Correlated Li-ion migration in the superionic conductor Li10GeP2S12†
Takeshi
Yajima
 *a,
Yoyo
Hinuma‡
b,
Satoshi
Hori
c,
Rui
Iwasaki
a,
Ryoji
Kanno
f,
Takashi
Ohhara
d,
Akiko
Nakao
e,
Koji
Munakata
e and
Zenji
Hiroi
*a,
Yoyo
Hinuma‡
b,
Satoshi
Hori
c,
Rui
Iwasaki
a,
Ryoji
Kanno
f,
Takashi
Ohhara
d,
Akiko
Nakao
e,
Koji
Munakata
e and
Zenji
Hiroi
 a
a
aInstitute for Solid State Physics, University of Tokyo, Kashiwa, Chiba 277-8581, Japan. E-mail: yajima@issp.u-tokyo.ac.jp
bCenter for Frontier Science, Chiba University, 1-33 Yayoi-cho, Inage, Chiba 263-8522, Japan
cInstitute of Innovative Research (IIR), All-Solid-State Battery Unit, Tokyo Institute of Technology, 4259 Nagatsuta, Midori, Yokohama 226-8502, Japan
dJ-PARC Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan
eCenter for Neutron Science and Technology, Comprehensive Research Organization for Science and Society (CROSS), Tokai 319-1106, Japan
fResearch Center for All-Solid-State Battery, Institute of Innovative Research (IIR), Tokyo Institute of Technology, 4259 Nagatsuta, Midori, Yokohama 226-8502, Japan
First published on 27th April 2021
Abstract
An all-solid-state Li-ion secondary battery is a promising device that provides a solution to existing energy problems. However, it remains far from practical application mainly because of the lack of our basic understanding of the conduction mechanism of Li ions in Li-rich superionic conductors used as solid electrolytes in place of liquid electrolytes for conventional batteries. Herein, we studied the crystalline compound Li10GeP2S12 with the largest Li-ion conductivity thus far via a novel route based on a combination of single-crystal neutron diffraction experiments at low temperature and first-principles calculations, and found that a correlated migration of the densely packed Li ions governs the overall Li-ion conduction. The correlated migration mechanism provides us with guidelines on how to design efficient superionic conductors for more efficient batteries.
Introduction
Electrochemical devices such as batteries, fuel cells, and sensors are technologically important in our daily life. To improve their performance, it is crucial to investigate the motions of ions in the electrolytes and control them appropriately. Superionic conductors (SICs) have been developed as solid electrolytes, which contain highly mobile ions embedded in rigid frameworks made of other atoms, giving a large ionic conductivity just like aqueous electrolytes.1 For example, β-alumina and α-AgI exhibit large ionic conductivities of monovalent sodium and silver ions, respectively.2,3 The ionic conduction mechanism in SICs is key for achieving large ionic conductivity but still remains controversial because of the complexity of the phenomena.4–7 Particularly, since SICs possess complicated crystal structures with mobile ions spreading over many crystallographic sites with partial occupancy, fundamental information about the crystal structure was often difficult to obtain.8Recently, SICs with mobile lithium ions have been extensively studied to apply them as electrolytes in all-solid-state Li-ion secondary batteries which potentially deliver both higher power density and improved safety.9,10 Nevertheless, a basic understanding of the Li-ion conduction mechanism has not yet been achieved.11–14 The main reason is the lack of information on the distribution of Li ions in the crystal structure. Since Li ions are highly mobile even at room temperature (RT), a delicate structural analysis using high-quality data taken at low temperature is required. However, it was difficult thus far because of the lack of sizable single crystals: the light Li ion cannot be easily detected by means of X-rays but by high-flux neutrons generated in modern facilities, which requires a reasonably large amount of sample. Thus, most studies on Li-ion SICs relied on first-principles calculations which guessed ideal structures and accordingly deduced conduction mechanisms.12,15–17 One of them is the concerted migration mechanism in which a correlation among densely packed Li ions reduces the effective energy barrier compared with that of conventional single-ion hopping so that the ionic conductivity is appropriately enhanced.12 However, we think that precise structural information from experiments is indispensable for the clarification of the true mechanism.
Here we focus on Li10GeP2S12 (LGPS) which is a promising SIC with the largest conductivity of 27 mS cm−1 at room temperature among all Li-ion SICs, comparable to those of liquid electrolytes;18 it has a general composition of Li10+δGe1+δP2−δS12, where 0 ≤ δ ≤ 0.7.19,20 Extensive studies were carried out to reveal the conduction mechanism there and aimed at increasing the conductivity, but fell into confusion as in the other SICs. Thanks to the recent success in growing high-quality single crystals of LGPS18 and also thanks to the recent progress in the advanced neutron source with a high flux, we were able to conduct precise structural determinations simultaneously using X-ray diffraction (XRD) and neutron diffraction (ND) data. Of particular note is that the ND data obtained at a low temperature of 10 K uncovered the exact positions of Li ions in the complex structure, which was impossible in the previous ND experiments at room temperature using polycrystalline samples.19,21–23 Based on the reliable structural data, we carried out sophisticated first-principles calculations which clearly showed how Li ions migrate in a correlated fashion different from the previous concerted mechanism.
Experimental
7Li-enriched LGPS single crystals for ND experiments were grown by the self-flux method using 7Li2S as one of the starting materials in a similar manner to that reported previously;18 the neutron absorption cross-section is much smaller for 7Li than for 6Li. The obtained LGPS crystal was yellow in color and a few mm in size. The average chemical composition of the crystals was examined by inductively coupled plasma atomic emission spectroscopy (ICP-AES) using 1–3 mg of crystals dissolved in water. The amounts of Li, Ge, and P were determined to be Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge
Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 11.2
P = 11.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.28
1.28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.72, which is Li-rich and Ge-rich compared with the ideal chemical composition of Li10GeP2S12; the precise composition of a single crystal was determined by XRD and ND experiments.
1.72, which is Li-rich and Ge-rich compared with the ideal chemical composition of Li10GeP2S12; the precise composition of a single crystal was determined by XRD and ND experiments.
To obtain reliable structural data, we performed both XRD and ND experiments using single crystals with sizes of 0.15 × 0.19 × 0.20 mm3 and 1.5 × 1.5 × 1.2 mm3, respectively. XRD data were collected at RT in a diffractometer (Rigaku R-AXIS RAPID) with graphite-monochromated Mo-Kα radiation. A crystal was sealed into a capillary with a diameter of 0.4 mm in an Ar-filled glovebox and used for the experiments. ND data were collected at RT and 10 K in the time-of-flight neutron diffractometer SENJU at beamline BL18 installed at the Materials and Life Science Experimental Facility (MLF) in the Japan Proton Accelerator Research Complex (J-PARC).24 The structure was solved by the direct method and refined with the Jana2006 program against Fo2 data using the full-matrix least-squares algorithm.25 Anisotropic thermal vibration factors were assumed for all the atoms. To find all possible Li positions from a negative scattering-length density map, MEM analysis was applied to the unit cell divided into 176 × 176 × 252 pixels using the Dysnomia program.26 The crystallographic data are given in Tables S1 and S2.† The joint probability density function (JPDF) of Li was calculated using the Jana2006 program. To understand the diffusion pathway landscapes of the Li ions, effective OPPs were calculated from the JPDF using the CalcOPP program.27
First-principles calculations were conducted using the projector augmented-wave method28 implemented in the VASP code29,30 with the Perdew–Burke–Ernzerhof generalized gradient approximation function tuned for solids (PBEsol).31 Plane-wave cut-off energies of 550 eV and 400 eV were used for calculations with and without lattice parameter calculations, respectively. Internal coordinates were allowed to relax in all the calculations. Calculations were conducted in a conventional cell containing two formula units, that is, Lix(Ge,P)6S24, and a gamma-centered 2 × 2 × 2 k-mesh was used. Charge compensation was achieved by changing the number of valence electrons in the supercell; the number of valence electrons was 0, 0, 0, and 8 for Li+, Ge4+, P5+, and S2−, respectively. Therefore, the number of valence electrons in the cell containing 24 S atoms was always 192 regardless of the adopted Li/vacancy and Ge/P ordering.
Results and discussion
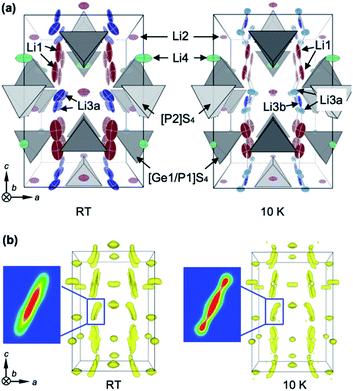
The high Li ion conductivity of LGPS has been ascribed to its specific crystal structure, as shown in Fig. 1a. There are four Li sites in the tetragonal structure at room temperature: the Li1 and Li3 sites have large amounts of vacancies and are aligned along the [001] direction to form a one-dimensional (1-D) channel, while two-dimensional (2-D) diffusion occurs via the Li4 site along the [110] direction. The Li2 site has a small number of vacancies, and so is inactive. Powder ND measurements at RT19,21–23 and molecular dynamics (MD) calculations16,17 showed that the 1-D pathway is dominant, with 2-D hopping being a secondary transport pathway. Nuclear magnetic resonance (NMR) experiments gave the activation energies Eas for the local hopping processes as 0.16 eV and 0.26 eV at RT for the 1-D and 2-D pathways, respectively,32 while recent AC impedance measurements using a single crystal of LGPS found weak anisotropic, long-range conduction with Ea ∼ 0.3 eV in both directions.18 In contrast, the Ea calculated for classical single-ion hopping along the 1-D channel is as high as 0.47 eV.12 The observed low value of Eas along the 1-D channel has been interpreted as demonstrating the concerted migration mechanism,12 which involves cooperative hopping that enhances Li ion conduction by significantly reducing the potential barrier. However, as noted above, this mechanism was based on previous structural data, and thus may have to be reconsidered.7Li-enriched single crystals of LGPS 1–2 mm in edge were grown by the flux method.18 To obtain reliable structural data, both XRD at RT and ND at RT and 10 K were performed. First, a chemical composition of Li10.34Ge1.34P1.66S12 (δ = 0.34) was determined via structural refinements of the XRD data at RT. Then, the positional parameters of all the atoms and the occupancies of the Li sites were refined using the ND data. Refined structural parameters are given in Tables S1a and b.† The refined structure at RT (Fig. 1a) is almost identical to those reported in previous studies.18,19,21,22,33 However, a significant deviation is the site splitting of Li3, which was not observed in previous studies using polycrystalline samples19,21,22 but was seen in single-crystal XRD analysis;18 we refer to the split site as Li3a (16h site) and the central site as Li3b (8f site).
Since the RT structure is seriously obscured by the large mobility of the Li ions as well as their large thermal atomic vibrations, ND data taken at 10 K were analyzed in detail to yield precise information regarding the true potential profiles for the Li atoms. A maximum-entropy method (MEM) analysis was carried out to capture the probable spatial distribution of the atomic densities, irrespective of the starting structural models. Fig. 1b shows maps of the negative scattering-length density of Li at RT and 10 K. The scattering-length density distributions around the Li2 and Li4 sites resemble the shapes of the corresponding thermal ellipsoids shown in Fig. 1a, while those around Li1 and Li3 are heavily elongated along the [001] direction. Note that the elongated distribution around Li3 at RT splits into three positions at 10 K, as shown in the density cross-sections in Fig. 1b.
Based on the MEM results, a structural analysis was carried out on the ND data at 10 K, assuming a triple-split model with Li atoms at the 16h (Li3a) and 8f (Li3b) sites. Refined structural parameters are given in Table S1c.† Since a significant improvement was achieved with notably smaller R values when compared with the double-split model, the Li3 triple-split model acts as a reasonable platform for discussing the diffusion pathways of Li ions in LGPS. The fact that the triple-split density at 10 K becomes a single elongated one at RT means that Li ions can easily migrate over the three positions via thermal excitations, implying that the potential barriers between them must be quite small. More details of the structural analysis are provided in the ESI.†
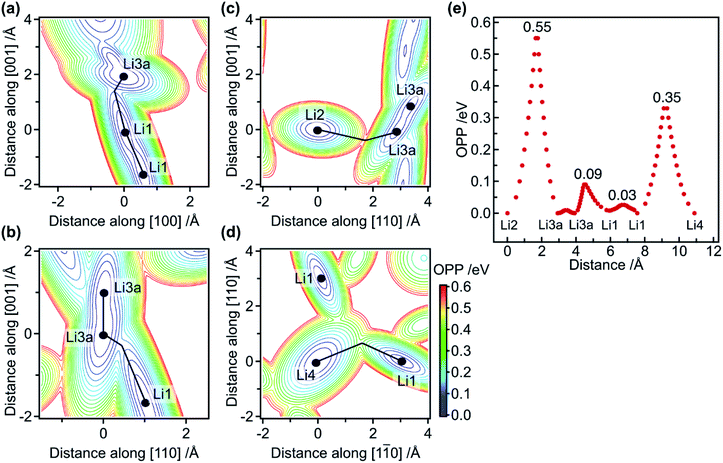
Based on the refined structure at 10 K, possible diffusion pathways for the migration of Li ions are considered. First, single-ion migration barriers in the 1-D and 2-D pathways are approximately evaluated via effective one-particle potential (OPP) calculations. The OPP maps at RT for the pathways along the [001] and [110] directions are shown in Fig. 2a–d, in which cross-sections via saddle points in the potential landscape are depicted. Fig. 2e shows the profile of the OPPs as a function of distance along various pathways. The energy barriers along the 1-D pathway are very small: approximately 0.03, 0.09, and 0.01 eV for Li1–Li1, Li1–Li3a, and Li3a–Li3a, respectively. Note that the potential profile along the channel is almost flat, with an effective barrier of 0.09 eV, which is much smaller than the 0.47 eV calculated for classical single-ion hopping based on previous structural data.12 Furthermore, it is smaller than the 0.29 eV obtained from AC impedance measurements,18 indicating that single-ion jumps are not critical. In contrast, the potential barrier for Li1–Li4–Li1 along the [110] direction is 0.35 eV, which is comparable to the experimental value of 0.30 eV,18 indicating that the single-ion jump mechanism is common for migration along the 2-D pathways.
Next, a complex diffusion process of Li ions along the 1-D channel via the Li1a, Li3a and Li3b sites is considered; hereafter, we use Li1a rather than Li1 for clarity. The Li1a–Li1a, Li1a–Li3a, and Li3a–Li3b inter-site distances are very short, at 1.688(9) Å, 1.68(2) Å, and 0.89(2) Å, respectively. Because of strong Coulomb repulsions between Li+ ions at such short distances, it is plausible that nearby positions would not be occupied simultaneously. In fact, these Li sites possess small occupation factors; g(Li1a) = 0.500(9), g(Li3a) = 0.20(2), and g(Li3b) = 0.40(4). The half occupancy of the Li1a site evidences that either of the pair of Li1a positions is occupied at any one time. This can also be applied to the closely located Li3a–Li3b–Li3a positions with a total deficiency of ∼20%, i.e., there are ∼0.8 Li ions on average over the three positions. Moreover, the neighboring Li1a and Li3a positions should not be occupied simultaneously. Thus, it is reasonable to assume that the 1-D pathway is segmented into block B/B′ [Li1a–Li1a] and block A/A′ [Li3a–Li3b–Li3a], each containing nearly one Li ion on average, as illustrated in Fig. 3a. Since the occupancy of each site in the blocks must be influenced by its surroundings, diffusion in the 1-D channel should not be described by classical single-ion jumps between nearby sites, but as occurring in a certain correlated manner.
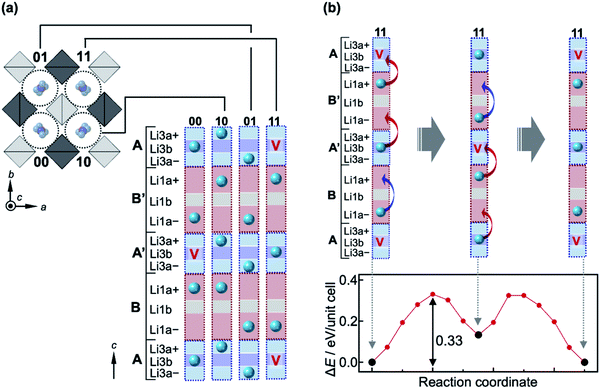 | ||
| Fig. 3 Correlated migrations of Li ions in LGPS. (a) Schematic representation of the crystal structure of LGPS viewed along the [001] direction, showing four 1-D channels labeled 00, 10, 01, and 11 in the unit cell. Each 1-D channel is divided into four blocks with two forms: blocks A and A′ contain Li3a+, Li3b, and Li3a−, while blocks B and B′ contain Li1a+, Li1b, and Li1a−; ‘+’ and ‘−’ distinguish the top and bottom positions, respectively, for the Li3a and Li1a sites. Every block contains either one Li ion, marked with a sphere, or a vacancy marked with a ‘V’, avoiding large Coulomb energies between Li ions. The distribution of the Li ions in the four channels in (a) shows the lowest-energy state when two vacancies are introduced in the unit cell [x = 22 in Lix(Ge,P)6S24] as calculated by the NEB method (Fig. S4†). The two vacancies are located far from each other in blocks A′ and A of channels 00 and 11, respectively, so as to reduce the Coulomb energy; the vacancies prefer block A/A′ rather than block B/B′ (Fig. S3†). (b) Correlated migration process of Li ions in channel 11 for x = 22 and the associated variation of potential as calculated by the NEB method. The Li ion initially jumps from block B′ to the vacancy above in block A, generating an unstable distribution with a vacancy at block B′. This transient state is recovered by pushing the Li ion in block A′ to B′, and also by moving the Li ion in block B from Li1a− to Li1a+ as the previously vacant site in the block A below it is now occupied. As a result, the three Li ions cooperatively jump upward along the channel, giving the arrangement shown in the middle. Similar cooperative jumps then take place as depicted in the figure to return to the original distribution. The energy barrier for this transition is 0.33 eV, and the intermediate state lies in a local minimum that is 0.13 eV higher than the initial state, as shown in the potential profile at the bottom of the figure. Note that this increase in energy from the initial state does not originate from the arrangement of Li ions in one channel, but from an increase in Coulomb energy among the channels: the two vacancies in channels 00 and 11 are now both in their respective block A′; in reality, a further relaxation in the distribution of Li ions must be induced in the nearby channels to reduce the total energy. | ||
A possible migration process is proposed based on first-principles nudged elastic band (NEB) calculations, which take into account cooperative migration of a few ions. Details of the calculations are provided in the ESI.† After full relaxation of the lattice parameters, internal coordinates, and occupancies for the Li sites, it is found that every block is occupied by one Li ion at its center [Li1b (hypothetical site between Li1a) or Li3b site] for x = 24 in Lix(Ge,P)6S24; no split sites are observed (Fig. S2†). Then, the formation energy of a vacancy when one Li ion is removed from the unit cell is calculated (i.e., x = 23). The Li deficiency preferably occurs in block A/A′ and causes site splitting in both blocks A/A′ and B/B′, as experimentally observed (Fig. S3†). Next, a model with two Li ions removed from blocks A/A′ is considered (i.e., x = 22) in order to examine any correlation between the two vacancies. The lowest energy state is obtained when they are separated as far as possible, as shown in Fig. 3a, which must reduce the total Coulomb energy arising from repulsions between the Li ions; other states with higher energies are shown in Fig. S4.† The average occupancies of the Li sites calculated for the lowest-energy model are g(Li1a) = 0.5, g(Li1b) = 0, g(Li3a) = 0.25, and g(Li3b) = 0.5, which are in good agreement with the experimental values of g(Li1a) = 0.500(9), g(Li3a) = 0.20(2), and g(Li3b) = 0.40(4) from the ND refinements at 10 K. The slightly smaller experimental values of g(Li3a) and g(Li3b) are due to the fact that the actual Li content in the examined crystal is x ∼ 21, that is, three Li ions are missing from the unit cell.
A possible migration process for Li ions in the 1-D channel is depicted for x = 22 in Fig. 3b. The migration occurs in two steps where three Li atoms in one channel cooperatively migrate in one direction along the channel (for details see the caption of Fig. 3). The potential profile of this correlated migration process as calculated by the NEB method shows a double peak with a height of 0.33 eV and a local minimum at 0.13 eV between the peaks. Therefore, the effective migration barrier is 0.33 eV, which is much larger than that of the single-ion jump from the OPP calculations and is in good agreement with the experimental value of 0.29 eV from our AC impedance measurements,18 indicating that such a correlated migration mechanism functions along the 1-D channel. We also considered 2-D pathways via Li1(Li3)–Li4–Li1(Li3) and Li3–Li2–Li3, and obtained potential profiles, as shown in Fig. S5.† The effective migration barriers deduced were relatively large, at 0.41 and 0.59 eV, respectively. These migration barriers are close to those obtained from the OPP calculations, suggesting that a single-ion hopping mechanism operated in the 2-D pathways.
A collective motion of Li ions via a concerted migration mechanism has been discussed to explain the observed Ea for LGPS determined via NMR (∼0.16 eV) which is much smaller than the Ea calculated for classical single-ion hopping (0.47 eV).12,34 However, the latter value is apparently an overestimate owing to imprecise structural information; in fact, we observed Ea = 0.09 eV for a single-ion jump based on our ND data. Therefore, in reality, many-body effects should cause an increase rather than a decrease in effective barrier height compared with those of single-ion jumps: in spite of the flat energy landscape for the single-ion jump, migration along the 1-D pathway is difficult in a “traffic jam”. Our NEB calculations strongly suggest that this increase in effective barrier height is due to a correlation arising from Coulomb interactions among Li ions in the 1-D channel. Thus, the correlated mechanism plays a critical role in Li ion conduction in LGPS.
The importance of collective motion of ions has been recognized in various SICs such as AgI, β-alumina, perovskite fluorides, and garnet oxides.35–38 In each case, it was theoretically proposed that the collective migration enhances the ion conductivity by reducing the effective barrier from that for single-ion hopping,36–39 as in the concerted migration mechanism for LGPS in which the collective motion reduces the effective barrier from 0.47 eV for single-ion hopping to the experimental value of ∼0.3 eV.12 However, here we showed that collective motions in LGPS in fact work in the opposite way to increase the effective barrier than for single-ion hopping (Fig. S6†); the effective barrier of 0.09 eV based on our single crystal neutron diffraction is much smaller than the experimental value, so the collective motion enhances the effective barrier. These novel findings were based on accurate structural refinements at low temperature revealing actual migration pathways and the sophisticated first-principles calculations. Such a combination of classical structural study and recently developing computational science as established in the present study will be a standard approach for the investigation of SICs. We think that this correlated migration mechanism is also important in other SICs; the previous suggestions might be based on poor structural data. It provides us a direction for improving the ion conductivity and for a new design of efficient SICs. For example, a compound with an appropriate arrangement of Li sites in 2-D or 3-D pathways is favorable as the correlation effects are weakened with increasing the dimensionality, as already suggested in previous studies.12,16,18,22
Conclusions
The precise crystal structures of LGPS at RT and 10 K were determined by XRD and ND experiments on a single crystal. The ND data obtained at 10 K revealed the exact positions of Li ions in the complex structure with the help of MEM analysis, which were difficult to obtain in the previous ND experiments at RT using polycrystalline samples: the Li-ion conduction path along the 1-D channel consists of a doubly split Li1 site and a triply split Li3 site.Our OPP calculations based on the obtained precise structure estimated the migration barriers at RT to be 0.09 and 0.35 eV along the c axis and ab plane, respectively, while the corresponding values from the NEB calculations were 0.33 and 0.41 eV; the latter values are in good agreement with the experimental values from AC impedance measurements on a single crystal.18 The large mismatch between the potential barriers along the c axis from the OPP and NEB calculations indicates that the classical single-ion hopping mechanism does not work in the 1D channel, suggesting that correlations between Li ions play a critical role in Li ion conduction. We propose a correlated migration mechanism in which the collective motions of Li ions enhance the effective potential barrier compared to that for single-ion hopping, which is distinguished from the concerted migration mechanism proposed before.12 This work could lead to a further understanding of collective ion motions in electrolyte materials and guide materials design to create a better SIC for use in all-solid-state Li-ion secondary batteries.
Author contributions
The crystal growth was performed by R. I. The XRD data were obtained by T. Y. The ND data were obtained by S. H., R. I., T. O., A. N., and K. M. Structural analyses of XRD and ND data, MEM analyses, and OPP calculations were performed by T. Y. The NEB calculations were performed by Y. H. R. K. and Z. H. supervised the project. All the authors discussed the results and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The ND experiment on SENJU at MLF J-PARC was conducted under a user program (Proposal No. 2017B0230). Computing resources of the Research Institute for Information Technology at Kyushu University, ACCMS at Kyoto University, and the Supercomputer Center in the Institute for Solid State Physics at the University of Tokyo were used. This work was partly supported by the Core-to-Core Program for Advanced Research Networks given by the Japan Society for the Promotion of Science (JSPS). One of the authors (R. K.) acknowledges the support by Grant-in-Aid for Scientific Research S (No. 17H06145).Notes and references
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- M. S. Whittingham and R. A. Huggins, J. Chem. Phys., 1971, 54, 414–416 CrossRef CAS.
- C. Tubandt and E. Lorenz, Z. Phys. Chem., 1914, 87, 513–542 CrossRef CAS.
- J. Maier, Nat. Mater., 2005, 4, 805–815 CrossRef CAS PubMed.
- O. Yamamoto, Sci. Technol. Adv. Mater., 2017, 18, 504–527 CrossRef PubMed.
- K. Funke, Sci. Technol. Adv. Mater., 2013, 14, 043502 CrossRef CAS PubMed.
- P. Knauth and H. L. Tuller, J. Am. Ceram. Soc., 2002, 85, 1654–1680 CrossRef CAS.
- D. A. Keen, J. Phys.: Condens. Matter, 2002, 14, R819 CrossRef CAS.
- K. Takada, Acta Mater., 2013, 61, 759–770 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- A. R. West, in Solid State Chemistry and its Application, John Wiley and Sons, Chichester, 1984, pp. 452–496 Search PubMed.
- S. Hull, Rep. Prog. Phys., 2004, 67, 1233–1314 CrossRef CAS.
- M. Catti, Chem. Mater., 2007, 19, 3963–3972 CrossRef CAS.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2011, 24, 15–17 CrossRef.
- S. Adams and R. Prasada Rao, J. Mater. Chem., 2012, 22, 7687–7691 RSC.
- R. Iwasaki, S. Hori, R. Kanno, T. Yajima, D. Hirai, Y. Kato and Z. Hiroi, Chem. Mater., 2019, 31, 3694–3699 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- S. Hori, M. Kato, K. Suzuki, M. Hirayama, Y. Kato and R. Kanno, J. Am. Ceram. Soc., 2015, 98, 3352–3360 CrossRef CAS.
- O. Kwon, M. Hirayama, K. Suzuki, Y. Kato, T. Saito, M. Yonemura, T. Kamiyama and R. Kanno, J. Mater. Chem. A, 2015, 3, 438–446 RSC.
- D. A. Weber, A. Senyshyn, K. S. Weldert, S. Wenzel, W. Zhang, R. Kaiser, S. Berendts, J. Janek and W. G. Zeier, Chem. Mater., 2016, 28, 5905–5915 CrossRef CAS.
- S. Hori, S. Taminato, K. Suzuki, M. Hirayama, Y. Kato and R. Kanno, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 727–736 CrossRef CAS PubMed.
- T. Ohhara, R. Kiyanagi, K. Oikawa, K. Kaneko, T. Kawasaki, I. Tamura, A. Nakao, T. Hanashima, K. Munakata, T. Moyoshi, T. Kuroda, H. Kimura, T. Sakakura, C.-H. Lee, M. Takahashi, K. Ohshima, T. Kiyotani, Y. Noda and M. Arai, J. Appl. Crystallogr., 2016, 49, 120–127 CrossRef CAS PubMed.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr.–Cryst. Mater., 2014, 229, 345–352 CrossRef.
- Dysnomia, 2000, DOI:10.1017/s088571561300002x.
- D. Wiedemann, OPP_CALC, 2015 Search PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- X. Liang, L. Wang, Y. Jiang, J. Wang, H. Luo, C. Liu and J. Feng, Chem. Mater., 2015, 27, 5503–5510 CrossRef CAS.
- A. Kuhn, J. Köhler and B. V. Lotsch, Phys. Chem. Chem. Phys., 2013, 15, 11620–11622 RSC.
- M. Xu, J. Ding and E. Ma, Appl. Phys. Lett., 2012, 101, 031901 CrossRef.
- G. E. Murch, Solid State Ionics, 1982, 7, 177–198 CrossRef CAS.
- J. C. Wang, M. Gaffari and S. I. Choi, J. Chem. Phys., 1975, 63, 772–778 CrossRef CAS.
- G. W. Watson, S. C. Parker and A. Wall, J. Phys.: Condens. Matter, 1992, 4, 2097 CrossRef CAS.
- K. Meier, T. Laino and A. Curioni, J. Phys. Chem. C, 2014, 118, 6668–6679 CrossRef CAS.
- Y. Deng, C. Eames, J. N. Chotard, F. Lalère, V. Seznec, S. Emge, O. Pecher, C. P. Grey, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2015, 137, 9136–9145 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: More details of experimental results and theoretical calculations. CCDC 2051650, 2051651 and 2051653. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ta00552a |
| ‡ Present address: Department of Energy and Environment, National Institute of Advanced Industrial Science and Technology (AIST), 1-8-31, Midorigaoka, Ikeda, Osaka 563-8577, Japan. |
| This journal is © The Royal Society of Chemistry 2021 |