Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Code generation in ORCA: progress, efficiency and tight integration†
Marvin H.
Lechner‡
 *,
Anastasios
Papadopoulos‡
*,
Anastasios
Papadopoulos‡
 *,
Kantharuban
Sivalingam
*,
Kantharuban
Sivalingam
 ,
Alexander A.
Auer
,
Alexander A.
Auer
 ,
Axel
Koslowski
,
Ute
Becker
,
Axel
Koslowski
,
Ute
Becker
 ,
Frank
Wennmohs
and
Frank
Neese
,
Frank
Wennmohs
and
Frank
Neese
 *
*
Department of Molecular Theory and Spectroscopy, Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: frank.neese@kofo.mpg.de
First published on 7th May 2024
Abstract
An improved version of ORCA's automated generator environment (ORCA-AGE II) is presented. The algorithmic improvements and the move to C++ as the programming language lead to a performance gain of up to two orders of magnitude compared to the previously developed PYTHON toolchain. Additionally, the restructured modular design allows for far more complex code engines to be implemented readily. Importantly, we have realised an extremely tight integration with the ORCA host program. This allows for a workflow in which only the wavefunction Ansatz is part of the source code repository while all actual high-level code is generated automatically, inserted at the appropriate place in the host program before it is compiled and linked together with the hand written code parts. This construction ensures longevity and uniform code quality. Furthermore the new developments allow ORCA-AGE II to generate parallelised production-level code for highly complex theories, such as fully internally contracted multireference coupled-cluster theory (fic-MRCC) with an enormous number of contributing tensor contractions. We also discuss the automated implementation of nuclear gradients for arbitrary theories. All these improvements enable the implementation of theories that are too complex for the human mind and also reduce development times by orders of magnitude. We hope that this work enables researchers to concentrate on the intellectual content of the theories they develop rather than be concerned with technical details of the implementation.
Introduction
The boundaries of what is possible in quantum chemistry are continually being expanded, not least through advancements in microprocessor technology. Over the last decades, feasible ab initio wave function-based calculations have progressed from simple, SCF-level calculations in small basis sets1,2 to production level application of advanced correlated methods. For instance, the coupled cluster (CC) model can now be applied to medium to large molecules in triple-ζ or even larger basis sets,3 or even very large molecules when local approximation techniques are employed.4,5 This development has been fostered in great part by the advances in CPU processing power, commonly described by Moore's law.6 It is the opinion of the authors that these advances bring more and more computationally demanding theories into the realm of “routinely feasible” computations. These theories include internally contracted7,8 (ic) multireference (MR) theories and gradients of higher-order CC models, the implementation of which is, in fact, beyond human capacity. Traditionally, a quantum chemical theory would be reformulated for and implemented in computer code entirely manually, which is an onerous and error-prone9 approach. In light of these challenges, tools have been developed that either simplify or completely automate the implementation process, which we will refer to as automatic code generation. These tools automate at least one of the following general steps needed to go from theory on paper to computer code: (i) derivation of the working equations from an Ansatz (equation generation), (ii) manipulation thereof to reduce the computational cost (factorization), and (iii) the actual code generation. We will adopt this distinction throughout the rest of this paper and expand on each of the steps below. For a more detailed introduction to the field of automatic code generation, we also recommend the excellent review of Hirata.10Automatic derivation of the working equations from a theoretical Ansatz is the most straightforward part, since it mostly relies on a fixed set of rules that can be applied deterministically. Very early on in the development of equation generation11 Wick's theorem12,13 was used in order to obtain the explicit forms of the tensor contractions. Even today most existing toolchains14–28 rely on the same principle. Despite this prevalence of Wick's theorem, the first automated equation generators used diagrammatic approaches, mainly to avoid tedious and error prone derivations by hand.29–31 However, these early developments lack further equation processing and code generation. A major benefit of diagrammatic generators is that only topologically different contractions are generated, i.e., less work needs to be done in finding equivalent terms in the factorization step.16 More recent examples of such equation generators are Smith16 by Shiozaki and co-workers or the arbitrary-order CC program by Kállay and Surján (MRCC).32 In our own work, we have used neither approach, but instead relied on plain and simple (anti-)commutation rules between second-quantized operators that are applied recursively until all non-target labels have been processed.33 This strategy was adopted in the first version of the ORCA-AGE toolchain and has the advantage that it can be applied equally well to single- or multireference reference functions.34
The factorization step is arguably the most crucial in the toolchains, since it ensures the proper, minimal computational scaling with system size and significantly reduces the computational cost of the generated code. Unfortunately, finding the global minimum in terms of computational cost constitutes an NP-hard problem.35 Hence, virtually all toolchains rely on heuristics to reduce the complexity of this problem. Core concepts were developed early on, e.g., by Janssen and Schaefer11 or Kállay and Surján.32 However, perhaps the most complete overview can be found in the literature describing the tensor contraction engine (TCE),14,15 which sequentially uses detection of duplicates, strength reduction, factorization (i.e., application of the distributive law), and common subexpression elimination to arrive at the final working equations before generating code.14 Tensor contractions are often canonicalized by relabelling and permuting the indices and tensors in order to aid in detecting duplicate terms, cancelling terms and common subexpressions, especially when taking tensor symmetry into account.11,14,35–37 A detailed analysis of common subexpression elimination was published by Hartono et al.38 Overall, these heuristics perform quite well,39 although they will generally not reach the same efficiency as the best hand-optimized40 code. More advanced schemes have been discussed,35 but, to the best of our knowledge, only a single tool that uses a genetic algorithm to sample the complete factorization space has been presented to date.39 An overview of the algorithms used in the AGE can be found in the original publication.34
Finally, the equations that have been derived, canonicalized and factorized in the previous steps must be evaluated (in the correct order) in order to arrive at the desired implementation of the target quantity, which may, for example, be an energy or a residual. To this end, we can either generate code (generally for a compiled programming language) or use an interpreter to evaluate the tensor contractions. Generated code frequently relies on further libraries, most often on the basic linear algebra subroutines (BLAS)41 to speed up the evaluation of the tensor contractions. BLAS can be extended to arbitrary (binary) tensor contractions,42 and even faster algorithms have been developed for the same sake.43 As an intermediate between low-level generated code and interpreters, specialized tensor contraction libraries have emerged that more or less completely take care of the computational kernel such that code generation can be greatly simplified. Examples of such libraries include the CTF,44,45 libtensor,46 LITF,47 TCL,43,48 and TiledArray.49,50 Interpreters even further remove the connection of the contractions to the (compiled) code or hardware by fully abstracting away the latter two, requiring just the contractions and the input quantities. This concept is perhaps best illustrated with the super instruction assembly language (SIAL) of ACES III, which is a full-fledged virtual machine and parallel programming model51 used to evaluate generated and handwritten contractions.52,53 An integrated tensor framework (ITF) has been reported by Werner and co-workers for the implementation of an internally contracted multireference configuration interaction (ic-MRCI) method.18,54 Other toolchains with interpreters using string-based methods31,55 include the general contraction engine (GeCCo) by Köhn and co-workers, first to appear in the context of explicitly correlated coupled cluster methods,27,28 and Kállay and Surján's arbitrary-order CC program.32,56
To conclude the introduction, we now briefly discuss applications of existing code generators. One of the most complete implementations remains the TCE,14,15 which encompasses all the steps outlined above. Generated code exists in NWChem,57,58 and examples include higher-order CC methods (up to (EOM)-CCSDTQ)59 or combined CC theory and MBPT.60 The SMITH generator by Shiozaki and co-workers,16,17 which can be viewed as the successor to the TCE,61 is another feature-complete tool that was initially used to implement CCSD-R12,61 and later extended to state-specific17 and multistate62 CASPT2 gradients. Around the same time, the SQA, used for the automatic implementation of CT theory19,20 and later for the MR-ADC(2) method,63,64 and FEMTO codes21–23 were introduced. FEMTO has specialized features to work with cumulant reconstructions that appear in internally contracted DMRG-MRCI theory, and has also been extended to pair-natural orbitals (PNOs).23 Also noteworthy are the GeCCo27,28 and APG24–26 codes, which have both been used to implement highly complex ic-MR methods, such as fully internally contracted multireference coupled cluster theory (fic-MRCC)65 and MR-EOMCC66–69 theory, respectively. More recently, GeCCo and ITF have been used together to develop an optimised fic-MRCC implementation.70 For a long time, the APG and SQA were the only tools that supported Kutzelnigg–Mukherjee normal order,71 with generalized normal order (GNO) being taken up more recently by the Wick&d program72 of Evangelista. Last but not least, the first version of the ORCA-AGE toolchain was introduced close to seven years ago.34 Different multireference contraction schemes were compared with its support,73 and the STEOM method based on an unrestricted Hartree–Fock (UHF) reference has been implemented74 with the aid of the APG into the ORCA75–77 program package.
In this article, we describe a completely rewritten and vastly improved ORCA-AGE toolchain, henceforth referred to as ORCA-AGE II. Thus, we first outline the differences to the previous version of the toolchain and the numerous improvements that have been incorporated. Furthermore, we will compare its features to other existing solutions. Then, we showcase recent developments, most of which have only been possible through the improvements made to the toolchain. We will finish with a holistic view of and perspective for the development process in quantum chemistry, including our vision for the ORCA75–77 program package. Lastly, we conclude by summarizing the main points of this article.
Software description
The ORCA-AGE II toolchain has been rewritten from scratch, a decision that has been motivated by the experience gained while working with its first version.34 In this section, we first recapitulate the layout of ORCA-AGE II, which has mainly undergone streamlining, before we discuss the new internal algorithms, equation and code generators. Further information on the code generation process can be found in the preceding publication.34From an architectural standpoint, ORCA-AGE II still uses the modular structure of its predecessor, organized into three groups: equation generation, equation processing (factorization), and code generation. Each of these three steps is further split into smaller executables that only perform a very specific subtask, e.g., merging several contractions into one by exploiting tensor symmetry. This layout allows highly flexible workflows, where each step can be turned on or off depending on the user's preference, although all steps are enabled by default to achieve the best possible performance of the generated code. In turn, each of these steps may have optional features like debug output or different contraction engines, which are controlled through easy-to-understand command line options as well. Furthermore, the user can easily verify or modify all intermediate stages, which are simply text files containing a single contraction per line, as necessary. An example of such an equation file is given in Scheme 1.
Here, the indices indicate the orbital space they belong to, using i, j, k, l for inactive, t, u, v, w for active, and a, b, c, d for virtual orbitals. Furthermore, any index has a number associated with it, so that a unique index can always be constructed. Finally, a capitalised label indicates a summation index.
While the general structure of the toolchain has remained largely unchanged, the code itself is an entirely new development. The main reason for redeveloping the software lies in the long code generation times of the previous version, which required about one month to generate highly complicated theories such as fic-MRCC, leading to a slow overall development and debugging process. This was addressed by improving the internal algorithms throughout all factorization and generation steps. For example, we introduced a hash-based data compaction method for eliminating duplicate intermediates generated by the initial, term-wise factorization step. This reduces the scaling from a quadratic to an expected linear-time algorithm, and consequently to a speedup of about two orders of magnitude for the fic-MRCC method in this step alone. While this example shows the biggest improvement over the old toolchain, other parts, such as the detection of tensor symmetry, have received improvements of up to one order of magnitude as well. To further ensure good use of multicore architectures, we use OpenMP to allow for thread-based parallelism in the toolchain. Lastly, the new toolchain has been written in the C++ programming language, which together with an improved factorization algorithm, is responsible for a large part of the speedups compared to the previous implementation that relied on PYTHON. Another benefit of relying on C++ is that ORCA-AGE II fits far better into the ORCA ecosystem through a more homogeneous and cleaner software structure. Taken together, the parallelized and improved C++ code allows us to generate and process highly complex equations in minutes rather than weeks that were required for the serial PYTHON code.
Internally, the executables rely on a core library that provides the required basic functionality to read/write, represent, and manipulate tensor contractions as a set of high-level classes and functions. This library, and by extension the entire toolchain, has no limitations in terms of number of indices per tensor, allowed tensor symmetries, or number of source tensors per contraction, to name a few features. Consequently, any theory that can be written as a set of tensor contractions can be implemented with ORCA-AGE II. Also, despite this generality, even costly operations such as determining the tensor symmetry of an intermediate based on its source tensors are so fast that they can be routinely used for hundreds of tensors with, for example, ten indices, as is the case in fic-MRCC theory (further discussed below).
In addition to the improvements to the underlying infrastructure, the functionality (especially of the code generator) has been extended as well. In terms of performance improvements, the recent work falls into the two categories of compute and I/O optimizations. We first discuss the compute optimizations, which are mainly geared towards making BLAS calls more pervasive in the generated code. To this end, we use the fact that essentially every binary tensor contraction can be written as a matrix–matrix multiplication,
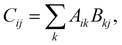 | (1) |
Also in the category of compute optimizations are further hand-coded routines. Additional contraction patterns have been added to the “ContractionEngine” functionality for increased performance, which complement the features already available since the first version of the code generator.34 These patterns are especially useful for the generation of analytic gradients components (vide infra).
On the note of I/O improvements, we should first delineate how ORCA-AGE II deals with a mixed strategy of keeping some tensors on disk and some entirely in memory. Ultimately, the decision is up to the end user, but by default 4-index quantities are stored on disk with two indices encoding disk access, for which a matrix can be retrieved. In the ORCA framework these objects are called “matrix containers” and they have been part of the ORCA infrastructure since the earliest days of the correlation modules. The matrix containers are intrinsically “smart”, in that they automatically take care of storage of the data in memory or on disk in an uncompressed or compressed format and they also distribute data across the available disks with the programmer that uses these objects having to write a single line of additional code. The tools can deal with symmetric or unsymmetric matrices, vectors and, ultimately, with arbitrary dimensional tensors via another tool, we have called “MultiIndex” that allows us to generate arbitrarily complex compound indices from any set of individual indices. For example, given Xrspq and using the lower indices for access, we can load matrices of r × s for a given index pair p, q. In ORCA-AGE II, these quantities are generally stored on disk to integrate nicely with the rest of the ORCA infrastructure as well as to avoid memory bottlenecks (e.g., the 4-external integrals (ab|cd) already exceed 10 GB for nvirt > 188 virtual orbitals in double precision).
We optimized the I/O performance by both hand-coded contractions and a new on-the-fly resorting scheme. The hand-coded functions are mostly geared towards copy/add operations,
| Cij… ← AΠ(ij…), | (2) |
| Xrspq ← Ypqrs, | (3) |
A more general scheme was also introduced that proceeds by resorting the on-disk quantities on the fly. The underlying inefficiency is the same as discussed above, namely, that non-matching indices are associated with I/O operations. In the general case, however, we do not opt for a batching scheme, but rather exploit the fact that reordering such a 4-index tensor only scales as 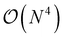 and can be done itself with efficient handwritten functions. Virtually all contractions that use such stored quantities scale higher than
and can be done itself with efficient handwritten functions. Virtually all contractions that use such stored quantities scale higher than 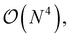 and hence the additional reordering step is negligible in cost. Furthermore, these resorted matrix containers can be kept until the end of the computation to be reused in multiple contractions, at the expense of additional disk space being used. Nonetheless, since disk space is generally not limiting for highly correlated theories, we found this strategy to improve computational efficiency by at least a factor of 10 for larger examples while increasing disk space by only a marginal amount.
and hence the additional reordering step is negligible in cost. Furthermore, these resorted matrix containers can be kept until the end of the computation to be reused in multiple contractions, at the expense of additional disk space being used. Nonetheless, since disk space is generally not limiting for highly correlated theories, we found this strategy to improve computational efficiency by at least a factor of 10 for larger examples while increasing disk space by only a marginal amount.
Compared to the first ORCA-AGE toolchain, the updated version has also been integrated much more tightly with the main ORCA source code. The philosophy of this approach will be discussed in detail at the end of this paper.
Comparison to other toolchains
To summarize the features of ORCA-AGE II and show how it relates to other code generators used in quantum chemistry, we summarized the main code generation features in Table 1. To keep the size of the table manageable, we only included other codes that are sufficiently complete or have been more widely used.| Program | Equation generation | Factorisation | Code generation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Commutation | Wick/NO | Diagrams | Duplicates | Strength reduction | Distributive law | (Sub)expression elimination | “Plain” code | Interpreter | String | BLAS | Parallel | Spatial symmetry | CSFs | Year | |
| a While generating terms with Wick's theorem, topologically equivalent terms (diagrams) can be recognized and combined. | |||||||||||||||
| FEMTO | — | x | — | x | x | Partial | Partial | x | — | — | x | x | x | — | 2013 |
| SQA | — | x | — | x | x | Limited | — | x | — | — | x | — | x | x | 2009 |
| Smith3 | — | x | Internal | n/a | x | x | x | x | — | — | x | x | — | x | 2015 |
| Smith | — | — | x | n/a | x | x | x | x | — | — | x | x | x | n/a | 2008 |
| TCE | — | x | — | x | x | x | x | x | — | — | x | x | x | n/a | 2003 |
| GeCCo | —— | x | Internal | x | x | x | x | — | x | x | x | — | x | — | 2008 |
| ORCA-AGE | x | In progress | — | x | x | x | x | x | — | — | x | x | — | x | 2017, 2024 |
| MRCC | — | — | x | n/a | x | x | x | — | x | x | — | x | x | — | 2001 |
We now highlight a few salient features of the tools from Table 1. First, only ORCA-AGE relies on a commutator-based engine to derive the working equations for simplicity and generality. However, using a Wick's theorem or diagram-based engine can be significantly faster and reduce the time required to remove equivalent contractions. Hence, efforts to develop such an engine are ongoing for ORCA-AGE II. Second, great care is placed by all toolchains on a complete factorization toolchain, which is a testament to the importance of this step in obtaining a performant implementation. Third, the actual evaluation part either relies on generation of actual code or simply interprets the factorized equations akin to a specialized virtual machine. To this end, all toolchains except for one rely on BLAS to maximize computational efficiency. Parallelization support, however, is not implemented for all toolchains since doing so in a completely automated fashion is highly non-trivial.
Recently implemented methods with ORCA-AGE II
With the new, improved ORCA-AGE II toolchain, we now find ourselves in a position where large, complicated theories can be implemented quickly into the ORCA software package. In this section, we will demonstrate a few examples, starting with the CCSDT method and its various approximations. Then, going on to theories that contain more tensor contractions, we show how ORCA-AGE II can also generate gradients for CI and CC theories with minimal effort. We then conclude this section with details of our fic-MRCC implementation, which contains so many terms that it is beyond human capacity to implement.CCSDT
As more powerful hardware and successively more efficient implementations of post-HF methods started being available, methods like CCSD(T) established themselves as what today is called “gold standard” in quantum chemistry.79 One aspect that can be considered as crucial in this respect is the availability of excitations higher than doubles, and hence, especially during the 1980s many pioneering efforts were made towards efficient and powerful implementations of variants of CCSDT methods and beyond, like CCSDT(Q).80 In line with some of the existing multireference approaches, CCSDT and CCSDTQ energies and their analytical derivatives are among the most complex and challenging algorithms that have been implemented and optimized by hand.81,82Hence, it is not surprising, that many of the early computer-aided implementation techniques in quantum chemistry focused on generating higher order coupled cluster methods or MR-CC implementations. The CCSDT method can be viewed as a standard example for high complexity of equations with numerous terms, complex tensor contractions and high-dimensional wavefunction parameters. For this reason, we will discuss the ORCA AGE implementation of the UHF CCSDT-1 and CCSDT energies in detail in the following. This does not only present an illustrative example but also demonstrates the versatility and simplicity of the tools available and allows for a conceptual comparison with other code generation tools.
Besides perturbative triples corrections, iterative CCSDT approximations like the CCSDT-N (N = 1,2,3 and 4) have been proposed as a systematic hierarchy of approximations with reduced computational effort.83–89 While CCSDT-1, 2 and 3 exhibit 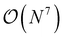 scaling, CCSDT-4 includes T3 → T3 terms which scale as
scaling, CCSDT-4 includes T3 → T3 terms which scale as 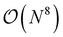 and only two contributions to the triples equations are excluded from the full CCSDT amplitude equations. In order to generate all of these approximations, it is essential that the generation tool allows to evaluate the nested commutator expressions from the Baker–Campbell–Hausdorff (BCH) expansion as well as the addition of separate commutator terms to an existing set of equations. ORCA-AGE II can do both as we will show in the following.
and only two contributions to the triples equations are excluded from the full CCSDT amplitude equations. In order to generate all of these approximations, it is essential that the generation tool allows to evaluate the nested commutator expressions from the Baker–Campbell–Hausdorff (BCH) expansion as well as the addition of separate commutator terms to an existing set of equations. ORCA-AGE II can do both as we will show in the following.
Before going into the full input listing for the CCSDT-N theories, we will start with UHF-CCSD to show a simplified connection to the conventional equations (Scheme 2). This is accomplished by simply specifying the maximum level of nested commutators that should appear in the energy and residual equations in $order_E and $order_residuals, respectively. Lastly, each $class line provides an identifier, an amplitude, the excitation operators contained in the cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) , and (optionally) contravariant projection functions90 for the residuals after a semi-colon. The E-operators contained therein typically refer to spin-traced operators Êpq, but in the case of UHF references they refer to pairs of elementary creation and annihilation operators in spin–orbital basis, âpσâqσ. The rest of the infrastructure is then able to set up and evaluate all nested commutator expressions of the defined amplitudes with the Hamiltonian in a BCH expansion. This represents the conventional CCSD expressions,
, and (optionally) contravariant projection functions90 for the residuals after a semi-colon. The E-operators contained therein typically refer to spin-traced operators Êpq, but in the case of UHF references they refer to pairs of elementary creation and annihilation operators in spin–orbital basis, âpσâqσ. The rest of the infrastructure is then able to set up and evaluate all nested commutator expressions of the defined amplitudes with the Hamiltonian in a BCH expansion. This represents the conventional CCSD expressions,
〈Φai|e−(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2)Ĥe( 2)Ĥe(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2)|0〉 = |0〉, 2)|0〉 = |0〉, | (4) |
〈Φabij|e−(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2)Ĥe( 2)Ĥe(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2)|0〉 = |0〉. 2)|0〉 = |0〉. | (5) |
The corresponding expression of all triples amplitudes is shown in Scheme 3. This will, in addition to the terms in eqn (4) and (5) include the triples equation and contributions to the singles and doubles amplitudes as:
〈Φai|e−(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)Ĥe( 3)Ĥe(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)|0〉 = 0, 3)|0〉 = 0, | (6) |
〈Φabij|e−(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)Ĥe( 3)Ĥe(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)|0〉 = 0, 3)|0〉 = 0, | (7) |
Φabcijk|e−(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)Ĥe( 3)Ĥe(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1+ 1+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2+ 2+![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3)|0〉 = 0. 3)|0〉 = 0. | (8) |
The CCSDT-1 (more specifically CCSDT-1a) equations are characterized by an approximate triples treatment for which, in addition to the CCSD equations, two terms are included in the triples equations, and one term is included which couples the T3 amplitudes to the singles and one term which couples T3 to the double amplitudes.
As any commutator, these can be added separately in a term-by-term manner as outlined in Schemes 3–6 (see the ESI†), this time, invoking our equation generation tool directly to generate each term.
tai ← 〈Φai|[Ĥ, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3]|0〉. 3]|0〉. | (9) |
tabij ← 〈Φabij|[Ĥ, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3]|0〉. 3]|0〉. | (10) |
tabcijk ← 〈Φabij|[![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) , , ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3] + [Ĥ, 3] + [Ĥ, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2]|0〉. 2]|0〉. | (11) |
This way, ORCA-AGE II has been used to extend the ORCA functionality by CCSDT-1,2,3,4 and CCSDT as well as CC2 and CC3 UHF energies. The implementations have been verified against CFOUR91 and MRCC.
In order to test the limits of these implementations and the performance, calculations were carried out on small alkene chains and compared to CFOUR. As can be seen in Table 2, our implementation shows turnaround times that are in the ballpark of the CFOUR implementation, which is hand-coded and known to be efficient. Further analysis of the computational bottlenecks is underway and is expected to lead to further efficiency gains in the generated code.
| Alkene | n basis | Program | t iteration (h) |
|---|---|---|---|
| Ethene | 116 | ORCA | 1.2 |
| CFOUR | 0.95 | ||
| Propene | 174 | ORCA | 37.3 |
| CFOUR | 16.8 |
Initially, our triples implementation has been restricted to spin–orbitals and UHF references. However, spin–orbital based wavefunctions, such as UHF-CCSDT, suffer from spin contamination, even with pure spin-references (such as ROHF references). Much research has already gone into eliminating spin contamination by spin adaptation, both for single and multireference methods.93–96 Since the resulting theory contains extra complexity, it is a prime candidate for code generation. Our work on spin-adapted triple excitation containing theories will be reported in due course.
Generation of analytic gradients
A plethora of useful molecular properties can be calculated as energy derivatives with respect to a certain perturbation, such as nuclear gradients, harmonic vibrational frequencies or nuclear magnetic shielding.97,98 While these derivatives can be computed straightforwardly using numerical finite difference methods, it is also quite costly. Calculating the first derivative numerically requires a minimum of two energy calculations along the perturbation, with more calculations needed for increased accuracy. This quickly makes numerical gradient calculations unfeasible for larger molecules. More importantly, perhaps, is the fact that (especially higher-order) numeric derivatives tend to become unstable. Therefore, being able to evaluate analytic gradients is of vital importance, as their cost should not exceed that of approximately a single energy calculation.99Especially relevant for computing properties accurately is obtaining accurate geometries, which can be obtained through geometry optimizations. This involves minimizing the nuclear gradient, the energy derivative with respect to the nuclear coordinates. Due to geometry optimizations being a routine procedure in computational chemistry, nuclear gradients are a logical target to apply code generation to.
Since one of the cornerstones of code generation and ORCA-AGE II is generality, the aim was to build a general framework that would support arbitrary-order CI and CC nuclear gradients (and other derivatives). The starting point for gradients of non-variational methods is to formulate a Lagrangian (CI is taken as an example),100–105
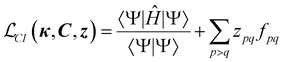 | (12) |
| γpq = 〈Ψ|Epq|Ψ〉. | (13) |
With this restriction in mind, the gradient components that have to be generated are the equations to determine the CI coefficients/CC amplitudes and the unrelaxed density matrices. Equation solvers, such as for the amplitude equations, will have to be implemented by hand, as the AGE is not (yet) able to incorporate them in the generated modules. This is also the case for the so-called Z-vector equation, of which the solving provides the orbital relaxation contribution, zpq.104 By reformulating the CI energy functional in terms of the unrelaxed 1-body reduced density matrix (1RDM), γ and the 2-body reduced density matrix (2RDM), Γ,
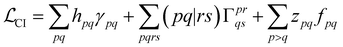 | (14) |
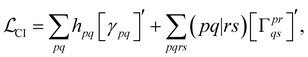 | (15) |
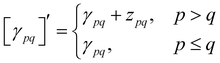 | (16) |
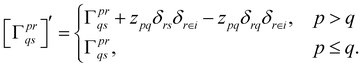 | (17) |
To obtain the final nuclear gradient expression, the derivative is taken with respect to the nuclear coordinates, R, while using the orthonormal molecular orbitals (OMO) approach to ensure that the overlap matrix, S, is well defined at every geometry.106 This leads to the final expression of
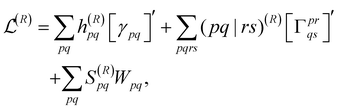 | (18) |
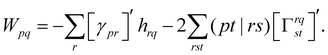 | (19) |
The major bottleneck of these nuclear gradients was the 2RDM due to the layout of the matrix containers involved in its computation. Many contractions incurred a heavy I/O penalty in addition to not being able to utilize BLAS. As described above, this is where matrix containers can usefully be resorted in  so that the most efficient BLAS operations are performed and the I/O operations are minimized. Given that already CCSD computationally scales as
so that the most efficient BLAS operations are performed and the I/O operations are minimized. Given that already CCSD computationally scales as  , resorting will not have a significant impact on the computational performance of CC and CI theories. More importantly, the cost of resorting will be heavily outweighed by the gain in performance from being able to use BLAS operations. This resorting algorithm also keeps track of other resorted containers, so that no duplicates are created and so that they can be reused in other contractions. As can be seen from Fig. 1, the speedup can easily exceed a factor of 10–20 for larger system sizes.
, resorting will not have a significant impact on the computational performance of CC and CI theories. More importantly, the cost of resorting will be heavily outweighed by the gain in performance from being able to use BLAS operations. This resorting algorithm also keeps track of other resorted containers, so that no duplicates are created and so that they can be reused in other contractions. As can be seen from Fig. 1, the speedup can easily exceed a factor of 10–20 for larger system sizes.
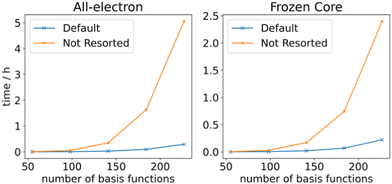 | ||
| Fig. 1 RHF CCSD 2RDM performance with and without resorting matrix containers. The calculations were performed on linear alkanes of increasing length with a def2-TZVP basis set. | ||
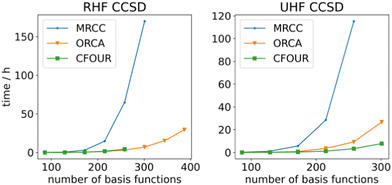
To determine the efficiency of ORCA's generated gradients, they have been compared against the MRCC program's, which is able to generate these gradients on-the-fly for arbitrary order CI/CC theories. This is in contrast with the AGE, which generates code for a specific order of CI/CC, which is compiled into binary form prior to computation. The performance of both gradients is rather similar for smaller systems (Fig. 2), but when more basis functions are present, ORCA runs up to 20 times faster. This is where the effect of the data resorting becomes apparent since (i) the time to resort becomes negligible and (ii) BLAS can generate significant returns on larger tensors due to specialized multiplication methods. The lower performance of the MRCC might be attributed to the in-core parts of the calculation. At most 8 GB of memory is used for RHF CCSD, which is sub-optimal according to the MRCC output. Thus, the calculation becomes unfeasible for larger systems, whereas ORCA stores everything on disk and only loads the tensors into memory when needed. The UHF CCSD calculations were performed with 50 GB of memory. ORCA outperforms the MRCC gradients here as well despite MRCC not having to resort to out-of-core algorithms. This could be ascribed to the AGE's ContractionEngine that is able to make optimal use of the available memory. A comparison has also been made against the hand-written CFOUR code.91,107 ORCA's generated gradients perform approximately the same as CFOUR's in the case of RHF CCSD. While larger calculations are certainly possible, we restricted the memory in CFOUR for consistency purposes such that CFOUR was not able to complete calculations with more than 258 basis functions. CFOUR does outperform ORCA by an approximate factor of 3 in the case of UHF CCSD. Overall, the generated code performs well, with it being able to handle system sizes of around 300–400 basis functions. Single gradient steps for these system sizes can be performed with a def2-TZVP108 basis set within days on an AMD EPYC 75F3 CPU. These results indicate that code generation is a viable way to obtain reliable and performant code.
Internally contracted multireference coupled-cluster theory
Throughout quantum chemistry, we always strive for faster and more accurate theories to aid in our understanding of chemical systems. As mentioned before, CCSD(T) has been quite universally established as the “gold standard” in the single reference domain. In the multireference regime, however, no clear-cut “best” approach exists yet. Various approaches to transfer the coupled cluster Ansatz to multireference wave functions have been introduced,109 some dating back to the late 1970s and early 80s.110–113 In our group, we focus on the internally contracted variant since it has several desirable properties, such as orbital invariance,114 a limited parameter space,65 and size-extensivity.115 Furthermore, fic-MRCC theory is known to be significantly more accurate than fic-MRCI theory, even when the BCH expansion of the similarity-transformed Hamiltonian is truncated at quadratic terms.116Given a zeroth-order wave function |0〉 obtained from a run of a complete active space self-consistent field (CASSCF) calculation,
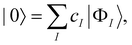 | (20) |
|Ψ = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |0〉, |0〉, | (21) |
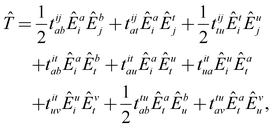 | (22) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) written in Einstein's summation convention for repeated indices. The energy and residuals are computed as in single-reference CC theory as the expectation value of the similarity-transformed Hamiltonian or by projecting the transformed Hamiltonian with functions from all excitation classes. To further simplify the theory, we also truncate the BCH expansion after quadratic terms.65,114 The resulting methodology is equivalent to scheme A from Hanauer and Köhn65 omitting the reference relaxation. The outlined theory is not size extensive, but can become fully size-extensive with a minor modification.115 The latter is not considered in the present implementation.
written in Einstein's summation convention for repeated indices. The energy and residuals are computed as in single-reference CC theory as the expectation value of the similarity-transformed Hamiltonian or by projecting the transformed Hamiltonian with functions from all excitation classes. To further simplify the theory, we also truncate the BCH expansion after quadratic terms.65,114 The resulting methodology is equivalent to scheme A from Hanauer and Köhn65 omitting the reference relaxation. The outlined theory is not size extensive, but can become fully size-extensive with a minor modification.115 The latter is not considered in the present implementation.
This theory is very difficult to implement due to its large number of terms.65 The working equations are derived with spatial orbitals using the elementary commutation rules of spin-traced excitation operators,33
| [Êpq, Êrs] = Êpsδrq − Êrqδps. | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173 terms before removing contractions redundant by symmetry, and 49
173 terms before removing contractions redundant by symmetry, and 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 terms after removal thereof. After factorization, the resulting 65
186 terms after removal thereof. After factorization, the resulting 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 tensor contractions are translated to 3
848 tensor contractions are translated to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765
765![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 lines of code. We remark that the number of equations is vastly different from the implementation of Hanauer and Köhn, who report 5020 terms prior factorization for a CAS(6,6).65 In the latter an additional truncation based on the number of active electrons limiting the rank of the reduced density matrix in the diagrammatic representation is employed, which can further reduce the number of equations, e.g. to 3523 terms for a CAS(2,2). The issue is presently under investigation.
810 lines of code. We remark that the number of equations is vastly different from the implementation of Hanauer and Köhn, who report 5020 terms prior factorization for a CAS(6,6).65 In the latter an additional truncation based on the number of active electrons limiting the rank of the reduced density matrix in the diagrammatic representation is employed, which can further reduce the number of equations, e.g. to 3523 terms for a CAS(2,2). The issue is presently under investigation.
A theory having so many terms places a high computational workload on the code generator, which was the primary reason for redeveloping the ORCA-AGE infrastructure. In particular, removing duplicate intermediates in the equation factorization step proved to be highly demanding, as that step creates 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803 intermediates in the case of fic-MRCC theory, which are eventually pruned to 15
803 intermediates in the case of fic-MRCC theory, which are eventually pruned to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 intermediates. In the previous version of ORCA-AGE, a simple algorithm for detecting duplicates was used that scaled as
987 intermediates. In the previous version of ORCA-AGE, a simple algorithm for detecting duplicates was used that scaled as 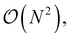 thus leading to impractically long generation times of about one month. In the updated version, this algorithm uses a hash table-based data compression technique with expected linear time instead, reducing the time to about 4 hours for the entire toolchain. In both cases, the toolchain, which has time-limiting steps parallelized with OpenMP threads, was run on 16 cores/32 threads.
thus leading to impractically long generation times of about one month. In the updated version, this algorithm uses a hash table-based data compression technique with expected linear time instead, reducing the time to about 4 hours for the entire toolchain. In both cases, the toolchain, which has time-limiting steps parallelized with OpenMP threads, was run on 16 cores/32 threads.
If we now look at the generator from an end user's perspective, generating the code is also much simpler. All that is required is to define the excitation classes from eqn (22) in a user-friendly input file, an example of which is given in Scheme 4. Each line corresponds to an excitation class with an identifier, the amplitudes, and the excitation operators for that class. Optionally, contravariant projection operators90 can be defined such that the projection functions are orthogonal to the excitation space. The generator itself features code that can create all necessary terms from the definition of the excitation classes, be it the similarity-transformed Hamiltonian through application of the BCH expansion, residuals through projection or the energy equations. Hence, everything from changing the cluster operator to the size of the BCH expansion is simple to program and quick to extend to other methods as well.
 | ||
| Scheme 4 Definition of the excitation classes for fic-MRCC theory (see also eqn (22)). | ||
To exemplify the efficiency of the generated code, we consider two limiting cases in fic-MRCC theory: first, large systems with small active spaces, and second, systems with large active spaces. We further note that the contractions given below are asymptotically limiting, i.e., they need not be the most expensive contractions for small systems. Large systems with small active spaces, e.g., using triple-ζ basis sets and a CAS(2,2), are dominated by the 4-external term, which also appears in single-reference CC theory,
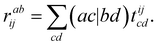 | (24) |
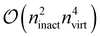 and thus dominates the computational time for nvirt ≫ ninact, nact. Therefore, it is crucial to fully optimize this term, which is complicated by the fact that the 4-external integrals must be stored on disk for their large size. This is where the hand-coded ContractionEngine functionality is employed: it minimizes I/O through reading large batches of the amplitudes and integrals (up to a given memory limit) and then applies a large-scale DGEMM operation to have maximum computational efficiency, consequently performing no worse than the best handwritten CC codes for this contraction.34
and thus dominates the computational time for nvirt ≫ ninact, nact. Therefore, it is crucial to fully optimize this term, which is complicated by the fact that the 4-external integrals must be stored on disk for their large size. This is where the hand-coded ContractionEngine functionality is employed: it minimizes I/O through reading large batches of the amplitudes and integrals (up to a given memory limit) and then applies a large-scale DGEMM operation to have maximum computational efficiency, consequently performing no worse than the best handwritten CC codes for this contraction.34
The other extreme is given by systems with large active spaces. In these cases, the runtime is dominated by contractions such as
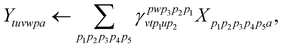 | (25) |
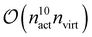 and consequently dominates the other contractions for nvirt > ninact, nact ≳ 6.
and consequently dominates the other contractions for nvirt > ninact, nact ≳ 6.
The tensor γ5 is difficult for the CPU to manage because of its complicated structure with ten dimensions as well as its size (e.g., 8.59 GB for nact = 8), thus leading to frequent cache misses if implemented naively with eleven nested loops. Such contractions are ideal candidates for the TTGT engine discussed above, as BLAS libraries carefully optimize both algorithms and cache usage. In this case, the generated code is reproduced in Scheme 5.
The TTGT engine first reorders the five-body density DC5 to optimally align and group the indices together, thus enabling a single large-scale DGEMM instruction to digest the contraction. As a result, explicit loops are only used to reorder the tensors, while the actual contraction is done with implicit loops in the DGEMM matrix–matrix multiplication. Compared to the same contraction implemented with plain for-loops, the TTGT scheme easily leads to a speedup by a factor >100. All tensors are kept in memory since the space requirements are not as high as for the 4-external term and the number of active indices is limited. The TTGT engine is also capable of accounting for indices associated with I/O and will dynamically adapt to load (sub-)tensors from disk in an optimal fashion and perform a DGEMM over the remaining non-I/O indices, if required.
The improvements made to the code generator in ORCA-AGE II now allow quite large systems to be computed with the fic-MRCC implementation. It should be noted that our generated code does not yet take advantage of point group symmetry and hence all calculations are performed under C1 symmetry. The implementation of point group symmetry is a logical next step that we are currently pursuing.
We will now present two calculations of tetradecene, C14H28, and naphthalene, C10H8, for which the requirements are close to the limits of computational resources for large systems with small active spaces and systems with large active spaces, respectively. Both systems were run in serial on an AMD EPYC™ 75F3 processor and use the def2-SVP basis set.108 The tetradecene system uses a small CAS(2,2) active space. Thus, its 112 electrons are filled into 14 frozen core, 41 inactive, 2 active, and 279 virtual orbitals (336 in total). On average, a single iteration takes 6.58 hours. The calculation converges smoothly in 12 iterations for a total runtime of 3.3 days, a timeframe that is manageable for routine calculations. The naphthalene system, on the other hand, uses a CAS(10,10), and distributes 68 electrons among 10 frozen core, 19 inactive, 10 active, and 141 virtual orbitals (180 in total). Each iteration requires 11.35 hours to complete, and an additional 17.46 hours are spent computing the five-body density, which takes up 80.00 GB of memory. The total runtime for all 16 iterations is 8.3 days.
Finally, we present a series of calculations on linear polyene chains (see Fig. 3) at the fic-MRCI and fic-MRCC levels of theory, starting from ethene up until tetradecaheptaene, to systematically try to find the limits of the current implementation. The active space consists of the conjugated π-system and is thus increasing in size in tandem with the polyenes. We can conclude that a CAS(14,14) calculation, which in this case corresponds to a system size of 276 basis functions, is at the very limit of what it achievable with our fic-MRCI. A single-point calculation on tetradecaheptaene takes 3.5 days for 16 iterations. As can be seen, fic-MRCC is an order of magnitude more expensive than fic-MRCI, meaning a CAS(14,14) calculation could not be completed. The largest possible calculation was performed on dodecahexaene (238 basis functions) which took 24.5 days for 11 iterations.
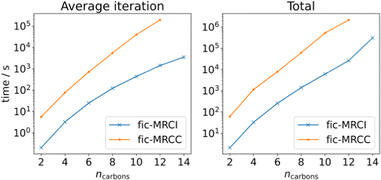 | ||
| Fig. 3 Polyene calculations at fic-MRCI and fic-MRCC level, using a def2-SVP basis set, while increasing the number of carbons and simultaneously the active space, meaning CAS(ncarbons, ncarbons). | ||
From these examples, we see that increasing the size of the active space severely limits the system size to remain computationally feasible. This is both due to the asymptotic scaling, 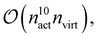 as well as the difficulty of handling a large, high-dimensional tensor like γ5 for the CPU, as discussed above. To this end, we are currently developing a version of fic-MRCC theory that only requires the four-body density.
as well as the difficulty of handling a large, high-dimensional tensor like γ5 for the CPU, as discussed above. To this end, we are currently developing a version of fic-MRCC theory that only requires the four-body density.
In summary, ORCA-AGE II has been proven to be a performant toolchain that generates near-optimal code for the time-limiting steps of fic-MRCC theory. The code optimization strategies illustrated here are, of course, also applied to the non-limiting contractions in the code. However, despite the performant implementation, fic-MRCC theory remains a very time-intensive method due to the large number of contractions it contains.
Parallel code generation with MPI
Quantum chemistry methods, such as CC theory, have a cost that scales polynomially with respect to the number of basis functions N,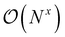 . Hence, systems with many basis functions will take a long time to compute, unless further steps are taken. One way to approach this is to reduce the scaling of the methods through local approximation schemes, ideally ending at x = 1.4 However, even then computational demands grow with system size, to which the solution is to distribute the work among multiple processors, ideally dividing the work and thus the time perfectly among them. In this section, we will show how parallelization can be achieved in a fully automated way across any input theory that can be handled by ORCA-AGE II.
. Hence, systems with many basis functions will take a long time to compute, unless further steps are taken. One way to approach this is to reduce the scaling of the methods through local approximation schemes, ideally ending at x = 1.4 However, even then computational demands grow with system size, to which the solution is to distribute the work among multiple processors, ideally dividing the work and thus the time perfectly among them. In this section, we will show how parallelization can be achieved in a fully automated way across any input theory that can be handled by ORCA-AGE II.
The most computationally demanding steps in electronic structure methods are typically the tensor contractions, so the parallelization effort should be focused on these. Considering that the parallelized code needs to be generated for an arbitrary number of contractions, a scheme is needed that would be efficient regardless of the number of contractions and would be able to handle the generality of the contractions. Hence, we opted for parallelization on per-contraction-basis, where the parallelization would occur only on the outermost loop. By additionally forcing the I/O to be restricted to the outermost loop (potentially by resorting matrix containers), it is ensured that no two processes will access the same target matrix simultaneously. A load-balancing scheme, in which one process works on a single expensive contraction while another process tackles multiple smaller contractions, is another route to solving this problem and is under active investigation.
An example of such parallelized code, based on eqn (26) can be found below in Scheme 6. In order to enforce the I/O of the target tensor to be restricted to the outermost loop, so-called pair or compound indices are used, which map a tuple of indices to a linear index and vice versa. In the case of eqn (26), the indices i, j are mapped to the pair index ij. Doing so also allows easy parallelization over restricted index lists, such as i > j. With the use of these compound indices, the contraction code for parallelized tensor contraction looks exactly like for a serial program. Tensors are loaded from disk, after which the contraction is evaluated (using BLAS) and the result is then stored on disk. The only extension that is needed is to distribute the list of compound indices to the processes in unique evenly sized batches, as defined by the pairIJAB_index_start and pairIJAB_index_stop variables.
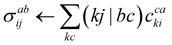 | (26) |
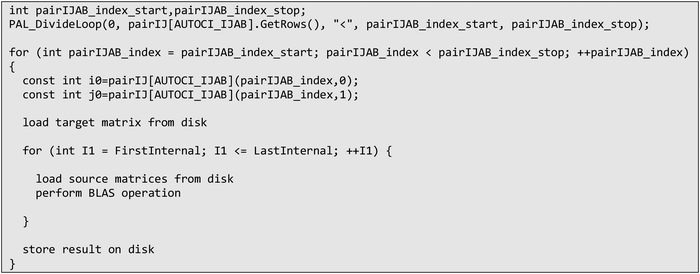 | ||
| Scheme 6 Semi-pseudo generated code of eqn (26) that has been parallelized over indices i, j using compound indices and ORCA parallel infrastructure. | ||
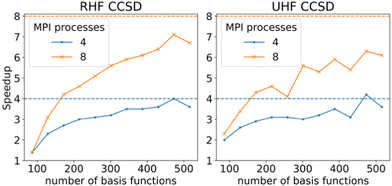
In order to check the performance of the parallelized code, benchmarks using the RHF- and UHF-CCSD methods were performed on a series of linear alkenes, from ethene to dodecene using the def2-TZVP basis set. Fig. 4 shows that the scaling for 4 processes is close to the ideal value when larger systems are treated. The situation is less ideal in the case of 8 processes, with the speed-up stagnating around 7 and 6 times for RHF- and UHF-CCSD, respectively. This is due to a small number of contractions incurring I/O penalties from forcing the target tensor to be accessed first.
A possible solution would be to gather the problematic contraction patterns and incorporate those in the ContractionEngine as well to ensure maximum efficiency. Regardless, the initial parallel implementation performs well, especially considering that all of the code is generated entirely automatically with no custom intervention.
Perspective: automated code generation in quantum chemistry
In this section, we wish to address a few of the aspects which, in our opinion, are of central importance for the future of correlated wavefunction theory and where automatic code generation offers unique opportunities. These considerations are only partially of a genuine scientific nature, but we feel that it is useful to spell them out in the present context as they have far-reaching consequences for the way that implementation projects might be handled in the immediate future.The art and science of writing computer programs that implement correlated wavefunction calculations began in the late 1960s and early 1970s. Ingenious programs were written by the best scientists in the field that took advantage of the state-of-the-art hardware at the time.117–121 Unfortunately, these programs became obsolete with the next or second next generation of hardware. Since writing a correlated wavefunction code is an extremely technical and time-consuming undertaking, the codes have never been rewritten and the science and the effort that went into it are partially lost. Today, we are facing the very same problem of legacy codes that are no longer optimally adapted to modern computer facilities such as highly parallel supercomputers. At the same time, in an academic environment the novelty of writing another (e.g.) coupled cluster code, is necessarily limited since it has been done so many times in the past. Yet, it is still a difficult and time-consuming task. Consequently, finding the financial and human resources to tackle long and complicated re-implementation projects of known quantum chemical theories will become more and more difficult. It is precisely this aspect that we regard as one of the most important missions of automatic code generation: to ensure that theories can be implemented in an ever-shifting hardware landscape without investing years of programmer time. This is a problem that automatic code generation, in principle, is able to solve. However, in order to ensure that up-to-date code can indeed be generated one must simultaneously tackle the problem of “deep-integration”.
In order to explain the concept of “deep integration”, consider the commonly met situation, in which a code generator has been written by a very talented co-worker inside an academic research group who has since moved on and may no longer be available to ask questions, fix bugs or add new features. Furthermore, if the code generator was written in an unstable language, it may not even be executable anymore in its original form. There may be some code inside a given program package that was generated using these tools. If it was not meticulously documented how exactly that code was generated with which exact input using a given well-documented state of the generation chain, it will be impossible to re-generate that code. If the generated code is facing some limitations (for example not being parallelized or not taking proper advantage of molecular symmetry) the whole project will start from scratch when the need arises to implement such features.
In order to avoid such unproductive cycles, it will therefore be necessary to more tightly integrate the code generator itself as well as the generated code with the host program. This does not preclude the possibility that a given code generator can generate code for different host programs. The ideal situation that we envision, and to a large extent have realized in the present incarnation of ORCA-AGE II, is that the developer only submits their Ansatz in the form of an input file and expressed in the language of second quantization into the source code repository. Everything else from this point must proceed automatically: generation and factorization of equations, generation of host specific high-level code and insertion of this code in the host program. In this way, it can be ensured that all generated code is of uniform quality and reflects the latest state of development of the code generation chain. It will also ensure that the origin of all generated code is unambiguous and hence, well documented and reproducible. Obviously, for this concept to work, the source code of the code generator itself must also be part of the source code repository. A master build then proceeds by first generating the code generation chain which subsequently triggers the generation of actual code as described above. To this end, ORCA has a module ORCA_AUTOCI, that essentially consists of a framework of solvers and task organizers that trigger the various generated codes to generate Sigma-vectors, energy expressions, gradients etc. No generated code is inserted elsewhere in the program.
We believe, that following this strategy, the curse of legacy code can be overcome and the generated code can be optimally adapted to different hardware. In fact, if new hardware emerges, the only thing that needs to change is the final step of the generation that translates factorized equations into high-level code. For a new hardware, a new module must be added to the code generation chain that produces hardware specific code. Alternatively, the new module could make use of emerging libraries such as Kokkos122 or HPX.123 This becomes an attractive possibility since no human time is involved in redoing quantum chemical code. Such a strategy would also allow for an optimal collaboration between quantum chemists and computer scientists since the chemistry and computer sciences tasks are cleanly separated from each other.
While we believe that solving the legacy code problem might be the most important mission for automatic code generation, there are other, more obvious advantages:
1. The generation of code implementing complex methods can proceed in a matter of hours instead of years.
2. Theories like fic-MRCC that are far too complex for humans, can be readily implemented in a reliable and efficient manner. This become more and more important since the readily implementable correlation methods tend to have been implemented already many times.
3. Once the toolchain is properly debugged, the generated code will be highly reliable and will produce correct results. This will save humongous amounts of debugging time that any human written code will have to go through.
Effectively, we envision a clearer partitioning of quantum chemistry codes in the future into low-level, mid-level, and high-level parts, to be explicated below. While the exact boundaries between the hierarchy of codes will be somewhat fluid, we nonetheless believe that we identified the three main (future) development areas of quantum chemistry codes.
Under “low-level,” we understand the foundational code of any quantum chemical software package that provides basic quantities such as molecular integrals and other general-purpose libraries used throughout the codes, e.g., a library for arbitrary-dimensional tensors. Integral libraries already exist (for example, Libint,124 SHARK125 and libcint,126 to name but a few) and have been extensively tuned for shortest possible runtimes. Interestingly, specialized code generation has also been employed for the integral libraries Libint124 and SHARK,77,127 as especially loop unrolling allows the compiler to generate the most efficient code. Other low-level libraries include BLAS, which allows peak efficiency for the ubiquitous matrix multiplications in modern-day quantum chemistry codes. As a side note, general BLAS-like libraries for arbitrary tensors that may become more pervasive in the future would also fall in this category. Noteworthy examples are TBLIS128 and GETT,43 among others.44,46
Under our classification, the mid-level code would mainly comprise common algorithms that are implemented by hand, such as general solvers and drivers. Given a flexible interface, these common algorithms enable the (iterative) computation of the desired molecular properties without needing to copy-and-paste code, possibly with minor modifications depending on the actual method. Doing so guarantees that these core algorithms are free from errors since there is only the library that needs to be tested; and not multiple, slightly different implementations. Also, any improvements also apply across all implemented methods in a consistent fashion. In ORCA, we are steadily moving in this direction, starting with the Davidson and DIIS algorithms, and expect more changes by the time the next major version releases.
The highest level is reserved for the actual implementation of quantum chemical theories such as CCSD, CCSDT, fic-MRCC, and gradients. This is ideally enabled through a high-level interface that more closely resembles the mathematical equations or Ansätze rather than computer code. This can be achieved in many possible ways, each with its own benefits and drawbacks. In our group, we decided to focus on code generation since all contractions and tensors (with all their dimensions) are already known at compile time. Thus, there is no need to interpret the data on-the-fly, and the generated code can still be tailored to different architectures and different framework backends such as the ones mentioned in the introduction (CTF,44,45 libtensor,46 LITF,47 TCL,43,48 and TiledArray49,50). Other approaches may include interpreters such as SIAL52,53,129,130 or direct usage of the aforementioned libraries. One might even generate code optimised for individual examples, given that the ideal factorisation depends on the size of the orbital subspaces. Eventually, only the mathematical equations would be stored in the code repository, which makes them easy to understand for new researchers as well as easy to validate and modify.
Our firm belief in these underlying trends has led us to significantly overhaul the entire architecture of ORCA, which has started with the code generator and the SHARK integral library77,127 for the fifth major version.127 Further work has been done on the algorithms library, with more to come for the next major release. In this article, we outlined the latest developments in ORCA-AGE's code generation capabilities, which showcases what we think will be representative of high-level interfaces in quantum chemical codes in the future.
Conclusions
In this article, we describe a newer version of ORCA-AGE, ORCA-AGE II, which is a complete overhaul of the previously introduced toolchain. Due to algorithmic improvements throughout the code (especially in the time-limiting steps) and a shift in programming language from PYTHON to C++, the toolchain is faster by a factor of ≈150 as measured while generating fic-MRCC theory. Its highly modular layout has also been refreshed, enabling us to add new code engines such as the TTGT scheme easily. It is also simpler to use than the old toolchain as external dependencies were removed and because of an even tighter integration with the main ORCA source code: all computational modules can be regenerated with a simple command, which automatically brings new features and better code to existing modules as well.The new toolchain has proven to be capable of generating even the most complicated theories, as demonstrated for fic-MRCC with its enormous number of terms generated through the commutation rules-based equation generator. We also showed that the toolchain is not tailored to specific problems, but rather general enough to allow a gradient framework for arbitrary theories to be developed with it. In both cases, the generated code is highly performant despite the large number of terms that must be computed. The AGE is even capable of producing well-performing parallelised code. Higher-order excitations, such as in CCSDT, can further be incorporated at minimal effort on the researcher's side.
In the end, developing automated code generators is beneficial for researchers as it allows them to spend their resources on their critical projects while at the same time transparently accounting for an efficient, production-level implementation. We believe that this is the direction in which ab initio quantum chemistry is evolving and will hence continue to align our development efforts on ORCA and ORCA-AGE with these trends.
Data availability
Original data from this work are provided as an open-access data set hosted by the Open Research Data Repository of the Max Planck Society at https://doi.org/10.17617/3.CWGUUL.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors greatly appreciate clarifying comments by Ondřej Demel, Mihály Kállay, Andreas Köhn, Eric Neuscamman, Masaaki Saitow, Toru Shiozaki, and Alexander Y. Sokolov on the features of code generators in Table 1. The authors thankfully acknowledge funding by the Max Planck Society. M. H. L. further thanks the Fonds der Chemischen Industrie as well as the Studienstiftung des deutschen Volkes for support. Finally, we gratefully acknowledge funding of this work by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) as part of the CRC 1639 NuMeriQS – project no. 511713970. Open Access funding provided by the Max Planck Society.References
- R. E. Watson, Phys. Rev., 1960, 118, 1036–1045 CrossRef CAS.
- R. E. Watson, Phys. Rev., 1960, 119, 1934–1939 CrossRef CAS.
- M. R. Silva-Junior, S. P. A. Sauer, M. Schreiber and W. Thiel, Mol. Phys., 2010, 108, 453–465 CrossRef CAS.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- R. R. Schaller, IEEE Spectrosc., 1997, 34, 52–59 Search PubMed.
- W. Meyer, in Methods of Electronic Structure Theory, ed. H. F. Schaefer III, Springer Science + Business Media, New York, 1977, vol. 3, pp. 413–446 Search PubMed.
- P. E. M. Siegbahn, Int. J. Quantum Chem., 1980, 18, 1229–1242 CrossRef CAS.
- T. Yanai, Y. Kurashige, M. Saitow, J. Chalupský, R. Lindh and P.-Å. Malmqvist, Mol. Phys., 2017, 115, 2077–2085 CrossRef CAS.
- S. Hirata, Theor. Chem. Acc., 2006, 116, 2–17 Search PubMed.
- C. L. Janssen and H. F. Schaefer III, Theor. Chim. Acta, 1991, 79, 1–42 CrossRef CAS.
- G. C. Wick, Phys. Rev., 1950, 80, 268–272 CrossRef.
- I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, Cambridge, 2009 Search PubMed.
- S. Hirata, J. Phys. Chem. A, 2003, 107, 9887–9897 CrossRef CAS.
- A. A. Auer, G. Baumgartner, D. E. Bernholdt, A. Bibireata, V. Choppella, D. Cociorva, X. Gao, R. Harrison, S. Krishnamoorthy, S. Krishnan, C.-C. Lam, Q. Lu, M. Nooijen, R. Pitzer, J. Ramanujam, P. Sadayappan and A. Sibiryakov, Mol. Phys., 2006, 104, 211–228 CrossRef CAS.
- T. Shiozaki, M. Kamiya, S. Hirata and E. F. Valeev, Phys. Chem. Chem. Phys., 2008, 10, 3358 RSC.
- M. K. MacLeod and T. Shiozaki, J. Chem. Phys., 2015, 142, 051103 CrossRef PubMed.
- K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- E. Neuscamman, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2009, 130, 124102 CrossRef PubMed.
- E. Neuscamman, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2009, 130, 169901 CrossRef.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Phys., 2013, 139, 044118 CrossRef PubMed.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Theory Comput., 2015, 11, 5120–5131 CrossRef CAS PubMed.
- M. Saitow and T. Yanai, J. Chem. Phys., 2020, 152, 114111 CrossRef CAS PubMed.
- M. Nooijen and V. Lotrich, J. Mol. Struct.: THEOCHEM, 2001, 547, 253–267 CrossRef CAS.
- L. Kong, K. R. Shamasundar, O. Demel and M. Nooijen, J. Chem. Phys., 2009, 130, 114101 CrossRef PubMed.
- L. Kong, PhD Thesis, University of Waterloo, 2009.
- A. Köhn, G. W. Richings and D. P. Tew, J. Chem. Phys., 2008, 129, 201103 CrossRef PubMed.
- A. Köhn, J. Chem. Phys., 2009, 130, 104104 CrossRef PubMed.
- J. Paldus and H. C. Wong, Comput. Phys. Commun., 1973, 6, 1–7 CrossRef.
- H. C. Wong and J. Paldus, Comput. Phys. Commun., 1973, 6, 9–16 CrossRef.
- Z. Csépes and J. Pipek, J. Comput. Phys., 1988, 77, 1–17 CrossRef.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945–2954 CrossRef.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, Ltd, Chichester, 2000 Search PubMed.
- M. Krupička, K. Sivalingam, L. Huntington, A. A. Auer and F. Neese, J. Comput. Chem., 2017, 38, 1853–1868 CrossRef PubMed.
- A. Hartono, A. Sibiryakov, M. Nooijen, G. Baumgartner, D. E. Bernholdt, S. Hirata, C.-C. Lam, R. M. Pitzer, J. Ramanujam and P. Sadayappan, in Computational Science – ICCS 2005, ed. V. S. Sunderam, G. D. van Albada, P. M. A. Sloot and J. J. Dongarra, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, vol. 3514, pp. 155–164 Search PubMed.
- P.-W. Lai, H. Zhang, S. Rajbhandari, E. Valeev, K. Kowalski and P. Sadayappan, Proc. Comput. Sci., 2012, 9, 412–421 CrossRef.
- A. D. Bochevarov and C. D. Sherrill, J. Chem. Phys., 2004, 121, 3374–3383 CrossRef CAS PubMed.
- A. Hartono, Q. Lu, X. Gao, S. Krishnamoorthy, M. Nooijen, G. Baumgartner, D. E. Bernholdt, V. Choppella, R. M. Pitzer, J. Ramanujam, A. Rountev and P. Sadayappan, in Computational Science – ICCS 2006, ed. V. N. Alexandrov, G. D. van Albada, P. M. A. Sloot and J. Dongarra, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, vol. 3991, pp. 267–275 Search PubMed.
- A. Engels-Putzka and M. Hanrath, J. Chem. Phys., 2011, 134, 124106 CrossRef PubMed.
- J. F. Stanton, J. Gauss, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1991, 94, 4334–4345 CrossRef CAS.
- C. L. Lawson, R. J. Hanson, D. R. Kincaid and F. T. Krogh, ACM Trans. Math. Software, 1979, 5, 308–323 CrossRef.
- M. Hanrath and A. Engels-Putzka, J. Chem. Phys., 2010, 133, 064108 CrossRef PubMed.
- P. Springer and P. Bientinesi, ACM Trans. Math. Software, 2018, 44, 1–29 Search PubMed.
- E. Solomonik, D. Matthews, J. Hammond and J. Demmel, 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, 2013 Search PubMed.
- E. Solomonik, D. Matthews, J. R. Hammond, J. F. Stanton and J. Demmel, J. Parallel Distrib. Comput., 2014, 74, 3176–3190 CrossRef.
- E. Epifanovsky, M. Wormit, T. Kuś, A. Landau, D. Zuev, K. Khistyaev, P. Manohar, I. Kaliman, A. Dreuw and A. I. Krylov, J. Comput. Chem., 2013, 34, 2293–2309 CrossRef CAS PubMed.
- D. Kats and F. R. Manby, J. Chem. Phys., 2013, 138, 144101 CrossRef PubMed.
- P. Springer, Tensor Contraction Library (TCL), https://github.com/springer13/tcl, (accessed September 20, 2021).
- J. A. Calvin and E. F. Valeev. TiledArray: A general-purpose scalable block-sparse tensor framework, https://github.com/valeevgroup/tiledarray, (accessed June, 30, 2021).
- J. A. Calvin, C. A. Lewis and E. F. Valeev, Proceedings of the 5th Workshop on Irregular Applications: Architectures and Algorithms, 2015 Search PubMed.
- N. Jindal, PhD Thesis, University of Florida, 2015 Search PubMed.
- E. Deumens, V. F. Lotrich, A. Perera, M. J. Ponton, B. A. Sanders and R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 895–901 CAS.
- E. Deumens, V. F. Lotrich, A. S. Perera, R. J. Bartlett, N. Jindal and B. A. Sanders, Annual Reports in Computational Chemistry, Elsevier, 2011, vol. 7, pp. 179–191 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- J. M. Herbert and W. C. Ermler, Comput. Chem., 1998, 22, 169–184 CrossRef CAS.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2000, 113, 1359–1365 CrossRef.
- K. Kowalski, J. R. Hammond, W. A. de Jong, P.-D. Fan, M. Valiev, D. Wang and N. Govind, in Computational Methods for Large Systems, ed. J. R. Reimers, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2011, pp. 167–200 Search PubMed.
- H. J. J. van Dam, W. A. de Jong, E. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma and M. Valiev, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 888–894 CAS.
- S. Hirata, J. Chem. Phys., 2004, 121, 51–59 CrossRef CAS PubMed.
- S. Hirata, P.-D. Fan, A. A. Auer, M. Nooijen and P. Piecuch, J. Chem. Phys., 2004, 121, 12197–12207 CrossRef CAS PubMed.
- T. Shiozaki, M. Kamiya, S. Hirata and E. F. Valeev, J. Chem. Phys., 2008, 129, 071101 CrossRef PubMed.
- B. Vlaisavljevich and T. Shiozaki, J. Chem. Theory Comput., 2016, 12, 3781–3787 CrossRef CAS PubMed.
- K. Chatterjee and A. Y. Sokolov, J. Chem. Theory Comput., 2019, 15, 5908–5924 CrossRef CAS PubMed.
- I. M. Mazin and A. Y. Sokolov, J. Chem. Theory Comput., 2021, 17, 6152–6165 CrossRef CAS PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed.
- D. Datta, L. Kong and M. Nooijen, J. Chem. Phys., 2011, 134, 214116 CrossRef PubMed.
- D. Datta and M. Nooijen, J. Chem. Phys., 2012, 137, 204107 CrossRef PubMed.
- O. Demel, D. Datta and M. Nooijen, J. Chem. Phys., 2013, 138, 134108 CrossRef PubMed.
- M. Nooijen, O. Demel, D. Datta, L. Kong, K. R. Shamasundar, V. Lotrich, L. M. Huntington and F. Neese, J. Chem. Phys., 2014, 140, 081102 CrossRef PubMed.
- J. A. Black, A. Waigum, R. G. Adam, K. R. Shamasundar and A. Köhn, J. Chem. Phys., 2023, 158, 134801 CrossRef CAS PubMed.
- W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1997, 107, 432–449 CrossRef CAS.
- F. A. Evangelista, J. Chem. Phys., 2022, 157, 064111 CrossRef CAS PubMed.
- K. Sivalingam, M. Krupička, A. A. Auer and F. Neese, J. Chem. Phys., 2016, 145, 054104 CrossRef PubMed.
- L. M. J. Huntington, M. Krupička, F. Neese and R. Izsák, J. Chem. Phys., 2017, 147, 174104 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- T. Shiozaki, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1331 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 054101 CrossRef PubMed.
- S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1992, 97, 4282–4288 CrossRef CAS.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 2002, 116, 1773–1782 CrossRef CAS.
- Y. S. Lee and R. J. Bartlett, J. Chem. Phys., 1984, 80, 4371–4377 CrossRef CAS.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1984, 81, 5906–5912 CrossRef.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1985, 82, 5761 CrossRef.
- M. Urban, J. Noga, S. J. Cole and R. J. Bartlett, J. Chem. Phys., 1985, 83, 4041–4046 CrossRef CAS.
- J. Noga, R. J. Bartlett and M. Urban, Chem. Phys. Lett., 1987, 134, 126–132 CrossRef.
- J. Gauss and J. F. Stanton, Phys. Chem. Chem. Phys., 2000, 2, 2047–2060 RSC.
- Y. He, Z. He and D. Cremer, Theor. Chem. Acc., 2001, 105, 182–196 Search PubMed.
- P. Pulay, S. Saebo and W. Meyer, J. Chem. Phys., 1984, 81, 1901–1905 CrossRef CAS.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T. C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- B. G. Adams and J. Paldus, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 1–17 CrossRef CAS.
- N. Herrmann and M. Hanrath, J. Chem. Phys., 2020, 153, 164114 CrossRef CAS PubMed.
- D. A. Matthews, J. Gauss and J. F. Stanton, J. Chem. Theory Comput., 2013, 9, 2567–2572 CrossRef CAS PubMed.
- D. A. Matthews and J. F. Stanton, J. Chem. Phys., 2015, 142, 064108 CrossRef PubMed.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, 2017 Search PubMed.
- P. Jørgensen and J. Simons, J. Chem. Phys., 1983, 79, 334–357 CrossRef.
- P. Pulay, in Modern Electronic Structure Theory, ed. D. R. Yarkony, World Scientific, Singapore, 1995, vol. 2, p. 1191 Search PubMed.
- E. Salter, G. W. Trucks and R. J. Bartlett, J. Chem. Phys., 1989, 90, 1752–1766 CrossRef.
- J. Gauss, W. J. Lauderdale, J. F. Stanton, J. D. Watts and R. J. Bartlett, Chem. Phys. Lett., 1991, 182, 207–215 CrossRef CAS.
- K. Hald, A. Halkier, P. Jørgensen, S. Coriani, C. Hättig and T. Helgaker, J. Chem. Phys., 2003, 118, 2985–2998 CrossRef CAS.
- A. C. Scheiner, G. E. Scuseria, J. E. Rice, T. J. Lee and H. F. Schaefer III, J. Chem. Phys., 1987, 87, 5361–5373 CrossRef CAS.
- N. C. Handy and H. F. Schaefer III, J. Chem. Phys., 1984, 81, 5031–5033 CrossRef CAS.
- K. Kristensen, P. Jørgensen, A. J. Thorvaldsen and T. Helgaker, J. Chem. Phys., 2008, 129, 214103 CrossRef PubMed.
- T. Helgaker and P. Jørgensen, in Methods in Computational Molecular Physics, ed. S. Wilson and G. H. F. Diercksen, Plenum, New York, 1992 Search PubMed.
- J. Gauss, J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1991, 95, 2623–2638 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS PubMed.
- I. Lindgren, Int. J. Quantum Chem., 1978, 14, 33–58 CrossRef.
- B. Jeziorski and H. J. Monkhorst, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 1668–1681 CrossRef CAS.
- W. D. Laidig and R. J. Bartlett, Chem. Phys. Lett., 1984, 104, 424–430 CrossRef CAS.
- A. Banerjee and J. Simons, Int. J. Quantum Chem., 1981, 19, 207–216 CrossRef CAS.
- F. A. Evangelista and J. Gauss, J. Chem. Phys., 2011, 134, 114102 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 137, 131103 CrossRef PubMed.
- J. A. Black and A. Köhn, J. Chem. Phys., 2019, 150, 194107 CrossRef PubMed.
- R. Ahlrichs, H. J. Böhm, C. Ehrhardt, P. Scharf, H. Schiffer, H. Lischka and M. Schindler, J. Comput. Chem., 1984, 6, 200–208 CrossRef.
- H. Lischka, R. Shepard, F. B. Brown and I. Shavitt, Int. J. Quantum Chem., Quantum Chem. Symp., 1981, 15, 91–100 CAS.
- J. Paldus, J. Čížek and I. Shavitt, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 50–67 CrossRef.
- W. Meyer, J. Chem. Phys., 1973, 58, 1017–1035 CrossRef CAS.
- R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581 CrossRef CAS.
- C. R. Trott, D. Lebrun-Grandie, D. Arndt, J. Ciesko, V. Dang, N. Ellingwood, R. Gayatri, E. Harvey, D. S. Hollman, D. Ibanez, N. Liber, J. Madsen, J. Miles, D. Poliakoff, A. Powell, S. Rajamanickam, M. Simberg, D. Sunderland, B. Turcksin and J. Wilke, IEEE Trans. Parallel Distrib. Syst., 2022, 33, 805–817 Search PubMed.
- H. Kaiser, P. Diehl, A. Lemoine, B. Lelbach, P. Amini, A. Berge, J. Biddiscombe, S. Brandt, N. Gupta, T. Heller, K. Huck, Z. Khatami, A. Kheirkhahan, A. Reverdell, S. Shirzad, M. Simberg, B. Wagle, W. Wei and T. Zhang, J. Open Source Software, 2020, 5, 2352 CrossRef.
- E. F. Valeev and J. T. Fermann. Libint: A high-performance library for computing Gaussian integrals in quantum mechanics, https://github.com/evaleev/libint, (accessed September 16, 2021).
- F. Neese, J. Comput. Chem., 2023, 44, 381–396 CrossRef CAS PubMed.
- Q. Sun, J. Comput. Chem., 2015, 36, 1664–1671 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- D. A. Matthews, arXiv, 2017, preprint, arXiv:1607.00291, DOI:10.48550/arxiv.1607.00291v4.
- V. Lotrich, N. Jindal, E. Deumens, R. J. Bartlett and B. A. Sanders, Final Report: The Super Instruction Architecture, 2013.
- V. F. Lotrich, J. M. Ponton, A. S. Perera, E. Deumens, R. J. Bartlett and B. A. Sanders, Mol. Phys., 2010, 108, 3323–3330 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00444b |
| ‡ These authors share first authorship. |
| This journal is © the Owner Societies 2024 |