On the performance of second-order approximate coupled-cluster singles and doubles methods for non-valence anions

Abstract

We investigate the capability of several variants of the second-order approximate coupled-cluster singles and doubles (CC2) method to describe dipole-bound, quadrupole-bound, and correlation-bound molecular anions. The binding energy of anions formed by electron attachment to closed-shell molecules is computed using the electron attachment variant of CC2 (EA-CC2), whereas anions with a closed-shell ground state are treated with the standard CC2 method that preserves the number of particles. We find that EA-CC2 captures the binding energies of dipole-bound radical anions quite well, whereas results for other types of non-valence anions are less reliable. We also test the performance of semi-empirical spin-scaling factors for all types of non-valence anions and observe that the spin-scaled CC2 variants generally do not provide more accurate binding energies for dipole-bound anions, while the binding energies of quadrupole-bound and correlation-bound anions are improved. As exemplary applications of EA-CC2, we investigate the dipole-bound anions of the steroids cortisol, progesterone, and testosterone. In addition, we characterize electron attachment to sym-tetracyanonaphthalene, a molecule that supports five anionic states, two of which can be interpreted as hitherto unobserved π-type quadrupole-bound states.

---

1 Introduction

The binding of an excess electron to a neutral molecule with positive electron affinity results in the formation of molecular anions, which can be categorized into valence anions and non-valence anions depending on the binding mechanism.^1,2 In valence anions, the extra electron occupies a compact valence orbital and short-range interactions dominate, whereas long-range interactions predominate in non-valence anions and the extra electron resides in a much more diffuse orbital. Among non-valence anions, one can distinguish dipole-bound states,^3–11 quadrupole-bound states,^12–17 and correlation-bound states.^18–25

In dipole-bound states, the excess electron is bound by interaction with the neutral molecule's large dipole moment and it has been established that there is a critical strength of the dipole of ca. 2.5 D for an extra electron to be bound,⁷ although a larger dipole moment is no guarantee that a dipole-bound anion exists. Quadrupole-bound states are formed by a similar electrostatic interaction as dipole-bound states, but with molecules that have a large quadrupole moment and zero dipole moment. Interestingly, it has been argued that a critical strength of the quadrupole moment for quadrupole-bound states to occur cannot been established.¹⁴ Finally, in correlation-bound anions the binding is not governed by electrostatic interactions but rather by dispersion. We add that there are many dipole-bound and quadrupole-bound states that are unbound if electron correlation is neglected, which makes the distinction between different types of non-valence anions debatable.²³

For all classes of molecular anions, the electron binding energy can vary substantially from less than 1 meV to several eVs. On average, however, valence anions are more strongly bound than non-valence anions. Also, there are numerous molecules that support a valence state alongside a non-valence state or, in other cases, the character of a state changes upon relaxation of the molecular structure. Non-valence anions are therefore believed to act as gateway to the capture of low-energy electrons and as precursors to the formation of valence anions.^1,2,26–37

As concerns the theoretical description of non-valence anions, it is well established that standard basis sets need to be augmented by additional shells of diffuse functions to capture the enormous extent of the wave function. In addition, a method that takes proper account of electron correlation is also important. While there are treatments based on a self-consistent field (SCF) wave function of the non-valence anionic state, for example using density functional theory,³⁸ it has been shown that approaches such as the equation-of-motion electron-attachment coupled-cluster (EOM-EA-CC) method^39,40 that base the description on an SCF wave function of the parent neutral molecule are especially well suited for non-valence anions. This applies in particular to correlation-bound anions, which are by definition unbound at the Hartree–Fock (HF) level of theory.^23,41

However, the application range of EOM-CC is limited because the computational cost and memory requirements scale with system size as N⁶ and N⁴, respectively, already in the singles and doubles approximation (EOM-CCSD). The problem is exacerbated for non-valence anions by the need to use large basis sets. An alternative to EOM-EA-CCSD that was successfully applied to correlation-bound anions^20–22,41 is EOM-EA-CCSD(2),⁴² also known as EOM-EA-MP2. For this method, the computational cost scales as N⁵, while the memory requirements are unchanged compared to EOM-EA-CCSD.

In this work, we explore the performance of the second-order approximate coupled-cluster singles and doubles method (CC2) for non-valence anions, which represents another alternative to EOM-EA-CCSD. CC2 is obtained from a perturbative analysis of the CCSD model and, in analogy to CCSD, it is possible to define a CC2 linear-response function whose poles correspond to the excitation energies.⁴³ The same CC2 excitation energies can alternatively be obtained in the spirit of the EOM-CC approach, where one considers the wave function of the excited target state explicitly. The computational cost of CC2 scales as N⁵ and the memory requirements can be reduced from N⁴ to N³ by applying the resolution-of-the-identity (RI) approximation or Cholesky decomposition to the electron-repulsion integrals.^44–46 As a consequence, CC2 and the closely related algebraic diagrammatic construction through second order (ADC(2))^47,48 are well established as excited-state methods for molecules beyond the application range of EOM-CCSD.

Besides the original CC2 method, where the excited target state and the reference state have the same number of α and β electrons, further CC2 methods have been introduced. This includes a spin–flip variant for the treatment of multiconfigurational wave functions⁴⁹ as well as ionization potential^50,51 (IP) and electron attachment⁵² (EA) variants in which the target state has one electron less or more, respectively, than the reference state. These latter variants can conveniently be obtained from the particle-number conserving method by means of the continuum orbital technique.⁵³

While the original CC2 method offers a good balance between accuracy and computational cost for valence excitations and, in some cases, even yields more accurate excitation energies than EOM-CCSD, the numerical performance of the IP-CC2 and EA-CC2 methods is not convincing. This shortcoming is related to the poor performance of CC2 for charge-transfer and Rydberg states. However, it was recently shown that spin scaling^54–57 improves ADC(2) results for vertical ionization energies and vertical electron attachment energies of valence anions considerably.⁵⁸ In view of the close connection between ADC(2) and CC2, the same improvements can be anticipated for CC2. It is, however, less clear a priori if attachment energies of non-valence anions are improved as well.

This latter question motivates the present study. In Section 2, we report the technical details of the computations that we carried out, while Section 3 discusses the numerical results for valence-bound, dipole-bound, quadrupole-bound, and correlation-bound anions. Our general conclusions are presented in Section 4.

2 Computational details

To assess the performance of RI-CC2 including its spin-scaled analogues for non-valence anions, we computed the vertical binding energies of different types of anionic states. The computations were carried out using a new implementation of RI-CC2 in the Q-Chem program package,⁵⁹ which is based on the formulation by Hättig and Weigend, in which the doubles amplitudes need not be stored.⁴⁴ Details of our implementation will be presented elsewhere.

Because RI-CC2 is an approximation to EOM-CCSD, we used the latter method to assess the accuracy of RI-CC2. The structures of all molecules were optimized with RI-MP2 using the cc-pVTZ basis set and the rimp2-cc-pVTZ auxiliary basis set and are provided in the ESI.† All CC2 and EOM-CCSD computations were done with the core electrons frozen. For the spin-scaled methods, we implemented the same scaling factors that were originally proposed for MP2 and are also used in the context of CC2 and ADC(2). For the spin-component scaling (SCS) method,⁵⁴ the values are c_ss = 1/3 and c_os = 6/5 for the same-spin and opposite-spin contributions, respectively, while they amount to c_ss = 0 and c_os = 1.3 for the scaled opposite-spin (SOS) method.⁵⁵

The vertical binding energies of the anionic states were determined using the following procedures:

• For valence radical anions of closed-shell neutral molecules, the binding energies were computed with EOM-EA-CCSD or RI-EA-CC2 with the aug-cc-pVTZ basis using the neutral ground state as CC reference state.

• For dipole-bound and quadrupole-bound radical anions of closed-shell neutral molecules, the same methods were combined with an aug-cc-pVTZ basis further augmented by 3 s-shells on hydrogen atoms and 6 s- and 3 p-shells on all non-hydrogen atoms.

• For correlation-bound radical anions of closed-shell neutral molecules, we used EOM-EA-CCSD and RI-EA-CC2 with an aug-cc-pVTZ + 7s7p basis set.²¹

• For excited dipole-bound states of closed-shell anions, we evaluated the binding energies as differences between EOM-IP-CCSD and EOM-EE-CCSD energies or RI-IP-CC2 and RI-CC2 energies. In this way, the CC treatment could be based on a closed-shell HF state. The same basis set as for dipole-bound radical anions was used.

The rimp2-cc-pVTZ auxiliary basis set was used for valence anions, while the rimp2-aug-cc-pVTZ auxiliary basis set was used for non-valence anions. To ensure that this latter auxiliary basis is appropriate for calculations in which additional diffuse functions are added to aug-cc-pVTZ, we carried out some calculations using larger auxiliary bases with additional diffuse functions. These yielded the same energies up to 10⁻⁶ a.u. The dipole moments and quadrupole moments of all molecules that support a corresponding anion were computed at the HF level using the same bases as in the correlated calculations. For selected anions, we additionally evaluated EOM-EA-CCSD Dyson orbitals.^60,61 Notably, we encountered in many calculations linear dependencies in the basis set as is typical when one uses many diffuse shells. We solve this problem by reorthogonalizing the basis set, which entails that the actual basis set is often smaller than what one would assume based on the information given above, in some cases by up to 20%. The number of orthogonal orbitals is given for each calculation in the ESI.† All calculations were carried out using the Q-Chem program package, version 6.0.⁵⁹ The irreducible representations of all states are reported according to Q-Chem convention, which differs from Mulliken's convention.⁶²

3 Results and discussion

3.1 Valence anions

We first investigated a set of 12 organic molecules that support conventional anions in which the excess electron resides in a valence orbital. This test set forms a subset of the one from ref. 58. The binding energies computed with EOM-EA-CCSD and RI-EA-CC2 are reported in Table 1. Our results illustrate that RI-EA-CC2 overestimates all electron affinities significantly with respect to EOM-EA-CCSD and that spin-scaling largely eliminates that shortcoming. The mean absolute error is reduced from 0.47 eV for RI-EA-CC2 to 0.07 eV for SCS-RI-EA-CC2. A very similar conclusion was drawn in ref. 58 about the accuracy of spin-scaled EA-ADC(2) with respect to CCSD(T) reference values. We note, however, that the CC2 results from Table 1 do not coincide with those from ref. 58 because an aug-cc-pVDZ basis was used there while we use aug-cc-pVTZ. Also, it is apparent from Table 1 that Koopmans' theorem captures only the most strongly bound anions that have an electron affinity of more than ca. 1.4 eV.

Table 1 Electron binding energies of valence anions computed using RI-EA-CC2, EOM-EA-CCSD, and Koopmans' theorem (KT). Energies are given in eV with a positive value corresponding to an electronically bound anion

Molecule		EOM-	RI-	SCS-RI-	SOS-RI-
		EA-CCSD	EA-CC2	EA-CC2	EA-CC2	KT
Tetrafluorobenzoquinone	C6F4O2	2.329	2.805	2.328	2.085	0.980
Benzoquinone	C6H4O2	1.540	2.016	1.534	1.288	0.082
1,4-Naphthoquinone	C10H6O2	1.424	1.955	1.489	1.254	−0.136
p-Nitrobenzonitrile	NC–C6H4–NO2	1.362	1.741	1.364	1.174	0.002
Phenazine	(C6H4)2N2	1.077	1.575	1.213	1.030	−0.435
Maleic anhydride	C4H2O3	1.006	1.439	0.990	0.764	−0.463
Fumaronitrile	C4H2N2	0.946	1.381	0.954	0.738	−0.408
Phthalic anhydride	C6H4(CO)2O	0.824	1.304	0.915	0.720	−0.762
Acridine	C13H9N	0.637	1.133	0.770	0.585	−0.898
Isophthalonitrile	C6H4(CN)2	0.628	1.089	0.748	0.576	−0.844
Phthalimide	C6H4(CO)2NH	0.579	1.063	0.666	0.468	−1.034
Azulene	C10H8	0.519	0.980	0.669	0.512	−1.034
Mean absolute error			0.468	0.068	0.140	1.485

---

Interestingly, two recent studies^63,64 reported substantially better performances for the EA-ADC(2) method with average deviations of ca. 0.1 eV from CCSD(T) and full CI. This difference to our results can be ascribed to two reasons: Firstly, our test set and that from ref. 58 only comprise bound electronic states, while the test sets from ref. 63 and 64 additionally include states in the detachment continuum, whose binding energy approaches zero in the limit of a full basis set. Secondly, our test set is formed by polyatomic molecules with up to 15 non-hydrogen atoms, whereas the two previous studies focused on diatomic and triatomic molecules. To address the latter point, we performed some additional RI-EA-CC2 calculations on valence anions of diatomic and triatomic molecules.⁶⁵ For these species, we indeed observe a better performance of RI-EA-CC2 with deviations from EOM-EA-CCSD in the range of 0.2 to 0.3 eV. However, we believe that the larger species from Table 1 are more representative of the application area of the RI-EA-CC2 method than diatomic and triatomic molecules.

3.2 Dipole-bound radical anions

As a second test set, we investigated 15 organic molecules that support dipole-bound radical anions. Notably, 6 of them (uracil, nitrobenzene, benzonitrile, nitromethane, benzaldehyde, acetone) also form a valence anion that is bound either vertically or at least adiabatically. The binding energies of the dipole-bound states computed with EOM-EA-CCSD and RI-EA-CC2 are reported in Table 2. Although the binding energies of dipole-bound anions are in general much smaller than those of valence anions, Table 2 shows that the values can vary over a wide range, from less than 1 meV for acetone to up to almost 80 meV for uracil within our test set. It is also apparent from Table 2 that the binding energy is only loosely connected to the strength of the dipole moment. For example, vinylene carbonate has a somewhat larger dipole moment than uracil but the binding energy of the anion is three times lower.

Table 2 Electron binding energies of dipole-bound radical anions computed using RI-EA-CC2, EOM-EA-CCSD, and Koopmans' theorem (KT). Energies are given in meV with a positive value corresponding to an electronically bound anion. Dipole moments in Debye computed at the HF level of theory are also given

Molecule		EOM-	RI-	SCS-RI-	SOS-RI-	KT	μ (D)
		EA-CCSD	EA-CC2	EA-CC2	EA-CC2
Uracil	C4H4N2O2	76.5	80.8	58.2	47.2	22.7	4.305
Nitrobenzene	C6H5NO2	25.7	34.8	17.1	13.8	5.4	4.436
Vinylene carbonate	C3H2O3	25.5	26.7	19.8	17.0	10.0	4.601
Benzonitrile	C6H5CN	23.8	19.8	14.7	12.1	3.2	4.540
Pyridazine	C4H4N2	19.0	26.3	15.3	10.2	1.7	4.254
Acetonitrile	CH3CN	18.4	17.2	12.3	9.9	4.2	3.948
Formamide	CH3NO	15.7	16.2	10.7	8.7	3.4	3.896
Dimethyl sulfoxide	(CH3)2SO	14.9	12.1	8.8	7.1	2.1	4.140
Nitromethane	CH3NO2	13.7	12.6	8.7	6.8	3.5	3.598
N,N-Dimethylformamide	(CH3)2NCHO	13.4	10.9	8.6	6.7	1.9	4.216
Phenyl isocyanide	C6H5NC	9.1	16.3	6.3	3.4	−4.9	4.077
Methyl isocyanide	CH3NC	8.9	10.0	6.0	4.5	−1.8	3.921
Nitrosobenzene	C6H5NO	5.9	11.4	3.1	0.7	−4.1	3.355
Benzaldehyde	C6H5CHO	4.1	8.9	1.6	−0.6	−4.9	3.228
Acetone	(CH3)2CO	0.8	1.3	−1.9	−3.1	−5.1	3.003
Mean absolute error			3.5	5.7	8.7	15.9

---

As concerns the comparison of the different methods, Table 2 shows that RI-EA-CC2 deviates from EOM-EA-CCSD on average by only 3.5 meV and never by more than 9 meV. In 10 cases, RI-EA-CC2 gives too high a value, in 5 cases too low a value. Notably, there is no single case in Table 2 in which RI-EA-CC2 fails to produce a positive binding energy. The method thus performs much better for dipole-bound anions than for valence anions (see Table 1). Spin-scaling, however, does not represent an improvement, the SCS and SOS variants of RI-EA-CC2 underestimate the binding energy systematically and the mean absolute error with respect to EOM-EA-CCSD is also larger as compared to unscaled RI-EA-CC2.

Whereas the step from EOM-EA-CCSD to RI-EA-CC2 apparently does not compromise the quality of the computed binding energies, Table 2 also illustrates that electron correlation and orbital relaxation cannot be neglected altogether for dipole-bound anions. According to Koopmans' theorem, i.e., using the energy of the lowest unoccupied molecular orbital as an estimate of the binding energy, all those anions that have an EOM-EA-CCSD binding energy of less than 10 meV become unbound. But also in the more strongly bound cases, Koopmans' theorem underestimates the binding energy considerably and captures, for example, in the case of nitrobenzene only 20%.

To illustrate the usefulness of RI-EA-CC2 for studying dipole-bound anions in larger molecules, we investigated electron attachment to the steroids testosterone, progesterone, and cortisol. These molecules have considerable dipole moments of 4–7 D so that the presence of a dipole-bound anion appears plausible. Yet, to the best of our knowledge, the electron affinity of these compounds has so far not been investigated, neither experimentally nor computationally.

Our calculations on these molecules use between 2009 and 2366 basis functions, which is beyond the range of EOM-EA-CCSD for a molecule in the C₁ point group but entirely feasible with RI-EA-CC2. Our results in Fig. 1 show that RI-EA-CC2 yields binding energies between 30 and 80 meV with the largest value obtained for cortisol, which also has the largest dipole moment. Interestingly, however, the electron affinities of testosterone and progesterone are almost identical even though the dipole moment of progesterone is 1.45-times larger. This demonstrates again that the binding energy of dipole-bound anions depends only loosely on the dipole moment as already discussed for Table 2.

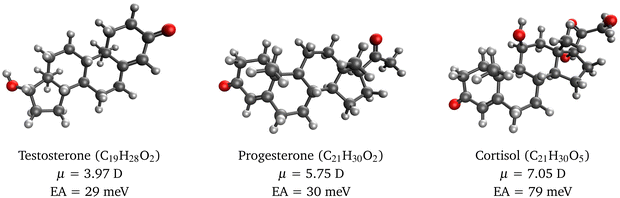Fig. 1 Molecular structures of selected steroids, their dipole moments, and electron affinities of the corresponding dipole-bound radical anions computed with RI-EA-CC2.

Finally, it is noteworthy that the equilibrium structures of dipole-bound anions are, in general, almost identical to those of the parent neutral molecules.^1,2 This implies that the differences between the vertical electron affinity, the vertical detachment energy, and the adiabatic electron affinity are negligible and the good performance of RI-EA-CC2 apparent from Table 2 applies to all three quantities.

3.3 Excited dipole-bound states of closed-shell anions

As a third test set we investigated closed-shell anions that support an excited dipole-bound state. This type of dipole-bound state is less common than the one discussed in Section 3.2 and the binding energies are typically lower. Our results for the binding energies of 4 such states computed with EOM-CCSD and RI-CC2 are summarized in Table 3. It is obvious that CC2 is unsuited as we obtain negative binding energies for all 4 examples. Spin-scaled CC2 does not yield better binding energies although the underlying RI-EE-CC2 and RI-IP-CC2 energies are significantly improved. Notably, EOM-CCSD also fails to reproduce the experimentally determined binding energies^9,66,67 and produces values that are consistently too low. A higher-order coupled-cluster method such as EOM-CCSDT is likely needed to fully recover the binding energies of the test cases from Table 3 or other examples with even lower binding energy.

Table 3 Electron binding energies (eBE) of excited dipole-bound states of closed-shell anions computed using RI-EE-CC2 and RI-IP-CC2 as well as EOM-EE-CCSD and EOM-IP-CCSD. Energies are given in meV with positive values corresponding to electronically bound states. Experimental binding energies and dipole moments in Debye of the anionic ground states computed at the HF level of theory are also given

Molecule		EOM-CCSD			RI-CC2			SCS-RI-CC2			SOS-RI-CC2			Expt.
		EE	IP	eBE	EE	IP	eBE	EE	IP	eBE	EE	IP	eBE	eBE	μ (D)
2-Naphthoxide	C10H7O^−	2404	2440	13.4	1978	1909	−69.2	2100	2036	−63.9	2162	2101	−61.4	25.0^66	7.676
9-Anthroxide	C14H9O^−	2217	2226	8.9	1870	1800	−69.9	1998	1934	−64.2	2065	2004	−61.2	23.7^9	3.746
Phenoxide	C6H5O^−	1527	1525	7.6	1016	937	−71.0	1103	1024	−65.8	1148	1068	−63.1	12.0^67	5.008
Cyanomethyl anion	CH2CN^−	1776	1778	1.4	1376	1312	−63.9	1482	1419	−62.6	1536	1474	−61.9		1.667

---

3.4 Quadrupole-bound anions

Next, we studied a set of 6 organic molecules that support quadrupole-bound radical anions. Interestingly, all of them except succinonitrile also support a valence anion and p-dinitrobenzene and tetracyanobenzene even support two valence anion states. The binding energies computed with EOM-EA-CCSD and RI-EA-CC2 are reported in Table 4. Similar to dipole-bound anions, the binding energies of quadrupole-bound states can vary over a wide range, from 1 meV for p-diisocyanobenzene to more than 170 meV for tetracyanobenzene, which is more than twice the largest binding energy of the dipole-bound anions from Table 2. We observe that the connection between the strength of the quadrupole moment and the binding energy is weak. Succinonitrile and p-diisocyanobenzene, for example, have similar quadrupole moments but the binding energy of the former anion is ten times larger.

Table 4 Electron binding energies of quadrupole-bound anions and valence anions computed using RI-EA-CC2, EOM-EA-CCSD, and Koopmans' theorem (KT). Energies are given in meV with a positive value corresponding to an electronically bound anion. Experimental binding energies and quadrupole moments in Debye·Ångström computed at the HF level of theory are also given

Molecule		State	EOM-	RI-EA-	SCS-RI-	SOS-RI-	KT	Expt.	Q xx	Q yy	Q zz
			EA-CCSD	CC2	EA-CC2	EA-CC2
Succinonitrile	C4H4N2	Ag	10.0	25.7	0.2	−4.6	−10.9	22.0^13/18.0^16	−20.69	5.93	14.76
Terephthalonitrile	C6H4(CN)2	Ag	23.6	59.3	14.7	3.6	−10.5		−27.61	14.94	12.67
p-Diisocyanobenzene	C6H4(NC)2	Ag	1.1	14.5	−2.5	−5.8	−11.6		−20.48	12.53	7.95
p-Dinitrobenzene	C6H4(NO2)2	Ag	7.0	33.5	1.9	−4.0	−11.3	25.0^27	−23.52	8.56	14.96
2,6-Dicyanonaphthalene	C10H6(CN)2	Ag	46.1	95.0	36.3	18.4	−8.2		−38.69	21.05	17.64
Tetracyanobenzene	C6H2(CN)4	Ag	171.6	321.6	167.0	107.9	−7.7	220.6^17	−31.94	3.12	28.82
Mean absolute error				48.4	7.0	24.0	53.3
Terephthalonitrile	C6H4(CN)2	B1u	905.2	1342.9	1001.1	828.5	−151.3
p-Diisocyanobenzene	C6H4(NC)2	B1u	385.8	820.5	476.3	304.0	−157.6
p-Dinitrobenzene	C6H4(NO2)2	B2g	100.1	513.1	110.3	−88.2	−11.3
		B1u	1650.9	1990.6	1603.4	1409.1	366.9
2,6-Dicyanonaphthalene	C10H6(CN)2	Bg	1135.4	1637.9	1274.1	1089.3	−247.8
Tetracyanobenzene	C6H2(CN)4	B1u	1610.3	2245.4	1850.3	1651.0	−27.4
		Au	2407.9	2939.5	2559.7	2366.7	971.1	2469.5^17
Mean absolute error				470.6	110.7	102.4	1098.6

---

To further characterize the quadrupole-bound states, we computed their Dyson orbitals with EOM-EA-CCSD. The plots in Fig. 2 show that the excess electron resides in a diffuse s-like orbital in each case. There is a weak trend between the size of the orbital and the binding energy: For the anions of 2,6-dicyanonaphthalene and in particular tetracyanobenzene, which have larger binding energies than the other quadrupole-bound anions, the Dyson orbital is somewhat more compact.

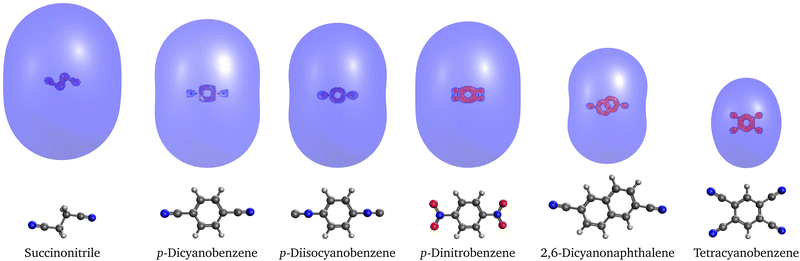Fig. 2 Dyson orbitals of quadrupole-bound anions of selected molecules computed with EOM-EA-CCSD and plotted at an isovalue of 0.001.

As concerns the performance of the different methods, the results for the valence states in Table 4 are by and large in line with those from Table 1. For the quadrupole-bound states, we observe that RI-EA-CC2 consistently overestimates the binding energies compared to EOM-EA-CCSD, on average by almost 50 meV. RI-EA-CC2 performs thus worse for quadrupole-bound anions than for dipole-bound anions for which the average deviation amounts to no more than 3.5 meV (see Table 2). Spin-scaling improves the RI-EA-CC2 results considerably; for the SCS variant the average deviation from EOM-EA-CCSD goes down to 7 meV. This picture changes when a comparison is made to experimentally determined binding energies. EOM-EA-CCSD underestimates them for succinonitrile, p-dinitrobenzene, and tetracyanobenzene alike, while the RI-EA-CC2 method without spin scaling gives a much better match. Finally, we note that according to Koopmans' theorem none of the 6 quadrupole-bound states from Table 4 is bound, which means that orbital relaxation and electron correlation are more important for quadrupole-bound anions than for dipole-bound anions.

3.5 The five anionic states of sym-tetracyanonaphthalene

In view of its large quadrupole moment (Q_xx = −55.39 D Å, Q_yy = 12.78 D Å, Q_zz = 42.61 D Å, computed with HF/aug-cc-pVTZ + 6s3p), the formation of a quadrupole-bound anion seems plausible for sym-tetracyanonaphthalene. This is indeed the case but we choose to discuss our results for this molecule separately because of its unique electronic structure, which to the best of our knowledge has hitherto not been studied. As Table 5 demonstrates, there are 5 anionic states in sym-tetracyanonaphthalene, which is remarkable given that most organic molecules support only one or, at most, two bound anionic states. The different nature of the 5 states is revealed by the EOM-EA-CCSD Dyson orbitals shown in Fig. 3. Whereas the two lowest-lying states (B_2g and B_3g) with large binding energies of 2.13 eV and 1.96 eV have valence character as indicated by their compact Dyson orbitals, the remaining three states (B_1u, A_g, B_2u) with much smaller binding energies of 0.29 eV, 0.25 eV, and 0.02 eV and more diffuse Dyson orbitals are clearly non-valence anions. Interestingly, the extent of the Dyson orbitals is again correlated with the binding energy.

Table 5 Electron binding energies of the five anionic states of sym-tetracyanonaphthalene computed using RI-EA-CC2, EOM-EA-CCSD, and Koopmans' theorem. Energies are given in meV with a positive value corresponding to an electronically bound anion

State	EOM-	RI-	SCS-RI-	SOS-RI-	KT
	EA-CCSD	EA-CC2	EA-CC2	EA-CC2
B2g	2128.9	2746.0	2338.2	2130.6	496.1
B3g	1962.7	2490.0	2133.3	1952.0	435.8
B1u	288.8	957.3	559.1	366.1	−94.4
Ag	247.2	394.1	243.3	181.8	10.4
B2u	18.0	71.3	7.4	−8.4	−20.0

---

Fig. 3 Dyson orbitals of the five anionic states of sym-tetracyanonaphthalene computed with EOM-EA-CCSD and plotted at an isovalue of 0.001. From left to right, the B_2g B_3g, B_1u, A_g, and B_2u states are shown.

The A_g state can be interpreted as a quadrupole-bound anion comparable to those discussed in Section 3.4, but this is not possible for the B_1u and B_2u states because their Dyson orbitals have nodal planes containing or bisecting the molecule, respectively. We propose to view the B_1u and B_2u anion states of sym-tetracyanonaphthalene as π-type quadrupole-bound anions akin to π-type dipole-bound anions,^4,68,69 which were experimentally confirmed only recently.^9,70,71 The comparison to the quadrupole-bound states from Table 4 illustrates that the B_1u and A_g states of sym-tetracyanonaphthalene have exceptionally large binding energies, but also the B_2u state is more strongly bound than, for example, the quadrupole-bound states of succinonitrile and p-dinitrobenzene.

As concerns the performance of RI-EA-CC2, Table 5 shows the same pattern discussed in Sections 3.1 and 3.4. While the ordering of the states is preserved, all binding energies are overestimated by 50 to 670 meV. Spin scaling remedies this problem to a large degree: SOS-RI-EA-CC2 recovers the EOM-EA-CCSD result up to 10 meV for the valence states and up to 70 meV for the B_1u and A_g quadrupole-bound states but fails to capture the B_2u state. Also, it is noteworthy that according to Koopmans’ theorem, only the two valence anion states and the totally symmetric quadrupole-bound state exist. The π-like B_1u and B_2u quadrupole-bound states of sym-tetracyanonaphthalene only become visible when orbital relaxation and electron correlation are accounted for.

On the basis of the discussion in Section 3.4, one may assume that EOM-EA-CCSD underestimates the binding energies of the quadrupole-bound states of sym-tetracyanonaphthalene as well and that the RI-EA-CC2 results are closer to the true values. This remains, however, speculation until electron attachment to sym-tetracyanonaphthalene has been characterized experimentally.

3.6 Correlation-bound anions

As a final test set, we studied the 4 molecules shown in Fig. 4 that support correlation-bound anions. The electron binding energies computed with EOM-EA-CCSD and RI-EA-CC2 are reported in Table 6. Notably, perfluorocubane has a much larger electron affinity than the other molecules, which has been explained by the cage-like structure of the molecule and an effect called σ-stellation.²⁵

Fig. 4 Selected molecules that support correlation-bound anions.

Table 6 Electron binding energies of correlation-bound anions computed with RI-EA-CC2 and EOM-EA-CCSD. Energies are given in meV with positive values corresponding to electronically bound states

Molecule	EOM-	RI-	SCS-RI-	SOS-RI-
	EA-CCSD	EA-CC2	EA-CC2	EA-CC2
C6F6	79.6	361.7	77.4	11.6
C6Cl6	67.7	637.3	136.9	14.3
C10F8	71.3	279.9	70.2	17.3
C8F8	1027.1	1675.4	1076.9	790.4

---

It is apparent from Table 6 that RI-EA-CC2 overestimates all binding energies greatly, in the case of hexachlorobenzene by a factor of almost 10. SOS-RI-EA-CC2 overcorrects that problem and yields energies that are consistently too low, while SCS-RI-EA-CC2 yields accurate energies for the perfluorinated compounds but overestimates the EOM-EA-CCSD result for hexachlorobenzene still by a factor of 2.

4 Conclusions

We explored the performance of the CC2 method for the computation of vertical binding energies of various types of molecular anions. For our test set of 12 valence anions, RI-EA-CC2 yields a mean absolute error with respect to EOM-EA-CCSD of 0.47 eV that can be reduced to 0.07 eV and 0.14 eV using SCS-RI-EA-CC2 and SOS-RI-EA-CC2, respectively, which is very well in line with recent ADC(2) results.⁵⁸

For non-valence anions, different trends are observed: RI-EA-CC2 performs well for dipole-bound radical anions with a mean absolute deviation from EOM-EA-CCSD of only 3.5 meV. Also, all states that are bound at the EOM-EA-CCSD level of theory stay bound with RI-EA-CC2. For excited dipole-bound states of closed-shell anions, however, a combination of RI-CC2 and RI-IP-CC2 yields poor results for the binding energies. Given that all states in our test set become unbound at the RI-CC2 level, this approach cannot be recommended. For quadrupole-bound anions, RI-EA-CC2 overestimates EOM-EA-CCSD binding energies by ca. 50 meV, which is too high for accurate modelling given that quadrupole-bound states usually have binding energies in the same range. A much more pronounced overestimation is observed for correlation-bound anions so that RI-CC2 cannot be recommended for this type of state either.

The spin-scaled CC2 variants do not present an improvement for dipole-bound states, but they do in general improve binding energies of quadrupole-bound and correlation-bound states. SCS-RI-EA-CC2 yields a mean absolute deviation from EOM-EA-CCSD of only 7 meV for quadrupole-bound states, although the method fails to produce a positive binding energy for the anion of p-diisocyanobenzene that is bound by 1 meV at the EOM-EA-CCSD level. For correlation-bound anions, SCS-RI-EA-CC2 improves binding energies considerably even though that of the anion of hexachlorobenzene is still overestimated by a factor of 2 as compared to EOM-EA-CCSD.

In sum, we can recommend without reservation the unscaled RI-EA-CC2 method for the study of dipole-bound radical anions, whereas SCS-RI-EA-CC2 is possibly useful for quadrupole-bound and correlation-bound anions. We illustrated the application area that we envision for RI-EA-CC2 by computing the binding energies of the dipole-bound anions of testosterone, progesterone, and cortisol. Judging by their dipole moments, many molecules in this size range should support dipole-bound anions and it appears reasonable to assume that they can act as doorway states similar to what is established for small molecules.

Finally, our work illustrates that there are still new types of molecular anions to be discovered. Specifically, we showed that sym-tetracyanonaphthalene supports a total of 5 anionic states, two of which we interpret as π-type quadrupole-bound states, which have not been identified in other molecules before.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Xintian Feng for help with the implementation of the RI-CC2 method in the Q-Chem program package. T.-C. J. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant 851766) and from the KU Leuven internal funds (grant C14/22/083).

Notes and references

1. J. D. Simons, J. Phys. Chem. A, 2008, 112, 6401–6511.
2. J. D. Simons, J. Phys. Chem. A, 2023, 127, 3940–3957.
3. E. Fermi and E. Teller, Phys. Rev., 1947, 72, 399–408.
4. R. F. Wallis, R. Herman and H. W. Milnes, J. Mol. Spectrosc., 1960, 4, 51–74.
5. C. Desfrançois, H. Abdoul-Carime and J.-P. Schermann, Int. J. Mod. Phys. B, 1996, 10, 1339–1395.
6. M. Gutowski, P. Skurski, A. I. Boldyrev, J. Simons and K. D. Jordan, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 1906.
7. K. D. Jordan and F. Wang, Annu. Rev. Phys. Chem., 2003, 54, 367–396.
8. C.-H. Qian, G.-Z. Zhu and L.-S. Wang, J. Phys. Chem. Lett., 2019, 10, 6472–6477.
9. D.-F. Yuan, Y. Liu, C.-H. Qian, Y.-R. Zhang, B. M. Rubenstein and L.-S. Wang, Phys. Rev. Lett., 2020, 125, 073003.
10. S. Slimak and K. D. Jordan, J. Phys. Chem. Lett., 2022, 13, 10331–10334.
11. D.-F. Yuan, Y. Liu, Y.-R. Zhang and L.-S. Wang, J. Am. Chem. Soc., 2023, 145, 5512–5522.
12. K. D. Jordan and J. F. Liebman, Chem. Phys. Lett., 1979, 62, 143–147.
13. C. Desfrançois, Y. Bouteiller, J. Schermann, D. Radisic, S. Stokes, K. Bowen, N. Hammer and R. Compton, Phys. Rev. Lett., 2004, 92, 083003.
14. T. Sommerfeld, K. M. Dreux and R. Joshi, J. Phys. Chem. A, 2014, 118, 7320–7329.
15. G.-Z. Zhu, Y. Liu and L.-S. Wang, Phys. Rev. Lett., 2017, 119, 023002.
16. G. Liu, S. M. Ciborowski, J. D. Graham, A. M. Buytendyk and K. H. Bowen, J. Chem. Phys., 2019, 151, 101101.
17. Y. Liu, G.-Z. Zhu, D.-F. Yuan, C.-H. Qian, Y.-R. Zhang, B. M. Rubenstein and L.-S. Wang, J. Am. Chem. Soc., 2020, 142, 20240–20246.
18. T. Sommerfeld, B. Bhattarai, V. P. Vysotskiy and L. S. Cederbaum, J. Chem. Phys., 2010, 133, 114301.
19. V. G. Bezchastnov, V. P. Vysotskiy and L. S. Cederbaum, Phys. Rev. Lett., 2011, 107, 133401.
20. V. K. Voora, L. S. Cederbaum and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 849–853.
21. V. K. Voora and K. D. Jordan, J. Phys. Chem. A, 2014, 118, 7201–7205.
22. V. K. Voora and K. D. Jordan, J. Phys. Chem. Lett., 2015, 6, 3994–3997.
23. V. K. Voora, A. Kairalapova, T. Sommerfeld and K. D. Jordan, J. Chem. Phys., 2017, 147, 214114.
24. S. M. Ciborowski, R. M. Harris, G. Liu, C. J. Martinez-Martinez, P. Skurski and K. H. Bowen, J. Chem. Phys., 2019, 150, 161103.
25. M. P. Krafft and J. G. Riess, Science, 2022, 377, 709.
26. J. Hendricks, S. Lyapustina, H. De Clercq and K. Bowen, J. Chem. Phys., 1998, 108, 8–11.
27. C. Desfrancois, V. Periquet, S. Lyapustina, T. Lippa, D. Robinson, K. Bowen, H. Nonaka and R. Compton, J. Chem. Phys., 1999, 111, 4569–4576.
28. T. Sommerfeld, Phys. Chem. Chem. Phys., 2002, 4, 2511–2516.
29. T. Sommerfeld, J. Phys. Chem. A, 2004, 108, 9150–9154.
30. T. Sommerfeld, J. Phys.: Conf. Ser., 2005, 4, 245–250.
31. T. Sommerfeld, J. Chem. Phys., 2007, 126, 124301.
32. E. F. Belogolova, G. Liu, E. P. Doronina, S. M. Ciborowski, V. F. Sidorkin and K. H. Bowen, J. Phys. Chem. Lett., 2018, 9, 1284–1289.
33. G. Liu, S. M. Ciborowski, C. R. Pitts, J. D. Graham, A. M. Buytendyk, T. Lectka and K. H. Bowen, Phys. Chem. Chem. Phys., 2019, 21, 18310–18315.
34. S. Gulania, T.-C. Jagau, A. Sanov and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 5002–5010.
35. J. R. R. Verlet, C. S. Anstöter, J. N. Bull and J. P. Rogers, J. Phys. Chem. A, 2020, 124, 3507–3519.
36. D. H. Kang, J. Kim, H. J. Eun and S. K. Kim, Acc. Chem. Res., 2022, 55, 3032–3042.
37. S. Z. Hassan, J. Tauch, M. Kas, M. Nötzold, H. L. Carrera, E. S. Endres, R. Wester and M. Weidemüller, Nat. Commun., 2022, 13, 818.
38. G. Thiam and F. Rabilloud, J. Chem. Theory Comput., 2023, 19, 2842–2849.
39. M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 3629–3647.
40. I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, Cambridge, UK, 2009.
41. V. P. Vysotskiy, L. S. Cederbaum, T. Sommerfeld, V. K. Voora and K. D. Jordan, J. Chem. Theory Comput., 2012, 8, 893–900.
42. J. F. Stanton and J. Gauss, J. Chem. Phys., 1995, 103, 1064–1076.
43. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
44. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
45. T. B. Pedersen, A. M. J. Sánchez de Merás and H. Koch, J. Chem. Phys., 2004, 120, 8887–8897.
46. C. Hättig, in Computational Nanoscience: Do It Yourself! ed. J. Grotendorst, S. Blügel and D. Marx, John von Neumann Institute for Computing, 2006, vol. 31, pp. 245–278.
47. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
48. A. Dreuw, A. Papapostolou and A. L. Dempwolff, J. Phys. Chem. A, 2023, 127, 6635–6646.
49. G. P. Paran, C. Utku and T.-C. Jagau, Phys. Chem. Chem. Phys., 2022, 24, 27146–27156.
50. G. Wälz, D. Usvyat, T. Korona and M. Schütz, J. Chem. Phys., 2016, 144, 084117.
51. A. K. Dutta, N. Vaval and S. Pal, Int. J. Quantum Chem., 2018, 118, e25594.
52. F. Ma, Z. Wang, M. Guo and F. Wang, J. Chem. Phys., 2020, 152, 124111.
53. J. F. Stanton and J. Gauss, J. Chem. Phys., 1999, 111, 8785–8788.
54. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
55. Y. Jung, R. C. Lochan, A. D. Dutoi and M. Head-Gordon, J. Chem. Phys., 2004, 121, 9793–9802.
56. A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127.
57. S. Grimme, L. Goerigk and R. Fink, WIREs Comput. Mol. Sci., 2012, 2, 886–906.
58. A. Shaalan Alag, D. P. Jelenfi, A. Tajti and P. G. Szalay, J. Chem. Theory Comput., 2022, 18, 6794–6801.
59. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, A. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
60. C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106.
61. T.-C. Jagau and A. I. Krylov, J. Chem. Phys., 2016, 144, 054113.
62. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1997–2011.
63. S. Banerjee and A. Y. Sokolov, J. Chem. Phys., 2019, 151, 224112.
64. A. L. Dempwolff, A. M. Belogolova, A. B. Trofimov and A. Dreuw, J. Chem. Phys., 2021, 154, 104117.
65. T.-C. Jagau, J. Chem. Phys., 2018, 148, 024104.
66. C.-H. Qian, G.-Z. Zhu, Y.-R. Zhang and L.-S. Wang, J. Chem. Phys., 2020, 152, 214307.
67. H.-T. Liu, C.-G. Ning, D.-L. Huang, P. D. Dau and L.-S. Wang, Angew. Chem., Int. Ed., 2013, 125, 9146–9149.
68. V. K. Voora and K. D. Jordan, Nano Lett., 2014, 14, 4602–4606.
69. A. Kairalapova, K. D. Jordan, M. F. Falcetta, D. K. Steiner, B. L. Sutter and J. S. Gowen, J. Phys. Chem. B, 2019, 123, 9198–9205.
70. D.-F. Yuan, Y.-R. Zhang, C.-H. Qian, Y. Liu and L.-S. Wang, J. Phys. Chem. A, 2021, 125, 2967–2976.
71. Y. Lu, R. Tang and C. Ning, J. Phys. Chem. Lett., 2021, 12, 5897–5902.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized molecular structures, Dyson orbitals, and basis-set details. See DOI: https://doi.org/10.1039/d3cp05923e

---