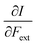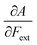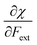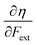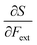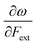Wandering through quantum-mechanochemistry: from concepts to reactivity and switches
Mercedes
Alonso
 *,
Tom
Bettens
*,
Tom
Bettens
 ,
Jochen
Eeckhoudt
,
Jochen
Eeckhoudt
 ,
Paul
Geerlings
,
Paul
Geerlings
 and
Frank
De Proft
and
Frank
De Proft
 *
*
Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: mercedes.alonso.giner@vub.be; fdeprof@vub.be
First published on 12th December 2023
Abstract
Mechanochemistry has experienced a renaissance in recent years witnessing, at the molecular level, a remarkable interplay between theory and experiment. Molecular mechanochemistry has welcomed a broad spectrum of quantum-chemical methods to evaluate the influence of an external mechanical force on molecular properties. In this contribution, an overview is given on recent work on quantum mechanochemistry in the Brussels Quantum Chemistry group (ALGC). The effect of an external force was scrutinized both in fundamental topics, like reactivity descriptors in Conceptual DFT, and in applied topics, such as designing molecular force probes and tuning the stereoselectivity of certain types of reactions. In the conceptual part, a brief overview of the techniques introducing mechanical forces into a quantum-mechanical description of a molecule is followed by an introduction to conceptual DFT. The evolution of the electronic chemical potential (or electronegativity), chemical hardness and electrophilicity are investigated when a chemical bond in a series of diatomics is put under mechanical stress. Its counterpart, the influence of mechanical stress on bond angles, is analyzed by varying the strain present in alkyne triple bonds by applying a bending force, taking the strain promoted alkyne–azide coupling cycloaddition as an example. The increase of reactivity of the alkyne upon bending is probed by Fukui functions and the local softness. In the applied part, a new molecular force probe is presented based on an intramolecular 6π-electrocyclization in constrained polyenes operating under thermal conditions. A cyclic process is conceived where ring opening and closure are triggered by applying or removing an external pulling force. The efficiency of mechanical activation strongly depends on the magnitude of the applied force and the distance between the pulling points. The idea of pulling point distances as a tool to identify new mechanochemical processes is then tested in [28]hexaphyrins with an intricate equilibrium between Möbius aromatic and Hückel antiaromatic topologies. A mechanical force is shown to trigger the interconversion between the two topologies, using the distance matrix as a guide to select appropriate pulling points. In a final application, the Felkin-Anh model for the addition of nucleophiles to chiral carbonyls under the presence of an external mechanical force is scrutinized. By applying a force for restricting the conformational freedom of the chiral ketone, otherwise inaccessible reaction pathways are promoted on the force-modified potential energy surfaces resulting in a diastereoselectivity different from the force-free reaction.
1. Introduction
Synthetic chemists are continuously updating their portfolio to increase the rate and steer the outcome of chemical reactions, in most cases by supplying energy in one or another form. Traditional approaches, each of them giving rise to a specific nomenclature of the resulting branch of chemistry, involve heat (thermochemistry), radiation (photochemistry), electric current (electrochemistry) and mechanical energy (mechanochemistry) (for a recent review, see ref. 1). Mankind has been aware for a very long time of the unique and fascinating outcomes in the latter field involving “the direct absorption of mechanical energy” according to IUPAC.2 Although already documented by Theophrastus (describing the formation of the liquid metal mercury by grinding cinnabar, a mineral of mercuric sulfide, in vinegar with a copper pestle and mortar3), the field has known hardly any progress for many centuries. However, in the 19th century, a revival can be noticed with the use of grinding techniques evolving to the present-day status with for example ball milling techniques allowing to gain control of the reaction conditions and obtain reproducible results. This renaissance of mechanochemistry4–7 has witnessed remarkable sustainability features, not requiring the use of solvents and reducing the generation of waste and pollution.1 It should however be recognized that still a veil of mystery is surrounding the way these mechanochemical transformations occur at the molecular level due to the bulk aspect of the aforementioned classical techniques.The introduction of the atomic force microscopy (AFM) technique has been a crucial step in understanding the effect of a mechanical force on a single molecule.8 Other ingenious experimental set ups were designed for example by incorporating a target molecule into polymer chains, allowing the transfer of mechanical force to the target molecule, thereby initiating a chemical transformation.6 The molecular level is then reached opening the gate to investigate the mechanical effect on the properties and reactions of an individual molecule, in contrast to the “classical” bulk mechanochemistry. These single-molecule mechanochemical experiments launched a subfield of mechanochemistry: molecular mechanochemistry, sometimes also called covalent mechanochemistry.3,9,10
At the time of these experimental developments, quantum chemistry had already reached a level of sophistication in which both via wavefunction techniques and density functional theory (DFT) accurate results can be obtained routinely for a variety of properties of individual molecules and reactions.11,12 DFT surpasses wavefunction methods from a quality/cost ratio point of view enabling studies on systems with a significantly larger number of atoms, although less trustworthy for systems with intricate bonding patterns or spin behavior. It bears no surprise that quantum chemical studies on the influence of mechanical forces on the geometrical and electronic structure, reactivity and even complete reaction pathways emerged from the beginning of the 21st Century with often a direct interplay between theory and experiment. In retrospect, it can be said that molecular mechanochemistry is a chemistry subfield characterized by a simultaneous development of experimental and theoretical techniques.
This short review on the entrance of quantum chemistry in mechanochemistry may not give the impression that the inclusion of a mechanical force in the quantum mechanical description of a molecule or a reacting pair of molecules was a trivial task, ready to be implemented in the existing quantum-chemical packages. The mechanical nature of the force without associated interaction terms in the electronic Hamiltonian, similar to pressure, is responsible for this theoretical challenge. Various techniques have been proposed to cope with this fundamental problem such as COGEF (constrained geometries simulate external force)13 and EFEI (external forces explicitly included)14 methods, as will be briefly summarized in Sections 2 and 3, resulting in a fair increase in quantum mechanochemical publications, sometimes also including the visualization of the distribution of the strain energy in the molecule (JEDI, Judgment of Energy Distribution).10,15 Studies vary from the initial investigation of the mechanical strength and bond rupture in small molecules,13 through papers on the possibility to control the stereoselectivity of pericyclic reactions including the violation of the Woodward Hoffmann rules,16–18 often in synergy with experimental studies,17,19,20 to studies on force-induced retro-click reactions,21 mechanically induced conductance switching,22 activation efficiency of mechanophores,23 mechanical activation of photo-reactivity24,25 and anthracene (4+4) cycloadducts,26 force-induced switching of aromaticity and homo-aromaticity,27 flex-activated mechanophores,28 among others.
In this contribution, we report on recent work on quantum mechanochemistry in the ALGC group,29–34 in which the mechanical force was put in as an extra ingredient in a Conceptual DFT (CDFT) framework, involving more fundamental aspects (concepts and reactivity) and more applied topics such as mechanically driven switches.
To put the conceptual aspect in a broader context, it is part of the ALGC research program35 on the inclusion of external “fields” in Conceptual DFT (CDFT),36–46 for many years one of the central topics of our research.39,42,44,45 Conceptual DFT is essentially a density-based reactivity theory in which the reactivity of a molecule is described in terms of a series of response functions. They quantify the propensity of a molecule to change its energy at the onset of a chemical reaction when it is perturbed by another molecule resulting in a change in its number of electrons N and/or the external potential v(r), i.e. the potential felt by the electrons due to the nuclei. These response functions, derivatives at different orders of the energy with respect to N or/and v(r), can often be traced back to well-known concepts such as the electron density itself,36 electronegativity,47 hardness and softness,48 the Fukui functions49 (a generalization of Fukui's frontier orbital concept50) and electrophilicity.51 In recent years, we have extended the scope of CDFT by introducing new external variables35 from which the mechanical force is one example that will be discussed in detail in the present work. In this broader context, the extension of CDFT to incorporate electric52,53 and magnetic fields54,55 and pressure56 was investigated, together with mechanical forces, to keep pace with recent experimental and theoretical work on extending the portfolio of reaction conditions. Examples include the use of oriented external electric fields (OEFFs)57 as “novel effectors of chemical change”,58 chemistry at very high pressure59–61 and the rising interest in the behavior of atoms and molecules in strong magnetic fields,62 as observed in white dwarfs and neutron stars.62,63 In the present contribution the inclusion of a mechanical force in a CDFT context is considered in Section 2. After a short introduction to CDFT and pinpointing the basic equations of the mechanochemical methods, we discuss the results of a proof-of-concept investigation on the change in chemical properties of diatomics, as described by CDFT concepts when an external stretching force is applied to a chemical bond.29 As a natural sequel, implying an extension of the COGEF approach, the reactivity of a bond is probed when it is bent by an external mechanical force, taking the CC triple bond as an example. The results are a guide to rationalize structural trends and the reactivity of cyclic alkynes of paramount importance in in vivo click reactions.30
Section 3 is more diverse and applied in nature and injects a mechanochemical component in existing research lines in our group involving pericyclic reactions64–70 (with studies on regioselectivity and a density only re-interpretation of the Woodward Hoffmann rules), expanded porphyrins71–82 (with an extensive series of studies on their topology, their Hückel vs Möbius switching behavior, conductance, photophysical and non-linear optical properties, with aromaticity as leitmotiv) and the reactivity of carbonyl groups for nucleophilic additions with the associated Fukui function,83–90 recently including its behavior under an electric field and the stereoselectivity of its hydride reduction. The two former research lines are extended with the inclusion of an external force in the design of force probes based on electrocyclization reactions in polyenes and mechanochemically triggered topology changes in extended porphyrins respectively, offering the possibility for mechanically driven switches.31,32 The final example shows how mechanical pulling can force the outcome of a nucleophilic addition to an α-chiral ketone to a diastereoselectivity opposed to the celebrated Felkin–Anh model,33 a situation comparable to the anti-Woodward Hoffmann ring opening of cyclobutene shifting from a conrotatory to a disrotatory mode upon mechanical stress.16
Our wandering through quantum mechanochemistry, from concepts to reactivity and switches thereby comes to an end.
2. Reconciling conceptual DFT with mechanochemistry
2.1. Quantum mechanochemistry: a short introduction
In this part, we provide a brief overview of the quantum mechanochemical approaches used in our work to describe the effect of an external force on the different molecular systems. Extensive and complete reviews on this topic are available elsewhere.3,9,10,34 We will focus on two static approaches as mentioned in the introduction. A first approach is the constrained geometries simulate external force (COGEF) methodology, introduced by Beyer and co-workers.13 This is an indirect method that uses a geometric constraint to simulate an external force. Applying an external force to a molecule results in a change of the nuclear constellation; the nuclear gradient computed at this deformed geometry is equal to the force that will mechanically lead to this geometry. When performing this type of calculation, one typically adjusts (i.e. elongate or decrease) the distance between two atoms on which an external force will act and the rest of the molecular framework is relaxed. Repeating this for different values of this interatomic distance will then allow to explore the effect of a changing external force. As such, COGEF indirectly simulates the influence of the mechanical force on the molecular framework.An example of a direct method used in our work to investigate the effect of an external force is the EFEI (external force explicitly included) method.14 In this approach, one minimizes the force modified potential energy expression:
| VEFEI(q,Fext) = VBO(q) − FextR | (1) |
The effect of the application of an external force to a molecule will result to a change of the complete geometry of the molecule with respect to the original Born–Oppenheimer equilibrium geometry. However, it is relevant to know the structural parameters that are most impacted by the application of the force. This information can be gained through the application of the so-called JEDI (Judgement of Energy DIstribution) analysis.10,15 In this approach, one computes, in a harmonic approximation, the energy stored in each internal coordinate q, of which there are M in total, through application of an external force as:
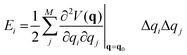 | (2) |
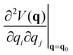 is a Hessian matrix element evaluated at the equilibrium geometry (q0) and Δqi is the change in the internal coordinate i upon mechanical deformation. The sum of each of these terms for all internal coordinates is called the harmonic stress energy. Analysis of the distribution of the stress energy can provide useful insights into local effects as a response to the application of a mechanical force.
is a Hessian matrix element evaluated at the equilibrium geometry (q0) and Δqi is the change in the internal coordinate i upon mechanical deformation. The sum of each of these terms for all internal coordinates is called the harmonic stress energy. Analysis of the distribution of the stress energy can provide useful insights into local effects as a response to the application of a mechanical force.
2.2. Conceptual DFT and its extension by a mechanical force: mechanochemical response functions
Density functional theory (DFT)12,91 is a branch of quantum mechanics which uses the electron density ρ(r) of the system, an observable quantity, function of three spatial coordinates, as the basic variable of an N-electron system instead of the wave function Ψ, which is a function of the spatial coordinates and spin coordinate of all the electrons. DFT was formally established through the Hohenberg–Kohn theorems which allow to write the electronic energy as a functional of the ground state electron density. Minimization of this energy with respect to variations in the electron density with the constraint that the electron density should at all times integrate to the number of electrons of the system yields the so-called DFT analogue to the Schrödinger equation:36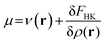 | (3) |
In this equation, μ is the Lagrange multiplier associated with the above-mentioned constraint, which is called the electronic chemical potential, v(r) is the potential due to the nuclei (i.e. the potential due to the nuclei in the absence of other external fields) and FHK is the so-called Hohenberg–Kohn functional, which contains the kinetic energy of the electrons and the electron–electron repulsion. This equation was turned into an orbital equation by Kohn and Sham in which the only unknown variable is the exchange–correlation functional.92 In the last 4 decades, many accurate approximations for this functional have been put forward enabling the use of Kohn–Sham DFT for the accurate calculation of many atomic, molecular, and material properties with high accuracy at a much lower computational cost than traditional wavefunction methods. However, density functional approximations also suffer from shortcomings for the calculation of certain properties [for a recent critical account on the different Density functional approximations (DFAs), see ref. 93]. Next to the attractive computational properties of DFT, the theory has also proven to be ultimately suited for the introduction of chemical concepts and principles, known to many chemists, but often previously defined only on qualitative grounds. As already mentioned in the introduction, this area known as conceptual DFT (CDFT)36–46 allows a sharp, mathematical definition of these chemical concepts which permits their first principles computation. Conceptual DFT started with the identification by Parr and co-workers of the electronic chemical potential μ47 with the negative of the Mulliken expression for the electronegativity χ, a quantity introduced by Pauling as the power of an atom in a molecule to attract electrons to itself.94 The electronic chemical potential can be proven to be equal to the derivative of the energy of the system with respect to the number of electrons at a constant external potential and can thus be seen as a response function:
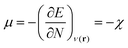 | (4) |
This CDFT expression for the electronegativity connects the definition to the expression put forward by Iczkowski and Margrave.95 In a finite difference approximation, the electronegativity definition equals the expression proposed by Mulliken96 for this quantity, the average of the vertical ionization energy I and electron affinity A of the system.
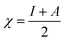 | (5) |
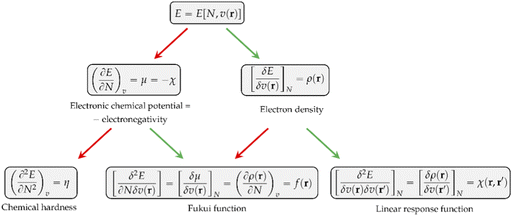
Other chemical quantities have in turn been introduced as response functions of the system's energy with respect to variations in the number of electrons, the external potential, or both. These functions can conveniently be collected in a so-called response function tree,35,38,39 given in Fig. 1 up to second order.
As can be seen, the first derivative of the energy with respect to the external potential equals the electron density, the central quantity of DFT. Other quantities find themselves a natural place in this tree:
• The chemical hardness η,48 the second derivative of the energy with respect to the number of electrons, an important quantity in Pearson’ hard and soft acids and bases97 and maximum hardness principles.98 The absolute hardness was introduced by Parr and Pearson as the half of the difference between I and A.† The inverse of the global chemical hardness is the global softness S.
• The Fukui function f(r) probes molecular regions prone to a nucleophilic, electrophilic or radical attack.49 This function is suited to describe intramolecular reactivity trends. To describe reactivity trends between different compounds, the Fukui function is turned into the so-called local softness, the product of the Fukui function with the global softness.99
• The linear response function χ(r,r′),36 a quantity which has been shown to provide insight into electron delocalization.44,100
Other additional quantities have also been introduced over the years. The dual descriptor, a third order energy derivative, was defined as the derivative of the Fukui function with respect to the number of electrons101,102 and can provide a “one-shot” picture of both the electrophilic and nucleophilic regions of the molecule. The electrophilicity index ω51 was introduced as the energy change when the system takes up the maximum amount of electrons possible from a perfect electron donor (i.e. a system with zero chemical potential). It was shown to be equal to the ratio of the square of the chemical potential and two times the hardness:
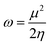 | (6) |
These reactivity indices have been used extensively to evaluate chemical reactivity in different fields of chemistry, ranging from organic to inorganic chemistry, biochemistry, catalysis and nanochemistry.38–46
In a first part of our work on mechanochemical reactivity, we wanted to evaluate the effect of an external mechanical force on these above-mentioned response functions. This will involve, among others, the evaluation of derivatives of the type:
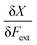 | (7) |
2.3. Chemical bonds and angles stressed by mechanical forces
| X(2)(Fext) = aFext2 + bFext + X(0) | (8) |
In Table 1, we list the linear parameters b of these second order polynomials, which represent the first order changes in X around the equilibrium position, i.e. corresponding to the absence of an external force, 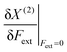 . Remark that both the (2), denoting the use of a second-order polynomial fit, and the condition Fext = 0 has been dropped in the notation of the response functions in Table 1.
. Remark that both the (2), denoting the use of a second-order polynomial fit, and the condition Fext = 0 has been dropped in the notation of the response functions in Table 1.
| H2 | −0.4037 | 0.0276 | −0.1881 | −0.4313 | 1.0196 | −0.0410 |
| HF | −0.1351 | 0.0327 | −0.0509 | −0.1672 | 0.4436 | −0.0058 |
| HCl | −0.0706 | 0.0516 | −0.0095 | −0.1222 | 0.5214 | 0.0084 |
| HBr | −0.0589 | 0.0723 | 0.0067 | −0.1312 | 0.6586 | 0.0169 |
| F2 | 0.2014 | 0.8709 | 0.5362 | −0.6695 | 1.9945 | 0.3621 |
| Cl2 | 0.2099 | 0.7473 | 0.4786 | −0.5374 | 3.4234 | 0.3655 |
| Br2 | 0.1467 | 0.5460 | 0.3464 | −0.3992 | 3.3898 | 0.3069 |
| FCl | 0.1796 | 0.5921 | 0.3858 | −0.4124 | 2.0071 | 0.2647 |
| FBr | 0.1574 | 0.5171 | 0.3373 | −0.3597 | 2.1888 | 0.2547 |
| ClBr | 0.2064 | 0.7045 | 0.4555 | −0.4981 | 3.7181 | 0.3741 |
| N2 | −0.0372 | 0.1332 | 0.0480 | −0.1457 | 0.3343 | 0.0252 |
| P2 | −0.1473 | 0.1464 | −0.0005 | −0.2937 | 2.2166 | 0.0437 |
| PN | 0.0147 | 0.0940 | 0.0545 | −0.0792 | 0.4265 | 0.0373 |
| BN | −0.1282 | 0.0025 | −0.0629 | −0.1307 | 1.4116 | −0.0030 |
| O2 | 0.1801 | 0.2090 | 0.1945 | −0.0289 | 0.1319 | 0.0975 |
| S2 | 0.1538 | 0.1997 | 0.1767 | −0.0459 | 0.5217 | 0.1306 |
| SO | 0.1278 | 0.1446 | 0.1362 | −0.0168 | 0.1346 | 0.0834 |
| CO | 0.0309 | 0.0568 | 0.0439 | −0.0259 | 0.0797 | 0.0196 |
| LiF | −0.4419 | 0.0893 | −0.1763 | −0.5312 | 3.3022 | −0.0186 |
| NaCl | −0.4534 | 0.1941 | −0.1297 | −0.6475 | 7.0596 | 0.0344 |
| MgO | −0.1065 | 0.0838 | −0.0114 | −0.1902 | 4.3190 | 0.0512 |
First, we will discuss the changes of the ionization energy and the electron affinity with an external force. Since these responses have the dimension of a distance, it is reasonable to investigate the relationship between the changes in I and A with the difference in bond equilibrium distance between the neutral species and the cation and anion, respectively, in order to gain insight into the sign and the magnitude of the responses. The correlation plots between the first-order derivative of I and A with respect to Fext and the difference between the equilibrium bond distance of the neutral and cationic and anionic species, respectively, are shown in Fig. 2. As can be seen, except for a small number of outliers, these quantities are correlated. One can infer that 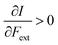 if the equilibrium bond distance of the neutral molecule is larger than the equilibrium bond distance of the cation, and vice versa. In addition, the sign of this derivative can be shown to be smaller than zero when the electron is removed from a bonding orbital and larger than zero when it is removed from an antibonding orbital. Analogously, one observes that,
if the equilibrium bond distance of the neutral molecule is larger than the equilibrium bond distance of the cation, and vice versa. In addition, the sign of this derivative can be shown to be smaller than zero when the electron is removed from a bonding orbital and larger than zero when it is removed from an antibonding orbital. Analogously, one observes that, 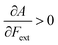 if the equilibrium bond distance of the neutral species is smaller than the equilibrium bond distance of the anion; similarly, the derivative is larger than zero when the electron is added to an antibonding orbital.
if the equilibrium bond distance of the neutral species is smaller than the equilibrium bond distance of the anion; similarly, the derivative is larger than zero when the electron is added to an antibonding orbital.
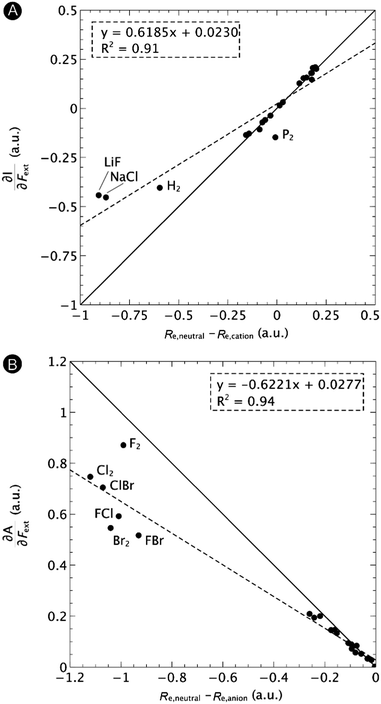 | ||
| Fig. 2 Correlation between (A) the first-order derivative of I with respect to Fext and the difference between the equilibrium bond distance of the neutral and cationic species and (B) the first-order derivative of A with respect to Fext and difference between the equilibrium bond distance of the neutral and anionic species. The solid lines indicate the lines with unit (1 or −1) slope and zero intercept, the dashed lines the regression curves. Reproduced from ref. 29 with permission from the PCCP Owner Societies. | ||
Both I and A are the basic ingredients of the finite difference estimates of the electronegativity and hardness; for the dependence of the Mulliken electronegativity, one can thus write:
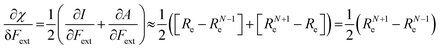 | (9) |
One might expect that the bond distance of the anion will always be larger than that of the cation, implying an increase of the molecular electronegativity with increasing force. In our test set of 21 diatomic molecules, seven molecules (H2, HF, HCl, BN, LiF, NaCl and MgO) have a larger equilibrium bond distance in the cation than in the anion leading to a decrease of the electronegativity with increasing force. For all other diatomics, except P2, a positive first order derivative of χ was found, in agreement with the larger bond distance in the anion than in the cation. In the case of P2, the inconsistency between the electronegativity change and the bond distance changes was shown to be due to an important high order effect.
In the case of the absolute hardness, one obtains:
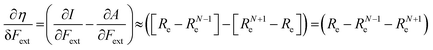 | (10) |
Without any exception, we find that 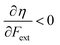 for the 21 diatomic molecules; the hardness of a diatomic molecule decreases when an external force is applied. This observation can be seen as a manifestation of the so-called principle of maximum hardness,98 which states that a system will evolve to a configuration of maximum hardness at constant external and chemical potential. It is pleasing to note that when replacing the external force by an external isotropic pressure p, expressions were found relating
for the 21 diatomic molecules; the hardness of a diatomic molecule decreases when an external force is applied. This observation can be seen as a manifestation of the so-called principle of maximum hardness,98 which states that a system will evolve to a configuration of maximum hardness at constant external and chemical potential. It is pleasing to note that when replacing the external force by an external isotropic pressure p, expressions were found relating 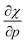 and
and 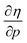 to the volume of the neutral, anionic and cationic systems, completely analogous to equations (9) and (10).56
to the volume of the neutral, anionic and cationic systems, completely analogous to equations (9) and (10).56
Finally, we investigate the influence of a mechanical force on the electrophilicity, a quantity which combines the electronegativity and the hardness (Eq. 6.). The change of electrophilicity with respect to an external mechanical force can be evaluated as follows:
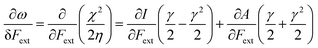 | (11) |
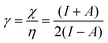 | (12) |
As I is usually much larger than A (typically a factor 8),36 the value of γ varies around 0.5. As a result, the change in the electrophilicity is mostly determined by the change of A. Since this quantity is always positive for the systems investigated, the electrophilicity change is positive in most cases, except for H2, HF, BN and LiF where the large negative response of I overcomes the small positive change of A. This result for the change of the electrophilicity nicely connects to a QM/MM study indicating that the redox potentials of cysteine dimers104 increases with the application of a pulling force. Since electrophilicity is positively correlated with redox potentials,105,106 this result is in line with the increasing electrophilicity with an increasing external force.
We consequently modelled the variation of strain present in an alkyne triple bond by applying an angular bending force of different magnitude to put this reaction into a mechanochemical perspective.30 Bending away from linearity in a syn fashion, both angles around the triple bond resembles a fragment of a cyclic alkyne. As such, the reactivity of the triple bond can be probed through CDFT reactivity indices when the alkyne is bent. The reactivity of cyclic alkynes with increasing ring strain was probed using substituted 2-butyne fragments. As can be seen from Fig. 3, the global softness S increased upon increasing bending angle, in line with the results for the softness variation found for stretching the covalent bonds in the diatomic molecules. Since increasing global softness implies decreasing hardness, this results already indicates an increasing chemical reactivity with increasing bending force.
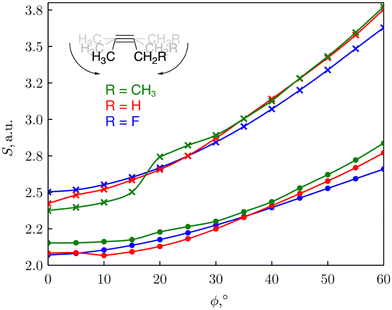 | ||
| Fig. 3 Plot of the global softness S of the 2-butyne fragments vs the triple bending angle ϕ. S was calculated as the inverse of I-A (•) or the inverse of the HOMO–LUMO gap (×). Reproduced from ref. 30 from the Royal Society of Chemistry. | ||
Next, the local reactivity, as probed by the local softness, was evaluated. In most cases, the alkyne behaves as the electrophile116 and thus we evaluated both the condensed Fukui function f+ and local softness s+ for a nucleophilic attack on both carbon atoms of the triple bond in order to probe the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C reactivity. The resulting plots of these quantities vs the bending angle is shown in Fig. 4. As can be seen from these plots, an increasing bending angle renders these alkynes more prone to a nucleophilic attack. Importantly, the angles of the alkyne must be distorted at least 15° to be significantly more reactive than the linear system and the influence of substituents on the electrophilic character of the triple bond diminishes when it is bent further away from linearity. From this study, we can thus conclude that not only the strain effect is important in SPAAC reactions but also the intrinsic increase of chemical reactivity upon changing the bending angle.
C reactivity. The resulting plots of these quantities vs the bending angle is shown in Fig. 4. As can be seen from these plots, an increasing bending angle renders these alkynes more prone to a nucleophilic attack. Importantly, the angles of the alkyne must be distorted at least 15° to be significantly more reactive than the linear system and the influence of substituents on the electrophilic character of the triple bond diminishes when it is bent further away from linearity. From this study, we can thus conclude that not only the strain effect is important in SPAAC reactions but also the intrinsic increase of chemical reactivity upon changing the bending angle.
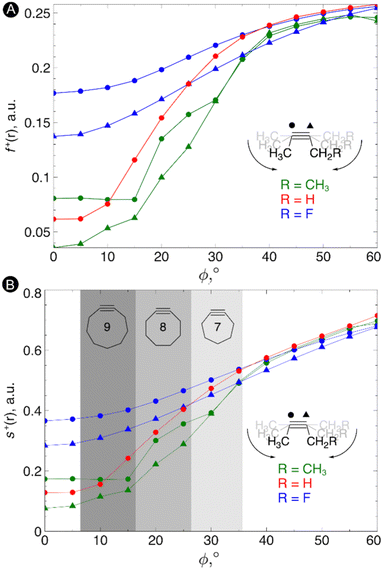 | ||
| Fig. 4 (A) Condensed Fukui functions f+(r) on the carbon atoms of the triple bond with increasing bending angle. (B) Condensed local softness s+(r) on the carbon atoms of the triple bond with increasing bending angle. Reproduced from ref. 30 from the Royal Society of Chemistry. | ||
3. Design of molecular force probes
Molecular force probes are a special type of mechanophores that allow for the detection and quantification of mechanical strain in a single molecule or material due to a measurable change in the properties, such as a variation of the color.3,117,118 The small molecular force probes can be incorporated into polymer chains providing a broad range of stress-responsive materials, which are very important for the understanding of mechanochemical reactivity.119–121 These exciting force-sensitive molecules can be designed using computational approaches by identifying species undergoing optical property changes upon application of an external mechanical force.3,24,28,122 The most intensively investigated mechanophore is based on the spiropyran-merocyanine interconversion via a force-induced pericyclic ring-opening reaction.123,124 Thus, application of a force in spiropyran results in the elongation of the spirocyclic C–O bond triggering a 6π-ring opening to the colored merocyanine form.125,126 When external forces are removed, the material's deformation recovers quickly but the color fades away slowly.122 Definitely, most of the mechanophores suffer from a slow mechanical deactivation, which limits the applicability of functional materials incorporating mechanophores.127In our work, an alternative intramolecular 6π-electrocyclization in constrained polyenes was explored for designing novel molecular force probes operating under thermal conditions.31 As illustrated in Fig. 5, our thermal force probe operates in 4 steps. In the first step, a spontaneous ring closure takes place yielding the closed product, which interrupts the π-conjugated system within the polyene. In step 2, an external force (Fext) is then applied at the terminal H-atoms of the polyene chain to strain the newly formed carbon–carbon bond, triggering the reverse ring-opening reaction in step 3. With the open form now promoted, the external force is removed in step 4 allowing the relaxation of the open structure that can undergo again the 6π-electrocyclization, reinitiating the mechanism. In principle, we can cycle through this force-probe mechanism by repeatedly applying and removing the external force.
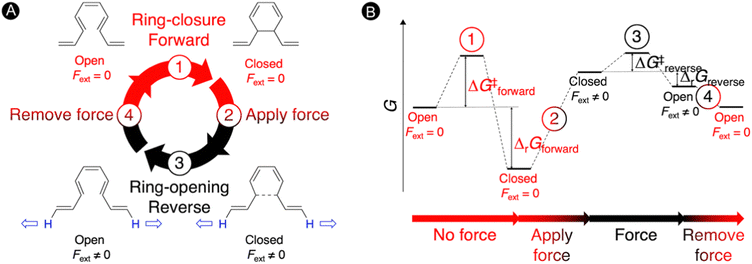 | ||
| Fig. 5 Molecular force probe based on 6π-electrocyclizations in constrained polyenes. (A) Force probe mechanism consisting of 4 steps. (B) Schematic Gibbs free energy diagram under thermal conditions. Reprinted with permission from the Journal of Organic Chemistry (ref. 31), Copyright 2021, American Chemical Society. | ||
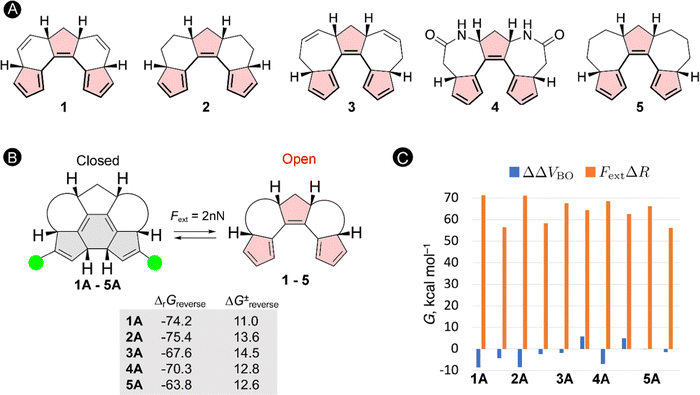
The schematic energy level diagram in Fig. 5B shows that the ring closure is spontaneous when no force is applied, i.e. ΔrGforward < 0; while the ring opening should be exergonic when an external force is active, i.e. ΔrGreverse < 0 (under Fext). Thus, the closed form must be sufficiently activated in the presence of the external force in step 2 for such force probe mechanism to be viable. To validate our hypothesis, we devised a set of constrained polyenes with a fused ring system to lock the orientation of the three π-bonds to promote the desired 6π-electrocyclization in the absence of an external force. Indeed, quantum mechanical calculations showed negative Gibbs free energies for the forward ring-closure reaction in compounds 1–5 possessing different ring fused structures (Fig. 6A). More importantly, strongly negative reaction barriers and low activation barriers were obtained for the reverse reaction upon application of an external pulling force of 2 nN, proving that the reverse ring opening becomes highly exergonic in this force regime (Fig. 6B).
To get further insight into the driving forces pushing the equilibrium towards the open form when Fext = 2 nN, we decompose the changes in the activation energies and reaction energies into two terms based on the EFEI eqn (1). According to this formalism, the shift of the energy differences (ΔΔV) of the stationary points due to the external force can be written as a sum of two terms:
| ΔΔV = ΔΔVBO − FextΔR | (13) |
As illustrated in Fig. 6C, the force-dependent term is significantly larger than the Born–Oppenheimer term and therefore governs the large shift in the thermochemical properties of the reverse ring-opening reaction. Because the mechanical work is the product of the force and the displacement along which the force is oriented, one can explain why ring-opening reactions are specifically triggered by a pulling force: a ring-opening reaction typically increases the distance between several atoms in a molecule (ΔR > 0) and the application of a pulling force to a pair of such atoms triggers the ring opening. Therefore, the efficiency of mechanical activation strongly depends on the magnitude of the applied external force and the distance between the pulling positions.
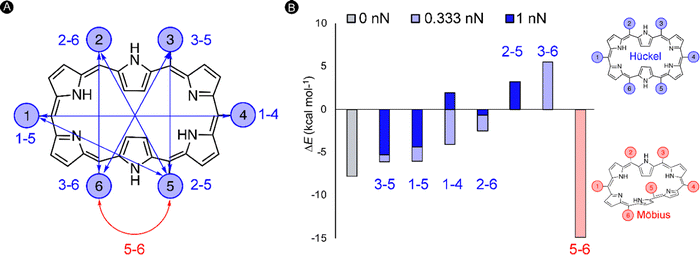
In the next study, we took this idea of the pulling point distances a step further. Herein, we assessed if internuclear distances can be used as a predictive tool for the identification of new mechanochemical processes. As a test bed, we focused on the [28]hexaphyrin, a flexible macrocycle for which aromatic Möbius and antiaromatic Hückel structures coexist in dynamic equilibrium as proven experimentally128 and theoretically.71,129 Expanded porphyrins are an unexplored class of compounds for molecular force probe applications despite its potential to act as conformational mechanophores, i.e. molecules that undergo a predictable conformational modification triggered by a mechanical force.130 The interest in conformational mechanophores has spiked in recent years as they do not require any bond cleavage and thus can be operated at lower force regimes and are less prone to mechanical degradation.131,132
Our quantum mechanochemical calculations demonstrated that mechanical force is an effective stimulus to trigger the interconversion between Hückel and Möbius topologies in [28]hexaphyrin,32 expanding the toolbox of stimuli to activate these unique molecular switches.81,133 A straightforward approach based on distance matrices of the unperturbed structures was proposed for the identification of appropriate pulling scenarios. Only the six meso-positions of the macrocycle were considered as pulling positions since such peripheral modifications are synthetically viable and applying force through meso-positions should retain the central macrocyclic framework.134 A total of six internuclear distances that are larger in the Hückel topology were identified and our hypothesis is that the application of a pulling force along these distances is expected to favor the Hückel topology. These meso carbon–carbon distances larger in the Hückel topology are indicated in blue in Fig. 7A. Additionally, one distance (5–6 in red) was found that is larger in all Möbius topologies and accordingly pulling along this distance is expected to enhance the stability of the Möbius topologies (Fig. 7B).
To verify our hypothesis, we computed the relative energies of Hückel and Möbius topologies at two force regimes (0.333 nN and 1 nN) with the EFEI formalism. Remarkably, the conformational equilibrium evolved in the expected direction for all pulling scenarios (Fig. 7B). For the pulling scenarios highlighted in blue, the energy differences between the Hückel and Möbius structures are reduced until full inversion of the conformational equilibrium when the force is applied through 2–5 and 3–6meso-positions. By contrast, pulling at carbons 5–6 increases even more the energy difference, locking the Möbius topology in a deeper minimum on the potential energy surface. In a stronger force regime of 1 nN, the shift in the relative energies is even more pronounced, but it is remarkable that certain conformations did not converge to the desired topology. Accordingly, the maximum force for this conformational mechanophore is about 1 nN.
Importantly, distance matrices are computed for unperturbed structures and can therefore only be used as a guiding principle for the identification of appropriate pulling scenarios. Two key assumptions need to be satisfied. First, if a distance is smaller in one conformer relative to another one, this trend must be preserved upon the application of a pulling force along this distance. Second, it is assumed that the Born–Oppenheimer term is small relative to the mechanical work, which is indeed the case for the force-triggered topology interconversions in [28]hexaphyrin.32
Having proved that [28]hexaphyrin can act as a novel conformational mechanophore operating at low force conditions, we asked ourselves why mechanical activation is so efficient to revert the conformational equilibrium towards the Hückel topology. To answer this question, we performed JEDI analyses10 to examine the distribution of the mechanical energy absorbed by bond, angles and dihedral angles. The JEDI analysis provides a color-coded distribution of the mechanical energy in the Möbius structures, where red areas correspond to large amounts of stored mechanical energy (Fig. 8). Even though the force was applied to the meso positions, the strain energy was allocated very locally. The change of topology in [28]hexaphyrin is achieved by variation of the internal dihedral angles71,129 and the regions around these dihedral angles of interest were strained more than the rest of the molecule, which is in line with the strong activation of the molecular switch. It is noteworthy that the dihedral angles account for a large portion of the total strain energy in this mechanophore.
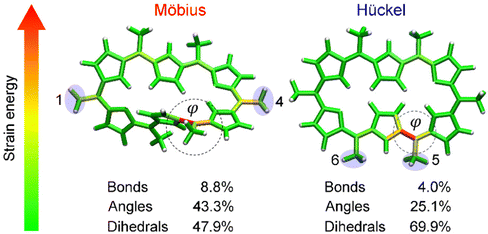 | ||
| Fig. 8 JEDI analysis showing the distribution of the mechanical energy stored in the Möbius structure in the 1–4 pulling scenario at 1.0 nN and the Hückel structure in the 5–6 pulling scenario at 0.333 nN. Circular contours highlight the most activated regions by the external force and correspond to the reaction coordinate triggering the topology interconversions. Reprinted from Chemistry – A European Journal, ref. 32. | ||
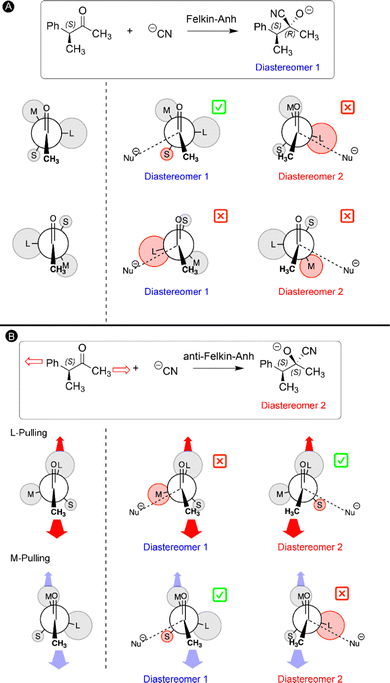
4. Mechanochemical Felkin–Anh model for the addition of nucleophiles to chiral carbonyls
In our final study, the ability to lock a molecule into one conformation with mechanical forces is used to challenge a well-established reaction mechanism in organic chemistry: the Felkin–Anh model for the nucleophilic attack to α-chiral carbonyls.33 Two diastereomers can be obtained upon such carbonyl addition reactions and the stereoselectivity can be predicted by the Felkin–Anh model by arranging the substituents on the Cα atom according to their size.135,136 It is assumed that the ketone can freely rotate around the C–Cα bond and the most stable rotamers are those in which the largest group (L) is positioned perpendicular with respect to the oxygen atom and methyl group of the ketone to minimize steric interactions (Fig. 9A). In the next step, the nucleophile approaches the carbonyl via either side of the ketone for both rotamers and hence a total of four transition states are possible (Fig. 9A). According to the Felkin–Anh model, the pathway with the least steric hindrance proceeds via the lowest activation barrier leading to the major diastereomer. In this case, the transition state in which the nucleophile approaches close to the small substituent is expected to be lower in energy. For our test reaction, the nucleophilic addition of CN− to (3S)-3-phenylbutan-2-one, our calculations confirm that this is indeed the lowest energy transition state, yielding predominantly the S,R-diastereomer (diastereomer 1 in Fig. 9A), in line with the Felkin–Anh model predictions.33The rotational freedom around the C–Cα bond is crucial in the Felkin–Anh model for achieving the different rotamers of the chiral ketone. Based on our work on force-induced electrocyclic ring openings and topological interconversions,31,32 we postulated that a mechanical force can be used to prevent the free rotation around the C–Cα bond and lock one conformation in order to influence the stereoselectivity of the nucleophilic addition. As illustrated in Fig. 9B, two pulling scenarios were considered in which the mechanical force is applied through the L or M substituent on Cα and the carbonyl methyl group. Upon application of an external force to the ketone chain, only one conformation becomes accessible in which the pulling positions are placed in an antiperiplanar arrangement to maximize the distance between the pulling groups (Fig. 9B). The second step in our mechanochemical model is identical to the Felkin–Anh model since the nucleophile can approach from either side of the carbonyl in the stretched chiral ketone and the preferred transition state is selected based on steric hindrance. In the case of M-pulling, the stretched conformation is very similar to the original Felkin–Anh model since L is almost perpendicular with respect to the oxygen atom and the methyl group. Consequently, the favored pathway involves a similar transition state and the diastereomeric selectivity is anticipated to be unaffected. By contrast, pulling to the L group leads to a drastic change in the stretched conformation of the ketone and the favored transition state. As shown in Fig. 9B, the nucleophile is expected to approach via the smaller substituent (S), yielding the opposite diastereomeric selectivity with respect to the original Felkin–Anh model.
This intuitive model was validated through quantum mechanochemical calculations. While the S,R-diastereomer is kinetically preferred when a force is applied to the two methyl groups, the S,S-diastereomer is preferred when the force is applied to the phenyl substituent on the Cα atom and the carbonyl methyl group. Remarkably, the conformation of the ketone was locked into one minimum on the force-modified potential energy surface at a very low force regime (0.50 nN) in both pulling scenarios. The pulling point distances in the optimized geometries at 0 nN were used to accurately predict the changes of the rotational potential curves. Overall, a novel mechanochemical Felkin–Anh model was proposed in which the force is solely applied for restricting the conformational freedom of the chiral ketone, promoting otherwise inaccessible reaction pathways on the force-modified potential energy surface.
5. Conclusions
The field of single-molecule mechanochemistry is only two decades old and its development has witnessed a remarkable interplay between theory and experiment. Some recent advances in the quantum chemical part of this evolution are highlighted in this contribution. Combined with the (extended) COGEF model, both global and local descriptors from the Conceptual DFT toolbox are capable to rationalize the behavior of a bond under mechanical stress, both for stretching and bending forces. In the former case, changes in global reactivity indices such as electronegativity, hardness and electrophilicity upon application of an external force can be related to the evolution of equilibrium distances of the unperturbed molecule when accepting or donating electrons. In the latter case, local descriptors (Fukui functions and local softness) are instrumental in modelling the influence of ring strain on the reactivity of cycloalkynes by mechanical bending forces.The idea of applying a force along the reaction coordinate already emerges from these more conceptual investigations and turns out to be a leitmotiv in the applications on molecular force probes. It is reminiscent of similar findings on the optimal use of electric fields as “effectors” of chemical reactivity, as presented in Shaik’ s work. In this part, local changes of potential energy surfaces are investigated using the EFEI approach to design force probes based on ring-opening and closure (6π electrocyclizations) and a Hückel-Möbius topological switch in [28]hexaphyrins. In both cases, the distance between the pulling points plays a decisive role. In the final application, triggering the diasteroselectivity in nucleophilic additions on α chiral ketones, the potential of the mechanical force on locking certain conformations is exploited, the distance between the pulling points being again of crucial importance.
Our studies indicate that the introduction of a mechanical force into a quantum chemical context, at first sight far from trivial as the associated interaction terms in the electronic Hamiltonian are not present, has been successful. Combined with reactivity theories, such as Conceptual DFT, this approach may be very rewarding to design and/or interpret experiments for synthetic chemists exploring molecules with unprecedented properties. A key issue in this endeavor is the position of the pulling points: their distance and their relation to the reaction coordinate. To put it in a more general context, molecular mechanochemistry is still in its infancy, but has a great potential for synthetic chemists when extending their traditional portfolio to increase the rate and steer the outcome of chemical reactions alongside with pressure, electric fields and, who knows, magnetic fields. The role of quantum mechanochemistry in this evolution can be expected to be preponderant.
A final reflection. The reader should realize that in the present contribution only a relatively small part of the emergent field of mechanochemistry has been discussed, namely quantum-mechanochemistry at the molecular level. Of course, the field of mechanochemistry is much broader as can be seen in the Introduction and the overall content of this Special Issue. When looking at the status of the field,1 some parallelism can however be drawn between the experimental and theoretical advances and prospects. At the single molecular level, theory often precedes experiment thanks to a series of solid theoretical methodologies developed in recent years, as evidenced in the present paper. This evolution should be compared with the intricacies of the experimental studies. For reactions with ball milling techniques, a theoretical interpretation, mechanistic insight into the reactions and support for optimizing the thermodynamical variables at stake (temperature and pressure) are still in their infancy. One may hope that breakthroughs along the theoretical side in that field may be accompanied by experimental progress in upscaling the single molecule mechanochemical processes. Having a look at the coverage of the new journal “Mechanochemistry” yields “Great Expectations” for the future of mechanochemistry in the development of new reactions and materials, all sharing a remarkable “greening”1 of chemical processes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
JE acknowledges support by the FWO (Fund for Scientific Research Flanders) under grant number 1148522N. MA thanks the Vrije Universiteit Brussel (VUB) for financial support. MA and FDP thanks the Vrije Universiteit Brussel (VUB) for the Strategic Research Program awarded to the ALGC research group. The resources and services used in this work were provided by the VSC (Flemish Super-computer Center), funded by the Research Foundation – Flanders (FWO) and the Flemish Government.References
- S. Pagola, Crystals, 2023, 13, 124 CrossRef CAS.
- K. Horie, M. Barón, R. B. Fox, J. He, M. Hess, J. Kahovec, T. Kitayama, P. Kubisa, E. Maréchal, W. Mormann, R. F. T. Stepto, D. Tabak, J. Vohlídal, E. S. Wilks and W. J. Work, Pure Appl. Chem., 2004, 76, 889–906 CrossRef CAS.
- T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137–14180 CrossRef CAS PubMed.
- S. L. James and T. Friščić, Themed collection Mechanochemistry, Chem. Soc. Rev., 2013, 42, 7487–7740 RSC.
- J. C. Robertson, M. L. Coote and A. C. Bissember, Nat. Rev. Chem., 2019, 3, 290–304 CrossRef.
- R. T. O'Neill and R. Boulatov, Nat. Rev. Chem., 2021, 5, 148–167 CrossRef PubMed.
- See the recent (2023) launching of “RSC Mechanocemistry – The first journal dedicated to the study of Mechanochemistry”, J. Batteas and T. Friščić Eds.
- M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727–1730 CrossRef CAS PubMed.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Acc. Chem. Res., 2017, 50, 1041–1048 CrossRef CAS PubMed.
- J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267–1274 CrossRef CAS (Nobel lecture).
- W. Koch and M. C. Holthausen, A Chemist ‘s Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2000 Search PubMed.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312 CrossRef CAS.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, J. Chem. Phys., 2014, 140, 134107 CrossRef PubMed.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377–6379 CrossRef CAS PubMed.
- C. L. Brown, B. H. Bowser, J. Meisner, T. B. Kouznetsova, S. Seritan, T. J. Martinez and S. L. Craig, J. Am. Chem. Soc., 2021, 143, 3846–3855 CrossRef CAS PubMed.
- W. Sakai, L. Gonnet, N. Haruta, T. Sato and M. Baron, J. Phys. Chem. A, 2023, 127, 5790–5794 CrossRef CAS PubMed.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. Niu, M. T. Ong, H. M. Klukovich, A. L. Rheingold, T. J. Martinez and S. L. Craig, Nat. Chem., 2015, 7, 323–327 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Chem. Sci., 2017, 8, 5567–5575 RSC.
- Y. Li, N. L. Haworth, L. Xiang, S. Ciampi, M. L. Coote and N. Tao, J. Am. Chem. Soc., 2017, 139, 14699–14706 CrossRef CAS PubMed.
- S. Kumar and T. Stauch, RSC Adv., 2021, 11, 7391–7396 RSC.
- C. García-Iriepa, D. Sampedro, F. Mendicuti, J. Léonard and L. M. Frutos, J. Phys. Chem. Lett., 2019, 10, 1063–1067 CrossRef PubMed.
- A. Jodra, C. García-Iriepa and L. M. Frutos, J. Org. Chem., 2022, 87, 12586–12595 CrossRef CAS PubMed.
- M. Walter, D. Linsler, T. König, C. Gäbert, S. Reinicke, M. Moseler and L. Mayrhofer, J. Phys. Chem. Lett., 2023, 14, 1445–1451 CrossRef CAS PubMed.
- T. Stauch, Chem. – Eur. J., 2018, 24, 7340–7344 CrossRef CAS PubMed.
- L. J. Mier, G. Adam, S. Kumar and T. Stauch, ChemPhysChem, 2020, 21, 2402–2406 CrossRef CAS PubMed.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2019, 21, 7378–7388 RSC.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Chem. Sci., 2020, 11, 1431–1439 RSC.
- T. Bettens, J. Eeckhoudt, M. Hoffmann, M. Alonso, P. Geerlings, A. Dreuw and F. De Proft, J. Org. Chem., 2021, 86, 7477–7489 CrossRef CAS PubMed.
- T. Bettens, M. Hoffmann, M. Alonso, P. Geerlings, A. Dreuw and F. De Proft, Chem. – Eur. J., 2021, 27, 3397–3406 CrossRef CAS PubMed.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, J. Org. Chem., 2023, 88, 2046–2056 CrossRef CAS PubMed.
- T. Bettens and F. De Proft, in Conceptual Density Functional Theory: Towards a New Reactivity Theory, ed. S. B. Liu, Wiley VCH, Weinheim Germany, 2022, ch. 13, 1 Search PubMed.
- P. Geerlings and F. De Proft, J. Comput. Chem., 2023, 44, 442–455 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, UK, 1989 Search PubMed.
- R. G. Parr and W. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701–728 CrossRef CAS PubMed.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quantum Chem., 2005, 101, 520–534 CrossRef CAS.
- J. L. Gázquez, J. Mex. Chem. Soc., 2008, 52, 3–10 Search PubMed.
- P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042 RSC.
- S. B. Liu, Acta Phys. Chem. Sin., 2009, 25, 590–600 CAS.
- P. Geerlings, S. Fias, Z. Boisdenghien and F. De Proft, Chem. Soc. Rev., 2014, 43, 4989–5008 RSC.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Theor. Chem. Acc., 2020, 139, 36 Search PubMed.
- Conceptual Density Functional Theory. Towards a new Reactivity Theory, ed. S. B. Liu, Wiley VCH, Weinheim Germany, 2022, vol. 1 and 2 Search PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- T. Clarys, T. Stuyver, F. De Proft and P. Geerlings, Phys. Chem. Chem. Phys., 2021, 23, 990–1005 RSC.
- R. Van Lommel, R. H. Verschueren, W. M. De Borggraeve, F. De Vleeschouwer and T. Stuyver, Org. Lett., 2022, 24, 1–5 CrossRef CAS PubMed.
- R. Francotte, T. J. P. Irons, A. M. Teale, F. De Proft and P. Geerlings, Chem. Sci., 2022, 13, 5311–5324 RSC.
- T. J. P. Irons, B. C. Huynh, A. M. Teale, F. De Proft and P. Geerlings, Mol. Phys., 2023, 121, e2145245 Search PubMed.
- J. Eeckhoudt, T. Bettens, P. Geerlings, R. Cammi, B. Chen, M. Alonso and F. De Proft, Chem. Sci., 2022, 13, 9329–9350 RSC.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642 CrossRef CAS PubMed.
- R. Cammi, V. Verdolino, B. Mennucci and J. Tomasi, J. Chem. Phys., 2008, 344, 135–141 CAS.
- R. Cammi, in Annu. Rep. Comput. Chem., ed. D. A. Dixon, Elsevier, 2017, 13, pp. 117–135 Search PubMed.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331 CrossRef CAS PubMed.
- D. Lai, Rev. Mod. Phys., 2001, 73, 629–662 CrossRef CAS.
- S. Damoun, G. Van de Woude, F. Méndez and P. Geerlings, J. Phys. Chem. A, 1997, 101, 886–893 CrossRef CAS.
- F. De Proft, P. W. Ayers, S. Fias and P. Geerlings, J. Chem. Phys., 2006, 125, 214101 CrossRef PubMed.
- P. W. Ayers, C. Morell, F. De Proft and P. Geerlings, Chem. – Eur. J., 2007, 13, 8240–8247 CrossRef CAS PubMed.
- F. De Proft, P. K. Chattaraj, P. W. Ayers, M. Torrent-Sucarrat, M. Elango, V. Subramanian, S. Giri and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 595–602 CrossRef CAS PubMed.
- N. Sablon, F. De Proft and P. Geerlings, Croat. Chem. Acta, 2009, 82, 157–164 CAS.
- P. Jaque, J. V. Correa, F. De Proft, A. Toro-Labbé and P. Geerlings, Can. J. Chem., 2010, 88, 858–865 CrossRef CAS.
- P. Geerlings, P. W. Ayers, A. Toro-Labbé, P. K. Chattaraj and F. De Proft, Acc. Chem. Res., 2012, 45, 683–695 CrossRef CAS PubMed.
- M. Alonso, P. Geerlings and F. De Proft, Chem. – Eur. J., 2012, 18, 10916–10928 CrossRef CAS PubMed.
- M. Alonso, P. Geerlings and F. De Proft, Chem. – Eur. J., 2013, 19, 1617–1628 CrossRef CAS PubMed.
- T. Stuyver, M. Perrin, P. Geerlings, F. De Proft and M. Alonso, J. Am. Chem. Soc., 2018, 140, 1313–1326 CrossRef CAS PubMed.
- T. Stuyver, S. Fias, P. Geerlings, F. De Proft and M. Alonso, J. Phys. Chem. C, 2018, 122, 19842–19856 CrossRef CAS.
- T. Woller, P. Geerlings, F. De Proft, B. Champagne and M. Alonso, J. Phys. Chem. C, 2019, 123, 7318–7335 CrossRef CAS.
- T. Woller, P. Geerlings, F. De Proft, B. Champagne and M. Alonso, Molecules, 2018, 23, 1333 CrossRef PubMed.
- D. Yu, C. Rong, T. Lu, P. Geerlings, F. De Proft, M. Alonso and S. Liu, Phys. Chem. Chem. Phys., 2020, 22, 4715–4730 RSC.
- T. Woller, A. Banerjee, N. Sylvetsky, G. Santra, X. Deraet, F. De Proft, J. M. L. Martin and M. Alonso, J. Phys. Chem. A, 2020, 124, 2380–2397 CrossRef CAS PubMed.
- N. Sylvetsky, A. Banerjee, M. Alonso and J. M. L. Martin, J. Chem. Theory Comput., 2020, 16, 3641–3653 CrossRef CAS PubMed.
- E. Desmedt, T. Woller, J. L. Teunissen, F. De Vleeschouwer and M. Alonso, Front. Chem., 2021, 9, 786036 CrossRef CAS PubMed.
- I. Casademont-Reig, T. Woller, V. García, J. Contreras-García, W. Tiznado, M. Torrent-Sucarrat, E. Matito and M. Alonso, Chem. – Eur. J., 2023, 29, e202202264 CrossRef CAS PubMed.
- E. Desmedt, D. Smets, T. Woller, M. Alonso and F. De Vleeschouwer, Phys. Chem. Chem. Phys., 2023, 25, 17128–17142 RSC.
- W. Langenaeker, K. Demel and P. Geerlings, J. Mol. Struct.: THEOCHEM, 1992, 259, 317–330 CrossRef.
- F. De Proft, J. M. L. Martin and P. Geerlings, Chem. Phys. Lett., 1996, 256, 400–408 CrossRef CAS.
- R. K. Roy, S. Krishnamurti, P. Geerlings and S. Pal, J. Phys. Chem. A, 1998, 102, 3746–3755 CrossRef CAS.
- P. W. Ayers, F. De Proft, A. Borgoo and P. Geerlings, J. Chem. Phys., 2007, 126, 224107 CrossRef PubMed.
- T. Fievez, N. Sablon, F. De Proft, P. W. Ayers and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 1065–1072 CrossRef CAS PubMed.
- W. Yang, A. J. Cohen, F. De Proft and P. Geerlings, J. Chem. Phys., 2012, 136, 144110 CrossRef PubMed.
- X. Deraet, T. Woller, R. Van Lommel, F. De Proft, G. Verniest and M. Alonso, ChemistryOpen, 2019, 8, 788–806 CrossRef CAS PubMed.
- X. Deraet, L. Voets, R. Van Lommel, G. Verniest, F. De Proft, W. De Borggraeve and M. Alonso, J. Org. Chem., 2020, 85, 7803–7816 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, A1133–A1138 CrossRef.
- A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. V. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone, P. Calaminici, E. Cancès, E. A. Carter, P. K. Chattaraj, H. Chermette, I. Ciofini, T. D. Crawford, F. De Proft, J. F. Dobson, C. Draxl, T. Frauenheim, E. Fromager, P. Fuentealba, L. Gagliardi, G. Galli, J. Gao, P. Geerlings, N. Gidopoulos, P. M. W. Gill, P. Gori-Giorgi, A. Görling, T. Gould, S. Grimme, O. Gritsenko, H. J. A. Jensen, E. R. Johnson, R. O. Jones, M. Kaupp, A. M. Köster, L. Kronik, A. I. Krylov, S. Kvaal, A. Laestadius, M. Levy, M. Lewin, S. Liu, P.-F. Loos, N. T. Maitra, F. Neese, J. P. Perdew, K. Pernal, P. Pernot, P. Piecuch, E. Rebolini, L. Reining, P. Romaniello, A. Ruzsinszky, D. R. Salahub, M. Scheffler, P. Schwerdtfeger, V. N. Staroverov, J. Sun, E. Tellgren, D. J. Tozer, S. B. Trickey, C. A. Ullrich, A. Vela, G. Vignale, T. A. Wesolowski, X. Xu and W. Yang, Phys. Chem. Chem. Phys., 2022, 24, 28700–28781 RSC.
- L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- R. P. Iczkowski and J. L. Margrave, J. Am. Chem. Soc., 1961, 83, 3547–3551 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 981–984 Search PubMed.
- W. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS PubMed.
- S. Fias, P. W. Ayers, F. De Proft and P. Geerlings, J. Chem. Phys., 2022, 157, 114102 CrossRef CAS PubMed.
- C. Morell, A. Grand and A. Toro-Labbé, J. Phys. Chem. A, 2005, 109, 205–212 CrossRef CAS PubMed.
- C. Morell, A. Grand and A. Toro-Labbé, Chem. Phys. Lett., 2006, 425, 342–346 CrossRef CAS.
- P. M. Morse, Phys. Rev., 1929, 34, 57–64 CrossRef CAS.
- I. B. Baldus and F. Gräter, Biophys. J., 2012, 102, 622–629 CrossRef CAS PubMed.
- J. Moens, P. Geerlings and G. Roos, Chem. – Eur. J., 2007, 13, 8174–8184 CrossRef CAS PubMed.
- J. Moens, G. Roos, P. Jaque, F. De Proft and P. Geerlings, Chem. – Eur. J., 2007, 13, 9331–9343 CrossRef CAS PubMed.
- C. Bertozzi, ACS Cent. Sci., 2023, 9, 558–559 CrossRef CAS PubMed.
- R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 565–598 CrossRef.
- V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596–2599 CrossRef CAS PubMed.
- M. Meldal and C. W. Tornøe, Chem. Rev., 2008, 108, 2952–3015 CrossRef CAS PubMed.
- E. M. Sletten and C. R. Bertozzi, Angew. Chem., Int. Ed., 2009, 48, 6974–6998 CrossRef CAS PubMed.
- J. M. Baskin, J. A. Prescher, S. T. Laughlin, N. J. Agard, P. V. Chang, I. A. Miller, A. Lo, J. A. Codelli and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16793–16797 CrossRef CAS PubMed.
- P. Thirumurugan, D. Matosiuk and K. Jozwiak, Chem. Rev., 2013, 113, 4905–4979 CrossRef CAS PubMed.
- J. C. Jewett and C. R. Bertozzi, Chem. Soc. Rev., 2010, 39, 1272–1279 RSC.
- K. Li, D. Fong, E. Meichsner and A. Adronov, Chem. – Eur. J., 2021, 27, 5052 CrossRef CAS.
- J. Dommerholt, O. van Rooijen, A. Borrmann, C. F. Guerra, F. M. Bickelhaupt and F. L. van Delft, Nat. Commun., 2014, 5, 5378 CrossRef CAS PubMed.
- R. Göstl and R. P. Sijbesma, Chem. Sci., 2016, 7, 370–375 RSC.
- Y. Zhou, S. P. Centeno, K. Zhang, L. Zheng, R. Göstl and A. Herrmann, Adv. Mater., 2023, 35, 2210052 CrossRef CAS PubMed.
- H. Zhang, F. Gao, X. Cao, Y. Li, Y. Xu, W. Weng and R. Boulatov, Angew. Chem., Int. Ed., 2016, 55, 3040–3044 CrossRef CAS PubMed.
- Z. S. Kean, G. R. Gossweiler, T. B. Kouznetsova, G. B. Hewage and S. L. Craig, Chem. Commun., 2015, 51, 9157–9160 RSC.
- Y. Chen, G. Mellot, D. van Luijk, C. Creton and R. P. Sijbesma, Chem. Soc. Rev., 2021, 50, 4100–4140 RSC.
- H. Qian, N. S. Purwanto, D. G. Ivanoff, A. J. Halmes, N. R. Sottos and J. S. Moore, Chem, 2021, 7, 1080–1091 CAS.
- L. Kortekaas and W. R. Browne, Chem. Soc. Rev., 2019, 48, 3406–3424 RSC.
- M. H. Barbee, T. Kouznetsova, S. L. Barrett, G. R. Gossweiler, Y. Lin, S. K. Rastogi, W. J. Brittain and S. L. Craig, J. Am. Chem. Soc., 2018, 140, 12746–12750 CrossRef CAS PubMed.
- G. R. Gossweiler, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2015, 137, 6148–6151 CrossRef CAS PubMed.
- M. Li, Q. Zhang, Y.-N. Zhou and S. Zhu, Prog. Polym. Sci., 2018, 79, 26–39 CrossRef CAS.
- S. Kumar, F. Zeller and T. Stauch, J. Phys. Chem. Lett., 2021, 12, 9470–9474 CrossRef CAS PubMed.
- J. Sankar, S. Mori, S. Saito, H. Rath, M. Suzuki, Y. Inokuma, H. Shinokubo, K. Suk Kim, Z. S. Yoon, J.-Y. Shin, J. M. Lim, Y. Matsuzaki, O. Matsushita, A. Muranaka, N. Kobayashi, D. Kim and A. Osuka, J. Am. Chem. Soc., 2008, 130, 13568–13579 CrossRef CAS PubMed.
- E. Marcos, J. M. Anglada and M. Torrent-Sucarrat, J. Phys. Chem. C, 2012, 116, 24358–24366 CrossRef CAS.
- M. Torelli, F. Terenziani, A. Pedrini, F. Guagnini, I. Domenichelli, C. Massera and E. Dalcanale, ChemistryOpen, 2020, 9, 261–268 CrossRef CAS PubMed.
- Y. Zhang, Z. Wang, T. B. Kouznetsova, Y. Sha, E. Xu, L. Shannahan, M. Fermen-Coker, Y. Lin, C. Tang and S. L. Craig, Nat. Chem., 2021, 13, 56–62 CrossRef CAS PubMed.
- Y. Sagara, M. Karman, E. Verde-Sesto, K. Matsuo, Y. Kim, N. Tamaoki and C. Weder, J. Am. Chem. Soc., 2018, 140, 1584–1587 CrossRef CAS PubMed.
- Y. M. Sung, J. Oh, W.-Y. Cha, W. Kim, J. M. Lim, M.-C. Yoon and D. Kim, Chem. Rev., 2017, 117, 2257–2312 CrossRef CAS PubMed.
- T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640 CrossRef CAS PubMed.
- M. Chérest, H. Felkin and N. Prudent, Tetrahedron Lett., 1968, 9, 2199–2204 CrossRef.
- N. T. Anh and O. Eisenstein, Nouv. J. Chim., 1977, 1, 61–70 Search PubMed.
Footnote |
| † In most papers, this arbitrary factor of ½ is dropped. |
| This journal is © the Owner Societies 2024 |