Novel two-dimensional magnets with an in-plane auxetic effect

Abstract

The auxetic effect in two-dimensional (2D) materials can not only enhance their mechanical properties but also brings additional tunability of their physical properties. Here, we employ density-functional-theory calculations to report on a class of auxetic 2D magnets, namely, the squarely packed transition metal dichlorides MCl₂ (M = Ti, V, Mn, Fe, Co, Ni). These magnets are dynamically stable and exhibit an intrinsic in-plane auxetic effect. Meanwhile, the transition metal disulfides MS₂ (M = V, Cr, Mn) with the same crystal structure exhibit a positive Poisson's ratio. This indicates that the auxetic effect in MCl₂ is not merely dominated by the crystal structure. We attribute the occurrence of such auxetic behavior to the weak bond stiffness governed by electronic coupling between nearest-neighboring atoms. We find that magnetic ordering of 2D magnets with an auxetic effect is robust under external strain due to the protection of super-exchange interaction coming from the auxetic effect. Super-exchange interaction is sensitive to the symmetry of the crystal structure while the auxetic effect can mitigate the variation of such symmetry. The abundant magnetic properties in combination with the auxetic effect exhibit potential for novel nanodevice applications.

---

Introduction

Intrinsic magnetism in two-dimensional (2D) layered materials has attracted tremendous interest for potential application in nanodevices.^1–4 In the process of nanodevice fabrication, especially for flexible magnetic devices, 2D layered magnets can be subjected to strain, which will affect the performance of the designed devices.^5–8 Meanwhile, the magnetic properties of 2D layered magnets, such as Curie temperature, magnetic anisotropy and magnetic exchange coupling, are relatively sensitive to this strain.^9–14 For example, the Curie temperature of 2D Cr₂Ge₂Se₆ can be up to room temperature (from 144 K to 326 K) under 3% strain,¹⁵ the spin orientation of CrPbTe₃ transitions from in-plane to out of plane under 4% compressive strain,¹⁶ the ferromagnetism of Fe₃GeTe₂ is weakened by compressive strain,¹⁷ and CrI₃ undergoes magnetic phase transition to a different AFM ordering under different magnitudes and directions of in-plane strain.¹⁸

The auxetic effect,¹⁹ which relates the resulting lateral stretch/compression to the applied transverse tensile/compressive axial strain, can result in enhanced mechanical properties, including shear modulus,²⁰ indentation resistance²¹ and fracture toughness.²² The auxetic effect has been predicted or observed in several 2D materials, such as phosphorene, GeS, monolayer arsenic and penta-graphene.^23–28 Associated with the enhanced mechanical properties, the in-plane auxetic effect is maintained and the crystal symmetry of 2D materials is less affected, and hence they retain their electronic properties.^29,30 Therefore, 2D layered magnetic materials with the auxetic effect may exhibit robust magnetic ordering for the designed devices.

In this paper, we report a new class of 2D layered magnetic materials, the squarely packed transition metal dichloride MCl₂ (M = Ti, V, Mn, Fe, Co, Ni) with auxetic effect and transition metal disulfide MS₂ (M = V, Cr, Mn) with non-auxetic effect. The squarely packed materials are reported to exhibit the auxetic effect due to their crystal structure.^25,31,32 By employing density-functional-theory calculations, we find that the intrinsic in-plane auxetic effect in transition metal dichlorides originates from not only the crystal structure but also the electronic structure. The projected density of states calculations reveal that the hybridization of M and Cl elements is weaker than that of M and S elements. The different stiffnesses of hybridization lead to different bond stiffnesses and further induce the movement of X atoms along the lateral direction via the release of strain energy under transverse axial strain. Hence, the occurrence of auxetic behavior is dominated by the bond stiffness governed by electronic coupling. Moreover, MX₂ with the auxetic effect exhibits stable magnetic ordering when a mono-axial strain is applied, which can be attributed to the protection offered by super-exchange interactions. Super-exchange interactions, which determine magnetic ordering, are sensitive to such symmetry. Therefore, stretch in the lateral direction in an auxetic material mitigates the variation of crystal symmetry, thus preventing the change of super-exchange interactions from FM to AFM under transverse tensile strain. These new 2D magnets with stable magnetic ordering under external strain exhibit potential applications in flexible magnetic devices.

Results and discussion

Crystal structure

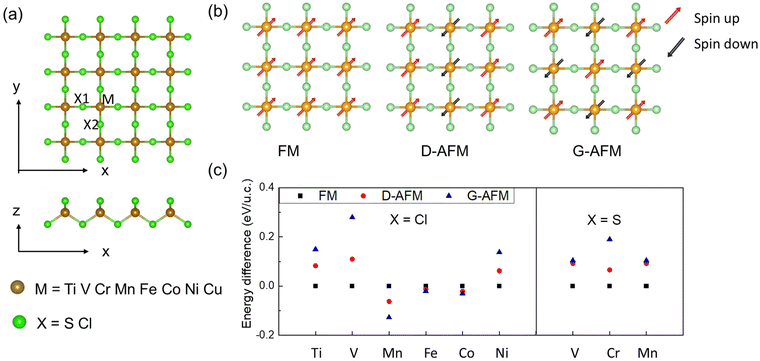
The single layers of transition metal monochlorides/monochalcogenides are formed by a squarely packed layer of metal (M) atoms sandwiched between two layers of chalcogen/sulfur (X) atoms. Each metal atom is connected to four chalcogen/sulfur (X) atoms, constituting a tetrahedron-like bulk SiO₂, as shown in Fig. 1(a). Their dynamic stability has been analyzed by calculating the phonon spectrum, which is shown in Fig. S1.† All the structures of chlorides except CrCl₂ are dynamically stable. Although there is a small acoustic imaginary mode near the Γ-point for MnCl₂ and FeCl₂ monolayers, this instability can be considered as that against long-wavelength transverse waves, and can be removed by ripples in structures. The similar structure observed in thin films has been synthesized using molecular beam epitaxy (MBE) on a substrate.^33,34

Fig. 1 Structure and magnetic states of monolayer MX. (a) Overview and sideview of monolayer MX, where the dark yellow and the green balls indicate the transition metal atoms and sulfur or chlorine, respectively. (b) Schematic top view of three possible magnetic orders of MX: FM order, checkerboard AFM order and collinear AFM order. The red and black arrows represent the up and down spins of transition metal atoms, respectively. (c) The magnetic order in the ground state of MX.

The magnetic ground state is evaluated by considering various magnetic configurations, i.e., ferromagnetic (FM), D-type antiferromagnetic (D-AFM) and G-type antiferromagnetic (G-AFM), and non-magnetic (NM) ordering, respectively, as shown in Fig. 1(b). Here, the D-AFM and G-AFM represent the magnetic strip lying along the [100]^s and [110]^s, respectively. NM ordering is energetically favorable for ZnCl₂ and TiS₂, while the other materials exhibit FM or G-AFM ground states. The relative energies calculated for the FM and two AFM configurations are listed in Fig. 1(c). FM ordering tends to be the ground state when M is Ti, V, Cr, Ni or Cu, whereas G-AFM ordering is more stable for MnCl₂, FeCl₂ and CoCl₂.

Poisson's ratio

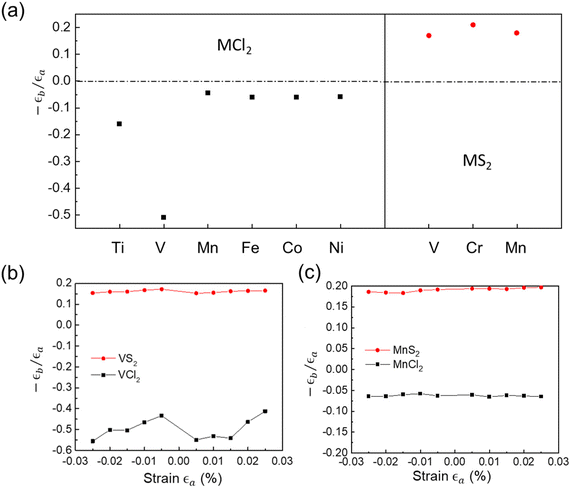
Fig. 2(a) shows our calculated a negative ratio of resulting strain and applied strain −ε_b/ε_a for 10 MX₂ compounds in the y-axis direction when the strain is applied along the x-axis direction from 2.5% compressive strain to 2.5% tensile strain. Remarkably, we find that the sign of the strain ratio is strongly related to the X elements. All MCl₂ compounds exhibit a negative strain ratio, ranging from −0.05 to −0.50. In particular, the strain ratio of VCl₂ is −0.50, which is much larger than that of the other 2D auxetic materials, making it a promising candidate in mechanical nanodevice applications. However, MS₂ compounds exhibit a positive strain ratio of around 0.2. The difference in strain ratios between MCl₂ and MS₂ indicates that MCl₂ exhibits the auxetic effect while MS₂ does not although they share the same crystal structure.

Fig. 2 Auxetic effect. (a) −ε_b/ε_a of MX, where the black and red dots indicate MCl₂ and MS₂, respectively. (b) −ε_b/ε_a of VCl₂ and VS₂ with the strain range from −2.5% to 2.5%. (c) −ε_b/ε_a of MnCl₂ and MnS₂ with the strain range from −2.5% to 2.5%.

We further plotted the calculated −ε_b/ε_a values for VCl₂/VS₂ and MnCl₂/MnS₂, as shown in Fig. 2(b) and (c). The values of −ε_b/ε_a and −ε_a/ε_b should be identical due to the isotropic crystal structure; however, here only, the −ε_b/ε_a value is considered for the auxetic effect calculation. For all compounds, the auxetic effect varies slowly with external strain between −2.5% and 2.5%. VCl₂ exhibits the most significant auxetic effect, in which the negative strain ratio ranges from −0.45 to −0.55. The variation in Poisson's ratio indicates a linear elastic stress response within the strain range considered. The nonlinear stress response of VCl₂ can be attributed to the soft mode from phonon dispersion, which leads to a smaller linear response region. Hence, the type of X element in MX₂, which can be attributed to the electronic structure, determines the existence of the auxetic effect. Similar phenomena have also been found in TMD materials.³⁵

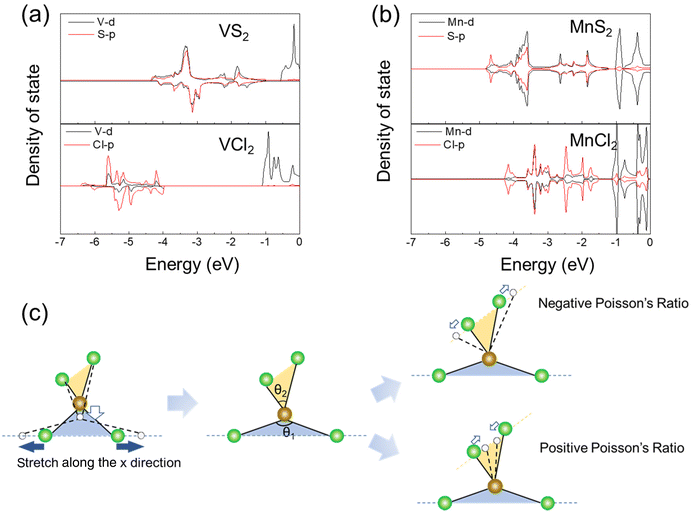
To understand how the electronic structure affects the sign of the Poisson's ratio, we calculate the projected density of states (DOS) of the d orbital of the M atoms and the p orbital of the X atoms, respectively. Here we use VCl₂/VS₂ and MnCl₂/MnS₂ as examples, as shown in Fig. 3(a) and (b). The majority of p orbitals of Cl compounds in MCl₂ are located at the deep states, which are far away from the Fermi level, whereas the majority of d orbitals of M compounds in MCl₂ are near the Fermi level. Comparing with Cl, the p orbitals of S are near the Fermi level, and exhibit stronger p–d hybridization. The hybridization of M–S is stronger than in M–Cl, and the different hybridization stiffnesses indicate different M–X bond stiffnesses, and hence M–S bonds exhibit a stronger bond stiffness than M–Cl bonds due to the stronger coupling of p–d orbitals. Meanwhile, VCl₂ exhibits weaker p–d orbital bonding than MnCl₂, which causes the stronger auxetic effect.

Fig. 3 Deformation mechanism. (a) DOS of VS₂ (upper panel) and VCl₂ (lower panel), (b) DOS of MnS₂ (upper panel) and MnCl₂ (lower panel), where the blue, black and red lines indicate the s and d orbitals of V/Mn atoms, and p orbital of S/Cl atoms, respectively. (c) Deformation mechanism of MX, where the grey and cyan arrows indicate the movement of X atom and M atom, respectively.

To further understand the underlying mechanism responsible for the dichotomy between auxetic and non-auxetic behavior, a schematic of the deformation mechanism is plotted as shown in Fig. 3(c) where the tensile strain is applied along the x-axis direction. The M atom will be less likely to maintain the bond length with the distance increase of X atoms along the x direction, and this leads to an increase of θ₁ and decrease of θ₂. Here, the strain energy is stored in the four M–X bonds, θ₁ and θ₂, which will be released in the subsequent step. The second step determines the sign of the Poisson's ratio. In the second step, the strain energy of MCl₂ stored in the increased θ₁ can be transmitted to the decreasing θ₂ through the elastic M–Cl bonds; thus the decrease in θ₂ releases the strain energy through the increase of θ₂ and leads to the auxetic effect. However, the strain energy of MS₂ stored in the increased θ₁ is released simultaneously due to the rigid M–S bonds, and the strain energy caused by the movement of M compounds is released through the decrease of M–S bond length in the resulting strain direction, further resulting in the decrease of θ₂, and leading to the non-auxetic effect.

Stability of magnetic ordering under strain

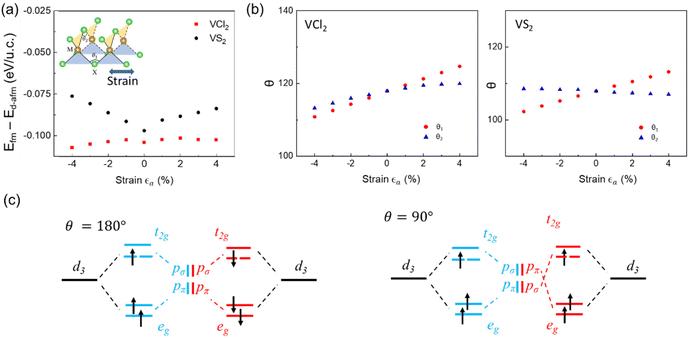
The magnetic properties can usually be tuned by strain, and even lead to magnetic phase transitions. 2D magnets undergo external strain when used in nanodevices. Hence, the stability of the magnetic ground state of 2D magnets can influence the performance of the nanodevices when the external strain is induced due to the mismatch of different composites. Moreover, 2D magnets and other components of the nanodevices are usually arranged via one side, and thus the 2D magnets undergo monoaxial strain. Here we use VCl₂ and VS₂ as examples to indicate that 2D magnets with the auxetic effect exhibit higher stability when a monoaxial external strain is applied. According to our previous calculation, both VCl₂ and VS₂ exhibit ferromagnetic ground states. We then apply 1–4% compressive and tensile strains along the x-axis, as shown in the inset image of Fig. 4(a). The energy difference of FM and D-AFM is shown in Fig. 4(a). With the increase of compressive strain up to 4%, the energy difference of VS₂ decreases from 0.09 eV per u.c. to 0.075 eV per u.c., while a similar phenomenon is also found when the tensile strain is applied, when the energy difference is 0.08 eV per u.c. with 4% tensile strain. This indicates that the stability of the magnetic ground states of VS₂ gradually becomes lower when external strain is applied. However, the energy difference of VCl₂ becomes almost constant (around 0.11 eV per u.c.) when the external strain is applied, which indicates that the FM ground state is stable with external strain.

Fig. 4 Stability of magnetic ground states under strain. (a) The energy difference of VCl₂ and VS₂ under external strain from −4% to 4%, where E_diff = E_FM − E_D-AFM. The inset image indicates a schematic of monoaxial strain along the x direction. (b) The change of θ₁ and θ₂ of VCl₂ and VS₂ under external strain from −4% to 4%, where θ₁ and θ₂ indicate the of M–X–M bond angle along the x- and y-axis directions, respectively. (c) Diagrams for super-exchange paths between the nearest-neighbour M 3d orbitals via X 3p ligands with different angles.

To explain the different stabilities of magnetic ground states under strain of VCl₂ and VS₂, we plotted the change of the M–X–M bond angle along the x- and y-axis directions (θ₁ and θ₂ for the x- and y-axis directions, as shown in the inset image of Fig. 4(a)) of VCl₂ and VS₂ with different external strains, respectively. As shown in Fig. 4(b), the trend of θ₂ is identical to that of θ₁ for VCl₂, where θ₁ and θ₂ increase with the tensile strain and decrease with the compressive strain, whereas the trend of θ₁ and θ₂ is in contrast for VS₂. This difference can be attributed to the auxetic effect of VCl₂ and non-auxetic effect of VS₂. Since the magnetic properties are due to electron–electron interactions, the relative position of M atoms and the nearest neighbor X atoms can change the magnetic ground states via the changing strength of electron–electron interactions.

The underlying physics of the magnetic ground states can be effectively described by the super-exchange interaction (SEI) with the nearest neighbor M atoms mediated by the X 3p orbital. Here, each d–p–d super-exchange interaction path can be viewed as the competitive interaction between θ = 180° and 90°, as shown in Fig. 4(c). When θ is 180°, M₁–X–M₂ can be viewed as sharing the same main axis, which indicates that the p_σ orbital for Cl in the M₁–X bond is also the p_σ orbital for X in the M₂–X bond while p_π follows the same rule. Given the orbital symmetry relationship, the t_2g orbital bonds with the p_σ orbital, while the e_g orbital bonds with the p_π orbital. The SEI can only be accessible through the t_2g–p_σ–t_2g path and the e_g–p_π–e_g path. Based on the Pauli exclusion principle, the electron jumps through the SEI path and forms an AFM interaction. The interaction is different when θ is 90°, when M₁–X–M₂ can be viewed as occupying a different axis, and the SEI path becomes t_2g–p_σ/p_π–e_g and e_g–p_π/p_σ–t_2g. Since p_σ and p_π are different orbitals, the electron jumps through the SEI path and forms an FM interaction based on Hund's rule, as shown by the dashed lines in Fig. 4(c).

Hence, the FM ground states of VCl₂ and VS₂ indicate that the two SEI paths are competitive and the t_2g–p_σ/p_π–e_g path dominates the SEI. When the external strain is applied, θ₁ and θ₂ change and exhibit different trends for VS₂, which indicate the break of crystal symmetry. The large variation of symmetry can more easily cause the SEI path along the y direction to change to the t_2g–p_σ–t_2g path and induce the instability of the FM interaction. However, θ₁ and θ₂ of VCl₂ exhibit identical change trends due to the auxetic effect, and the crystal symmetry is less affected. The auxetic effect weakens the change in the SEI path and promotes the stability of FM ground states.

Conclusion

We investigated the mechanical and magnetic properties of a family of 2D layered magnetic material transition metal dichlorides, MCl₂, with the auxetic effect. In particular, the Ti₂, V₂ and Ni compounds exhibit ferromagnetic ordering while the Mn, Fe and Co compounds exhibit antiferromagnetic ordering. Among the MCl₂ compounds, VCl₂ exhibits the largest negative Poisson's ratio (−0.5). In contrast, with many auxetic materials, the Poisson's ratio of MCl₂ compounds also depends on the electronic structure, especially p–d orbital hybridization. Weak hybridization stiffness induces weak bond stiffness; hence the strain energy is stored in the bond instead of the angle and leads to the auxetic effect. Meanwhile, the auxetic effect can promote the stability of magnetic ground states under external strain, which can be attributed to the prevention of changes to the super-exchange interaction path. Our work enriches the knowledge of 2D magnets and paves a new way to maintain the stability of magnetic ordering for future nanodevice applications.

Computational methods

The calculations were performed using the Vienna ab initio simulation package (VASP).^36,37 The projector augmented wave (PAW) method was applied.^38,39 A plane wave basis set with a cutoff energy of 700 eV was used to expand the wave functions. For the exchange and correlation, we mainly employed the Perdew–Burke–Ernzerhof (PBE) functionals.⁴⁰ Atomic coordinates were fully optimized until the forces were smaller than 0.001 eV Å⁻¹. We used a vacuum spacing of 20 Å, which reduced the image interactions caused by the periodic boundary conditions. The Brillouin-zone integration was carried out using 24 × 24 × 1 Monkhorst–Pack k-point meshes for the monolayer MX₂. The structure figures were produced using VESTA.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by grants from the National Key R&D Program of China (No. 2019YFA0308500), the National Natural Science Foundation of China (52250402 and 61888102), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB30000000), and the CAS Project for Young Scientists in Basic Research (YSBR-003).

References

1. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, et al., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270.
2. I. A. Verzhbitskiy, H. Kurebayashi, H. Cheng, J. Zhou, S. Khan, Y. P. Feng and G. Eda, Controlling the Magnetic Anisotropy in Cr₂Ge₂Te₆ by Electrostatic Gating, Nat. Electron., 2020, 3, 460.
3. C. Gong and X. Zhang, Two-dimensional magnetic crystals and emergent heterostructure devices, Science, 2019, 363, 4450.
4. B. Huang, G. Clark, D. R. Klein, D. MacNeill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. McGuire, D. H. Cobden and D. Xiao, et al., Electrical control of 2D magnetism in bilayer CrI₃, Nat. Nanotechnol., 2018, 13, 544.
5. N. Pérez, M. Melzer, D. Makarov, O. Ueberschär, R. Ecke, S. E. Schulz and O. G. Schmidt, High-performance giant magnetoresistive sensorics on flexible Si membranes, Appl. Phys. Lett., 2015, 106, 153501.
6. Y. Ling, Y. Hu, H. Wang, B. Niu, J. Chen, R. Liu, Y. Yuan, G. Wang, D. Wu and M. Xu, et al., Strain Control of Phase Transition and Exchange Bias in Flexible Heusler Alloy Thin Films, ACS Appl. Mater. Interfaces, 2021, 13, 24285–24294.
7. H. Matsumoto, S. Ota, T. Koyama and D. Chiba, Control of magnetic anisotropy in a Co thin film on a flexible substrate by applying biaxial tensile strain, Appl. Phys. Lett., 2021, 118, 022406.
8. B. Miranda-Silva, P. H. C. Taveira, A. W. Teixeira, J. M. Fonseca, L. N. Rodrigues, R. G. Elías, A. Riveros, N. Vidal-Silva and V. L. Carvalho-Santos, Manipulating the shape of flexible magnetic nanodisks with meronlike magnetic states, Phys. Rev. B, 2022, 105, 104430.
9. M. Šiškins, S. Kurdi, M. Lee, B. J. M. Slotboom, W. Xing, S. Mañas-Valero, E. Coronado, S. Jia, W. Han and T. van der Sar, et al., Nanomechanical probing and strain tuning of the Curie temperature in suspended Cr₂Ge₂Te₆-based heterostructures, npj 2D Mater. Appl., 2022, 6, 41.
10. Z. Wu, Z. Shen, Y. Xue and C. Song, Strain-induced topological phase transition and enhanced Curie temperature in MnBi₂Te₄/CrI₃ heterojunction, Phys. Rev. Mater., 2022, 6, 014011.
11. M. X. Guo, C. K. Cheng, Y. C. Liu, C. N. Wu, W. N. Chen, T. Y. Chen, C. T. Wu, C. H. Hsu, S. Q. Zhou and C. F. Chang, et al., Single-crystal epitaxial europium iron garnet films with strain-induced perpendicular magnetic anisotropy: Structural, strain, magnetic, and spin transport properties, Phys. Rev. Mater., 2022, 6, 054412.
12. J. Cenker, S. Sivakumar, K. Xie, A. Miller, P. Thijssen, Z. Liu, A. Dismukes, J. Fonseca, E. Anderson and X. Zhu, et al., Reversible strain-induced magnetic phase transition in a van der Waals magnet, Nat. Nanotechnol., 2022, 17, 256–261.
13. L. Wu, L. Zhou, X. Zhou, C. Wang and W. Ji, In-plane epitaxy-strain-tuning intralayer and interlayer magnetic coupling in CrSe₂ and CrTe₂ monolayers and bilayers, Phys. Rev. B, 2022, 106, L081401.
14. W.-R. Liu, X.-J. Dong, Y.-Z. Lv, W.-X. Ji, Q. Cao, P.-J. Wang, F. Li and C.-W. Zhang, Magnetic anisotropy and ferroelectric-driven magnetic phase transition in monolayer Cr₂Ge₂Te₆, Nanoscale, 2022, 14, 3632.
15. X.-J. Dong, J.-Y. You, B. Gu and G. Su, Strain-Induced Room-Temperature Ferromagnetic Semiconductors with Large Anomalous Hall Conductivity in Two-Dimensional Cr₂Ge₂Se₆, Phys. Rev. Appl., 2019, 12, 014020.
16. I. Khan and J. Hong, High Curie temperature and strain-induced semiconductor-metal transition with spin reorientation transition in 2D CrPbTe₃ monolayer, Nanotechnology, 2020, 31, 195704.
17. X. Hu, Y. Zhao, X. Shen, A. V. Krasheninnikov, Z. Chen and L. Sun, Enhanced Ferromagnetism and Tunable Magnetism in Fe₃GeTe₂ Monolayer by Strain Engineering, ACS Appl. Mater. Interfaces, 2020, 12, 26367.
18. M. Pizzochero and O. V. Yazyev, Inducing Magnetic Phase Transitions in Monolayer CrI₃ via Lattice Deformations, J. Phys. Chem. C, 2020, 124, 7585.
19. K. E. Evans, M. A. Nkansah, I. J. Hutchinson and S. C. Rogers, Molecular network design, Nature, 1991, 353, 124.
20. J. B. Choi and R. S. Lakes, Non-linear properties of metallic cellular materials with a negative Poisson's ratio, J. Mater. Sci., 1992, 27, 5375.
21. R. S. Lakes and K. Elms, Indentability of conventional and negative Poisson's ratio foams, J. Compos. Mater., 1993, 27, 1193.
22. J. B. Choi and R. S. Lakes, Fracture toughness of re-entrant foam materials with a negative Poisson's ratio: experiment and analysis, Int. J. Fract., 1996, 80, 73.
23. J. W. Jiang and H. S. Park, Negative poisson's ratio in single-layer black phosphorus, Nat. Commun., 2014, 5, 7.
24. X. Kong, J. Deng, L. Li, Y. Liu, X. Ding, J. Sun and J. Z. Liu, Tunable auxetic properties in group-IV monochalcogenide monolayers, Phys. Rev. B, 2018, 98, 184104.
25. Z. Gao, X. Dong, N. Li and J. Ren, Novel two-dimensional silicon dioxide with in-plane negative Poisson's ratio, Nano Lett., 2017, 17, 772.
26. J. Mannix Andrew, X.-F. Zhou, B. Kiraly, D. Wood Joshua, D. Alducin, D. Myers Benjamin, X. Liu, L. Fisher Brandon, U. Santiago and R. Guest Jeffrey, et al., Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs, Science, 2015, 350, 1513.
27. V. O. Özçelik, S. Cahangirov and S. Ciraci, Stable single-layer honeycomblike structure of silica, Phys. Rev. Lett., 2014, 112, 246803.
28. Y. Wang, F. Li, Y. Li and Z. Chen, Semi-metallic Be₅C₂ monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson's ratio, Nat. Commun., 2016, 7, 11488.
29. L. Kou, Y. Ma, C. Tang, Z. Sun, A. Du and C. Chen, Auxetic and Ferroelastic Borophane: A Novel 2D Material with Negative Possion's Ratio and Switchable Dirac Transport Channels, Nano Lett., 2016, 16, 7910.
30. M. E. Kilic and K.-R. Lee, Tetrahex carbides: Two-dimensional group-IV materials for nanoelectronics and photocatalytic water splitting, Carbon, 2021, 174, 368–381.
31. X. Chen, D. Wang, X. Liu, L. Li and B. Sanyal, Two-Dimensional Square-A₂B (A = Cu, Ag, Au, and B = S, Se): Auxetic Semiconductors with High Carrier Mobilities and Unusually Low Lattice Thermal Conductivities, J. Phys. Chem. Lett., 2020, 11, 2925–2933.
32. W. Jin, W. Sun, X. Kuang, C. Lu and L. Kou, Negative Poisson Ratio in Two-Dimensional Tungsten Nitride: Synergistic Effect from Electronic and Structural Properties, J. Phys. Chem. Lett., 2020, 11, 9643–9648.
33. V. H. Etgens, P. C. de Camargo, M. Eddrief, R. Mattana, J. M. George and Y. Garreau, Structure of Ferromagnetic CrAs Epilayers Grown on GaAs(001), Phys. Rev. Lett., 2004, 92, 167205.
34. V. F. Agekyan, P. O. Holz, G. Karczewski, V. N. Katz, E. S. Moskalenko, A. Y. Serov and N. G. Filosofov, Magnetoluminescence of CdTe/MnTe/CdMgTe heterostructures with ultrathin MnTe layers, Semiconductors, 2011, 45, 1301–1305.
35. L. Yu, Q. Yan and A. Ruzsinszky, Negative Poisson's ratio in 1T-type crystalline two-dimensional transition metal dichalcogenides, Nat. Commun., 2017, 8, 15224.
36. G. Kresse and J. Furthmuller, Efficient Iterative Schemes for ab Initio Total-energy Calculations Using a Plane-wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
37. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15.
38. P. E. Blochl, Projector Augmented-wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr01458d

---