Ultraflexible two-dimensional Janus heterostructure superlattice: a novel intrinsic wrinkled structure†
Kai
Ren
 *a,
Guoqiang
Zhang
b,
Lifa
Zhang
c,
Huasong
Qin
*a,
Guoqiang
Zhang
b,
Lifa
Zhang
c,
Huasong
Qin
 *b and
Gang
Zhang
*b and
Gang
Zhang
 *d
*d
aSchool of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing, Jiangsu 210037, China. E-mail: kairen@njfu.edu.cn
bLaboratory for Multiscale Mechanics and Medical Science, SV LAB, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: huasongqin@xjtu.edu.cn
cNNU-SULI Thermal Energy Research Center, and Center for Quantum Transport and Thermal Energy Science (CQTES), School of Physics and Technology, Nanjing Normal University, Nanjing 210023, China
dInstitute of High Performance Computing, A*STAR, Singapore 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
First published on 17th April 2023
Abstract
The recently reported two-dimensional Janus transition metal dichalcogenide materials present promising applications such as in transistors, photocatalysts, and thermoelectric nanodevices. In this work, using molecular dynamics simulations, the self-assembled in-plane MoSSe/WSSe heterostructure superlattice is predicted with a natural sinusoidal structure constructed by an asymmetric interface. Such a sinusoidal structure shows extraordinary mechanical behavior where the fracture strain can be enhanced up to 4.7 times than that of the symmetrical interface. Besides, the deformational structure of all these MoSSe/WSSe heterostructure superlattice are in accordance with the Fourier function curve; the fracture strength and fracture strain also demonstrate pronounced size dependence. Our investigations proposed an ultrastretchable assembled heterostructure superlattice and provided a desirable strategy to tune the mechanical properties of such an in-plane two-dimensional heterostructure.
1. Introduction
Nowadays, two-dimensional (2D) materials are explored by abundant efforts, encouraged by graphene, which was found to possess extraordinary properties.1 Although the Dirac cone in graphene contributes to ultrafast mobility,2 such zero bandgap characteristic also restricts some applications such as field-effect transistors.3 Thus, transition metal dichalcogenide (TMD) materials (MoS2, WS2, etc.) have attracted extensive research attention and also have high carrier mobility.4 Besides, the decent bandgap of TMDs results in novel physical and chemical properties, such as photocatalyst for water splitting.5,6 Recently, Janus MoSSe monolayer was prepared to reveal out-of-plane piezoelectricity for future spintronics7 because of the broken symmetry. MoSSe and WSSe monolayers present thermal conductivity of about 51.27 W m−1 K−1 and 47.90 W m−1 K−1, respectively, which still has obvious temperature dependence.8 MoSSe was also found to be promising in various applications, such as photocatalyst,9 electronics,10 and energy conversion.11,12 Besides, the novel magnetic and thermal performances are also explored for other 2D materials.13–15For 2D materials, the effective strength of the monolayer used in engineering is decided by the fracture toughness instead of the intrinsic strength of atomic bonds. The failure characteristic of graphene results from a brittle manner, and the measured fracture toughness of graphene is about 4.0 MPa.16 Negative Poisson's ratio is found in some 2D materials, such as δ-SiSe (about −0.29),17 Li2B12 (about −0.03),18 B4N (about −0.02),19 and δ-CS (about −0.19),20 which is contributed by their particular structure. Such auxetic materials are promising candidates for composites and aviation.21 Besides, 2D materials also illustrate desirable external strain-dependence on thermal22 and electronic23 performances. To create more applications for 2D materials, heterostructures are constructed. For example, van der Waals heterostructure possessing type-II band alignment can separate the photogenerated charges and prolong the lifetime of electrons and holes.24 Differently, in-plane heterostructure is built by covalent bonding between the two materials. The in-plane MoS2/WSe2 heterostructure was recently synthesized,25 and the fracture stress of the heterostructure can be tuned by interface, temperature, and introduced cracks.26 The in-plane Janus MoSSe/WSSe heterostructure is also successfully prepared,27 suggesting an intrinsic thermomechanical coupled interface.28 Furthermore, the in-plane self-assembled heterostructure superlattice is obtained in experiments, such as WSe2/WS2,29,30 which possesses diode characteristics with an ultrahigh rectification ratio of about 105. These heterostructure superlattices have excited critical consideration because of the novel quantum phenomena, such as mini-Dirac points,31 Mott insulator states,32 minimized lattice thermal conductivity,33 and moiré exciton bands.34 In particular, the band structure of the Janus MoSSe/WSSe superlattice can be changed from type-I to type-II by intrinsic structural parameters and used as a photocatalyst for water splitting,35 which can also be effectively tuned by external strain and electric field.36 The Janus MoSSe/WSSe superlattice nanoribbon can even be transformed as half-metal and magnetic material using decent ribbon width,37 while the influence of superlattice configuration on the mechanical behaviors of the 2D in-plane heterostructure is rarely reported. In addition, the intrinsic bending at the interface of in-plane Janus MoSSe/WSSe heterostructure decides the mechanical strength, which can provide a theoretical guidance for further devices. However, the bending characteristic of the in-plane Janus MoSSe/WSSe heterostructure is not well investigated.
In this work, the in-plane Janus MoSSe/WSSe heterostructure superlattice is predicted to be stable with an almost sinusoidal structure by a decent interface. Then, the tunable mechanical behaviors of the heterostructure superlattice are investigated by different size parameters of the MoSSe and WSSe using molecular dynamics method, which shows an ultrastretchable characteristic.
2. Geometric structure and computational methods
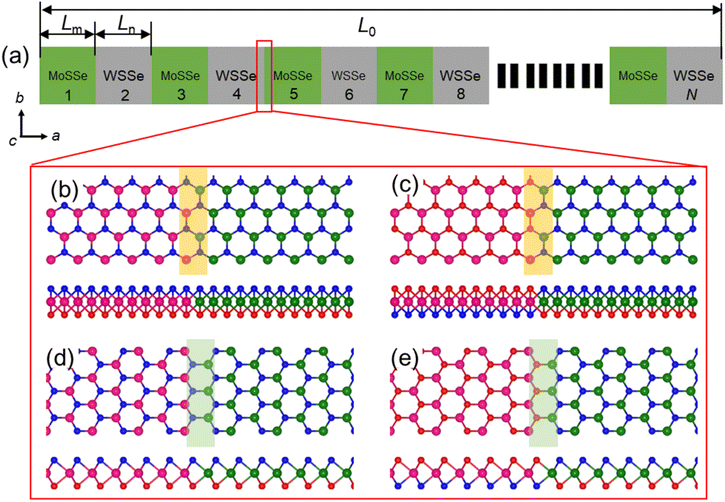
In our investigation, all the simulations are implemented by Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).38 The visualization of the atomic structure was obtained by the OVITO package.39 The interatomic interactions of the in-plane MoSSe/WSSe heterostructure were employed by the Stillinger–Weber (SW) potential, which was proposed by Jiang and can provide the accurate prediction of the structure and mechanical properties of TMDs.40,41 The stress–strain curve and the Young's modulus of MoS2 calculated using this SW potential developed by Jiang is comparable with the experimental data,42,43 which demonstrates the accuracy of the SW potential in studying the mechanical properties of this type of materials. The in-plane MoSSe/WSSe heterostructure superlattice was constructed referring in Fig. 1(a), where the total number of MoSSe and WSSe components is decided by N. Besides, the periodic boundary condition was set along the a, b, and c directions in the simulations. The length of the MoSSe, WSSe, and MoSSe/WSSe heterostructure was denoted as Lm, Ln, and L0, respectively. Importantly, the possible interfacial types of the MoSSe/WSSe heterostructure were further demonstrated by Fig. 1(b)–(e), named as armchair-A (AA), armchair-B (AB), zigzag-A (ZA), and zigzag-B (ZB), respectively. For AA MoSSe/WSSe heterostructure in Fig. 1(b), the Se and S atoms are arranged on the same side in the MoSSe and WSSe with the armchair interface. To obtain the AB MoSSe/WSSe heterostructure, the Se and S atoms are located on the opposite sides in the MoSSe and WSSe. Similarly, the ZA and ZB MoSSe/WSSe heterostructure can be constructed. It is worth noting that the interfacial structure of the lateral MoSSe/WSSe can be synthesized in the experiment.27,44–47 The size and periodicity of the TMDs heterostructure superlattice also can be controlled down to the nanometer scale.30 Furthermore, to obtain a stable superlattice structure, the structure was relaxed by NPT ensemble (isothermal and isobaric) for 40 ns at 300 K with the time step of 1 fs. During the relaxation process, the temperature and energy of the system are monitored and reached a steady state. In addition, the layer thickness of the studied system was 0.61 nm.41For the mechanical test, the uniaxial tension was conducted under a strain rate of 2 × 108 s−1 along the a direction using the fix/deform procedure in LAMMPS.38 The temperature of the system was set as 300 K and zero pressure was applied along the b direction for the tensile deformation. To study the mechanical properties of the MoSSe/WSSe heterostructure superlattice, the normal stress was monitored in the calculations. The atomic virial stress of the Se, S, Mo, and W atoms is decided by
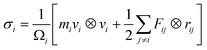 | (1) |
3. Results and discussion
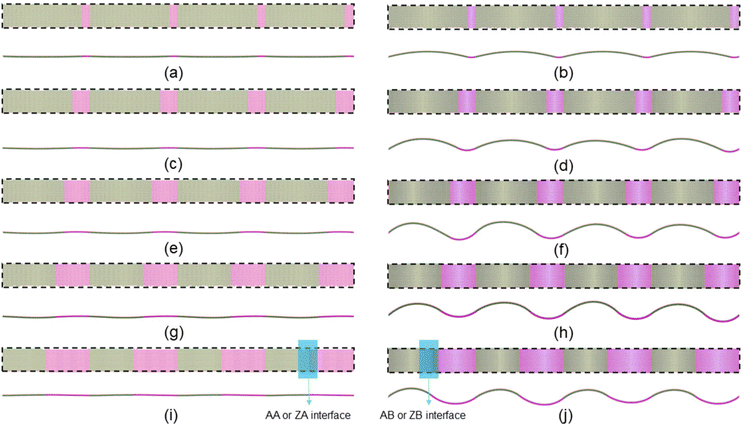
The lattice constants of the MoSSe and WSSe monolayers are 3.228 Å and 3.269 Å, respectively, which have been reported in our previous work by first-principles calculations.28 Thus, the lattice mismatch is about 1.26% for armchair and zigzag MoSSe/WSSe interface. Then, we design the self-assembled AA, AB (ZA and ZB) MoSSe/WSSe heterostructure superlattices. For the AA and AB MoSSe/WSSe heterostructure superlattices, the initial length and the width are 619.776 Å and 50.3195 Å, respectively. Besides, the initial length and width are 715.656 Å and 51.648 Å, respectively, for the ZA and ZB MoSSe/WSSe heterostructure superlattices. The periodic boundary condition is applied for the a, b, and c directions. In this work, the initial length and width of the total MoSSe/WSSe heterostructure superlattice are fixed, and the length of the MoSSe and WSSe sections is considered as a variable parameter.Firstly, we explore the impact of the length ratio Lm/Ln on the optimized structure. After the structural relaxation, the intrinsic configurations of the AA and AB MoSSe/WSSe heterostructure superlattice with different Lm/Ln are presented in Fig. 2. Obviously, the AA heterostructure superlattice still presents an almost smooth monolayer, as shown in Fig. 2(a), (c), (e), (g), and (i), while the AB heterostructure superlattice folds regularly because of the interface bending, as shown in Fig. 2(b), (d), (f), (h), and (j). In particular, when Lm/Ln increases to 1, the nearly perfect sinusoidal structure monolayer is obtained, as shown in Fig. 2(j). This intrinsic characteristic is different from other analogous folding or wrinkled monolayers through external strain.48–50 The same phenomenon also occurs in the heterostructure superlattice with a zigzag interface.
Inspired by the spontaneous bending structure of the MoSSe/WSSe heterostructure superlattice, the quantitative characteristics of such a trajectory were addressed. Here, to explore the tunable properties of the heterostructure superlattice, the length of the MoSSe and WSSe sections is fixed as L = Lm = Ln, as demonstrated in Fig. 1. Then, N is considered as 4, 8, 16, 32, and 64, which means that L should be 15.49 nm, 7.75 nm, 3.87 nm, 1.94 nm, and 0.97 nm, respectively, in AA and AB MoSSe/WSSe heterostructure superlattices. Similarly, L is 17.92 nm, 8.95 nm, 4.48 nm, 2.24 nm, and 1.12 nm in the calculations for the ZA and ZB MoSSe/WSSe heterostructure superlattices. We extracted the coordinate of the atoms in the c direction; after averaging them, the intermediate atomic coordinates are set as zero. Thus, the trajectories of the MoSSe/WSSe heterostructure superlattice is obtained. After the fitting method, we found that the side-view curves of all these relaxed structures follow Fourier function perfectly, the fitted Fourier function of the armchair and zigzag MoSSe/WSSe heterostructure superlattice with different L (L = Lm = Ln) is presented in Fig. 3(a). Clearly, the curve amplitude of these obtained MoSSe/WSSe heterostructure superlattices can be enlarged by increased L, as shown in Fig. 3(b). This is because both sides of the individual MoSSe (or WSSe) section are applied to opposite intrinsic forces; when Lm (or Ln) is not long enough, the MoSSe (or WSSe) is hard to be bend. Thus, the curve amplitude decreases when L decreases. Furthermore, the functions of trajectories of the MoSSe/WSSe heterostructure superlattice in the Fig. 3(a) are also defined as y = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(bx) + c
sin(bx) + c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(dx) + e, which were fitted, and the details are presented in Table 1.
cos(dx) + e, which were fitted, and the details are presented in Table 1.
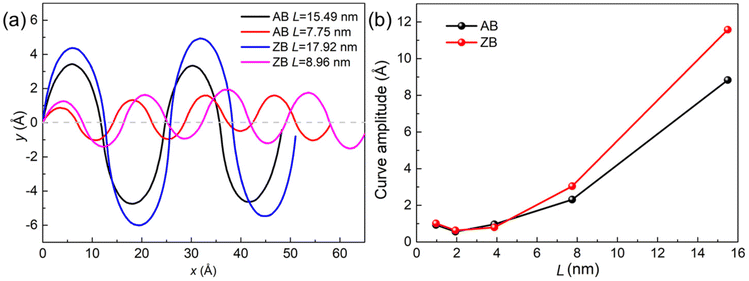 | ||
| Fig. 3 (a) The fitted Fourier curve for the structural trajectory of the MoSSe/WSSe heterostructure superlattice and (b) the amplitude value of the Fourier curve versus L. | ||
| a | b | c | d | e | |
|---|---|---|---|---|---|
| AB L = 15.49 | 0.67 | 0.26 | −4.36 | 0.26 | 0.071 |
| AB L = 7.75 | 0.84 | 0.43 | −0.79 | 0.43 | 0.050 |
| ZB L = 17.92 | −4.22 | 0.24 | −3.97 | 0.24 | −0.01 |
| ZB L = 8.96 | 0.78 | 0.38 | −1.31 | 0.38 | −0.01 |
The fracture behaviors of the MoSSe and WSSe monolayers are calculated. For uniaxial tension along the armchair direction, the fracture strain of the MoSSe (or WSSe) monolayer is 0.113 (or 0.140) with the fracture stress of 12.66 GPa (or 19.85 GPa). While for uniaxial tension along the zigzag direction, the fracture strain of the MoSSe (and WSSe) monolayers is 0.100 (and 0.120) with the fracture stress of 11.25 GPa (and 17.06 GPa), respectively. Obviously, the WSSe monolayer has higher mechanical strength than the MoSSe monolayer. Thus, the initial crack emerges in the MoSSe section in the MoSSe/WSSe heterostructure superlattice, as shown in Fig. 4, when the heterostructure superlattice is applied to the external strain. The crack nucleation of the MoSSe/WSSe heterostructure superlattice with AA, AB, ZA, and ZB interfaces are demonstrated by Fig. 4(a)–(d), respectively. Note that the atomic stress under tension along the zigzag MoSSe/WSSe heterostructure superlattice is larger, and the initial crack length is also longer. Furthermore, compared with the AA (or ZA) MoSSe/WSSe heterostructure superlattice, the required fracture stress is enhanced in AB (or ZB) heterostructure superlattice.
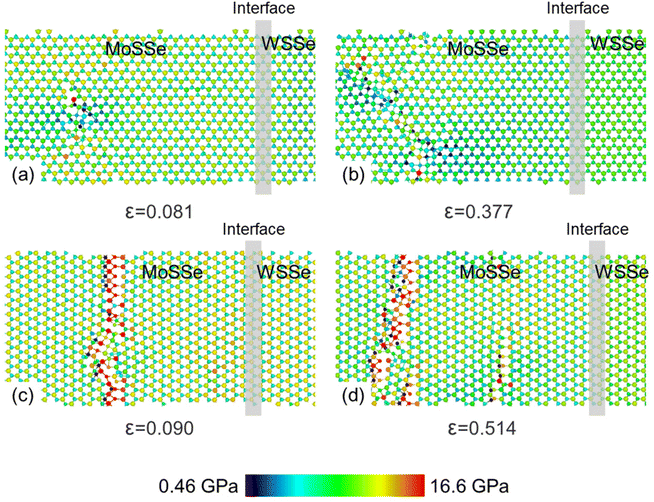 | ||
| Fig. 4 The crack nucleation of the MoSSe/WSSe heterostructure superlattice with (a and c) AA and (b and d) AB interfaces. L is 15.494 nm and 17.92 nm, respectively, in (a and b) and (b and d). | ||
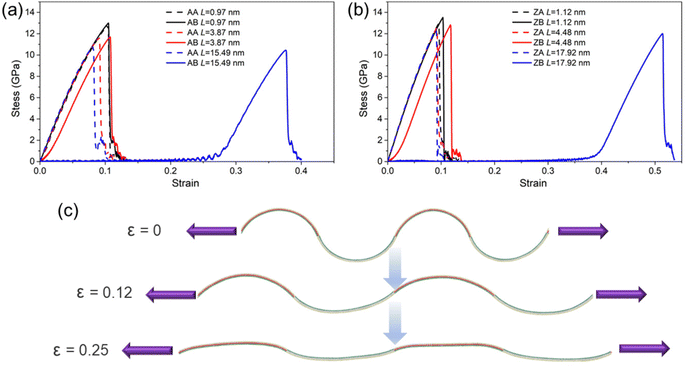
To further investigate the tunable strain–stress relationships of the MoSSe/WSSe heterostructure superlattice, the response of the stress on external uniaxial strain of the armchair and zigzag heterostructure superlattice is studied. The nonlinear elastic behavior is shown in Fig. 5. It is worth noting that the fracture strength of the AA (or ZA) and the AB (or ZB) MoSSe/WSSe heterostructure superlattice is comparable when L is 0.97 nm (or 1.12 nm). On the other side, the process of tension fracture for the AB and ZB MoSSe/WSSe heterostructure superlattice is prolonged substantially, as shown in Fig. 5(a) and (b); even the stress of the AB and ZB MoSSe/WSSe heterostructure superlattice remains very low before the strain increases to 0.28 and 0.38, respectively. This is because the relaxed state of the AB and ZB MoSSe/WSSe heterostructure superlattice is the bending structure; then, it needs to go through the process of being flattened before catastrophic damage, as shown in Fig. 5(c). Besides, the fracture stress MoSSe/WSSe heterostructure superlattice is higher than that of the MoS2/WS2 heterostructure (11.95 GPa along the zigzag direction and 12.55 GPa along the armchair direction) with N = 4.26 Furthermore, the fracture strain with N = 4 is also much higher than that of the MoS2/WS2 heterostructure (9.6% along the zigzag direction and 9.4% along the armchair direction). Moreover, the stress–strain relationship of the AA MoSSe/WSSe heterostructure superlattice with L = 0.97 nm is also calculated by density functional theory (DFT) calculations. As shown in Fig. S1 in the ESI,† the results calculated using empirical potential agree well with those calculated using DFT, further demonstrating the accuracy of the SW potential used in this work.
The fracture stress of the MoSSe/WSSe heterostructure superlattice with armchair and zigzag interfaces with different L (here, we set L = Lm = Ln) are presented in Fig. 6(a). It can be seen that the MoSSe/WSSe heterostructure superlattice with zigzag interfaces possesses stronger fracture stress than that of armchair one, and all these heterostructure superlattices present a decreased fracture stress with L increasing. Importantly, the fracture stress of the AA (or ZA) MoSSe/WSSe heterostructure superlattice can exceed that of the AB (or ZB) with increased L. Besides, the size-dependent fracture strain (σF) of the MoSSe/WSSe heterostructure superlattice is also studied. We use the fracture strain growth ratio (η), which is defined as η = (σF-AB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (or
(or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZB) − σF-AA
ZB) − σF-AA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (or
(or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZA))/σF-AA
ZA))/σF-AA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (or
(or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZA), to evaluate the response of the fracture strain on L. As shown in Fig. 6(b), the rapid growth of η is obtained when L increases. In detail, the fracture strain of the AA (or ZA) MoSSe/WSSe heterostructure superlattices can be greatly improved by 3.7 (or 4.7) times using the AB (or ZB) interface. Therefore, the toughness of the MoSSe/WSSe heterostructure superlattice can be significantly enhanced by the asymmetric (AB and ZB) interface, which also illustrates the ultraflexible behavior. Furthermore, the exponential function relationship is found between the fracture strain growth and L, as shown in Fig. 6(b).
ZA), to evaluate the response of the fracture strain on L. As shown in Fig. 6(b), the rapid growth of η is obtained when L increases. In detail, the fracture strain of the AA (or ZA) MoSSe/WSSe heterostructure superlattices can be greatly improved by 3.7 (or 4.7) times using the AB (or ZB) interface. Therefore, the toughness of the MoSSe/WSSe heterostructure superlattice can be significantly enhanced by the asymmetric (AB and ZB) interface, which also illustrates the ultraflexible behavior. Furthermore, the exponential function relationship is found between the fracture strain growth and L, as shown in Fig. 6(b).
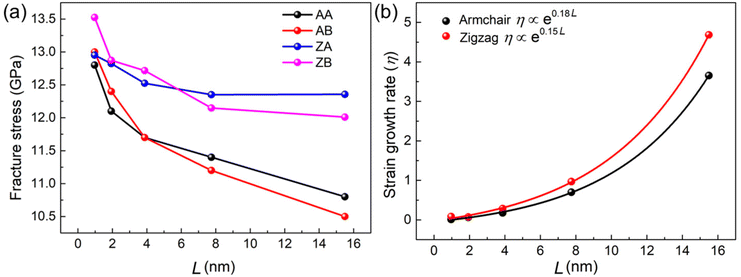 | ||
| Fig. 6 (a) The obtained fracture of the MoSSe/WSSe heterostructure superlattice versus L; (b) the strain growth rate between the AA (or ZA) and AB (or ZB) at different L. | ||
4. Conclusion
In this work, molecular dynamics calculations were performed to propose a new in-plane assembled heterostructure superlattice based on Janus MoSSe and WSSe. Four different interfaces are considered to construct the heterostructure superlattice and present thermal stability at 300 K. Interestingly, the AB and ZB MoSSe/WSSe heterostructure superlattice demonstrate excellent mechanical properties compared with that of the AA and ZA interfaces as they need to overcome the intrinsic curved structure. The calculated fracture strain and the strength of the AB (or ZB) MoSSe/WSSe heterostructure superlattice are 0.38 (or 0.51) and 10.5 GPa (or 12.0 GPa) with N = 4. Besides, the configuration of such bending AB and ZB MoSSe/WSSe heterostructure superlattice agrees with the Fourier curve. Our results reveal an effective method to tune the mechanical characteristics of the in-plane Janus TMDs heterostructure by engineering the size and interface type for decent applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Natural Science Foundation of Jiangsu (no. BK20220407), the financial support of National Natural Science Foundation of China (12102323, 11890674), the Fundamental Research Funds for the Central Universities (sxzy012022024) and the China Postdoctoral Science Foundation (2021M692574).References
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- J. Wang, S. Deng, Z. Liu and Z. Liu, The rare two-dimensional materials with Dirac cones, Natl. Sci. Rev., 2015, 2, 22–39 CrossRef CAS.
- T. Roy, M. Tosun, J. S. Kang, A. B. Sachid, S. B. Desai, M. Hettick, C. C. Hu and A. Javey, Field-effect transistors built from all two-dimensional material components, ACS Nano, 2014, 8, 6259–6264 CrossRef CAS PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Single-layer MoS2 transistors, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- H. L. Zhuang and R. G. Hennig, Computational search for single-layer transition-metal dichalcogenide photocatalysts, J. Phys. Chem. C, 2013, 117, 20440–20445 CrossRef CAS.
- Y. Ouyang, C. Ling, Q. Chen, Z. Wang, L. Shi and J. Wang, Activating Inert Basal Planes of MoS2 for Hydrogen Evolution Reaction through the Formation of Different Intrinsic Defects, Chem. Mater., 2016, 28, 4390–4396 CrossRef CAS.
- A. Y. Lu, H. Zhu, J. Xiao, C. P. Chuu, Y. Han, M. H. Chiu, C. C. Cheng, C. W. Yang, K. H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M. Y. Chou, X. Zhang and L. J. Li, Janus monolayers of transition metal dichalcogenides, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed.
- H. Qin, K. Ren, G. Zhang, Y. Dai and G. Zhang, Lattice thermal conductivity of Janus MoSSe and WSSe monolayers, Phys. Chem. Chem. Phys., 2022, 24, 20437 RSC.
- K. Ren, S. Wang, Y. Luo, J.-P. Chou, J. Yu, W. Tang and M. Sun, High-efficiency photocatalyst for water splitting: a Janus MoSSe/XN (X = Ga, Al) van der Waals heterostructure, J. Phys. D: Appl. Phys., 2020, 53, 185504 CrossRef CAS.
- R. Peng, Y. Ma, S. Zhang, B. Huang and Y. Dai, Valley Polarization in Janus Single-Layer MoSSe via Magnetic Doping, J. Phys. Chem. Lett., 2018, 9, 3612–3617 CrossRef CAS PubMed.
- H. Cai, Y. Guo, H. Gao and W. Guo, Tribo-piezoelectricity in Janus transition metal dichalcogenide bilayers: A first-principles study, Nano Energy, 2019, 56, 33–39 CrossRef CAS.
- C. Shang, X. Lei, B. Hou, M. Wu, B. Xu, G. Liu and C. Ouyang, Theoretical Prediction of Janus MoSSe as a Potential Anode Material for Lithium-Ion Batteries, J. Phys. Chem. C, 2018, 122, 23899–23909 CrossRef CAS.
- L. Shi, C. Ling, Y. Ouyang and J. Wang, High intrinsic catalytic activity of two-dimensional boron monolayers for the hydrogen evolution reaction, Nanoscale, 2017, 9, 533–537 RSC.
- J. He, S. Li, A. Bandyopadhyay and T. J. N. L. Frauenheim, Unravelling photoinduced interlayer spin transfer dynamics in two-dimensional nonmagnetic-ferromagnetic van der Waals heterostructures, Nano Lett., 2021, 21, 3237–3244 CrossRef CAS PubMed.
- J. He and T. Frauenheim, Optically driven ultrafast magnetic order transitions in two-dimensional ferrimagnetic MXenes, J. Phys. Chem. Lett., 2020, 11, 6219–6226 CrossRef CAS PubMed.
- P. Zhang, L. Ma, F. Fan, Z. Zeng, C. Peng, P. E. Loya, Z. Liu, Y. Gong, J. Zhang, X. Zhang, P. M. Ajayan, T. Zhu and J. Lou, Fracture toughness of graphene, Nat. Commun., 2014, 5, 3782 CrossRef CAS PubMed.
- K. Ren, X. Ma, X. Liu, Y. Xu, W. Huo, W. Li and G. Zhang, Prediction of 2D IV–VI semiconductors: auxetic materials with direct bandgap and strong optical absorption, Nanoscale, 2022, 14, 8463–8473 RSC.
- K. Ren, Y. Yan, Z. Zhang, M. Sun and U. Schwingenschlögl, A family of LixBy monolayers with a wide spectrum of potential applications, Appl. Surf. Sci., 2022, 604, 154317 CrossRef CAS.
- B. Wang, Q. Wu, Y. Zhang, L. Ma and J. Wang, Auxetic B4N Monolayer: A Promising 2D Material with in-Plane Negative Poisson's Ratio and Large Anisotropic Mechanics, ACS Appl. Mater. Interfaces, 2019, 11, 33231–33237 CrossRef CAS PubMed.
- M. Sun and U. Schwingenschlögl, Unique Omnidirectional Negative Poisson's Ratio in δ-Phase Carbon Monochalcogenides, J. Phys. Chem. C, 2021, 125, 4133–4138 CrossRef CAS.
- R. Lakes, Advances in negative Poisson's ratio materials, Adv. Mater., 1993, 5, 293–296 CrossRef CAS.
- Y. Cheng, X. Wu, Z. Zhang, Y. Sun, Y. Zhao, Y. Zhang and G. Zhang, Thermo-mechanical correlation in two-dimensional materials, Nanoscale, 2021, 13, 1425–1442 RSC.
- K. Ren, H. Shu, W. Huo, Z. Cui, J. Yu and Y. Xu, Mechanical, electronic and optical properties of a novel B2P6 monolayer: ultrahigh carrier mobility and strong optical absorption, Phys. Chem. Chem. Phys., 2021, 23, 24915–24921 RSC.
- R. Zhang, L. Zhang, Q. Zheng, P. Gao, J. Zhao and J. Yang, Direct Z-scheme water splitting photocatalyst based on two-dimensional Van Der Waals heterostructures, J. Phys. Chem. Lett., 2018, 9, 5419–5424 CrossRef CAS PubMed.
- Y. Gong, J. Lin, X. Wang, G. Shi, S. Lei, Z. Lin, X. Zou, G. Ye, R. Vajtai, B. I. Yakobson, H. Terrones, M. Terrones, B. K. Tay, J. Lou, S. T. Pantelides, Z. Liu, W. Zhou and P. M. Ajayan, Vertical and in-plane heterostructures from WS2/MoS2 monolayers, Nat. Mater., 2014, 13, 1135–1142 CrossRef CAS PubMed.
- H. Qin, Q. X. Pei, Y. Liu and Y. W. Zhang, The mechanical and thermal properties of MoS2-WSe2 lateral heterostructures, Phys. Chem. Chem. Phys., 2019, 21, 15845–15853 RSC.
- D. B. Trivedi, G. Turgut, Y. Qin, M. Y. Sayyad, D. Hajra, M. Howell, L. Liu, S. Yang, N. H. Patoary, H. Li, M. M. Petric, M. Meyer, M. Kremser, M. Barbone, G. Soavi, A. V. Stier, K. Muller, S. Yang, I. S. Esqueda, H. Zhuang, J. J. Finley and S. Tongay, Room-Temperature Synthesis of 2D Janus Crystals and their Heterostructures, Adv. Mater., 2020, 32, e2006320 CrossRef PubMed.
- K. Ren, H. Qin, H. Liu, Y. Chen, X. Liu and G. Zhang, Manipulating Interfacial Thermal Conduction of 2D Janus Heterostructure via a Thermo-Mechanical Coupling, Adv. Funct. Mater., 2022, 32, 2110846 CrossRef CAS.
- C. Jin, E. C. Regan, A. Yan, M. Iqbal Bakti Utama, D. Wang, S. Zhao, Y. Qin, S. Yang, Z. Zheng, S. Shi, K. Watanabe, T. Taniguchi, S. Tongay, A. Zettl and F. Wang, Observation of moire excitons in WSe2/WS2 heterostructure superlattices, Nature, 2019, 567, 76–80 CrossRef CAS PubMed.
- Z. Zhang, P. Chen, X. Duan, K. Zang, J. Luo and X. Duan, Robust epitaxial growth of two-dimensional heterostructures, multiheterostructures, and superlattices, Science, 2017, 357, 788–792 CrossRef CAS PubMed.
- L. Ponomarenko, R. Gorbachev, G. Yu, D. Elias, R. Jalil, A. Patel, A. Mishchenko, A. Mayorov, C. Woods and J. Wallbank, Cloning of Dirac fermions in graphene superlattices, Nature, 2013, 497, 594–597 CrossRef CAS PubMed.
- Z. Shi, C. Jin, W. Yang, L. Ju, J. Horng, X. Lu, H. A. Bechtel, M. C. Martin, D. Fu and J. Wu, Gate-dependent pseudospin mixing in graphene/boron nitride moiré superlattices, Nat. Phys., 2014, 10, 743–747 Search PubMed.
- G. Ding, J. He, G. Y. Gao and K. Yao, Two-dimensional MoS2-MoSe2 lateral superlattice with minimized lattice thermal conductivity, J. Appl. Phys., 2018, 124, 165101 CrossRef.
- F. Wu, T. Lovorn and A. H. MacDonald, Topological exciton bands in moiré heterojunctions, Phys. Rev. Lett., 2017, 118, 147401 CrossRef PubMed.
- H. Zhang, D. Deng, D. F. Zou, X. B. Li, Z. K. Tang, X. L. Wei, Q. X. Ge and W. J. Yin, The unique photoelectronic properties of the two-dimensional Janus MoSSe/WSSe superlattice: a first-principles study, Dalton Trans., 2022, 51, 16102–16110 RSC.
- L. Yu, W. Guo, S. Sun and X. Ye, The Strain and Electric Field Effects on the Electronic and Optical Properties of Armchair MoSSe/WSSe Superlattice Nanoribbon: A First-Principles Study, Phys. Status Solidi B, 2021, 258, 2000361 CrossRef CAS.
- L. Yu, S. Sun and X. Ye, Electronic and magnetic properties of the Janus MoSSe/WSSe superlattice nanoribbon: a first-principles study, Phys. Chem. Chem. Phys., 2020, 22, 2498–2508 RSC.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- J.-W. Jiang, Misfit Strain-Induced Buckling for Transition-Metal Dichalcogenide Lateral Heterostructures: A Molecular Dynamics Study, Acta Mech. Solida Sin., 2018, 32, 17–28 CrossRef.
- J.-W. Jiang, H. S. Park and T. Rabczuk, Molecular dynamics simulations of single-layer molybdenum disulphide (MoS2): Stillinger-Weber parametrization, mechanical properties, and thermal conductivity, J. Appl. Phys., 2013, 114, 064307 CrossRef.
- R. C. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Nonlinear elastic behavior of two-dimensional molybdenum disulfide, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035423 CrossRef.
- S. Bertolazzi, J. Brivio and A. Kis, Stretching and breaking of ultrathin MoS2, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS PubMed.
- C. Zhang, M. Y. Li, J. Tersoff, Y. Han, Y. Su, L. J. Li, D. A. Muller and C. K. Shih, Strain distributions and their influence on electronic structures of WSe2-MoS2 laterally strained heterojunctions, Nat. Nanotechnol., 2018, 13, 152–158 CrossRef CAS PubMed.
- J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen, J. Xia, H. Wang, Y. Xie, H. Yu, J. Lei, D. Wu, F. Liu, Q. Fu, Q. Zeng, C. H. Hsu, C. Yang, L. Lu, T. Yu, Z. Shen, H. Lin, B. I. Yakobson, Q. Liu, K. Suenaga, G. Liu and Z. Liu, A library of atomically thin metal chalcogenides, Nature, 2018, 556, 355–359 CrossRef CAS PubMed.
- C. Huang, S. Wu, A. M. Sanchez, J. J. Peters, R. Beanland, J. S. Ross, P. Rivera, W. Yao, D. H. Cobden and X. Xu, Lateral heterojunctions within monolayer MoSe2-WSe2 semiconductors, Nat. Mater., 2014, 13, 1096–1101 CrossRef CAS PubMed.
- T. Ma, W. Ren, X. Zhang, Z. Liu, Y. Gao, L.-C. Yin, X.-L. Ma, F. Ding and H.-M. Cheng, Edge-controlled growth and kinetics of single-crystal graphene domains by chemical vapor deposition, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20386–20391 CrossRef CAS PubMed.
- H. Li, A. W. Contryman, X. Qian, S. M. Ardakani, Y. Gong, X. Wang, J. M. Weisse, C. H. Lee, J. Zhao, P. M. Ajayan, J. Li, H. C. Manoharan and X. Zheng, Optoelectronic crystal of artificial atoms in strain-textured molybdenum disulphide, Nat. Commun., 2015, 6, 7381 CrossRef CAS PubMed.
- Q. Song, M. An, X. Chen, Z. Peng, J. Zang and N. Yang, Adjustable thermal resistor by reversibly folding a graphene sheet, Nanoscale, 2016, 8, 14943–14949 RSC.
- N. Yang, X. Ni, J.-W. Jiang and B. Li, How does folding modulate thermal conductivity of graphene?, Appl. Phys. Lett., 2012, 100, 093107 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00429e |
| This journal is © The Royal Society of Chemistry 2023 |