Size-dependent chiro-optical properties of CsPbBr₃ nanoparticles

Abstract

Chiral metal halide perovskites have garnered substantial interest because of their promising properties for application in optoelectronics and spintronics. Understanding the mechanism of chiral imprinting is paramount for optimizing their utility. To elucidate the nature of the underlying chiral imprinting mechanism, we investigated how the circular dichroism (CD) intensity varies with nanoparticle size for quantum confined sizes of colloidal CsPbBr₃ perovskite nanoparticles (NPs) capped by chiral β-methylphenethylammonium bromide ligands. We find that the CD intensity decreases strongly with increasing NP size, which, along with the shape of the CD spectra, points to electronic interactions between ligand and NP as the dominant mechanism of chiral imprinting in smaller NPs. We observe that as the NP size increases and crosses the quantum confinement threshold, the dominant mechanism of chirality transfer switches and is dominated by surfaces effects, e.g., structural distortions. These findings provide a benchmark for quantitative models of chiral imprinting.

---

Introduction

Metal halide perovskite nanomaterials have garnered attention over the past decade because of their promising optoelectronic properties such as tunable bandgaps,^1,2 long carrier diffusion length,^3,4 high defect tolerance,⁵ near unity fluorescence quantum yield (in cases),⁶ and long spin lifetimes,^7,8 which make them useful for photovoltaics,⁹ lasers,^10–12 light emitting diodes (LEDs),^13–15 and photodetectors.^16,17 Recently, metal halide perovskites imprinted with chiro-optical properties by chiral organic ligands have added to the desirable optoelectronic properties of perovskite materials for applications in spin-dependent optoelectronic devices,¹⁸ spin-polarized charge transport,^19–21 and circularly polarized light emission^22–24 and detection.^25–27 Moon et al. reported the first synthesis of chiro-optically active hybrid organic–inorganic 2D metal halide perovskite thin films in 2017.²⁸ Since then, a gamut of 2D^19,29–31 and 3D^32–37 chiral perovskites which display a range of interesting chiro-optical and spintronic properties have been synthesized. However, the underlying mechanism of chiral imprinting on perovskite nanoparticles (NPs) is still not well understood.

Researchers often discuss two potential mechanisms for imprinting chiro-optical properties onto perovskites: (i) chirality transfer through structural distortion³⁵ and (ii) electronic coupling between the perovskite and the organic ligand.^19,32,38 For example, Chen et al. showed that chiral α-octylamine modified cesium lead bromide (CsPbBr₃) NPs display circular dichroism (CD) and circularly polarized luminescence (CPL) signals, which they attributed to the asymmetric distortion of surface atoms by the chiral ligand.³⁴ In a similar study, Kim et al. reported CPL activity for chiral methylbenzylammonium bromide passivated CsPbBr₃ bulk nanocrystals (NCs) and attributed the chirality to a distortion of the surface lattice which penetrates up to five atomic unit cells deep into the NCs.³⁹ In order to improve the chiro-optical properties of perovskite nanomaterials, researchers have explored the importance of structural aspects, such as using mixed ligand shells,³⁶ manipulating the perovskite lattice-spacing (d-spacing) and halogen–halogen interaction,⁴⁰ and changing the concentration of chiral ligand during post-synthetic ligand exchange.³⁸ While structural distortions can provide a straightforward mechanism for symmetry breaking, it does not necessarily translate into the significant “electronic” chirality that is probed by CD and CPL spectroscopy. Thus, one must also consider how the electronic interactions between chiral ligands and the NP contribute to the chiro-optical response. The contribution of electronic coupling to chiral imprinting in perovskites has been discussed in several works.^32,41,42 Ma et al. recently demonstrated that controlling the electronic interaction between chiral organic ligands and the inorganic framework of 2D organic–inorganic halide perovskite NCs was key to controlling their chiro-optical response.⁴² Zhang et al. have reported that π-orbitals of the organic ligand can couple with the p-orbitals of the perovskite iodide to modify the electronic configuration of quasi-two-dimensional perovskites.⁴³ We have recently demonstrated the importance of the exciton's spatial extent and the surface chiral ligand coverage on the induced circular dichroism (CD) response of perovskite nanoplatelets.⁴¹ The findings in this work suggest that electronic interactions between the ligand and perovskite electronic states may play an important role in chirality transfer for NPs, especially in the quantum confined regime.

To date, no studies have explored the effect of nanoparticle size on the chiral imprinting strength of quantum confined perovskite NPs. Studies of chiral II–VI quantum dots (QDs) display a correlation between the size of QDs and their observed CD signal intensities. Zhou et al. demonstrated the size-dependence of the CD signal intensity for CdSe/CdTe colloidal QDs stabilized by chiral biomolecules.⁴⁴ Also, Ben-Moshe et al. reported the tuning of the CD intensity over a wide wavelength range by adjustment to the sizes of CdS and CdSe QDs that were capped with chiral penicillamine ligands.⁴⁵ In both studies, a decrease in the CD intensity was seen with increasing QD size, with the latter study showing an exponential decrease. A similar effect has been reported for CdSe/CdS core shell structures, where the CdS shell thickness was varied and the chiro-optical properties were examined.⁴⁶ These researchers proposed that chiral imprinting involves coupling between the HOMO of the ligand and the valence band of the semiconductor QD. As a clear understanding of the mechanistic process behind chiral imprinting in perovskite NPs has not yet been elucidated, investigating the dependence of chiro-optical activity on properties such as NP size is important, as it can reveal whether structural distortion or electronic coupling plays a bigger role in imprinting chirality. The change in chiro-optical properties introduced by structural distortion of the NP surface should have a different dependence on NP size than those arising from electronic interaction with the NP's exciton, thus allowing their relative importance to be assessed.

The importance of a size-dependent study is further suggested by consideration of different literature reports on the chiro-optical properties of CsPbBr₃ perovskites of different sizes. In 2021, we reported chiral 2 nm sized CsPbBr₃ with a strong CD peak at the first excitonic energy of the NP, and correlated it with the electronic properties of the chiral ligands.³³ In contrast, CsPbBr₃ NPs with an edge length of ∼10 nm show only a broad CD signature in the UV region and no peaks at the first excitonic transition energy.³⁹ In this study, we examine how the chiro-optical response of perovskite NPs changes as a function of NP size and surface ligand coverage. We examine the size dependence of the CD spectrum for chiral CsPbBr₃ perovskite NPs of four different sizes, circa 2.2 nm, 4.1 nm, 5.2 nm, and 6 nm edge lengths. We observe a strong decrease of the CD intensity of the first exciton band as the NP size increases. The observed size dependence of such chiro-optical properties is a feature that must be accounted for by theoretical descriptions of chiral imprinting for a complete understanding of the imprinting mechanism.

Experimental methods

Materials

Cesium carbonate (Cs₂CO₃ 99.9% trace metals basis), lead(II) bromide (PbBr₂, 99.999% trace metals basis), zinc(II) bromide (ZnBr₂, 99.999% trace metals basis), oleic acid (OA, technical grade, 90%), oleylamine (OAm, technical grade, 70%), octadecene (ODE, 90%), ethyl acetate, and hydrobromic acid (HBr, 48%) were purchased from Sigma Aldrich. S-(−)-β-methylphenethylamine (S-MPEA, >98.0%) and R-(+)-β-methylphenethylamine (R-MPEA, >98.0%) were purchased from TCI. Dimethyl sulfoxide (DMSO)-d6 was purchased from Cambridge Isotope Laboratories Inc. Ferrocene (99%), toluene, and tert-butanol were purchased from Thermo Fisher Scientific.

Synthesis of precursor salts

Bromide salts of R- and S-MPEA were synthesized by mixing equimolar amounts of the desired chiral amine and HBr in 15 mL of absolute ethanol. The reaction was stirred in an ice bath for 2 hours, then the solvent was removed via rotary evaporation until crystals were formed. The crystals were collected, recrystallized with chlorobenzene, and then vacuum filtered and washed several times with toluene. The product was dried in a vacuum desiccator for several hours before storage.

Synthesis of CsPbBr₃ NPs

For all syntheses, 0.2 g Cs₂CO₃, 0.7 mL OA, and 10 mL ODE were added to a 50 mL three neck round bottom flask and flushed with argon for 1 hour at 120 °C. The reaction was then sealed in an Ar atmosphere and the temperature was raised to 140 °C until the complete dissolution of Cs₂CO₃ and the formation of Cs-oleate. The reaction temperature was then maintained at 120 °C to prevent precipitation.

To obtain NPs in the 2 nm size regime, 160 mg PbBr₂, 1.20 g ZnBr₂, 4 mL OA, 4 mL OAm, and 10 mL ODE were flushed with argon for 1 h at 130 °C after which the reaction was sealed in an Ar atmosphere and heated at 140 °C for an additional 45 minutes. The temperature was then decreased to 85 °C and after equilibration, 1.2 mL Cs-oleate was rapidly injected. The reaction was quenched after 180 seconds by cooling the flask in an ice bath.

To obtain NPs in the 4 nm size regime, 138 mg PbBr₂ and 10 mL ODE were combined in a round bottom flask and flushed with argon for 1 h at 120 °C, after which the reaction was sealed in an Ar atmosphere. OA and OAm were added to the reaction in a 2 : 1 ratio to a total volume of 1.8 mL and the reaction mixture was heated at 140 °C for an additional 45 minutes until complete dissolution of the PbBr₂. The temperature was then decreased to 90 °C, and after equilibration, 1.6 mL Cs-oleate was rapidly injected. The reaction was quenched after 20 seconds by cooling the flask in an ice bath.

To obtain NPs in the 5 nm size regime, 140 mg PbBr₂ and 10 mL ODE were combined in a round bottom flask and flushed with argon for 1 h at 120 °C, after which the reaction was sealed in an Ar atmosphere. OA and OAm were added to the reaction in a 1 : 1 ratio to a total volume of 2.0 mL and the reaction mixture was heated at 140 °C for an additional 45 minutes until complete dissolution of the PbBr₂. The temperature was then decreased to 130 °C, and after equilibration, 1.6 mL Cs-oleate was rapidly injected. The reaction was quenched after 10 seconds by cooling the flask in an ice bath.

To obtain NPs in the 6 nm size regime, 140 mg PbBr₂, and 10 mL ODE were combined in a round bottom flask and flushed with argon for 1 h at 120 °C after which the reaction was sealed in the Ar atmosphere. OA and OAm were injected into the flask in a 1 : 1 ratio to a total volume of 2.0 mL and the reaction mixture was heated at 140 °C for an additional 45 minutes until complete dissolution of the PbBr₂. While maintaining the reaction temperature at 140 °C, 1.6 mL Cs-oleate was rapidly injected. The reaction was quenched after 10–15 seconds by cooling the flask in an ice bath.

Purification of achiral NPs and ligand exchange

For 2 nm NPs, 2 ml of the as-synthesized mixture was dispersed in 5 ml of toluene and then centrifuged at 6500 rpm for 15 minutes at room temperature to remove any unreacted precursors. The supernatant was collected and stored overnight to allow for NP ripening. The ripened NP mixture was then centrifuged at 11 000 rpm for an hour at −3 °C. The precipitate was resuspended in toluene and diluted to an absorbance intensity of 2 a.u. at the first exciton's λ_max. R- or S-MPEABr was added to the NPs as a solution in tert-butanol to reach a total chiral ligand concentration of 1.85 mM. The NP-ligand mixture was allowed to rest for 2 h, then centrifuged at 6000 rpm for 15 minutes at 10 °C. The precipitate was collected for measurements.

For 4 nm NPs, the as-synthesized mixture was centrifuged at 10 000 rpm for 15 minutes at 15 °C. The supernatant was collected, and ethyl acetate was added in a 3 : 1 ratio by volume, then centrifuged at 10 000 rpm for 20 minutes at 10 °C. The precipitate was resuspended in toluene and diluted to an absorbance intensity of 2 a.u. at the first exciton's λ_max. R- or S-MPEABr was added to the NPs as a solution in tert-butanol to reach a total chiral ligand concentration of 0.46 mM. The NP-ligand mixture was allowed to rest for 1 h, then centrifuged at 11 000 rpm for 45 minutes at −5 °C. The precipitate was collected for measurements.

For 5 nm NPs, the as-synthesized mixture was centrifuged at 6500 rpm for 20 minutes at room temperature. The precipitate was resuspended in toluene and diluted to an absorbance intensity of 2 a.u. at the first exciton's λ_max. R- or S-MPEABr was added to the NPs as a solution in tert-butanol to reach a total chiral ligand concentration of 1.85 mM. The NP-ligand mixture was allowed to rest overnight (∼18 hours), then centrifuged at 11 000 rpm for 20 minutes at room temperature. The precipitate was collected for measurements.

For 6 nm NPs, the as-synthesized mixture was centrifuged at 7000 rpm for 25 minutes at room temperature. The precipitate was resuspended in toluene and diluted to an absorbance intensity of 2 a.u. at the first exciton's λ_max. R- or S-MPEABr was added to the NPs as a solution in tert-butanol to reach a total chiral ligand concentration of 1.85 mM. The NP-ligand mixture was allowed to rest overnight (∼18 hours), then centrifuged at 11 000 rpm for 20 minutes at room temperature. The precipitate was collected for measurements.

Characterization of NPs

UV-Visible absorption spectra were collected on an Agilent 8453 spectrometer. Circular dichroism spectra were collected on a Jasco J-810 spectropolarimeter with a scan speed of 100 nm min⁻¹ and up to 15 averaged scans for each spectrum.

TEM images were acquired using a JEOL JEM-2100F and a Thermo Fisher Scientific Titan Themis 200 aberration corrected TEM operated at an acceleration potential of 200 kV. The samples were prepared by drop-casting a 10 μl NP dispersion in toluene onto a Cu TEM grid with ultra-thin carbon supporting film and dried in air.

Powder X-Ray diffraction patterns were collected on a Bruker D8 Discover XRD instrument equipped with a PSD (LYNXEYE) detector and operated with a Cu Kα source (λ = 1.54187 Å) at an X-ray generator voltage and current of 40 kV and 40 mA respectively. Concentrated NP dispersions were drop-cast on a clean glass substrate and then dried before acquiring the spectra at room temperature. Data analysis was performed on the EVA and HighScore XRD analysis software.

¹H NMR spectra were obtained using a Bruker Advance 400 MHz spectrometer. The spectra were calibrated to the residual solvent peak (DMSO-d6, 2.50 ppm). To prepare NP samples for NMR, purified suspensions of NPs in toluene were centrifuged into a pellet, then dried under an Ar flow and stored in a vacuum desiccator. DMSO-d6 (∼1 g) was added to the dried NPs and mixed until complete digestion occurred, as indicated by the formation of a clear solution. A standard solution was prepared by dissolving ferrocene in DMSO-d6 in a volumetric flask and a known amount was added to the NMR sample.

Calculating ligand coverage

Concentrations of chiral and achiral ligands were obtained via¹H-NMR measurements as described in the ESI. The mass of the NP pellet for each NMR sample was recorded and the total mass of ligands, as estimated from NMR measurements, was subtracted to yield the mass of CsPbBr₃ only. Calculated values for the orthorhombic CsPbBr₃ unit cell mass and volume, as well as the measured edge length of NPs in the sample, were used to convert the NP mass to the total number of NPs and total surface area. The total number of chiral ligands (derived from NMR measurements) was then divided by the total surface area of the dissolved NPs.

Results and discussion

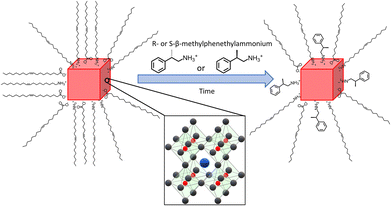
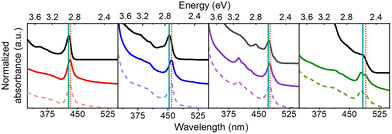
Four different sizes of achiral CsPbBr₃ NPs were synthesized using modifications of previously published hot injection procedures.^33,47,48 In order to imprint chirality onto the achiral NPs, they were post-synthetically ligand-exchanged with solutions of R-(+)-β-methylphenethylammonium bromide (R-MPEABr) or S-(−)-β-methylphenethylammonium bromide (S-MPEABr) in tert-butanol following the procedure outlined in the Experimental methods section. Fig. 1 illustrates the ligand exchange procedure.

Fig. 1 Schematic of post-synthetic ligand exchange on CsPbBr₃ NPs (represented by red cubes). The insert depicts the crystal structure of the NPs where the Pb²⁺ (red) and Br⁻ (black) ions arranged in corner-sharing octahedra, with Cs⁺ ions (blue) surrounded by the PbBr₆⁴⁻ octahedra. The achiral NP shown on the left is capped by oleic acid and oleylamine, while after ligand exchange, some of the native achiral ligands are replaced by R/S-methylphenethylammonium ligands (as shown on the right).

The sizes of the NPs were determined using UV-Visible absorption spectroscopy and transmission electron microscopy (TEM) data. A calibration plot was used for determining the edge length of colloidal CsPbBr₃ NPs from their lowest energy absorbance maxima (λ_max), i.e. the first excitonic transition. Details of the plot and analysis are provided in the ESI (see Fig. S1†). Fig. 2 shows absorption spectra of the chiral and achiral NPs of different sizes. The NPs exhibit a size-dependent bandgap shift that is typical of structures in the quantum-confined regime, with their absorbance maxima red-shifting with increasing NP size. Achiral NPs in the small size regime have absorbance maxima at 428 nm, which shifts to 453 nm, 475 nm, and 483 nm for the medium and larger sized NPs. These λ_max values correspond to NP edge lengths of 2.1 ± 0.2 nm, 3.7 ± 0.3 nm, 5.0 ± 0.4, and 5.4 ± 0.5 nm respectively. Upon ligand exchange, a small, additional red-shift in the absorbance maximum of a few nanometers is observed for all NP sizes, with larger sizes seeing a somewhat greater shift in wavelength. Thus, the absorbance maxima for the chiral NPs increase to 431 nm, 458 nm, 477 nm, and 490 nm. If this shift is attributed to a size change, then the small, medium, and larger sized chiral NPs increase their edge lengths modestly to 2.2 ± 0.2 nm, 4.1 ± 0.4 nm, 5.2 ± 0.5 nm, and 6.0 ± 0.5 nm respectively. The size-dependent shift in the absorbance peaks of the achiral and chiral NPs is presented in more detail in Fig. S2.† To ensure that the integrity of the NPs is not compromised upon ligand exchange, X-ray diffraction (XRD) patterns of the different sized perovskites were collected. Fig. S3† shows that the perovskites adopt a primarily orthorhombic CsPbBr₃ crystal structure, consistent with other works.^49,50

Fig. 2 UV-Vis spectra for 2 nm (red), 4 nm (blue), 5 nm (purple) and 6 nm (green) sized NPs. Achiral NPs are shown in black while chiral NPs with R-MPEABr and S-MPEABr on the surface are shown using colored solid and dotted lines respectively. The solid teal and dotted brown lines mark the absorbance maxima for the achiral and chiral NPs respectively. The NPs were dispersed in toluene for the measurements.

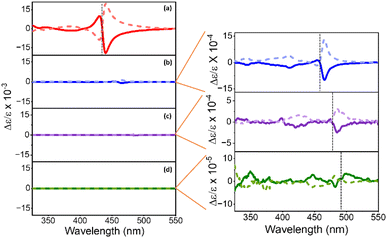
Representative CD spectra for the chiral NPs are shown in Fig. 3a, b, c, and d. The CD intensity is reported in units of the dimensionless dissymmetry, or g-factor (Δε/ε), which is derived by dividing the differential absorbance of circularly polarized light of each sample by their respective concentrations and molar extinction coefficients. This processing eliminates differences in concentration and molar absorptivity across NP sizes. The R- and S-chiral NPs produced mirror image CD signatures for all four NP sizes (see enlarged plots for 4 nm, 5 nm, and 6 nm sized NPs), with a bisignate (consisting of a positive and negative lobe) feature occurring at the energy of the first exciton of the NP and weaker features in the near-UV region. A bisignate CD shape can arise from the electronic coupling between two chiral chromophores or between a chiral and an achiral chromophore.^51,52 Despite these similarities, CD intensities (defined as the trough to peak value for Δε/ε of the bisignate band) decrease strongly with increasing NP size. That is, we observe a 10-fold decrease in CD intensity between the 2 nm and the 4 nm/5 nm NPs (Fig. 3a, b, and c), and a 100-fold decrease between the 2 nm and the 6 nm NPs (Fig. 3a and d). Moreover, the first exciton peak becomes less bisignate in shape i.e., the two lobes become less equal in area. For the 2 nm NPs, the ratio of the area under the positive and the negative lobes of the bisignate peak is 0.31 ± 0.07, while for the 4 nm, 5 nm, and 6 nm NPs, the ratios are at 0.12 ± 0.08, 0.06 ± 0.03 and 0.19 ± 0.07 respectively. An ideal bisignate peak would have a ratio of 1 between the areas under the two lobes. The 2 nm NPs show a ratio closest to one, followed by the 6 nm, 4 nm and the 5 nm NPs. It should be noted that the sign of the bisignate peak flips for the 6 nm NPs. In previous work, the change in the sign of the bisignate peak (as shown by the 6 nm NPs) has been attributed to changes in chiral ligand orientation and coverage on the NP surface.⁴¹ The 6 nm chiral NPs also appear to have two close lying absorbance peaks near the first exciton transition, at 480 nm and 489 nm respectively (Fig. 2). This can occur due to an increase in the polydispersity of the NPs upon ligand exchange, where there is a broader distribution of NP sizes and morphologies in the sample (Fig. S5†). The presence of two peaks in such close vicinity can affect the resulting CD peak; i.e. a superposition of the CD peaks due to the two separate absorbance maxima could lead to abnormalities in the resulting bisignate feature,⁵³ such as the slightly larger separation in energy between the positive and the negative lobes as observed for both the R and S enantiomers of the large chiral NPs in Fig. 3d. The disruption in the trend of reduction in the bisignate nature of the exciton CD peak with size could also be a result of such superimposition of neighboring absorbance peaks. Nevertheless, the reduction of bisignate feature with increasing NP size is evident from the data presented for the 2 nm, 4 nm and 5 nm NPs, and the anisotropy for the 6 nm NPs follows the same trend; see Fig. 4.

Fig. 3 Circular dichroism (CD) spectra for (a) 2 nm, (b) 4 nm, (c) 5 nm, and (d) 6 nm NPs in toluene are shown. Orange lines indicate zoomed in spectra of the 4 nm, 5 nm (×10), and 6 nm (×100) NPs shown in panels to the right. Chiral NPs with R-MPEABr and S-MPEABr on the surface are shown using solid and dotted lines respectively. The wavelength for the first excitonic transition is marked by black dotted line in each spectrum.

Fig. 4 (a) Average CD intensity plotted on a logarithmic scale as a function of average edge length for a chiral NP in the 2 nm (red), 4 nm (blue), 5 nm (purple), and 6 nm (green) size regimes. The brown dashed line shows a line of best fit, with a slope of −1.35 nm⁻¹. (b) CD intensity plotted on a logarithmic scale as a function of chiral ligand (MPEABr) coverage for the different NP sizes.

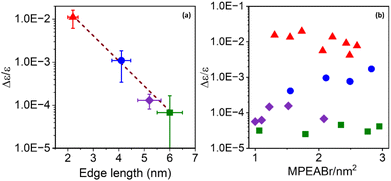
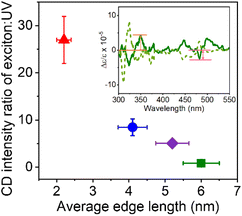
To further explore this size dependence of chiro-optical activity in CsPbBr₃ NPs, the average CD intensities observed for each of the four size regimes in this work are plotted as a function of the average edge length of the chiral NPs. Plotting the average CD intensities on a logarithmic scale (Fig. 4a) shows a linear decrease with increasing NP size, suggesting that the CD intensities of the NPs decay exponentially with size. This large, nonlinear decrease in CD intensity with increasing NP edge length is similar to that reported for II–VI materials.^45,54 Recently, Georgieva et al. showed that the CD intensity in perovskite nanoplatelets can change strongly with chiral ligand surface coverage, before plateauing at a high coverage.⁴¹ To examine whether chiral ligand coverage is causing the intensity change, we quantified the chiral ligand coverage on the NP surface via¹H-NMR spectroscopy and correlated it with changes in the CD intensities for different sized NPs. The procedure and analysis for this quantification are provided in the ESI.†Fig. 4b shows a compilation of CD intensity (plotted on a logarithmic scale) and ligand coverage data measured for this work. The standard deviation in Δε/ε of ±5 × 10⁻³ for 2 nm NPs, ±7 × 10⁻⁴ for 4 nm NPs, ±5 × 10⁻⁵ for 5 nm NPs, and ±8 × 10⁻⁶ for 6 nm NPs over the coverage range shown indicates a small variation. While CD intensity fluctuates modestly with changing chiral ligand coverage, these variations are small compared to the change in average CD intensity with size and are attributed to the variation in chiral ligand coverage between samples.

The CD spectra for the quantum confined NPs studied here contrast sharply with the CD spectra of “bulk” CsPbBr₃ NPs. CsPbBr₃ NPs with sizes >7 nm do not display significant or strong CD activity at the first exciton transition energy;^35,36,39 rather, they sometimes display broad features at higher energies, which have been attributed to structural distortion in the NP surface region near the ligand binding site.³⁹ Similar broad features in the UV region of the CD spectrum have also been reported for II–VI QDs, which were attributed to localized structural distortion.^55–57 In contrast to these findings, the CD spectra presented in this work are dominated by the transition at the first exciton energy. The data in Fig. 3 and 4a show that the CD signal strength decreases strongly with increasing NP size. To understand this trend, we posit that the bisignate features at the first exciton transition energy in chiral CsPbBr₃ perovskite NPs (Fig. 3) originate from a coupled oscillator interaction between the ligand and the NP. The mechanism for a bisignate shape comprises the coupling of the electronic transitions of two chromophores (e.g., the chiral ligand and the achiral NP) via a dipole–dipole interaction.^54,58 This interaction should change strongly with the distance between the two interacting chromophores. As the NPs grow larger in size, the effective distance of the NP exciton from the chiral ligands on the surface increases.

For strongly quantum confined NPs, such as the 2 nm sized ones, bisignate features dominate the CD spectrum; however, as the NP size gets closer to the quantum confinement threshold (6 nm NPs), the CD spectra are less dominated by the bisignate band of the first exciton. This change is shown in Fig. 5 by plotting the CD strength at the first exciton divided by that in the near UV (∼350 nm) as a function of NP size. When the NP edge length exceeds the Bohr diameter of the exciton, little to no quantum confinement occurs; and the strength of the CD signals in the UV, which have been attributed to localized structural distortions on the NP surface,³⁹ increase in relative magnitude. Note that Kim et al.³⁹ have reported that structural distortion of the NP surface structures by chiral ligands can run up to five octahedral layers deep into the NP crystal lattice. Considering the size of an octahedron to be 0.67 nm,³⁹ the smallest NPs in this work comprise ∼3 octahedral layers, while the largest NPs are made up of ∼9 octahedral layers, so structural distortion throughout the NP is expected. Nevertheless, we observe a strong decrease of the exciton CD strength with size, whereas the CD strength of the NPs in the near-UV change much less (only half as much as the exciton) with size, indicating that chiro-optical response (CD strength) is not derived solely from the chiral distortions of the lattice. The claim of electronic interactions being the major source of chirality in these quantum confined NP sizes is further strengthened by the proportionality seen between excitonic state splitting and the dissymmetry factor in the CD spectra (Table S1†), which has been used as an indication of chirality due to electronic interactions in II–VI QDs.⁵³

Fig. 5 Plot of the ratio of the exciton: UV region CD intensity versus the NP edge length for 2 nm (red), 4 nm (blue), 5 nm (purple), and 6 nm (green) NPs. Inset shows a representative CD spectrum with the UV and the exciton intensity marked in orange and pink respectively.

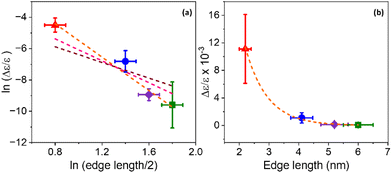
A coupled oscillator model predicts that the Coulomb interaction between two interacting chromophores should decay as a power law of the distance between them; for point dipoles it is inversely proportional to the square of the distance.⁵⁹ If the NP exciton and the chiral ligand are taken as the two chromophores, and we approximate the distance by the separation between the surface (where the ligands are attached) and the center of the NP (where the exciton is centered), then the rotatory strength should scale inversely with a power of the NP edge length.⁵¹ To determine how the CD intensity scales with this distance, the natural log of both variables were plotted against each other, as shown in Fig. 6a. We consider the relationship

CD intensity ∝ rⁿ

where r is the distance between NP exciton and ligand and thus equal to half of the NP edge length. Fig. 6a shows a best fit with n ≈ −2, and a best fit in which n is allowed to vary. This analysis shows that the CD intensity scales more strongly than 1/r² and that the coupled oscillator model, when approximating the chromophores as point dipoles, cannot fully account for the behavior. The coupled oscillator model primarily focuses on the interaction between electric dipole transitions of the chromophores. Recently, however, it was reported that 2D lead-halide perovskites show bright magnetic dipole transitions from self-trapped excitons.^60,61 If these transitions are present in the quantum-confined 3D perovskites, then dynamic coupling can occur between the magnetic dipole transition moment of an achiral chromophore and the electric transition dipole moment of a chiral chromophore to generate a CD response.⁵¹ In the point dipole limit, this kind of interaction gives rise to a dissymmetry that scales as 1/r⁴,⁵¹ which better mimics the data in Fig. 6a; i.e. a best fit value of n = −5.3 ± 0.7 (orange dashed line). These considerations suggest that a coupled oscillator model can account for the decay of CD strength with distance if it is elaborated to include the extended nature of the charge distribution and/or coupling to magnetic dipole transitions.

Fig. 6 (a) The natural log of average CD intensity plotted as a function of the natural log of half of the average edge length for a chiral NP in the 2 nm (red), 4 nm (blue), 5 nm (purple), and 6 nm (green) size regimes. The brown dashed line shows a line of best fit with a slope fixed at −2, the pink dashed line shows a line of best fit with a slope fixed at −3, while the orange dashed line shows a line of best fit where the slope is allowed to float, which gives a best fit slope of −5.3. (b) Average CD intensity vs. NP edge length fitted to an exponential decay law of y = ae^−bx, where a = 0.22 and b = 1.35, with an adjusted R² fit of 0.98.

The use of an extended charge distribution to describe a chiral molecule and its imprint on a nanoparticle was reported by Goldsmith et al.⁶² In their model, the chiral adsorbates produce a dissymmetric or chiral electrostatic field which perturbs the electronic states of a gold nanocluster. They used an electron in a cubic box model to mimic the gold's electronic structure, and then computed the perturbed wavefunction by the interaction between the absorbates (approximated to surface charges) and the electron box states, from which they could calculate the CD spectrum. They found that the calculated CD strength scales as 1/r³ (pink dotted line in Fig. 6a) with increasing gold nanocluster size when eight point charges are placed on the surface; in contrast to the scaling of 1/r² that is expected for two point dipoles. Note that the coupled oscillator and the dissymmetric chiral adsorbate models account for the chiral imprinting by Coulomb interactions, though the major difference lies in whether the NP and ligand are modelled as interacting dipoles or as extended charge distributions. The considerations above and the fact that the exciton is spread over the entire NP and interacting with multiple chiral ligands indicate that models which account for the extended nature of the chiral ligand and NP charge distributions will be needed for more quantitative comparisons.

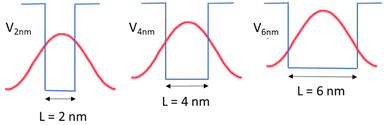
Another mechanism that may explain the chiral imprinting involves wavefunction overlap between the chiral ligand and the NP exciton, which leads to electronic state mixing and chiral symmetry transfer between the chiral ligands and the CsPbBr₃ NP.⁵³ Consider a particle-in-a box (PIB) model, with the NP size acting as the length of the box (L) and the ionization potential of the NPs acting as the height of the box or potential barrier (V). As the NP size decreases, the ionization potential should increase modestly,⁶³ which would increase the height of the potential barrier of the box. The exciton wavefunction is confined within the potential well, but some of the wavefunction amplitude tunnels into the ligand shell on the NP surface and decays in an exponential manner. Even though the height of the box is bigger for smaller NPs, the length of the box is smaller, which can lead to an increase in the amplitude of the wavefunction tunneling as the NP size decreases; see Fig. 7. Assuming that a larger overlap between the NP exciton wavefunction and the chiral ligand wavefunction increases the electronic coupling between the exciton and the ligand, then the electronic coupling should increase exponentially with decreasing NP size. If the chiral imprinting increases with the magnitude of wavefunction mixing between the chiral ligand and the exciton, it should be roughly proportional to the electronic coupling and decay exponentially with distance also. A fit of the data by an exponential decay law is shown in Fig. 6b and gives an inverse decay length of 1.35 nm⁻¹, a decay length of 0.75 nm. The decay length can act as a measure of the electronic coupling strength between the interacting electronic states, and how it depends on the distance between interacting species.

Fig. 7 Schematic of proposed mechanism of how wavefunction overlap in a PIB model differs with NP size in small (L = 2), medium (L = 4), and large (L = 6) size regimes. The rectangles shown represent the comparative size of the boxes for each NP size. The red curve represents a simple n = 1 wavefunction for the NP exciton if it were not confined. V_{2 nm}, V_{4 nm}, and V_{6 nm} represent the height of the boxes or the potential barriers, and are dependent on the ionization potentials of the respectively sized NPs.

Conclusions

We studied the effect of size on chiro-optical properties in CsPbBr₃ perovskite NPs that were capped by chiral organic ligands. The average CD intensity was found to decrease dramatically with NP size, a factor of 100 for a diameter change of 3 times. Differences in NP size and surface ligand coverage were examined as potential sources of this phenomenon. While chiral ligand coverage affects the observed CD signals, the size of the NPs is the major factor in determining the chiral imprinting strength. Comparison of these findings with literature results on chiral perovskites and chiral II–VI quantum dots points towards electronic interactions being the major contributor in the decay of the first exciton's CD intensity with NP size. We identified different mechanisms of electronic imprinting that may explain the observed trend; however, determining the correct mechanism will require extensive theoretical modelling and can be the focus of future work. Ligand induced structural distortion of the NP lattice is discounted as the origin of the strong size effect on the NP's exciton transition, because the CD transitions in the near UV, which are thought to arise from structural distortions, display a weaker intensity decay with NP size. As the NP size increases and evolves from being strongly quantum confined to weakly quantum confined, the dominant mechanism giving rise to chiral imprinting switches from electronic modification of the NP exciton to surface localized effects, previously rationalized as structural distortion. Understanding this size dependence of chiro-optical properties in perovskite NPs and the underlying mechanisms giving rise to chirality for different NP size regimes should enable the optimization of such properties to produce more efficient NP-containing devices for circularly polarized light absorption and emission, as well as for spintronics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge U.S. Department of Energy (grant no. ER46430) for supporting this work. We thank B. P. Bloom and D. N. Beratan for helpful comments and discussions.

References

1. Q. A. Akkerman, V. D'Innocenzo, S. Accornero, A. Scarpellini, A. Petrozza, M. Prato and L. Manna, J. Am. Chem. Soc., 2015, 137, 10276–10281.
2. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
3. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344.
4. J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. Al-Jassim, M. van Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475–479.
5. H. Huang, M. I. Bodnarchuk, S. V. Kershaw, M. V. Kovalenko and A. L. Rogach, ACS Energy Lett., 2017, 2, 2071–2083.
6. F. Di Stasio, S. Christodoulou, N. Huo and G. Konstantatos, Chem. Mater., 2017, 29, 7663–7667.
7. P. Odenthal, W. Talmadge, N. Gundlach, R. Wang, C. Zhang, D. Sun, Z.-G. Yu, Z. V. Vardeny and Y. S. Li, Nat. Phys., 2017, 13, 894–899.
8. D. Giovanni, H. Ma, J. Chua, M. Gratzel, R. Ramesh, S. Mhaisalkar, N. Mathews and T. C. Sum, Nano Lett., 2015, 15, 1553–1558.
9. A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103.
10. H. Dong, C. Zhang, X. Liu, J. Yao and Y. S. Zhao, Chem. Soc. Rev., 2020, 49, 951–982.
11. Z. Li, J. Moon, A. Gharajeh, R. Haroldson, R. Hawkins, W. Hu, A. Zakhidov and Q. Gu, ACS Nano, 2018, 12, 10968–10976.
12. H. Zhang, Q. Liao, Y. Wu, Z. Zhang, Q. Gao, P. Liu, M. Li, J. Yao and H. Fu, Adv. Mater., 2018, 30, 1706186.
13. Q. Van Le, H. W. Jang and S. Y. Kim, Small Methods, 2018, 2, 1700419.
14. J. Cui, Y. Liu, Y. Deng, C. Lin, Z. Fang, C. Xiang, P. Bai, K. Du, X. Zuo, K. Wen, S. Gong, H. He, Z. Ye, Y. Gao, H. Tian, B. Zhao, J. Wang and Y. Jin, Sci. Adv., 2021, 7, eabg8458.
15. B. Zhao, S. Bai, V. Kim, R. Lamboll, R. Shivanna, F. Auras, J. M. Richter, L. Yang, L. Dai, M. Alsari, X.-J. She, L. Liang, J. Zhang, S. Lilliu, P. Gao, H. J. Snaith, J. Wang, N. C. Greenham, R. H. Friend and D. Di, Nat. Photonics, 2018, 12, 783–789.
16. Y. Fang, Q. Dong, Y. Shao, Y. Yuan and J. Huang, Nat. Photonics, 2015, 9, 679–686.
17. Q. Lin, A. Armin, P. L. Burn and P. Meredith, Nat. Photonics, 2015, 9, 687–694.
18. J. Wang, H. Lu, X. Pan, J. Xu, H. Liu, X. Liu, D. R. Khanal, M. F. Toney, M. C. Beard and Z. V. Vardeny, ACS Nano, 2021, 15, 588–595.
19. H. Lu, J. Wang, C. Xiao, X. Pan, X. Chen, R. Brunecky, J. J. Berry, K. Zhu, M. C. Beard and Z. V. Vardeny, Sci. Adv., 2019, 5, 7.
20. Z. Huang, B. P. Bloom, X. Ni, Z. N. Georgieva, M. Marciesky, E. Vetter, F. Liu, D. H. Waldeck and D. Sun, ACS Nano, 2020, 14, 10370–10375.
21. H. Lu, C. Xiao, R. Song, T. Li, A. E. Maughan, A. Levin, R. Brunecky, J. J. Berry, D. B. Mitzi, V. Blum and M. C. Beard, J. Am. Chem. Soc., 2020, 142, 13030–13040.
22. Y. H. Kim, Y. Zhai, H. Lu, X. Pan, C. Xiao, E. A. Gaulding, S. P. Harvey, J. J. Berry, Z. V. Vardeny, J. M. Luther and M. C. Beard, Science, 2021, 371, 1129–1133.
23. C. T. Wang, K. Chen, P. Xu, F. Yeung, H. S. Kwok and G. Li, Adv. Funct. Mater., 2019, 29, 1903155.
24. J. Wang, C. Fang, J. Ma, S. Wang, L. Jin, W. Li and D. Li, ACS Nano, 2019, 13, 9473–9481.
25. G. Long, R. Sabatini, M. I. Saidaminov, G. Lakhwani, A. Rasmita, X. Liu, E. H. Sargent and W. Gao, Nat. Rev. Mater., 2020, 5, 423–439.
26. C. Chen, L. Gao, W. Gao, C. Ge, X. Du, Z. Li, Y. Yang, G. Niu and J. Tang, Nat. Commun., 2019, 10, 1927.
27. H. Kim, R. M. Kim, S. D. Namgung, N. H. Cho, J. B. Son, K. Bang, M. Choi, S. K. Kim, K. T. Nam, J. W. Lee and J. H. Oh, Adv. Sci., 2022, 9, 2104598.
28. J. Ahn, E. Lee, J. Tan, W. Yang, B. Kim and J. Moon, Mater. Horiz., 2017, 4, 851–856.
29. J. Ahn, S. Ma, J. Y. Kim, J. Kyhm, W. Yang, J. A. Lim, N. A. Kotov and J. Moon, J. Am. Chem. Soc., 2020, 142, 4206–4212.
30. J. Ma, C. Fang, C. Chen, L. Jin, J. Wang, S. Wang, J. Tang and D. Li, ACS Nano, 2019, 13, 3659–3665.
31. G. Long, C. Jiang, R. Sabatini, Z. Yang, M. Wei, L. N. Quan, Q. Liang, A. Rasmita, M. Askerka, G. Walters, X. Gong, J. Xing, X. Wen, R. Quintero-Bermudez, H. Yuan, G. Xing, X. R. Wang, D. Song, O. Voznyy, M. Zhang, S. Hoogland, W. Gao, Q. Xiong and E. H. Sargent, Nat. Photonics, 2018, 12, 528–533.
32. Z. N. Georgieva, B. P. Bloom, S. Ghosh and D. H. Waldeck, Adv. Mater., 2018, 30, 1800097.
33. G. H. Debnath, Z. N. Georgieva, B. P. Bloom, S. Tan and D. H. Waldeck, Nanoscale, 2021, 13, 15248–15256.
34. W. Chen, S. Zhang, M. Zhou, T. Zhao, X. Qin, X. Liu, M. Liu and P. Duan, J. Phys. Chem. Lett., 2019, 10, 3290–3295.
35. T. He, J. Li, X. Li, C. Ren, Y. Luo, F. Zhao, R. Chen, X. Lin and J. Zhang, Appl. Phys. Lett., 2017, 111, 151102.
36. Y. H. Kim, Y. Zhai, E. A. Gaulding, S. N. Habisreutinger, T. Moot, B. A. Rosales, H. Lu, A. Hazarika, R. Brunecky, L. M. Wheeler, J. J. Berry, M. C. Beard and J. M. Luther, ACS Nano, 2020, 14, 8816–8825.
37. A. Hubley, A. Bensalah-Ledoux, B. Baguenard, S. Guy, B. Abécassis and B. Mahler, Adv. Opt. Mater., 2022, 10, 2200394.
38. S. Jiang, Y. Song, H. Kang, B. Li, K. Yang, G. Xing, Y. Yu, S. Li, P. Zhao and T. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 3385–3394.
39. Y. H. Kim, R. Song, J. Hao, Y. Zhai, L. Yan, T. Moot, A. F. Palmstrom, R. Brunecky, W. You, J. J. Berry, J. L. Blackburn, M. C. Beard, V. Blum and J. M. Luther, Adv. Funct. Mater., 2022, 32, 2200454.
40. J. T. Lin, D. G. Chen, L. S. Yang, T. C. Lin, Y. H. Liu, Y. C. Chao, P. T. Chou and C. W. Chiu, Angew. Chem., Int. Ed., 2021, 60, 21434–21440.
41. Z. N. Georgieva, Z. D. Zhang, P. Zhang, B. P. Bloom, D. N. Beratan and D. H. Waldeck, J. Phys. Chem. C, 2022, 126, 15986–15995.
42. S. Ma, Y. K. Jung, J. Ahn, J. Kyhm, J. Tan, H. Lee, G. Jang, C. U. Lee, A. Walsh and J. Moon, Nat. Commun., 2022, 13, 3259.
43. Y. Zhang, M. Sun, N. Zhou, B. Huang and H. Zhou, J. Phys. Chem. Lett., 2020, 11, 7610–7616.
44. Y. Zhou, Z. Zhu, W. Huang, W. Liu, S. Wu, X. Liu, Y. Gao, W. Zhang and Z. Tang, Angew. Chem., Int. Ed., 2011, 50, 11456–11459.
45. A. Ben-Moshe, D. Szwarcman and G. Markovich, ACS Nano, 2011, 5, 9034–9043.
46. F. Purcell-Milton, A. K. Visheratina, V. A. Kuznetsova, A. Ryan, A. O. Orlova and Y. K. Gun'ko, ACS Nano, 2017, 11, 9207–9214.
47. G. H. Debnath, B. P. Bloom, S. Tan and D. H. Waldeck, Nanoscale, 2022, 14, 6037–6051.
48. C. Bi, Z. Yao, X. Sun, X. Wei, J. Wang and J. Tian, Adv. Mater., 2021, 33, 2006722.
49. M. C. Brennan, J. E. Herr, T. S. Nguyen-Beck, J. Zinna, S. Draguta, S. Rouvimov, J. Parkhill and M. Kuno, J. Am. Chem. Soc., 2017, 139, 12201–12208.
50. Y. Dong, T. Qiao, D. Kim, D. Parobek, D. Rossi and D. H. Son, Nano Lett., 2018, 18, 3716–3722.
51. A. Rodger and B. Norden, Circular Dichroism and Linear Dichroism, Oxford University Press, New York, 1997.
52. P. R. Schimmel and C. R. Cantor, Biophysical Chemistry Part II: Techniques for the Study of Biological Structure and Function, Freeman, New York, 1st edn, 1980.
53. A. Ben-Moshe, A. Teitelboim, D. Oron and G. Markovich, Nano Lett., 2016, 16, 7467–7473.
54. X. Gao, X. Zhang, K. Deng, B. Han, L. Zhao, M. Wu, L. Shi, J. Lv and Z. Tang, J. Am. Chem. Soc., 2017, 139, 8734–8739.
55. S. D. Elliott, M. P. Moloney and Y. K. Gun'ko, Nano Lett., 2008, 8, 2452–2457.
56. T. Nakashima, Y. Kobayashi and T. Kawai, J. Am. Chem. Soc., 2009, 131, 10342–10343.
57. Y. Zhou, M. Yang, K. Sun, Z. Tang and N. A. Kotov, J. Am. Chem. Soc., 2010, 132, 6006–6013.
58. N. Berova, L. Di Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931.
59. J. L. Greenfield, J. Wade, J. R. Brandt, X. Shi, T. J. Penfold and M. J. Fuchter, Chem. Sci., 2021, 12, 8589–8602.
60. R. A. DeCrescent, X. Du, R. M. Kennard, N. R. Venkatesan, C. J. Dahlman, M. L. Chabinyc and J. A. Schuller, ACS Nano, 2020, 14, 8958–8968.
61. R. A. DeCrescent, N. R. Venkatesan, C. J. Dahlman, R. M. Kennard, X. Zhang, W. Li, X. Du, M. L. Chabinyc, R. Zia and J. A. Schuller, Sci. Adv., 2020, 6, eaay4900.
62. M. R. Goldsmith, C. B. George, G. Zuber, R. Naaman, D. H. Waldeck, P. Wipf and D. N. Beratan, Phys. Chem. Chem. Phys., 2006, 8, 63–67.
63. B. P. Bloom, L.-B. Zhao, Y. Wang, D. H. Waldeck, R. Liu, P. Zhang and D. N. Beratan, J. Phys. Chem. C, 2013, 117, 22401–22411.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr06751j

---