DNA origami tubes with reconfigurable cross-sections

Abstract

Structural DNA nanotechnology has enabled the design and construction of complex nanoscale structures with precise geometry and programmable dynamic and mechanical properties. Recent efforts have led to major advances in the capacity to actuate shape changes of DNA origami devices and incorporate DNA origami into larger assemblies, which open the prospect of using DNA to design shape-morphing assemblies as components of micro-scale reconfigurable or sensing materials. Indeed, a few studies have constructed higher order assemblies with reconfigurable devices; however, these demonstrations have utilized structures with relatively simple motion, primarily hinges that open and close. To advance the shape changing capabilities of DNA origami assemblies, we developed a multi-component DNA origami 6-bar mechanism that can be reconfigured into various shapes and can be incorporated into larger assemblies while maintaining capabilities for a variety of shape transformations. We demonstrate the folding of the 6-bar mechanism into four different shapes and demonstrate multiple transitions between these shapes. We also studied the shape preferences of the 6-bar mechanism in competitive folding reactions to gain insight into the relative free energies of the shapes. Furthermore, we polymerized the 6-bar mechanism into tubes with various cross-sections, defined by the shape of the individual mechanism, and we demonstrate the ability to change the shape of the tube cross-section. This expansion of current single-device reconfiguration to higher order scales provides a foundation for nano to micron scale DNA nanotechnology applications such as biosensing or materials with tunable properties.

---

Introduction

Structural DNA nanotechnology^1,2 provides a platform to design and construct complex geometries. DNA origami^3,4 has enabled the production of nanodevices integrating complex geometry with programmable mechanical and dynamic properties. Many of these dynamic DNA nanostructures can achieve reconfigurability using single-stranded DNA (ssDNA) inputs to displace regions of double-stranded DNA (dsDNA). This technique, called DNA strand displacement,^5,6 provides a platform for controlling the configuration, motion, and rigidity of DNA nanodevices.⁷ For example, this approach has been used to open and closed nanoscale hinges or containers,^8–10 extend or retract pistons,^10,11 or shape transformations in 2D or 3D mechanisms.^12,13 Recent efforts have extended actuated reconfiguration to larger scale assemblies leveraging strand displacement^7,12,14,15 or switchable base-stacking interactions;¹⁶ However, studies that have extended dynamic DNA devices to higher order structures rely on relatively simple motion (largely assembling devices with one degree of rotational motion) compared to what has been demonstrated with individual devices. Here we focus on expanding complex shape transformations to higher order DNA origami assemblies.

Actuated reconfiguration is well-established for individual DNA nanodevices to achieve motions on the scale of one to tens of nanometers.^7,17 In particular, well-defined motions can be achieved by integrating rigid dsDNA and flexible ssDNA components to achieve rotation or translation, allowing for robotic devices¹⁸ that can even mimic the design of some macroscopic-machines.^10–12 DNA nanostructure actuation has largely focused on the nanoscale, while other technologies like soft robotics and polymer-based responsive materials exhibit structural features and motions at micron-scales and larger.^19,20 Hence, bridging DNA devices from nano- to micron length scales could provide a foundation for DNA based material and robotic components with shape-morphing or dynamically tunable mechanical properties.

A number of recent efforts have expanded DNA origami to larger scales through controlled hierarchical assemblies^21–26 thus expanding DNA origami to well-defined structures on the gigadalton scale. More recent works have showcased DNA nanostructures capable of combinatorial multi-micron DNA nanostructures via crisscross polymerization,²² DNA origami–nanoparticle composites,²⁷ activatable hydrogel devices,¹⁴ or polymers with local reconfiguration or switchable components.^21,28 For example, DNA nanostructures via crisscross polymerization^{16,22,27,29,30} formed “megastructures” up to ∼5 gigadalton and periodic assemblies containing ∼10 000 DNA origami structures. Some studies have demonstrated integration of reconfigurable constructs into arrays and wireframe tubes.^{15,16,27,29,30} Some functional DNA construct examples include placing and shaping liposomes³¹ with reconfigurable DNA cages to provide various bending transitions, and recent assembly of three distinct DNA origami structures to create a rotary motor.³²

These dynamic assemblies take critical steps to expand the design capabilities of DNA origami to material scales, but a large gap remains between the complex reconfiguration that has been demonstrated with individual devices and the relatively simpler motions of higher order assemblies. To address this limitation, we report the design and characterization of a 6-bar DNA origami mechanism that can adopt different cross-sections and be assembled into a tube such that the shape of the device forms the cross-section of the tube. The shape of the 6-bar mechanism is determined by a set of struts, which can be reconfigured to morph the mechanism into four representative distinct shapes: rectangle, triangle, hexagon and compact configuration (i.e. “flat-closed”). The struts are decorated with toehold strands to mediate strand displacement, allowing for shape changes. We demonstrate high yield folding into several distinct shapes as well as multiple transformations between these shapes based on DNA strand displacement to reconfigure the struts. We quantified the shape preferences of the 6-bar when multiple strut strand inputs were introduced to study the relative free energies of the distinct shapes. Finally, we demonstrate polymerization of the devices to form tubes with specific shape cross sections, and demonstrate reconfiguration of the tubes into new cross-sections to establish higher order reconfigurability in multi-device assemblies.

Results

6-Bar DNA origami mechanism design and characterization

We designed the 6-bar mechanism in MagicDNA,³³ a computer-aided design software for dynamic assemblies of DNA structures, and fine-tuned features like the assembly overhangs in cadnano³⁴ (ESI Fig. S.1–S.5†). The 6-bar is single loop of 6-links, or arms, each with a 3 × 4 dsDNA helix bundle cross section (Fig. 1A), connected with six hinge joints. Since the stiffness of the arms is several orders of magnitude higher than that of the hinges, the 6-bar mechanism is considered a planar three degrees-of-freedom mechanism that requires three inputs for kinematically controlling the configuration; hence, we devised a design strategy to provide three spatial inputs by constraining inter-arm angles to lock the mechanism into a target configuration, similar to a prior strategy used to form tripods with tunable angles.³⁵ Each arm contains a 172 nt scaffold loop (i.e. 6 total scaffold loops) protruding toward the center of the mechanism. The scaffold loops can be connected by ssDNA staple strands that fold two of the loops into a stiff strut to hold two of the links at a defined relative angle. Hence, the configuration of these struts determines the shape of the 6-bar mechanism. The staple strands forming the struts also contain ssDNA overhangs to serve as toeholds for DNA strand displacement, allowing for resetting to the flexible state and reconfiguration into another shape by the addition of new strut staples. We designed the device to adopt four different shapes: a rectangle, triangle, hexagon, and “flat closed” configuration, each defined by a distinct set of three struts (Fig. 1B). Additional staples were included in two of the shapes (rectangle and triangle) to bridge pairs of arms that are held straight end-to-end (e.g., cyan and orange arms in rectangle or cyan and magenta arms in triangle). The shapes were simulated using oxDNA^36–38 to visualize the intended link angles and overall shape (Fig. 1C). We then fabricated structures through a 2.5-day thermal annealing ramp with varying salt concentrations dependent on shape to determine the optimal folding conditions for each shape. Folding results were characterized via agarose gel electrophoresis (ESI Fig. S.6–S.9†) and transmission electron microscopy (TEM). TEM imaging showed a high yield of well-folded structures of the desired shapes (ESI Fig. S.6–S.9†). TEM image averages revealed the clear formation of struts that lock the mechanism into the desired configuration (Fig. 1D) illustrating the ability to fold the 6-bar mechanism into a variety of different shapes.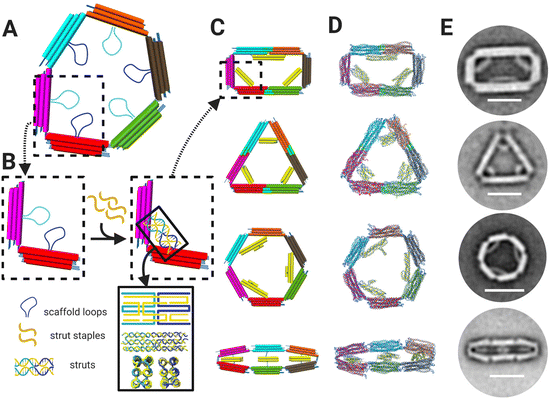

Fig. 1 (A) 6-Bar mechanism is comprised of six bars/arms connected by six hinges. Each arm contains a 172 nt scaffold loops protruding towards the middle of the mechanism. (B) The 172 nt scaffold loops can be combined and folded via addition of staple strands (yellow) to form struts, which are depicted schematically and in oxDNA^36–38 simulations (bottom of lower right inset). (C) CAD models with dsDNA helices depicted as cylinders and (D) oxDNA^36–38 simulations of the 6-bar mechanism showing four shapes: rectangle, triangle, hexagon, and flat-closed. (E) TEM image averages of each shape validating designs and simulations where each shape is formed by distinct strut configurations. Scale bars = 50 nm. CAD models visualized in UCSF Chimera.³⁹ Schematics created with BioRender.com.

Shape preference of 6-bar mechanism

The 6-bar strut regions contain the same scaffold sequences among each shape, but the scaffold loops are arranged and paired differently for each design. All four shapes contain 3 struts; however, these are arranged differently and may contain different cross sections. For example, the cross section of the rectangle has 2 struts with a 2 × 3 dsDNA bundles and 1 strut with a 2 × 2 dsDNA bundle, whereas the flat close and triangle struts have 2 × 4 dsDNA bundle cross sections arranged differently, and the hexagon struts are arranged in a 3 × 2 dsDNA bundle cross section. The cross-section was determined based on the strut length for the desired angle.

Since the different shapes are folded from a common set of strands that make up the 6 arms and a distinct set of strands that make up the struts (and in some cases fortify two neighboring straight arms), we hypothesized that the differences in the strut arrangements and the added staple strands to hold two arms straight (e.g. as in the rectangle) could lead to a relative difference in the free energy of each shape, which could make it easier to adopt one particular shape over the other. To study the shape preferences, we performed a folding reaction using a long temperature annealing ramp where we mixed the core staples for the 6-bar (i.e., common staples that make up the 6 arms) in equimolar ratio to the sets of strut strands for the rectangle, hexagon, and flat close shapes in competitive folding reaction. We focused the shape preference and reconfiguration studies on the hexagon, rectangle, and flat-closed configurations since they folded with higher yield (ESI Fig. S.6–S.9†). This competitive folding mixture was subjected to a 2.5 day annealing temperature ramp (details in Methods) and evaluated by gel electrophoresis and TEM (Fig. S.10†). Gel electrophoresis revealed structures from the competitive folding ran similar to the direct fold of the rectangle configuration. This result is consistent with TEM images, which revealed a large majority of rectangle shapes (75%) with minor populations of flat closed (2.3%) (Fig. S.10†). Some structures were folded into an undefined shape (22%), where one or more struts were visibly misfolded, or the mechanism was twisted likely due to staples from distinct shapes binding to struts. It is also possible that the mechanisms that we prescribe as a particular shape may still have some fraction of staples from the other struts, but here we reported mechanisms that were clearly observed in a target shape. The preference for folding into a particular shape is likely due to the distinct strut configurations and the corresponding staple strands that define each shape. The observed trend that most shapes fold into the rectangle is consistent with the total hybridization free energies of the staple strand sequences (calculated using the nearest neighbor model⁴⁰), where the rectangle exhibits the strongest hybridization free energy followed by the flat closed configuration and then the hexagon (ESI Table 1†). These hybridization free energies assume binding of staple strands directly to reverse complements. While this is distinct from hybridization to form struts in the 6-bar mechanism and does not account for free energy contributions due to constraining the 6-bar into different shapes, our results suggest the hybridization strength is important in regulating the shape preference.

In addition to studying the preferred shapes during the folding reaction, we also tested the case of actuating the 6-bar into a target shape. For these experiments, we first folded the 6-bar mechanism in the flexible configuration mechanism (i.e. with all struts single-stranded), and then added the mixture of strut staples for forming the rectangle, hexagon, and flat-closed configurations. We subjected these mixed strut folding reactions to low temperature thermal annealing (max temperature in thermal ramp is 45 °C) to facilitate strut folding while avoiding melting of the 6-bar structure. Quantitative analysis from TEM imaging after each annealing cycle (Fig. S.11–S.13†) shows that after three annealing cycles, ∼70% of the final shapes are the rectangle and the rest a mixture of undefined and flat-closed shapes. The twisted configuration shown as an undefined structure (Fig. 2A TEM image and Fig. S.11–S.13†) may be twisting out of plane due to a mixture of strut staples corresponding to different shapes. Our results show the structures again fold primarily into rectangle shapes with the three annealing cycles converging to nearly the same results as the 2.5-day folding reaction (Fig. 2B). While we cannot be certain the observed target shapes are not hybrids (i.e., observed rectangles may contain some fraction of hexagon strut staples), these results suggest the rectangle is strongly preferred.

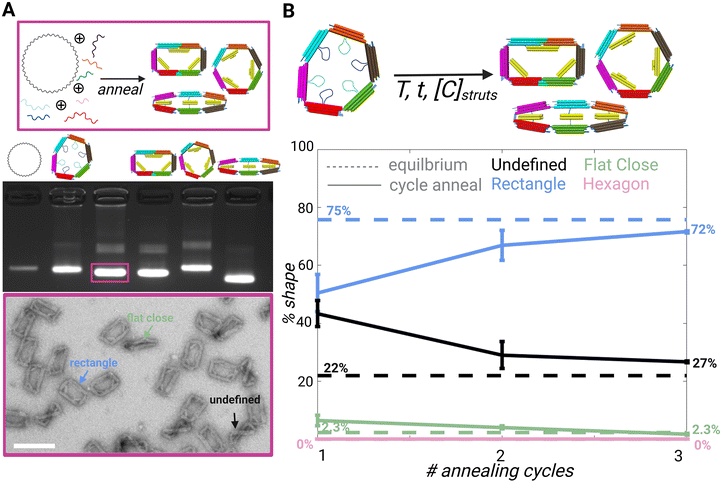Fig. 2 (A) Schematic showing competitive folding of 6-bar with scaffold and all core and strut staples. (Top) Agarose gel electrophoresis image left to right: 7249 m13p18 scaffold, direct fold of 6-bar with no strut staples, competitive fold as shown in schematic above, direct fold of rectangle shape, direct fold of hexagon shape, and direct fold of flat close (middle) TEM image of competitive fold showing the preferred shapes (bottom) scale bar = 50 nm. (B) Schematic showing folded 6-bar open configuration added with strut strands and annealed to form a mixture of rectangle, hexagon, and flat close shapes. (Top) Plot of competitive fold of 6-bar compared to cycle annealing of folded 6-bar mechanism with strut staples; dotted line = equilibrium average, solid line = cycle annealing (bottom). CAD models visualized in UCSF Chimera³⁹ Created with BioRender.com.

Although the mixed actuation results agree well with the competitive folding results, it is difficult to ensure the observed shape ratios represent equilibrium conditions reflective of true free energy differences. However, we can estimate apparent free energy differences between 6-bar configurations based on these experimental results. Based on the observed shape distributions in the competitive folding, we estimated an apparent free energy difference of 14.3 pN nm between the rectangle and flat-closed conformation (from eqn (1)). K_eq corresponds to the equilibrium constant defined by the ratio of rectangles to flat-closed shapes and related to ΔG, the free energy difference between the rectangle and flat-closed configurations, and the thermal energy k_bT = 4.1 pN nm (Boltzmann constant multiplied by absolute temperature).

The nearest neighbor approximation results in hybridization free energies of −1377 kcal mol⁻¹ and −1363 kcal mol⁻¹ (details in ESI Table 1†), respectively, for the rectangle and flat-closed accounting for hybridization for all of the additional staples that define each shape. The difference in these total hybridization free energies is 14 kcal mol⁻¹, or 97 pN nm, which is larger than but on a similar order of magnitude as the experimentally determined apparent free energy difference. The discrepancy is likely due to additional free energy contributions from scaffold topology, strut bundle configuration (e.g. different cross-sections, shorter versus longer bundles, and potential steric hindrances) and 6-bar mechanism deformation leading to local stresses (i.e. distinct joint angles), which have been shown to play a role in folding.⁴¹ It is also possible that some structures contain defects (i.e. some fraction of hexagon strut staples binding to rectangle shapes). In addition, it could be that some mechanisms are still kinetically trapped and longer annealing protocols might converge more of the undefined structures to the rectangle, which would lead to a larger apparent free energy difference.

Reconfiguration of 6-bar mechanism

We chose two shape transformations to illustrate the versatility of this design. We tested both conversion from a more preferred to less preferred shape and a less preferred to a more preferred state by selecting the intermediate shape as the target shape (flat close) and starting from either more (rectangle) or less (hexagon) preferred shapes. For both shape transformations, we first release the initial shape constraints to convert to the flexible mechanism, and then reconfigure to the target shape through the incorporation of new strut staple strands.

The reconfiguration of the 6-bar mechanism relies on toehold-mediated strand-displacement⁵ to remove the strut staple strands and convert to the flexible 6-bar mechanism (Fig. 3A). During the displacement, we use a short incubation of 37 °C to displace the staples connected to the struts. Then, transformation staples are introduced and incubated in a low temperature annealing cycle (highest temp. 45 °C) to refold the strut scaffold loops and form a new cross-section (Fig. 3A). TEM and agarose gel electrophoresis were used to verify the displacement and transformation of strut strands. TEM images were used to produce galleries (Fig. S.14 and S.15†) of individual particles and counted as transformed or not transformed with the criteria that at least 2/3 struts were clearly transformed (Methods section). Fig. 3C shows gel images depicting the gel shifts between each transformation step: displacement, intermediate, and transformation. The final band on the gels shows the compact configuration and the band to the left shows the transformed structure, showing clearly that the transformed structure band is running similarly to the compact configuration. Fig. 3B (top) shows the transformation from the rectangle configuration to the compact configuration with 91% transformation efficiency. Fig. 3B (bottom) shows transformation from the hexagon configuration to the compact configuration with 98% transformation efficiency. The lower transformation efficiency for the rectangle-to-flat-closed condition is consistent with the observed result that the rectangle shape is preferred and may be due to the relatively stronger binding free energies of the rectangle strut staples, which suggest those may not displace as readily. In contrast, the hexagon-to-flat-closed transition has a higher efficiency, which is consistent with the flat-closed being preferred.

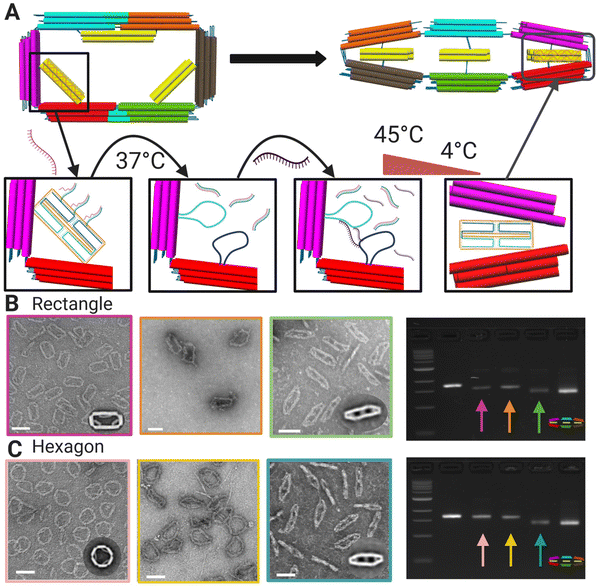Fig. 3 (A) Schematic of toe-hold mediated strand displacement in a rectangle with the introduction of a displacement strand attaching to toe-hold strands on the strut region subjected to incubation. The transformation strand is introduced and subjected to the annealing incubation showing the final configuration as flat-closed. (B) TEM image of rectangle (left) to displaced rectangle (middle) to final transformed shape flat-closed (right) and agarose gel electrophoresis showing each configuration with arrow colors matching borders of TEM images. (C) TEM image of hexagon (left) to displaced hexagon (middle) to final transformed shape flat-closed (right) and agarose gel electrophoresis showing each configuration with arrow colors matching borders of TEM images. Insets are TEM image averages. Scale bars = 100 nm. CAD models visualized in UCSF Chimera.³⁹ Created with BioRender.com.

Since our shape preference results indicated one transition is energetically favorable (hexagon to flat-closed), we hypothesized that the flat-closed strut staples may directly be able to transform the hexagon strut staples without the need for the strand displacement step (i.e., flat-closed staples outcompete hexagon staples for binding the scaffold). To test this, we exposed the rectangle and hexagon shapes to the actuation incubation with and without strut displacement staples, then incubated the mixtures with flat-closed strut transformation strands. We visualized the results on an agarose gel to analyze the shapes at each step and directly compare to the flat-closed shape (Fig. S.16 and S.17†). The results revealed the toehold strand displacement steps are needed, even for energetically favorable shape transformations with our transformation protocol.

Polymerization and reconfiguration of 6-bar tubes

To assemble the 6-bar mechanism into filaments with varying cross sections, we designed the 6-bar structures to form tubes via “sticky-end” hybridization, where there are two monomeric units “A” and “B” (Fig. 4A) with complementary ssDNA sticky-ends on the outer face of each link pointing in the direction normal to the cross-section. The sticky-ends allow the formation of DNA origami tubes where the cross-section of the tube is defined by the shape of the 6-bar mechanism. Formation of tubes was verified via TEM (Fig. 4B). The “A” and “B” units were mixed in equimolar ratios and incubated for ∼26 hours in a thermal annealing cycle where the highest temperature reached 45 °C. ESI Fig. S.22–S.24, S.25–S.27, and S.28, S.29† show flat-closed, rectangle, and hexagon cross-section tubes respectively at varying salt conditions. The tubes reach lengths on the scale of ∼0.1–1 μm, translating to 10s of individual devices. Given the large aspect ratio of the tubes, they deposited onto the TEM imaging grid with the long axis of the tube laying on the grid. Hence the cross-section is not observable. In some cases, the shape of one of the end structures was visible (e.g., Fig. 4B(iii)); however, each shape had a clear signature of the top-down intensity profile. This lateral (i.e., across the width orthogonal to the long-axis) intensity profile was qualitatively apparent in images, and we further quantified the intensity profile of each cross-section (Fig. S.18–S.21†).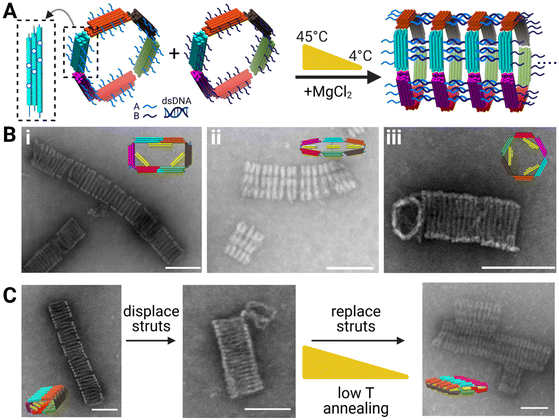

Fig. 4 (A) Left to right: Schematic showing polymerization scheme of the 6-bar tubes (inset showing in-plane location of polymerization strands on each arm) with each arm having 6 in-plane and 6 out-of-plane polymerization strands. Unit “A” and “B” polymerize via complementary sticky ends and subjected to a low temperature thermal annealing ramp to form tubes with distinct cross-sections. (B) TEM images of DNA origami tubes with (i) with rectangle cross-section (ii) flat-closed-cross section (iii) hexagon cross-section (insets are CAD models of each tubes cross-section shape). (C) Reconfiguration schematic of DNA origami tubes with TEM images. (Left) Rectangle cross-section (middle) rectangle cross-section subjected to displacement staples and incubation (right). Displaced tubes mixed with transformation strut staples to reconfigure to flat-closed cross-section. Scale bars = 100 nm. CAD models visualized in UCSF Chimera.³⁹ Created with BioRender.com.

We tested the ability to reconfigure the tubes cross sections and used the lateral intensity profile to confirm what shapes the tubes were in. Fig. 4C depicts TEM images of the reconfiguration of rectangular tubes into flat-closed tubes. ESI Fig. S.18–S.21† provide intensity profiles for the rectangle initial tube cross-section, intermediate tube cross-section, final flat-closed cross-section, and flat-closed initial tube cross-section to confirm reconfiguration of the tubes. Previous literature focused on singular device formation and reconfiguration,¹² whereas here we show tubes on the order of 100s of nanometers capable of reconfiguration. Reconfiguration of the DNA origami tubes provides fundamental work to enable higher order devices capable of reconfiguration.

Conclusions

DNA nanotechnology, specifically DNA origami is a powerful approach to design reconfigurable devices while leveraging actuation methods to dynamically control structure and mechanical properties. These actuation methods have largely focused on the nanoscale while soft robotics and bio-based polymers reach micron-length scale motion. DNA origami devices are capable of coupling across these length scales, however, the reconfigurability and complex motion of higher order DNA origami assemblies remained significantly limited compared to individual device reconfiguration and actuation. This work addresses these limitations with the design and fabrication of a 6-bar DNA origami device capable of higher order assembly to hundreds of nanometer long tubes with a variety of cross-sections and reconfiguration of individual devices as well as tubes.

As a key design feature, the reconfiguration of the 6-bar occurs in plane, whereas the polymerization of the 6-bar mechanism is occurring out of plane. This decouples the primary modes of motion from the polymerization allowing for large assemblies while maintaining the capability for versatile reconfiguration. The shapes transformations in this work occur either at the scale of tens of nanometers on the single-device scale or hundreds of nanometers on the higher order tube assemblies. Future outlooks and advancement include combining DNA origami tubes with other materials^42–44 or tubes for molded structures^45–47 (e.g. gold molding) or coating with silicon.⁴⁸ Reconfiguring these DNA origami tubes provides fundamental work to enable higher order assembly of DNA devices^23,26,49 capable of reconfiguration for many research areas relating to soft robotics,^18–20 bio-inspired polymers,^19,50–52 and drug delivery systems.^45,53,54

Methods

Design and fabrication of DNA origami 6-bar device

Design and simulation. The DNA origami 6-bar device was designed in the software MagicDNA³³ (Fig. S.5†) and modified in cadnano³⁴ (Fig. S.1–S.4†) and uploaded to nanobase.org.⁵⁵ Each core arm of the 6-bar consists of 12 dsDNA helices with a 3 × 4 helix-bundle cross section. The arms are connected on the internal bundles by scaffold connections between arms with various scaffold topology defined by the shape angle. Scaffold loops on the internal bundles are connected by two arms to create the strut regions. Sticky end locations along the internal planar bundle were designed in MagicDNA where sequences were designed in an in-house MATLAB code to prevent secondary structures with other structure sequences.

Simulation files were generated from the cadnano design of the 6-bar mechanism through the python code caDNAno interface.py, provided by the oxDNA group (https://dna.physics.ox.ac.uk). We used a custom MATLAB code, as previously described,⁵⁶ to manipulate design components into the target shape to form the initial configuration for simulation. The code was used to manually apply rigid body transformations to the individual components of the 6-bar mechanism to position them near the desired target shape. The rigid-body transformations were introduced to reduce the length of over-stretched bonds between components from the 2D caDNAno design as well as define the overall initial configuration for the MD. The coarse-grained MD simulations were performed as previously described.⁵⁶ Briefly, after the relaxation step, simulations were run using the oxDNA2 package³⁸ at a temperature of 303 K with no external forces. The total number of steps was set to 1 × 10⁷ for each simulation with a simulation time step for integration of 15.15 fs, the Newtonian step of an Andersen-like thermostat was 103, and a monovalent NaCl concentration of 0.5 M NaCl. A scaling factor α ≈ 330 was used to convert the simulation time to the physical time.⁵⁷ To reduce computation time, the oxDNA simulation was run with GPU acceleration⁵⁸ on a computer with a NVIDIA GPU. The UCSF Chimera³⁹ software was used to render all 3D coarse-grained models.

Fabrication. DNA staples were ordered and synthesized through Integrated DNA Technologies (Coralville, IL, USA) at 25 nmol scale with standard desalting purification. The scaffold was fabricated in-house derived from an M13mp18 bacteriophage as described in previous literature.⁵⁹ The DNA origami structures were folded (thermal-cycler C1000 from Bio-Rad) and optimized for optimal salt, scaffold, and staple concentrations. The structures were folded with 200 nM staples and 40 nM scaffold concentrations with folding reactions containing buffer solutions consisting of 5 mM Tris, 5 mM NaCl (pH 8), 1 mM EDTA and varying found in the respective ESI captions for magnesium screens (Fig. S.6–S.9†). The appropriate MgCl₂ concentrations for subsequent folds are as followed: rectangle folded at 20 mM MgCl₂, the triangle folded at 12 mM MgCl₂, the hexagon folded at 26 mM MgCl₂, and flat close folded at 18 mM MgCl₂. The annealing ramp used was a 2.5-day fold beginning with a melt phase at 1 hour per °C from 65 °C to 61 °C followed by an anneal phase at 2 hours per °C from 60 °C to 40 °C and finally a cool step at 30 minutes per °C from 39 °C to 4 °C. Folding reactions were then verified through agarose gel electrophoresis and transmission electron microscopy (TEM) as described below. While a range of MgCl₂ concentrations resulted in well-folded structures, we selected particular concentrations based on high yield of well-folded structures in TEM images (Fig. S.6–S.9†).

Purification of DNA origami

Agarose gel electrophoresis. Well-folded DNA origami structures were verified through agarose gel electrophoresis. Buffer conditions included 0.5× TBE (Tris, borate, and EDTA) buffer containing 45 mM boric acid, 45 mM tris(hydroxymethyl)aminomethane base, and 1 mM (ethylenedinitrilo)tetraacetic acid with 11 mM MgCl₂ and 2% agarose with 0.5 μg ml⁻¹ ethidium bromide. The gel was run at 90 V for 90–120 minutes in an ice water bath. The agarose gel electrophoresis images in Fig. 2 and ESI Fig. S.15, S.16† were purified using a 0 mM EDTA loading dye to prevent chelation of MgCl₂. Agarose gel electrophoresis images in ESI Fig. S.6–S.9† used 1 mM EDTA loading dye. Agarose gels were imaged on an analytik jena UVP GelStudio touch, 12 MP or a FotoDyne Express FOTO/Analyst system.

Amicon centrifugation purification. Once structures were verified as well-folded, unpurified folded structures were placed into amicon centrifugation tubes. The amicon centrifugation tubes were initially conditioned with 500 μL of 1× FOB (buffer solution containing 5 mM Tris, 5 mM NaCl (pH 8), and 1 mM EDTA) and 10 mM MgCl₂ buffer and spun for 8 minutes at 5000g. 100 μL of well-folded, unpurified structures and 400 μL of conditioning buffer were then placed in the centrifugation tubes and spun for 8 minutes at 5000g. This process was repeated 2× until finally the filter containing the purified structures was flipped upside down into a new centrifuge tube and spun for 2 minutes at 10 000g. Purified structures were subsequently used in reconfiguration and polymerization.

Competitive folding reactions and mixture actuation

Competitive folding reaction. The competitive folding reaction is a mixture of 20 nM scaffold, 200 nM core staples (6-bar link staples), 10× excess rectangle, hexagon, and flat-closed strut staples relative to the scaffold (i.e., each set of strut staples was added to final concentration of 200 nM in mixture), buffer solutions consisting of 5 mM Tris, 5 mM NaCl (pH 8), 1 mM EDTA, and 20 mM MgCl₂. The mixture was then subjected to a 2.5-day thermal annealing cycle as described above. The structures were purified via agarose gel electrophoresis to visualize the band shift and amicon purified for TEM image analysis.

Mixture actuation. The 6-bar open configuration (i.e. no strut staples) is folded as a mixture of 20 nM scaffold, 200 nM core staples (6-bar link staples), buffer solutions consisting of 5 mM Tris, 5 mM NaCl (pH 8), 1 mM EDTA, and 20 mM MgCl₂. The mixture was then subjected to a 2.5-day thermal annealing cycle as described above. The structures were then purified via agarose gel electrophoresis to confirm well-folded structures and amicon purified for the mixture actuation. The mixture actuation consisted of a mixture containing amicon purified 6-bar open configuration structures, 10× excess rectangle, hexagon, and flat-closed strut staples relative to the scaffold (also the same as folded structure concentration), and buffer solutions consisting of 5 mM Tris, 5 mM NaCl (pH 8), 1 mM EDTA, and 20 mM MgCl₂. The mixture actuation was then subjected to a low temperature thermal annealing ramp starting at 45 °C followed by an anneal phase at −2 hours per °C until 20 °C for 1-cycle, 2-cycle, and 3-cycle annealing ramps.

Reconfiguration of DNA origami

Purified individual structures were mixed with 10× excess displacement strands relative to the structure concentration and subjected to an incubation of 2 hours at 37 °C with a buffer consisting of 1× FOB and 8 mM MgCl₂. The DNA origami tubes were also subjected to a similar transformation protocol post polymerization, however, the tubes were incubated for 4 hours at 37 °C. Once displaced, the monomers and tubes were mixed with 75× excess transformation strands relative to the structure/tube concentration, 200 mM MgCl₂ for a final MgCl₂ concentration of 20 mM and subjected to a 2-cycle low temperature cycle annealing ramp starting at 45 °C followed by an anneal phase at −2 hours per °C until 20 °C and repeated 2× total.

Polymerization of DNA origami

Polymerization of the “A” and “B” units were performed after amicon purification of the well-folded structures. “A” and “B” units were mixed at equal volume and equal concentration with a final buffer concentration of 5 mM MgCl₂, 10 mM MgCl₂, or 20 mM MgCl₂, with 45 mM boric acid, 45 mM tris(hydroxymethyl)aminomethane base, and 1 mM (ethylenedinitrilo)tetraacetic acid. The mixtures were then subjected to a 2-cycle low temperature annealing ramp starting at 45 °C followed by an anneal phase at −2 hours per °C until 20 °C and repeated 2× total.

Analysis and TEM imaging of DNA origami

TEM sample preparation. The individual 6-bar devices and reconfigured devices were imaged post agarose gel electrophoresis or amicon purification. Polymers were made from previously purified structures. A sample volume of 4 μL was deposited onto a plasma-cleaned Formvar-coated 400 mesh copper grid (Ted Pella) with incubation times between 4–8 min before wicking away the solution with filter paper. For the polymer images in Fig. 4B. A 4 μL droplet of 30 mM MgCl₂ was added to the plasma cleaned grid before sample incubation for ∼1 minute then wicked away on filter paper followed by a 4 μL droplet of polymer sample. The polymer samples were incubated on the grid for 8 minutes for sufficient surface deposition, whereas the individual devices from folds or reconfiguration were incubated for 4 minutes. The sample was then wicked away on filter paper, followed by the addition of a 10 μL droplet of staining solution consisting of 2% uranyl formate plus 25 mM NaOH, immediately wicked away, then followed by the addition of a 20 μL droplet of the same staining solution incubated for 40 s and finally wicking away the stain solution. The samples were allowed to dry for at least 20 minutes at room temperature before imaging, the structures were imaged at the Ohio State University Campus Microscopy and Imaging Facility on a FEI Tecnai G2 Spirit TEM with an acceleration of 80 kV.

TEM image analysis. TEM images for the reconfiguration were analyzed in EMAN2.3 ⁶⁰ and galleries were created using EMAN2.3 as described previously.³³ EMAN2.3 was also used as described previously³³ to create image averages shown in Fig. 1 and 2. ImageJ 1.53e⁶¹ was used to measure the polymer intensity profiles using the plot profile tool in the analyze tab. At least 10 polymer intensity profile plots were averaged and plotted for ESI Fig. S.17–S.20.† ImageJ 1.53e was used to enhance contrast/brightness and measure scale bars on TEM images using the set scale function in the analyze tab.

TEM image sorting for reconfiguration. TEM images from reconfiguration experiments were sorted into galleries of individual particles where manual sorting was used to determine transformation efficiency. Particles were deemed transformed if 2 or more struts were visibly transformed to the final shape. Transformed and untransformed particles were then separated and counted to measure efficiency. At least 200 particles were quantified as transformed or untransformed for both reconfiguration pathways.

Author contributions

This work was conceived by C. E. C. and H. S. The initial design of the 6-bar mechanism and the simulations were performed by C. M. H. All experiments were led by A. K., and J. W. supported optimization of the actuation reactions. A. K. and C. E. C. drafted the manuscript with feedback and editing from all authors.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the National Science Foundation through grants #1536862 to HJS and CEC, #1916740 to CEC, and #1921881 to CEC. We acknowledge the Campus Microscopy and Imaging Facility (CMIF) of the Ohio State University for imaging support. We also thank members of the Castro Lab and Su Lab for valuable feedback. Main Article figures were created using Biorender.com.

References

1. N. C. Seeman, Nucleic acid junctions and lattices, J. Theor. Biol., 1982, 99(2), 237–247,  DOI:10.1016/0022-5193(82)90002-9.
2. N. C. Seeman and H. F. Sleiman, DNA nanotechnology, Nat. Rev. Mater., 2017, 3(1), 1–23,  DOI:10.1038/natrevmats.2017.68.
3. P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440(7082), 297–302,  DOI:10.1038/nature04586.
4. S. Dey, C. Fan and K. V. Gothelf, et al., DNA origami, Nat. Rev. Methods Primers, 2021, 1(1), 1–24,  DOI:10.1038/s43586-020-00009-8.
5. B. Yurke, A. J. Turberfield, A. P. Mills, F. C. Simmel and J. L. Neumann, A DNA-fuelled molecular machine made of DNA, Nature, 2000, 406(6796), 605–608,  DOI:10.1038/35020524.
6. D. Y. Zhang and G. Seelig, Dynamic DNA nanotechnology using strand-displacement reactions, Nat. Chem., 2011, 3(2), 103–113,  DOI:10.1038/nchem.957.
7. H. Ijäs, S. Nummelin, B. Shen, M. A. Kostiainen and V. Linko, Dynamic DNA origami devices: From strand-displacement reactions to external-stimuli responsive systems, Int. J. Mol. Sci., 2018, 19(7), 2114,  DOI:10.3390/ijms19072114.
8. E. S. Andersen, M. Dong and M. M. Nielsen, et al., Self-assembly of a nanoscale DNA box with a controllable lid, Nature, 2009, 459(7243), 73–76,  DOI:10.1038/nature07971.
9. M. Liu, J. Fu and C. Hejesen, et al., A DNA tweezer-actuated enzyme nanoreactor, Nat. Commun., 2013, 4(1), 2127,  DOI:10.1038/ncomms3127.
10. A. E. Marras, L. Zhou, H. J. Su and C. E. Castro, Programmable motion of DNA origami mechanisms, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(3), 713–718,  DOI:10.1073/pnas.1408869112.
11. A. Mills, N. Aissaoui and D. Maurel, et al., A modular spring-loaded actuator for mechanical activation of membrane proteins, Nat. Commun., 2022, 13(1), 3182,  DOI:10.1038/s41467-022-30745-2.
12. L. Zhou, A. E. Marras, C. M. Huang, C. E. Castro and H. J. Su, Paper Origami-Inspired Design and Actuation of DNA Nanomachines with Complex Motions, Small, 2018, 14(47), 1802580,  DOI:10.1002/smll.201802580.
13. D. Lei, A. E. Marras and J. Liu, et al., Three-dimensional structural dynamics of DNA origami Bennett linkages using individual-particle electron tomography, Nat. Commun., 2018, 9(1), 592,  DOI:10.1038/s41467-018-03018-0.
14. J. Fern and R. Schulman, Modular DNA strand-displacement controllers for directing material expansion, Nat. Commun., 2018, 9(1), 3766,  DOI:10.1038/s41467-018-06218-w.
15. X. Lan, T. Liu, Z. Wang, A. O. Govorov, H. Yan and Y. Liu, DNA-Guided Plasmonic Helix with Switchable Chirality, J. Am. Chem. Soc., 2018, 140(37), 11763–11770,  DOI:10.1021/jacs.8b06526.
16. T. Gerling, K. F. Wagenbauer, A. M. Neuner and H. Dietz, Dynamic DNA devices and assemblies formed by shape-complementary, non-base pairing 3D components, Science, 2015, 347(6229), 1446–1452,  DOI:10.1126/science.aaa5372.
17. M. Deluca, Z. Shi, C. E. Castro and G. Arya, Dynamic DNA nanotechnology: Toward functional nanoscale devices, Nanoscale Horiz., 2020, 5(2), 182–201,  10.1039/c9nh00529c.
18. S. Nummelin, B. Shen, P. Piskunen, Q. Liu, M. A. Kostiainen and V. Linko, Robotic DNA Nanostructures, ACS Synth. Biol., 2022, 9(8), 1923–1940,  DOI:10.1021/acssynbio.0c00235.
19. S. Coyle, C. Majidi, P. LeDuc and K. J. Hsia, Bio-inspired soft robotics: Material selection, actuation, and design, Extreme Mech. Lett., 2018, 22, 51–59,  DOI:10.1016/j.eml.2018.05.003.
20. Y. Lee, W. J. Song and J. Y. Sun, Hydrogel soft robotics, Mater. Today Phys., 2020, 15, 100258,  DOI:10.1016/j.mtphys.2020.100258.
21. S. Gentile, E. Del Grosso, L. J. Prins and F. Ricci, Reorganization of Self-Assembled DNA-Based Polymers using Orthogonally Addressable Building Blocks, Angew. Chem., Int. Ed., 2021, 60(23), 12911–12917,  DOI:10.1002/anie.202101378.
22. C. M. Wintersinger, D. Minev and A. Ershova, et al., Multi-micron crisscross structures from combinatorially assembled DNA-origami slats, bioRxiv, 2022 DOI:10.1101/2022.01.06.475243.
23. W. Pfeifer and B. Saccà, From Nano to Macro through Hierarchical Self-Assembly: The DNA Paradigm, ChemBioChem, 2016, 17(12), 1063–1080,  DOI:10.1002/cbic.201600034.
24. S. Groeer and A. Walther, Switchable supracolloidal 3D DNA origami nanotubes mediated through fuel/antifuel reactions, Nanoscale, 2020, 12(32), 16995–17004,  10.1039/D0NR04209A.
25. S. Loescher and A. Walther, Supracolloidal Self-Assembly of Divalent Janus 3D DNA Origami via Programmable Multivalent Host/Guest Interactions, Angew. Chem., Int. Ed., 2020, 59(14), 5515–5520,  DOI:10.1002/anie.201911795.
26. A. E. Marras, Hierarchical assembly of DNA origami nanostructures, MRS Commun., 2022, 12(5), 543–551,  DOI:10.1557/s43579-022-00248-8.
27. J. A. Johnson, A. Dehankar, J. O. Winter and C. E. Castro, Reciprocal Control of Hierarchical DNA Origami-Nanoparticle Assemblies, Nano Lett., 2019, 19(12), 8469–8475,  DOI:10.1021/acs.nanolett.9b02786.
28. W. Pfeifer, P. Lill, C. Gatsogiannis and B. Saccà, Hierarchical Assembly of DNA Filaments with Designer Elastic Properties, ACS Nano, 2018, 12(1), 44–55,  DOI:10.1021/acsnano.7b06012.
29. K. F. Wagenbauer, C. Sigl and H. Dietz, Gigadalton-scale shape-programmable DNA assemblies, Nature, 2017, 552(7683), 78–83,  DOI:10.1038/nature24651.
30. M. Matthies, N. P. Agarwal and T. L. Schmidt, Design and Synthesis of Triangulated DNA Origami Trusses, Nano Lett., 2016, 16(3), 2108–2113,  DOI:10.1021/acs.nanolett.6b00381.
31. Z. Zhang, Y. Yang, F. Pincet, M. C. Llaguno and C. Lin, Placing and shaping liposomes with reconfigurable DNA nanocages, Nat. Chem., 2017, 9(7), 653–659,  DOI:10.1038/nchem.2802.
32. A. K. Pumm, W. Engelen and E. Kopperger, et al., A DNA origami rotary ratchet motor, Nature, 2022, 607(7919), 492–498,  DOI:10.1038/s41586-022-04910-y.
33. C. M. Huang, A. Kucinic, J. A. Johnson, H. J. Su and C. E. Castro, Integrated computer-aided engineering and design for DNA assemblies, Nat. Mater., 2021, 1–8,  DOI:10.1038/s41563-021-00978-5.
34. S. M. Douglas, A. H. Marblestone, S. Teerapittayanon, A. Vazquez, G. M. Church and W. M. Shih, Rapid prototyping of 3D DNA-origami shapes with caDNAno, Nucleic Acids Res., 2009, 37(15), 5001–5006,  DOI:10.1093/nar/gkp436.
35. R. Iinuma, Y. Ke, R. Jungmann, T. Schlichthaerle, J. B. Woehrstein and P. Yin, Polyhedra self-assembled from DNA tripods and characterized with 3D DNA-PAINT, Science, 2014, 344(6179), 65–69,  DOI:10.1126/science.1250944.
36. J. P. K. Doye, T. E. Ouldridge and A. A. Louis, et al., Coarse-graining DNA for simulations of DNA nanotechnology, Phys. Chem. Chem. Phys., 2013, 15(47), 20395–20414,  10.1039/c3cp53545b.
37. T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model, J. Chem. Phys., 2011, 134(8), 085101,  DOI:10.1063/1.3552946.
38. B. E. K. Snodin, F. Randisi and M. Mosayebi, et al., Introducing improved structural properties and salt dependence into a coarse-grained model of DNA, J. Chem. Phys., 2015, 142(23), 234901,  DOI:10.1063/1.4921957.
39. E. F. Pettersen, T. D. Goddard and C. C. Huang, et al., UCSF Chimera—a visualization system for exploratory research and analysis, J. Comput. Chem., 2004, 25(13), 1605–1612,  DOI:10.1002/jcc.20084.
40. J. SantaLucia, A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics, Proc. Natl. Acad. Sci. U. S. A., 1998, 95(4), 1460–1465,  DOI:10.1073/pnas.95.4.1460.
41. R. Kosinski, A. Mukhortava, W. Pfeifer, A. Candelli, P. Rauch and B. Saccà, Sites of high local frustration in DNA origami, Nat. Commun., 2019, 10(1), 1061,  DOI:10.1038/s41467-019-09002-6.
42. F. M. Anastassacos, Z. Zhao, Y. Zeng and W. M. Shih, Glutaraldehyde Cross-Linking of Oligolysines Coating DNA Origami Greatly Reduces Susceptibility to Nuclease Degradation, J. Am. Chem. Soc., 2020, 142(7), 3311–3315,  DOI:10.1021/jacs.9b11698.
43. N. Ponnuswamy, M. M. C. Bastings and B. Nathwani, et al., Oligolysine-based coating protects DNA nanostructures from low-salt denaturation and nuclease degradation, Nat. Commun., 2017, 8(1), 15654,  DOI:10.1038/ncomms15654.
44. A. Buchberger, C. R. Simmons, N. E. Fahmi, R. Freeman and N. Stephanopoulos, Hierarchical assembly of DNA origami nanostructures using coiled-coil peptides, J. Am. Chem. Soc., 2019, 142(3), 1406–1416,  DOI:10.1021/jacs.9b11158.
45. Q. Jiang, Y. Shi and Q. Zhang, et al., A Self-Assembled DNA Origami-Gold Nanorod Complex for Cancer Theranostics, Small, 2015, 11(38), 5134–5141,  DOI:10.1002/smll.201501266.
46. J. Sharma, R. Chhabra, C. S. Andersen, K. V. Gothelf, H. Yan and Y. Liu, Toward Reliable Gold Nanoparticle Patterning On Self-Assembled DNA Nanoscaffold, J. Am. Chem. Soc., 2008, 130(25), 7820–7821,  DOI:10.1021/ja802853r.
47. V. V. Thacker, L. O. Herrmann and D. O. Sigle, et al., DNA origami based assembly of gold nanoparticle dimers for surface-enhanced Raman scattering, Nat. Commun., 2014, 5(1), 3448,  DOI:10.1038/ncomms4448.
48. G. Thomas, C. Tidiane Diagne, X. Baillin, T. Chevolleau, T. Charvolin and R. Tiron, DNA Origami for Silicon Patterning, ACS Appl. Mater. Interfaces, 2022, 12(32), 36799–36809,  DOI:10.1021/acsami.0c10211.
49. J. F. Berengut, C. K. Wong, J. C. Berengut, J. P. K. Doye, T. E. Ouldridge and L. K. Lee, Self-Limiting Polymerization of DNA Origami Subunits with Strain Accumulation, ACS Nano, 2020, 14(12), 17428–17441,  DOI:10.1021/acsnano.0c07696.
50. S. V. Ahir and E. M. Terentjev, Photomechanical actuation in polymer-nanotube composites, Nat. Mater., 2005, 4(6), 491–495,  DOI:10.1038/nmat1391.
51. W. Engelen, S. P. W. Wijnands and M. Merkx, Accelerating DNA-Based Computing on a Supramolecular Polymer, J. Am. Chem. Soc., 2018, 140(30), 9758–9767,  DOI:10.1021/jacs.8b06146.
52. H. T. Maune, R. D. Barish, M. Bockrath, G. A. William, P. W. K. Rothemund and E. Winfree, Self-assembly of carbon nanotubes into two-dimensional geometries using DNA origami templates, Nat. Nanotechnol., 2010, 5(1), 61–66,  DOI:10.1038/nnano.2009.311.
53. P. D. Halley, C. R. Lucas and E. M. McWilliams, et al., Daunorubicin-Loaded DNA Origami Nanostructures Circumvent Drug-Resistance Mechanisms in a Leukemia Model, Small, 2016, 12(3), 308–320,  DOI:10.1002/smll.201502118.
54. S. Li, Q. Jiang and S. Liu, et al., A DNA nanorobot functions as a cancer therapeutic in response to a molecular trigger in vivo, Nat. Biotechnol., 2018, 36(3), 258–264,  DOI:10.1038/nbt.4071.
55. E. Poppleton, A. Mallya, S. Dey, J. Joseph and P. Šulc, Nanobase.org: a repository for DNA and RNA nanostructures, Nucleic Acids Res., 2022, 50(D1), D246–D252,  DOI:10.1093/nar/gkab1000.
56. C. M. Huang, A. Kucinic, J. V. Le, C. E. Castro and H. J. Su, Uncertainty quantification of a DNA origami mechanism using a coarse-grained model and kinematic variance analysis, Nanoscale, 2019, 11(4), 1647–1660,  10.1039/C8NR06377J.
57. Z. Shi, C. E. Castro and G. Arya, Conformational Dynamics of Mechanically Compliant DNA Nanostructures from Coarse-Grained Molecular Dynamics Simulations, ACS Nano, 2017, 11(5), 4617–4630,  DOI:10.1021/acsnano.7b00242.
58. L. Rovigatti, P. Šulc, I. Z. Reguly and F. Romano, A comparison between parallelization approaches in molecular dynamics simulations on GPUs, J. Comput. Chem., 2015, 36(1), 1–8,  DOI:10.1002/jcc.23763.
59. C. E. Castro, F. Kilchherr and D. N. Kim, et al., A primer to scaffolded DNA origami, Nat. Methods, 2011, 8(3), 221–229,  DOI:10.1038/nmeth.1570.
60. G. Tang, L. Peng and P. R. Baldwin, et al., EMAN2: An extensible image processing suite for electron microscopy, J. Struct. Biol., 2007, 151(1), 38–46,  DOI:10.1016/j.jsb.2006.05.009.
61. M. D. Abràmoff, P. J. Magalhães and S. J. Ram, Image processingp with imageJ, Biophotonics Int., 2004, 11(7), 36–42,  DOI:10.1201/9781420005615.ax4.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr05416g

---