Terahertz cavity optomechanics using a topological nanophononic superlattice
Haonan
Chang
ab,
Zhenyao
Li
ab,
Wenkai
Lou
ab,
Qifeng
Yao
c,
Jia-Min
Lai
ab,
Bing
Liu
d,
Haiqiao
Ni
ab,
Zhichuan
Niu
abd,
Kai
Chang
ab and
Jun
Zhang
 *ab
*ab
aState Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China. E-mail: zhangjwill@semi.ac.cn
bCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
cBeijing Academy of Quantum Information Sciences, Beijing 100193, China
dJoint Laboratory of Advanced Semiconductor, Nanjing Guoke Semiconductor Co., Ltd, China
First published on 17th August 2022
Abstract
Cavity optomechanical systems operating at the quantum ground state provide a novel way for the ultrasensitive measurement of mass and displacement and provide a new toolbox for emerging quantum information technologies. The high-frequency optomechanical devices could reach the quantum ground state at a high temperature because the access to high frequency is favorable for the cavity optomechanical devices to decouple from the thermal environment. However, reaching ultra-high frequency (THz) is extremely difficult due to the structure of cavity optomechanical devices and properties of materials. In this paper, by introducing acoustic topological interface states, we designed a THz mechanical frequency semiconductor pillar microcavity optomechanical device based on a GaAs/AlAs nanophononic superlattice. In the optomechanical system, multi-optical cavity modes are obtained and the frequency separation between adjacent optical modes is equal to the frequency of the mechanical mode (optomechanical frequency matching). By detuning the laser pump to a lower (higher) energy-resolved sideband to make a spontaneously scattering photon doubly resonate with optical cavity modes at an anti-Stokes (Stokes) frequency and pump frequency, we can achieve an anti-Stokes (Stokes) scattering efficiency 2600 (1800) times larger than that of Stokes (anti-Stokes) scattering, which provides potential for laser cooling and low threshold phonon lasing in the optomechanical system.
1. Introduction
The cavity optomechanics field explores the interactions between optical modes and mechanical motion.1 Many novel physical phenomena have been discovered in the optomechanical systems, such as nonlinear optical phenomena, chaos, optomechanical cooling and so on.1–5 The preparation of mechanical oscillators in the quantum ground state is the basic starting step for the quantum control of mechanical motion.6 However, how to cool a mechanical oscillator to its quantum ground state is a long-standing difficulty in investigating this problem because of spurious laser heating, which threatens the robust ground-state operation within microscale and nanoscale optomechanical systems.7–11 Moreover, cooling a mechanical resonator to its quantum ground state requires temperature T ≪ hνm/kB, where νm is the eigenfrequency of the mechanical mode and h and kB are respectively Planck's and Boltzmann's constants.7 For example, a mechanical mode at νm = 1 MHz would need to be cooled to T ≪ 50 μK, which relies on cryogenic pre-cooling and optical cooling, while a mechanical mode at 1 THz only needs to be cooled to T ≪ 50 K via standard cryogenic techniques. Hence, the high-frequency optomechanical system paves the way to robust quantum control of phonons and provides the implementation of efficient ultrafast quantum information protocols,6,12 which would stimulate the development of emerging quantum information technologies. In current optomechanical systems, the mechanical frequency of membrane resonators could reach several MHz and the mechanical frequency of microdisk and optomechanical crystals can reach several GHz magnitudes.1,13–17 Reaching higher mechanical frequencies, up to the extremely high frequency range (∼1 THz), has been hampered so far by the structure of optomechanical devices and properties of materials.18 In this paper, we designed a nanophononic system where the mechanical frequency could reach several terahertz by numerical calculation. Besides, the nanophononic system could be grown by the well-established molecular beam epitaxy (MBE) technology.18,19Among all the cavity optomechanical systems, GaAs/AlAs semiconductor pillar microcavities have been presented as novel optomechanical resonators with an unprecedented 18–300 GHz mechanical frequency range, showing highly promising features such as state-of-the-art quality factor-frequency products from numerical calculation and experiments.18–28 The high refractive index contrast between GaAs and AlAs allows defining optical Bragg mirrors surrounding a cavity spacer, confining light in one direction. The high refractive index contrast between the semiconductor pillar and air confines light in the two other directions.18,21 The pillar microcavities can be designed flexibly: the optical mode volume can be changed through the spacer thickness and pillar lateral size and the optical quality factor (Q) can be optimized through the number of layers in the mirrors.20 In the optomechanical system, phonons can be confined by the phonon impedance Z = ρv contrast between GaAs and AlAs, where ρ and v are density and sound velocity, respectively.20 For the material choice of GaAs/AlAs, the optical and acoustic impedance contrasts are almost equal. The phonons and photons both can be confined in the cavity.21 In our work, the mechanical topological interface state, which is protected against any perturbation that does not change the underlying topological invariants of the structures,29 at the terahertz frequency was obtained by concatenating two GaAs/AlAs superlattices with inverted spatial mode symmetries at the band edges around a common minigap, without a mechanical resonant spacer. The topological invariants (Zak phases) corresponding to the two concatenated systems determine the existence of an interface mode confined between them.30–33 Hence, the Zak phases are calculated to determine whether the topological interface state exists.
In the optomechanical system, narrow-band filters can be realized by two DBRs and one spacer layer.34,35 When the spacer layer is thick enough, the transmission of semiconductor microcavity is comb-like with the peak separation being approximately inversely proportional to the thickness (mλ0/2), where λ0 is the optical wavelength in the spacer material and m is an integer number. Since the transmission peaks are in the band gap of the DBR, multiple optical modes can be obtained by increasing the thickness of the spacer layer in this system.34 In this case, the semiconductor microcavity can serve as a multichannel optical filter. By inserting the nanophononic system we designed between two optical DBRs, the nanophononic system acts as an optical cavity. The eigenfrequency of the mechanical modes can be changed by tuning the thickness of the unit cells in the nanophononic system. Meanwhile, multi-optical cavity modes can be obtained by adjusting the period number of the unit cell of the nanophononic system. Prashanta Kharel et al. reported that they achieved optomechanical frequency matching by bulk phonons at 13 GHz.17 In this work, we realized optomechanical frequency matching by nanophononic topological interface state at terahertz. It would be used to mediate resonant coupling between two adjacent modes of an optical cavity through inelastic scattering interactions. Hence, the symmetry of the Stokes and anti-Stokes scattering processes could be broken by unequal frequency differences between one optical mode and its adjacent optical modes,36,37 which enables splitter and entanglement interactions as the basis for the quantum optical control of phonons.17
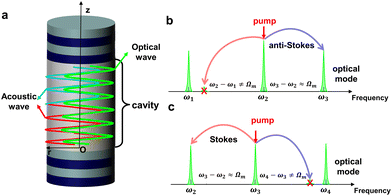
2. Simulation model
The model studied in this paper is shown in Fig. 1(a). It consists of an optical microcavity with two DBRs enclosing a resonant spacer with an optical path length of mλ/2 at a resonance wavelength of around λ = 900 nm, where λ is the vacuum wavelength of an optical wave. The bottom (top) optical DBR is formed by 20 (18) GaAs/AlAs bilayers and the optical spacer of the cavity is composed of two concatenated GaAs/AlAs acoustic superlattices. The thickness of the GaAs (AlAs) layers is 62.6 nm (75.3 nm). In this system, the acoustic superlattice is also an optical cavity, which can confine the acoustic and optical modes in three directions. According to previous literature,34 a multi-optical mode cavity optomechanical system can be obtained by adjusting the parameter m. Calculation of the mechanical and optical properties was performed by a commercial finite element method software (COMSOL Multiphysics). The numerical calculation model is a two-dimensional axisymmetric geometry. GaAs and AlAs are considered here to be isotropic materials, both for optical and mechanical properties and no absorption process was considered.21In this multi-optical mode cavity optomechanical system, there is a frequency separation between the two optical modes (ω3 − ω2) equal to the eigenfrequency of the acoustic mode (Ωm), where Ωm = 2πνm. However, the frequency separation between these two optical modes and the other two adjacent optical modes (ω2 − ω1 and ω4 − ω3) is not equal to the eigenfrequency of the mechanical mode (Ωm). Therefore, when the pump laser frequency is equal to ω2, the frequency of the anti-Stokes scattering is ω2 + Ωm, which is equal to ω3 (one of the resonant frequencies of the cavity). As shown in Fig. 1(b and c), the anti-Stokes scattering process would be enhanced by tuning the frequency of the pump laser from ω3 to ω2, whereas the Stokes scattering process is not enhanced, which results in a higher intensity of anti-Stokes scattering than that of the Stokes scattering process. Achieving a stronger anti-Stokes scattering than Stokes scattering of high frequency optical phonons in solids is not an easy task due to the large dissipation. By using the strong Fröhlich coupling between excitons and phonons in some semiconductors, Zhang et al. demonstrated the reverse of the energy-flow direction and resolved the sideband Raman cooling of longitudinal optical phonons (LOPs) in zinc telluride (ZnTe) nanobelts.39 Similar enhanced anti-Stokes scattering phenomena also were reported in GaN38 and CdS.43 These reports open a door towards a possible experimental solution to achieve a net Raman cooling of solids under anti-Stokes resonance or THz phonon lasing under Stokes resonance.37,40
3. Results and discussion
3.1 Multi-optical modes
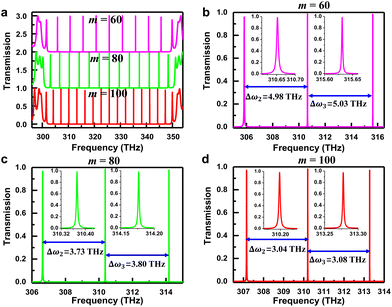
The transmission spectra of the structure in Fig. 1(a) are shown in Fig. 2. The thickness of the cavity is designed to make the optical path in the cavity equal to mλ/2, i.e., in the optical domain the acoustic superlattice represents the resonant spacer of a cavity. In Fig. 2(a), we show three transmission spectra corresponding to cases of different values for m (60, 80 and 100). As the cavity thickness increases, i.e., the optical path length increases, the number of resonant frequencies in the DBR band gap increases and the frequency difference Δωj between adjacent resonant frequencies decreases. The thickness of the optical cavity is set to 60, 80, and 100 (λ/2) respectively, where the frequency difference between adjacent optical modes varies from around 3 THz to 5 THz. The transmission spectra from around 305 to 315 THz are shown in Fig. 2(b–d) and the insets are the enlarged transmission peaks. For an optical cavity in vacuum, the optical cavity modes are spaced equally and the frequency spacing between the adjacent modes is c/Lopt, where c is light speed in vacuum and Lopt is optical length.17 When a crystal medium with a refractive index n is placed in between the mirrors and is placed in the cavity, the frequency spacing between the optical modes decreases and the adjacent mode spacing becomes unequal.17 Hence, we can conclude that the unequal frequency spacing is due to the existence of a medium in the optical resonance cavity.3.2 Nanophononic topological interface states
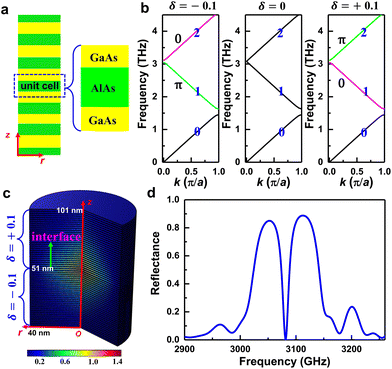
In order to make the mechanical eigenfrequency equal to the frequency difference between two adjacent optical modes, the thickness of the optical cavity should be quite large, which brings great difficulties to the subsequent growth of the structure by molecular beam epitaxy. Hence it is necessary to obtain high-frequency mechanical modes. In previous literature,30 a nanophononic system supporting a robust topological interface state at 350 GHz was designed. In this work, we obtained the acoustic mode at several terahertz frequency, which is the first to be designed in an optomechanical system. The structure of the nanophononic microcavity is shown in Fig. 3(a). The unit cell consists of two GaAs layers and an AlAs layer. The thickness of the GaAs layer is dGaAs = λGaAs(1 + δ)/8 and the thickness of the AlAs layer is dAlAs = λAlAs(1 + δ)/4, where λ denotes the wavelength of sound at the design frequency of the mechanical mode in the corresponding material. The total acoustic path length of the unit cell is set to half a phonon wavelength, λac/2, and δ depicts the distribution of the overall acoustic path length between the two materials. The thickness of the nanophononic superlattice layer is determined by the design mechanical eigenfrequency, ν0 and δ. The design frequency is set to ν0 = 1.54 THz in order to match m = 100. The acoustic band structures of the superlattice corresponding to δ = 0 and ±0.1 are calculated. As shown in Fig. 3(b), the first minigap is open for δ = 0 and ±0.1. The second minigap for δ = 0 is closed, while for δ = ±0.1, the second minigap is open. In a one-dimensional system, a topological transition is usually characterized by topological invariants such as the Zak phase. The Zak phases of the acoustic bands can be calculated by an integration across the Brillouin zone as follows:33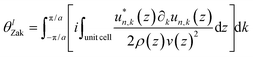 | (1) |
Subsequently, we concatenated two superlattices with inverted bands as shown in Fig. 3(a) with δ = ±0.1. When two different superlattices are concatenated directly, in order to generate a topological interface state, the reflection phases φleft and φright of the individual reflectors have to add up to an integer multiple of 2π,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 that is,
41 that is,
φleft + φright = 2mπ,m∈![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) | (2) |
The sign reflection phase of the minigap around 3.08 THz is determined by the Zak phases of the zeroth and first bands surrounding the minigap:32
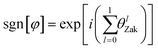 | (3) |
The reflection phase of δ = −0.1 is π and the reflection phase of δ = +0.1 is −π. Hence, the resonance condition eqn (2) is fulfilled in the second minigap. In Fig. 3(c), we show the absolute value of the volumetric strain |dV/V| corresponding to a confined acoustic topological interface mode around 3.08 THz in three dimensions. The mechanical mode envelope shows a maximum at the interface between the two superlattices and decays evanescently in both directions away from the interface with different topological phases. In Fig. 3(d), we display the calculated phonon reflectivity for energies around the second minigap and a phonon-transmission stop band is observed at around 3.08 THz. Within this stop band a phonon mode exists (as shown in Fig. 3(c)), characterized by the nearly complete transmission of the vibrational energy.
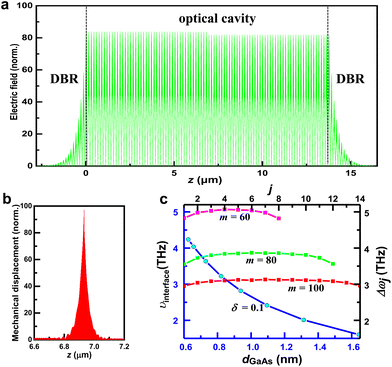
The electric field distribution and mechanical displacement corresponding to m = 100 are presented in Fig. 4(a). The frequency ω0 of the confined optical mode is 310 THz and the frequency of the confined acoustic topological interface mode is 3.08 THz. The energy of the optical mode is mostly confined in the cavity, and the acoustic mode is concentrated at the interface of the acoustic superlattice as shown in Fig. 4(b), so this structure can achieve both the optical mode and the acoustic mode confinement. The cavity and mechanical damping rates are critical for the design of an optomechanical system. The loss of mechanical excitations can be quantified by the energy dissipation rate Γm. According to the phonon reflectance spectra in Fig. 3(d), the energy dissipation rate Γm of the topological interface state is around 10 GHz and the quality factor Qm is around 300. Besides, the Qmνm product plays an important role in the phase noise performance of oscillators. The Qmνm product for this topological interface state is around 900 THz, which means that the mechanical resonator is easy to decouple from the thermal environment. The optical quality factor and energy dissipation rate for the optical eigenfrequency at 307.15 THz for m = 100 is 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 0.02 THz, respectively.
000 and 0.02 THz, respectively.
3.3 Optomechanical frequency matching and potential applications
The frequencies of the acoustic interface states corresponding to different GaAs layer thicknesses in the acoustic superlattice are shown in the blue curve of Fig. 4(c). As the thickness of the GaAs layer decreases, the frequency of the acoustic topological interface states increases. Therefore, making the frequency separation of adjacent optical modes equal to the acoustic frequency can be achieved by adjusting the thickness of the GaAs/AlAs layer in the acoustic superlattice. The frequency spacing between adjacent optical modes corresponding to m = 60, 80 and 100 is shown in Fig. 4(c). There are several optical modes whose frequency differences to the left and right adjacent optical modes are not equal, such as the four adjacent free spectral ranges Δω1, Δω2, Δω3 and Δω4 at m = 100 (red curve) shown in Fig. 4(c), which are essential to break the symmetry of the Stokes and anti-Stokes processes.We semi-quantitatively investigated the Raman scattering efficiency of Stokes and anti-Stokes processes and described the potential of this structure to enhance the anti-Stokes scattering for laser cooling. In the case where the medium is transparent with respect to the pump and scattered light, the total Raman scattering efficiencies per unit length IS and IAS can be calculated by equations:36,37
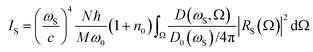 | (4) |
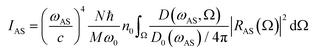 | (5) |
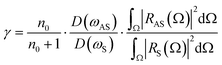 | (6) |
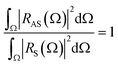 . According to the above approximation, eqn (7) becomes
. According to the above approximation, eqn (7) becomes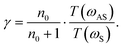 | (7) |
At room temperature (300 K), the phonon frequency is 3081.6 GHz, and the frequency of the pump laser is 310.198 THz, then we calculated the value of γ and found it to be 2600 approximately, which means that the scattering efficiency of the anti-Stokes scattering is 2600 times larger than that of Stokes scattering.
The minimum requirements to achieve Raman cooling in solids is:
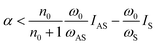 | (8) |
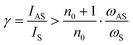 | (9) |
When the system is pumped at a blue-resolved sideband, this cavity optomechanical system is also a very suitable platform for phonon laser generation.44,45 In the case of m = 100 and νm = 3.0816 THz, if the frequency of the pump laser is set to 311.278 THz, the ratio of the Raman scattering efficiency between anti-Stokes and Stokes processes is 5.37 × 10–4 according to eqn (7), which means that the scattering efficiency of the Stokes scattering is 1863 times larger than that of anti-Stokes scattering. Moreover, the pump laser at the resonant frequency would be intensified in the cavity, which provides great potential to get a high conversion efficiency and low threshold phonon lasing.
4. Conclusion
We designed an unprecedented ultrahigh frequency THz GaAs/AlAs pillar multi-optical mode microcavity optomechanical structure by numerical calculation. The high phonon frequency range obtained in this work might even allow preparing our devices in the quantum mechanical ground state of motion at liquid-nitrogen temperatures, which would stimulate the development of manipulating the quantum states of mechanical motion and light through optomechanical interactions. Besides, the frequency of the mechanical mode is equal to the frequency separation between two adjacent optical modes, while the frequency difference between the optical mode and its two adjacent optical modes is unequal. Hence, this optomechanical system can be used to enhance the anti-Stokes scattering or Stokes scattering selectively in an inelastic scattering process by detuning the frequency of the pump laser to an optical resonance mode and the scattering efficiency of the anti-Stokes (Stokes) scattering is 2600 (1800) times larger than that of Stokes (anti-Stokes) scattering when the Stokes (anti-Stokes) process is suppressed, which provides a new platform for laser cooling and phonon lasing.Author contributions
Jun Zhang conceived the project. Haonan Chang, and Zhenyao Li, performed the experiments. Haonan Chang and Jun Zhang analyzed the data and wrote the paper. All the authors have discussed the results and revised the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the funding support from the National Key Research and Development Program of China (2017YFA0303401, 2018YFA0306101), CAS Interdisciplinary Innovation Team, National Natural Science Foundation of China (12074371, 11974340), Strategic Priority Research Program of Chinese Academy of Sciences (XDB28000000).References
- M. Aspelmeyer, T. J. Kippenberg and F. Marquardt, Cavity optomechanics, Rev. Mod. Phys., 2014, 86, 1391–1452 CrossRef.
- W. Qin, A. Miranowicz, P. B. Li, X. Y. Lü, J. Q. You and F. Nori, Exponentially enhanced light-matter interaction, cooperativities, and steady-state entanglement using parametric amplification, Phys. Rev. Lett., 2018, 120, 093601 CrossRef CAS PubMed.
- X. Y. Lü, H. Jing, J. Y. Ma and Y. Wu, PT -symmetry-breaking chaos in optomechanics, Phys. Rev. Lett., 2015, 114, 253601 CrossRef PubMed.
- X. Y. Lü, Y. Wu, J. R. Johansson, H. Jing, J. Zhang and F. Nori, Squeezed optomechanics with phase-matched amplification and dissipation, Phys. Rev. Lett., 2015, 114, 093602 CrossRef PubMed.
- Y. J. Guo, K. Li, W. J. Nie and Y. Li, Electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system, Phys. Rev. A, 2014, 90, 053841 CrossRef.
- S. Barzanjeh, A. Xuereb, S. Gröblacher, M. Paternostro, C. A. Regal and E. M. Weig, Optomechanics for quantum technologies, Nat. Phys., 2021, 18, 15–24 Search PubMed.
- A. D. O'Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang, M. Weides, J. Wenner, J. M. Martinis and A. N. Cleland, Quantum ground state and single-phonon control of a mechanical resonator, Nature, 2010, 464, 697–703 CrossRef PubMed.
- X. W. Xu, L. N. Song, Q. Zheng, Z. H. Wang and Y. Li, Optomechanically induced nonreciprocity in a three-mode optomechanical system, Phys. Rev. A, 2018, 98, 063845 CrossRef CAS.
- M. Wu, N. L. Wu, T. Firdous, F. Fani Sani, J. E. Losby, M. R. Freeman and P. E. Barclay, Nanocavity optomechanical torque magnetometry and radiofrequency susceptometry, Nat. Nanotechnol., 2017, 12, 127–131 CrossRef CAS PubMed.
- K. C. Lee, B. J. Sussman, M. R. Sprague, P. Michelberger, K. F. Reim, J. Nunn, N. K. Langford, P. J. Bustard, D. Jaksch and I. A. Walmsley, Macroscopic non-classical states and terahertz quantum processing in room-temperature diamond, Nat. Photonics, 2011, 6, 41–44 CrossRef.
- J. D. Teufel, D. Li, M. S. Allman, K. Cicak, A. J. Sirois, J. D. Whittaker and R. W. Simmonds, Circuit cavity electro-mechanics in the strong-coupling regime, Nature, 2011, 471, 204–208 CrossRef CAS PubMed.
- V. Villafañe, S. Anguiano, A. E. Bruchhausen, G. Rozas, J. Bloch, C. G. Carbonell, A. Lemaître and A. Fainstein, Quantum well photoelastic comb for ultra-high frequency cavity optomechanics, Quantum Sci. Technol., 2018, 4, 014011 CrossRef.
- G. Bahl, J. Zehnpfennig, M. Tomes and T. Carmon, Stimulated optomechanical excitation of surface acoustic waves in a microdevice, Nat. Commun., 2011, 2, 403 CrossRef PubMed.
- Y. F. Gao, J. M. Lai and J. Zhang, Optical control of bulk phonon modes in crystalline solids, Adv. Quantum Technol., 2021, 5, 2100103 CrossRef.
- J. T. Hill, A. H. Safavi-Naeini, J. Chan and O. Painter, Coherent optical wavelength conversion via cavity opto-mechanics, Nat. Commun., 2011, 3, 1196 CrossRef PubMed.
- F. R. Lamberti, M. Esmann, A. Lemaître, C. G. Carbonell, O. Krebs, I. Favero, B. Jusserand, P. Senellart, L. Lanco and N. D. Lanzillotti-Kimura, Nanomechanical resonators based on adiabatic periodicity-breaking in a superlattice, Appl. Phys. Lett., 2017, 111, 173107 CrossRef.
- G. I. H. P. Kharel, E. A. Kittlaus, W. H. Renninger, N. T. Otterstrom, J. G. E. Harris and P. T. Rakich, High-frequency cavity optomechanics using bulk acoustic phonons, Sci. Adv., 2019, 5, eaav0582 CrossRef PubMed.
- S. Anguiano, A. E. Bruchhausen, B. Jusserand, I. Favero, F. R. Lamberti, L. Lanco, I. Sagnes, A. Lemaitre, N. D. Lanzillotti-Kimura, P. Senellart and A. Fainstein, Micropillar resonators for optomechanics in the extremely high 19-95-GHz frequency range, Phys. Rev. Lett., 2017, 118, 263901 CrossRef CAS PubMed.
- M. Esmann, F. R. Lamberti, A. Harouri, L. Lanco, I. Sagnes, I. Favero, G. Aubin, C. G. Carbonell, A. Lemaître, O. Krebs, P. Senellart and N. D. Lanzillotti-Kimura, Brillouin scattering in hybrid optophononic Bragg micropillar resonators at 300 GHz, Optica, 2019, 6, 854–859 CrossRef CAS.
- A. Fainstein, N. D. Lanzillotti-Kimura, B. Jusserand and B. Perrin, Strong optical-mechanical coupling in a vertical GaAs/AlAs microcavity for subterahertz phonons and near-infrared light, Phys. Rev. Lett., 2013, 110, 037403 CrossRef CAS PubMed.
- F. R. Lamberti, Q. Yao, L. Lanco, D. T. Nguyen, M. Esmann, A. Fainstein, P. Sesin, S. Anguiano, V. Villafane, A. Bruchhausen, P. Senellart, I. Favero and N. D. Lanzillotti-Kimura, Optomechanical properties of GaAs/AlAs micropillar resonators operating in the 18 GHz range, Opt. Express, 2017, 25, 24437–24447 CrossRef CAS PubMed.
- N. D. Lanzillotti-Kimura, A. Fainstein and B. Jusserand, Towards GHz-THz cavity optomechanics in DBR-based semiconductor resonators, Ultrasonics, 2015, 56, 80–89 CrossRef CAS PubMed.
- N. D. Lanzillotti-Kimura, A. Fainstein, A. Lemaitre, B. Jusserand and B. Perrin, Coherent control of sub-terahertz confined acoustic nanowaves: Theory and experiments, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115453 CrossRef.
- A. Maznev, F. Hofmann, A. Jandl, K. Esfarjani, M. T. Bulsara, E. A. Fitzgerald, G. Chen and K. A. Nelson, Lifetime of sub-THz coherent acoustic phonons in a GaAs-AlAs superlattice, Appl. Phys. Lett., 2013, 102, 041901 CrossRef.
- G. Rozas, M. F. Winter, B. Jusserand, A. Fainstein, B. Perrin, E. Semenova and A. Lemaitre, Lifetime of THz acoustic nanocavity modes, Phys. Rev. Lett., 2009, 102, 015502 CrossRef CAS PubMed.
- M. Trigo, A. Bruchhausen, A. Fainstein, B. Jusserand and V. Thierry-Mieg, Confinement of acoustical vibrations in a semiconductor planar phonon cavity, Phys. Rev. Lett., 2002, 89, 227402 CrossRef CAS PubMed.
- S. Sandeep, S. L. Heywood, R. P. Campion, A. J. Kent and R. N. Kini, Resonance of terahertz phonons in an acoustic nanocavity, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 98, 235303 CrossRef.
- A. Fainstein, M. Trigo, D. Oliva, B. Jusserand, T. Freixanet and V. Thierry-Mieg, Standing optical phonons in finite semiconductor superlattices studied by resonant Raman scattering in a double microcavity, Phys. Rev. Lett., 2001, 86, 3411–3414 CrossRef CAS PubMed.
- O. Ortiz, P. Priya, A. Rodriguez, A. Lemaitre, M. Esmann and N. D. Lanzillotti-Kimura, Topological optical and phononic interface mode by simultaneous band inversion, Optica, 2021, 8, 598–605 CrossRef.
- M. Esmann, F. R. Lamberti, P. Senellart, I. Favero, O. Krebs, L. Lanco, C. G. Carbonell, A. Lemaître and N. D. Lanzillotti-Kimura, Topological nanophononic states by band inversion, Phys. Rev. B, 2018, 97, 155422 CrossRef.
- M. Esmann and N. D. Lanzillotti-Kimura, A topological view on optical and phononic Fabry–Perot microcavities through the Su–Schrieffer–Heeger model, Appl. Sci., 2018, 8, 527 CrossRef.
- V. Peano, C. Brendel, M. Schmidt and F. Marquardt, Topological phases of sound and light, Phys. Rev. X, 2015, 5, 031011 Search PubMed.
- M. Xiao, G. Ma, Z. Yang, P. Sheng, Z. Q. Zhang and C. T. Chan, Geometric phase and band inversion in periodic acoustic systems, Nat. Phys., 2015, 11, 240–244 Search PubMed.
- X. Zhao, Y. Zhang, Q. Zhang, B. Zou and U. Schwingenschlogl, Transmission comb of a distributed Bragg reflector with two surface dielectric gratings, Sci. Rep., 2016, 6, 21125 Search PubMed.
- S. O'Brien, Comb transmission filters defined by phase-shifted superstructure Bragg gratings, Opt. Lett., 2014, 39, 1085–1088 CrossRef PubMed.
- S. Kim and G. Bahl, Role of optical density of states in Brillouin optomechanical cooling, Opt. Express, 2017, 25, 776–784 CrossRef PubMed.
- Y. C. Chen and G. Bahl, Raman cooling of solids through photonic density of states engineering, Optica, 2015, 2, 893–899 CrossRef CAS.
- Y. J. Ding and J. B. Khurgin, From anti-Stokes photo-luminescence to resonant Raman scattering in GaN single crystals and GaN-based heterostructures, Laser Photonics Rev., 2012, 6, 660–677 CrossRef CAS.
- J. Zhang, Q. Zhang, X. Wang, L. C. Kwek and Q. Xiong, Resolved-sideband Raman cooling of an optical phonon in semiconductor materials, Nat. Photonics, 2016, 10, 600–605 CrossRef CAS.
- J. B. Khurgin, Feasibility of resonant Raman cooling and radiation balanced lasing in semiconductors, J. Opt. Soc. Am. B, 2022, 39, 338–344 CrossRef CAS.
- M. Xiao, Z. Q. Zhang and C. T. Chan, Surface impedance and bulk band geometric phases in one-dimensional systems, Phys. Rev. X, 2014, 4, 021017 Search PubMed.
- K. Papatryfonos, T. Angelova, A. Brimont, B. Reid, S. Guldin, P. R. Smith, M. Tang, K. Li, A. J. Seeds, H. Liu and D. R. Selviah, Refractive indices of MBE-grown AlxGa(1−x)As ternary alloys in the transparent wavelength region, AIP Adv., 2021, 11, 025327 CrossRef CAS.
- J. Zhang, D. Li, R. Chen and Q. Xiong, Laser cooling of a semiconductor by 40 kelvin, Nature, 2013, 493, 504–508 CrossRef CAS PubMed.
- K. Vahala, M. Herrmann, S. Knünz, V. Batteiger, G. Saathoff, T. W. Hänsch and Th. Udem, A phonon laser, Nat. Phys., 2009, 5, 682–686 Search PubMed.
- G. Bahl, J. Zehnpfennig, M. Tomes and T. Carmon, Stimulated optomechanical excitation of surface acoustic waves in a microdevice, Nat. Commun., 2011, 2, 403 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |