A biopolymer-gated ionotronic junctionless oxide transistor array for spatiotemporal pain-perception emulation in nociceptor network†
Yanran
Li‡
a,
Kai
Yin‡
 a,
Yu
Diao
a,
Mei
Fang
a,
Yu
Diao
a,
Mei
Fang
 a,
Junliang
Yang
a,
Junliang
Yang
 a,
Jian
Zhang
a,
Jian
Zhang
 b,
Hongtao
Cao
b,
Hongtao
Cao
 c,
Xiaoliang
Liu
c,
Xiaoliang
Liu
 *a and
Jie
Jiang
*a and
Jie
Jiang
 *a
*a
aHunan Key Laboratory of Nanophotonics and Devices, School of Physics and Electronics, Central South University, 932 South Lushan Road, Changsha, Hunan 410083, P. R. China. E-mail: xl_liu@csu.edu.cn; jiangjie@csu.edu.cn
bSchool of Material Science and Engineering, Guilin University of Electronic Technology, Guilin, 541004, P. R. China
cLaboratory of Advanced Nano Materials and Devices, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, P. R. China
First published on 17th January 2022
Abstract
Capable of reflecting the location and intensity of external harmful stimuli, a nociceptor network is of great importance for receiving pain-perception information. However, the hardware-based implementation of a nociceptor network through the use of a transistor array remains a great challenge in the area of brain-inspired neuromorphic applications. Herein, a simple ionotronic junctionless oxide transistor array with pain-perception abilities is successfully realized due to a coplanar-gate proton-coupling effect in sodium alginate biopolymer electrolyte. Several important pain-perception characteristics of nociceptors are emulated, such as a pain threshold, the memory of prior injury, and sensitization behavior due to pathway alterations. In particular, a good graded pain-perception network system has been successfully established through coplanar capacitance and resistance. More importantly, clear polarity reversal of Lorentz-type spatiotemporal pain-perception emulation can be finally realized in our projection-dependent nociceptor network. This work may provide new avenues for bionic medical machines and humanoid robots based on these intriguing pain-perception abilities.
Introduction
Sensation is the response of individual areas of the human brain to objective things that directly act on the sensory organs.1–3 It arises from a nerve impulse produced by the receptor that receives the stimulus and expresses the internal and external experience of the human body.3 Pain, as interoception of an unpleasant sensory experience, normally starts with the activation of a subpopulation of peripheral nerve fibers known as nociceptors.4–6 These nociceptors can not only trigger pain signals in the central nervous system (CNS) but they can also locally convey information at the periphery, meaning that adjacent nociceptors are possibly evoked in this spreading.5–7 The network that consists of these nociceptors shapes the initial process of pain perception, playing an important role in intelligent cognition. With this in mind, the hardware-based realization of a nociceptor-based neural network using solid-state electronics is of great significance for developing next-generation human–machine interactive devices and systems. However, up to now, the development of artificial nociceptor networks still remains a great challenge due to the following issues: (i) a lack of efficient electronic materials for mimicking information transmission in the nociceptor network and (ii) a lack of a simple device architecture for integrating nociceptor neurons.In this work, using a sodium alginate (SA) biopolymer electrolyte as the common neurotransmitter layer for ion transmission, an artificial nociceptor network with pain-perception and threshold-regulated abilities is successfully demonstrated using a 5 × 5 array of ionotronic junctionless indium-tin oxide (ITO) transistors. This coplanar-gate array not only realizes a nociceptor network based on simple device architecture, but it also further establishes extensive soft connections between individual devices through a common electrolyte. Based on these coplanar connections, several important characteristics of nociceptor networks can be realized, such as the pain threshold shown by biological nociceptors, memory of prior injury, and spatiotemporal sensitization due to pathway alterations in the nociceptor network. Interestingly, a tunable pain threshold, corresponding to graded pain perception, can be achieved via controlling the gate-to-channel distance. More importantly, the nociceptor network exhibits spatiotemporally-correlated Lorentz-type polarity reversal. The proposed device may provide a good opportunity for use in human–machine interactive devices aimed towards potential applications in intelligent medical equipment, enabling future smart robots to protect themselves from damage in hazardous environments. Therefore, this work may provide a new form of artificial neural network integration and extend the use of artificial neural functionality to future neuromorphic electronics.
Results and discussion
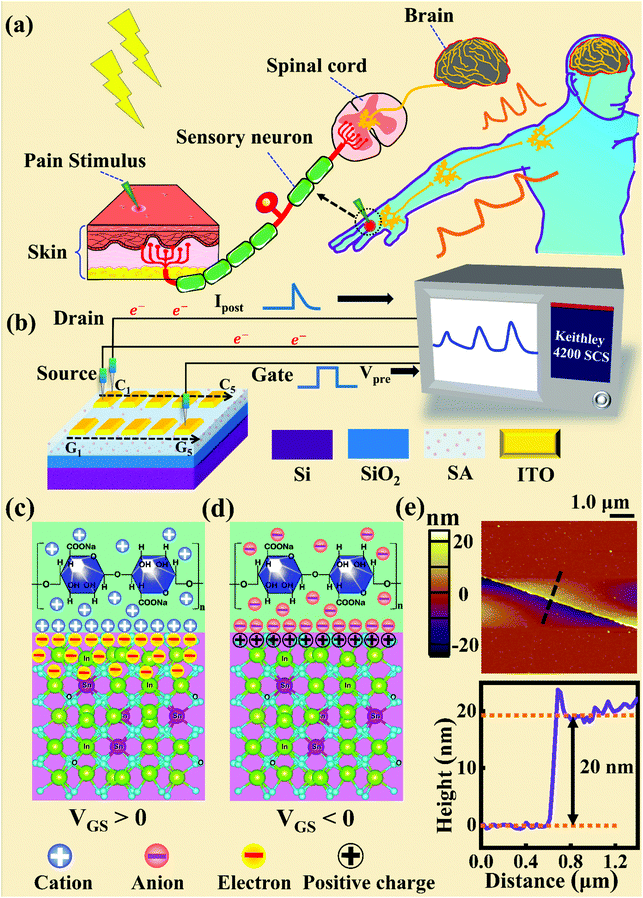
Fig. 1a and b illustrate schematic diagrams of the nociceptor network based on an ion-modulated transistor array and its analogous biological counterpart. The skin is an area dominated by nociceptors, and they are more densely distributed there than in other tissues. There are a wide variety of pain receptors in the epidermis.8–11 These nociceptors are only evoked when a harmful stimulus exceeds a certain value that could potentially injure tissues, such as extreme temperature, large mechanical stress, the presence of undesirable chemical molecules, etc.12–14 Acting as a threshold switch, this network that consists of peripheral stimulated nociceptors not only selectively provides a rapid warning to the CNS but also contributes to a motor response to avoid imminent threat or injury from the environment.1In our transistor network, the external stimulus is emulated by electrical pulse events triggering the device, as shown in Fig. 1b. The thin SA film mimics the synaptic cleft while SA ions can act as neurotransmitters. The migration of SA ions is similar to the release of glutamate (Glu) from the presynaptic membrane into the synaptic cleft when nociceptors are activated by harmful stimuli.15 When Glu is released in a sustained manner, it binds to post-synaptic glutamate receptors localized on second-order neurons in the dorsal horn and mediates a fast excitatory post-synaptic current.16 This process can be successfully emulated by our transistor network based on the ion-induced electric double layer (EDL) effect.17,18 The application of a voltage to the gate electrode causes the migration and accumulation of ions at the gate-electrolyte and semiconductor-electrolyte interfaces, and then equal mirror-image charges are induced at the other side of the interface. As shown in Fig. 1c, when a positive VGS is applied, the SA cations will accumulate at the SA/ITO interface, thus inducing many electrons on the other side of the SA/ITO interface, ultimately increasing the channel current. However, anions will gather at the SA/ITO interface to induce the depletion of charge at the ITO surface under the influence of a negative voltage, as described in Fig. 1d. In biological synapses, the process of information processing and signal delivery between neurons can be adjusted precisely via fluxes relating to ionic species, which closely resembles the process of ion migration in an EDL transistor. Fig. 1e displays the thickness of the ITO film based on atomic force microscopy (AFM). From this figure, it is observed to be ∼20 nm. The experimental details can be found in the ESI.† Here, we should point out that the specific features of this device can be summarized as follows: (i) the source, drain, and channel are made of common heavily-doped ITO film (i.e., a junctionless transistor)19,20 and (ii) the different gates and channels are directly coupled in the transistor network through a common SA bio-electrolyte.
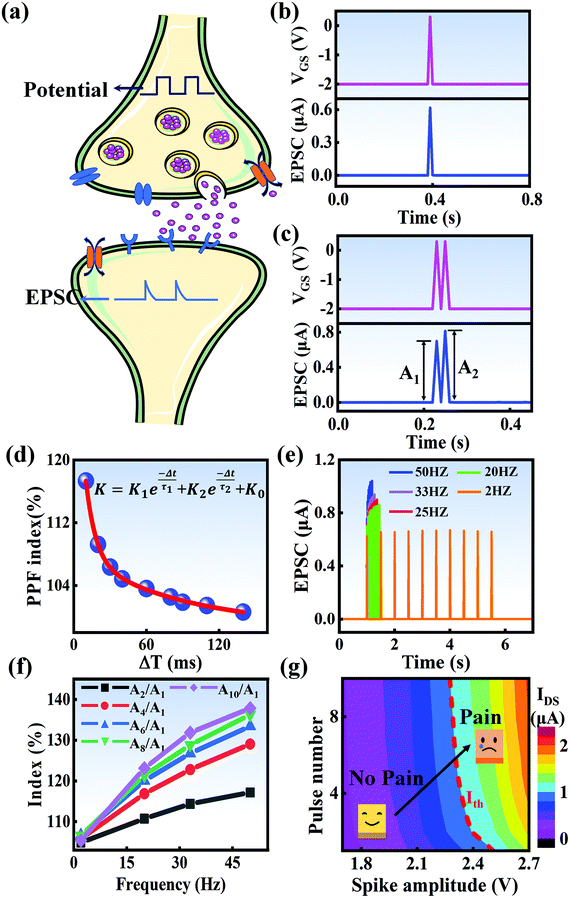
In a neural system, once a nociceptor is activated, pain information is transduced into long-range electrical signals and propagated into the spinal cord dorsal horn, thalamus, and cerebral cortex, respectively.4,9 In this complex pain circuitry, the synapse as a junction between two adjacent neurons plays an irreplaceable role in regulating pain transmission.21,22 The intrinsic mechanism of this regulating behavior is synaptic plasticity, which refers to corresponding changes in the synaptic morphological structure and function under the conditions of harmful stimuli or environmental changes.23,24 As shown in Fig. 2a, the neurotransmitters in a nociceptor are released from synaptic vesicles into the synaptic cleft when the action potential in the presynaptic neuron is triggered, resulting in an electrical signal as the output response. The resulting current is usually called an excitatory postsynaptic current (EPSC), and it is connected with basic synaptic plasticity over the entire information transmission route.25 Inspired by this architecture, the basically synaptic characteristics of nociceptors can be successfully emulated using our device. Herein, a coplanar gate is developed as the presynaptic terminal, while the ITO channel with source/drain electrodes can be regarded as the postsynaptic terminal. A typical EPSC is generated via a presynaptic spiking event (pulse amplitude: 2.3 V; pulse duration: 10 ms) from a constant voltage reading of VGS = −2 V, as shown in Fig. 2b. The EPSC amplitude evoked by the presynaptic potential spike rapidly reaches a maximum value of ∼0.62 μA and then drops back to the initial current state; this resembles a biological excitatory synapse.18 This spike can be ascribed to the ion migration effect, which is attributed to the accumulation of ions at the SA electrolyte/ITO channel layer interface.26,27 The distribution of ions gradually returns to its equilibrium state after the spike, resulting in the channel current decreasing back to its resting state.28 In a biological system, paired pulse facilitation (PPF) is another form of short-term synaptic behavior.29,30 This is the phenomenon in which the peak EPSC activated by a second presynaptic spike is larger than that induced by the previous spike when a neuron is subjected to two stimulus events at a certain interval.31–33 This behavior plays an essential role in recognizing and decoding temporal information in a neural nociceptor system.34 Interestingly, such neural behavior can be successfully emulated using our artificial synaptic transistor. As presented in Fig. 2c, two successive spike pulses (spike amplitude: 2.3 V, spike duration: 10 ms) at an interval (Δt) of 10 ms are applied to the gate electrode. From this figure, it is clear that the second EPSC response is obviously higher than the first one, indicating that PPF behavior has been well emulated. To further reveal the degree of facilitation for this artificial nociceptor, as shown in Fig. 2d, the PPF index (K) can be defined as A2/A1 × 100%, where A2 and A1 are the EPSC values triggered by the first and second spike events, respectively. We notice that the maximum PPF index is observed at Δt = 10 ms. With an increase in the spike interval, the index gradually approaches a value of 100%. The underlying mechanism of this behavior is based on the interval time being smaller than the relaxation time and, as a result, the ions triggered by the first pulse have not completely returned to their equilibrium state.34–36 The decline in the PPF index over time can be fitted by a dual exponential model:
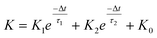 | (1) |
In biological synapses, the spike rate can also lead to a change in synaptic weight, which is a key attribute of synaptic plasticity.18 Interestingly, a pain perception process normally requires peripheral information to reach a higher center, and this depends on the frequency of action potentials in primary afferents.4,9Fig. 2e illustrates that varying the frequency can lead to information-filtering gates, affecting the transmission of pain information. Here, the spike width and number of spikes during the stimulus train at each frequency are fixed at 10 ms and 10, respectively. As seen in Fig. 2e, the EPSC response maintains an unchanged value of 650 nA over the entire stimulus train at a spike frequency of 2 Hz. However, when the stimulus frequency increases to 50 Hz, a maximum EPSC of 1.04 μA is clearly observed. Here, the relationship between the EPSC amplitude gain, defined using AN/A1, and the stimulus frequency is further shown in Fig. 2f, where AN and A1 represent the EPSC amplitudes after the Nth and 1st stimulus pulses, respectively. As seen in Fig. 2f, the index increases with an increase in the stimulus number and frequency, whereas the data points almost coincide at a low stimulus frequency of 2 Hz. The above results reveal that both the frequency and stimulus number have a significant effect on the synaptic weight. According to previous reports, a pain-perception signal only occurs when the pulse response currents triggered by the stimulus signal reach/exceed a certain threshold.2 For our device, the key pain perception function of the nociceptor is experimentally demonstrated through pulse measurements from the device. To mimic this specific feature, we can define a “threshold current line” of 1 μA in the contour map to mimic pain-perception behavior, as shown in Fig. 2g. An Ith value of 1 μA can be used to suitably categorize pain-perception processes into painful and non-painful at different gate terminals. As seen in Fig. 2g, typical non-painful behavior is located on the left side of the threshold line, whereas clear painfully perceived behavior can be observed on the opposite side of threshold line. Hence, these results strongly indicate that pain perception may be possibly realized using the proposed device.38,39
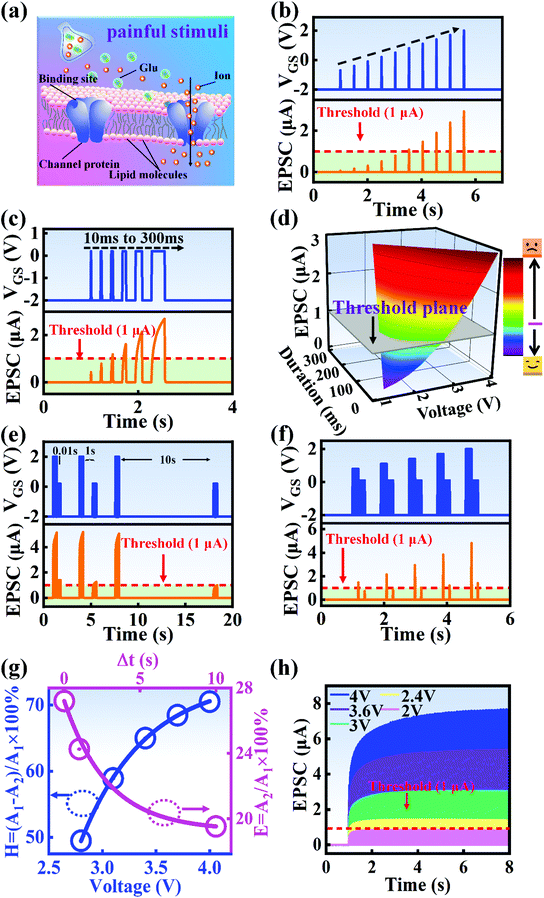
A nociceptor, which is one of the most crucial and distinguishing detectors, can rapidly respond to potentially injurious stimuli affecting the human body and help the organism to avoid injury.8 Three key aspects relating to nociceptors are threshold, sensitization, and desensitization.40 During the activation of the nociceptor, many mediators are released. These chemicals primarily act on metabotropic G-protein-coupled receptors and change the threshold and kinetics via activating intracellular voltage-gated calcium pathways, as described in Fig. 3a.41,42 In a biological nociceptor, the stimulus intensity is one of the most dependent threshold conditions affecting triggering. Thus, a spike train with different voltage amplitudes is used to emulate external stimuli in our artificial nociceptor, as shown in Fig. 3b. When a single electrical spike with a pulse duration of 10 ms is applied to our transistor, the EPSC response does not reach the trigger threshold (Ith = 1 μA) until the pulse amplitude reaches 2.70 V. In a previous biological experiment based on rats, when high-intensity noxious stimuli were applied to the knee joints of rats, a hindlimb-withdrawal reflex was evoked in awake rats. However, when low-intensity noxious stimuli were applied, the nociceptor neurons exhibited weak responses, resulting in innoxious-perception behavior. In our work, our device also exhibited a weak response to voltage stimuli below the threshold. This is consistent with the results obtained experimentally when examining the pain-perception nociceptors of rats.43 Here, the voltage that can cause the device to exactly exceed Ith is regarded as the pain-trigger threshold voltage (Vth). Therefore, Vth in this artificial nociceptor can be calculated to be 2.70 V. From this point, a further increase in the stimulus voltage results in clear pain-cognition behavior. At the same time, the spike duration also plays an important role in triggering pain-perception abilities, as shown in Fig. 3c. Using a fixed pulse amplitude of 2.2 V, as seen in Fig. 3c (i.e., a non-painful stimulus), it is clearly observed that a longer pulse duration (40 ms) is required to exceed the pain-perception threshold when a spike train of different spike widths (10–300 ms) is applied to the gate terminal. This is very consistent with the fact that a neural system cannot detect pain based on a short-term external injury with a short duration, whereas an non-painful response changes to a pain-perception event if the noxious stimulus duration is continually increased.43,44Fig. 3d depicts the fascinating pain-perception behavior in response to different spike amplitudes and durations. The dark grey plane at 1 μA is defined as the “threshold plane” in this 3D image. In this figure, we can see that the non-painful cognition turns to painful cognition upon an increase in the stimulus amplitude and duration. In general, to protect the human body, an injured area possesses sensitization characteristics after the nociceptor responds to a prior harmful stimulus.45–47 Peripheral sensitization (abbreviated as sensitization) is an important property of nociceptors, as it can help injured tissue to further avoid exposure to potential damage. This sensitization can be observed through a lowering of the threshold level (i.e., “allodynia”) and an increase in the response magnitude to harmful stimuli (i.e., “hyperalgesia”).4 During these biological processes, the recovery time after injury and the severity of the injury are two important factors affecting sensitization. Such characteristics can be successfully emulated in our artificial nociceptor upon using different spike pairs with various time intervals, as shown in Fig. 3e–g. In Fig. 3e, the first spike during each pulse pair is set with a voltage amplitude of 4 V and a pulse duration of 10 ms (pain-perception stimulus), resulting in a large EPSC (∼5.13 μA). After the first stimulus, the device is exposed to a second non-painful stimulus with a voltage amplitude of 2.2 V after different time intervals (0.01, 1, and 10 s). From Fig. 2e, it can be seen that the pain response caused by the second stimulus shifts towards a higher value with a decrease in the stimulus interval. Most notably, the current induced by the second unpainful stimulus can even reach Ith if the spike interval is small enough; this can be attributed to the “ion relaxation” process not being fully complete after the harmful stimulus has been removed.26 However, when the spike interval grows large enough, the EPSC response induced by the second stimulus gradually decreases and even falls below the threshold. This phenomenon resembles the hyperalgesia and allodynia shown by nociceptors during the relaxation period, which can allow a potentially harmful stimulus to be detected with increased sensitivity right after responding to a prior harmful stimulus.48,49 In addition, using the same interval of 10 ms, a train consisting of a varied stimulus (2.8–4 V spike amplitudes) followed by a fixed of 2.1 V (subthreshold stimulus) is employed to emulate the dependence of injury severity on pain sensitization, as shown in Fig. 3f. From this, it is found that the response triggered by the second stimulus of each spike pair exhibits a gradual stepwise increase and finally exceeds Ith as the first spike amplitude is increased. This result implies that the threshold shifts towards a lower voltage after experiencing a more harmful stimulus, once again mimicking the hyperalgesia and allodynia of nociceptors. These behaviors make the system hyperalert after injury, so that tissue is highly protected. Here, as shown in the pink curve in Fig. 3g, the sensitization degree (E) can be defined by A2/A1 × 100%, where A2 and A1 are the EPSC amplitudes resulting from the first and second stimulus, respectively, of each spike pair. To further reveal the sensitization and desensitization features of this artificial pain-perception device, an exponential equation based on the ion migration model is proposed as follows:
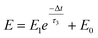 | (2) |
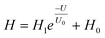 | (3) |
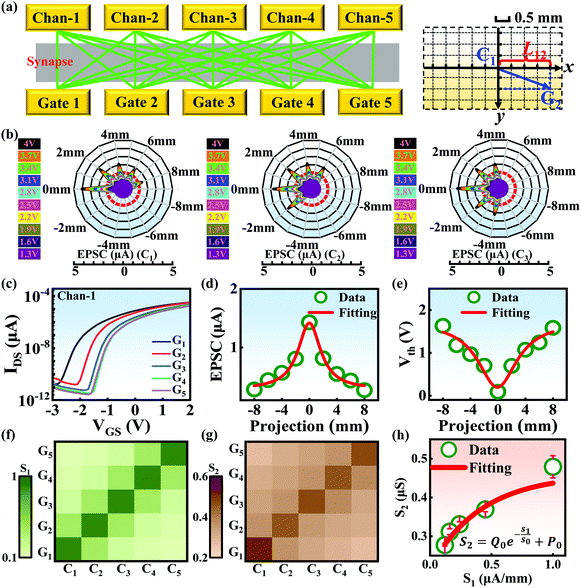
Compared with other tissues, the skin is more densely dominated by nociceptors, and they are widely distributed in the dermis of the skin.10 When skin is stressed by an external painful stimulus, vesicles in the C-fibers of skin are released and this can cause physiological effects in surrounding tissue. Nearby neurons may also be recruited in this physiological effect, diffusing the action potential of the stimulus to adjacent branches of nociceptor neurons.8,45 Inspired by this biological mechanism, a 5 × 5 coplanar-gate transistor array is constructed to emulate the pain-perception abilities of the neural network system. As shown in the schematic diagram in Fig. 4a, Chan-1 to Chan-5 correspond to the different positions of 5 channels, and Gate 1 to Gate 5 are the different gate terminals. The film length of ITO is 1000 μm, while the film width of ITO is 150 μm. Furthermore, as shown in Fig. S5 (ESI),† the stability of the junctionless transistor was demonstrated upon subjecting different gate terminals (G1–G5) to a fixed bias of VDS = 2 V for five successive measurements. A coordinate system can be established with the channel itself as the origin of the coordinates and Lij representing the typical x-axis projection of the distance between “channel i” and “gate j”, where “i” and “j” indicate the channel and gate positions, respectively. The distance between adjacent channels is 2 mm, and the distance between the vertical alignment channel and the gate is 1 mm. The projection of the distances between different channels and the gate on the corresponding abscissa is summarized in Table S4 (ESI).† Herein, as shown in Fig. 4b and Fig. S7 (ESI),† the pain-perception behavior of nociceptor networks can be successfully emulated in our oxide transistor array. Five torus graphs display the current responses of these different channels after series of spike stimuli are applied to the gate terminals with different projections. In these figures, different colors from purple to black indicate the current response to stimuli ranging from 1.3 V to 4 V with a step size of 0.3 V. The red circular line represents the Ith threshold for a pain response. It is found that when the stimulus voltage is fixed, the current response decreases significantly with a continuous increase in the projection, resulting in an increase in Vth. Interestingly, the largest current response is observed for a projection of 0 mm. From these results, we can conclude that the EPSC response and Vth of pain perception are strongly dependent on the projection. The variation of Vth can be further illustrated as shown in Fig. S8–S12 (ESI).† This above regularity is most likely due to the following reason: the capacitive-coupling effect gets stronger as the gate-to-channel projection decreases, making Vth smaller and thus leading to more significant pain-perception behavior.45Fig. 4c shows the transfer characteristics of Chan-1 for the 5 different gates at a fixed VDS of 2 V. From this, one can clearly see that with a decrease in the distance between the gate and Chan-1, the on-state current (Ion) becomes larger. This phenomenon is ascribed to EDL modulation in electrolyte-gated thin-film transistors (TFTs).54,55 A short distance between the channel and gate can enhance the EDL coupling effect and thus increase the response current, causing the device to require a larger negative voltage to turn off. As mentioned before, pain perception typically begins with the activation of a network of nociceptors. Hence, these corresponding activities in this network would constitute a direct and objective measure of the actual experience of pain.2,46 Herein, the EPSC and corresponding Vth can be further extracted, as shown in Fig. 4d and e, respectively. From these, it is interestingly observed that the EPSC trend exhibits open-down Lorentz-type characteristics, while Vth shows open-up characteristics. Based on these specific features, a mathematic Lorentz equation can be proposed as follows:
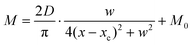 | (4) |
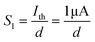 | (5) |
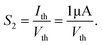 | (6) |
Using this equation, S2 can be extracted, as shown in Fig. 4g. It is interesting to note that the diagonal positions also exhibit large values. In fact, our transistor array is directly coupled through a lateral ion-conducting film, and each path between a gate and a channel has different capacitance.45 Hence, these phenomena can be attributed to the fact that as the distance between the gate and the channel increases, the ion-coupling effect becomes weak, leading to a decrease in the electrolyte capacitance.45 Interestingly, the underlying mechanism of the relationship between S1 and S2 can be further revealed from the following equation:
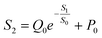 | (7) |
Conclusions
A multiterminal junctionless transistor array with SA biopolymer electrolyte as the gate dielectric is developed to mimic a pain-perceiving nociceptor network. The ionotronic biopolymer electrolyte endows the neuromorphic transistor network with intriguing position-sensitive characteristics due to the different channel-to-gate spatial distances, resulting in the good ability to tune the pain-perception threshold. The important pain-perception functions of nociceptors in response to peripheral stimuli, such as a pain threshold, pain sensitization, and desensitization, were successfully emulated. More importantly, the device can not only establish a good pain-sensitive network system based on graded pain-perception abilities, but it also exhibits the emulation of sensitivity-modulated spatiotemporal pain perception in a nociceptor network. Finally, the clear polarity reversal of the Lorentz-type spatiotemporal characteristics can be realized in our projection-dependent nociceptor network. This special artificial pain-perception network can provide new opportunities for applications in bionic medical machines, humanoid robots, etc.Experimental section
Firstly, sodium alginate (SA) solution (4 wt%) was drop-casted onto a Si/SiO2 substrate and dried to form a homogeneous film in ambient air as the top electrolyte. The thickness of the SA film is about 15.5 μm. Next, indium tin oxide (ITO) film with in-plane source, drain, channel, and gate components was deposited on the SA-based solid electrolyte via radio-frequency (RF) magnetron sputtering, where the RF power, Ar flow rate, and working pressure were set to 50 W, 15 sccm, and 0.65 Pa, respectively. The time of the sputtering process for all the in-plane components (gates, source, drain, and channels) was 2.5 min. The dimensions of the nickel shadow mask were 150 μm × 1000 μm. Electrical performance data were measured using a semiconductor parameter characterization system (Keithley 4200 SCS) in the dark at room temperature.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (52172169) and the Central South University Research Fund for Innovation-Driven Program (2019CX024). Y. Li thanks the Fundamental Research Funds for the Central Universities of Central South University (2020zzts374). K. Yin thanks the Natural Science Foundation of Hunan Province (Grant No. 2021JJ20067).References
- A. I. Basbaum, D. M. Bautista, G. Scherrer and D. Julius, Cell, 2009, 139, 267–284 CrossRef CAS PubMed.
- P. Cortelli, G. Giannini, V. Favoni, S. Cevoli and G. Pierangeli, Neurol. Sci., 2013, 34, 41–46 CrossRef PubMed.
- L. Wei, Y. Li, C. Tian and J. Jiang, Phys. Status Solidi A, 2021, 218, 2100204 CrossRef CAS.
- K. Hagiwara, L. Garcia-Larrea, L. Tremblay, A. Montavont, H. Catenoix, S. Rheims, M. Guénot and J. Isnard, Pain, 2020, 161, 502–508 CrossRef PubMed.
- D. D. Ridder, D. Adhia and S. Vanneste, Neurosci. Biobehav. Rev., 2021, 130, 125–146 CrossRef PubMed.
- S. N. Raja, D. B. Carr, M. Cohen, N. B. Finnerup, H. Flor, S. Gibson, F. J. Keefe, J. S. Mogil, M. Ringkamp, K. A. Sluka, X. Song, B. Stevens, M. D. Sullivan, P. R. Tutelman, T. Ushida and K. Vader, Pain, 2020, 161, 1976–1982 CrossRef PubMed.
- V. Neugebauer and W. Li, J. Neurophysiol., 2002, 87, 103–112 CrossRef PubMed.
- W. D. Tracey Jr., Curr. Biol., 2017, 27, R129–R133 CrossRef PubMed.
- M. A. Rahman, S. Walia, S. Naznee, M. Taha, S. Nirantar, F. Rahman, M. Bhaskaran and S. Sriram, Adv. Intell. Syst., 2020, 2, 2000094 CrossRef.
- C. Tian, L. Wei, Y. Li and J. Jiang, Curr. Appl. Phys., 2021, 31, 182 CrossRef.
- H. Abdo, L. Calvo-Enrique, J. M. Lopez, J. Song, M. Zhang, D. Usoskin, A. E. Manira, I. Adameyko, J. Hjerling-Leffler and P. Ernfors, Science, 2019, 365, 695–699 CrossRef CAS PubMed.
- H. Wei, H. Han, K. Guo, H. Yu, J. Gong, M. Ma, Y. Ni, J. Feng, Z. Xu and W. Xu, Mater. Today Phys., 2021, 18, 100329 CrossRef CAS.
- R. A. John, N. Yantara, S. E. Ng, M. I. B. Patdillah, M. R. Kulkarni, N. F. Jamaludin, J. Basu, Ankit, S. G. Mhaisalkar, A. Basu and N. Mathews, Adv. Mater., 2021, 33, 2007851 CrossRef CAS.
- F. Wang, S.-B. Ma, Z.-C. Tian, Y.-T. Cui, X.-Y. Cong and W.-B. Wu, Pain, 2021, 162, 135–151 CrossRef CAS PubMed.
- C. Henneberger, L. Bard, A. Panatier, J. P. Reynolds, O. Kopach, N. I. Medvedev, D. Minge, M. K. Herde, S. Anders, I. Kraev, J. P. Heller, S. Rama, K. Zheng, T. P. Jensen, I. Sanchez-Romero, C. J. Jackson, H. Janovjak, O. P. Ottersen, E. A. Nagelhus, S. H. R. Oliet, M. G. Stewart, U. V. Nagerl and D. A. Rusakov, Neuron, 2020, 108, 919–936 CrossRef CAS PubMed.
- J. R. Barnes, B. Mukherjee, B. C. Rogers, F. Nafar, M. Gosse and M. P. Parsons, J. Neurosci., 2020, 40, 2793–2807 CrossRef CAS PubMed.
- J. Jiang, J. Guo, X. Wan, Y. Yang, H. Xie, D. Niu, J. Yang, J. He, Y. Gao and Q. Wan, Small, 2017, 13, 1700933 CrossRef PubMed.
- C. Ge, C. Liu, Q. Zhou, Q. Zhang, J. Du, J. Li, C. Wang, L. Gu, G. Yang, K. Jin and C. Ge, Adv. Mater., 2019, 31, 1900379 CrossRef PubMed.
- Y. Zhao, G. Feng and J. Jiang, Solid-State Electron., 2020, 165, 107767 CrossRef CAS.
- Z. Zheng, J. Jiang, J. Guo, J. Yang and Y. Gao, Org. Electron., 2016, 37, 474–478 CrossRef CAS.
- Y. Q. Wang, J. Wang, S. Xia, H. B. Gutstein, Y. H. Huang, O. M. Schlüter, J. Cao and Y. Dong, Pain, 2021, 162, 1322–1333 CrossRef CAS PubMed.
- Q. Lu, F. Sun, L. Liu, L. Li, M. Hao, Z. Wang and T. Zhang, npj Flexible Electron., 2020, 4, 3 CrossRef CAS.
- A. Payeur, J. Guerguiev, F. Zenke, B. A. Richards and R. Naud, Nat. Neurosci., 2021, 24, 1010–1019 CrossRef CAS PubMed.
- A. C. E. Shibata, H. H. Ueda, K. Eto, M. Onda, A. Sato, T. Ohba, J. Nabekura and H. Murakoshi, Nat. Commun., 2021, 12, 751 CrossRef CAS PubMed.
- J. Li, C. Ge, J. Du, C. Wang, G. Yang and K. Jin, Adv. Mater., 2020, 32, 1905764 CrossRef CAS PubMed.
- G. Feng, J. Jiang, Y. Zhao, S. Wang, B. Liu, K. Yin, D. Niu, X. Li, Y. Chen, H. Duan, J. Yang, J. He, Y. Gao and Q. Wan, Adv. Mater., 2020, 32, 1906171 CrossRef CAS PubMed.
- J. Guo, Y. Liu, F. Zhou, F. Li, Y. Li and F. Huang, Adv. Funct. Mater., 2021, 31, 2102015 CrossRef CAS.
- P. C. Trettenbrein, Front. Syst. Neurosci., 2016, 10, 88 Search PubMed.
- L. Leng, R. Martel, O. Breitwieser, I. Bytschok, W. Senn, J. Schemmel, K. Meier and M. A. Petrovici, Sci. Rep., 2018, 8, 10651 CrossRef PubMed.
- J. Du, D. Xie, Q. Zhang, H. Zhong, F. Meng, X. Fu, Q. Sun, H. Ni, T. Li, E. Guo, H. Guo, M. He, C. Wang, L. Gu, X. Xu, G. Zhang, G. Yang, K. Jin and C. Ge, Nano Energy, 2021, 89, 106439 CrossRef CAS.
- Q. Ou, B. Yang, J. Zhang, D. Liu, T. Chen, X. Wang, D. Hao, Y. Lu and J. Huang, Small, 2021, 17, 2007241 CrossRef CAS PubMed.
- H. Huang, C. Ge, Q. Zhang, C. Liu, J. Du, J. Li, C. Wang, L. Gu, G. Yang and K. Jin, Adv. Funct. Mater., 2019, 29, 1902702 CrossRef.
- W. Hu, J. Jiang, D. Xie, B. Liu, J. Yang and J. He, J. Mater. Chem. C, 2019, 7, 682–691 RSC.
- S. Jiang, Y. He, R. Liu, C. Chen, L. Zhu and Y. Zhu, IEEE Trans. Electron Devices, 2021, 68, 415–420 CAS.
- Q. B. Zhu, B. Li, D. D. Yang, C. Liu, S. Feng, M. L. Chen, Y. Sun, Y. Tian, X. Su, X. Wang, S. Qiu, Q. Li, X. Li, H. Zeng and H. Cheng, Nat. Commun., 2021, 12, 1798 CrossRef CAS PubMed.
- S. E. Ng, J. Yang, R. A. John and N. Mathews, Adv. Funct. Mater., 2021, 31, 2100807 CrossRef CAS.
- R. S. Zucker and W. G. Regehr, Annu. Rev. Physiol., 2002, 64, 355–405 CrossRef CAS PubMed.
- F. Li, S. Gao, Y. Lu, W. Asghar, J. Cao, C. Hu, H. Yang, Y. Wu, S. Li, J. Shang, M. Liao, Y. Liu and R. Li, Adv. Sci., 2021, 8, 2004208 CrossRef PubMed.
- J. Ge, S. Zhang, Z. Liu, Z. Xie and S. Pan, Nanoscale, 2019, 11, 6591–6601 RSC.
- R. Yu, Y. Yan, E. Li, X. Wu, X. Zhang and J. Chen, Mater. Horiz., 2021, 8, 2797–2807 RSC.
- S. J. Macedo-Junior, F. P. Nascimento, M. Luiz-Cerutti and A. R. S. Santos, Purinergic Signalling, 2021, 17, 303–312 CrossRef CAS PubMed.
- M. Toyota, D. Spencer, S. Sawai-Toyota, J. Wang, T. Zhang, A. J. Koo, G. A. Howe and S. Gilroy, Science, 2018, 361, 1112–1115 CrossRef CAS PubMed.
- Y. Cheng, K. Shan, Y. Xu, J. Yang, J. He and J. Jiang, Nanoscale, 2020, 12, 21798 RSC.
- H. Wei, Y. Ni, L. Sun, H. Yu, J. Gong, Y. Du, M. Ma, H. Han and W. Xu, Nano Energy, 2021, 81, 105648 CrossRef CAS.
- G. Feng, J. Jiang, Y. Li, D. Xie, B. Tian and Q. Wan, Adv. Funct. Mater., 2021, 31, 2104327 CrossRef CAS.
- A. Parvizi-Fard, N. Salimi-Nezhad, M. Amiri, E. Falotico and C. Laschi, Sci. Rep., 2021, 11, 2109 CrossRef CAS PubMed.
- D. Copot and C. Ionescu, IEEE Trans. Biomed. Eng., 2019, 66, 718–726 Search PubMed.
- R. R. Ji, T. Kohno, K. A. Moore and C. J. Woolf, Trends Neurosci., 2003, 26, 696–705 CrossRef CAS PubMed.
- M. de Tommaso, L. L. Sito, O. D. Fruscolo, M. Sardaro, M. P. Prudenzano, P. Lamberti and P. Livrea, Clin. Neurophysiol., 2005, 116, 1254–1264 CrossRef PubMed.
- X. Deng, S. Q. Wang, Y. X. Liu, N. Zhong, Y. H. He, H. Peng, P. Xiang and C. Duan, Adv. Funct. Mater., 2021, 31, 2101099 CrossRef CAS.
- T. Hucho and J. D. Levine, Neuron, 2007, 55, 365–376 CrossRef CAS PubMed.
- S. Ke, Y. He, L. Zhu, Z. Jiang, H. Mao, Y. Zhu, C. Wan and Q. Wan, Adv. Electron. Mater., 2021, 7, 2100487 CrossRef CAS.
- N. A. Temour'yants, A. S. Kostyuk and K. N. Tumanyants, Neurophysiology, 2011, 42, 276–285 CrossRef.
- L. Zhu, Y. He, C.1900379. Chen, Y. Zhu, Y. Shi and Q. Wan, IEEE Trans. Electron Devices, 2021, 68, 1659–1663 CAS.
- Y. Zhao, B. Liu, J. Yang, J. He and J. Jiang, Chin. Phys. Lett., 2020, 37, 088501 CrossRef CAS.
- H. Bastuji, M. Frot, C. Perchet, M. Magnin and L. Garcia-Larrea, Hum. Brain Mapp., 2016, 37, 4301–4315 CrossRef PubMed.
- Y. Kim, A. Chortos, W. Xu, Y. Liu, J. Y. Oh, D. Son, J. Kang, A. M. Foudeh, C. Zhu, Y. Lee, S. Niu, J. Liu, R. Pfattner, Z. Bao and T. Lee, Science, 2018, 360, 998–1003 CrossRef CAS PubMed.
- D. Xie, L. Wei, M. Xie, L. Jiang, J. Yang, J. He and J. Jiang, Adv. Funct. Mater., 2021, 31, 010655 Search PubMed.
- Y. Chen, Z. Shu, S. Zhang, P. Zeng, H. Liang, M. Zheng and H. Duan, Int. J. Extreme Manuf., 2021, 3, 032002 CrossRef CAS.
- W. Hu, D. Xie, J. Yang, J. He, Y. Gao, Q. Wan and J. Jiang, Nanoscale, 2019, 11, 1360 RSC.
- G. Feng, Y. Zhao and J. Jiang, Solid-State Electron., 2019, 153, 16 CrossRef CAS.
- W. Hu, J. Jiang, D. Xie, S. Wang, K. Bi, H. Duan, J. Yang and J. He, Nanoscale, 2018, 10, 14893 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr07896h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |