Optimised spectral pre-processing for discrimination of biofluids via ATR-FTIR spectroscopy†
Holly J.
Butler
 ab,
Benjamin R.
Smith
ab,
Benjamin R.
Smith
 c,
Robby
Fritzsch
c,
Robby
Fritzsch
 d,
Pretheepan
Radhakrishnan
e,
David S.
Palmer
*bc and
Matthew J.
Baker
d,
Pretheepan
Radhakrishnan
e,
David S.
Palmer
*bc and
Matthew J.
Baker
 *ab
*ab
aWestCHEM, Department of Pure and Applied Chemistry, University of Strathclyde, Technology and Innovation Centre, 99 George Street, Glasgow, G1 1RD, UK. E-mail: matthew.baker@strath.ac.uk; Fax: +44(0)141 548 4700,; Web: http://www.twitter.com/ChemistryBaker
bClinSpec Diagnostics Limited, Technology and Innovation Centre, 99 George St, Glasgow, G1 1RD, UK
cWestCHEM, Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, 295 Cathedral Street, Glasgow, G1 1XL, UK
dDepartment of Physics, University of Strathclyde, 107 Rottenrow East, Glasgow, G4 0NG, UK
eDepartment of Biomedical Engineering, University of Strathclyde, 50 George Street, Glasgow, G1 1QE, UK
First published on 19th November 2018
Abstract
Pre-processing is an essential step in the analysis of spectral data. Mid-IR spectroscopy of biological samples is often subject to instrumental and sample specific variances which may often conceal valuable biological information. Whilst pre-processing can effectively reduce this unwanted variance, the plethora of possible processing steps has resulted in a lack of consensus in the field, often meaning that analysis outputs are not comparable. As pre-processing is specific to the sample under investigation, here we present a systematic approach for defining the optimum pre-processing protocol for biofluid ATR-FTIR spectroscopy. Using a trial-and-error based approach and a clinically relevant dataset describing control and brain cancer patients, the effects of pre-processing permutations on subsequent classification algorithms were observed, by assessing key diagnostic performance parameters, including sensitivity and specificity. It was found that optimum diagnostic performance correlated with the use of minimal binning and baseline correction, with derivative functions improving diagnostic performance most significantly. If smoothing is required, a Sovitzky–Golay approach was the preferred option in this investigation. Heavy binning appeared to reduce classification most significantly, alongside wavelet noise reduction (filter length ≥6), resulting in the lowest diagnostic performances of all pre-processing permutations tested.
Introduction
A single IR spectrum obtained from a biological specimen contains not only the information of interest, but also underlying contributions from unwanted signals. Optimised sampling methods are essential to reducing this variability; however, these contributions are often still apparent in the subsequent dataset. Pre-processing can be defined as the reduction of these uncontrolled variables and can improve the experimental outcomes of spectral investigations.Extracting biological variance arising from the sample itself is often the key aim of spectroscopic studies of biological materials. Whether this is exploratory or diagnostic, differences in biological content, molecular structure and distribution can allow differences to be observed within the dataset. However, spectra can also contain variance as a result of environmental, experimental and technical conditions. Respectively, factors such as humidity, sample morphology, and instrumental drift can all have negative impacts on spectral quality, repeatability and reproducibility.1
The purpose of pre-processing is to reduce this unwanted variance, thus exposing the important underlying information from the spectral dataset. Consequently, pre-processing can improve exploratory analysis, classification and calibrations models, and interpretability whilst also removing outliers and trends, and reducing dimensionality.2 It is important to acknowledge that pre-processing is not a solution to poor spectral data that arises from inherent issues with sample preparation and spectral acquisition. Whilst pre-processing may improve poor spectra, it is first imperative to obtain the highest quality spectra possible, within the constraints of sample and instrument.3
Fourier-transform Infrared (FTIR) spectroscopy has been widely applied to biological applications, due to its ability to identify chemical bonds characteristic of biological samples. More specifically, FTIR spectroscopy has been increasingly used as a tool to identify and differentiate disease status, in combination with machine learning and classification algorithms.4 For such approaches to perform optimally – that is with the highest sensitivity, specificity, accuracy and precision, in combination with low false positive and negative rates – the data must be pre-processed to ensure the important biological information is not concealed or diluted by systematic variance. Different combinations of pre-processing techniques have been shown to have a drastic impact on the diagnostic performance of machine learning algorithms, and thus an optimised approach to data handling must be employed prior to this form of analysis.5–7
Sources of variance in FTIR spectroscopy
One of the primary sources of unwanted variance in an infrared (IR) spectrum derives from the phenomena of light scattering. Biological molecules absorb light in the mid-IR (MIR) region due matched frequencies between the incoming light and specific chemical bond vibrations.8 FTIR spectroscopy is able to produce an information rich spectrum that is indicative of the sample's discrete biochemical fingerprint. Due to this, the technology is widely implemented in the field of biological sciences, with applications spanning clinical, microbiological, pharmaceutical and food fields.9,10 However, despite the suitability of MIR light for analysing molecular vibrations of interest, the wavelength of this light (2.5–25 μm) is also highly correlated with the size of many biological samples, including cells and their subcellular components. These are ideal conditions for light scattering which can cause aberrations to the spectral baseline, and thus presents one of the most common issues in FTIR investigations.11 This particular form of scattering is defined as Mie scattering and results in spectra that do not obey the principles of Beer–Lambert's Law, often altering the intensity and position of the amide I band.12,13 Scattering is also apparent in the analysis of powders, or other solids with uneven surfaces. As scattering is wavelength dependent (shorter wavelengths are more prone to scattering), a subsequent spectrum will often have higher absorption in the high wavenumber region.14Furthermore, noise is an inherent issue with FTIR and other photonic techniques, that is apparent as high frequency signals within a spectrum. This noise can arise from electrical signals, mechanical vibrations, and environmental parameters, which are often unavoidable. A cooled detector, such as a deuterated triglycine sulfate detector (DGTS) can reduce thermal, or dark, noise in an IR system although not entirely.3 Increased spectral noise can often overshadow subtle spectral features, and thus spectral quality is often assessed as a value of signal-to-noise, or the signal-to-noise ratio (SNR).
The optical pathlength of a system is directly implicated in Beer–Lambert's Law, and as such, FTIR spectra can also contain evidence of pathlength heterogeneity. This can commonly arise as a consequence of disparity in sample thickness, but can also occur due to intensity changes in the IR source.2 The evidence of this is what may initially appear are gross spectral differences in absorbance, but are in actual fact indicative of inconsistencies in the sampling. Although not exhaustive, these factors can conceal interesting biological information by reducing the quality, accuracy and precision of IR spectra. By pre-processing data with evidence of such spectral features, the repeatability and reproducibility of the approach can be improved dramatically, leading to more insight in the data.
Pre-processing for FTIR spectroscopy
There is a wealth of pre-processing options available for spectral datasets, often providing more than one solution. Although this flexibility allows for optimised signal processing, the number of processing options available can often prove too large to systematically determine the best approach.15 In this instance, we focus upon relevant pre-processing steps for FTIR spectroscopy, although this may draw from information from other techniques. Some processes are technique-specific, such as cosmic ray removal in Raman spectroscopy, but many are applicable to a wide range of spectroscopies including NMR and near-infrared (NIR) spectroscopy.16 The development of spectral pre-processing methods has been largely developed in the field of NIR spectroscopy, and also has much overlap with Raman spectroscopy, due to similar susceptibilities to scattering and noise.14For an in depth overview of pre-processing applications in IR (and Raman) spectroscopy, the authors direct the reader to the following comprehensive review, which covers an array of pre-processing steps, namely: exclusion, normalisation, filtering, de-trending, transformations, feature selection, folding and other methods.2 In short, FTIR datasets often first undergo a form of quality control; an exclusion step where spectra with poor SNR or high water contributions for example, can excluded from the subsequent analysis. It is often important to undergo this step first, so that highly variable spectra do not influence subsequent analysis (such as processes that use the dataset mean, such as mean centering).17 Normalisation steps are required to negate differences in optical pathlength, allowing spectra to scaled relative to each other.18 Baseline correction procedures are also commonly acquired to remove scattering as well as additive or multiplicative baselines.19 Additionally, filtering, or smoothing, can reduce the appearance of noise regions, thus potentially improving the clarity of spectral features and SNR. Spectral derivation is a useful filtering tool that can be remove baseline effects and deconvolute complex spectra, whilst also improving diagnostic performances of classification algorithms.20,21
As spectral datasets are highly dimensional, with a single spectrum alone often containing around 3600 absorbance values, the computational burden of data processing can be high. A feature selection step that selects only the variables that are important to the post-analysis can often make a large dataset more manageable, whilst also improving overall analysis accuracy.22 This can often be as simple as reducing the spectral range under investigation, or more sophisticated multivariate approaches such as principal component analysis (PCA) and partial least squares (PLS) which can also describe spectral differences between given experimental classes.23
Consensus in the community
Although, there have been several attempts to unify the field of biological FTIR spectroscopy,3,24 there still remains a distinct lack of consensus with regards to pre-processing.16 This issue has been directly highlighted as one of the key objectives of The International Society of Clinical Spectroscopy, stressing the importance of establishing consensus between researchers.25Due to the variability between biological samples, spectral artefacts will be specific for each sample type, and even each individual experimental set-up. This therefore requires a priori knowledge of the sample, and the spectral response, in order to apply appropriate pre-processing steps. Through visual inspection of the dataset, indicators of unwanted spectral variance may be noticeable and thus pre-processing steps can be applied when deemed necessary by the analyst.16
This highly subjective approach may be the efficient with regards to analysis time, but will be variable between individuals. It has been shown that this may be improved using a trial-and-error based approach which systematically implements a range of pre-processing options, with the highest performing choice determined as the optimum protocol.26 A search algorithm, such as a genetic algorithm (GA), can optimise this process using machine learning to predict the optimal pre-processing steps.27 However, despite the obvious benefits of this method, it can still be considered computationally heavy and is often not easily implemented in each spectroscopic experiment.
The order in which pre-processing steps are implemented is also another aspect of pre-processing to be optimised. It could be suggested that the largest source of spectral variance is minimised in the first instance, so that this is not influential in the next stage of analysis. For instance it is suggested that baseline effects should be removed prior to a normalisation step.15,28 It has also been suggested that the most effective approach for pre-processing is often the simplest, and as such the number of processes in a pre-processing protocol should be kept to the minimum.15
The optimum sample pre-processing procedure is likely entirely sample specific, with suggestions that this may even be specific to the classification question being asked of the dataset.29 For instance, samples prone to contamination, such as paraffin embedded tissue, may undergo specific quality tests to automatically exclude spectra containing evidence of the contaminant (in this case, paraffin).30 Whereas in contrast, a cell based investigation may be more prone to scattering and thus require a specific baseline correction.31
Biofluid FTIR spectroscopy
The analysis of biofluids, such as blood serum, using IR spectroscopy is a rapidly progressing field that is nearing ever closer to clinical translation.17,32,33 Due to its simplicity and robust methodology, the analysis of easily obtained bodily fluids using ATR-FTIR spectroscopy lends itself well to a rapid and cost-effective technology for clinical diagnostics.34,35The diagnostic capabilities of this approach have been explored in a range of cancers and disease.6,22,36–41 The application of ATR-FTIR serum analysis for the early detection of brain tumour provides an example of where a spectroscopic technique is distinctly addressing an unmet clinical need. Due to a combination of non-specific symptoms, pressure in the health service diagnostic pathway, expensive neuroimaging and highly invasive biopsies – the diagnosis of brain tumours is often made in the case of an emergency, when the patient will likely have a well-developed tumour. A method of early detection would greatly benefit this patient pathway, allowing screening or triage into secondary healthcare.33 Recently, we have shown that glioblastoma (GBM) patients can be correctly identified at sensitivities and specificities of 91.5% and 83% respectively, using a feature-fed support vector machine (SVM) analysis.42 This same dataset was reanalysed using a random forest (RF) approach, which resulted in an improved classification performance (92.8% and 91.5%, sensitivity and specificity respectively).43 The classification process was iterated up to 96 times to generate a robust result, and thus small differences in sensitivity and specificity can be expected due to effectively altering the population of patients in the training and test sets.
The range of pre-processing methods for biofluid spectroscopy described in the literature are variable, with a baseline correction, normalisation step the most commonly implemented. A specific review of pre- and post-processing in ATR-FTIR has been recently published, highlighting technique specific approaches to data analysis.44 It is evident therefore, that even in this highly specific application there is no defined pre-processing approach that has been accepted.
This study aims to optimise the spectral pre-processing approach for biofluid ATR-FTIR spectroscopy, for the purpose of improving a subsequent classification model. Although largely specific to this sample-technique scenario, the optimum pre-processing approach as defined by this thorough investigation may also be applicable to other sample types and techniques, as the approaches highlighted address many sources of variance non-discriminately. The spectral investigation of samples, such as bodily fluids, using techniques that are sensitive to differences in sample thickness and inherent heterogeneity, would be considered the best suited application of this approach.
Experimental
Data processing was conducted using the PRRFECT toolbox written the R programming language (https://github.com/Palmer-Lab/PRFFECT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45). The aim of this programme is to provide a comprehensive, robust, and interpretable system for pre- and post-processing of spectral datasets. In its current format, this programme follows pre-processing steps commonly implemented in the field of biospectroscopy, with scope for altering the order and parameters inputted into the processing options available. An overview of the pre-processing dataflow investigated in this study can be seen in Fig. 1.
45). The aim of this programme is to provide a comprehensive, robust, and interpretable system for pre- and post-processing of spectral datasets. In its current format, this programme follows pre-processing steps commonly implemented in the field of biospectroscopy, with scope for altering the order and parameters inputted into the processing options available. An overview of the pre-processing dataflow investigated in this study can be seen in Fig. 1.
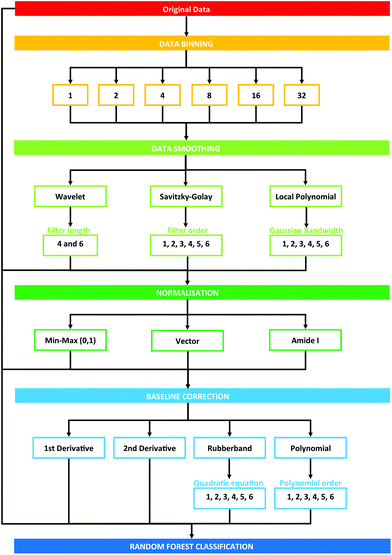 | ||
| Fig. 1 Schematic overview of pre-processing steps explored in this study. Numbers describe the cumulative total of pre-processing combinations. | ||
Each pre-processing permutation from this point onwards will be described by a 6 (or 7, in the case of binning with a factor of 16 or 32) identifier, which is described by Table 1. The calculations were run in serial on Dual Intel Xeon X5650 2.66 GHz processors at the ARCHIE-WeSt supercomputing center located at the University of Strathclyde in Glasgow, Scotland and each run performed took approximately 2–3 minutes.
| Binning factor | Smoothing | Smoothing parameters | Normalisation | Baseline correction | Baseline correction parameters |
|---|---|---|---|---|---|
| 1 | 0 – none | 0 – none | 0 – none | 0 – none | 0 – none |
| 2 | 1 – SG filter | 1,2,3,4,5,6 filter order | 1 – min/max | 1–1st derivative | |
| 4 | 2 – wavelet denoise | 4 or 6 length of filter | 2 – vector | 2–2nd derivative | |
| 8 | 3 – local polynomial | 1,2,3,4,5,6 bandwidth of gaussian | 3 – amide I | 3 – rubberband | 1, 2, 3, 4, 5, 6 factor of quadratic equation |
| 16 | 4 – polynomial | 1, 2, 3, 4, 5, 6 polynomial degree | |||
| 32 |
Dataset and spectral acquisition
The dataset explored in this study is that from Hands et al. 2016,42 where more detail can be found. In short, ATR-FTIR spectra obtained from 433 patients; 122 control patients and 311 brain cancer patients. Each patient was analysed in triplicate, with three spectra obtained per sample, providing a total of 3897 spectra. Spectra were obtained at a spectral resolution of 4 cm−1, and a data spacing of 1.9 cm−1.42 Spectra were collected using a triangular apodization, no zero filling factor, a 5 kHz collection speed, 1.28 kHz electronic low pass filter, an interferogram sample interval of 2, a sensitivity factor of 1 and an asymmetric single sided interferogram symmetry. Primarily, the binary classification between cancer and control is explored as an indicator of pre-processing optimisation. However, as a further post-comparative analysis, the effect of pre-processing on determining more difficult clinical questions, specifically differentiating between primary and metastatic brain cancer, is also explored. The research described in this paper was performed with full ethical approval (Walton Research Bank BTNW/WRTB 13_01/BTNW Application #1108).Pre-processing options
A concise overview of the pre-processing options explored in this study are presented; full details are described here can be found in the article by Smith et al., 2018.45 The options that have been selected for this study encompass a range of approaches that are commonly implemented in IR studies of biological materials. A total of 3528 possible pre-processing permutations were considered initially in this study, each generating a new dataset that is subsequently fed into the same classification algorithm (Fig. 1). Some permutations were excluded from the study due to an insufficient number of data points that resulted in unviable spectral outputs; this was particularly significant with increased binning and larger processing parameters.Assessment of performance
Initially, each pre-processing combination was analysed using a random forest (RF) machine learning algorithm. This approach uses a defined number of decision trees (in this case, 500 trees), which subdivide during training at each or fork, or node, using randomly chosen descriptors (wavenumbers). The number of descriptors used was determined as the square root of the total number of wavenumbers in the dataset, and a minimum of 5 nodes for each tree was chosen.45 Each of the pre-processed datasets were split into training and test sets at a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 based upon patient identity, with no spectra from a single patient appearing in both the training and test sets. The process is iterated a total of 96 times, in order to produce the average results of the classification for both the training and test sets. It is possible to identify which descriptors contribute to the split at each node using the relative Gini importance. This useful aspect of RF is considered in ‘Further classification’.
1 based upon patient identity, with no spectra from a single patient appearing in both the training and test sets. The process is iterated a total of 96 times, in order to produce the average results of the classification for both the training and test sets. It is possible to identify which descriptors contribute to the split at each node using the relative Gini importance. This useful aspect of RF is considered in ‘Further classification’.
The output of this process is a binary classification between cancer versus non-cancer (and afterwards metastatic versus GBM) with the following metrics; prediction accuracy (PAC), sensitivity, specificity, Matthew's correlation coefficient (MCC), positive predictive value (PPV) and negative predictive value (NPV). A description of each of these metrics can be found in the following articles.43,45 There are also corresponding standard error values for each metric. The model is iterated 96 times in order to ensure the population of the training and test set is changed at each iteration, providing results more representative of the total patient population. As such, there is less opportunity for bias in the test set. To encompass all measures of performance, a representative metric was created (eqn (1)). This found the cumulative total of the standard error (se) for all test measures, and subtracted this value from the cumulative total performance of each measure over 96 iterations. As such, a simple method of observing overall stability of the pre-processing method, as well as overall performance can be conducted.
Equation representing the Overall Metric.
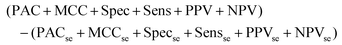 | (1) |
In order to visualise the overall results for each of these metrics, the performance of each combination was ranked in terms of test performance, and displayed as a line chart of decreasing efficiency. The corresponding validation dataset performance was shown for comparative purposes. Standard error bars are shown to display the variance across the 96 iterations.
Order of pre-processing
The initial processing ordered as described, with first binning (B), followed by smoothing (S), normalisation (N) and baseline correction (C). However, as this order is somewhat debated in the literature, the impact of order was assessed. The top 12 performing pre-processed datasets were re-analysed using RF classification in a variety of orders, denoted by their ‘B’, ‘S’, ‘N’, ‘C’ label. Re-analysis of the data results in alterations to performance values previously derived. The overall performance metric, sensitivity and specificity were compared against the default ‘BSNC’ results ascertained through this reanalysis. To reduce the number of order options and to take advantage of data reduction, binning was kept at the first position throughout. Net percentage change was used to visualise these differences.Further classification
The 12 permutations that had the best diagnostic performance occording to the overall metric were recorded, as were the worst performing permutations. These best performing pre-processing combinations were than re-analysed using; (i) a RF-fed support vector machine (SVM), and (ii) a genetic algorithm (GA) fed SVM.This was conducted to compare alternative classification approaches and to observe any relationships between specific pre-processing protocols and classifiers. A SVM was employed as a non-linear model that is known to minimise empirical error and maximise inter-class geometric margin.52 The top 30 Gini descriptors that were extracted from the original RF analysis were thus fed into the SVM, producing a feature-fed classification system which should focus on wavenumbers that best describe the variance in the dataset. 30 Gini descriptors were chosen due to preliminary investigation that suggested this provided the optimum performance in comparison to higher and lower values (data not shown). A GA was used as a comparison to the trial-and-error based approach described here, in order to optimise the pre-processing combination. The output of this was then also fed into an SVM. Net percentage change in the overall performance metric was used to describe the effect of alternative classifiers on overall classification.
Results and discussion
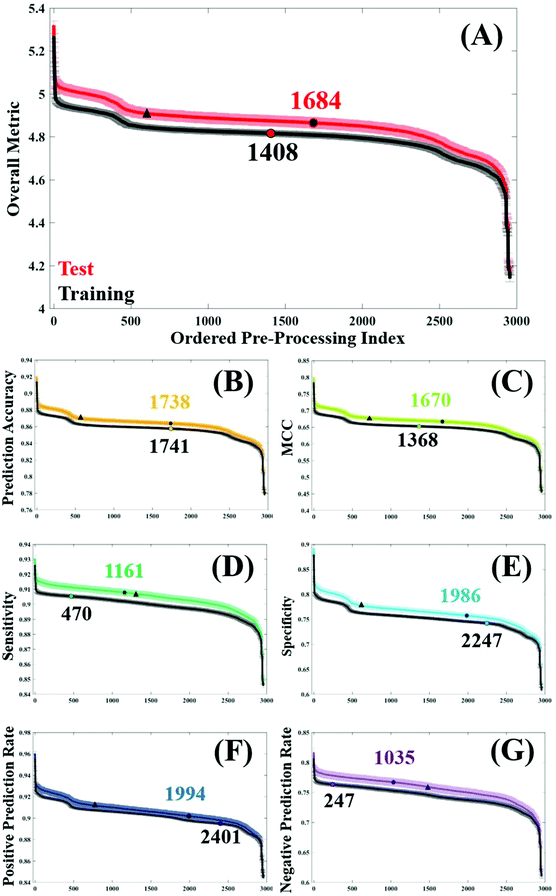
In order to assess general trends in classification performance of the pre-processed datasets, test and training sets were ranked according to each metric (Fig. 2). By plotting the distribution of each pre-processing permutation it is possible to identify how pre-processing effects the overall classification between brain cancer and control, in comparison to the raw data (shown as a circle on each plot). Both training and test datasets are displayed in order to identify any discrepancies and stability within the model. The raw, unprocessed dataset is highlighted as a marker for classification performance, as is a standard processing step commonly used in the literature.3Initially it is clear that the trend in overall performance is similar across the board, with a number of permutations yielding higher results than the vast majority, and similarly a number of permutations that have detrimental effects on the overall classification. Generally, it appears that around 2000 or so options in the central area do not drastically alter the classification. What is also apparent in Fig. 2, is a dip in efficiency at around the 500th ranked combination. From investigating the data further (data not shown), this corresponds with the use of a min–max normalisation and subsequent rubberband or polynomial baseline correction. The combination of these approaches may be well suited to diagnostic studies using IR spectra.
The overall metric (Fig. 2A) encompasses this trend, and is also evident in each of the other performance measures. It is noticeable that the unprocessed dataset appears at a slightly higher rank in both the training dataset, coinciding with smaller standard error in this dataset too. This is as expected given the cross validation of the training dataset will not be as variable as the predicting test data. The sharp incline represents the best performing combinations, of which the top 12 are given in Table 2. Consistently, the top performing processing combination was a simple vector normalised and second derivative filtered dataset. Similarly, the second best classification result also came from the dataset only corrected using a second derivative, indicating the suitability of this processing step for the analysis of FTIR data. As this method removes baseline effects, has an in-built smoothing SG step, and also has the ability to resolve spectral features, it is a simple yet powerful approach for diagnostic applications. The minimal number of steps in these approaches could also be considered preferable.15
| Rank | Overall Metric | Prediction Accuracy | Matthew's CC | Sensitivity | Specificity | PPV | NPV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 100220 | 5.319 ± 0.021 | 100220 | 0.920 ± 0.002 | 100220 | 0.799 ± 0.005 | 100220 | 0.930 ± 0.002 | 100220 | 0.892 ± 0.004 | 100220 | 0.960 ± 0.002 | 100220 | 0.817 ± 0.006 |
| 2 | 100020 | 5.262 ± 0.021 | 100020 | 0.913 ± 0.002 | 100020 | 0.783 ± 0.005 | 100020 | 0.925 ± 0.002 | 100020 | 0.884 ± 0.005 | 100020 | 0.957 ± 0.002 | 100020 | 0.805 ± 0.006 |
| 3 | 416220 | 5.215 ± 0.023 | 416220 | 0.907 ± 0.002 | 416220 | 0.769 ± 0.006 | 416210 | 0.924 ± 0.002 | 416210 | 0.868 ± 0.006 | 100210 | 0.951 ± 0.002 | 3215310 | 0.802 ± 0.006 |
| 4 | 100210 | 5.192 ± 0.021 | 416320 | 0.905 ± 0.002 | 416320 | 0.762 ± 0.005 | 100210 | 0.924 ± 0.002 | 100210 | 0.857 ± 0.004 | 416210 | 0.946 ± 0.002 | 416320 | 0.801 ± 0.006 |
| 5 | 416210 | 5.172 ± 0.021 | 100210 | 0.902 ± 0.002 | 100210 | 0.757 ± 0.005 | 416320 | 0.923 ± 0.002 | 416320 | 0.847 ± 0.005 | 416320 | 0.941 ± 0.002 | 100210 | 0.799 ± 0.006 |
| 6 | 416310 | 5.122 ± 0.023 | 416210 | 0.895 ± 0.002 | 416310 | 0.742 ± 0.005 | 416220 | 0.923 ± 0.002 | 3215310 | 0.830 ± 0.005 | 416220 | 0.935 ± 0.002 | 416220 | 0.798 ± 0.005 |
| 7 | 100010 | 5.101 ± 0.023 | 416310 | 0.894 ± 0.002 | 416210 | 0.735 ± 0.005 | 3215310 | 0.919 ± 0.002 | 416310 | 0.825 ± 0.005 | 3215310 | 0.934 ± 0.002 | 415032 | 0.797 ± 0.005 |
| 8 | 416133 | 5.084 ± 0.024 | 100010 | 0.891 ± 0.002 | 100010 | 0.731 ± 0.006 | 416310 | 0.918 ± 0.002 | 134136 | 0.824 ± 0.005 | 416310 | 0.934 ± 0.002 | 416310 | 0.790 ± 0.005 |
| 9 | 414144 | 5.060 ± 0.023 | 416133 | 0.889 ± 0.002 | 424210 | 0.724 ± 0.005 | 134136 | 0.918 ± 0.002 | 416220 | 0.824 ± 0.005 | 213035 | 0.933 ± 0.002 | 416210 | 0.790 ± 0.006 |
| 10 | 413132 | 5.060 ± 0.022 | 414144 | 0.888 ± 0.002 | 414010 | 0.724 ± 0.005 | 132143 | 0.918 ± 0.002 | 815042 | 0.823 ± 0.006 | 412136 | 0.933 ± 0.003 | 416335 | 0.790 ± 0.006 |
| 11 | 413136 | 5.058 ± 0.024 | 413132 | 0.888 ± 0.002 | 413132 | 0.723 ± 0.005 | 100010 | 0.918 ± 0.002 | 435042 | 0.821 ± 0.005 | 235043 | 0.932 ± 0.002 | 135135 | 0.789 ± 0.006 |
| 12 | 414132 | 5.053 ± 0.021 | 413136 | 0.888 ± 0.002 | 413136 | 0.722 ± 0.005 | 234144 | 0.917 ± 0.002 | 435034 | 0.820 ± 0.005 | 114134 | 0.932 ± 0.002 | 132035 | 0.789 ± 0.006 |
Below the two highest ranked pre-processing options, there is less uniformity across the different classification metrics (Table 2). Whilst simple procedures such as first order derivation with and without a normalisation step appear spordically in this table, the majority of pre-processing permutations have multiple steps. Using PAC as an example, options ranked 3 to 12 vary quite significantly, with binning, smoothing, normalisation, and baseline corrections having a positive effect on the overall accuracy. This metric is indicative of the correct prediction of true positives and negatives, in this case predicting the presence or absence of brain cancer, and ranges from 92.0–88.8% in the top pre-processing approaches. Interestingly, a binning factor of 4 appears more regularly than any other binning option, representing a four-fold reduction in the number of data points within the dataset. Binning is known to improve the SNR across the spectrum, by averaging out the signal of a given number of wavenumbers. With a data spacing of every four wavenumbers, closer matched to the original spectral resolution of 4 cm−1, this binning option may increase SNR without smoothing out spectral features important for classification.
In this clinical dataset, a binning step is usually associated with a smoothing procedure, with SG filtering being the most commonly chosen option. Looking at the top 12 permutations with regards to optimum MCC, SG filtering with a filter order of 6 generates the best classification. It is worth noting that the value of MCC is lower than the other metrics, with values ranging between 0.799–0.722 (Table 2). Rather than being expressed as a percentage, MCC is representative of a scale between −1 and +1; with positive values indicating a strong correlation between the observed and predicted classifications and negative values indicating a worse performance than random choice. As expected, in the test dataset the classification error is higher than in cross validation, and unprocessed spectra as a comparison differ between these two datasets (Fig. 2C).
For the remaining classification metrics, a number of processing combinations already mentioned also perform well. For sensitivity, our ability to detect brain cancer patients in this case, ranges from 93.0–91.7%. Local polynomial smoothing appear to have a positive impact on sensitivity on this dataset, as well as on the NPR. However, it appears as though pre-processing generally has a greater impact on sensitivity of the classifier, shown by a steady increase in performance from the unprocessed dataset (Fig. 2E). In cross validation of the algorithm, this raw dataset is ranked 470th in specificity, compared to a 2247th in sensitivity; indicating that our ability to identify true negatives, or control patients, without pre-processing is higher than our ability to detect disease patients. This may be an inherent characteristic of this classifier, also influenced by the patient population. An unbalance in patient numbers in each class may be further investigated with up- or down-sampling methods.53
Somewhat surprisingly, data processed with a binning factor of 32 appears to perform favourably with regards to sensitivity (7th), specificity (6th), PPR (7th), and NPR (3rd). Whilst ‘heavy’ binning has the benefit of improved SNR in the dataset, there is also the likelihood of removing spectral information, with some spectral features broader than the 32 wavenumber spacing. The evidence for this can be seen when exploring the pre-processing permutations that contribute to the worst classification values, visualised as the steep drop in performance across Fig. 2. Of the 12 least efficient pre-processing models, a binning factor of 32 appears in every combination (Table 3), as well as wavelet denoising (with a filter length of 6), min–max normalisation and a baseline correction of either rubberband or polynomial corrections (with varying parameters). It is likely that the binning aspects of these permutations is reducing spectral resolution to a point where few features are visible, and thus classification is reduced. However, in the instance where a binning factor of 32 performs well, it is coupled with a standard SG filter (filter order of 5), but also with Amide I normalisation and a first derivative filter. The latter of these processes can resolve spectral features and may account for an improvement in classification, whilst amide I may be amplifying subtle differences between cancer and control patients.
| Rank | Overall Metric | Prediction Accuracy | Matthew's CC | Sensitivity | Specificity | PPV | NPV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3226141 | 4.179 ± 0.023 | 3226141 | 0.782 ± 0.002 | 3226144 | 0.465 ± 0.005 | 3226141 | 0.849 ± 0.002 | 3226141 | 0.618 ± 0.004 | 3226136 | 0.847 ± 0.003 | 3226134 | 0.615 ± 0.005 |
| 2 | 3232131 | 4.187 ± 0.020 | 3232131 | 0.783 ± 0.002 | 3226132 | 0.468 ± 0.004 | 3226132 | 0.849 ± 0.002 | 3226132 | 0.618 ± 0.004 | 3226135 | 0.847 ± 0.003 | 3226145 | 0.616 ± 0.006 |
| 3 | 3226134 | 4.195 ± 0.020 | 3226134 | 0.784 ± 0.002 | 3226131 | 0.470 ± 0.005 | 3226146 | 0.850 ± 0.002 | 3226146 | 0.619 ± 0.004 | 3226146 | 0.847 ± 0.003 | 3226144 | 0.617 ± 0.006 |
| 4 | 3226136 | 4.195 ± 0.021 | 3226145 | 0.784 ± 0.002 | 3226131 | 0.470 ± 0.005 | 3226136 | 0.850 ± 0.002 | 3226131 | 0.620 ± 0.004 | 3226133 | 0.848 ± 0.003 | 3226135 | 0.620 ± 0.005 |
| 5 | 3226145 | 4.195 ± 0.023 | 3226136 | 0.784 ± 0.002 | 3226145 | 0.470 ± 0.004 | 3226131 | 0.850 ± 0.002 | 3226145 | 0.621 ± 0.004 | 3226132 | 0.849 ± 0.003 | 3226131 | 0.621 ± 0.006 |
| 6 | 3226143 | 4.197 ± 0.020 | 3226133 | 0.785 ± 0.002 | 3226143 | 0.471 ± 0.004 | 3226143 | 0.851 ± 0.002 | 3226144 | 0.621 ± 0.004 | 3226141 | 0.849 ± 0.003 | 3226141 | 0.621 ± 0.006 |
| 7 | 3226133 | 4.198 ± 0.020 | 3226143 | 0.785 ± 0.002 | 3226146 | 0.471 ± 0.005 | 3226145 | 0.851 ± 0.002 | 3226136 | 0.621 ± 0.004 | 3226143 | 0.849 ± 0.003 | 3226132 | 0.621 ± 0.005 |
| 8 | 3226132 | 4.201 ± 0.019 | 3226142 | 0.786 ± 0.002 | 3226134 | 0.471 ± 0.004 | 3226133 | 0.851 ± 0.002 | 3226143 | 0.621 ± 0.004 | 3226131 | 0.849 ± 0.003 | 3226146 | 0.622 ± 0.005 |
| 9 | 3226146 | 4.202 ± 0.022 | 3226146 | 0.786 ± 0.002 | 3226135 | 0.472 ± 0.005 | 3226135 | 0.851 ± 0.002 | 3226134 | 0.624 ± 0.004 | 3226145 | 0.851 ± 0.003 | 3226136 | 0.622 ± 0.006 |
| 10 | 3226135 | 4.208 ± 0.021 | 3226135 | 0.786 ± 0.002 | 3226141 | 0.474 ± 0.005 | 3226134 | 0.851 ± 0.002 | 3226135 | 0.625 ± 0.004 | 3226142 | 0.853 ± 0.003 | 3226142 | 0.624 ± 0.006 |
| 11 | 3226142 | 4.214 ± 0.020 | 3226132 | 0.786 ± 0.002 | 3226133 | 0.476 ± 0.005 | 3226144 | 0.853 ± 0.002 | 3226133 | 0.626 ± 0.004 | 3226144 | 0.853 ± 0.003 | 3226143 | 0.626 ± 0.006 |
| 12 | 3226144 | 4.235 ± 0.023 | 3226144 | 0.789 ± 0.002 | 3226136 | 0.482 ± 0.005 | 3226142 | 0.854 ± 0.002 | 3226142 | 0.631 ± 0.005 | 3225134 | 0.854 ± 0.003 | 3226133 | 0.630 ± 0.006 |
To further explore the impact of pre-processing on classification of IR spectra, the un-processed dataset was used to split the ranked pre-processing permutations into two portions; a list of pre-processing protocols that improves classification performance compared to the raw data, and a list that reduced classification performance. The frequency that each processing option occurred to both increase or decrease the performance was recorded. Fig. 3A displays the how frequently each binning choice occurred, and how this impacted the overall classification with regards to the overall metric. It is clear to see that when an increase in diagnostic performance was seen overall, a binning factor of 2 or 4 was more common, whilst no binning made up a total of 22%. Increasing the binning factor was more influential in decreasing the overall classification in comparison to raw spectra, with a clear shift towards 16 and 32 seen.
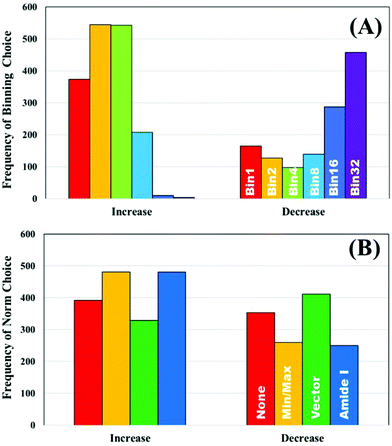 | ||
| Fig. 3 The frequency of pre-processing options that increase and decrease the classification performance of the unprocessed clinical dataset; (A) binning and (B) normalisation choices. | ||
Normalisation looks to have less influence on the overall metric, as the frequency of each of the options appears relatively equally. Min–max and amide I normalisation contribute to improved classification more commonly than no or vector normalisation, yet both only make up 57% of the overall selections (Fig. 3B). The parameters are all standard choices for use in pre-processing and have been used extensively in the literature. This could indicate that normalisation, in any capacity, is beneficial to diagnostic performance, regardless of the approach chosen. It is also of considerable interest that no normalisation performs well. Comparisons of smoothing and baseline correction, as well as their respective parameters are shown in ESI.† As some steps, such as rubberband baseline correction, have multiple parameters compared to others, these graphs are not shown to avoid confusion. For smoothing, the parameters have little effect on overall performance particularly in SG filtering, which appears equally across all the ranked permutations (ESI: Fig. S1†). Local polynomial smoothing has a more positive impact on classification, although again the relative parameters have little effect. The same is seen with baseline corrections that have tuneable parameters, namely rubberband and polynomial corrections (ESI: Fig. S2†).
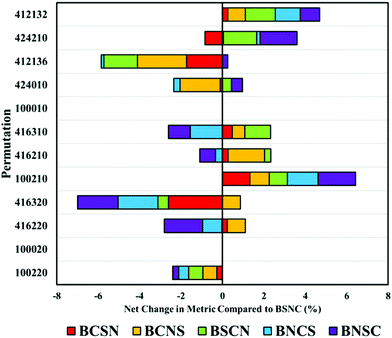
The order in which processing steps are implemented is explored in the top twelve processing combinations. By comparing each new arrangement of these processing steps against the default order described previously (binning (B), smoothing (S), normalisation (N) and baseline correction (C)), the impact of order can be seen. It is important to note that these comparisons are made from BSCN values generated separately from the previously described analyses. This can result in slight variations in performance metrics and can suggest unexpected variance in some combinations. A full breakdown of these comparisons can be found in ESI; Tables S1, 2 and Fig. S3–5.†
As expected, when only a single processing step is conducted, such as a first or second derivative (100020 and 100010), order has no impact on the overall performance. Some permutations are equivalent yet not identical; for example, BSNC, BNSC and BNSC for ‘100220’, and other combinations where only two variables are altered. The result of this is only small changes to overall performance values.
Beginning with the highest ranked combination (100220: no binning or smoothing, vector normalised and second derivative correction), it is clear that any alteration to the default order has a negative impact on the overall classification by an average of 5% (Fig. 4). Most significantly affected was the permutation ‘416320’, that appears sensitive to order of implementation. Other pre-processing protocols with smoothing steps also appear to be sensitive to order, suggesting that smoothing may be better implemented earlier in the processing order.
Altering the order can also have positive impacts, shown particularly in ‘100210’ representative of a vector normalisation and a first derivative filter. Each different arrangement improved the overall classification, illustrating that each processing protocol may require bespoke tuning with regards to order. With regards to the analysis of clinical data of biofluids, it remains clear that the top permutation of 100220 is well suited for this application, however, may lose diagnostic accuracy if re-ordered.
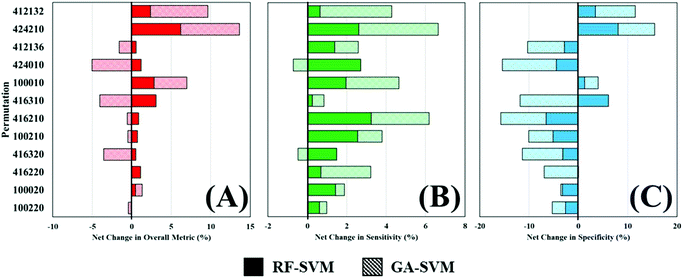
Throughout this study, a RF model has been used to classify patients as either cancer or non-cancer; the computational burden of such approach is low and allows rapid analysis of multiple datasets and was thus ideal for this application. However, there are a wide variety of machine learning algorithms available, which may be more appropriate for this study and yield better diagnostic results. To investigate this, two additional algorithms were explored as alternatives to a standalone RF classifier (Table 4). Comparing the overall metric, sensitivity and specificity of all three approaches shows that feature fed classification can improve overall performance. This is more clearly visualised in Fig. 5, where the percentage change in diagnostic performance (compared to RF) is illustrated. The pattern described by the overall metric indicates that for each of the permutations, RF-SVM improves classification to some degree, whereas GA-SVM has a more variable response (Fig. 5A). It is also clear that the top performing pre-processing combinations do not vary much between the three classifiers. This could indicate stability in the dataset due to pre-processing steps revealing an optimum level of diagnostic information.
| Permutation | Random forest | Random forest – SVM | Genetic algorithm – SVM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Overall | Sens | Spec | Overall | Sens | Spec | Overall | Sens | Spec | |
| 100220 | 5.319 | 0.930 | 0.892 | 5.315 | 0.936 | 0.869 | 5.300 | 0.934 | 0.868 |
| 100020 | 5.262 | 0.925 | 0.884 | 5.289 | 0.938 | 0.855 | 5.307 | 0.929 | 0.881 |
| 416220 | 5.215 | 0.923 | 0.868 | 5.273 | 0.929 | 0.868 | 5.215 | 0.946 | 0.807 |
| 416320 | 5.192 | 0.923 | 0.857 | 5.219 | 0.937 | 0.829 | 5.008 | 0.919 | 0.787 |
| 100210 | 5.172 | 0.924 | 0.847 | 5.209 | 0.947 | 0.803 | 5.147 | 0.935 | 0.806 |
| 416310 | 5.101 | 0.918 | 0.830 | 5.146 | 0.948 | 0.776 | 5.072 | 0.945 | 0.754 |
| 416210 | 5.122 | 0.924 | 0.824 | 5.279 | 0.927 | 0.874 | 4.915 | 0.930 | 0.727 |
| 100010 | 5.084 | 0.918 | 0.825 | 5.229 | 0.936 | 0.835 | 5.294 | 0.942 | 0.848 |
| 424210 | 5.023 | 0.913 | 0.811 | 5.083 | 0.937 | 0.775 | 4.770 | 0.906 | 0.723 |
| 424010 | 5.044 | 0.914 | 0.817 | 5.071 | 0.927 | 0.794 | 4.964 | 0.925 | 0.756 |
| 412132 | 5.009 | 0.913 | 0.805 | 5.320 | 0.937 | 0.870 | 5.380 | 0.950 | 0.864 |
| 412136 | 5.038 | 0.917 | 0.807 | 5.159 | 0.923 | 0.835 | 5.403 | 0.951 | 0.872 |
In contrast, RF-SVM and GA-SVM both dramatically increase the sensitivity of these pre-processed datasets, with only small decreases apparent (Fig. 5B). Sensitivity was found to be high in this clinical dataset using RF classification, tentatively associated with the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 imbalance of cancer to control patients. This may contribute to heightened sensitivity with feature fed classifiers, which should contain specific information for distinguishing cancer. Specificity on the other hand is more likely to be decreased when using these classifiers (Fig. 5C). Apart from a couple of improvements in performance, on the whole RF-SVM and GA-SVM reduce the specificity of the model. Again, this could be attributed to the fact that these approaches extract disease specific information from the dataset, and thus the capabilities of identifying true negatives, or control patients, is inhibited.
1 imbalance of cancer to control patients. This may contribute to heightened sensitivity with feature fed classifiers, which should contain specific information for distinguishing cancer. Specificity on the other hand is more likely to be decreased when using these classifiers (Fig. 5C). Apart from a couple of improvements in performance, on the whole RF-SVM and GA-SVM reduce the specificity of the model. Again, this could be attributed to the fact that these approaches extract disease specific information from the dataset, and thus the capabilities of identifying true negatives, or control patients, is inhibited.
Conclusions
For all metrics, it is evident that there are a number of highly favourable pre-processing permutations, a larger group of that have incremental improvements in classification, and a group of unfavourable pre-processing combinations. The overall metric is a good method of viewing all the statistical patterns in the data, and mimics the morphology of all performance curves. Variability between the validation and test sets is evident throughout, however this is expected due to the nature of predictions on unknown populations.With regards to the best pre-processing combination for discriminatory biofluid analysis, two clear permutations came out on top; a simple second order derivative filter, or a first derivative filter with a vector normalisation. Differentiation, of first or second order, has the benefit of removing baseline effects as well as revealing further spectral information by peak deconvolution.
Although no binning features highly in the top performing combinations, a binning factor of 4, also appears to be a beneficial step in pre-processing. This moderate binning factor has the benefit of dimension reduction, thus improving analysis times, as well as enhancing SNR across the spectral; all of which can have a positive influence on the diagnostic performance of the RF classifier. On the other hand, binning factors above four tend to have a detrimental effect on diagnostic performance. This approach may reduce the information contained in the spectrum and is consistent with the worst diagnostic performers. A normalisation step appears to be preferable, although of the approaches discussed in this study, none are clear frontrunners. The same can also be said for smoothing and baseline correction approaches, despite derivative and SG filters featuring prominently in the top twelve pre-processing permutations. The order in which pre-processing steps are implemented can have significant impact on overall classification. This could be dependent on specific combinations of processes, such as normalisation alongside derivative filters.
Whilst it is important to explore the range of classification algorithms available, it is important to first note the desired output of the study. In this given example, the diagnosis of brain cancer would require a high level of sensitivity, in order to ensure the false negative rate is low and no tumours are missed. The use of feature fed algorithms that have been trained on datasets with a higher proportion of positives, may provide this higher sensitivity. However, if sensitivity, or another metric is desirable, the choice of machine learning approach should be carefully considered.
Abbreviations
| ATR | Attenuated total reflectance |
| FTIR | Fourier-transform infrared |
| GA | Genetic algorithm |
| IR | Infrared; biofluid |
| MCC | Matthew's correlation coefficient |
| MIR | Mid-IR |
| NIR | Near infrared |
| NPV | Negative predictive value |
| PAC | Prediction accuracy |
| PCA | Principal component analysis |
| PLS | Partial least squares |
| PPV | Positive predictive value |
| RF | Random Forest |
| SG | Savitzky-golay |
| SNR | Signal-to-noise ratio |
Conflicts of interest
There are no conflicts to declare.References
- D. Naumann, H. Fabian and P. Lasch, FTIR spectroscopy of cells, tissues and body fluids, Biol. Biomed. Infrared Spectrosc., 2009, 2, 312 CAS.
- P. Lasch, Spectral pre-processing for biomedical vibrational spectroscopy and microspectroscopic imaging, Chemom. Intell. Lab. Syst., 2012, 117(Supplement C), 100–114 CrossRef CAS . Available from: http://www.sciencedirect.com/science/article/pii/S0169743912000561.
- M. J. Baker, J. Trevisan, P. Bassan, R. Bhargava, H. J. Butler and K. M. Dorling, et al., Using Fourier transform IR spectroscopy to analyze biological materials, Nat. Protoc., 2014, 9, 1771, DOI:10.1038/nprot.2014.110.
- L. Wang and B. Mizaikoff, Application of multivariate data-analysis techniques to biomedical diagnostics based on mid-infrared spectroscopy, Anal. Bioanal. Chem., 2008, 391(5), 1641–1654 CrossRef CAS PubMed.
- J. Trevisan, P. P. Angelov, P. L. Carmichael, A. D. Scott and F. L. Martin, Extracting biological information with computational analysis of Fourier-transform infrared (FTIR) biospectroscopy datasets: current practices to future perspectives, Analyst, 2012, 137(14), 3202–3215, 10.1039/C2AN16300D.
- K. Gajjar, J. Trevisan, G. Owens, P. J. Keating, N. J. Wood and H. F. Stringfellow, et al., Fourier-transform infrared spectroscopy coupled with a classification machine for the analysis of blood plasma or serum: a novel diagnostic approach for ovarian cancer, Analyst, 2013, 138(14), 3917–3926 RSC.
- G. Theophilou, K. M. G. Lima, P. L. Martin-Hirsch, H. F. Stringfellow and F. L. Martin, ATR-FTIR spectroscopy coupled with chemometric analysis discriminates normal, borderline and malignant ovarian tissue: classifying subtypes of human cancer, Analyst, 2016, 141(2), 585–594 RSC.
- B. Stuart, Infrared Spectroscopy. in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Inc., 2000, DOI:10.1002/0470011149.
- Z. Movasaghi, S. Rehman and D. I. ur Rehman, Fourier transform infrared (FTIR) spectroscopy of biological tissues, Appl. Spectrosc. Rev., 2008, 43(2), 134–179 CrossRef CAS.
- B. Singh, R. Gautam, S. Kumar, B. N. V. Kumar, U. Nongthomba and D. Nandi, et al., Application of vibrational microspectroscopy to biology and medicine, Curr. Sci., 2012, 102(2), 232–244 CAS.
- N. K. Afseth and A. Kohler, Extended multiplicative signal correction in vibrational spectroscopy, a tutorial, Chemom. Intell. Lab. Syst., 2012, 117, 92–99 CrossRef CAS.
- B. Mohlenhoff, M. Romeo, M. Diem and B. R. Wood, Mie-Type Scattering and Non-Beer-Lambert Absorption Behavior of Human Cells in Infrared Microspectroscopy, Biophys. J., 2005, 88(5), 3635–3640 CrossRef CAS PubMed . Available from: http://internal-pdf://157.156.226.121/RSC_(5).ris.
- P. Bassan, H. J. Byrne, F. Bonnier, J. Lee, P. Dumas and P. Gardner, Resonant Mie scattering in infrared spectroscopy of biological materials–understanding the “dispersion artefact”, Analyst, 2009, 134(8), 1586–1593 RSC.
- Å. Rinnan, Pre-processing in vibrational spectroscopy–when, why and how, Anal. Methods, 2014, 6(18), 7124–7129 RSC.
- J. Gerretzen, E. Szymańska, J. J. Jansen, J. Bart, H.-J. van Manen and E. R. van den Heuvel, et al., Simple and Effective Way for Data Preprocessing Selection Based on Design of Experiments, Anal. Chem., 2015, 87(24), 12096–12103 CrossRef CAS PubMed . Available from: http://internal-pdf://107.58.44.223/RSC_(6).ris.
- J. Engel, J. Gerretzen, E. Szymańska, J. J. Jansen, G. Downey and L. Blanchet, et al., Breaking with trends in pre-processing?, TrAC, Trends Anal. Chem., 2013, 50, 96–106 CrossRef CAS . Available from: http://internal-pdf://213.82.153.163/RSC_.bib.
- M. J. Baker, S. R. Hussain, L. Lovergne, V. Untereiner, C. Hughes and R. A. Lukaszewski, et al., Developing and understanding biofluid vibrational spectroscopy: a critical review, Chem. Soc. Rev., 2016, 45(7), 1803–1818 RSC.
- R. Aruga, Closure of analytical chemical data and multivariate classification, Talanta, 1998, 47(4), 1053–1061 CrossRef CAS PubMed . Available from: http://www.sciencedirect.com/science/article/pii/S003991409800126X.
- Å. Rinnan, F. van den Berg and S. B. Engelsen, Review of the most common pre-processing techniques for near-infrared spectra, TrAC, Trends Anal. Chem., 2009, 28(10), 1201–1222 CrossRef.
- P. Heraud, B. R. Wood, J. Beardall and D. McNaughton, Effects of pre-processing of Raman spectra on in vivo classification of nutrient status of microalgal cells, J. Chemom., 2006, 20(5), 193–197 CrossRef CAS.
- H. J. Butler, M. R. McAinsh, S. Adams and F. L. Martin, Application of vibrational spectroscopy techniques to non-destructively monitor plant health and development, Anal. Methods, 2015, 7(10), 4059–4070 RSC.
- J. Ollesch, S. L. Drees, H. M. Heise, T. Behrens, T. Brüning and K. Gerwert, FTIR spectroscopy of biofluids revisited: an automated approach to spectral biomarker identification, Analyst, 2013, 138(14), 4092–4102 RSC.
- F. Vogt and M. Tacke, Fast principal component analysis of large data sets, Chemom. Intell. Lab. Syst., 2001, 59(1), 1–18 CrossRef CAS . Available from: http://www.sciencedirect.com/science/article/pii/S0169743901001307.
- F. L. Martin, J. G. Kelly, V. Llabjani, P. L. Martin-Hirsch, I. I. Patel and J. Trevisan, et al., Distinguishing cell types or populations based on the computational analysis of their infrared spectra, Nat. Protoc., 2010, 5(11), 1748 CrossRef CAS PubMed.
- The International Society of Clinical Spectroscopy. Objective 5 | CLIRSPEC Network [Internet]. 2018 [cited 2018 Jul 17]. Available from: https://clirspec.org/uk-network/objectives/objective-5/.
- T. Bocklitz, A. Walter, K. Hartmann, P. Rösch and J. Popp, How to pre-process Raman spectra for reliable and stable models?, Anal. Chim. Acta, 2011, 704(1), 47–56 CrossRef CAS PubMed.
- R. M. Jarvis and R. Goodacre, Genetic algorithm optimization for pre-processing and variable selection of spectroscopic data, Bioinformatics, 2005, 21(7), 860–868, DOI:10.1093/bioinformatics/bti102.
- H. J. Byrne, P. Knief, M. E. Keating and F. Bonnier, Spectral pre and post processing for infrared and Raman spectroscopy of biological tissues and cells, Chem. Soc. Rev., 2016, 45(7), 1865–1878 RSC.
- O. Preisner, J. A. Lopes, R. Guiomar, J. Machado and J. C. Menezes, Fourier transform infrared (FT-IR) spectroscopy in bacteriology: towards a reference method for bacteria discrimination, Anal. Bioanal. Chem., 2007, 387(5), 1739–1748 CrossRef CAS PubMed . Available from: http://internal-pdf://222.249.218.220/RSC_ (4).ris.
- E. Ly, O. Piot, R. Wolthuis, A. Durlach, P. Bernard and M. Manfait, Combination of FTIR spectral imaging and chemometrics for tumour detection from paraffin-embedded biopsies, Analyst, 2008, 133(2), 197–205 RSC.
- P. Bassan, A. Sachdeva, A. Kohler, C. Hughes, A. Henderson and J. Boyle, et al., FTIR microscopy of biological cells and tissue: data analysis using resonant Mie scattering (RMieS) EMSC algorithm, Analyst, 2012, 137(6), 1370–1377 RSC.
- M. J. Baker, H. J. Byrne, J. Chalmers, P. Gardner, R. Goodacre and A. Henderson, et al., Clinical applications of infrared and Raman spectroscopy: state of play and future challenges, Analyst, 2018, 143(8), 1735–1757, 10.1039/C7AN01871A.
- E. Gray, H. J. Butler, R. Board, P. M. Brennan, A. J. Chalmers and T. Dawson, et al., Health economic evaluation of a serum-based blood test for brain tumour diagnosis: exploration of two clinical scenarios, BMJ Open, 2018, 8(5) DOI:10.1136/bmjopen-2017-017593.
- A. L. Mitchell, K. B. Gajjar, G. Theophilou, F. L. Martin and P. L. Martin-Hirsch, Vibrational spectroscopy of biofluids for disease screening or diagnosis: translation from the laboratory to a clinical setting, J. Biophotonics, 2014, 7(3–4), 153–165 CrossRef CAS PubMed.
- M. J. Baker, Photonic biofluid diagnostics, J. Biophotonics, 2014, 7(3–4), 151–152 CrossRef PubMed.
- M. Paraskevaidi, C. L. M. Morais, K. M. G. Lima, J. S. Snowden, J. A. Saxon and A. M. T. Richardson, et al., Differential diagnosis of Alzheimer's disease using spectrochemical analysis of blood, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(38), E7929–E7938 CrossRef CAS PubMed.
- R. Goodacre, M. J. Baker, D. Graham, Z. D. Schultz, M. Diem and M. P. Marques, et al., Biofluids and other techniques: general discussion, Faraday Discuss., 2016, 187, 575–601 RSC.
- B. H. Menze, W. Petrich and F. A. Hamprecht, Multivariate feature selection and hierarchical classification for infrared spectroscopy: serum-based detection of bovine spongiform encephalopathy, Anal. Bioanal. Chem., 2007, 387(5), 1801–1807, DOI:10.1007/s00216-006-1070-5.
- E. Scaglia, G. D. Sockalingum, J. Schmitt, C. Gobinet, N. Schneider and M. Manfait, et al., Noninvasive assessment of hepatic fibrosis in patients with chronic hepatitis C using serum Fourier transform infrared spectroscopy, Anal. Bioanal. Chem., 2011, 401(9), 2919 CrossRef CAS PubMed.
- J. Ollesch, M. Heinze, H. M. Heise, T. Behrens, T. Brüning and K. Gerwert, It's in your blood: spectral biomarker candidates for urinary bladder cancer from automated FTIR spectroscopy, J. Biophotonics, 2014, 7(3–4), 210–221 CrossRef CAS PubMed.
- F. Bonnier, H. Blasco, C. Wasselet, G. Brachet, R. Respaud and L. F. C. S. Carvalho, et al., Ultra-filtration of human serum for improved quantitative analysis of low molecular weight biomarkers using ATR-IR spectroscopy, Analyst, 2017, 142(8), 1285–1298 RSC.
- J. R. Hands, G. Clemens, R. Stables, K. Ashton, A. Brodbelt and C. Davis, et al., Brain tumour differentiation: rapid stratified serum diagnostics via attenuated total reflection Fourier-transform infrared spectroscopy, J. Neurooncol., 2016, 127(3), 463–472 CrossRef PubMed.
- B. R. Smith, K. M. Ashton, A. Brodbelt, T. Dawson, M. D. Jenkinson and N. T. Hunt, et al., Combining random forest and 2D correlation analysis to identify serum spectral signatures for neuro-oncology, Analyst, 2016, 141(12), 3668–3678 RSC.
- L. C. Lee, C.-Y. Liong and A. A. Jemain, A contemporary review on Data Preprocessing (DP) practice strategy in ATR-FTIR spectrum, Chemom. Intell. Lab. Syst., 2017, 163(Supplement C), 64–75 CrossRef CAS . Available from: http://www.sciencedirect.com/science/article/pii/S0169743916305500.
- B. R. Smith, M. J. Baker and D. S. Palmer, PRFFECT: A versatile tool for spectroscopists, Chemom. Intell. Lab. Syst., 2018, 172, 33–42 CrossRef CAS.
- B. K. Alsberg, A. M. Woodward, M. K. Winson, J. Rowland and D. B. Kell, Wavelet denoising of infrared spectra, Analyst, 1997, 122(7), 645–652 RSC.
- T. W. Randolph, Scale-based normalization of spectral data, Cancer Biomarkers, 2006, 2(3–4), 135–144 CAS.
- S. Wartewig, IR and Raman spectroscopy: fundamental processing, John Wiley & Sons, 2006 Search PubMed.
- C. Hughes, M. Brown, G. Clemens, A. Henderson, G. Monjardez and N. W. Clarke, et al., Assessing the challenges of Fourier transform infrared spectroscopic analysis of blood serum, J. Biophotonics, 2014, 7(3), 180–188 CrossRef CAS PubMed.
- H. J. Butler, L. Ashton, B. Bird, G. Cinque, K. Curtis and J. Dorney, et al., Using Raman spectroscopy to characterize biological materials, Nat. Protoc., 2016, 11(4), 664–687 CrossRef CAS PubMed.
- C. A. Lieber and A. Mahadevan-Jansen, Automated method for subtraction of fluorescence from biological Raman spectra, Appl. Spectrosc., 2003, 57(11), 1363–1367 CrossRef CAS PubMed.
- O. Devos, G. Downey and L. Duponchel, Simultaneous data pre-processing and SVM classification model selection based on a parallel genetic algorithm applied to spectroscopic data of olive oils, Food Chem., 2014, 148, 124–130 CrossRef CAS PubMed . Available from: http://www.sciencedirect.com/science/article/pii/S0308814613014520.
- V. Ganganwar, An overview of classification algorithms for imbalanced datasets, Int. J. Emerg. Technol. Adv. Eng., 2012, 2(4), 42–47 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8an01384e |
| This journal is © The Royal Society of Chemistry 2018 |