Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantitative local state of charge mapping by operando electrochemical fluorescence microscopy in porous electrodes†
Anton M.
Graf‡
 a,
Thomas
Cochard‡
a,
Thomas
Cochard‡
 a,
Kiana
Amini§
a,
Kiana
Amini§
 a,
Michael S.
Emanuel
a,
Michael S.
Emanuel
 a,
Shmuel M.
Rubinstein
a,
Shmuel M.
Rubinstein
 *b and
Michael J.
Aziz
*b and
Michael J.
Aziz
 *a
*a
aHarvard John A. Paulson School of Engineering and Applied Sciences, 29 Oxford St., Cambridge, MA02138, USA. E-mail: maziz@harvard.edu
bRacah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem, Israel
First published on 28th August 2024
Abstract
We introduce operando quantitative electrochemical fluorescence state of charge mapping (QEFSM), a non-invasive technique to study operating electrochemical systems along with a new design of optically transparent microfluidic redox flow cells compatible with the most demanding optical requirements. QEFSM allows quantitative mappings of the concentration of a particular oxidation state of a redox-active species within a porous electrode during its operation. In this study, we used confocal microscopy to map the fluorescence signal of the reduced form of 2,7-anthraquinone disulfonate (AQDS) in a set of multistep-chronoamperometry experiments. Calibrating these images and incorporating an analytical model of quinhydrone heterodimer formation with no free parameters, and accounting for the emission of each species involved, we determined the local molecular concentration and the state of charge (SOC) fields within a commercial porous electrode during operation. With this method, electrochemical conversion and species advection, reaction and diffusion can be monitored at heretofore unprecedented transverse and axial resolution (1 μm and 25 μm, respectively) at frame rates of 0.5 Hz, opening new routes to understanding local electrochemical processes in porous electrodes. We observed pore-scale SOC inhomogeneities appearing when the fraction of electroactive species converted in a single pass through the electrode becomes large.
1. Introduction
To respond to the growing concerns over environmental consequences of the consumption of fossil fuels, our economy needs to rapidly undergo a transition to sustainable energy sources and technologies. Electrochemical devices and related systems are playing an increasing part in this energy transition. Electrochemical flow cells operate, for example, in redox flow batteries, fuel cells, electrolyzers and desalinators. Most such systems employ high surface area porous electrodes as the central neighborhood for electrochemical conversion, specifically to facilitate mass transport and increase reaction rates in 3D architectures.Whereas considerable amounts of research have been conducted on macroscopic reaction-flow properties1–3 and the microscopic properties such as surface functionalization and nano pores,4–6 more work is required to understand the mesoscopic length scales in between, e.g. the concentrations, transport, and conversion of chemical species at scales from fibers to microstructures, which could make electrochemical flow devices more viable. Conventional electrochemical techniques, such as voltammetry, typically lack spatial resolution.7 Voltage probes provide only sparse sample sets and are often invasive. Although, from voltage probes, losses can be attributed to processes occurring within porous electrodes,8 the understanding of how these losses depend on the electrode microstructure, i.e. pore size or fiber diameter and their respective distributions and orientations, is still missing. Other in situ analytical methods, e.g. UV/Vis spectrophotometry,9 nuclear magnetic resonance spectroscopy (NMR),10,11 electron paramagnetic resonance spectroscopy (EPR),12 or X-ray imaging13,14 are under ongoing development but have not yet yielded data spatially resolved inside porous electrodes over mesoscopic length-scales.
A promising technique to overcome the current limitations and gain further insight into geometric effects of electrochemical conversion inside porous electrodes is offered by coupling in situ fluorescence microscopy with electrochemical monitoring. A variety of studies from the last decades utilized fluorescence microscopy coupled to electrochemistry15 have been performed mainly to study electrochemical processes on planar electrodes in 2D,16–20 defects21,22 or for application in biomolecules.23–28
Recently, the remarkable ability of confocal microscopes to quantify optical information from three spatial dimensions has been harnessed in electrochemical reactions. This advancement has enhanced the interpretation of variations in the adsorption patterns of organic agents, informed by surface morphology, and enabled the quantification of pH gradients in proximity to the electrode surface.21,29,30
Electrochemical reaction layers and microscopic heterogeneities on microelectrodes have been imaged in static electrochemical devices with a confocal fluorescence microscope.31 Confocal fluorescence microscopy has also been used to map the local pH in the electrolyte near an operating gas diffusion electrode during electrochemical CO2 reduction showcasing the effect of the micro-scale morphology on mass transport and hence the local electrochemical performance.32,33
Recently, 2D widefield fluorescence microscopy revealed substantial heterogeneities in the state of charge and electrolyte velocity field within commercial electrodes operating inside a flow cell.34 The scale of these heterogeneities exceeded the characteristic pore size (∼50 μm) by more than an order of magnitude, reaching length scales relevant to commercial flow batteries. This work called into question the validity of assuming a homogeneous Darcy-like flow and the use of Newman's porous electrode model in practical electrochemical devices at these scales.35 The real-time investigation of electrochemical conversion was performed with 2,7-anthraquinone disulfonate (AQDS) and its corresponding hydroquinone, H2AQDS, which results from a two-electron, two proton reduction and is accompanied by a significant change in its fluorescence signal.
The study of anthraquinone derivatives in flow batteries is also of great interest due to their synthetically controllable properties,36–38 potential low cost,39–41 earth-abundant building blocks and chemically mild operation.42 Their realized lab-scale power densities, however, remain below those of vanadium flow batteries43 and, in some cases, their internal resistance has been shown to be due, in large part, to the losses within the porous electrode imbibed with flowing aqueous organic electrolyte.8 Such power losses are inherent obstacles in most electrochemical flow devices, underscoring the demand for the development of novel techniques to comprehend these losses across diverse length scales through accurate quantification of electrochemical conversion and local transport coefficients. Given that many organic-based, redox-active systems are optically active, they are amenable to analysis using operando confocal microscopy. Achieving spatial resolution in the quantification of electrochemical conversion provides a valuable opportunity to gain deeper insight into the nature and extent of these power losses.
Here, we introduce a non-invasive operando technique, namely quantitative electrochemical fluorescence state of charge mapping (QEFSM), to precisely quantify electrochemical conversion of redox active molecules at the single-digit micron scale and over time within electrochemical flow systems.
We transcended previous techniques by employing confocal fluorescence microscopy inside an operating porous electrode during the reduction of AQDS to quantify and map the local state of charge (SOC). This entails quantitatively differentiating the signal contributions originating from the various molecular species present. The incorporation of a confocal microscope enhances previous studies by providing depth-focused imaging which, in turn, enables accurate measurement of fluorescence intensity within a specified volume; this is crucial in relating the local species concentrations to spatial features of the electrode. Along with the technique we present a new microfluidic flow cell compatible with the optical requirements of the confocal microscope. Except for the electrode, current collector and the membrane, the flow cell is fully transparent, enabling excellent optical access to the pore space. The high porosity of the electrode allows access to the volume inside except for the regions where light is blocked by electrode fibers. Shadows and artifacts due to opaque fibers were removed throughout calibration and post-processing of the images. The SOC is evaluated locally at these optically accessible positions inside the porous electrode.
We further demonstrate that the dimerization of one AQDS molecule with one H2AQDS molecule to form quinhydrone (QH) affects the fluorescence intensity. While this can be quantified by our visualization technique, it cannot be discerned with the electrochemical measurements of the cell alone. The SOC is estimated by iteratively calibrating observed image intensities using a model with no free parameters, which includes a reversible 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (AQDS
1 (AQDS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2AQDS) binding dimer, which is further supported by prior experimental work.9 Whereas the heterodimer can influence the intensity, it should not impact the detected current or the accessible storage capacity in AQDS solutions at concentrations used in this study, as over 90% of theoretical capacity has been demonstrated in 1 M solutions.44 By employing a calibration technique that incorporates dimer formation and enables the separation of distinct signal contributions of AQDS, H2AQDS and dimer, we develop a consistent quantification of fluorescence, the local optical environment, and all three concentrations.
H2AQDS) binding dimer, which is further supported by prior experimental work.9 Whereas the heterodimer can influence the intensity, it should not impact the detected current or the accessible storage capacity in AQDS solutions at concentrations used in this study, as over 90% of theoretical capacity has been demonstrated in 1 M solutions.44 By employing a calibration technique that incorporates dimer formation and enables the separation of distinct signal contributions of AQDS, H2AQDS and dimer, we develop a consistent quantification of fluorescence, the local optical environment, and all three concentrations.
Under the operating conditions considered in this study, the spatially averaged and dimer-corrected image intensity monotonically increases with (and is approximately linear in) the total current. The resulting local SOC maps offer a robust tool for quantifying and evaluating local variations in electrochemical conversion and transport within complex porous electrodes. Our findings contrast with the simple assumption of a constant gradient along the macroscopic flow direction. Such insights are valuable for future research evaluating the domain of suitability of such assumptions. We expect QEFSM to not only improve the understanding of electrochemical conversion and transport of other redox-active species, but also to greatly aid in the understanding of porous electrodes and their microstructures as active materials in electrochemical devices.
2. Working principles and experimental setup of operando QEFSM
2.1 Design and fabrication of transparent microfluidic flow cells
Our microfluidic electrochemical cell design, shown in Fig. 1, enables the synchronous study of electrochemical reaction with a conventional potentiostat and the spatially resolved fluorescence intensity. The non-invasive operando study of optically active electrolytes via confocal fluorescence microscopy necessitates the design of an electrochemical cell that is compatible with optical imaging. The cell we introduce in this study is optically transparent and permits optical access to the entire electrode, as shown in Fig. 1(A) and (B). Two half cells are fabricated from PDMS (Polydimethylsiloxane) with acrylic backing. To visualize the inside of the electrode, a relatively long working distance (<11 mm), high-resolution microscope objective used.The flow cell is designed for small working electrodes (3 × 6 mm2) allowing an effective study of the entire electrode under high magnification (10×). A single flow channel transports the electrolyte into, through, and out of the electrochemical cell, as shown in Fig. 1(A) and (B). The cell was constructed of two half cells, an anode and a cathode, each embedded in a thin, optically transparent PDMS slab (see ESI,† Section 1 for details). The anode side includes 1 × 1 mm2 channels in a serpentine geometry supplying the Pt-coated carbon electrode with humidified hydrogen gas. This electrode is much larger (10 × 20 mm2) than the one on the cathode side, ensuring that the cathodic reaction on the working electrode remains rate limiting. Hydrogen flow was controlled via a manual pressure adjusted to ensure that a bubble emerged approximately every two seconds from a plastic tube at the cell exit, which was immersed in water. Hydrogen underwent oxidation on a Pt-coated carbon electrode, with resulting protons crossing the membrane for net charge neutrality.
The cathode or working electrode side, the PDMS contained a 1.0 × 0.5 mm2 flow channel that supplied the porous electrode with electrolyte as shown in Fig. 1(A). The aqueous electrolyte on the cathode side consisted of 10, 20, 30 and 40 mM of AQDS in 1 M sulfuric acid. The acid served as a supporting electrolyte whose protons were involved in the proton-coupled electron transfer in the AQDS reduction reaction (see Section 2.2). A syringe pump was used to drive the electrolyte flow at constant flow rate. The superficial flow velocity, defined as the ratio of the volumetric flow rate Q to the nominal cross-sectional area A of the electrode by the formula us = Q/A and without correcting for the porosity or the compression of the electrode, was 2.3 mm s−1. A Reynolds number of ∼14 indicates laminar flow, suggesting steady-state conditions with no expected time-dependent variations in the flow. A commercial AvCarb MGL 190 carbon paper of nominal thickness 190 μm was used as the working electrode. This electrode has a disordered fiber microstructure held together by a binder material, as shown in Fig. 1(C). The electrode was baked for 24 h at 400 °C to increase its hydrophilicity.2 The proton-conducting separator (Nafion 212) was soaked in 1 M sulfuric acid prior to the experiments. The PDMS half cells, electrodes, and membrane were compressed by transparent acrylic endplates and screws, providing an excellent seal that obviates the use of gaskets, as shown in Fig. 1(B).
Experimentally, we showcased the capabilities of QEFSM utilizing the AQDS/H2AQDS redox system as the optically active electrolyte. In all experiments, the electrochemical cell was placed on top of an inverted spinning disk confocal microscope with a 10 × 0.3 NA air objective and 50 μm pinhole size. Transverse (x–y) and axial (z) resolution are 1 μm and 25 μm, respectively. The short depth of field is one of the major advantages of QEFSM compared to previous studies that used fluorescence microscopy as it allows us to determine a precise volume for each frame. In this study, images of fluorescence intensity were captured simultaneously over a 1.2 × 1.2 mm2 field of view close to the center of the working electrode. The transparent PDMS casing allowed the study of an arbitrary position inside the electrode as well as an arbitrary depth from the surface toward the opaque membrane as the focal plane is adjusted. For orientation inside the electrode, we located the interface between PDMS and electrolyte and moved toward the membrane to a depth of 50 μm. The electrochemistry was controlled and measured by a potentiostat (see ESI,† 1 and 2). We acquired dynamical fluorescence image stacks at 2 seconds exposure time spanning over pre-defined volumes within the porous electrode while varying the applied potential. While it is possible to significantly reduce the exposure time, a deliberate choice was made to employ a longer exposure time in this study in order to enhance signal resolution and generate high-quality maps.
2.2 Properties of the optically active AQDS electrolyte
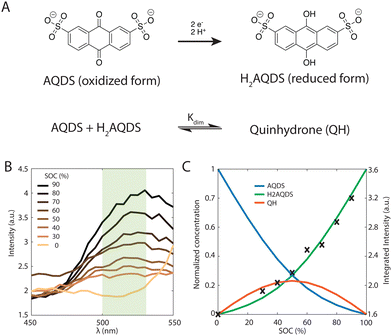
The redox-active species AQDS in its various oxidation states, shown in Fig. 2(A), is a suitable molecular system to study electrochemical conversion inside porous electrodes.9,34 We distinguish between the oxidized and reduced species (AQDS and H2AQDS, respectively) by imaging at an emission band dominated by H2AQDS as shown in Fig. 2(B). Calibration was performed with samples of known concentrations of AQDS, the stable form in equilibrium with air, and then reducing it by controlled amounts to obtain electrolyte emissions spectra at various proportions between the species.We obtained the emission spectra of the 40 mM AQDS electrolyte at multiple SOCs using a plate reader after different amounts of electrochemical reduction aiding the quantitative correlation between state of charge (SOC) and fluorescence intensity, as shown in Fig. 2(B) and (C). Electrolytes were prepared from a pure and degassed 40 mM AQDS stock solution. The electrolytes were charged in a conventional bench scale flow battery vs. V3+/V4+ across a Nafion 212 membrane to obtain a series of different SOCs (0, 30, 40, 50, 60, 70, 80 and 90%). A 405 nm wavelength laser was used to excite the optically active molecules in the system. H2AQDS exhibits an absorption peak proportional to its concentration.9 The emission spectra of the AQDS/H2AQDS system at various SOC, shown in Fig. 2(B), showed a broad peak whose height increases with SOC. This broad emission peak was captured by the microscope's imaging sensor with a green bandpass filter with a range between 500 and 525 nm and integrated in the microscopy studies described below. Contrary to initial expectations,34 the integrated raw fluorescence intensity measured by the microscope as a function of SOC shows a nonlinear increase, as illustrated in Fig. 2(C).
If the only contribution to the SOC were from H2AQDS, we would expect the fluorescence intensity to be linearly increasing with SOC. Thus, the observed nonlinear response indicates that competitive photophysical processes due to chemical electrolyte interactions, such as self-absorption, fluorescence quenching, molecular decomposition or electrolyte interactions, should be considered. We eliminated electrolyte decomposition as an explanation because the capacity fade rate of the AQDS/H2AQDS systems lies around 0.08%/day and we were not reusing any of the electrolyte from day to day.45 Although we were not able to exclude other mechanisms with certainty, the dynamical formation of quinhydrone dimers (QH), as shown in Fig. 2(A) provides a logical and quantitative explanation of the nonlinearity measured in fluorescence intensity. In previous studies9 measuring the absorption spectra for these species, it was found that when both are present, one molecule of AQDS and one molecule of H2AQDS can reversibly bind to form a quinhydrone heterodimer (QH) as shown in Fig. 2(A). A value of 80 M−1 was deduced for the equilibrium constant Kdim of the association reaction.
We propose that the dimer species does not contribute significantly to the detected fluorescence and therefore reduces the measured intensity by lowering the concentration of H2AQDS, the only significantly fluorescent species in the mixture. Based on this hypothesis we are able to construct an effective 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (AQDS
1 (AQDS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2AQDS) binding dimer model that quantitatively corrects the SOC by the amount of reduced electrolyte that became invisible due to dynamic dimer incorporation (see ESI,† Section 4). During the electrochemical reduction of AQDS, some of the charge resides in the H2AQDS and some in the dimer. Thus, the dimer should be regarded as another reduced species. If [QH] represents the concentration of the QH, then the state of charge (SOC) may be defined as
H2AQDS) binding dimer model that quantitatively corrects the SOC by the amount of reduced electrolyte that became invisible due to dynamic dimer incorporation (see ESI,† Section 4). During the electrochemical reduction of AQDS, some of the charge resides in the H2AQDS and some in the dimer. Thus, the dimer should be regarded as another reduced species. If [QH] represents the concentration of the QH, then the state of charge (SOC) may be defined as
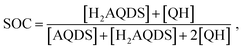 | (2.1) |
The results shown in Fig. 2(C) demonstrate that overlaying the experimental intensity data with the theoretical normalized H2AQDS concentrations predicted from the dimer model reproduces this nonlinear increase closely. Hence, we concluded that the fluorescence intensity is proportional to [H2AQDS] and [QH] does not significantly contribute to the total intensity of the redox-system. Whereas the dimer formation lowers the measured fluorescence intensity, it participates in the current extracted. For the given dimerization mechanism, the ratio of dimer formed to [AQDS]0 increases as [AQDS]0 grows, as shown for all experimentally relevant cases in ESI,† 4. Because of the thermodynamic equilibrium of the equation shown in Fig. 2(A), the dimer fraction as a function of the SOC has the functional form of an inverted parabola. The dimer concentration initially grows and is the largest at 50% SOC when the concentrations of AQDS and H2AQDS are equal, beyond which it decreases to 0 M at 100% SOC, as shown in Fig. 2(C). In experimental data with sufficiently high [AQDS]0, such as the presented case of 40 mM, the concentration of QH can surpass that of H2AQDS indicating a prevalence of charged species in the form of dimer rather than H2AQDS, which affects the fluorescence intensity significantly. As a consequence, the intensity calibration vs. SOC, which must account for the amount of dimer that contributes to the SOC but only weakly to the emitted intensity, varies with [AQDS]0. This calibration qualifies the AQDS/H2AQDS system as a suitable system to exactly quantify SOC maps through QEFSM.
3. Results and discussion
3.1 Multi-step chronoamperometry studies with operando confocal fluorescence microscopy
With electrolyte flowing steadily, we imposed stepped cell voltages and measured the resulting current according to a multi-step chronoamperometry (MSC) protocol (vide infra). Simultaneously, we measured the varying fluorescence intensity field with the optical apparatus of a confocal fluorescence microscope, from which we obtained the concentration fields. In a flow cell, the temporal change of the concentration field Cj of species j has contributions from advection Aj, diffusion Dj, and electromigration εj in addition to the electrochemical source Sj, which is proportional to the faradaic component of the electrical current.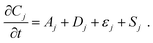 | (3.1) |
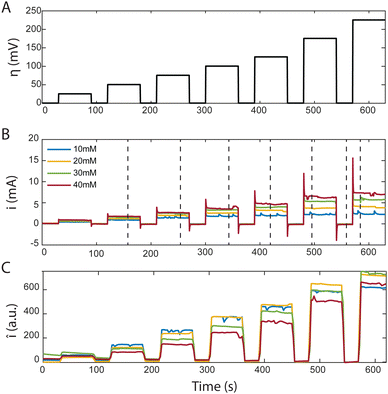
In the MSC experiment each potential step was held constant for 60 seconds to obtain a stable steady-state-current as shown in Fig. 3(A). We measured the current i as we increased the overpotential η successively from 25 to 225 mV in increments of 25 or 50 mV, which increased the electrochemical driving force that governs the reaction rate, as shown in Fig. 3(B). To prevent hydrogen evolution, we refrained from using higher overpotentials. Before each change in the step-potential we set the cell potential to open-circuit voltage (OCV), the potential at which no current is passing, for 30 seconds maintaining the flow of degassed electrolyte.
The current spike following each change in cell potential was caused by capacitive current. This event was followed by a steady-state faradaic current that was monitored for the remainder of each potential step. The faradaic current is governed by the reaction rate at the electrode. Despite maintaining a steady voltage, we observed small fluctuations in the current over time, which are captured in Fig. 3(B). These fluctuations can be caused by the competing reaction of hydrogen evolution from the electrolyte. For increasing values of [AQDS]0, higher steady-state currents were observed because greater reactant concentrations were available to become reduced in each time interval.
The confocal microscope simultaneously produced raw intensity maps Iraw for each image. To investigate the relationship between the current and the fluorescence intensity we first quantified the average fluorescence of each image (sampling time interval Δt = 2.5 s). Our initial analysis entailed averaging Iraw, across the entire image, yielding Īraw. For better visualization in Fig. 3(C) we subtracted the background fluorescence image captured at OCV prior to the spatial averaging of the intensity in each individual frame. The resulting mean background-corrected fluorescence intensity Î follows the current response closely for all potentials applied. Interestingly, the small variations in current were relatively well captured by the average fluorescence intensity Î. Any negative intensity fluctuation was correlated to a positive current fluctuation. This supports the hypothesis that hydrogen evolution competes with AQDS reduction. Small hydrogen bubbles, nucleating in pockets of presumably inhibited flow, transiently cross the image, momentarily decreasing average intensity, despite contributing to the overall detected current through water reduction to hydrogen. This behavior, depicted in Fig. 3 comparing (B) and (C), exhibits minor variations relative to their average values at each chronoamperometry step.
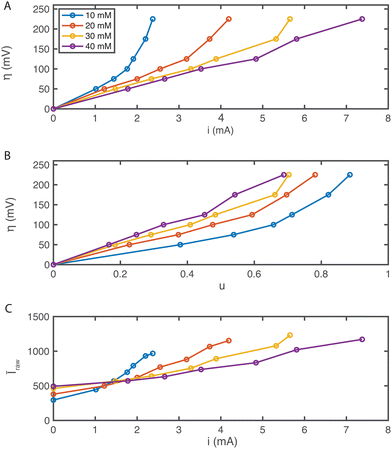
The current, sampled in steady state after each potential step, indicated by the dashed lines in Fig. 3(B) and reported in the polarization curves in Fig. 4(A), increased linearly with overpotential for the first ∼100 mV. Superlinear behavior, apparent at higher potentials, is indicative of mass transport limitations. The overall utilization of electrolyte, u, defined as the faradaic charge passed to the electrolyte on a single pass through the device divided by its theoretical maximum value set by the charge capacity of the molecules, decreased for increasing [AQDS]0, as shown in Fig. 4(B). When the electrolyte at the inlet is fully oxidized, as it always is in work reported here, the utilization can be expressed analytically in terms of the total current J, the volumetric flow rate Q, the concentration of species available for reduction in the entering electrolyte given by [AQDS]0, Faraday's constant F and the number of transferred charges per molecule n:
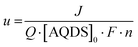 | (3.2) |
3.2 Local SOC and concentration mapping
| Pri = α[AQDS]ri + β[H2AQDS]ri + γ[QH]ri + δ | (3.3) |
| Iri = FiPri | (3.4) |
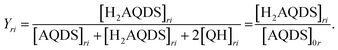 | (3.5) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , across the image cannot be solely attributed to a straightforward multiplicative effect on each pixel. Instead, specific regions where the SOC appears less sensitive to variations in overpotential can be identified. These areas have a lower contribution to the overall electrochemical conversion process, highlighting the opportunity for a better understanding of their mass transport characteristics in future studies.
, across the image cannot be solely attributed to a straightforward multiplicative effect on each pixel. Instead, specific regions where the SOC appears less sensitive to variations in overpotential can be identified. These areas have a lower contribution to the overall electrochemical conversion process, highlighting the opportunity for a better understanding of their mass transport characteristics in future studies.
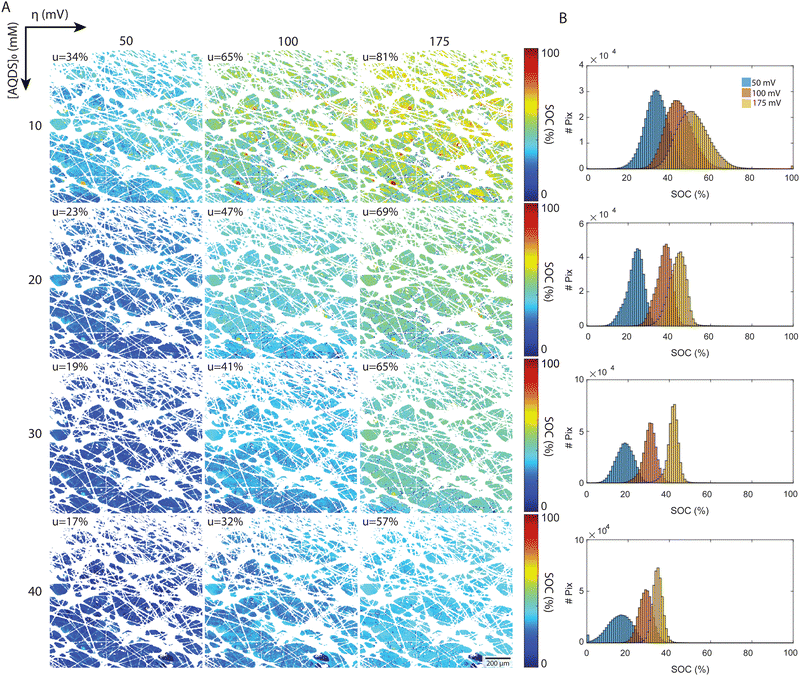
The local SOC maps of the 1.2 × 1.2 mm2 field reveal a field of increasing SOC, transitioning from the lower left to the upper right of each image. Given that the optical factor Fi corrects for spatial variations in emitted and detected light, we believe that this trend represents real physical processes and suggests that Darcy flow is an inadequate description of flow at these length scales. The 2D SOC maps at the highest utilization show pronounced local variation at length-scales from the fiber diameter to the characteristic pore size. These are the length scales where reactant depletion should be most severe. That this pattern is not apparent at lower utilizations might be related to the fact that we are working with integrated intensity through a slab of roughly 25 μm in the direction of the optical path. Large regions exhibiting uniform SOC may indicate low electrochemical conversion, suggesting the possibility of low electrode and flow path efficacy in the region.
A more detailed quantitative look is reported in the histograms, which depict the distribution of pixels by their SOC values. All experimental distributions resemble normal or skewed distributions, as shown in Fig. 5(B). In the low concentration experiments ([AQDS]0 = 10 mM), the histograms exhibit broader distributions than in the other cases. For [AQDS]0 = 30 and 40 mM, histograms show that the SOC distributions become narrower as overpotential and utilization increase. At these higher concentrations, the SOC histograms have a distinct peak, indicating a mostly uniform SOC across the entire image.
For comparison, in the simple picture with a constant gradient in SOC along x, the macroscopic flow direction, the expected SOC histograms result in rectangular distributions centered at ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) and a width given by uΔx/L, where Δx is the width of the image and L is the length of the entire electrode in x. For our setup with Δx = 1.2 mm and L = 6 mm, those rectangular distributions would have a width of 0.2u SOC values for each histogram (see ESI,† 6 for comparison). The histograms derived from the experiments are typically narrower than this. Intriguingly, for the specimen with the highest utilization, [AQDS]0 = 10 mM, under conditions where mass-transport limitations become apparent (Fig. 4(A)), the width of the SOC distributions from experiment exceeds the width of the hypothetical rectangular distributions.
and a width given by uΔx/L, where Δx is the width of the image and L is the length of the entire electrode in x. For our setup with Δx = 1.2 mm and L = 6 mm, those rectangular distributions would have a width of 0.2u SOC values for each histogram (see ESI,† 6 for comparison). The histograms derived from the experiments are typically narrower than this. Intriguingly, for the specimen with the highest utilization, [AQDS]0 = 10 mM, under conditions where mass-transport limitations become apparent (Fig. 4(A)), the width of the SOC distributions from experiment exceeds the width of the hypothetical rectangular distributions.
Remarkably, combined analysis of the experimental histograms and SOC maps reveals that under varying conditions, we can observe either heightened local heterogeneity or enhanced uniformity. While these deviations might average out across larger areas, they are significant at the scale of the displayed 1.2 × 1.2 mm image frame. Such nuances might impact mesoscopic transport in electrochemical flow devices operating under practical conditions. Because this particular experiment collected the fluorescence from only a limited depth range of the electrode – the focal plane is set at z = 50 μm within the 190 μm thick electrode, with the z = 190 μm coordinate denoting the interface of the electrode with the membrane – we cannot determine the average state of charge throughout the entire thickness. We expect more comprehensive investigations to provide further insight, guide model development and, ultimately, permit the design of higher-performance electrodes. These investigations might encompass imaging across the entire x–y plane of the electrode, and at varied z-depths, and to examine transient, in addition to steady-state, behavior. For an example of visualization of transient concentration field evolution, dynamical videos are shown in the ESI,† 7.
Utilizing the SOC maps, we can infer the concentration fields of other species involved in the electrochemical process, specifically AQDS, H2AQDS, and QH. Fig. 6 illustrates the average concentrations of these species within the imaging frame as functions of the average SOC, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) . These plots reflect the close alignment with the average concentrations predicted by the dimer model discussed in Section 2.2 and ESI,† 3. This reaffirms the pronounced influence of dimer formation at elevated concentrations. Such influence introduces non-linearities in the concentration profiles which, in turn, have implications for the measured intensities, emphasizing the necessity for precise calibration.
. These plots reflect the close alignment with the average concentrations predicted by the dimer model discussed in Section 2.2 and ESI,† 3. This reaffirms the pronounced influence of dimer formation at elevated concentrations. Such influence introduces non-linearities in the concentration profiles which, in turn, have implications for the measured intensities, emphasizing the necessity for precise calibration.
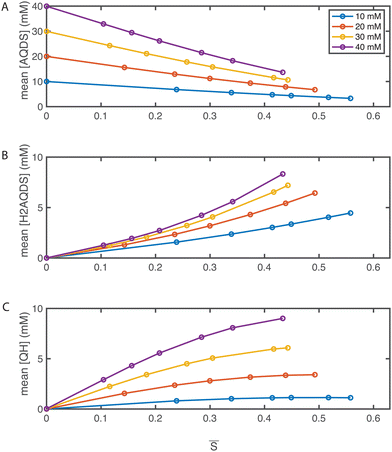 | ||
Fig. 6 Operando concentration profiles. Mean concentrations of (A) AQDS; (B) H2AQDS; (C) QH as functions of the mean SOC ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) within in the field of view. within in the field of view. | ||
The formation of dimers has previously been discussed as having a limiting impact on accessible capacity, even at low electrolyte concentrations.46,47 This is in contradiction with other findings, where over 90% of theoretical capacity has been accessed in a flow battery utilizing 1 M AQDS concentration.8 In the present study, we reached electrolyte utilizations of 70% or more at all concentrations, and 88% utilization at 10 mM despite dimer formation at concentrations shown in Fig. 6(C). As dimerization is concentration-dependent, QEFSM at higher concentrations of active material might reveal dimer effects on electrochemical behavior.
In this first demonstration of QEFSM, we show the potential this technique holds for mapping the concentrations of electrochemically active species within complex architectures, such as in electrochemical flow cell porous electrodes. This approach allows for in-depth examination of these systems across a range of operating conditions, offering valuable insights into intricate transport phenomena. Although not demonstrated here, by obtaining two-dimensional (2D) SOC maps at different depths within the porous electrode, we have the potential to reconstruct three-dimensional (3D) volumes encompassing local SOC and concentration fields.
As research in this domain becomes more rigorous, it will require more precise quantification, such as that provided by QEFSM, of local transport behavior and a deeper understanding of structure–function relationships from the pore-scale to the macro-scale. Such advancements are poised to enhance the design and performance of the forthcoming generation of electrochemical devices.
4. Conclusions
In this study, we have demonstrated a non-invasive operando technique for the precise mapping of concentration fields within a functioning porous electrode. By coupling electrochemistry and confocal microscopy inside the device we are able to derive spatially and temporally resolved SOC maps in well-defined volumes inside the electrode architecture. Transverse and axial resolution of 1 and 25 μm, respectively, were achieved.We developed an optically transparent flow cell that facilitates the investigation of the entire electrode and is compatible with the confocal microscope hardware. The versatility of the setup makes it suitable for a wide range of porous architectures and optically active electrolytes. We demonstrated an effective image processing technique to address challenges associated with the presence of opaque components, including fibers at various z-heights and heterophase artifacts. Because the detected signal comprises distinct contributions from reactants, products, other interacting species, and background, we developed a calibration technique that enables quantification of concentration fields for all relevant molecular species within the system: the oxidized species [AQDS], the reduced species [H2AQDS], and the dynamically formed heterodimer [QH]. Consideration of individual species concentration fields yields quantitative local SOC maps.
We have demonstrated that 2D mapping techniques offer a powerful method for characterizing local heterogeneity in concentration and SOC fields over mesoscopic areas inside of porous electrodes. This technique should permit experimental testing of multiphysics transport models from sub-pore scale to the scale of the field of view, which may be tiled to study larger areas. Within the limited 1.2 × 1.2 mm2 field of view of these experiments, we observed the average gradient in the SOC field not parallel to the nominal flow direction, suggesting that Darcy flow is too simple a model for this length scale. We identified more uniform SOC fields at high concentrations and low utilization and broad SOC distributions for the lowest concentration with – particularly at the highest utilization – significant local heterogeneities at length scales from the fiber diameter to the characteristic pore size.
QEFSM is a valuable method to quantitively study porous electrodes as active materials during electrochemical transformations. It should facilitate the understanding of local voltage losses and the development of structure–function relationships for various electrode architectures. It may lead to electrochemical systems with improved performance and a new generation of electrode designs.
Author contributions
AMG, TC, KA, SMR and MJA designed and conceptualized the project. MJA and SMR supervised the project. TC and AMG developed cell prototypes. TC designed and fabricated the final version of the transparent PDMS electrochemical flow cell. AMG performed the operando confocal experiments and acquired the data. AMG and KA conducted ex situ and plate reader experiments and acquired the data. AMG, TC, MSE and KA developed and implemented the dimer model. TC performed initial image processing for SOC mapping. MSE developed the pixel-by-pixel calibration method and performed the final image processing. TC, MSE and AMG made the figures. AMG wrote the original draft of the manuscript. AMG, TC, KA, MSE, SMR and MJA revised the manuscript.Data availability
Data for this article, including micrograph images and Python source code for data analysis, are available at qefsm at https://doi.org/10.5281/zenodo.11505668.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by U.S. Department of Energy, Office of Science, through grant DE-SC0020170. K.A. was supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC) Postdoctoral Fellowship (PDF) program [application number PDF – 557232 – 2021]. We thank everyone who helped in any way or contributed valuable discussions: Jennifer A. Lewis, Chris H. Rycroft, David A. Weitz, Dylan Barber, Bok Yeop Ahn, Simone Dussi, Meisam Bahari, Andrew Wong, Will Wang and Eric M. Fell.References
- M.-A. Goulet, M. Eikerling and E. Kjeang, Direct measurement of electrochemical reaction kinetics in flow-through porous electrodes, Electrochem. Commun., 2015, 57, 14–17 CrossRef CAS
.
- K. V. Greco, A. Forner-Cuenca, A. Mularczyk, J. Eller and F. R. Brushett, Elucidating the nuanced effects of thermal pretreatment on carbon paper electrodes for vanadium redox flow batteries, ACS Appl. Mater. Interfaces, 2018, 10(51), 44430–44442 CrossRef CAS PubMed
.
- H. Park, G. Kwon, H. Lee, K. Lee, S. Y. Park and J. E. Kwon,
et al., In operando visualization of redox flow battery in membrane-free microfluidic platform, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(9), e2114947119 CrossRef CAS PubMed
.
- X. Huang, Q. Wang, X. Y. Chen and Z. J. Zhang, The effects of amine/nitro/hydroxyl groups on the benzene rings of redox additives on the electrochemical performance of carbon-based supercapacitors, Phys. Chem. Chem. Phys., 2016, 18(15), 10438–10452 RSC
.
- A. J. Slate, D. A. Brownson, A. S. A. Dena, G. C. Smith, K. A. Whitehead and C. E. Banks, Exploring the electrochemical performance of graphite and graphene paste electrodes composed of varying lateral flake sizes, Phys. Chem. Chem. Phys., 2018, 20(30), 20010–20022 RSC
.
- X. Zhou, T. Zhao, Y. Zeng, L. An and L. Wei, A highly permeable and enhanced surface area carbon-cloth electrode for vanadium redox flow batteries, J. Power Sources, 2016, 329, 247–254 CrossRef CAS
.
- Y. A. Gandomi, D. Aaron, T. Zawodzinski and M. Mench, In situ potential distribution measurement and validated model for all-vanadium redox flow battery, J. Electrochem. Soc., 2015, 163(1), A5188 CrossRef
.
- Q. Chen, M. R. Gerhardt and M. J. Aziz, Dissection of the voltage losses of an acidic quinone redox flow battery, J. Electrochem. Soc., 2017, 164(6), A1126 CrossRef CAS
.
- L. Tong, Q. Chen, A. A. Wong, R. Gómez-Bombarelli, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, UV-Vis spectrophotometry of quinone flow battery electrolyte for in situ monitoring and improved electrochemical modeling of potential and quinhydrone formation, Phys. Chem. Chem. Phys., 2017, 19(47), 31684–31691 RSC
.
- E. W. Zhao, T. Liu, E. Jónsson, J. Lee, I. Temprano and R. B. Jethwa,
et al., In situ NMR metrology reveals reaction mechanisms in redox flow batteries, Nature, 2020, 579(7798), 224–228 CrossRef CAS PubMed
.
- Y. Jing, E. W. Zhao, M.-A. Goulet, M. Bahari, E. M. Fell and S. Jin,
et al., In situ electrochemical recomposition of decomposed redox-active species in aqueous organic flow batteries, Nat. Chem., 2022, 14(10), 1103–1109 CrossRef CAS PubMed
.
- E. Zhao, E. Jónsson, R. Jethwa, D. Hey, D. Lyu, A. Brookfield, P. A. Klusener, D. Collison and C. P. Grey, Coupled In Situ NMR and EPR Studies Reveal the Electron Transfer Rate and Electrolyte Decomposition in Redox Flow Batteries, J. Am. Chem. Soc., 2021, 143(4), 1885–1895 CrossRef CAS PubMed
.
- J. Chuankun, L. Qi, S. Cheng-Jun, Y. Fan, R. Yang and L. Yadong,
et al., In Situ X-ray Near-Edge Absorption Spectroscopy Investigation of the State of Charge of All-Vanadium Redox Flow Batteries, ACS Appl. Mater. Interfaces, 2014, 6(20), 17920–17925 CrossRef PubMed
.
- R. Jervis, L. D. Brown, T. P. Neville, J. Millichamp, D. P. Finegan and T. M. Heenan,
et al., Design of a miniature flow cell for in situ X-ray imaging of redox flow batteries, J. Phys. D: Appl. Phys., 2016, 49(43), 434002 CrossRef
.
- L. Bouffier and T. Doneux, Coupling electrochemistry with in situ fluorescence (confocal) microscopy, Curr. Opin. Electrochem., 2017, 6(1), 31–37 CrossRef CAS
.
- R. C. Engstrom, S. Ghaffari and H. Qu, Fluorescence imaging of electrode-solution interfacial processes, Anal. Chem., 1992, 64(21), 2525–2529 CrossRef CAS
.
- W. J. Bowyer, J. Xie and R. C. Engstrom, Fluorescence imaging of the heterogeneous reduction of oxygen, Anal. Chem., 1996, 68(13), 2005–2009 CrossRef CAS PubMed
.
- J. E. Vitt and R. C. Engstrom, Imaging of oxygen evolution and oxide formation using quinine fluorescence, Anal. Chem., 1997, 69(6), 1070–1076 CrossRef CAS
.
- J. C. O'Brien, J. Shumaker-Parry and R. C. Engstrom, Microelectrode control of surface-bound enzymatic activity, Anal. Chem., 1998, 70(7), 1307–1311 CrossRef PubMed
.
- J. P. Guerrette, S. J. Percival and B. Zhang, Fluorescence coupling for direct imaging of electrocatalytic heterogeneity, J. Am. Chem. Soc., 2013, 135(2), 855–861 CrossRef CAS PubMed
.
- N. C. Rudd, S. Cannan, E. Bitziou, I. Ciani, A. L. Whitworth and P. R. Unwin, Fluorescence confocal laser scanning microscopy as a probe of pH gradients in electrode reactions and surface activity, Anal. Chem., 2005, 77(19), 6205–6217 CrossRef CAS PubMed
.
- C. Renault, K. Marchuk, H. S. Ahn, E. J. Titus, J. Kim, K. A. Willets and A. J. Bard, Observation of nanometer-sized electro-active defects in insulating layers by fluorescence microscopy and electrochemistry, Anal. Chem., 2015, 87(11), 5730–5737 CrossRef CAS PubMed
.
- J. L. Shepherd, A. Kell, E. Chung, C. W. Sinclar, M. S. Workentin and D. Bizzotto, Selective reductive desorption of a SAM-coated gold electrode revealed using fluorescence microscopy, J. Am. Chem. Soc., 2004, 126(26), 8329–8335 CrossRef CAS PubMed
.
- A. Musgrove, A. Kell and D. Bizzotto, Fluorescence imaging of the oxidative desorption of a BODIPY-alkyl-thiol monolayer coated Au bead, Langmuir, 2008, 24(15), 7881–7888 CrossRef CAS PubMed
.
- J. R. Casanova-Moreno and D. Bizzotto, What happens to the thiolates created by reductively desorbing SAMs? An in situ study using fluorescence microscopy and electrochemistry, Langmuir, 2013, 29(6), 2065–2074 CrossRef CAS PubMed
.
- A. Meunier, E. Triffaux, D. Bizzotto, C. Buess-Herman and T. Doneux, In Situ Fluorescence Microscopy Study of the Interfacial Inhomogeneity of DNA Mixed Self-Assembled Monolayers at Gold Electrodes, ChemElectroChem, 2015, 2(3), 434–442 CrossRef CAS
.
- Z. L. Yu, J. Casanova-Moreno, I. Guryanov, F. Maran and D. Bizzotto, Influence of surface structure on single or mixed component self-assembled monolayers via in situ spectroelectrochemical fluorescence imaging of the complete stereographic triangle on a single crystal Au bead electrode, J. Am. Chem. Soc., 2015, 137(1), 276–288 CrossRef CAS PubMed
.
- C. Amatore, S. Arbault, Y. Chen, C. Crozatier, F. Lemaître and Y. Verchier, Coupling of electrochemistry and fluorescence microscopy at indium tin oxide microelectrodes for the analysis of single exocytotic events, Angew. Chem., Int. Ed., 2006, 45(24), 4000–4003 CrossRef CAS PubMed
.
- D. S. Chung and R. C. Alkire, Confocal microscopy for simultaneous imaging of Cu electrodeposit morphology and adsorbate fluorescence, J. Electrochem. Soc., 1997, 144(5), 1529 CrossRef CAS
.
- S. Cannan, I. D. Macklam and P. R. Unwin, Three-dimensional imaging of proton gradients at microelectrode surfaces using confocal laser scanning microscopy, Electrochem. Commun., 2002, 4(11), 886–892 CrossRef CAS
.
- M. Yang, C. Batchelor-McAuley, E. Kätelhön and R. G. Compton, Reaction layer imaging using fluorescence electrochemical microscopy, Anal. Chem., 2017, 89(12), 6870–6877 CrossRef CAS PubMed
.
- A. J. Welch, A. Q. Fenwick, A. Bohme, H.-Y. Chen, I. Sullivan and X. Li,
et al., Operando local pH measurement within gas diffusion electrodes performing electrochemical carbon dioxide reduction, J. Phys. Chem. C, 2021, 125(38), 20896–20904 CrossRef CAS
.
- A. Böhme, J. C. Bui, A. Q. Fenwick, R. Bhide, C. N. Feltenberger and A. J. Welch,
et al., Direct observation of the local microenvironment in inhomogeneous CO2 reduction gas diffusion electrodes via versatile pOH imaging, Energy Environ. Sci., 2023, 16(4), 1783–1795 RSC
.
- A. A. Wong, S. M. Rubinstein and M. J. Aziz, Direct visualization of electrochemical reactions and heterogeneous transport within porous electrodes in operando by fluorescence microscopy, Cell Rep. Phys. Sci., 2021, 2(4), 100388 CrossRef CAS
.
- J. S. Newman and W. Tiedemann, Flow-through porous electrodes, Adv. Electrochem. Electrochem. Eng., 1978, 11(4), 353–438 CAS
.
- Y. Jing, E. M. Fell, M. Wu, S. Jin, Y. Ji and D. A. Pollack,
et al., Anthraquinone flow battery reactants with nonhydrolyzable water-solubilizing chains introduced via a generic cross-coupling method, ACS Energy Lett., 2021, 7(1), 226–235 CrossRef
.
- D. G. Kwabi, Y. Ji and M. J. Aziz, Electrolyte lifetime in aqueous organic redox flow batteries: a critical review, Chem. Rev., 2020, 120(14), 6467–6489 CrossRef CAS PubMed
.
- P. Symons, Quinones for redox flow batteries. Current Opinion in, Electrochemistry, 2021, 29, 100759 CAS
.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt and C. J. Galvin,
et al., A metal-free organic–inorganic aqueous flow battery, Nature, 2014, 505(7482), 195–198 CrossRef CAS PubMed
.
- M. Wu, M. Bahari, E. M. Fell, R. G. Gordon and M. J. Aziz, High-performance anthraquinone with potentially low cost for aqueous redox flow batteries, J. Mater. Chem. A, 2021, 9(47), 26709–26716 RSC
.
- Z. Yang, L. Tong, D. P. Tabor, E. S. Beh, M. A. Goulet and D. De Porcellinis,
et al., Alkaline benzoquinone aqueous flow battery for large-scale storage of electrical energy. Advanced Energy, Materials, 2018, 8(8), 1702056 Search PubMed
.
- D. G. Kwabi, K. Lin, Y. Ji, E. F. Kerr, M.-A. Goulet and D. De Porcellinis,
et al., Alkaline quinone flow battery with long lifetime at pH 12, Joule, 2018, 2(9), 1894–1906 CrossRef CAS
.
- M. L. Perry, R. M. Darling and R. Zaffou, High power density redox flow battery cells, ECS Trans., 2013, 53(7), 7 CrossRef
.
- Q. Chen, L. Eisenach and M. J. Aziz, Cycling analysis of a quinone-bromide redox flow battery, J. Electrochem. Soc., 2015, 163(1), A5057 CrossRef
.
- M.-A. Goulet and M. J. Aziz, Flow battery molecular reactant stability determined by symmetric cell cycling methods, J. Electrochem. Soc., 2018, 165(7), A1466–A1477 CrossRef CAS
.
- C. Wiberg, T. J. Carney, F. Brushett, E. Ahlberg and E. Wang, Dimerization of 9,10-anthraquinone-2,7-Disulfonic acid (AQDS), Electrochim. Acta, 2019, 317, 478–485 CrossRef CAS
.
- T. J. Carney, S. J. Collins, J. S. Moore and F. R. Brushett, Concentration-dependent dimerization of anthraquinone disulfonic acid and its impact on charge storage, Chem. Mater., 2017, 29(11), 4801–4810 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00362d |
| ‡ These authors contributed equally to this work. |
| § Present address: Department of Materials Engineering, University of British Columbia, Vancouver, BC, Canada V6T 1Z4. |
| This journal is © The Royal Society of Chemistry 2024 |