Towards the universal use of DOSY as a molar mass characterization tool: temperature dependence investigations and a software tool to process diffusion coefficients†
Igor W. F.
Silva
 a,
Alasdair
McKay
a,
Alasdair
McKay
 b,
Anna
Sokolova
b,
Anna
Sokolova
 c and
Tanja
Junkers
c and
Tanja
Junkers
 *a
*a
aPolymer Reaction Design Group, School of Chemistry, Monash University, Clayton VIC 3800, Australia. E-mail: tanja.junkers@monash.edu
bSchool of Chemistry, Monash University, Clayton VIC 3800, Australia
cAustralian Centre for Neutron Scattering, ANSTO, Lucas Heights, NSW 2234, Australia
First published on 12th February 2024
Abstract
Two aspects of molar mass determination via diffusion ordered spectroscopy (DOSY) are described in this work. Firstly, we investigated how far the temperature of measurement affects the outcome of the DOSY experiment. For this, we performed molar mass calibrations of diffusion coefficients obtained for a series of narrowly distributed polystyrene samples in the temperature range of 0 to 40 °C. While a linear calibration is obtained at each temperature, a profound dependence of the obtained diffusion coefficient on temperature is first identified. We then demonstrated that this effect is an artifact created from convection in an NMR tube during the experiment and is dependent on the pulse sequence program. Using the dstebpgp3s pulse sequence, the available molar mass range and the temperature window for calibration are extended, and a reasonable agreement of all data with the Stokes–Einstein equation is found. To verify the validity of the chosen pulse sequence, we further determined the radii of gyration for different polymers via small-angle neutron scattering (SANS) experiments. SANS confirms the expected change in the radius with the molar mass, and no significant temperature dependence of the coil size is seen, in agreement with the results obtained using the dstebpgp3s pulse sequence. Secondly, we discuss different modes of calibration that scientists can use to determine molar masses from their individually measured diffusion coefficients. In addition, we provide a freely available software tool that allows one to directly transform diffusion coefficients into molar masses by applying a variety of calibrations and by guiding researchers as to which calibration is most suitable for their specific case.
Introduction
The accurate determination of the molecular masses of polymers has been a critical task ever since the field of polymer chemistry was established 100 years ago.1 Several different methods have matured over time, and without doubt, size exclusion chromatography (SEC) has become the gold standard in molecular mass characterization.2,3 While SEC is superior when it comes to the determination of molecular mass distribution shapes, it is a technique that is highly dependent on the good solubility of polymers to be analysed and on the precise calibration of individual machines.4 SEC, in combination with each specific analyte and solvent, in principle must be calibrated individually, unless sophisticated and not-easy-to operate detectors such as multi-angle light scattering are used. Without going into too much detail, SEC is equally flawed in its detail as it has proven to be essential for any polymer synthesis laboratory.5 It is the current consensus that SEC is accurate to only 10–20% at best, and is often probably much less accurate when it comes to absolute molar mass determination.6 Thus, researchers use a variety of other methods to confirm molar masses, especially to derive the accurate number or weight average molar masses of polymers. In the realm of controlled polymerization, where end groups are often known, 1H-NMR in combination with end group analysis is often used as an alternative; however, it is yet often associated with considerable errors due to the integration of peaks close to the baseline. MALDI-TOF has proved to be useful but is again quite limited in its applicability.7 More recently, diffusion ordered NMR spectroscopy (DOSY) has been extensively applied for molar mass determination. Grubbs and coworkers had demonstrated impressively how a polystyrene calibration could be established to follow the progress of reactions in NMR.8 Other specialists have reported similar ideas and provided calibrations for various materials and solvents.9–14 Thereby, the molar mass is plotted as a function of the determined diffusion coefficient in a double logarithmic fashion, yielding a linear relationship that then allows for the correlation of any diffusion coefficient with an unknown molar mass. This linearity can be understood based on a combination of the Rouse–Zimm model and the Stokes–Einstein equation (eqn (2)) (eqn (1)):| Rh ∼ bMv | (1) |
 | (2) |
| log(D) = log(b) − v·log(M) | (3) |
| log(D) = log(η) = log(c) − v·log(M) | (4) |
Here, eqn (3) gives the generic calibration for a given polymer/solvent combination, while eqn (4) accounts for the solvent according to its bulk viscosity, where c is an adjusted axis intercept. We had previously shown that eqn (4) is very powerful and allows one to compare DOSY calibrations for any solvent in a kind of solvent-universal calibration.10
While in principle, polymer physics suggests that the hydrodynamic radius is dependent on the type of polymer, it was a very interesting observation that most polymers, once corrected for their solvent viscosity following eqn (4), fall very closely together in their respective DOSY calibrations. This allows one to use an entirely universal calibration, as discussed in the context of low-field online NMR monitoring.15 Several examples, ranging from homopolymers to block copolymers, have shown that the errors made in molar mass determination are rather small, even if analytes are characterized based on another polymer calibration. Errors often below 20% are obtained in this way, which is an excellent result compared to the difficulties of SEC.10,16 As a further advantage, DOSY calibrations are applicable across laboratories, and don't require constant individual recalibrations as SEC does. This has huge potential for the standardization of molar mass determination and also provides the chance to create simple yet highly accurate tools that researchers can use in any laboratory to deduce molecular masses from a single DOSY experiment.
As positive as this sounds, two issues remain unresolved so far. The first being that while DOSY calibrations should in principle be lab-independent, a certain deviation between labs is in practice observed.16 This can be due to the differences in the methodology (for example, polymer concentration), yet it is worthwhile to study this further. In this work, we identified temperature as a very crucial factor.
Another issue that we identified is that researchers are used to SEC software to report molar masses. They usually do not deal in practice with calibrations and recalculations much, even if the math behind an SEC or DOSY calculation is fairly straightforward. We hence developed a software tool that is available for download and will allow one to calculate molar masses from a given diffusion coefficient. Users only need to choose a certain calibration type (direct, solvent-corrected or universal calibration based on polystyrene) to receive results directly.
Results and discussion
Temperature sensitivity of DOSY calibrations
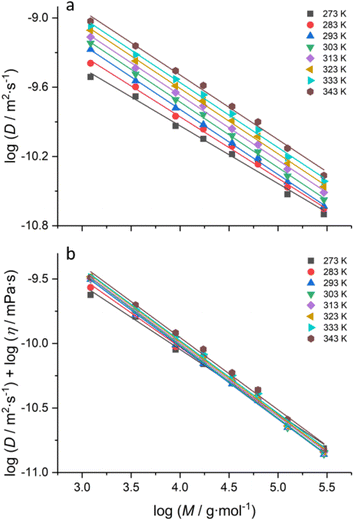
Fig. 1a shows the logarithm of diffusion coefficients obtained via DOSY plotted against the logarithm of molar masses for a series of polystyrene standards at different probe temperatures. In each case, linear relationships were obtained for the whole tested molar mass range of 1000 to 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1.
000 g mol−1.
At first glance, all temperatures yielded an individual calibration. A closer inspection further reveals that the highest and the lowest temperature under investigation almost match. Hence, whatever the temperature variation is, the dependency is complex. The largest deviation from the mentioned 273 and 313 K (0 and 40 °C) measurements is seen for 295 K (22 °C). Another interesting fact is that at 273 K (0 °C), it was impossible to measure any sample with higher molar masses, and the experiment essentially failed. This is surprising given that the viscosity of the solvent at that temperature is not too high, and the polymer remains well soluble.
Regardless, the Stokes–Einstein relation predicts changes in viscosity, and the bulk viscosity of the solvent (D-toluene) obviously changes with the temperature; hence, we corrected for this effect using eqn (4) (see Fig. S1 in the ESI†). The temperature dependence data of viscosity were taken from a report by Santos and co-workers24 and fitted with a third-order polynomial to obtain a functional form for η(T) (see Fig. S1 and Table S3†). Even with correction, no fundamental change in the order of the plots for the temperature series was observed. This first result, despite the rather narrow temperature window under investigation, is quite worrying as it implies quite large errors of the calibration if it is applied to the data measured at a different temperature.
Fig. 1b shows a different representation of the calibration data of Fig. 1a, in which we plotted the diffusion coefficients corrected for solvent viscosity as a function of temperature. In this representation, it becomes quite clear that for each temperature, log(Dη) goes through a minimum for all polymer standards at around 295 (22 °C) ± 3 K. Again, this is a peculiar observation. Since Rh is directly correlated with the radius of gyration (Rg),25 one would usually expect that Rh would continuously increase with temperature. A minimum, as observed, usually would only allow for the interpretation that the solvent quality changes, leading to a more collapsed state of polymer coils at around room temperature. However, the literature does not suggest any specific change in the solvent quality in this range for toluene. The estimated theta temperature of toluene is expected to be much lower (around 150 °C);26 hence a switch from good to bad solvent conditions must not be expected here. As a further question, it is also striking that higher molar mass samples only yield diffusion coefficients from the experiment at higher temperatures. This cannot be explained by any visually observable shift in the solubility of the sample. Why the DOSY experiment does not yield a reasonable result remains unclear at this point. In any case, it is interesting to see that a rise in temperature apparently allows for extending the accessible range of molar masses dramatically, and it seems advisable to exploit this feature for polymers where high molecular masses are difficult to assess through DOSY.
Yet, the fact that the data show a non-linear progression with temperature and optimal conditions appear around room temperature made us look closer at the applied NMR pulse sequence. Clearly, the data discussed above suggest a methodology or instrument dependence. Usually, the so-called Longitudinal Eddy-current Delay Bipolar Gradient Pulse (ledbpgp2s) program27 is largely used in the molar mass estimation of polymers10,14,16,22,28 because it is possible to get optimised results in lower gradient strength pulses,29 which can be essential for performing DOSY on macromolecules. We found that by applying this sequence, using the ledbpgp2s program, significant temperature deviations occur at the extremes of the temperature range studied, 273 and 313 K, despite care being taken to ensure the samples had sufficient time to thermally equilibrate, with the measurement undertaken at a high gas flow rate. The variability at the temperature extremes is consistent with those reported by Morris and coworkers, who elegantly showed evidence of convection both at temperatures above and below the quiescent temperature.30 Sample convection has long been known to be a major source of artefacts in DOSY-NMR. Convection is caused by temperature gradients within the sample, which may lead to extra signal attenuation in pulse field gradient experiments, thus leading to the overestimation of diffusion coefficients.31
A wide variety of different experimental methods have been proposed to minimise the effects of convection in NMR experimental results, which are given more detail in the ESI.† Since the theme of our research has been to see the wider employment of DOSY measurements in molar mass estimations amongst the polymer community, we have restricted our methods to those that are inexpensive, readily accessible and require only moderate NMR expertise.
We initially explored acquiring diffusion data whilst rotating the sample and by acquiring data in 3 mm NMR tubes rather than a more typical 5 mm tube. Both methods have been shown to reduce the artefacts caused by convection such that reliable data can be obtained over a wider temperature window (see the ESI†); however, convection effects were still present at around 323 and 333 K (60 and 70 °C).
We then explored the aforementioned convection compensation sequences. Whilst several sequences have been designed over the years, we restricted our study to the double-stimulated-echo sequence, a default sequence on Bruker spectrometers (dstebpgp3s). This sequence splits the sequence element into two symmetrical halves generating equal and opposite flow effects.32–34 Our diffusion data, obtained using this sequence, show seemingly little effect of convection across a wide temperature range (273 to 343 K), see the data shown in Fig. 2 and the discussion below. Switching the pulse sequence not only seemingly improved the measurement of diffusion coefficients with less influence of convection but also increased the available temperature range. The only downside of its application is that the signal-to-noise ratio is generally less favourable, giving concerns for the measurement of particularly high molar masses because it may not be possible to achieve the required signal attenuation. However, the dstebpgp3s sequence proved to be reliable for a very significant range of molar masses.
Fig. 2 shows the outcome of the DOSY calibrations using the better dstebpgp3s pulse sequence. Compared to the situation in Fig. 1, much more consistent data were obtained. The available molar mass range of the calibration is enlarged, and also higher temperatures (up to 343 K) became accessible. Again, each individual calibration shows good linearity. This time, however, changes with temperature are monotonous. More importantly, eqn (4) again is holding well, showing that the differences in diffusion coefficients correlate almost perfectly with the viscosity change with temperature. Yet, a small but noticeable influence of the temperature on the calibration remains.
In order to provide a temperature sensitive calibration, we fitted the combined data of Fig. 2b on a 3-dimensional scale, yielding the following mathematical relation of a plane surface (r2 = 0.9987) as the best fit to the data (visualization in Fig. 3). The fit function was arbitrarily chosen based on the best representation of the experimental values:
log(Dη) = −8.09358 – 0.5542![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(M) + 9.93965 × 10−4 T log(M) + 9.93965 × 10−4 T | (5) |
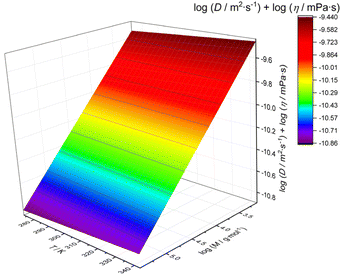 | ||
| Fig. 3 3D calibration fit of viscosity-corrected diffusion coefficients (obtained using dstebpgp3s) as a function of temperature and the molar mass of polystyrene standards. | ||
The best fit of the data to the above equation is shown in Fig. 3. As expected, the temperature influence is relatively small, leaving the otherwise known linear relationship. Still, a slight temperature influence beyond viscosity effects exists, and hence eqn (5) should be used rather than a single temperature calibration. Eqn (5) can hence be used to calibrate the molar mass from DOSY over the entire temperature range.
SANS investigation into the temperature dependence of polymer coiling
Despite the seemingly large improvement of the data by switching the pulse sequence, doubt may still exist on the validity of data shown in Fig. 2 and 3. Hence, we performed independent experiments to directly access information on the coil size of the polystyrene standards as a function of temperature with the aim to validate the calibration of eqn (5). This was performed using small angle neutron scattering experiments (SANS).Fig. 4a shows the Rg acquired from SANS data, processed using the Primus and SasView software (see the ESI† for procedures and fitting, p(r) and Kratky curve analysis) obtained for the standard polystyrene solutions under the same conditions as used in DOSY (average molar masses of 9, 33, 62, and 120 kg mol−1). As expected, a monotonous increase in the radius of the polymer coils is observed with increasing molar masses. However, with respect to temperature, only small changes are observed, as could be expected theoretically. Only slight fluctuations of Rg are noticeable in the covered temperature range and within error limits. This data can be directly compared to the DOSY results. Rather than applying the Zimm relation, one can directly calculate the hydrodynamic radius of a chain using the Stokes–Einstein relation. Fig. 4b depicts Rh derived from DOSY and calculated from eqn (1) for direct comparison with the SANS data. Overall, a good match between the two datasets is observed, with only small deviations in the absolute size. The DOSY data indicate a slight temperature dependence, which is also reflected in the temperature of eqn (5). Individual error bars are relatively small for both methods, yet also represent only the fitting error for a single experiment and the overall scatter of data is larger (as also indicated by the fluctuation of, for example, the SANS data with temperature). Regardless, in conclusion one can assume that both datasets are in very good general agreement, underpinning the validity of the dstebpgp3s sequence to obtain accurate diffusion coefficients without the disturbance of convection in the NMR tube. At this stage, however, it would still be beneficial to see if other laboratories can confirm the data we present herein to rule out further method dependencies. This is particularly important since we have seen a good match of data between laboratories when measurements are obtained at 298 K (25 °C), as we have shown in our interlaboratory work.16,28
Development of a software tool
Overall, the above discussed temperature dependence shows that using 298 K (25 °C) as a DOSY standard temperature is a good choice, which is underpinned by many individual studies using this condition.8,10,13,14,17–20,22,23,28 Yet, as mentioned above, polymer chemists who want to use DOSY to determine molar masses face difficulties when they want to use the methodology. Even though an individual calibration is not required, and despite the fact that the mathematical transformation is quite simple, one still needs to have a good overview on the state of the literature regarding calibration results. Also, it requires some expert knowledge to be able to choose the right calibration type to transform a diffusion coefficient of a polymer sample of interest. Generally, three types of calibration can be distinguished:Using these three different types of calibrations requires the knowledge of solvent viscosities, and as mentioned, the latest known calibration parameters. We have thus designed software that calculates molar masses for a polymer based on an entered diffusion coefficient. All the user needs to do is to select the type of polymer, and the deuterated solvent used in the experiment. The dropdown menu shows all polymers for which calibrations are known to the software. Also, all solvents that are known to the software are listed. The user can select the type of polymer and solvent that were used to determine the diffusion coefficient. If a polymer/solvent combination is chosen for which a direct calibration is available, then the result is calculated based on method (I). Since we deem that this method is the safest to use, an error is estimated based on calibration fit errors, if known from the literature. While errors can, at this point, appear to be sometimes high, we do believe that with more calibration data becoming available from various labs, the accuracy will increase.
If the user selects a polymer/solvent combination that is not known to the software, method (ii) is automatically applied and an error calculation is omitted. This choice was made based on the reason that a combined viscosity corrected calibration is always based on a larger number of data than an individual direct calibration. This results automatically in higher ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) 2 of the fits, even if the overall accuracy may not be higher. Future versions of the software might implement statistically better methods of error estimation for this method and introduce an estimate to be displayed for the expected error. However, if a user wants to check for a known polymer/solvent combination what the difference in result between method (I) and (II) is, one can activate the according tick box on the side of the solvent dropdown menu. If ticked, method II is always applied.
2 of the fits, even if the overall accuracy may not be higher. Future versions of the software might implement statistically better methods of error estimation for this method and introduce an estimate to be displayed for the expected error. However, if a user wants to check for a known polymer/solvent combination what the difference in result between method (I) and (II) is, one can activate the according tick box on the side of the solvent dropdown menu. If ticked, method II is always applied.
Method (III) is selected by keeping the polymer type open (“other”) in the dropdown menu. This is also the pre-set choice when opening the program. In this case, the solvent-corrected calibration of polystyrene is automatically applied to keep the statistical relevance high and ticking the box to activate method (II) has no effect.
In all three cases, the output of the software is a molar mass, together with a notation of what calibration was used. A reference to the source of the calibration behind the calculation is also provided to allow the user to identify which data are used, and to simplify proper referencing. It must be noted that in all cases, the molar mass is a peak molar mass rather than a true statistical number or weight average. At this stage, DOSY is not able to produce reliable distribution shape information, and hence information must be used with caution when polymers with significant dispersity are analysed.
Regarding temperature, the software offers a field to enter the temperature of the DOSY measurement. It must be stressed that though this was introduced based on the above-described investigations, no temperature specific calculation is offered in the current build of the program (version 1.5) (Fig. 5).
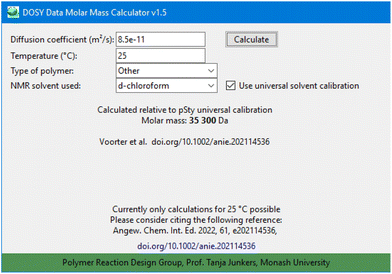 | ||
| Fig. 5 Screenshot of the DOSY Data Molar Mass Calculator software (version 1.5) for calculation of molar masses following the outlined procedure. | ||
The software is published as a stand-alone executable file, and is available in the ESI,† or from the PRD group github account: https://github.com/PRDMonash/DOSYto_mass_converter
We are aware that an .exe file is not what most researchers with a digital chemistry affinity would use. However, we decided in this case to cater for a broader user base that we can reach if we provide a program that works without the installation of a coding language-dependent environment. A python function that will allow one to directly implement the calculation into other codes is currently under development and will be added later. The executable file comes with three csv files in which the calibration data and viscosity data are stored. This allows one to update calibrations easily when new data become available, and allows the user to try different literature sources if they disagree with our selection of the literature. Changing the values in the csv file is straightforward, allowing users to apply their own calibration information wherever needed. We will periodically provide updates for the csv files to keep this in line with new research being published. We also anticipate the development of further software versions in time. The software is provided free of charge, and we only ask users to cite either this publication, or the mentioned paper in the software if they use the tool in their work.
Conclusions
In our strive to test the suitability of diffusion ordered spectroscopy as a molar mass determination tool for synthetic chemists, we have tested the applicability of the Stokes–Einstein equation further to the molar mass calibrations of diffusion coefficients. We have shown that the influence of temperature on the outcome of a DOSY experiment is far from trivial when standard pulse sequences are employed. Strong variations of the observable diffusion coefficient with temperature were identified at first, which can be related to convection playing an important role in disturbing the measurement. When a pulse sequence is chosen that corrects for convection, a low temperature dependence is observed, and the data are in overall good agreement with independent SANS data. A 3D correlation is provided for the molar mass determination of polystyrene via DOSY in a broad temperature range, allowing for a much more detailed comparison of literature data in the future.As an independent goal, we also present a software tool that we have developed to transform diffusion coefficients into molar masses. The software offers three different calibration methods and stores currently available calibration information in supplementary files. While the mathematical transformation for each calibration is not overly difficult, we hope that the provision of such a tool will help researchers apply the methods. Already in discussions with researchers at our own institution, we realized that the choice of appropriate calibration is not straightforward for scientists who are not fully up to date with the DOSY literature on polymer characterization. The software tool fills this gap and we hope that it will find widespread use.
Author contributions
Investigation, data analysis and writing – review & editing were carried out by IWFS. Experimental support and data analysis were provided by AM and AS. AS also helped in writing – review & editing and supervision. Software development, data curation, funding acquisition, supervision and writing – original draft and the revision of the draft were done by TJ. GPT4 was used for developing the described software.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Monash University for providing support in the form of a scholarship for IWF Silva. The authors are also grateful for a beamtime (proposal 15506) from the Australian Centre for Neutron Scattering, ANSTO, to perform SANS experiments.References
- H. Frey and T. Johann, Polym. Chem., 2020, 11, 8–14 RSC.
- M. T. R. Laguna, R. Medrano, M. P. Plana and M. P. Tarazona, J. Chromatogr., A, 2001, 919, 13–19 CrossRef CAS PubMed.
- D. Held and P. Kilz, Chem. Teach. Int., 2021, 3, 77–103 CrossRef.
- N. T. McManus, Can. J. Chem. Eng., 2023, 101, 5365–5381 CrossRef CAS.
- K. Philipps, T. Junkers and J. J. Michels, Polym. Chem., 2021, 12, 2522–2531 RSC.
- L. D'Agnillo, J. B. P. Soares and A. Penlidis, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 905–921 CrossRef.
- M. E. Payne and S. M. Grayson, J. Vis. Exp., 2018, 136, e57174 Search PubMed.
- W. Li, H. Chung, C. Daeffler, J. A. Johnson and R. H. Grubbs, Macromolecules, 2012, 45, 9595–9603 CrossRef CAS PubMed.
- F. M. Arrabal-Campos, P. Oña-Burgos and I. Fernández, Polym. Chem., 2016, 7, 4326–4329 RSC.
- P. J. Voorter, A. McKay, J. Dai, O. Paravagna, N. R. Cameron and T. Junkers, Angew. Chem., Int. Ed., 2022, 61, e202114536 CrossRef CAS PubMed.
- J. H. Vrijsen, I. A. Thomlinson, M. E. Levere, C. L. Lyall, M. G. Davidson, U. Hintermair and T. Junkers, Polym. Chem., 2020, 11, 3546–3550 RSC.
- C. Chamignon, D. Duret, M. T. Charreyre and A. Favier, Macromol. Chem. Phys., 2016, 217, 2286–2293 CrossRef CAS.
- J. G. Rosenboom, J. De Roo, G. Storti and M. Morbidelli, Macromol. Chem. Phys., 2017, 218, 1600436 CrossRef.
- E. Ruzicka, P. Pellechia and B. C. Benicewicz, Anal. Chem., 2023, 95, 7849–7854 CrossRef CAS PubMed.
- O. Tooley, W. Pointer, R. Radmall, M. Hall, V. Beyer, K. Stakem, T. Swift, J. Town, T. Junkers, P. Wilson, D. Lester and D. Haddleton, Macromol. Rapid Commun., 2024, 2300692 CrossRef PubMed.
- P.-J. Voorter, M. Wagner, C. Rosenauer, J. Dai, P. Subramanian, A. McKay, N. R. Cameron, J. J. Michels and T. Junkers, Polym. Chem., 2023, 14, 5140–5146 RSC.
- H. N. Nguyen, H. T. Nguyen, M. N. Nguyen and Q. T. Pham, VNU Journal of Science: Natural Sciences and Technology; Tạp chí Khoa học Đại học Quôc gia Hà Nọi: Khoa học, 2020, 36, 16–21 Search PubMed.
- E. Durand, M. Clemancey, J.-M. Lancelin, J. Verstraete, D. Espinat and A.-A. Quoineaud, J. Phys. Chem. C, 2009, 113, 16266–16276 CrossRef CAS.
- B. Grabe and W. Hiller, Macromolecules, 2022, 55, 8014–8020 CrossRef CAS.
- S. Beckert, F. Stallmach, R. Bandari and M. R. Buchmeiser, Macromolecules, 2010, 43, 9441–9446 CrossRef CAS.
- J. R. Montgomery, C. S. Lancefield, D. M. Miles-Barrett, K. Ackermann, B. E. Bode, N. J. Westwood and T. Lebl, ACS Omega, 2017, 2, 8466–8474 CrossRef CAS PubMed.
- T. F. Nelson and C. P. Ward, Anal. Chem., 2023, 95(22), 8560–8568 CrossRef CAS PubMed.
- X. Guo, E. Laryea, M. Wilhelm, B. Luy, H. Nirschl and G. Guthausen, Macromol. Chem. Phys., 2017, 218, 1600440 CrossRef.
- F. J. V. Santos, C. A. Nieto de Castro, J. H. Dymond, N. K. Dalaouti, M. J. Assael and A. Nagashima, J. Phys. Chem. Ref. Data, 2005, 35, 1–8 CrossRef.
- C. M. Kok and A. Rudin, Makromol. Chem., Rapid Commun., 1981, 2, 655–659 CrossRef CAS.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer Handbook, Wiley, New York, 1999 Search PubMed.
- D. Wu, A. Chen and C. S. Johnson, J. Magn. Reson., Ser. A, 1995, 115, 260–264 CrossRef CAS.
- J. De Neve, J. J. Haven, S. Harrisson and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 13869–13873 CrossRef CAS PubMed.
- P. Groves, Polym. Chem., 2017, 8, 6700–6708 RSC.
- I. Swan, M. Reid, P. Howe, M. A. Connell, M. Nilsson, M. Moore and G. Morris, J. Magn. Reson., 2015, 252, 120–129 CrossRef CAS PubMed.
- G. H. Sørland and D. Aksnes, Magn. Reson. Chem., 2002, 40, S139–S146 CrossRef.
- A. Jerschow and N. Müller, J. Magn. Reson., 1997, 125, 372–375 CrossRef CAS.
- A. Jerschow and N. Müller, J. Magn. Reson., 1998, 132, 13–18 CrossRef CAS.
- G. H. Sørland, J. G. Seland, J. Krane and H. W. Anthonsen, J. Magn. Reson., 2000, 142, 323–325 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, density calculations and SANS data fitting procedures. See DOI: https://doi.org/10.1039/d3py01172k |
| This journal is © The Royal Society of Chemistry 2024 |