 Open Access Article
Open Access ArticleSize analysis of large DNA molecules by relaxation time measurement using a nanoslit channel†
Hongdong Yi a,
Shintaro Itoh*ab,
Kenji Fukuzawaa,
Hedong Zhang
a,
Shintaro Itoh*ab,
Kenji Fukuzawaa,
Hedong Zhang c and
Naoki Azuma
c and
Naoki Azuma a
a
aDepartment of Micro-Nano Mechanical Science and Engineering, Nagoya University, Japan. E-mail: shintaro.itoh@mae.nagoya-u.ac.jp
bPRESTO, Japan Science and Technology Agency, Japan
cDepartment of Complex Systems Science, Nagoya University, Japan
First published on 1st July 2025
Abstract
Determining the size of DNA molecules >10 kbp continues to be challenging, as conventional methods, such as pulsed-field gel electrophoresis require time-consuming analysis and artificial gel structures increase the risk of mechanical fragmentation to DNA molecules during repeated hooking and stretching. Herein, we developed a new analytical method for identifying the size of DNA molecules by measuring the time required for a stretched large DNA molecule to relax into a random coil, using nanoslit channels with depths of 130–49 nm. By maintaining the initial stretching ratio of the collected DNA molecules at <30%, we successfully differentiated a mixed DNA sample containing λ and T4 DNAs into two distinct peaks in the relaxation-time histogram. Furthermore, we explored the influence of the number of collected relaxation times and nanoslit depths on the resolution of size analysis. Our findings indicated that the nanoslit depth was the primary factor affecting the size determination resolution. Reducing the nanoslit depth enhanced resolution, whereas the number of effective relaxation times did not impact the resolution once a critical data threshold was reached. A nanoslit channel of depth 49 nm exhibited superior performance, with a maximum resolution of 2.33 and a short analysis time of 60 s, surpassing both conventional methods in terms of resolution and time efficiency. The proposed method shows great potential for accurate, large-scale DNA size analysis.
Introduction
The global spread of infections caused by antibiotic-resistant bacteria has notably affected public health.1–3 Rapid and accurate bacterial genotyping is essential for epidemiological analyses. In bacterial genotyping, first, genomic DNA extracted from cells is usually cut into fragments using restriction enzymes. The molecular size of these fragments is typically larger than 10 kbp. The size distribution of these large molecular weight DNAs is measured to determine the genotype. Additionally, there is a pressing demand for the production of nucleic acid medicines and the development of artificial genomes. Compared with other antibody drugs, nucleic acid medicines can intervene at the source and block the expression of disease-related genes into pathological proteins, which is the characteristic of “treating the root cause”. Artificial genomes have attracted attention as a new method for genome editing. As they allow more flexible design than genome editing, they can be used to design organisms with high precision and functions that meet specific needs, efficiently use genes that incorporate only the necessary genetic information, and create new biological functions. In developing these genome-related technologies, the synthesis of large DNA molecules plays a crucial role. The process begins with designing a target DNA sequence tailored to the requirements of the intended application. Following this design, large DNA molecules are synthesized stepwise through multiple rounds of amplification, ligation, and assembly reactions. A rigorous purification protocol is employed to ensure that the synthesized DNA is free from residual impurities, enzymes, or other contaminants from the reaction process. This purification step is essential to maximize the effectiveness of DNA molecules in downstream applications. After purification, a DNA molecular size analysis is necessary. In nucleic acid therapeutics and synthetic gene applications, the size of the DNA molecule is a major factor that influences its cellular stability, transcription efficiency, and gene expression efficacy. Therefore, precise molecular size analysis is required post-synthesis to confirm that DNA meets the specific requirements of the application.Over the past few decades, pulsed-field gel electrophoresis (PFGE) has been widely used as a highly accurate genotyping method for large DNA fragments.4–6 However, PFGE has several limitations. It is time-consuming and labor-intensive, requiring hours for preparation by skilled operators and 1–2 d for the analysis. This is because PFGE relies on a biased reptation mechanism that requires the application of small electric fields in various directions to separate long DNA molecules, resulting in slower electrophoretic velocities. Consequently, developing fast and accurate analytical methods for identifying the size of large DNA molecules may expand the range of possible applications in genotyping drug-resistant bacteria and large DNA molecule synthesis.
Recent advancements in micro and nanofabrication techniques have sparked renewed interest in artificial gel structure development.7–9 Volkmuth and Austin pioneered the use of optical microlithography to create two-dimensional arrays.10 They demonstrated that DNA molecules of up to approximately 100 kbp can be separated in a DC field, surpassing the conventional gel electrophoresis limitations. This breakthrough has opened new avenues for bioanalysis and detection. Subsequent research has showcased various artificial molecular sieves for biomolecule separation that employ different separation mechanisms. A commonly utilized mechanism is Ogston sieving,11–13 where DNA molecules smaller than the constriction can freely move with their coiled conformation intact. Smaller DNA molecules exhibit higher velocity through the gel matrix owing to weaker steric hindrance than that faced by larger DNA molecules. However, Ogston sieving is typically effective only under low electric fields and for small DNA molecules. Han and Craighead devised a nanofluidic channel with alternating thin and thick regions to efficiently separate long DNA ladder samples (5–50 kbp) within 30 min based on the mechanism of entropic trapping.14 In this method, contrary to that in Ogston separation, larger DNA molecules move across entropy barriers with greater velocities than smaller ones because they have more contact area with the barrier and a higher likelihood of escaping it. Similarly, various novel artificial sieving structures have been explored for biomolecule separation, such as nanoscale deterministic lateral displacement arrays,15–17 self-assembled magnetic arrays,18 self-assembled nanowire arrays,19 size exclusion chromatography (SEC) separation chip,20,21 and nanorod-sieving matrices.22 Cao et al. developed a highly regular integrated glass capillary system to replace the traditional slit-well motif for faster separation in just a few minutes.23–25 However, several artificial sieving matrices rely on expensive, high-resolution photolithography techniques. Additionally, achieving DNA separation within different size ranges requires devices with constriction sizes comparable to the radius of gyration of DNA molecules, leading to increased costs. To tackle the challenges posed by the high-resolution and stringent fabrication requirements of traditional lithography in nanofluidics, Shiri et al. developed a nano-injection molding approach utilizing UV-resin mold inserts replicated from silicon masters. This strategy removes the need for nickel electroplating and enables cost-effective, rapid prototyping of nanofluidic devices with sub-30 nm accuracy features.26 Furthermore, separation using these gel materials presents an inherent trade-off between separation time and resolution.27 The increased driving force can compromise the separation efficiency and heighten the risk of DNA breakage due to frequent interactions between large DNA molecules and artificial gel structures. Therefore, due to these challenges, artificial sieving nanostructure-based microchips have not yet replaced conventional PFGE as a widely used method for large DNA size analysis.
In this study, a novel size analysis approach for long DNA molecules was proposed, utilizing relaxation-time measurements of DNA molecules. The relaxation time (τ) represents the duration for which the molecules transition from a stretched to a coiled state upon stress removal. Previous research has examined the correlation between the relaxation time of a single DNA molecule confined in a nanoslit and molecular weight (M).28–30 Relaxation times can be expressed as a function of molecular weight and degree of confinement.28 Therefore, we aimed to establish a method for determining the molecular size of DNA by measuring relaxation times in nanofluidic channels at a designed nanometer-sized depth.
Experimental section
Conceptual design
A schematic representation of the proposed method is shown in Fig. 1. A nanoslit device was employed to elongate DNA molecules. Fig. 1a illustrates the process of capturing videos of DNA molecule relaxation. DNA was introduced into the nanoslit channel when the voltage was “ON” and moved along the channel. Upon reaching the observation position, the voltage was turned off, causing the DNA conformation to transition from a stretched to a coiled state. Multiple videos documenting the relaxation process of DNA molecules were recorded. To ensure sufficient data collection, a pulse signal was used to repeat the experimental procedure described above. Fig. 1b shows the image data analysis process. Initially, the relaxation process of each DNA molecule was recorded individually to create a time series of images depicting the conformation. The stretching rate (S) of each DNA molecule at different time points was calculated. Then, the relaxation time of each DNA molecule was determined by fitting it to a single-exponential decay function.31 Finally, a histogram of the relaxation time was generated, with size discrimination achieved by identifying two distinct peaks in the histogram. The proposed device can measure molecular size, however, cannot separate molecules according to their size. This is because the concept of our device is to avoid the difficulty of creating complex nanoscale molecular sieve structures and to specialize in efficiently identifying their size. As the purpose of most conventional size separation methods is to identify size distributions, our device can perform this function more accurately and efficiently.The nanoslit channel had a depth of less than 130 nm and a width of 14 μm. To completely stretch the DNA, the width should also be on the nanometer scale, which is a two-dimensional nanoconfinement. However, our proposed method aims for a DNA stretching rate of up to 30%, which can be achieved with nanoslit channels that are 130 nm or less in depth (one-dimensional nanoconfinement). Nanoslit geometries with such dimensions can be produced using general microfabrication equipment, as described in the next section. Our method employs a simple one-dimensional nanoslit created using standard photolithography and dry etching, rather than intricate 2D or 3D nanostructures such as nanopillars or nanowires. This straightforward and commonly used fabrication technique eliminates the need for costly tools, resulting in a low-cost and easily reproducible process. The cause for a maximum stretching rate of approximately 30% is that excessive stretching not only increases the DNA breakage risk but also complicates the relaxation process, making it difficult to identify a single relaxation time. Although the lateral confinement in a nanoslit with a width of 14 μm is weak, it can reduce the significant effect from entropic entry barriers and hydrodynamic interactions. When the width is reduced to a few microns, hydrodynamic effects and entropic confinement will increase. Narrower nanoslit may cause stronger shear gradients, thereby increasing DNA molecules' stretching and changing their dynamics behavior. The relaxation time of DNA molecules near the boundary will increase due to hydrodynamic effects. This will affect the resolution of DNA size analysis. In addition, smaller geometries also raise fabrication complexity and entropic entry barriers. The risk of molecular damage also increases. Furthermore, the 14 μm width increases the probability of a large amount of DNA being introduced into the nanoslit channel, enabling the simultaneous acquisition of a large amount of relaxation process data, which may speed up the analysis.
Nanoslit channel fabrication
Fig. 2a outlines the steps in the fabrication process of the nanoslit channel device. Initially, the silicon wafer was prebaked at 180 °C for 5 min to eliminate moisture. Then, hexamethyldisilazane (HMDS “OAP”, Tokyo Ohka Kogyo Co., Ltd., Kanagawa, Japan), as an adhesion prompter and a positive photoresist (OFPR-800LB 34 cP, Tokyo Ohka Kogyo Co., Ltd., Kanagawa, Japan) were spin-coated onto the Si wafer at 800 rpm for 5 s and then at 3000 rpm for 20 s. The wafer was then baked at 90 °C for 5 min to enhance adhesion. The nanoslit structures were patterned using a maskless lithography system (DL-1000; Nanosystem Solutions Inc., Okinawa, Japan). Following exposure, the photoresist was developed in a 2.38% developer solution (NMD-3, Tokyo Ohka Kogyo Co., Ltd., Kanagawa, Japan) for 3 min at 25 °C and then post-baked at 120 °C for 30 min. The pattern was etched using reactive-ion etching (RIE-10NR, Samco International, Kyoto, Japan) at a rate of 4 Å s−1. Subsequently, the residual photoresist was removed through 5 min ultrasonic cleaning in acetone followed by cleaning with buffered hydrofluoric acid to eliminate surface contaminants. To enhance the wettability, a silicon dioxide layer was formed by thermal oxidation at 1057 °C for 20 min. The nanoslit surface was then cleaned using oxygen plasma and 5% hydrofluoric acid. Finally, the nanoslit was sealed with a glass plate via anodic bonding at 0.5 kV and 400 °C for 20 min. The nanoslit channel depth was measured using atomic force microscopy (AFM). Fig. 2b and e show a typical image of a nanoslit channel measured using AFM, which comprises two channels of the same size. The width and length of the single channel were 14 μm and 9 mm, respectively. To investigate the correlation between the depth of the nanoslit and the size analysis resolution, nanoslits with different depths (130, 110, 69, and 49 nm) were fabricated by varying the etching time to 325, 125, 175, and 250 s, respectively.Sample preparation
The λ DNA (48.5 kbp, Takara Bio) and T4 DNA (166 kbp, Nippon Gene) were diluted in pure water to a concentration of 10 ng μL−1. Subsequently, all the DNA samples were stained with 0.1 μM YOYO-1 (Thermo Fisher Scientific) at a dye-to-base pair ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for at least 30 min to ensure that dye binding reached equilibrium, resulting in a concentration of 0.322 ng μL−1. A 1× Tris-borate-EDTA buffer was used for DNA electrophoresis. Lipidure®-BL203 (NOF) was added to the buffer to suppress electroosmotic flow. To validate the principle of the proposed method, samples containing only λ DNA and those containing only T4 DNA were prepared separately. Moreover, to assess the resolution of the size analysis when mixed, a sample containing a 1
5 for at least 30 min to ensure that dye binding reached equilibrium, resulting in a concentration of 0.322 ng μL−1. A 1× Tris-borate-EDTA buffer was used for DNA electrophoresis. Lipidure®-BL203 (NOF) was added to the buffer to suppress electroosmotic flow. To validate the principle of the proposed method, samples containing only λ DNA and those containing only T4 DNA were prepared separately. Moreover, to assess the resolution of the size analysis when mixed, a sample containing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of λ and T4 DNAs was also prepared.
1 volume ratio of λ and T4 DNAs was also prepared.
Experimental setup and data analysis
A fluorescence microscope (Olympus BX51N-33F-2-SP) equipped with an LED light source emitting light at a wavelength of 460 nm was used to observe labeled DNA molecules. Time-series images were captured using an electron-multiplying charge-coupled device camera (iXonEM+, Andor) with an exposure time of 60 ms and an electron-multiplying gain of 500. The applied voltage was regulated by a signal generator (NF WF1948) and amplifier (MESS-TEK M-2617). To collect enough relaxation data, a periodic pulse with a period of 3 s and a duty cycle of 30% was set. The voltage values were adjusted so that the stretching rate did not exceed 30%, depending on the depth of the nanoslit channel. Images depicting the relaxation process were analyzed using image processing software (ImageJ; NIH, Bethesda) to generate a time series of images describing the conformation of each DNA molecule. A noise filtration method was employed to eliminate bright noise pixels surrounding the DNA without altering the image of the DNA itself.28 To determine the length of the DNA molecule in the stretching direction (x-direction), the intensity distribution along x-direction I(x) was obtained, which was defined as the average value of non-zero pixels in the vertical direction at each point along x-direction. Then, the following function32 was fitted to the intensity distribution I(x) (Fig. S1†):
 | (1) |
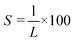 | (2) |
Results and discussion
Relaxation time measurement of a single DNA molecule
We first measured the relaxation time using a 130 nm nanoslit channel for λ and T4 DNAs separately. A total of 50 μL of each DNA sample was utilized. The voltage used to introduce DNA molecules into the nanoslit was set to 15 V. When the voltage was switched off, the DNA molecules transitioned from the stretched to the coiled state. Fig. 3a and d show time-series images describing the relaxation process of λ and T4 DNAs, respectively. The time difference between the images was 0.5 s. The stretching ratio was calculated for each DNA molecule at each time point throughout the relaxation process using eqn (1) and (2). The relationship between time (t) and stretching ratio (S) can be depicted as a single-exponential decay function (Fig. 3b and e), as follows:
 | (3) |
The relaxation time can be obtained by fitting a single-exponential decay function within the limit of a small stretching ratio (S < 30%),34 as the DNA chain behaves like an entropic spring that follows Hooke's law in this regime. In this linear elasticity region, the relaxation dynamics are analytically simple and can be well described by a single time constant. Furthermore, a moderate extension (approximately 30%) ensures a measurable change in observed DNA length during relaxation, improving the signal-to-noise ratio and fitting accuracy. In contrast, higher stretching ratios may induce nonlinear elastic responses or structural deformation of the DNA, especially under strong confinement. In principle, the relaxation time becomes independent of the stretching ratio immediately after the voltage is switched off and relaxation begins (initial stretching ratio). Fig. 4 shows the relationship between the initial stretching ratio and relaxation time for λ DNA and T4 DNA. The initial stretching ratio of λ DNA and T4 DNA were 13–30% and 3–14%, respectively, under the same conditions. In both cases, the measured relaxation times were randomly distributed and there was no significant dependence on the initial stretching ratio. This result demonstrates the advantages of the proposed method as a robust measurement method that allows for variations in the initial stretching rate. However, if the initial stretching rate is too low, the accuracy of the fitting is reduced, which reduces the relaxation time identification accuracy.
Relaxation time measurement using a mix of DNA samples
To further verify the effectiveness of the proposed size analysis scheme, we measured the relaxation time of a mix of DNA samples (50 μL), including λ and T4 DNA molecules, using a nanoslit channel of depth 130 nm. A periodic pulse consisting of 40 pulses with a period of 3 s and a duty cycle of 30% at 15 V was used to obtain sufficient data on the relaxation time. The number of DNA molecules analyzed was 150. The relaxation-time histogram revealed two distinct peaks (Fig. 5a). Moreover, we adopted this Gaussian-based resolution calculation to maintain consistency with the results of previous studies. In previous studies involving size analysis, Gaussian fitting is the standard approach. By applying the same method, we ensured comparability and methodological consistency across studies. The average and full width at half maximum (FWHM) of the two peaks were obtained by fitting two different Gaussian distributions. As shown in Fig. 5a, τ2 and τ1 are the average values of the two peaks and W1 and W2 are the FWHW values of the two peaks. The τ1 was 0.073 s (Fig. 5a), similar to the average value measured solely using λ DNA molecules (Fig. 3c), and the W1 was 0.034 s. The τ2 was 0.129 s (Fig. 5a), which was also similar to the value measured using T4 DNA molecules alone (Fig. 3f) and the W2 was 0.038 s. Therefore, these two peaks τ1 and τ2, correspond to the relaxation times of λ and T4 DNAs, respectively. The resolution (R) of size analysis is defined as follows:
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of λ to T4 DNA in nanoslit channels of 130 nm and 49 nm depth. As shown in Fig. S2,† distinct relaxation time peaks corresponding to the two DNA species were observed under both conditions. These results further confirm the robustness of our proposed method across different mixing ratios.
1 volume ratio of λ to T4 DNA in nanoslit channels of 130 nm and 49 nm depth. As shown in Fig. S2,† distinct relaxation time peaks corresponding to the two DNA species were observed under both conditions. These results further confirm the robustness of our proposed method across different mixing ratios.
Dependence of size analysis resolution on the nanoslit depth
The nanoslit depth affects the resolution of size analysis because when the depth of the nanoslit channel changes, the relaxation time of the DNA molecules also changes owing to the effective drag coefficient of the molecules being modified by their interaction with the channel walls. We experimentally verified this effect using nanoslit channels of four different depths: 130, 110, 69, and 49 nm. At the same electrophoresis voltage, when the channel depth became shallower, the stretching rate of the DNA molecule increased owing to an increase in the migration velocity. To maintain the elongation rate below 30% for all nanoslit channels, the pulse voltages were set to 15, 12, 8, and 6 V, respectively, corresponding to the channel depth.The proposed methodology determines the size distribution by analyzing the peaks in the histogram. Consequently, the resolution of this analysis is influenced by the number of DNA molecules whose relaxation times are evaluated. Therefore, when comparing the size analysis resolution based on the depth, the dependence on the number of molecules to be analyzed must also be simultaneously verified. As mentioned earlier, DNA stretching and relaxation were achieved by applying pulsed voltage. Approximately five DNA molecules were simultaneously observed to relax within the microscopic field of view during a single pulse. We recorded observations for 80 pulses and obtained the video data of 400 relaxing DNA molecules for each nanoslit channel. The period and duty ratio of the pulse voltage were 3 s and 30%, respectively.
From 400 datasets, we used the number of datasets increased in order, drew histograms for each, and calculated the resolution using eqn (4), as described in the previous section (Fig. S3–S6†). The relationship between the number of analyzed data and the resolution of size analysis is shown in Fig. 6. For all nanoslit channels, the resolution fluctuated when the dataset size was small; however, above a certain dataset size, it converged to a constant value. When the curvature on both the left and right sides of a given point and all subsequent points fall below a specified threshold, we can consider that the curve has flattened out, indicating that changes in resolution are no longer significant beyond this point. The resolutions were compared for those calculated over the minimum number of datasets, which were 150, 175, 200, and 100 for nanoslit depths of 130, 106, 69, and 49 nm, respectively. The relationship between the resolution calculated for the 400 datasets and the nanoslit channel depth is shown in Fig. 7. Error bars were added based on the standard errors of Gaussian fitting, but p-values were not calculated because each resolution value was derived from a single fitted distribution rather than repeated independent measurements. Decreasing the nanoslit depth led to an increase in the resolution of the DNA size analysis. As shown in eqn (4), the resolution was obtained by dividing the difference between τ1 and τ2 by the sum of the FWHMs. Regarding the depth dependence of the resolution, Fig. 7b shows the nanoslit depth dependence of τ1, τ2, and the differences (τ2 − τ1); with decreasing channel depth, the difference in relaxation times increased. Consequently, a maximum resolution of 2.33 was achieved in nanoslit channels with a depth of 49 nm.
 | ||
| Fig. 6 Size analysis resolution versus the number of DNA molecules analyzed using nanoslits of different depths: (a) 130 nm, (b) 110 nm, (c) 69 nm, and (d) 49 nm. | ||
Fig. 7c shows the sum of the FWHM. With the decreasing nanoslit depth, the FWHM increases. This trend may be caused by HI. Based on previous studies,36–38 DNA segments near the channel walls experience stronger hydrodynamic drag due to the no-slip boundary condition, which increases the local shear rate. When the slit is narrow, hydrodynamic reflections become stronger and more frequent. This leads to increased drag which reduces DNA mobility and slower relaxation. In our experiments, we did not distinguish whether the DNA molecules were located near the boundary of the nanoslit. Therefore, DNA molecules located at different positions may exhibit larger variations in relaxation time.
The relaxation time scaling of λ-DNA and T4-DNA is not a single decay. λ-DNA demonstrated a dependence of h−3.17 and T4-DNA showed a dependence of h−4.15 when the depth decreased from 125 nm to 106 nm. Since nanoslit height h is larger than the persistence length of DNA (∼100 nm), this range is categorized as weak confinement and DNA can be described as a series of blobs, which is known as de Gennes' blob model.29 When hydrodynamic interaction (HI) is assumed to dominate within a blob, the system follows the Zimm-blob model where the theoretical scaling of the longest relaxation time is follows h−7/6. When HI is completely suppressed throughout the chain, including inside blobs, the system follows the Rouse-blob model where its theoretical scaling of the longest relaxation time follows h−1/2. Our experimental results, which is h−3.17 for λ-DNA and h−4.15 for T4-DNA, differ from both the Zimm-blob model (h−7/6) the Rouse-blob model (h−1/2).
When nanoslit depth was reduced from 106 nm to 69 nm, the slope of relaxation time for λ-DNA and T4-DNA was h0.66 and h0.22 respectively. In addition, when the depth of the nanoslit decreased from 69 nm to 49 nm, the relaxation time for λ DNA decreased correspondingly, whereas for T4 DNA, the relaxation time increased. When nanoslit depth is less than 100 nm, DNA enters a strong confinement regime. The DNA chain segments are highly restricted vertically. The assumptions in the blob model including anisotropy and self-avoiding behavior are not applicable. This is considered as the transition from de Gennes to the Odijk regime. Following the theoretical analysis by Tang,39 the DNA molecule relaxation time in the Odijk regime can be defined as:
| τ ∼ ηLc5/2 | (5) |
The quantitative discrepancy observed between the experimental results and theoretical predictions was attributed to the complex factors influencing DNA relaxation during the experiments. These factors typically encompass the interaction between the surface and the DNA molecule, the ionic strength of the buffer, and alterations in the stiffness of the DNA molecule resulting from fluorescent staining. Previous studies41–43 have shown that electrostatic interactions between DNA and the nanoslit walls may contribute to variations in relaxation time. In our experiments, Lipidure®-BL203, which is a zwitterionic polymer, was added to the sample to inhibit electroosmotic flow. The polymer is adsorbed on the channel surface, thereby neutralizing the surface charge. Therefore, although the effects of electrostatic interactions are unlikely in our experimental system, there is an intermolecular interaction between the polymer and DNA. The quantitative effects of this interaction are challenging to predict, and we believe that this is the primary factor contributing to the observed discrepancies between the experimental and theoretical outcomes.
Moreover, Balducci et al. verified that the ionic strength of the buffer plays a critical role in DNA relaxation kinetics.44 As a polyelectrolyte, electrostatic repulsion between DNA molecular chain segments can be electrostatically screened by ions in solution. Therefore, the relaxation time of DNA molecules will be significantly influenced by electrostatic screening. Moreover, the experiment results suggest that the decreasing of ions strength will increase the relaxation time of DNA molecules. This may be because weaker electrostatic screening at low ionic strength enhances repulsion between DNA segments, which results in slowing down the relaxation process. This previous research indicates that an optimal reduction in the ionic strength of the buffer may extend the relaxation time, thereby facilitating measurements and enhancing resolution. Nonetheless, this adjustment may result in instability of the pH and ionic strength of the buffer during electrophoresis. Consequently, we used the ionic strength of the buffer that is typically employed in standard electrophoresis.
Various labeling dyes can influence the conformation and dynamics of DNA, particularly its relaxation behavior. YOYO-1, which binds to DNA through bis-intercalation, has been observed to increase the contour length, potentially impacting the relaxation time.45 In contrast, SYTO dyes, such as SYTO-13 and SYTO-82, bind to the minor groove or externally and do not intercalate deeply into DNA.46 A previous study showed that SYTO-13 and SYTO-82 do not significantly alter the DNA melting temperature or inhibit enzymatic activity. These dyes have a minimal influence on DNA conformation and stiffness. Based on the E. Shin et al. study,47 non-intercalating dyes, such as truncated TALE-FP (tTALE-FP), which bind to DNA without inserting between base pairs, do not alter DNA conformation, length, or mechanical properties. In our study, we opted to utilize YOYO-1, a non-intercalating dye, due to its high fluorescence quantum yield. This characteristic renders it particularly effective for single-molecule detection, including the analysis of stretching and folding dynamics. While relaxation measurements using non-intercalating dyes may provide insights that align more closely with the intrinsic dynamics of native DNA, YOYO-1's capabilities make it an optimal choice for our research objectives. In our proposed method, efficient data collection in a short time is essential because it allows the rapid capture of multiple relaxation trajectories. From this perspective, YOYO-1 offers practical advantages for the current experimental design.
As described above, the relaxation of DNA molecules in nanoslit channels depends on complex factors. However, our main goal is not to quantify the true relaxation time of DNA molecules. Instead, the focus is on utilizing relaxation time to determine their size. Consequently, our priority is to design conditions that are experimentally reproducible and have high resolution for size identification.
Analysis time and resolution of the proposed method
The total analysis time required to obtain the histogram was proportional to the number of molecules for which the relaxation time was analyzed. Therefore, the shortest analysis times corresponding to the minimum number of datasets for each channel depth were 90, 105, 120, and 60 s for depths of 130, 106, 69, and 49 nm, respectively. In the future, analysis times can be reduced by optimizing the structure of nanoslit devices and improving the image analysis techniques.Table 1 presents a comparison of different DNA size analysis techniques for a mixture of λ and T4 DNAs, focusing on the resolution, time, number of DNA molecules required for the analysis, and fabrication method. We also compared the advantages and disadvantages of different methods. The proposed DNA size analysis method, based on relaxation time measurement, outperformed the regular array of nanometer-sized pillars and solid nanowires in terms of resolution, with a processing time of less than 1 min. Compared to SEC, which uses microstructures, the proposed method demonstrated higher efficiency and improved resolution. Moreover, the proposed technique requires only 200 DNA molecules, with a significant reduction from approximately 1012 molecules required by other analysis methods. Furthermore, the device fabrication method employed in our device is notably simpler than previous approaches, thereby facilitating practical applications and large-scale production.
| Method | Resolution | Time | Number of molecules | Fabrication method | Advantages | Disadvantages |
|---|---|---|---|---|---|---|
| 100–500 nm wide pillars8 | 0.89 | 30 s | 1012 | Electron beam lithography | Simple sieving structure; relatively fast analysis | Low throughput; low resolution; large molecule number |
| Size exclusion chromatography20 | 1.8 | 80 min | Photolithography and FIB trimming | Gentle for large DNA; integrated pre-concentration; suitable for size-based separation in microscale channels | Long analysis time; large molecule number | |
| Nanorod sieving matrix22 | 2.1 | 10.6 s | Photolithography and oblique angle deposition | High resolution; fast analysis; simple nanorod integration; flexible design | Fabrication-dependent pore sizes; moderate cost; large molecule number | |
| Solid nanowires35 | 0.91 | 4 s | Photolithography and nanowire VLS growth | Ultrafast analysis; tunable 3D structure; wide DNA range | Low resolution; limited efficiency for short DNA fragments in sparse networks | |
| Relaxation time by nanoslit with 49 nm | 2.33 | 60 s | 200 | Photolithography | High resolution; fast; minimal sample requirement; simple photolithographic fabrication | No physical separation; relies on statistical sampling and relaxation dynamics analysis |
The separation of λ DNA and T4 DNA serves as a standard reference for assessing the effectiveness of microdevices in analyzing the molecular weight of large DNA molecules. In this study, we focused on experiments using mixed samples of λ and T4 DNA to verify the principle of our proposed method and to demonstrate its superiority over methods developed in previous studies by clarifying the dependence on channel depth, which has the greatest impact on performance. A future task will be to confirm the versatility of the proposed method. We plan to demonstrate its usefulness for DNA samples with diverse molecular weight distributions, for example, using high-molecular-weight DNA ladders.
Based on eqn (4), we can estimate from the results of this experiment the limiting value of the molecular weight at which the peaks can be separated, R = 0.5. Assuming that the sum of the peak widths shown in Fig. 7(c), i.e., W1 + W2, does not depend significantly on the molecular size and is approximately 0.15, and assuming the difference between molecular weight and relaxation time with a linear relationship, limiting value of peak separation is estimated to be 25 kbp. In principle, the resolution of our proposed method increases with increasing molecular weight, because the relaxation time becomes exponentially delayed with increasing molecular weight.
Recent developments in microscopy, such as super-resolution technology, have led to the development of techniques for optical mapping and optical measurement of DNA sizes.48 Especially, optical mapping is suitable for comprehensive genome-wide structural mapping and genotyping. However, optical mapping generally requires the use of advanced instruments and high-resolution imaging techniques, and the analysis duration is typically extensive. Our method, however, is optimized for efficient, high-resolution size analysis, which is particularly beneficial in applications such as nucleic acid medicine manufacturing, artificial genome construction, and rapid genotyping of large DNA fragments.
Conclusions
In this study, we proposed a novel method for the size analysis of large DNA molecules by measuring the relaxation time of DNA molecules using nanoslit channels. Using DNA samples containing two different sizes (λ and T4 DNAs), we showed that size discrimination can be realized at high resolution by generating histograms of relaxation times measured in nanoslit channels. In addition, we found that the resolution of the size analysis improved as the channel depth decreased. The maximum resolution of 2.33 was achieved with a nanoslit depth of 49 nm in 60 s. Furthermore, the minimum sample volume required for size analysis was systematically investigated and it was shown that 100–200 molecules are sufficient for the proposed method at any depth. This new measurement method represents a highly effective and accurate DNA size analysis technique with promising applications in genotyping drug-resistant bacteria and large DNA molecule synthesis. Furthermore, it effectively prevents the mechanical damage of large DNA molecules by reducing the risk of collision between DNA molecules and nanostructures, which is crucial for the recycling and reuse of large DNA molecules.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
H. Yi and S. Itoh designed and conducted the overall experiments and performed the data analysis. K. Fukuzawa provided the resources. H. Zhang contributed to the validation of the results. N. Azuma helped with the methodology and visualization. S. Itoh conceived and acquired the funding for this project. H. Yi wrote the paper and all authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was partially supported by KAKENHI [grant number 23K17717].Notes and references
- T. U. Berendonk, C. M. Manaia, C. Merlin, D. Fatta-Kassinos, E. Cytryn, F. Walsh, H. Bürgmann, H. Sørum, M. Norström, M. N. Pons, N. Kreuzinger, P. Huovinen, S. Stefani, T. Schwartz, V. Kisand, F. Baquero and J. L. Martínez, Nat. Rev. Microbiol., 2015, 13, 310–317 CrossRef CAS PubMed.
- R. C. MacLean and Á. San Millán, Science, 2019, 365, 1082–1083 CrossRef CAS PubMed.
- M. Naddaf, Nature, 2024, 633, 747–748 CrossRef CAS PubMed.
- R. V. Goering, Infect., Genet. Evol., 2010, 10, 866–875 CrossRef CAS PubMed.
- H. M. Neoh, X. E. Tan, H. F. Sapri and T. L. Tan, Infect., Genet. Evol., 2019, 74, 103935 CrossRef CAS PubMed.
- J. Herschleb, G. Ananiev and D. C. Schwartz, Nat. Protoc., 2007, 2, 677–684 CrossRef CAS PubMed.
- T. Yasui, N. Kaji, R. Ogawa, S. Hashioka, M. Tokeshi, Y. Horiike and Y. Baba, Anal. Chem., 2011, 83, 6635–6640 CrossRef CAS PubMed.
- N. Kaji, Y. Tezuka, Y. Takamura, M. Ueda, T. Nishimoto, H. Nakanishi, Y. Horiike and Y. Baba, Anal. Chem., 2004, 76, 15–22 CrossRef CAS PubMed.
- J. Fu, R. B. Schoch, A. L. Stevens, S. R. Tannenbaum and J. Han, Nat. Nanotechnol., 2007, 2, 121–128 CrossRef CAS PubMed.
- W. D. Volkmuth and R. H. Austin, Nature, 1992, 358, 600–602 CrossRef CAS PubMed.
- J. Fu, J. Yoo and J. Han, Phys. Rev. Lett., 2006, 97, 018103 CrossRef PubMed.
- Y. Zeng and D. J. Harrison, Anal. Chem., 2007, 79, 2289–2295 CrossRef CAS PubMed.
- J. Fu, P. Mao and J. Han, Appl. Phys. Lett., 2005, 87, 263902 CrossRef PubMed.
- J. Han and H. G. Craighead, Science, 2000, 288, 1026–1029 CrossRef CAS PubMed.
- B. H. Wunsch, S. C. Kim, S. M. Gifford, Y. Astier, C. Wang, R. L. Bruce, J. V. Patel, E. A. Duch, S. Dawes, G. Stolovitzky and J. T. Smith, Lab Chip, 2019, 19, 1567–1578 RSC.
- A. Hochstetter, R. Vernekar, R. H. Austin, H. Becker, J. P. Beech, D. A. Fedosov, G. Gompper, S.-C. Kim, J. T. Smith, G. Stolovitzky, J. O. Tegenfeldt, B. H. Wunsch, K. K. Zem-ing, T. Krüger and D. W. Inglis, ACS Nano, 2020, 14, 10784–10795 CrossRef CAS PubMed.
- B. H. Wunsch, J. T. Smith, S. M. Gifford, C. Wang, M. Brink, R. L. Bruce, R. H. Austin, G. Stolovitzky and Y. Astier, Nat. Nanotechnol., 2016, 11, 936–940 CrossRef CAS PubMed.
- P. S. Doyle, J. Bibette, A. Bancaud and J. L. Viovy, Science, 2002, 295, 2237–2237 CrossRef CAS PubMed.
- T. Yasui, S. Rahong, K. Motoyama, T. Yanagida, Q. Wu, N. Kaji, M. Kanai, K. Doi, K. Nagashima, M. Tokeshi, M. Taniguchi, S. Kawano, T. Kawai and Y. Baba, ACS Nano, 2013, 7, 3029–3035 CrossRef CAS PubMed.
- N. Azuma, S. Itoh, K. Fukuzawa and H. Zhang, Jpn. J. Appl. Phys., 2016, 55, 06GN01 CrossRef.
- N. Azuma, S. Itoh, K. Fukuzawa and H. Zhang, Jpn. J. Appl. Phys., 2018, 57, 027002 CrossRef.
- Z. Cao, Y. Zhu, Y. Liu, S. Dong, J. Zhao, Y. Wang, S. Yang and J. Fu, Biosens. Bioelectron., 2019, 137, 8–14 CrossRef CAS PubMed.
- Z. Cao and L. Yobas, ACS Nano, 2015, 9, 427–435 CrossRef CAS PubMed.
- L. Duan, Z. Cao and L. Yobas, Anal. Chem., 2017, 89, 10022–10028 CrossRef CAS PubMed.
- Z. Cao and L. Yobas, Anal. Chem., 2014, 86, 737–743 CrossRef CAS PubMed.
- F. Shiri, J. Choi, C. Vietz, C. Rathnayaka, A. Manoharan, S. Shivanka, G. Li, C. Yu, M. C. Murphy, S. A. Soper and S. Park, Lab Chip, 2023, 23, 4876–4887 RSC.
- T. Yasui, N. Kaji, R. Ogawa, S. Hashioka, M. Tokeshi, Y. Horiike and Y. Baba, Nano Lett., 2015, 15, 3445–3451 CrossRef CAS PubMed.
- A. Balducci, C. C. Hsieh and P. S. Doyle, Phys. Rev. Lett., 2007, 99, 238102 CrossRef CAS PubMed.
- C. C. Hsieh, A. Balducci and P. S. Doyle, Macromolecules, 2007, 40, 5196–5205 CrossRef CAS.
- D. J. Bonthuis, C. Meyer, D. Stein and C. Dekker, Phys. Rev. Lett., 2008, 101, 108303 CrossRef PubMed.
- J. Hartmann, T. Roy, K. Szuttor, J. Smiatek, C. Holm and S. Hardt, Soft Matter, 2018, 14, 7926–7933 RSC.
- J. O. Tegenfeldt, C. Prinz, H. Cao, S. Chou, W. W. Reisner, R. Riehn, Y. M. Wang, E. C. Cox, J. C. Sturm, P. Silberzan and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 10979–10983 CrossRef CAS PubMed.
- K. Jo, D. M. Dhingra, T. Odijk, J. J. de Pablo, M. D. Graham, R. Runnheim, D. Forrest and D. C. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2673–2678 CrossRef CAS PubMed.
- T. T. Perkins, S. R. Quake, D. E. Smith and S. Chu, Science, 1994, 264, 822–826 CrossRef CAS PubMed.
- S. Rahong, T. Yasui, T. Yanagida, K. Nagashima, M. Kanai, A. Klamchuen, G. Meng, Y. He, F. Zhuge, N. Kaji, T. Kawai and Y. Baba, Sci. Rep., 2014, 4, 5252 CrossRef CAS PubMed.
- D. Stigter, Biophys. Chem., 2002, 101–102, 447–459 CrossRef CAS PubMed.
- Q. He, H. Ranchon, P. Carrivain, Y. Viero, J. Lacroix, C. Blatché, E. Daran, J.-M. Victor and A. Bancaud, Macromolecules, 2013, 46, 6195–6202 CrossRef CAS.
- P.-K. Lin, J.-F. Chang, C.-H. Wei, P. H. Tsao, W. S. Fann and Y.-L. Chen, Phys. Rev. E, 2011, 84, 031917 CrossRef PubMed.
- J. Tang, S. L. Levy, D. W. Trahan, J. J. Jones, H. G. Craighead and P. S. Doyle, Macromolecules, 2010, 43, 7368–7377 CrossRef CAS.
- W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101 CrossRef PubMed.
- Y. Ren and D. Stein, Phys. Rev. Lett., 2011, 106, 068302 CrossRef PubMed.
- C. Manneschi, P. Fanzio, T. Ala-Nissila, E. Angeli, L. Repetto, G. Firpo and U. Valbusa, Biomicrofluidics, 2014, 8, 064121 CrossRef PubMed.
- K. D. Dorfman, D. Gupta, A. Jain, D. M. Mannion, T. M. Squires and D. E. Smith, Eur. Phys. J.: Spec. Top., 2014, 223, 3179–3200 CAS.
- C.-C. Hsieh, A. Balducci and P. S. Doyle, Nano Lett., 2008, 8, 1683–1688 CrossRef CAS PubMed.
- M. L. Bennink, O. D. Schärer, R. Kanaar, K. Sakata-Sogawa, J. M. Schins, J. S. Kanger, B. G. de Grooth and J. Greve, Cytometry, 1999, 36, 200–208 CrossRef CAS PubMed.
- H. Gudnason, M. Dufva, D. D. Bang and A. Wolff, Nucleic Acids Res., 2007, 35, e127 CrossRef PubMed.
- E. Shin, W. Kim, S. Lee, J. Kim, H. Jeon and D. Kim, Sci. Rep., 2019, 9, 17197 CrossRef PubMed.
- N. Azuma, K. Fukuzawa and S. Itoh, Appl. Phys. Lett., 2021, 119, 023701 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00998c |
| This journal is © The Royal Society of Chemistry 2025 |






