Particularly strong C–H⋯π interactions between benzene and all-cis 1,2,3,4,5,6-hexafluorocyclohexane

Abstract

We present the first high-level ab initio benchmark study of the interaction energy between fluorocyclohexanes and benzene. These compounds form CH⋯π interactions with aromatic solvents which causes notable shielding of the axial cyclohexane protons. For the recently synthesised all-cis 1,2,3,4,5,6-hexafluorocyclohexane the interaction energy with benzene amounts to −7.9 kcal mol⁻¹ and −6.4 kcal mol⁻¹ at the MP2 and SCS-MP2 levels, respectively (extrapolated to the complete basis set limit), which according to dispersion-corrected density functional calculations, is largely due to dispersion.

---

When fluorine atoms are added to organic compounds, interesting physicochemical properties may arise, which cannot be obtained using other elements from the periodic table.¹ Indeed, it was recently shown both experimentally² by ¹H NMR and theoretically³ that the all-cis 1,2,4,5- (1) and the 1,2,3,4-tetrafluorocyclohexanes (2, Fig. 1a and b) form CH⋯π interactions with molecules of aromatic solvents. These interactions arise from the high polarity of these all-cis tetrafluoro species, which have a “negative face” on the side of the axial fluorine atoms and a “positive face” on the hydrogen side (Fig. 1c). Such CH⋯π interactions lead to a close contact between the axial hydrogens and the arene π electrons. Thus, the axial hydrogen atoms show unusually large upfield shifts caused by anisotropic diamagnetism originating from the arene ring current (Fig. 1d).

Fig. 1 Schematic representations of (a) all-cis 1,2,4,5-tetrafluorocyclohexane (1), (b) all-cis 1,2,3,4-tetrafluorocyclohexane (2); (c) the “negative” and “positive” faces for compound 1; and (d) the induced ring-current effect on axial ¹H atoms of 1 interacting with a benzene molecule.

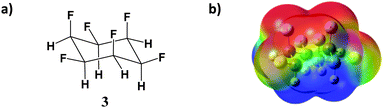
Recently, the synthesis of all-cis 1,2,3,4,5,6-hexafluorocyclohexane (3) was reported.⁴ This compound (Fig. 2a) was found to bear a very high dipole moment for a non-ionic organic compound, calculated to be 6.2 D at the M11/6-311G(2d,p) level. This hexafluorocyclohexane will reasonably have an even higher interaction energy with benzene compared to the tetrafluorocyclohexanes 1 and 2.

Fig. 2 (a) Structural representation of all-cis 1,2,3,4,5,6-hexafluorocyclohexane (3). (b) Electrostatic potential (ESP) of 3 [B3LYP-D3/def2-TZVP] color-coded on a scale from −0.03 au (red) to +0.03 au (blue) and mapped onto an isodensity surface ρ = 0.001 au.

Our previous DFT analysis of those CH⋯π interactions for the complex formed between 1 or 2 and benzene indicated a binding energy of ca. −1.5 kcal mol⁻¹ at the B3LYP/def2-TZVP level and a CH⋯π distance of ca. 3.10–3.25 Å.³ When one includes Grimme's DFT-D or DFT-D3 dispersion corrections⁵ the binding energies for those complexes rises to ca. −6 kcal mol⁻¹ and much closer C–H⋯π contacts of ca. 2.6–2.7 Å result. However, the NMR chemical shifts computed for the B3LYP-optimised complexes appeared to reproduce the upfield shifts observed in aromatic solvents better than those using the tighter geometries obtained with dispersion corrections.

In order to validate these DFT results and to arrive at a more confident value for the interaction energy between these polar fluorocyclohexanes and aromatics, high-level ab initio benchmarks are necessary. The newly synthesised hexafluorocyclohexane 3 is an ideal target for this purpose, because its complex with the simplest aromatic, benzene, can have high symmetry (C_3v, Fig. 3), all CH⋯π contacts being equivalent. We now present such a high-level ab initio benchmark for the CH⋯π binding energies between compound 3 and benzene at MP2 and SCS-MP2 levels, extrapolated to the complete basis set (CBS) limit. In addition, the ¹H chemical shift values for 3 were recorded in CD₂Cl₂ and benzene-d₆, and the resulting upfield shifts were compared with those computed on going from free 3 to the complex with benzene.

Fig. 3 Calculated geometries of benzene with: (a) all-cis 1,2,3,4,5,6-hexafluorocyclohexane (3), (b) all-cis 1,3,5-trifluorocyclohexane (4) and (c) cyclohexane (5). Geometries shown have C_3v symmetry.

In order to more fully evaluate the effect of fluorine atoms on the binding energy of 3 with benzene, two additional model systems were calculated, namely all-cis 1,3,5-trifluorocyclohexane (4) and cyclohexane (5) (Fig. 3).

Initial calculations were performed at B3LYP, B3LYP-D3 and MP2 levels in conjunction with the def2-TZVP basis set, similar to the levels used in our previous studies of compounds 1 and 2.³ With tight optimisation criteria and an “ultrafine” integration grid (see Computational details in the ESI†), the complexes of 3 and 4 with benzene are true minima at the B3LYP level in C_3v symmetry. At B3LYP-D3 a very small imaginary frequency appears, which describes rotation of the two rings relative to each other about the C₃ axis. This rotation is indicated to lower the energy by just fractions of a kcal mol⁻¹, implying essentially free rotation of the two parallel rings. Thus, we kept C_3v symmetry imposed throughout.

Consistent with our previous work on 1 and 2,³ the B3LYP functional showed much longer contacts between the cyclohexanes and benzene, as well as smaller energy values than B3LYP-D3 and also MP2 (Table 1). Indeed, as expected, B3LYP fails to find an interaction between the parent cyclohexane (5) and benzene. On the other hand, B3LYP-D3 and MP2 find strong CH⋯π binding energies with short distances for all compounds 3–5. When converted into enthalpies and Gibbs free energies using standard thermodynamic corrections from the frequency calculations from each level, the binding energy becomes weaker for enthalpies and even endergonic for Gibbs free energies (Table S1 in the ESI†). Still, for the complexes between benzene and 3 or 4, B3LYP-D3 and MP2 indicate binding energies approaching and even exceeding strengths of typical hydrogen bonds (e.g. ca. 5 kcal mol⁻¹ for the water dimer⁶). This binding energy increases steadily with the number of fluorines, from ca. −3 kcal mol⁻¹ for n = 0 via −5 kcal mol⁻¹ and −6 kcal mol⁻¹ for n = 3 and 4, respectively, to −7 kcal mol⁻¹ for n = 6 (B3LYP-D3/def2-TZVP level, Table 1). From these data, it is evident that it is not only the bond dipoles from the axial fluorine atoms in 3·C₆H₆ that are responsible for the strong binding, but that both equatorial and axial fluorine atoms are important. Comparison of B3LYP and B3LYP-D3 results (Table 1) indicates that the largest fraction of this interaction stems from dispersion rather than from electrostatic (e.g. dipole–quadrupole) interactions.

Table 1 Calculated distances and binding energies obtained at B3LYP/def2-TZVP, B3LYP-D3/def2-TZVP and MP2/aug-cc-pVDZ levels for complexes of 1–5 and benzene. Complexes for compounds 3–5 have C_3v symmetry. Optimised C–H⋯π distance in angstroms were obtained with basis set superposition error (BSSE) corrections included through the counterpoise method

		C–H⋯π distance (Å)	Binding energy (kcal mol^−1)
a Average of three C–H⋯π distances. b Unbound (no minimum found).
B3LYP	1	3.27^a	−1.26
	2	3.35^a	−1.28
	3	3.11	−2.12
	4	3.44	−0.75
	5	n.a.^b	n.a.^b
B3LYP-D3	1	2.77	−5.76
	2	2.90^a	−6.05
	3	2.69	−7.06
	4	2.79	−4.84
	5	2.83	−3.40
MP2	1	2.78	−5.71
	2	2.90^a	−6.34
	3	2.71	−6.95
	4	2.81	−4.88
	5	2.87	−3.17

---

The close correspondence between B3LYP-D3 and MP2 data in Table 1 is noteworthy. Because MP2 results tend to be much more basis-set dependent than DFT, we decided to perform extrapolations to the CBS limit for compounds 3 and 4 following a protocol by Helgaker et al.⁷ This protocol involves single-point calculations with correlation-consistent basis sets (up to aug-cc-pVQZ; for details see ESI,† Tables S2–S5 and Fig. S1). It has recently been reported that while standard MP2 may overestimate weak intermolecular interactions relative to CCSD(T) benchmarks (e.g. for the benzene dimer),⁸ the parametrised spin-component-scaled (SCS) variant⁹ performs much better. We therefore performed both MP2/CBS and SCS-MP2/CBS extrapolations (Table 2).

Table 2 Binding energies (kcal mol⁻¹) obtained at the HF, MP2 and SCS-MP2 ab initio methods with the complete basis set (CBS) for compounds 3 and 4

	3	4
a Estimated uncertainty ±0.4 kcal mol^−1 (see ESI for details).
HF/CBS	−0.13	+1.41
MP2/CBS^a	−7.93	−5.75
SCS-MP2/CBS^a	−6.39	−4.33

---

At the MP2-optimised distance, the HF method shows essentially vanishing or even repulsive interactions for both compounds 3 and 4 with benzene.¹⁰ Predicted binding energies for 3 at MP2/CBS and SCS-MP2/CBS levels are ca. −8 kcal mol⁻¹ and −6 kcal mol⁻¹, respectively, (ca. −6 kcal mol⁻¹ and −4 kcal mol⁻¹, respectively, for 4), bracketing the B3LYP-D3 values in Table 1, thus reinforcing the reliability of that level. The SCS-MP2 predicted binding energy of −6.4 kcal mol⁻¹ for 3·C₆H₆ is, to our knowledge, the largest C–H⋯π interaction energy between benzene and an aliphatic hydrocarbon, larger than that between benzene and chloroform.¹¹ In view of the dominance of dispersion discussed above one may argue that the overall interaction energy is not arising from three local C–H⋯π interactions,¹² but should rather be attributed to the large molecular size of 3. Irrespective of the individual contributions to the total interaction energy, however, topological analysis indicates the presence of three distinct bond paths between the axial H atoms of 3 and C atoms of benzene, and a weakly attractive noncovalent interaction between them (MP2/aug-cc-pVDZ density, see Fig. S2 in the ESI†).

¹H NMR chemical shift (δ) values for compound 3 have been obtained theoretically at the BHandH/6-311+G(2d,p) level¹³ and are compared to experimentally obtained data in Table 3 (more details in Tables S6–S8 in the ESI†). Observed solvent shifts Δδ on going from dichloromethane to benzene are modelled as the difference between pristine 3 and its complex with benzene. Irrespective of the source geometry, optimised at either B3LYP, B3LYP-D3 or MP2 levels, the computed trends are in qualitative agreement with experimental values (Table 3) accounting for roughly half of the observed upfield shift. In order to simulate the entire shielding effect exerted by the arene solvent, more solvent molecules would have to be included in a dynamic description. Calculations for a single benzene molecule placing “ghost atoms” at the positions of axial and equatorial H atoms in the complex with 3 indicate that the observed shifts are largely (but not exclusively) due to the anisotropy (ring current) effect in the aromatic solvent (Table S9 in the ESI†).

Table 3 Theoretical chemical shift (δ) values obtained from BHandH/6-311+G(2d,p) calculations on B3LYP, B3LYP-D3 and MP2 optimised geometries with the def2-TZVP basis set for pristine compound 3 and its complex with benzene, as well as the experimental values in dichloromethane and benzene

	δ(Hax)		δ(Heq)		Δδ(Hax)	Δδ(Heq)
	Gas/CH2Cl2	C6H6	Gas/CH2Cl2	C6H6
a Pristine 3. b 3·C6H6 complex.
B3LYP	4.90^a	3.79^b	6.10^a	5.45^b	−1.11	−0.65
B3LYP-D3	3.74^a	2.86^b	4.92^a	4.39^b	−0.88	−0.53
MP2	4.01^a	3.17^b	5.17^a	4.67^b	−0.84	−0.50
Exp.	4.53	2.88	5.32	4.41	−1.65	−0.91

---

As observed previously for the benzene complexes of 1 and 2, the results for the B3LYP geometry for 3 seem to fit better to the observed solvent shifts than those using the more optimal B3LYP-D3 structure. Apparently, the shorter CH⋯π separations in the B3LYP-D3 minimum (Table 1) bring the axial H atoms out of the shielding cone. From the anharmonicity of the 3⋯C₆H₆ stretching potential (Fig. 4a), thermal averaging might be expected to increase the intermolecular distance somewhat (approaching the B3LYP value), but from the small computed variation of the chemical shifts in the distance range of interest, 2.6–3.1 Å, little effect on the Δδ values is expected upon thermal averaging over this single coordinate. Again, full dynamics and more solvent molecules would have to be included for quantitative modelling. In any event, the upfield shifts of the axial H atoms for compound 3 in aromatic solvents are of similar magnitude (ca. −1.7 ppm) to those observed in the all-cis tetrafluoro derivatives 1 and 2.^3a

Fig. 4 (a) Binding energies of the 3·C₆H₆ complex vs. C–H⋯π distances. (b) Dependence of the chemical shifts in the 3·C₆H₆ complexation vs. the C–H⋯π distance. Energies calculated at B3LYP-D3/def2-TZVP level and shielding tensors on BHandH/6-311+G(2d,p) levels. BSSE corrections included.

Conclusions

In summary, we have presented the first high-level ab initio benchmark study (MP2/CBS and SCS-MP2/CBS) for the CH⋯π interaction energies between fluorocyclohexanes and benzene. The interaction energies proved to be strong (ca. 6–8 kcal mol⁻¹ in total for 3), and are well described by dispersion-corrected DFT functionals. The affinity toward aromatic solvents is reflected in notable changes in ¹H chemical shifts that are rationalised by way of ring current effects. This affinity could clearly be exploited in crystal engineering or liquid crystal design.

Theoretical and experimental procedures

Geometries were fully optimised in C_3v symmetry at the B3LYP/def2-TZVP, B3LYP-D3/def2-TZVP and MP2/aug-cc-pVDZ levels including BSSE corrections; single point energies for the MP2 geometries refined at MP2 and SCS-MP2 levels using auc-cc-pVxZ basis sets (X = D, T, Q) and extrapolated to the CBS limit.⁷¹H NMR measurements were carried out on a Bruker Avance III 700 spectrometer, operating at 700 MHz, using the deuterated solvent as the reference for internal deuterium lock. See ESI† for further details and references.

Acknowledgements

We thank EaStCHEM and the University of St Andrews for access to a computing facility managed by Dr H. Fruchtl, CNPq and FAPESP for the studentship for R. A. C. (#2011/01170-1, FAPESP) and for financial support (#2014/25903-6), as well as CNPq for the fellowship for R. R. DO'H thanks the Royal Society for a Wolfson Research Merit Award.

Notes and references

1. (a) D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308; (b) P. A. Champagne, J. Desroches, J.-D. Hamel, M. Vandamme and J.-F. Paquin, Chem. Rev., 2015, 115, 9073.
2. (a) A. J. Durie, A. M. Z. Alexandra, T. Lebl, P. Kirsch and D. O'Hagan, Chem. Commun., 2011, 47, 8265; (b) A. J. Durie, A. M. Z. Slwein, T. Lebl, P. Kirsch and D. O'Hagan, Chem. Commun., 2012, 48, 9643; (c) A. J. Durie, T. Fujiwara, R. Cormanich, M. Bühl, A. M. Z. Slawin and D. O'Hagan, Chem. – Eur. J., 2014, 20, 6259.
3. (a) R. A. Cormanich, A. J. Durie, R. Bjornsson, R. Rittner, D. O'Hagan and M. Bühl, Helv. Chim. Acta, 2014, 97, 797; (b) R. A. Cormanich, R. Rittner, D. O'Hagan and M. Bühl, J. Phys. Chem. A, 2014, 118, 7901.
4. N. S. Keddie, A. M. Z. Slawin, T. Lebl, D. Philp and D. O'Hagan, Nat. Chem., 2015, 7, 483.
5. (a) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456; (b) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
6. M. W. Feyereinsen, D. Feller and D. A. Dixon, J. Phys. Chem., 1996, 100, 2993.
7. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639.
8. E. Miliordos, E. Apra and S. S. Xantheas, J. Phys. Chem. A, 2014, 118, 7658.
9. S. J. Grimme, Chem. Phys., 2003, 118, 9095.
10. A small net binding should prevail at the HF level upon full optimisation, given the large dipole moments of the fluorocyclohexanes (calculated dipole moments for 3 and 4 are 5.15 D and 5.94 D, respectively, at B3LYP-D3/def2-TZVP).
11. −5.2 kcal mol⁻¹ (expt.: (a) A. Fujii, K. Shibasaki, T. Kazama, R. Itaya, N. Mikami and S. Tsuzuki, Phys. Chem. Chem. Phys., 2008, 10, 2836 ); stronger individual C–H⋯π interactions exceeding 6 kcal mol⁻¹ are known, but these involve larger aromatic systems (review: ; (b) M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873 ).
12. In line with observations that the number of C–H groups of aliphatic hydrocarbons in contact with a benzene ring does not correlate with the magnitude of the interaction energy: A. Fujii, H. Hayashi, J. W. Park, T. Kazama, N. Mikamia and S. Tsuzuki, Phys. Chem. Chem. Phys., 2011, 13, 14131.
13. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details, NMR spectra and experimental details, extrapolation details and data, calculated isotropic shielding data. See DOI: 10.1039/c5cp04537a

---