DOI:
10.1039/C3RA46697C
(Paper)
RSC Adv., 2014,
4, 9064-9071
Convection and mass transfer enhanced rapid capacitive serum immunoassay
Received
14th November 2013
, Accepted 2nd December 2013
First published on 2nd December 2013
Abstract
The mechanism of conventional serum immunoassay typically relies on the nature of diffusion of the target analytes, which can cause slow specific binding and long detection times. This work presents a rapid capacitive immunoassay which enhances analyte transport by integrating the AC electrothermal (ACET) flow stirring and capacitive biosensing. The ACET flow conveys target molecules towards the probe-coated electrode surface, and leads to rapid preconcentration of target analytes and an instant capacitance change at the electrode–fluid interface. Numerical simulation of ACET convection and mass transfer is provided to analyze how the ACET flow affects the target molecule flux and binding with immobilized receptors. Bovine progesterone diagnosis is demonstrated as an experimental validation. Pregnancy positive and negative serum can be distinguished in 60 seconds. This rapid, sensitive label-free immunoassay can be readily integrated into many microsystems for the detection of many other immunoglobulins.
1 Introduction
Clinical diagnosis requires highly sensitive, quantitative, and rapid detection platforms1,2 for the multiplexed monitoring of target analytes. Conventional optical immunosensors usually need fluorescence/enzyme3 or metallic particle tagging, thus label-free detection is necessary for in-situ diagnoses that can avoid large and expensive optical systems. Capacitive sensing can be integrated towards these needs for real-time monitoring of analytes without requiring any labels or surface modifications.4,5 The underlying mechanism of capacitive immunoassay is that material changes on the surface will cause changes in the impedance of the electrode–fluid system,6,7 providing a direct means to detect binding reactions on the electrode surface.5,8 However, the ultimate performance of the capacitive sensors can often be limited by the diffusion of the target analytes due to a lack of turbulence on a small scale.9 For example, the capacitance change was monitored for 70 min in Shen's work.10 Exciting with a voltage could decrease the time required per measurement and is suited for real time measurements due to the convection and mass transfer in the fluid.11,12 Thus the trapping efficiency of the target analytes is increased by means of fluid motion or particle pre-concentration. Numerical simulations show that 6 Vrms applied to electrodes near a binding region can increase binding in the first few minutes by a factor of seven,13 making the optical immunoassay rapid and much more sensitive. However this voltage may cause an undesirable temperature rise or chemical reactions, which are not suitable for capacitive sensing.
Here we present a novel capacitive serum immunoassay, in which an appropriate voltage is applied not only for capacitive sensing, but also for the excitation voltage to generate electrothermal flow. As a result, a single-step rapid operation is achieved without any risk of harmful temperature rise or chemical reactions. The unique feature of this capacitive biosensing is that the convection and mass transfer enhanced target analytes preconcentration step is not separate from the capacitance measurement step, and this differs our work from others.14 The single-step operation provides a simple, robust technique of small form factor, which is mass production ready with various materials and can be readily integrated into many microsystems at a low cost.
The mechanism of convection and mass transfer enhanced capacitive immunoassay is presented in Section 2, and the detailed numerical simulation of target pre-concentration enhanced by convection and mass transfer is given in Section 3. As a proof-of-concept, rapid progesterone detection by real time capacitive measurements is described in Section 4. The preliminary test verifies that the mechanism of convection and mass transfer enhanced rapid capacitive immunoassay. Specifically, the capacitive immunoassay is indicated by electrode–fluid interfacial capacitance change rate in the experiments, while the target concentration distribution is investigated in the simulation parts. According to the mechanism of capacitive immunoassay, the target particle concentration distribution in the micro channel or on the electrode surface directly reflects the amount of deposited particles and the binding efficiency. Thus it is reasonable to use the target particle concentration to represent the electrode–fluid interfacial capacitance in the numerical investigations.
2 Mechanism of particle preconcentration for rapid capacitive biosensing
2.1 Capacitive sensing of particle deposition
When the electrodes are immersed into a liquid electrolyte, a thin layer of counter ions is formed at the interface of the electrode and the fluid to neutralize the surface charges at the electrode, which is commonly known as the electric double layer (EDL) with a thickness of Debye length, λD. The impedance between a pair of electrodes immersed in liquid can be approximated as a series connection of the interfacial capacitor, Cint, and resistive components including charge transfer, Rct, resistance and electrolyte resistance, Rm. As long as macromolecules are adsorbed on to the electrode surface, the electrode–electrolyte interfacial capacitance will change, which can be correlated to the deposition of macromolecules or particles on the electrode as well as the macromolecule/particle concentration in the fluid.15 The interfacial capacitance response is generally proportional to the amount of bound macromolecules, thus can potentially be used for quantitative measurements. The relative change in capacitance, (C′int − Cint0)/Cint0 (here Cint0, C′int denotes the interfacial capacitance before and after target analyte deposition), can reveal the target particle deposition thus the specific binding.8 This is the main mechanism of capacitive sensing. However, conventional capacitive sensing typically relies on analyte diffusion for transport, thus it needs a long detection time (i.e. hours) and lacks sensitivity.
2.2 Analyte preconcentration for rapid biosensing
The flow-through microfluidic system, in which the flow is always confirmed as laminar flow, has a limited positive effect to enhance the surface binding. When the AC electric field is applied to the serum, the ACET effect would generate vortices that give positive guidance to the target progesterone towards the surface functionalized electrodes, leading to a high local concentration near the electrode surface.16 Fig. 1 provides the schematic diagram of particle movements generated by convection and mass transfer under a nonuniform AC electric field. Target particles are transported towards the electrode surface under an AC electric field.7,17 The EDL thickness before and after particle deposition is λD and dp + λD, where dp is the particle diameter. As a result, the interfacial capacitance decreases with time during the particle deposition process. For affinity binding which follows sandwich-like procedures, the EDL thickness values before and after affinity binding are drec + λD, and drec + dtar + λD, respectively, where drec, dtar stand for diameter of receptors and targets. Consequently, the capacitance change will be −dtar/[(drec + dtar) + λDεtar/εm], in which εtar and εm are permittivity of target and medium, respectively.
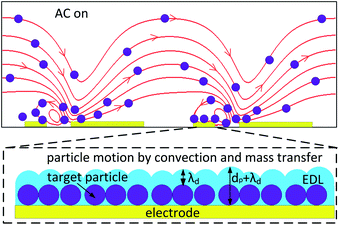 |
| | Fig. 1 Schematic diagram of particle movements under the effect of electrothermal fluid flow near the electrodes (indicated with yellow bars). The EDL thickness increases to dp + λD after particle deposition, thus the interfacial capacitance decreases. This figure is not drawn to scale. | |
2.3 Interfacial capacitance and analyte concentration
The changes of interfacial capacitance and target analyte concentration are two of the most important factors needed to judge the surface binding. Undoubtedly, the amount of analyte bonded with receptors is positively correlated with the interfacial capacitance change. Meanwhile, the target concentration in the microchamber (especially on the channel bottom) adequately reflects the amount of analyte bonded with receptors. In this way, the interfacial capacitance change is intimately associated with the analyte concentration distribution. Thus the target analyte concentration makes the interfacial capacitance known in an indirect manner. The target analyte concentration is affected by the specific association rate. Besides target movement caused by diffusion, the application of an AC electrokinetics force also drives more immuno interactions for the immunoassay. The main reason for the rapid immuno reaction is ACET convection and mass transfer. So the electrokinetics of the biomolecule capture process enhanced by the AC electric field can be analyzed by investigations into the concentration distribution of target analyte.
3 Theory and simulation
The model provides an example of an ACET adjusted fluid flow in a microchannel with a surface specific binding reaction on the array bottom. The microchannel and electrode pattern are set the same as those in the experimental setup. A full understanding of the process requires an extensive model which couples the physics of the electrostatics, the energy equation, incompressible flow, and the adsorption kinetics. Numerical study is acquired via the commercial finite element program Comsol Multiphysics 3.5a.
3.1 Geometry, meshing and basic physics
Since the electrode has a large slenderness ratio (1 mm in length, 25 μm in width, but only 100 nm in thickness), the numerical simulation is processed under 2D conditions. Two geometries (the 2D model is for the channel,18 and the 1D model is for the reaction surface) are used to simulate the experimental work. The proposed 2D model consists of a micro channel with pairs of micro-stirring ACET electrodes on its bottom. In the 2D geometry, the electrostatics, convection and conduction, incompressible Navier–Stokes, convection and diffusion equations are used to solve the static electric potential V in the channel, the temperature distribution T, ACET flow field u = (u, v), pressure p, concentration c, the concentration of the progesterone in the channel. While the surface concentration, B, the concentration of the bound progesterone on the reaction surface, is solved in the 1D surface geometry.
Triangular mesh is used throughout the domain and is refined near the reactive boundaries (i.e. the channel bottom where the electrode locates) to capture the high gradients of the concentration. The simulation was carried out in the following steps: first the electric field is solved, then the resulting electrothermal flow velocity field is solved from the ‘convection and conduction’ equation coupled with the Navier–Stokes equation.19,20 Finally the time-depended concentration field was solved from the flow field, convection and diffusion equation and surface binding reaction equations.21
3.2 Governing equations and boundary conditions
3.2.1 Electric field: conductive media DC. The electric problem can be treated as quasi-electrostatic and solved without employing time harmonics (i.e., V = V0eiωt) for AC electrothermal conditions. The applied electric potential V in the conductive media can be calculated by solving Laplace's equation of the conductive media DC module.The boundary conditions of two electrodes are set to be ±V0/2 (V0 is the AC voltage amplitude), the inlet and outlet are set to be symmetric boundaries, and the other walls are insulating boundaries.
3.2.2 Temperature: convection and conduction. The temperature profile, T, generated due to Joule heating of the suspending media, Q, can be calculated from the solution of the energy balance equation, which is simplified as,in which k is the thermal conductivity, Q = 〈σE2〉 (σ denotes the media conductivity) is the Joule heating source term, and E = −∇V is the electric field strength.Convection is caused by heat transfer between a solid surface and an adjacent fluid, and it occurs by conduction of heat within the fluid near the wall, accompanied by bulk motion of the fluid u,
| | |
∇·(−k∇T) = Q − ρmCpu·∇T
| (3) |
where
ρm,
Cp is mass density and heat capacity of media at constant pressure, respectively. The silicon substrate and PDMS channel are set as heat flux boundaries,
| | |
n·(k∇T) = ksi(T − T0) + nxuρmCpT
| (4) |
| | |
n·(k∇T) = kPDMS(T − T0) + nxuρmCpT
| (5) |
where
ksi and
kPDMS are heat transfer coefficient of silicon substrate and PDMS, respectively. The inlet and outlet are set to be convection flux,
3.2.3 Flow field: incompressible Navier–Stokes. The buffer liquid is assumed to flow through a rectangular microchannel in the presence of a body force exerted due to an external electric field. The inhomogeneous AC electric field can generate volume forces in the media by producing gradients in conductivity and permittivity due to local heating.22 The Navier–Stokes equation, derived from moment and mass conservation arguments, describes the fluid motion. For an incompressible, Newtonian fluid,| |
 | (7) |
where the body force f can be written in terms of temperature gradient,19| |
 | (8) |
in which α = (1/ε)(∂ε/∂T) ≈ −0.004 and β = (1/σ)(∂σ/∂T) ≈ 0.02. For Navier–Stokes equation, the inlet and outlet are periodic open boundaries (p = 0). Others are set to be wall (no slip) boundary conditions.
3.2.4 Concentration: convection and diffusion. The electric, temperature, energy balance and flow field velocity equations are couples solved via the finite element method. With current results, the distribution of the target progesterone within the channel can be described as,| |
 | (9) |
where c is the target antibody (progesterone) concentration, u is the fluid velocity and D is the diffusivity of antibody (progesterone), relating to the viscosity coefficient of the fluid, temperature and the particle size.As discussed previously, with the mass transfer enhanced by the AC electrothermal stirring effect, the target antibody will be delivered towards the well functionalized electrode surface and antigen–antibody specific binding occurs23 within a few minutes.
3.2.5 Surface specific binding reactions: diffusion. To describe the specific reaction on the surface, probe antigen (protein G with α-PAG, named as A) and target antibody (progesterone, named as B) are reacted to reaction product (protein G with α-PAG bonded with progesterone, named as AB) via a reversible reaction equation,and the concentration can be expressed as,| |
 | (11) |
where the reaction source Ri is calculated using the association rate constant kon, the dissociation rate constant koff, the surface probe concentration cA, the target concentration cB, and the product concentration cAB.| | |
Ri = −koncAcB + koffcAB, i = A, B
| (12) |
| | |
Rj = koncAcB − koffcAB, j = AB
| (13) |
All the bottom boundaries are set as reaction probe sites and the inlets are set to the initial concentration c0 and the outlet set as convection flux. AC voltage is essential to enhance the convection and mass transfer in the channel, leading to a rapid immunoassay. First we analyzed the target progesterone concentration distribution in the channel with and without AC voltages. Subsequently, we focused on the amount of bound target progesterone on the channel bottom, serving to validate the experimental results. The parameters in the numerical model are set in Table 1
Table 1 Parameter settings in the simulation model
| Symbols |
Value [unit] |
Note |
| V0 |
0–1 [V] |
AC voltage amplitude |
| k |
0.598 [W m−1 K−1] |
Thermal conductivity of medium |
| σ |
0.184 [S m−1] |
Conductivity of medium |
| ρm |
1000 [kg m−3] |
Mass density of medium |
| Cp |
4.484 [kJ kg−1 K−1] |
Heat capacity of medium |
| ksi |
149 [W m−1 K−1] |
Thermal conductivity of silicon |
| kPDMS |
0.15 [W m−1 K−1] |
Thermal conductivity of PDMS |
| η |
1.08 × 10−3 [Pa s] |
Viscosity of medium |
| c0 |
1 [pM] |
Initial concentration of probes |
| D |
1 × 10−13 [m2 s−1] |
Diffusion coefficient of targets |
| kon |
1 × 105 [m3 mol−1 s−1] |
Association rate constant |
| koff |
0.02 [s−1] |
Dissociation rate constant |
3.3 Simulation results and discussions
In this section, the immunoassay efficiency under different conditions are evaluated using numerical methods. Biological analysis generally involves biofluids with high salt concentration and hence high conductivity. However, the application of voltage to high conducting aqueous solutions leads to a high risk of electrolytic reactions and bubbles. Thus we should avoid the problems by lowering the voltage and increasing the frequency as the ionic concentration increases. The average flow velocity is defined as,| |
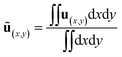 | (14) |
where ∫∫dxdy is the area of the channel in the model. Then the dimensionless ACET velocity is expressed as,| |
 | (15) |
As shown in Fig. 2(a), the maximum temperature rise is only 0.12 K, this means it will not be harmful for the proteins and the surrounding fluid. The maximum ACET velocity happens at the electrode corners and it can be more than 9.37 times bigger than the average value (not shown here). Define the dimensionless concentration of target analytes as,
| |
 | (16) |
 |
| | Fig. 2 Simulation results of ACET effects (t = 60 s). (a) Temperature rise. (b) Dimensionless target concentration distribution without AC field and (c) with AC signal of 1 V at 100 kHz. The surface plot, streamline and arrow stands for dimensionless concentration, flow pattern and flow direction, respectively. | |
Fig. 2(b) and (c) demonstrated the dimensionless concentration of targets with and without the AC signal applied. Since the flow field in the micro channel is laminar flow, there is no net flow or stirring in the channel, so the tangential and perpendicular flow in the micro channel is near zero for microfluidics without disturbance. Because there is no net flow or vortex in the channel, the Péclet number is accordingly much less than cut-off value, then the mass transfer in the channel is mainly caused by natural diffusion only. As a result, the target progesterone, which is supposed to bind the α-PAG on the array bottom, is transported mainly by natural diffusion. The stirring vortices transports the target molecule in the channel, resulting in a vortex-like concentration distribution rather than laminar flow. The maximum concentration in Fig. 2(b) and (c) is 1.0 and 1.029 respectively, showing strong preconcentration effects of ACET convection and mass transfer. Driven by the applied electric field, 1 V at 100 kHz for example, the convective fluid moves towards the exit of the channel and the motion of the fluid stops when it gets close to the bottom of the array. Meanwhile, local vortex generated by AC electrothermal flow will deliver the target progesterone towards the channel bottom and meet with the antigen (protein G with α-PAG) probes, then specific binding occurs. In addition, more fresh serum with progesterone of initial concentration are pumped continually due to net flow caused by the ACET effect.
To illustrate the advantage of ACET convection and mass transfer enhanced immunoassay, a comparative numerical analysis is presented in Fig. 3. There are two pairs of periodic array in Fig. 3(a) and (b): no ‘protein-G and α-PAG’ probes are coated on the left side of the dashed line while there are well coated probes on the right side. Fig. 3 shows flow pattern and target progesterone concentration in the micro channel. Since there is no probe antigen coated on the left side of the channel shown in Fig. 3(a) and (b), it is easy to understand that there is no progesterone consumed, whether the AC voltage is applied or not. The dimensionless progesterone concentration keeps 1 on the left side of the dashed line and the channel top where no specific binding occurs. On the other hand, the concentration decreases with time on the right side of the dashed line, especially on the channel bottom where specific binding takes place. Fig. 3(c) provides the dimensionless concentration, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , at t = 5 s, 60 s, 120 s, 180 s and 240 s, showing the changing of target concentration during the immunoassay.
, at t = 5 s, 60 s, 120 s, 180 s and 240 s, showing the changing of target concentration during the immunoassay.
 |
| | Fig. 3 Simulation results of dimensionless progesterone concentration in the channel for (a) no AC signal and (b) 1 volt potential is applied. The gray scale represents the concentration distribution. Streamline and arrows stand for AC electrothermal flow, the length of arrows indicates the relative fluid velocity. The yellow bars (not drawn to scale) stand for the electrodes. (c) The dimensionless concentration, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , at t = 5 s, 60 s, 120 s, 180 s and 240 s. , at t = 5 s, 60 s, 120 s, 180 s and 240 s. | |
An important characteristic of AC capacitive sensing is that the sensor response should increase with increasing electric field strength. Fig. 4(a) shows the dimensionless target concentration as a function of time with different AC voltages. The dimensionless target concentration, which behaves like the dimensionless interfacial capacitance, also shows linear approximation relationship with time, as shown in Fig. 7(a). The interfacial capacitance is related to the target preconcentration caused by convection and mass transfer, although the function Cint = F(σm, E, c, kon, koff,…) is not yet explicitly established. The target concentration decreased 0.92, 0.95 and 0.995 in 2 minutes with an exciting voltage of 1 V, 0.5 V, and 5 mV, respectively. This demonstrated that the voltage of 5 mV is too low to induce any ACET effects and convection to enhance the specific binding. The stirring vortex and the channel height also influence the target molecular concentration, as provided in Fig. 4(b). The target progesterone is almost exhausted at the channel bottom, while there still many targets available above the array bottom. The dimensionless concentration at the height of 10 μm is about 1.0, 0.78, 0.6, 0.5 and 0.4 for t = 5 s, 60 s, 120 s, 180 s and 240 s conditions, showing that the binding reaction at the first minute is stronger.
 |
| | Fig. 4 Simulation results of dimensionless concentration of target analytes. (a) Dimensionless concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) as a function of time with voltage of 5 mV, 0.5 V and 1 V. (b) Dimensionless concentration as a function of time with voltage of 5 mV, 0.5 V and 1 V. (b) Dimensionless concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) as a function of channel height. as a function of channel height. | |
4 Experimental validation
Progesterone is a steroid hormone involved in the female menstrual cycle, pregnancy and embryogenesis of humans and other species. In humans and other mammals, increasing amounts of progesterone are produced during pregnancy, so the concentration level detected is one of the common methods for pregnancy tests. However, progesterone concentration in the first few weeks of gestational period are very low (i.e. ng mL−1), making the detection process more complicated and time consuming.24 Here experimental observations of the rapid capacitive immunoassay of bovine progesterone is presented as a proof-of-concept. The detection takes only a few minutes following loading the target serum into the microchip.
4.1 Reagents and devices
4.1.1 Buffer solutions. Our progesterone assay is based on dilute phosphate-buffered saline (PBS) solutions, denoted as 0.1× PBS in this work. 0.1× PBS is made by 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 volume diluting physiological strength PBS with deionized water to obtain 1 mM phosphate buffer (pH 7.0) containing 15 mM NaCl. PBS–T is PBS containing 0.05% (volume ratio) Tween 20 (Fisher Scientific, Pittsburgh, PA), and buffer B is PBS–T containing 10% (volume ratio) SuperBlock (PIERCE Biotechnology, Rockford, IL). 0.1× buffer B is used to dilute antibody samples and to prevent non-specific binding.
10 volume diluting physiological strength PBS with deionized water to obtain 1 mM phosphate buffer (pH 7.0) containing 15 mM NaCl. PBS–T is PBS containing 0.05% (volume ratio) Tween 20 (Fisher Scientific, Pittsburgh, PA), and buffer B is PBS–T containing 10% (volume ratio) SuperBlock (PIERCE Biotechnology, Rockford, IL). 0.1× buffer B is used to dilute antibody samples and to prevent non-specific binding.
4.1.2 Protein G. The protein G (MP Biochemicals, Cat # 672651, Lot # M2909, Solou, OH, stock 1 mg mL−1) samples is diluted with 1× PBS to obtain the objective concentration, 10 μg mL−1.
4.1.3 Antibody. IDEXX pregnancy test kits 2nd antibody (no dilution). (IDEXX HerdCheck bovine pregnancy test kit, Lot 41169-W62, Detector solution.)
4.1.4 Serum samples. Ten pregnancy-positive serum samples were obtained from 5 different dairy cows (breed, Holstein; average age, 2.8 years old; gender, female) tested pregnant. The 5 pregnancy-negative serum samples were obtained from 5 different cows (breed, Holstein; average age, 2.4 years old; gender, female) tested non-pregnant. The original serum are diluted (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 volume ratio) with 0.1× buffer B.
5 volume ratio) with 0.1× buffer B.
4.1.5 Electrode array and microchannel. As a traditional electrothermal pump design, a planner, periodic, interdigitated asymmetric electrode layout is used in this work. The thin planner interdigitated electrode array fabricated on a silicon wafer and a soft-lithography PDMS chamber (40 μm height, 200 μm width and 1 mm length) is the covering layer of the enclosed fluid. The size of interdigitated electrode array is 5 μm–5 μm–25 μm–25 μm, meaning the narrow and wide electrode is 5 μm and 25 μm while the gap between adjacent electrode is 5 μm, the gap between adjacent electrode pair is 25 μm, as shown in Fig. 5.
 |
| | Fig. 5 The microfluidic device and electrode array used in the experiments. (a) The microfluidic chip and PDMS channel. (b) The electrode array under the microscope. | |
4.2 Procedures and methods
The experimental procedures are as shown in Fig. 6. To get a protein G coated electrode surface, 5 μL protein G sample was loaded into the PDMS chip chamber and incubated in a humidor at room temperature (20–25 °C) overnight. Then the channel is washed with 0.1× PBST twice to flush the extra protein G away. After that α-PAG (namely anti-PAG in Fig. 6) is loaded and kept for 1 hour at room temperature, α-PAG will bind with the protein G. Then the channel is washed with 0.1× PBST twice to wash out unbound α-PAG. Then 0.1× buffer B was loaded and incubated for 30–60 minutes at room temperature for blocking purposes. Then 0.1× PBST (Phosphate Buffered Saline with Tween) was loaded into the chamber to flush away excessive antigen and blocker that were not bound to the electrode surface. The last step is the binding process on the assay. Diluted serum was introduced into the chamber and capacitance change (representing antibody binding) was measured by high accuracy impedance analyzer (Agilent 4294A, USA) at specified frequencies and magnitudes. Each test was repeated for 3 to 5 times and the complex impedance was measured. The serum are as positive/negative experimental groups while 0.1× buffer B is the control buffer. Of note, the specific binding occurs not only on the electrode surface, but also on the substrate surface of the silicon wafer.
 |
| | Fig. 6 Procedures for progesterone detection. | |
During the impedance measurements in the specific binding process, the impedance and capacitance data were continuously recorded at 100 kHz and at an elevated voltage level of 1 V for 1 min, which is much higher than the typically used 5 mV in traditional impedance measurements. Such a voltage level is sufficient to induce ACET effects at that frequency and provide us with information on the impedance change as a result of specific binding on the electrodes.25 The impedance data were acquired using a precision impedance analyzer, and an oscilloscope (TDS2024, Tektronix, USA) was used to verify that the specified voltages were applied on the electrodes in all tests. In quantitative ELISA (Enzyme Linked Immunosorbent Assay), the optical density (OD) value of the sample is the measurable indicator, OD value of each serum sample, sample (450) is tested. For negative control groups, the mean value of negative control groups (0.1× buffer B),  , and OD value of each serum, sample (450), is expressed as,
, and OD value of each serum, sample (450), is expressed as,
| |
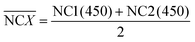 | (17) |
| |
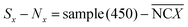 | (18) |
Similarly, capacitance changes in per minute, dC/dt in percentage, is calculated using least squares linear fitting method (the capacitance decreases with time linearly), as demonstrated in our previous work. The mean value of capacitance changes of negative control groups (0.1× buffer B), 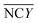 , and capacitance change per minute of each serum, sample (cap) is defined as,
, and capacitance change per minute of each serum, sample (cap) is defined as,
| |
 | (19) |
| |
 | (20) |
4.3 Experimental results and discussion
Fig. 7 gives the preliminary experimental results of the capacitive immunoassay. The capacitance decreases with time approximately linearly. When an AC field is applied on the positive serum the capacitance change could reach ∼−11% in 2 minutes, while the change is only −0.5% without AC voltage excitation (5 mV is used for measurement), as shown in Fig. 7(a). The capacitance change rate, namely the slope of ‘dimensionless capacitance–time’ is calculated by least square linear fitting methods, as reported in our previous work.8 The capacitance change per minute of blank control buffer (0.1× buffer B), positive and negative serum is (−0.242 ± 0.341)%, (−4.45 ± 0.48)%, (0.055 ± 0.0469)% respectively, showing that the positive serum can be well distinguished from negative or control buffers within 2 minutes.
 |
| | Fig. 7 Preliminary experimental results of rapid progesterone detection. (a) Dimensionless capacitance, C/C0, as a function of time. C0 is the initial capacitance value at time zero. (b) Capacitance change rate of blank control buffer, positive serum and negative serum with AC signal applied. | |
Compared with standard ELISA results, the capacitance assay shows good consistency. There are 5 positive serum (sample ID: 1–5), and 5 negative serum (sample ID: 6–10) used in the proof-of-concept tests. Positive serum has a bigger OD value (by ELISA) than the negative serum, as shown in Fig. 8(a), and serum with more target progesterone (i.e. samples 8 and 9) leading to a higher light intensity in ELISA operations. As shown in Fig. 8(b), all the 5 negative serum show small capacitance change per minute (less than −0.5%), agreeing with the ELISA results. For positive serum, the capacitance decreases after specific binding, and the capacitance change per minute of positive serum can reach as high as −5.5% per minute.
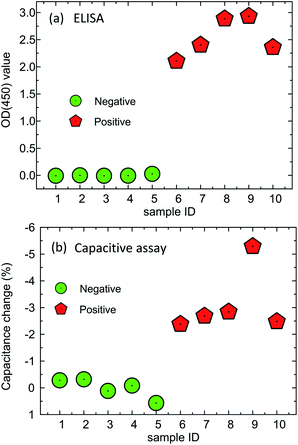 |
| | Fig. 8 Proof of concept experimental results of the capacitive assay compared with ELISA. | |
Usually, an at-home pregnancy test kit consists of a plastic device of three parts: a urine well, an opening that displays the test results, and a plastic-shielded region containing the tracer antibody. If hCG (human chorionic gonadotropin, for human beings) is presented in the urine poured into the urine well, it migrates toward and binds to the tracer antibody. This complex will then continue to flow to the immobilized capture antibody, which will glow to indicate a positive pregnancy test.26 Our proof of concept approach is no more sensitive and convenient than some established methods for detecting progesterone, such as pregnancy test kit detection. However, the capacitance based sandwich assays, can detect low micro molecular concentrations in minutes, directly in conductive bio-samples such as blood, serum, or cellular lysate. This concept can be extended to detect a range of other bio-particles based on convection and mass transfer enhanced specific binding on a microfluidic chip.
Particle transporting can be caused by fluid flow or dielectrophoresis (DEP) moving towards the electrode surface. As a main kind of fluid flow induced by AC electric field, ACEO (Alternating Current ElectroOsmosis) refers to the interaction between the electric field and induced charges at the diffusion layer,27 and is limited to pump fluid with low ionic concentration only.28,29 While ACET arising from the interaction of the electric field and the temperature gradient,19 plays a major role in the pumping of liquid with a higher ionic concentration. The conductive buffer here compresses the thickness of the electric double layer, making electroosmosis ineffective while the Joule heating flow dominates the flow. Positive DEP force is another possibility to deliver the biomolecule immersed in the surrounding buffer towards the electrodes. As the biomolecule moves across the channel height and becomes close to the electrode surfaces, it may be trapped in the presence of a capturing zone. However, the DEP forces only effect for molecules which locate within a very short distance to the electrode,30 mean that the DEP preconcentration would benefit from fluid flow that delivers target analytes to the electrodes for specific binding. Each of these effects (ACET and DEP) may make its own contribution to the rapid capacitive immunoassay, and their respective merits are unclear, thus further study on their contributions is the subject of ongoing investigations, as well as the quantitative determination, repeatability and sensitivity tests of progesterone.
5 Conclusions
A rapid capacitive immunoassay is presented and the basic mechanism for rapid detection relies on the convection and mass transfer caused by ACET flow stirring. Numerical simulation and a proof-of-concept experiment are described and the proposed array includes one cuboid micro chamber and pairs of interdigital electrodes. The external electric field induces vortices around the electrodes and enhances the mass transfer while pumping the conductive serum through the channel continuously. The numerical study provides the influences of AC voltages to the concentration of target molecules in the microchannel, showing proper AC voltage (i.e. 1 V) can greatly reduce the detection time. To sum up, convection and mass transfer enhanced capacitive immunoassay can provide simple, robust, and easy-to-operate detection of proteins.
Acknowledgements
This project is supported by the National Natural Science Foundation of China (Grant no. 51075087), the State Key Lab of Fluid Power Transmission and Control, Zhe Jiang University (no. GZKF-201107). All the authors want to thank Prof. Jayne Wu in Department of Electrical Engineering and Computer Science, and Prof. Shigetoshi Eda in the Center for Wildlife Health, Department of Forestry, Wildlife and Fisheries, the University of Tennessee, Knoxville, and Dr Ashutosh Wadhwa in the Center of Disease Control for the equipment support and sample processing.
References
- K. F. Lei, J. Lab. Autom., 2012, 17, 330–347 CAS.
- W. Zhao, L. Zhang, W. Jing, S. Liu, H. Tachibana, X. Cheng and G. Sui, Biomicrofluidics, 2013, 7, 011101 CrossRef PubMed.
- J. Hirota, Y. Shimoji and S. Shimizu, Clin. Vaccine Immunol., 2012, 19, 277–283 CrossRef CAS PubMed.
- A. Warsinke, A. Benkert and F. Scheller, Fresenius' J. Anal. Chem., 2000, 366, 622–634 CrossRef CAS.
- M. Wang, L. Wang, G. Wang, X. Ji, Y. Bai, T. Li, S. Gong and J. Li, Biosens. Bioelectron., 2004, 19, 575–582 CrossRef CAS.
- S. Li, Q. Yuan, B. I. Morshed, C. Ke, J. Wu and H. Jiang, Biosens. Bioelectron., 2012, 41, 649–655 CrossRef PubMed.
- Y. T. Ho, C. L. Pan, J. T. Sheu, Y. K. Wang and T. K. Wu, Biomedical Circuits and Systems Conference (BioCAS), IEEE, 2012, pp. 49–52 Search PubMed.
- S. Li, H. Cui, Q. Yuan, J. Wu, A. Wadhwa, S. Eda and H. Jiang, Biosens. Bioelectron., 2013, 51, 437–443 CrossRef CAS PubMed.
- M. L. Sin, T. Liu, J. D. Pyne, V. Gau, J. C. Liao and P. K. Wong, Anal. Chem., 2012, 84, 2702–2707 CrossRef CAS PubMed.
- Z. Wu, J. Li, T. Deng, M. Luo, G. Shen and R. Yu, Anal. Biochem., 2005, 337, 308–315 CrossRef CAS PubMed.
- G. Hu, Y. Gao, P. M. Sherman and D. Li, Microfluid. Nanofluid., 2005, 1, 346–355 CrossRef CAS.
- G. Hu, Y. Gao and D. Li, Biosens. Bioelectron., 2007, 22, 1403–1409 CrossRef CAS PubMed.
- M. Sigurdson, D. Wang and C. D. Meinhart, Lab Chip, 2005, 5, 1366–1373 RSC.
- I.-F. Cheng, H.-L. Yang, C.-C. Chung and H.-C. Chang, Analyst, 2013, 138, 4656–4662 RSC.
- J. Wu, Y. Ben and H. C. Chang, Microfluid. Nanofluid., 2005, 1, 161–167 CrossRef.
- X. Liu, K. Yang, A. Wadhwa, S. Eda, S. Li and J. Wu, Sens. Actuators, A, 2011, 171, 406–413 CrossRef CAS PubMed.
- N. Sasaki, Anal. Sci., 2012, 28, 3 CrossRef CAS.
- R. Zhang, C. Dalton and G. A. Jullien, Microfluid. Nanofluid., 2011, 10, 521–529 CrossRef.
- N. G. Green, A. Ramos, A. González, A. Castellanos and H. Morgan, J. Electrost., 2001, 53, 71–87 CrossRef.
- N. G. Green, A. Ramos, A. Gonzalez, H. Morgan and A. Castellanos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 026305 CrossRef CAS.
- K. R. Huang and J. S. Chang, Heat Mass Transfer, 2013, 49, 1647–1658 CrossRef CAS.
- J. Wu, M. Lian and K. Yang, Appl. Phys. Lett., 2007, 90, 234103 CrossRef PubMed.
- K. Yang and J. Wu, Biomicrofluidics, 2010, 4, 034106 CrossRef PubMed.
- A. Denicol, G. Lopes, L. Mendonça, F. Rivera, F. Guagnini, R. Perez, J. Lima, R. Bruno, J. Santos and R. Chebel, J. Dairy Sci., 2012, 95, 1794–1806 CrossRef CAS PubMed.
- H. C. Feldman, M. Sigurdson and C. D. Meinhart, Lab Chip, 2007, 7, 1553–1559 RSC.
- K. Kelley, Embryo Project Encyclopedia, 2012 Search PubMed.
- A. Ramos, H. Morgan, N. Green and A. Castellanos, J. Phys. D: Appl. Phys., 1999, 31, 2338 CrossRef.
- J. Wu, Y. Ben, D. Battigelli and H. C. Chang, Ind. Eng. Chem. Res., 2005, 44, 2815–2822 CrossRef CAS.
- H. Jiang, S. Li, Z. Hou, Y. Ren and Y. Sun, Chin. Phys. B, 2011, 60, 020702 Search PubMed.
- R. Pethig, Biomicrofluidics, 2010, 4, 022811 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. 



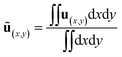


![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , at t = 5 s, 60 s, 120 s, 180 s and 240 s, showing the changing of target concentration during the immunoassay.
, at t = 5 s, 60 s, 120 s, 180 s and 240 s, showing the changing of target concentration during the immunoassay.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 volume diluting physiological strength PBS with deionized water to obtain 1 mM phosphate buffer (pH 7.0) containing 15 mM NaCl. PBS–T is PBS containing 0.05% (volume ratio) Tween 20 (Fisher Scientific, Pittsburgh, PA), and buffer B is PBS–T containing 10% (volume ratio) SuperBlock (PIERCE Biotechnology, Rockford, IL). 0.1× buffer B is used to dilute antibody samples and to prevent non-specific binding.
10 volume diluting physiological strength PBS with deionized water to obtain 1 mM phosphate buffer (pH 7.0) containing 15 mM NaCl. PBS–T is PBS containing 0.05% (volume ratio) Tween 20 (Fisher Scientific, Pittsburgh, PA), and buffer B is PBS–T containing 10% (volume ratio) SuperBlock (PIERCE Biotechnology, Rockford, IL). 0.1× buffer B is used to dilute antibody samples and to prevent non-specific binding.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 volume ratio) with 0.1× buffer B.
5 volume ratio) with 0.1× buffer B. , and OD value of each serum, sample (450), is expressed as,
, and OD value of each serum, sample (450), is expressed as,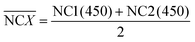
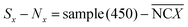
 , and capacitance change per minute of each serum, sample (cap) is defined as,
, and capacitance change per minute of each serum, sample (cap) is defined as,









