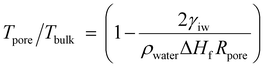Exploring the Mpemba effect: a universal ice pressing enables porous ceramics

Abstract

Piezoceramics with global porosity and local compaction are highly desired to exploit the combination of mechanical and electrical properties. However, achieving such a functional combination is challenging because of the lack of techniques for applying uniform pressure inside porous ceramic green parts. Nature provides many examples of generating strong forces inside the macro and micro channels via the state transformation of water. Inspired by these phenomena, we present a technique of “ice and fire”, that is, water freezing (ice pressing) and high-temperature sintering (fire), to produce ideal porous piezoceramics. We introduce a new compaction method called the “ice pressing method”, which manipulates liquid phase transition for compaction. This method has several advantages, including uniform pressure distribution, a wide pressure range, high effectiveness, and selective freezing. It can generate an ultrahigh pressure of up to 180 MPa on the piezoceramic green skeletons in minutes while retaining their functional pore structures. By exploiting the Mpemba phenomenon, we further accelerate the compaction procedure by 11%. The first ice-pressed and second fire-consolidated lead zirconate titanate (PZT) ceramics are highly densified and exhibit an outstanding piezoelectric response (d₃₃ = 531 pC N⁻¹), comparable to conventional pressed bulk counterparts and 10–20 times higher than those of unpressed materials. The novel ice pressing method breaks the limitation of lacking a compaction technique for porous ceramics. The versatile and effective ice pressing method is a green and low-cost route promoting applications in sensors, acoustics, water filtration, catalyst substrates, and energy harvesting.

---

New concepts

Porous ceramics are widely used in energy harvesters, sensors, batteries, electronics, and filters. The existing technologies cannot manufacture 3D globally porous but locally compact ceramics in a highly efficient and low-cost way. It is challenging to generate uniform and controllable pressure inside porous ceramic microstructures. Inspired by the frost weathering and Mpemba effect, this work develops an “ice and fire” technique as a new solution to fabricate globally porous and locally compact structural and functional ceramics. The term “ice and fire” mimics the classic manufacturing process of piezoceramic of “force and fire”: force pressing and high temperature sintering. Accordingly, two new concepts are emphasized. One is the ice pressing method, which breaks the limitation of lacking a compaction technique for porous ceramics. The other is the unique Mpemba effect for manipulating the freezing process. The fabricated PZT exhibits an outstanding piezoelectric response of d₃₃ = 531 pC N⁻¹, 10–20 times higher than that of its counterparts. Moreover, the ice pressing strategy is compatible with other manufacturing processes, like the sacrificed template, gel casting, additive manufacturing, etc. Thus, applications in thermal insulation, catalyst substrates, filtration systems, and biomedical and energy storage and conversion are expected to expand. This study underscores the versatility and efficacy of the ice-pressing method and highlights its potential as a valuable tool for manufacturing complex structures.

1. Introduction

It is generally recognized that the lower the water temperature is, the sooner it freezes. However, in 1963, a Tanzanian junior high school student, Mpemba, stumbled upon hot milk in a refrigerator frozen before cold milk.^1–3 After that, the Mpemba effect was named to describe the phenomenon of an initially hot system freezing faster in a cold bath than an initially cool one. Water lends itself to various explanations for the Mpemba effect, ranging from evaporation to dissolved gasses,⁴ hydrogen bonding to convection,⁵ to conduction with the environment.⁶ Although the phenomenon's origin is controversial, its exploration sheds much light on scientific research and engineering. Here we optimize the water-freezing process and establish a new rapid-freezing fabrication method.

Water and ice are known to have many unusual features. For instance, volume expansion is inevitable during the water freezing process. During frost weathering,⁷ when water fills the gaps in rocks and freezes in place, the resulting ice growth can exert pressures of up to 207 MPa inside cracks in the rock, assuming a temperature of −22 °C.^8–10 The stress caused by water expansion induces damage to rocks, plants, buildings, and infrastructure, revealing the enormous energy involved in water transformation.⁷ For another instance, freezing does not always occur even when cooling. Anderson discovered in 1968 that frozen clay mineral–water mixtures contain a significant amount of unfrozen water, which creates a movable surface layer that separates the mineral surfaces from the ice.¹¹ The unfrozen water can also be explained by the Gibbs–Thomson effect: containing liquids within porous materials lowers the freezing point. The smaller the pore size is, the lower the freezing temperature becomes.^9,12,13 This effect provides a path to realize regional selectivity via regulating the pore size.

Here, we explore the liquid–solid transformation for fabricating compact piezoceramics. Piezoceramics are key enabling materials in actuators, sensors, transducers, and memory devices.^14,15 Compact piezoceramics usually exhibit high piezoelectric responses^16,17 but a low hydrostatic figure of merit and poor acoustic coupling.^18–23 To attain balanced performance or abnormal responses, researchers have designed three-dimensional (3D) microstructures such as holes and tunnels in piezoelectric ceramics and formed metamaterials, smart composites, and transducers.^17,18,23,24 Unfortunately, the construction of lightweight porous bodies usually suffers from the significant loss of mechanical properties and piezoelectricity, thus making the integration of compactness and porosity contradictory.²⁵ Is it possible to fabricate globally porous but locally compact materials? Nature shows its intelligence in such delicate materials as bones and shells; we human intelligence still cannot. Existing technologies, such as uniaxial compression, sintering, and cold isostatic pressing (CIP), cannot generate pressure inside micro holes locally without causing damage to the global structures.^10,16,26,27

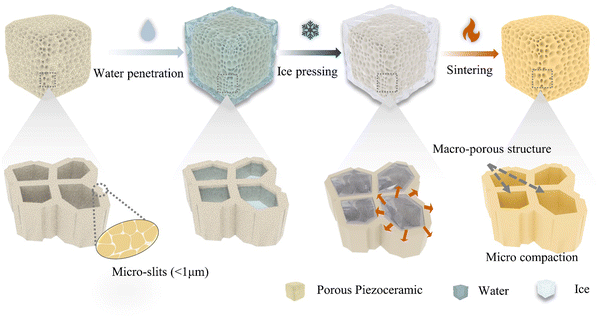
Inspired by the natural phenomena mentioned above, we present a technique of “ice and fire”, that is, manipulation of force via water freezing (ice) and high-temperature sintering (fire) to produce materials with global porosity and local compaction. The term “ice and fire” mimics the classic manufacturing process of piezoceramic products of “force and fire”: force pressing and high-temperature sintering. Here we use the pervasiveness of water flow to penetrate microstructures, and then freeze water to generate uniform pressure on the ceramic green bodies while maintaining the global porous structure, ending it with a sintering process (Fig. 1).

Fig. 1 Schematic of the technique “ice and fire”. The process involves pushing water to penetrate the microstructures, followed by freezing the water to generate uniform pressure on the ceramic green bodies while maintaining the global porous structure. This is followed by a sintering process to complete the manufacturing process. The ice pressing method used in this technique shows selective freezing, which allows the functional macro-pore structure to be retained during consolidation, while the slit or crack (pore diameters less than 1 μm) between the particles can be compressed.

2. Results and discussion

2.1 Design of the “ice and fire” process

To develop the “ice and fire” technique for producing porous piezoceramics, we have devised a novel compaction process that is refers to as the “ice pressing method”. This method is composed of a rapid cooling system and a sealable container containing a liquid medium, as illustrated in Fig. S1 (ESI†). The liquid medium generates uniform and controllable pressure inside the porous ceramic green parts. To execute the ice pressing method, a shaped precursor is first put inside a sealed container filled with a liquid medium. On cooling down, the liquid medium undergoes a phase transition to a solid state, resulting in a specific volume expansion. In this work, we have utilized water as the liquid medium due to its huge volumetric expansion upon freezing. Subsequently, frozen water creates numerous randomly oriented tiny ice crystals and generates a uniform force, owing to a liquid nitrogen bath and conduction system that ensures a uniform low-temperature environment. Afterward, the container is then removed from the liquid nitrogen and allowed to thaw at room temperature. As the temperature gradually increases, the applied pressure unloads in a controlled manner. Finally, the green compact undergoes high-temperature sintering, resulting in a fully formed ceramic structure. As highlighted in the magnified image in Fig. 1, the porous piezoceramics possess two distinct pore structures. One is a functional pore structure (usually a macro-pore structure) that is essential to be retained for optimal performance. The others are the slits or cracks (pore diameters less than 1 μm) between the particles that need to be compressed. The ice pressing method deliberately eliminates these slits and defects, resulting in denser solid parts while maintaining the desired porous structure that ultimately enhances the piezoelectric performance of the material.

2.2 Observation of the water freezing

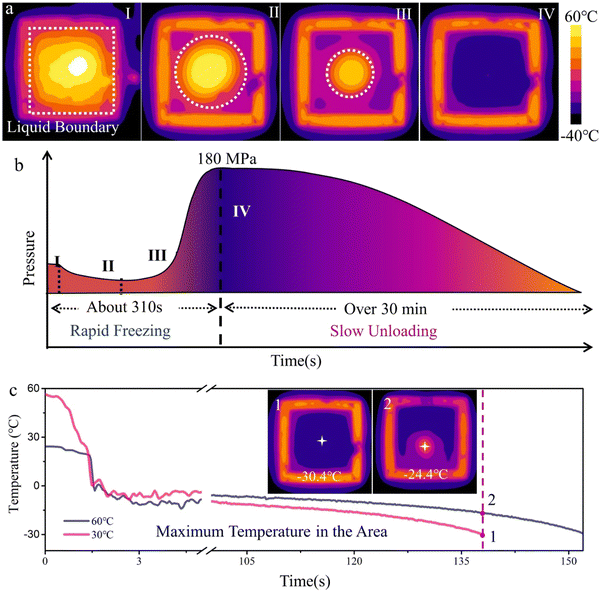
Understanding the freezing process helps evaluate the factors influencing ice pressing. To facilitate clear observation, the vessel lid is open during water-freezing. An infrared thermal mapping is taken from the top side to record the temperature variation in real time. As shown in Fig. 2a and Fig. S2 (ESI†), the solid–liquid interface slowly moves inward during ice pressing until the liquid completely transforms into a solid. The principle of ice pressing is analogous to that of isostatic pressing. According to Pascal's law,²⁸ the pressure acts equally over the sample's surface, uniformly squeezing the green body.

Fig. 2 Observation of water freezing and pressing process. (a) The infrared thermal mappings are taken from the top side to record the temperature. Water is in a liquid state during stage I; it is pseudo-solid (ice–water mixture) during stage II–III, and solid ice in stage IV. The temperature distribution mappings from I to IV demonstrate the pressure direction during the ice pressing process. (b) The pressure–time curve exhibits the main stages of the ice pressure process. First, there is a noticeable pressure drop from I to II, which is caused by the cooling of the equipment. Then stage II and III correspond to water freezing until it transforms into ice totally. We stopped cooling when water is completely frozen. In stage IV, ice starts to thaw and pressure unloads slowly. (c) The typical thermal mapping of the system with water in different initial temperatures (60 °C and 20 °C). The hot system (60 °C) takes less time (∼15 seconds) to be frozen in the system. (c inset) The thermal mapping of the hot system (left) and cool system (right) at 143 s.

A wide pressure range is one of the remarkable features of the ice-pressing process. The pressure range during water freezing is challenging to measure using a single liquid or solid pressure sensor, since water transforms from liquid to solid during the process. To address this issue, we designed a setup to measure the force during ice pressing indirectly. The main element is a steel vessel with a removable lid. The pressure of ice expansion on the lid can be easily determined using a pressure sensor, which is considered approximately equivalent to the pressure generated by ice expansion (detailed in Fig. S3, ESI†). And the pressure generated by ice expansion on the cover is approximately equivalent to the pressure generated by ice expansion. According to the pressure–time curve, the ice pressing process can be divided into two segments: rapid freezing and slow unloading (Fig. 2b). The first segment (from I–III) corresponds to rapid freezing, in which the ice and water phases co-exist simultaneously. The pressure–time curve drops and then rises due to the competition between ice expansion and water shrinkage. When water is completely frozen, the system stops cooling down and comes to the second segment. Ice starts to thaw and unload slowly. This is consistent with the corresponding density of water/ice at different temperatures (Fig. S3c, ESI†). The phase transformation can provide an ultrahigh pressure of up to 180 MPa (Fig. S3c, ESI†), that is, 1800 times atmospheric pressure. For comparison, the pressure range of dry pressing is typically between 13 and 100 MPa,^29–32 while the pressure range for CIP generally is between 100 and 500 MPa.^25,33,34 The pressure supplied by the ice pressing method is not as wide as CIP. However, overpressure may result in the formation of a closed pore and reduce densification. For practical application, the pressure produced from the ice pressing method is more than enough to prepare many piezoceramics. It is worth noting that the high-pressure generation only requires rapid water cooling down. Besides adequate pressure from the ice–water transition, homogeneous pressure distribution originating from the fast freezing in liquid nitrogen is also vital to improve the ice-pressing method. As illustrated in Fig. S4 (ESI†), the ice-template structures, resulting from the freeze-drying of the sodium alginate solution, reveal that the freezing process produces locally oriented ice crystals with a high degree of order. Fast freezing in liquid nitrogen enables randomly oriented tiny ice crystals to form, resulting in homogeneous pressure.^35–37

Rapid freezing of the ice pressing process is essential to prevent the collapse of the internal framework of the sample during solidification. The Mpemba effect is utilized to achieve fast freezing.^36,38 To evaluate this, water with different initial temperatures is introduced into a container, and its temperature changes are observed as it freezes entirely in a liquid nitrogen bath. According to the results of in situ temperature mappings (Movie S1, ESI†) and temperature curves (Fig. 2c & inset), hot water shows an exponentially faster cooling rate to reach the relative equilibrium than that in the cool case, which takes less time (about 15 seconds) to freeze. We can accelerate the compaction procedure by 11% by exploiting the Mpemba phenomenon. Research conducted by J. D. Brownridge's group suggests that convection likely played a role in facilitating the faster freezing of water at higher temperatures.²¹ That is to say, the cooling rate depends on the temperature gradient between the sample and its surroundings. Therefore, the temperature of hot water cools exponentially at the beginning and then slows down. At the same time, the cooling rate slows down considerably during the last few degrees for the cool water (Fig. 2c). Notably, the freezing temperature is below 0 °C, indicating supercooling, which could be attributed to the ambient cooling temperatures provided by a liquid nitrogen cooling vessel, typically ranging between −10 °C and −20 °C. In addition, in the absence of ice nucleators (i.e., ice crystals, dust particles, or other particles), pure water does not freeze at 0 °C. Sometimes, the temperature may fall below −39 °C before ice crystals form. Given these circumstances, hot water would tend to slightly supercool and spontaneously freeze.³⁹

The evidence presented above suggests that the Mpemba effect observed in this system is attributed to both thermal convection and supercooling. Overall, these findings provide new insights into engineering optimization based on the Mpemba effect. Researchers could potentially develop new strategies for rapidly removing heat from localized sources by engineering this effect into technologically relevant materials.

2.3 Ice pressing process for dense piezoceramics

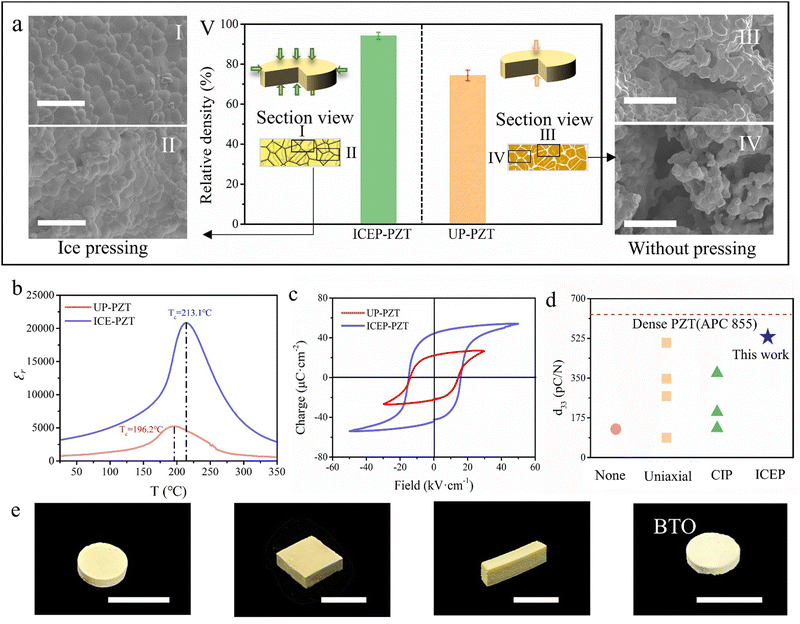
As previously highlighted, the ice pressure method is a highly effective compaction process. It has the potential to replace conventional compaction techniques to prepare bulk ceramics. To demonstrate this, the most widely used piezoceramic lead zirconate titanate (PZT) is adopted as the experimental subject. For comparison, we prepare PZT ceramic flakes using the ice pressing process (ICEP-PZT) and without using such a process (UP-PZT). Compared with the conventional uniaxial pressing, UP-PZT does not undergo a high-pressure compaction process, which aims to distinguish the effects of ice pressing. As shown in Fig. 3aI, II and Fig. S5a, b (ESI†), the section view of ICEP-PZT displays a well-densified morphology without significant porosity in the different sections. In sharp contrast, many slits and pores can be observed in Fig. 3aIII, IV and Fig. S5c, d (ESI†), as UP-PZT can only be shaped by mold with slight and inhomogeneous pressure. The comparison of the section view reveals that the ice pressing method generates a uniform force, which is consistent with Fig. 2b. As a result, ICEP-PZT presents a higher bulk density (7.35 g cm⁻³) than that of UP-PZT (5.796 g cm⁻³). The green body can be well-densified under an ice-enabled homogeneous pressure, acting through a suitable force-transmitting medium comparable to CIP.

Fig. 3 Ice pressing method for dense piezoceramic manufacturing. (a) The density comparison of ice-pressed ICEP-PZT and unpressed UP-PZT pellet. (I and II) The FESEM images show two different regions of the ICEP-PZT at the section view, which indicate uniform pressure and a well-densified morphology. (III and IV) The FESEM images show the two section view regions of the UP-PZT. A large amount of the slits and pores can be observed. (V) Density of the ICEP-PZT and UP-PZT pellets. The inset displays the influence of compaction process on the morphology of products (scale bar = 10 μm). (b) Temperature dependence of the relative dielectric constant (ε_r) at 1 kHz. (c) P–E hysteresis loops of the ICEP-PZT and UP-PZT at room temperature and 10 Hz. (d) Comparison of piezoelectric coefficient of the PZT bulk ceramics prepared without pressing (None), and by uniaxial pressing (uniaxial), cold isostatic pressing (CIP) and ice pressing method (ICEP). (e) Photographs of bulk PZT ceramics in different shapes and bulk BTO prepared by the ice pressing method (scale bar = 1 cm).

The compaction of the green body influences piezoelectric performance. Fig. 3b and Fig. S6 (ESI†) highlight the variation of the dielectric constant (ε) and dielectric loss (tan δ) versus the frequency. The ICEP-PZT shows a higher dielectric constant and a slightly lower dielectric loss within the whole frequency ranges, due to the improvement of the grain boundary after the ice-pressing process. The polarization levels versus applied electrical field (P–E) hysteresis loops are shown in Fig. 3c. The ICEP-PZT performs well-saturated P–E loops with a higher maximum polarization (53.9 μC cm⁻²), remanent polarization (44.07 μC cm⁻²), and a lower coercive field (15.83 kV cm⁻²), indicating that ICEP-PZT is easier to be poled.⁴⁰ It is commonly accepted that higher porosity results in lower Pr due to a lower quantity of active components compared to the dense counterpart, leading to a reduced level of polarization.^21,22 The high diffraction peaks can be identified from the XRD patterns, indicating good crystallinity (Fig. S7, ESI†). The easy reversal of polarization under DC bias can directly result in the improvement of piezoelectric responses.^41,42 Therefore, ICEP-PZT also exhibits a higher piezoelectric coefficient d₃₃ of 531 pC N⁻¹ (Fig. 3d and Table S1, ESI†), which is over four times higher than that of UP-PZT (125 pC N⁻¹). ICEP-PZT is comparable to conventional pressed bulk counterparts (i.e., uniaxial pressing^{31,32,43–45} and CIP^30,34). Theoretically, the properties of the piezoceramic depend to a great extent on the densification degrees of the green compact. For low densification degrees, the electric field is concentrated in the pores with lower permittivity. This reduces the effective electric charge in the ceramic bulk, leading to a reduction of remanent polarization Pr and piezoelectric properties, and vice versa. The improved piezoelectric performance observed above is attributed to the ice pressure method, which generates a uniform and high pressure that acts equally over the surface of the green bodies, eliminating defects or voids in the final products. Therefore, the increased density of ICEP-PZT allows for sufficient polarization, thereby further improving the piezoelectric properties of the piezoceramics.⁴¹ Overall, we believe the ice pressing method is a promising compaction process for manufacturing bulk ceramics. It can increase the densification degree of green bodies to prepare high-performing piezoelectric ceramics.

It is important to note that the new ice pressing method described herein is not only compatible with other processing techniques, but also enables the manufacturing of piezoceramics in a diverse range of shapes. To illustrate this, we successfully fabricate cylindrical-, square-, and strip-like PZT and barium titanate (BTO), as depicted in Fig. 3e. When preparing piezoceramics with a high aspect ratio, the structure may be prone to collapse during the ice pressing process. However, this challenge can be overcome by increasing the mechanical strength of the precursor. For example, the proportion of binders may be increased, or a pre-sintering step may be implemented. These measures enhance the precursor's mechanical strength, ultimately mitigating the risk of structural collapse during the ice-pressing process.

2.4 Ice pressing process enabled porous piezoceramics

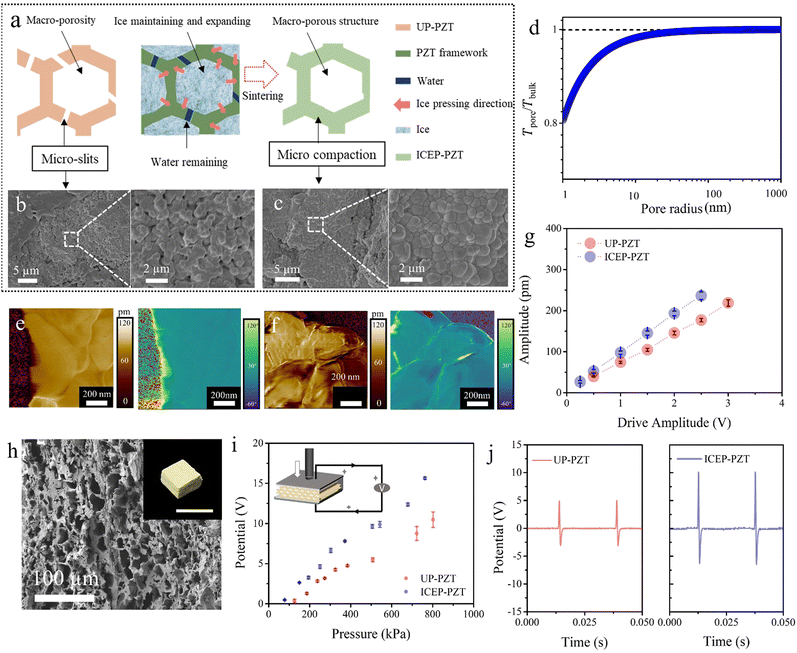
Besides dense piezoceramics, the versatile ice pressing method offers a unique way to create globally porous but locally compact piezoceramics that traditional densification methods cannot achieve. In general, porous piezoceramics exhibit subordinate piezoelectric properties compared with their bulk counterparts due to incompact local bodies, originating from their fabrication route. One of the most employed methods is the template-assisted process, in which a polymer template is first coated or infiltrated with a suspension, followed by sintering and template removal to obtain piezoceramics with a morphology similar to the original template. Unfortunately, the precursor is sintered while free shrinkage of the template co-occurs, leading to the existence of pores and defects within the internal structure and struts of the porous skeleton (Fig. 4a).^23,46 The need for a general and cost-effective strategy for compacting porous ceramic green skeletons is urgent, as existing compression processes such as uniaxial compression and CIP are limited by their reliance on solid-to-solid load paths, which cannot generate forces inside random microchannels. To end this, we introduce the compatible “ice and fire” technology into the manufacturing of porous piezoceramics. Porous PZT ceramics are prepared via an ice-pressing assisted template method¹⁸ (ICEP-PZT) and a case without ice pressing treatment (UP-PZT) for comparison. As demonstrated, UP-PZT presents cracks in the framework and many micro-slits caused by the free shrinkage and release of organic gases upon sintering (Fig. 4a, b and Fig. S8, ESI†). In sharp contrast, a continuous framework with closely arranged grains in the solid parts can be observed in ICEP-PZT (Fig. 4a, c and Fig. S9, ESI†).

Fig. 4 Effect of the ice pressing method on piezoceramic composites. (a) Structure evolution of porous piezoceramics UP-PZT and ICEP-PZT. The preparation of UP-PZT involves sintering the precursor while the template undergoes uncontrolled shrinkage, resulting in cracks and micro-slits in specific framework regions. In contrast, ICEP-PZT processing the ice pressing method, shows selective freezing: water in the macropore structure will preferentially transform into ice, followed by the water in the slits. A continuous framework with closely arranged grains can be observed in the ICEP-PZT. (b) FESEM images presents the structure of UP-PZT with separated framework and micro-slits, due to free shrinkage and release of organic gases during sintering. (c) FESEM images of micro-structure compaction of ICEP-PZT, owing to the ice protection and internal stress generated via ice pressure. (d) Variation of freezing temperature with pore size at the micro-scale. The smaller pore radius, the lower frozen temperate. (e) PFM amplitude map and PFM phase image of UP-PZT composites in the out-of-plane direction. The driven voltage is 1 V. (f) PFM amplitude map and phase image of the ICEP-PZT composites in the out-of-plane direction. The driven voltage is 1 V. (g) PFM amplitude responses ICEP-PZT and UP-PZT composite at different drive amplitudes, indicating that ICEP-PZT with local compaction presents a higher piezoelectric response. (h) FESEM images and (inset) photograph of the structure of ICEP-PZT with global pore structures. Noted that the scale bar represents 1 cm. (i) The open circuit output voltage of the porous PZT devices under pressure from 0.01 MPa to 0.8 MPa. The load frequency is 40 Hz. The insect image displays the measurement device, force application direction, and output signal. (j) Open circuit output voltage of the two porous PZT devices excited by the same force.

The ice pressing method, in particular, exhibits selective freezing, with water initially transforming into ice in the macropore structure and subsequently in the slits (Fig. 4a). The pore preference originates from the evolution of the ice–water interface (Fig. S10, ESI†).^9,13,36,37 At the micro-scale, the ice–water interface moves into the pore only when the surface temperature drops lower than the critical temperature. The freezing temperature T_pore in pore always performs a depression than that in bulk. The depression can be described using the Gibbs–Thomson equation (see full discussion in the ESI†):⁴⁷

where γ_iw is the surface energy between ice and water, ρ_water is the density of water, ΔH_f is the enthalpy of melting, and R_pore is the pore radius. The equation reveals the crucial factor for selective freezing, that is, the pore radius. In a word, the smaller the pore radius, the lower the frozen temperate (Fig. 4d). Accordingly, the structural pores are preserved globally while the cracks are compressed locally.

Piezoresponse force microscopy (PFM) is adopted to characterize the piezoelectric variation of porous PZT, so as to reveal the local structure and piezoelectric properties (Fig. 4e and f). The magnitude of the out-of-plane displacement images is shown on the left, while the right section displays their corresponding phase images. The ICEP-PZT shows an enhanced piezoelectric response corresponding to the out-of-plane polarization. In order to evaluate their average piezoelectric properties, piezoresponse of the region at different driven voltages is measured.⁴⁸ The average values of displacement are obtained from all measurements, as a function of the amplitude of the applied voltage (Fig. 4g). Thus, the piezoelectric coefficient (d₃₃) of UP-PZT and ICEP-PZT can be calculated to be 71.1 and 93.4 pm V⁻¹, respectively.

The local compaction structure can improve the local piezoelectric properties and contribute to the overall output. We further characterize the overall piezoelectric responses by assembling the piezoelectric composite device. As the inset image in Fig. 4i displays, a vibration generator is used to conduct a special frequency and compressing force onto the piezoceramic devices. As shown in Fig. 4i, the porous ICEP-PZT-based composite exhibits a stronger pressure sensitivity than the porous UP-PZT-based composite at the wide pressure range from 0.01 MPa to 0.8 MPa. The comparison of UP-PZT and ICEP-PZT further demonstrates that the local compaction increases the connectivity of the framework and dramatically benefits improved piezoelectric responses. This is due to the simultaneous internal and external stress generated during freezing, which maintains the porous structure while locally densifying. Therefore, the compatible “ice and fire” technique makes it possible to manufacture materials including but not limited to high-performance porous piezoceramics.

3. Conclusions

The “ice and fire” technology provides an alternative method for fabricating lightweight and high-performance porous ceramics and their composites. However, several essential factors must be considered when adopting it. First, water at a high initial temperature is preferred to achieve rapid freezing according to the Mpemba effect. Second, the loading force can be easily regulated by the volume of water in the vessel rather than the temperature. Finally, freezing functional pores while compressing the defects is possible for defects under 1 μm according to the Gibbs–Thomson effect. It is worth noting that while the ice pressing method can achieve homogeneous pressure and high pressing rates, the maximum pressure generated in the system may not reach the theoretical value (approximately 202 MPa). The primary reason is the supercooling phenomenon observed during the freezing process. Once water is supercool, the freezing temperature of ice becomes lower than 0 °C. Only when water completely transforms into ice at 0 °C, the stress reaches the maximum. Additionally, the ice pressing method may not work if the functional pore size is smaller than 1 μm, because the difference in freezing temperature caused by the pore size is not significant enough.

In this work, piezoceramics with global porosity and local compaction are obtained by the “ice and fire” process, which displays a satisfactory combination of mechanical and electrical properties. The ice pressing method is a novel compaction process with advantages such as uniform pressure distribution, wide pressure range, highly effective and selective freezing. It breaks the compaction limitation of current ceramic manufacturing methods, since there is no relevant compaction technique for porous ceramics. This study underscores the versatility and efficacy of the ice pressing method and highlights its potential as a valuable tool for manufacturing complex structures. Moreover, the ice pressing method is compatible with other manufacturing processes, like the sacrificed template, gel casting, additive manufacturing, etc. Thus, applications in thermal insulation, catalyst substrates, filtration systems, and biomedical and energy storage and conversion are expected to expand. The study also explores the potential use of the Mpemba effect in creating technologically relevant materials that can rapidly remove heat from localized sources, offering new and essential strategies for materials engineering.

4. Experimental section

4.1 The preparation of ICEP-PZT by ice pressing process

The setup of the ice pressing method is composed of a Dewar flask and a steel container (internal volume of 3 × 3 × 3 cm³) with a horizontal movement lid. A Dewar flask is used for a liquid nitrogen bath. PZT green bodies (see preparation detail in the ESI Text,†) are packed in a plastic bag and put into a sealed container filled with water. The container is submerged in liquid nitrogen and then directly frozen for 5 min. Afterward, it is removed from the liquid nitrogen until the ice fully melts under room temperature. After ice pressing, the green compacts are sintered at 1200 °C for 2 hours after debinding at 600 °C for 2 hours. The sintered pellets (ICEP-PZT) are polished, with Pt coated on both sides as electrodes for performance evaluation through magnetron sputtering (Q150TS). As a comparison, UP-PZT (use the above PZT green bodies directly) is prepared by the same procedure except for the ice pressing step.

4.2 The preparation of the porous PZT framework and composites

The chemical-treated wood template and PZT sol-powder suspension are prepared by our previously reported method.¹⁸ The wood template is immersed in PZT sol-powder suspension until the whole wood template is infiltrated with the PZT suspension within a few seconds. After squeezing to remove extra PZT suspension, the sample is dried in an oven at 70 °C for 1 hour. With the sol immersed in the wood template converting to gel, the precursor is sintered at 800 °C for 2 hours to remove the wood template. After ice pressing and sintering again at 1000 °C for 2 hours in Pb atmosphere, the aligned lamellar piezoelectric framework is obtained. In comparison, the porous UP-PZT framework is prepared similarly, except for the ice pressing step.

To prepare piezocomposites based on the porous PZT framework, uncured polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning Co., Ltd) with 10 wt% curing agent is fully mixed and then vacuumed to remove the bubbles. Then the prepared piezoceramic framework is immersed in uncured PDMS until the piezoceramic framework is fully infiltrated with uncured PDMS. After curing at 70 °C for 2 h, the PZT composite is finally obtained. With silver film sputtered as the electrode and PDMS film spin coated as the protective layer, the prepared PZT device is polarized at 85 °C for 1 hour under an electric field of 5 kV mm⁻¹ and then naturally cooled down to room temperature.

4.3 Materials and piezoelectric performance characterization

The scanning electron microscopic morphologies of the materials are examined using a scanning electron microscope (FESEM; FEI Quanta 450). The energy dispersive spectroscopic (EDS) mapping of the PZT piezoceramic framework is characterized using an energy dispersive spectrometer (Oxford Instruments, INCA Energy 200). The bulk density was measured using a Gas Displacement Pycnometry System (AccuPyc 1340, Micromeritics, America). The quasi-static piezoelectric constants are measured using a quasi-static piezoelectric meter (YE2730A d₃₃ meter). Before testing, the PZT flakes are sputtered with silver film on each side as the electrode and then polarized at 130 °C for 1 hour under the electric field of 3.5 kV mm⁻¹. The crystal structures of the PZT ceramic are characterized by X-ray diffraction (XRD, Rigaku SmartLab) with a scan speed of 4° per min. The ferroelectric hysteresis loop was tested using a ferroelectric analyzer (PK-CPE 1701, PolyK Technologies, USA). Temperature dependence of the relative dielectric constant and the corresponding dielectric loss tan δ are detected using a high-temperature dielectric property test system (DPTS-AT-600, Wuhan Yanhe Technology Co., Ltd). To assess the piezoelectric behavior of the samples, an Asylum Cypher ES AFM system is used in the DART mode to minimize noise and topography crosstalk. A conductive Nano world Arrow-EFM probe with Pt/Ir coating on both cantilever and tip, featuring a nominal resonance frequency of 75 kHz and nominal stiffness of 3 N m⁻¹, is used for all PFM and SKPM measurements. The contact resonance frequency is around 50 kHz. To determine the effective piezoelectric coefficient d₃₃ of the composites, a small area of 1 × 1 μm² is scanned under AC voltages ranging from 0.2 to 3 V. The open circuit output voltage of porous composite is measured using a digital oscilloscope (Rohde & Schwarz RTE1024) and the force is detected using a mechanical force sensor. A vibration generator is used to generate controllable oscillation frequency and compressing force.

Author contributions

Conceptualization: X. D. Yang, Y. Shan, Z. B. Yang. Methodology: X. D. Yang, Y. Shan, Y. Hong. Investigation: X. D. Yang, S. Y. Liu, Z. M. Zhang, X. D. Yan, X. T. Gong, G. Z. Zhang. Supervision: Z. B. Yang. Writing—original draft: X. D. Yang, Y. Shan, Y. Hong, Z. B. Yang. Writing – review & editing: all the authors.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The work described in this paper was supported by the Hong Kong Research Grants Council (GRF project no. 11212021 and 11210822), the Innovation and Technology Fund (project no. ITS/065/20; GHP/096/19SZ) from Innovation and Technology Commission of Hong Kong Special Administrative Region, and the International and Regional Science and Technology Cooperation Project (project no. kh2304005) from Department of Science and Technology of Hunan Province.

References

1. S. Deville, J. Mater. Res., 2013, 28, 2202–2219.
2. P. Xu, B. Cui, Y. Bu, H. Wang, X. Guo, P. Wang, Y. R. Shen and L. Tong, Science, 2021, 373, 187–192.
3. G. Bai, D. Gao, Z. Liu, X. Zhou and J. Wang, Nature, 2019, 576, 437–441.
4. M. Jeng, Am. J. Phys., 2006, 74, 514–522.
5. J. Jin and W. A. I. I. I. Goddard, J. Phys. Chem. C, 2015, 119, 2622–2629.
6. M. Vynnycky and S. Kimura, Int. J. Heat. Mass Transf., 2015, 80, 243–255.
7. J. G. Dash, A. W. Rempel and J. S. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695–741.
8. N. Matsuoka and J. Murton, Permafr. Periglac. Process., 2008, 19, 195–210.
9. M. J. Powell-Palm, B. Rubinsky and W. Sun, Commun. Phys., 2020, 3, 39.
10. J. Zheng, L. Winnubst, Velianti, S. Fang and D. Salamon, Adv. Eng. Mater., 2011, 13, 77–81.
11. N. Lahav and S. Chang, J. Mol. Evol., 1976, 8, 357–380.
12. H. Ozawa and S. Kinosita, J. Colloid Interface Sci., 1989, 132, 113–124.
13. R. O. David, C. Marcolli, J. Fahrni, Y. Qiu, Y. A. Perez Sirkin, V. Molinero, F. Mahrt, D. Brühwiler, U. Lohmann and Z. A. Kanji, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8184–8189.
14. Y. Shan, S. Liu, B. Wang, Y. Hong, C. Zhang, C. W. Lim, G. Zhang and Z. Yang, Nat. Commun., 2021, 12, 6066.
15. Z. Yang, S. Zhou, J. Zu and D. Inman, Joule, 2018, 2, 642–697.
16. C. Melo, A. Moraes, F. Oliveira Rocco, F. S. Montilha and R. Canto, J. Eur. Ceram. Soc., 2018, 38, 2928–2936.
17. R. Oberacker, Ceram. Sci. Technol., 2011, 3, 3–37.
18. Y. Hong, L. Jin, B. Wang, J. Liao, B. He, T. Yang, Z. Long, P. Li, Z. Zhang, S. Liu, Y. Lee, B. L. Khoo and Z. Yang, Energy Environ. Sci., 2021, 14, 6574–6585.
19. Y. Hong, B. Wang, W. Lin, L. Jin, S. Liu, X. Luo, J. Pan, W. Wang and Z. Yang, Sci. Adv., 2021, 7, eabf0795.
20. H. Cui, R. Hensleigh, D. Yao, D. Maurya, P. Kumar, M. G. Kang, S. Priya and X. Zheng, Nat. Mater., 2019, 18, 234–241.
21. J. I. Roscow, Y. Zhang, M. J. Kraśny, R. W. C. Lewis, J. Taylor and C. R. Bowen, J. Phys. D: Appl. Phys., 2018, 51, 225301.
22. Y. Zhang, J. Roscow, R. Lewis, H. Khanbareh, V. Y. Topolov, M. Xie and C. R. Bowen, Acta Mater., 2018, 154, 100–112.
23. M. Yan, Z. Xiao, J. Ye, X. Yuan, Z. Li, C. Bowen, Y. Zhang and D. Zhang, Energy Environ. Sci., 2021, 14, 6158–6190.
24. A. R. Studart, U. T. Gonzenbach, E. Tervoort and L. J. Gauckler, J. Am. Ceram. Soc., 2006, 89, 1771–1789.
25. E. Mercadelli, A. Sanson and C. Galassi, Porous piezoelectric ceramics, INTECH Open Access Publisher, 2010.
26. N. F. K. Bahanurddin, J. J. Mohamed and Z. A. Ahmad, J. Mater. Sci.: Mater. Electron., 2018, 29, 5439–5445.
27. U. M. Attia, Crit. Rev. Solid State Mater. Sci., 2021, 46, 587–610.
28. D. A. Issitt and P. J. James, Powder Metall., 1986, 29, 259–264.
29. P. K. Panda and B. Sahoo, Ferroelectrics, 2015, 474, 128–143.
30. M. Siddiqui, J. J. Mohamed and Z. A. Ahmad, J. Aust. Ceram. Soc., 2020, 56, 371–377.
31. Ľ. Medvecký, M. Kmecová and K. Saksl, J. Eur. Ceram. Soc., 2007, 27, 2031–2037.
32. L. B. Kong and J. Ma, Mater. Lett., 2001, 51, 95–100.
33. J. Li, Y. Yang, H. Jiang, Y. Wang, Y. Chen, S. Jiang, J.-M. Wu and G. Zhang, Composites, Part B, 2022, 232, 109617.
34. M. A. Zaghete, J. A. Varela, M. Cilense, C. O. Paiva-Santos, W. C. Las and E. Longo, Ceram. Int., 1999, 25, 239–244.
35. S. Miao, Y. Wang, L. Sun and Y. Zhao, Nat. Commun., 2022, 13, 4044.
36. A. Kumar and J. Bechhoefer, Nature, 2020, 584, 64–68.
37. R. Chen, C. Wang, Y. Huang, L. Ma and W. Lin, J. Am. Ceram. Soc., 2007, 90, 3478–3484.
38. Z. Tang, W. Huang, Y. Zhang, Y. Liu and L. Zhao, InfoMat, 2022, e12352.
39. H. Kanno, R. J. Speedy and C. A. Angell, Science, 1975, 189, 880–881.
40. M. Zheng, Y. Hou, M. Zhu, M. Zhang and H. Yan, J. Eur. Ceram. Soc., 2014, 34, 2275–2283.
41. X. Chen and Y. Liao, Materials, 2023, 16.
42. M.-P. Zheng, Y.-D. Hou, F.-Y. Xie, J. Chen, M.-K. Zhu and H. Yan, Acta Mater., 2013, 61, 1489–1498.
43. N. Jaitanong, A. Chaipanich and T. Tunkasiri, Ceram. Int., 2008, 34, 793–795.
44. A. Benčan, B. Malič, S. Drnovšek, J. Tellier, T. Rojac, J. Pavlič, M. Kosec, K. G. Webber, J. Rödel and D. Damjanovič, J. Am. Ceram. Soc., 2012, 95, 651–657.
45. J. Du, C. Yang, Y. Li, J. Yan, L. Qiu, L. Wang and K. Zhu, J. Mater. Sci.: Mater. Electron., 2023, 34, 780.
46. C. Vakifahmetoglu, D. Zeydanli and P. Colombo, Mater. Sci. Eng., R, 2016, 106, 1–30.
47. P. Buffat and J. P. Borel, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 2287–2298.
48. Z. Zhang, S. Liu, Q. Pan, Y. Hong, Y. Shan, Z. Peng, X. Xu, B. Liu, Y. Chai and Z. Yang, Adv. Mater., 2022, 34, 2200864.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh01869e

‡ These authors are co-first authors in this work.

---