Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical models for dense solutions
J.-F.
Dufrêche
 *,
B.
Siboulet
and
M.
Duvail
*,
B.
Siboulet
and
M.
Duvail
ICSM, University of Montpellier, CEA, CNRS, ENSCM, Marcoule, France. E-mail: jean-francois.dufreche@umontpellier.fr
First published on 22nd May 2024
Abstract
Here we examine the question of the chemical models widely used to describe dense solutions, particularly ionic solutions. First, a simple macroscopic analysis shows that, in the case of weak interactions, taking into account aggregated species amounts to modelling an effective attraction between solutes, although the stoichiometry used does not necessarily correspond to atomic reality. We then use a rigorous microscopic analysis to explain how, in the very general case, chemical models can be obtained from an atomic physical description. We show that there are no good or bad chemical models as long as we consider exact calculations. To obtain the simplest possible description, it is nevertheless advisable to take the speciation criterion that minimises the excess terms. Molecular simulations show that, very often, species can be defined simply by grouping ions which are in direct contact. In some cases, the appearance of macroscale clusters can be predicted.
1 Introduction
Electrolytes in aqueous solution or in other solvents are modelled differently depending on the concentration regime.• Firstly, in the case of dilute electrolytes, we generally follow the formalism proposed by Debye, Hückel1 and Onsager.2 Dilution means that long-range effects predominate. It is therefore a regime in which electrostatics is predominant, but as the ions are far apart, it is dominated by thermal agitation and the equations can therefore be linearised, allowing them to be solved. This is the domain of the limiting laws in the square root of the concentration, which control the equilibrium properties (chemical potentials, for example) and transport coefficients (conductivity, diffusion coefficients, viscosity, for example).3 These laws are exact in this limit and are very useful for analytical chemistry, but in practice their range of validity is very small, typically for the concentrations of less than 10−1 mol L−1 for the best case, which is that of weakly charged 1–1 electrolytes in a solvent such as water, which has a very high dielectric constant. This area shows that the interaction between ions is mainly attractive, which is rather stabilising for the solution.
• Then there is the regime of high concentrations, and in particular that of dense media. If we stay around average concentrations, simple extensions of Debye and Hückel laws are possible. The most obvious effect is due to the size of the ions. The purely attractive nature of the Debye–Hückel model is not valid anymore. It is counterbalanced by repulsive forces that increase the chemical potentials, forces that can be described, for example, as steric forces. In this context, the primitive model of electrolytes, in which they are described as charged hard spheres, is of particular interest.4–6
• For the highest concentrations, this description needs to be completed. First of all, the sizes of the ions are not necessarily additive.7 There are preferential interaction8 effects between ions (generally called Hofmeister’s effects) and new specific attractive forces can then appear. At high concentrations, the behaviour of solutions is very different. For some electrolytes, which are highly repulsive, the activity coefficient increases sharply, while for others it remains close to 1 and may even decrease.
The attractive effects at high concentration are often described by a chemical model.9–11 It is assumed that ion pairs are formed at high concentrations due to the interaction between cations and anions. This new species12 significantly reduces the chemical potential and conductivity. It is therefore possible to measure association constants. These association effects often seem to be directly linked to the charge of the ions, the most charged and smallest electrolytes generally being the most associated. In that case, the ion pairs are known as Bjerrum13 pairs. Bjerrum proposed the first model to predict these association constants KBj by assuming a mainly electrostatic interaction occurring from the contact distance σ of the ions:
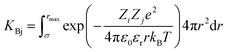 | (1) |
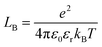 is Bjerrum’s length because this distance corresponds to the inflexion point of the ionic distribution. KBj is the Mass Action Law (MAL) constant where the activity is defined as the number concentration. The dimensionless MAL constant K° is K° = NAC°KBj with NA the Avogadro constant and C° the molar concentration defining the standard state, generally taken to be 1000 mol m−3. Bjerrum’s concept of electrostatic pairs can be generalised to charged interfaces. We can thus define adsorption constants14–17 for adsorbed ions, which are of great practical use in predicting surface charge states, and which can be roughly predicted by extending the Bjerrum model to interfaces, as the MUSIC model18 does, for example.
is Bjerrum’s length because this distance corresponds to the inflexion point of the ionic distribution. KBj is the Mass Action Law (MAL) constant where the activity is defined as the number concentration. The dimensionless MAL constant K° is K° = NAC°KBj with NA the Avogadro constant and C° the molar concentration defining the standard state, generally taken to be 1000 mol m−3. Bjerrum’s concept of electrostatic pairs can be generalised to charged interfaces. We can thus define adsorption constants14–17 for adsorbed ions, which are of great practical use in predicting surface charge states, and which can be roughly predicted by extending the Bjerrum model to interfaces, as the MUSIC model18 does, for example.
This shows that Bjerrum’s concept of ion pairs is not historically a rigorous one: the interactions are certainly not mainly ionic at short distances and the definition of the pair is problematic. Experimentally, the values measured are not always consistent. They may depend on the quantity under consideration, unlike speciation defined by covalent bonds. It is therefore necessary to question these chemical models19 for weak interactions such as those between ions in a dense medium.
The most spectacular way of doing this is to use molecular dynamics simulation. For some years now, it has not only been possible to simulate these concentrated solutions, but above all to build chemical models on a molecular basis.20–22 In particular, the use of biased simulations makes it possible to calculate the effective interaction between ions, and therefore to calculate chemical speciation more rigorously. Generally, the previous Bjerrum relation (1) is used directly, replacing the Coulomb potential with the effective potential (Potential of Mean Force PMF) calculated by averaging over the solvent configurations.
In a nutshell, generally speaking, chemical models for non-covalent interactions are an extremely common way of modelling complex solutions, since they provide both a chemical microscopic image of the solution and a way of estimating all the thermodynamic quantities. However, despite recent advances in simulation, their justification is not obvious, which makes the interpretation of their results problematic. What do the species modelled in this way really represent?
The purpose of this article is to provide an answer to this question:
• Firstly, we will show how, in all generality and without approximation, a chemical model can be defined on the basis of a physical model in which only elementary components and their interactions are considered. It will then be shown that chemical species can always be defined in principle, whatever the criteria used to define them. We can then determine the thermodynamic quantities for this chemical model where ions or molecules are possibly formed. At chemical equilibrium, these give exactly the same thermodynamic quantities as the original physical model which does not take these chemical species into account. The results here are quite general and applicable to all types of associating solutes, charged or not, monoatomic or polyatomic, rigid or not, small or large. On the other hand, the proposed method is not necessarily simpler than the original physical model, and in practice can require a numerical solution.
• Finally, we will apply this formalism to the case of simple systems. This will mainly involve describing simple, spherical or roughly spherical ions in bulk or confined aqueous solutions. We will show in which situation these chemical models can claim to represent dense ionic media rigorously in practice.
The central question is how to define chemical species in a concentrated environment controlled by weak interactions. More generally, is it possible to define a species rigorously? Is there a good criterion for defining species? What do multiple associations mean? What is the role of excess terms in speciation?
This article is organised as follows. First of all, we will study macroscopic models of association and their relevance for obtaining thermodynamic quantities in the case of weak interactions. In the following section we propose a rigorous microscopic theory of chemical association in this case. The calculation is quite general and the aim is to deduce a chemical model from an atomic microscopic model. In particular, it will be shown that, in principle, there is no good or bad association criterion, since they can all give exactly the same physical model. The problem is therefore to choose this criterion in practice. We will see in the next section that this is often quite simple at high temperatures, and we will show a few examples. The case of multiple associations typical of concentrated solutions is also discussed. For the sake of simplicity, we will consider mainly the thermodynamic properties. First of all, we will study macroscopic models of association and their relevance for obtaining thermodynamic quantities in the case of weak interactions. In the following section we propose a rigorous microscopic theory of chemical association in this case. The calculation is quite general and the aim is to deduce a chemical model from an atomic microscopic model. In particular, it will be shown that, in principle, there is no good or bad association criterion, since they can all give exactly the same physical model. The problem is therefore to choose this criterion in practice.
2 What it means to write a chemical reaction: the macroscopic level
2.1 Writing a chemical reaction is a simple way of modelling attractive forces in concentrated solution… except for electrostatic forces!
Let us first consider the case of a solution where two species A and B can form a pair P. The associated chemical kinetics are assumed to be rapid. There are two ways of looking at the problem thermodynamically:• First of all, we can make a physical model where we only consider the two elementary species A and B, supporting all the forms (free or in pairs). In this case, The Gibbs free energy total differential reads (at constant temperature and pressure)
| dG1 = μAtotdnAtot + μBtotdnBtot | (2) |
• We then have a chemical model where we consider three species, the two species A and B when they are free Afree and Bfree, and the pair, P. Using notations similar to the previous eqn (2), we obtain the Gibbs free energy total differential:
| dG2 = μAfreednAfree + μBfreednBfree + μPdnP | (3) |
If chemical equilibrium is reached, it can be shown that the two models are strictly equivalent. Indeed, the MAL is μP = μAfree + μBfree. We also have nAtot = nAfree + nP and nBtot = nBfree + nP so that
| dG2 = μAfreednAtot + μBfreednBtot | (4) |
| α = γAtot = γBtot | (5) |
This is what modellers very often do to represent complex solutions: they add species (pairs, triplets, quadruplets, etc.) as a function of concentration to reproduce experimental data as closely as possible over a wide range of concentrations. However, this does not mean that these data necessarily have a microscopic reality.
An important exception to this method is the case of ionic fluids when their equilibrium properties are to be treated rigorously. Since the chemical reactions involve integer numbers of species to form an entity, expansion of the activity coefficient in concentration c cannot have half-integer powers. However, this is required by the Debye–Hückel limiting law for dilute solutions. For example, in the formation of a simple pair, the Mass Action Law (MAL) gives 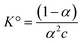 . The activity coefficient of A or B is thus
. The activity coefficient of A or B is thus
| γ = α = 1 − K°c + 2(K°c)2 + O(c3) | (6) |
2.2 The stoichiometry of the species can be obtained for the lowest molecularities from measurements at low concentration
Thermodynamic measurements can therefore, at least in principle, provide the value of the equilibrium constants by adjusting the data as a function of concentration. Can they also give the nature of the resulting species? In principle, this is a much trickier problem. In fact, for dilute solutions, it is sufficient to plot the activity of one species as a function of the logarithm of the concentration of another with which it associates. For example, if an ion A binds with a ligand B by a simple chemical reaction A + nB = C, the resulting MAL shows that the global activity coefficient of ion A is ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = −ln
γ = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K° − n
K° − n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CB. The coordination number n can be obtained by plotting ln
CB. The coordination number n can be obtained by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ as a function of ln
γ as a function of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CB, where CB is the concentration of B.
CB, where CB is the concentration of B.
This is the advantage of the slope method,26 which is widely used to characterise solvent phases during the extraction of metal ions. However, the method is rather tricky to implement, as it often requires considerable dilution for the method to be meaningful when the aim is to characterise concentrated solutions. The method could also be used to characterise the aggregation number of micelles, but in practice the sensitivity is very low and a pseudophase model where the aggregated species are considered as a second liquid phase is generally preferred.
3 What it means to write a chemical reaction: the microscopic level
It is not at first sight very simple to propose a similar method on a microscopic scale. In this case, it is necessary to define an atomic model in which the aggregated chemical species are explicitly present, from another atomic model in which this chemistry is implicit. As before, for the sake of simplicity, the model in which the aggregated species are explicitly considered will be called the chemical model, and the model in which this speciation is not distinguished but simply described by interactions will be called the physical model. Both models are atomic but with different species. The physical model is the original molecular model, which can be explored by molecular dynamics. The chemical model, on the other hand, is intended to be simplified, e.g. by neglecting correlations between species to arrive at a simpler chemical description. We therefore need to transform the partition function of the physical model, which is the simplest because it contains the smallest number of species, into a more complex partition function because it contains more species. The aim of this transformation is to make the two partition functions strictly equivalent.As we pointed out in the introduction, a central problem is the criterion used to determine the chemical species present. How, for example, can we say that two monoatomic ions are associated? Is it enough to say that they are less than a certain distance apart? And if so, what is the limit value? There are many possible criteria and the recipe for determining the right one is not known. Generally speaking, it can even be said that the right criterion does not exist. Chemistry is not a matter of Nature. It is the observer who, according to their point of view, decides which atoms are associated or not. Chemical species only really exist in the mind (or eyes) of the observer. As pointed out by Onsager27 at the conference in electrochemistry in Montpellier (France) in 1968, when discussing the Bjerrum association model, the definition of a “pair” is completely arbitrary: “The distinction between the free ions and associated pairs depends on an arbitrary convention (…) In a complete theory this would not matter; what we remove from one page of the ledger would be entered elsewhere with the same effect.” Indeed, the aim of this part is to show that all the criteria defining chemistry are in fact possible, at least theoretically. There are an infinite number of possible chemical models, but at chemical equilibrium, they all yield exactly the same physical model, provided that the calculations are carried out exactly. Note that this problem also arises when defining solvent molecules, and more generally when defining any molecule from atoms. However, the choice is much less delicate in the case of molecules linked by covalent bonds than in the case of aggregates formed by weak interactions between solutes, which may be dominated by thermal agitation.
3.1 The golden rule to define chemical potential in statistical thermodynamics
To keep the formulae as general as possible without making them long and unreadable, we will consider here a case where a compound A is formed from ν1 atoms (or ions) 1 and ν2 atoms (or ions) 2. Generalization to the case where several associated compounds and/or with more atoms in the compound are present will be immediate. Thus the equilibrium between species reads:| ν11 + ν22 = A | (7) |
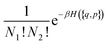 | (8) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ({q, p}) which is equal to H({q, p}) if the point in phase space has the correct number of A’s and equal to +∞ if this is not the case.
({q, p}) which is equal to H({q, p}) if the point in phase space has the correct number of A’s and equal to +∞ if this is not the case.
To simplify the calculation, we take another route and define an ordered chemical Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (NA, {q, p}). It is only equal to the Hamiltonian H({q, p}) if not only is NA correct, but also the particles are well ordered. The first compound A must thus be made up of the first ν1 atoms (or ions) 1 and the first ν2 atoms (or ions) 2, the second compound A is made up of the next ν1 atoms (or ions) 1 and the next ν2 atoms (or ions) 2, and so on. If the point in the phase space {q, p} does not verify this, then
(NA, {q, p}). It is only equal to the Hamiltonian H({q, p}) if not only is NA correct, but also the particles are well ordered. The first compound A must thus be made up of the first ν1 atoms (or ions) 1 and the first ν2 atoms (or ions) 2, the second compound A is made up of the next ν1 atoms (or ions) 1 and the next ν2 atoms (or ions) 2, and so on. If the point in the phase space {q, p} does not verify this, then ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (NA, {q, p}) = +∞. The term for partition functions (8) thus becomes:
(NA, {q, p}) = +∞. The term for partition functions (8) thus becomes:
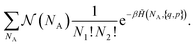 | (9) |
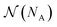 is a combinatorial term equal to the number of ways of choosing the NA compounds A and putting them in order:
is a combinatorial term equal to the number of ways of choosing the NA compounds A and putting them in order: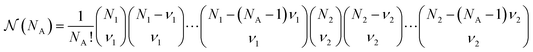 | (10) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (NA, q, p), the order of the aggregates is irrelevant: if we exchange two of them, they correspond to the same state in the original physical Hamiltonian H({q, p}). We obtain:
(NA, q, p), the order of the aggregates is irrelevant: if we exchange two of them, they correspond to the same state in the original physical Hamiltonian H({q, p}). We obtain: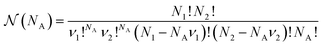 | (11) |
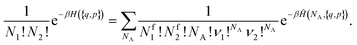 | (12) |
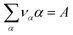 | (13) |
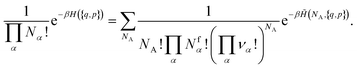 | (14) |
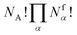 . However, there are three important points to make this link.
. However, there are three important points to make this link.
• A sum over all possible chemical species distributions is necessary. This means that the two models can only be equivalent if they are averaged over all possible chemistry, as in the grand canonical ensemble. This brings us back to the idea that the physical and chemical models are only equivalent at chemical equilibrium.
• The chemical Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (NA, {q, p}) is a hard Hamiltonian. In practice, its definition is very simple: it is exactly the physical Hamiltonian H({q, p}) as long as the configuration respects the correct chemistry, and it is equal to +∞ if it is not the case.
(NA, {q, p}) is a hard Hamiltonian. In practice, its definition is very simple: it is exactly the physical Hamiltonian H({q, p}) as long as the configuration respects the correct chemistry, and it is equal to +∞ if it is not the case.
• Internal indistinguishability factors 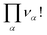 must also be taken into account. They correspond to the possible exchanges of identical particles in the aggregates which do not modify the number of microstates if the particles α are assumed to be indistinguishable.
must also be taken into account. They correspond to the possible exchanges of identical particles in the aggregates which do not modify the number of microstates if the particles α are assumed to be indistinguishable.
The previous formula can be directly extended to the general case where several chemical species can be formed. In this case, we obtain:
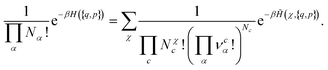 | (15) |
3.2 Chemical equilibria
In the grand-canonical ensemble, the grand partition function calculated using eqn (14) reads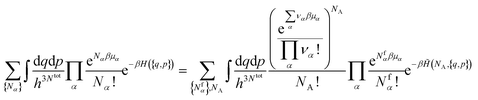 | (16) |
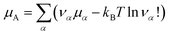 | (17) |
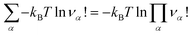 is an internal exchange entropic term that can be included in the standard chemical potential of the aggregate A to recover the standard MAL
is an internal exchange entropic term that can be included in the standard chemical potential of the aggregate A to recover the standard MAL 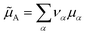 .
.
The two models, physical, with no chemical species, and chemical, where the chemical species A is explicitly considered, are therefore strictly equivalent at chemical equilibrium. We have therefore demonstrated Onsager’s assertion: there is no good or bad chemical model as long as we make exact calculations in statistical thermodynamics, since they all give the same properties at equilibrium. We just have to remember that in the chemical model the Hamiltonian is the hard chemical Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and that we have to consider an additional entropy term for the chemical potential of the chemical species A
and that we have to consider an additional entropy term for the chemical potential of the chemical species A ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A.
A.
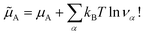 | (18) |
3.3 Equilibrium constants
The equilibrium constants depend on the convention defining the standard state under consideration. They are related to the standard chemical potentials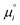 of the various species i involved in the chemical equilibrium. So the problem is to evaluate the latter quantity.
of the various species i involved in the chemical equilibrium. So the problem is to evaluate the latter quantity.
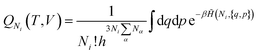 | (19) |
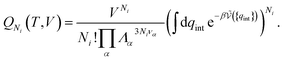 | (20) |
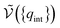 is the potential energy as a function of the internal degrees of freedom. The associated free energy F = −kBT
is the potential energy as a function of the internal degrees of freedom. The associated free energy F = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QNi(T, V) leads to the chemical potential
QNi(T, V) leads to the chemical potential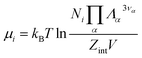 | (21) |
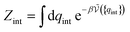 | (22) |
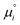 is defined from the limiting law:
is defined from the limiting law: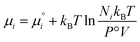 | (23) |
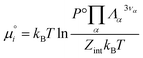 | (24) |
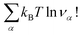 must be added to this term to obtain the true chemical potential:
must be added to this term to obtain the true chemical potential: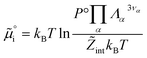 | (25) |
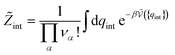 | (26) |
The standard chemical potentials, and therefore the equilibrium constants, are directly related to the internal correlations of the different species involved in the reaction. In practice, the de Broglie length terms do not affect the equilibrium constant and can be omitted. In fact, due to the conservation of matter, they appear in the same quantities on the reactants and products of the reaction and their effect is cancelled out. For example, for a chemical reaction between two atoms, 1 + 2 = 3, we get 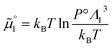 ,
, 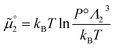 , and
, and 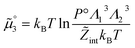 . We obtain
. We obtain
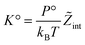 | (27) |
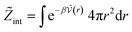 | (28) |
Let us start with a point solute, made up of a single atom. Neglecting edge effects, when the solute is sufficiently dilute, the ratio of the canonical partition function of the solution by the one of pure solvent is
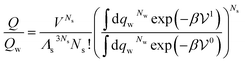 | (29) |
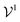 is the potential energy of the solution when only one solute particle is localized at the origin of the coordinate system and
is the potential energy of the solution when only one solute particle is localized at the origin of the coordinate system and 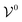 is the potential energy of the pure solvent (without solute particles). Then the resulting Helmholtz free energy F = −kBT
is the potential energy of the pure solvent (without solute particles). Then the resulting Helmholtz free energy F = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q yields
Q yields 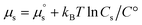 where Cs is the molar concentration of the solute. The standard chemical potential of the solute is
where Cs is the molar concentration of the solute. The standard chemical potential of the solute is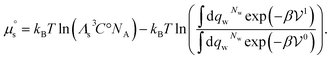 | (30) |
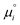 is also valid when the solvent is a mixture of molecules as can be shown by a trivial generalization of this calculation. Consequently eqn (30) is the general expression of the standard chemical potential of a point solute in a solvent.
is also valid when the solvent is a mixture of molecules as can be shown by a trivial generalization of this calculation. Consequently eqn (30) is the general expression of the standard chemical potential of a point solute in a solvent.
If the solute is made up of several atoms or ions α, the Hamiltonian of the chemical model must be considered for the partition function. The relationship (29) becomes:
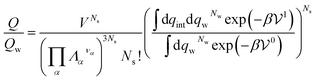 | (31) |
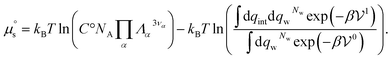 | (32) |
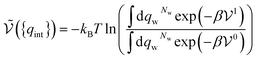 | (33) |
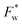 . It therefore corresponds to the potential of mean force between the solute particles averaged over the positions of the solvent when the solutes are infinitely dilute (there is only one solute here). Consequently, this term is nothing but the McMillan–Mayer potential between the α solute molecules. By adding the internal entropic indistinguishability factor we finally obtain:
. It therefore corresponds to the potential of mean force between the solute particles averaged over the positions of the solvent when the solutes are infinitely dilute (there is only one solute here). Consequently, this term is nothing but the McMillan–Mayer potential between the α solute molecules. By adding the internal entropic indistinguishability factor we finally obtain: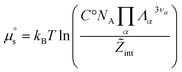 | (34) |
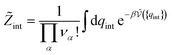 | (35) |
As before, the equilibrium constant for any reaction can be obtained from these expressions for the standard chemical potentials. Here again, the result does not depend on the de Broglie’s lengths, but it may depend on the choice of standard state (C°), depending on the reaction. For a reaction between two monoatomic ions in solution, we obtain as above
K° = C°NA![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) int int | (36) |
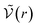 is the McMillan–Mayer potential between the two ions. This relationship corresponds precisely to the Bjerrum’s relationship. Once again, if the two ions are the same, divide
is the McMillan–Mayer potential between the two ions. This relationship corresponds precisely to the Bjerrum’s relationship. Once again, if the two ions are the same, divide ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) int by 2.
int by 2.
4 Results and discussion
4.1 What criteria should be used to define chemical species?
The calculation of association constants in solution is therefore possible by thermodynamic integration if we calculate the effective McMillan–Mayer potential between the solutes. To establish a complete chemical model, it is also necessary to calculate the activity coefficients between the solutes, which can be done by the usual methods of liquid physics.31 Nevertheless, an important issue is the choice of the criterion to define the chemical species. The formalism we derived is quite general and exact. It can be used for any criterion, but in itself it is of no use because the associated model is no simpler than the initial model: there are more species present and the associated free energy is therefore more complex because it depends on more parameters.If we consider a simple association between two ions, the criterion is often to consider that the pair is defined when the two ions are at a distance less than a certain limiting distance d. But which d should we take? Bjerrum’s choice (d = ZiZjLB/2) consists in considering the inflection point in the coordination number curve as a function if the distance between the two ions when the McMillan–Mayer potential is supposed to be purely coulombic. Criteria based on coordination numbers are very popular to distinguish solvation layers, but there is no guarantee that the resulting activity coefficients are weak. Another criterion for the choice of d is such that at low concentration, the free energy of the chemical model is equivalent to that of the physical model. This the strategy proposed by Ebeling.24 For a simple neutral solute, at low solute density ρ the (osmotic) pressure P can be calculated either from the second virial coefficient or from the chemical model:
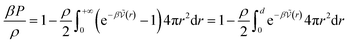 | (37) |
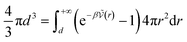 | (38) |
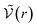 for distances r < d corresponding to internal correlations within the pair. This brings us back to the idea that the criterion defining the chemical species is defined in order to minimise the activity coefficients which depend in the chemical model on the interactions for d > r.
for distances r < d corresponding to internal correlations within the pair. This brings us back to the idea that the criterion defining the chemical species is defined in order to minimise the activity coefficients which depend in the chemical model on the interactions for d > r.
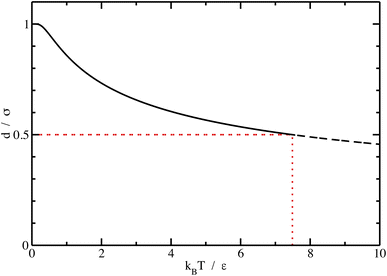
We can see what happens to a square-well potential. In that case, we have a solute for which 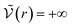 for r < δ,
for r < δ, 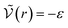 for δ < r < σ and
for δ < r < σ and 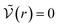 for r > σ. At low temperature, d > δ and we obtain:
for r > σ. At low temperature, d > δ and we obtain:
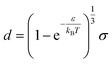 | (39) |
For low temperatures (kBT < ε), the size of the pair d corresponds to σ. The pair is thus unambiguously defined and corresponds to pairs of molecules with an association energy of −ε. If T increases, d gradually decreases. In an exact model, we could keep the d = σ criterion, but if we want to neglect the activity coefficients, it is no longer valid. The system is effectively less attractive. When the temperature reaches 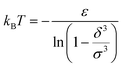 , d = δ. Thermal agitation is sufficient to completely compensate for the attraction and there is no need to consider pairs. This corresponds to the temperature where the second virial coefficient is zero. Beyond that, no chemical model without activity correction is possible. Overall, the solutes repel each other by contact forces, with thermal agitation completely dominating attraction. A chemical model can be retained but activity coefficients greater than 1 must be introduced to take account of this predominant physical effect. In this case, the chemical model may be useful for characterising solute pairs in the attractive domain, but it does not simplify the estimation of thermodynamic properties.
, d = δ. Thermal agitation is sufficient to completely compensate for the attraction and there is no need to consider pairs. This corresponds to the temperature where the second virial coefficient is zero. Beyond that, no chemical model without activity correction is possible. Overall, the solutes repel each other by contact forces, with thermal agitation completely dominating attraction. A chemical model can be retained but activity coefficients greater than 1 must be introduced to take account of this predominant physical effect. In this case, the chemical model may be useful for characterising solute pairs in the attractive domain, but it does not simplify the estimation of thermodynamic properties.
This analysis cannot be used directly for charged solutions. The formula (38) cannot be used because the second virial coefficient diverges and another density expansion has to be considered, with a mandatory Debye–Hückel term. Nevertheless, the fact that association constants are well defined at low temperature (or for high charge) where thermal agitation is not enough to overcome attraction is still important.
4.2 Association from molecular descriptions
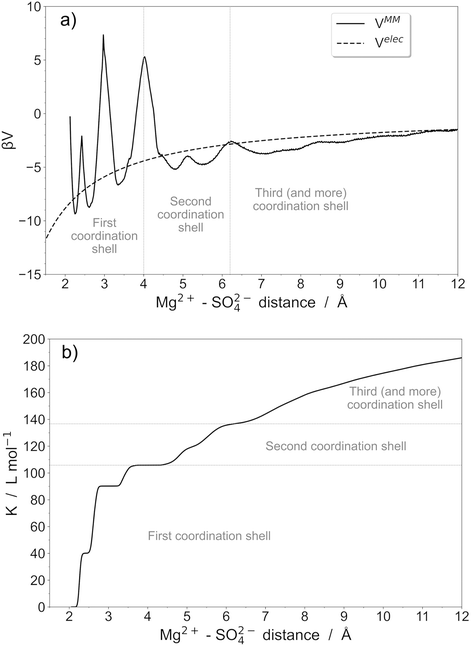
An important point is that the McMillan–Mayer potential in solution is complex because it reflects the molecular nature of the solvent. Even for single ions, it is often not monotonic. In fact, the predominant association is often the formation of Contact Ion Pairs (CIP) in the system. In a CIP, there are no solvent molecules between the two ions and the interaction is often very strong.As an example, we focus now on the description of the MgSO4 pair in water by performing explicit polarization molecular dynamics simulations. The effective McMillan–Mayer potential is calculated from the free energy profile associated with the interaction between Mg2+ and SO42− ions (Fig. 2). This quantity has been calculated using umbrella sampling simulations. Molecular dynamics simulations were performed using Sander10, a module of Amber10,32 using explicit polarization in the NVT ensemble. Water molecules were described using the polarizable rigid water model POL3,33,34 while polarizable force fields of Mg2+ and SO42− were the ones developed in ref. 35.
For the umbrella sampling simulations, we defined the distance between Mg2+ and the sulfur atom of SO42− ions as the equilibrium reaction coordinate, ranging from 1 to 12 Å with a step size of 0.5 Å. A harmonic restraining force constant of 2 kcal mol−1 Å−2 was applied. To overcome activation barriers located at approximately 3.2 Å (transition from bidentate to monodentate configurations) and 4.0 Å (transition from the first to the second coordination shell), a constant force of 50 kcal mol−1 Å−2 was applied. Umbrella sampling simulations were conducted in a simulation box containing 1001 water molecules (31 × 31 × 31 Å3). Production runs were collected for 1 ns. The umbrella sampling simulation protocols were optimized to ensure sufficient overlap of equilibrium windows, ensuring accurate representation of reaction pathways. Free energy profiles were then calculated using the Weighted Histogram Analysis Method36–39 (WHAM).
The potential can therefore exhibit marked oscillations around the coulombic curve, reflecting different kinds of ion pairs. Several shells (at least two) can be distinguished but they are divided into well-defined domains that correspond to different coordination modes. We can therefore propose a global model or, in contrast, a model with several types of pairs. If we stop at the CIP, the value of K° is close to 110 and reaches 140 if we take the second shell, which is also strongly associated.
The choice of chemistry depends on how it will be used, but globally for ions it has to be coupled to the way the electrostatic potential is modelled. Numerous macroscopic theories, such as the Mean Spherical Approximation40 generalise the Debye–Hückel approach and they are valid only at high temperature. These theories cannot describe the strong electrostatic attractions and they must be modified by considering, for example, the pair explicitly.41–44 In that case, the criterion can be obtained by comparing the potential depth to kBT. When compared with experimental data45 for transport properties, the important point is the lifespan of species, which should diffuse together. Thus, the comparison with kBT also makes sense, but we must also look at the activation energy barriers when they are significant.
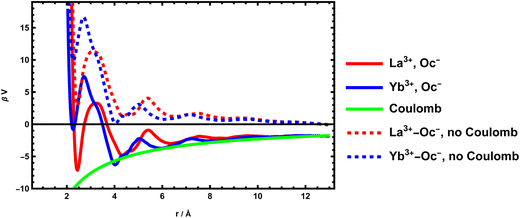
Chemical association is also important for confined solutions. In particular, in the case of surfaces, recent studies have shown that the important point in describing electrical double layers (EDL), when simple models based on the Poisson–Boltzmann equation are no longer valid, is to take into account a Stern layer made up of ions specifically bonded to the surface. This gives us ion pairs in contact comprising a charged atom of the surface and an ion of opposite charge. This association can also be calculated from molecular dynamics from the same method. For silica surfaces, cations are generally associated to negatively charged oxygen atoms of the surfaces (silanolate groups). The McMillan–Mayer potential can also be calculated. We show here the case of two free energy profiles of lanthanides interacting with a negatively charged silica surface. We use a classical simulation, with LAMMPS. The system and the method46 has been originally derived for divalent cations. The methodology has been adapted to lanthanide potentials.47 The potential of mean force is determined from Umbrella Sampling using the WHAM algorithm.
Overall, the profiles presented in Fig. 3 are no different from those of single ions in solution. There are fewer coordination modes than for the MgSO4 pair because the anion is not molecular. We still mainly find the presence of this CIP around r = 2 Å. The value of the constant is trickier to calculate here because it depends on the model that considers it. In EDL, generally, the long-ranged electrostatic force is considered in a non-local way, by solving the Poisson equation. The MAL defining the pairs associated with the surface are therefore defined using not the global chemical potentials but the local electrochemical potentials, which treat the electrostatic term separately. The free ions are therefore assumed to have the same potential as those associated. The coulombic contribution of the McMillan–Mayer potential must therefore be removed to calculate the association constants on a charged surface.
Despite their similarities, the two lanthanide cations have very different adsorption intensities, La3+ being less bound than Yb3+. In terms of adsorption constant, we obtain 10−3.72 for La3+ and 10−6.75 for Yb3+. In terms of Gibbs energy difference, which represents the specificity of the site, it corresponds to a difference of 7 kBT ≈ 17 kJ mol−1 which is important. An important point to note here is that the ratio of constants (or the difference in Gibbs energies) are more important than the absolute values of the constants, as they are entirely modulated by the electrostatic potential, which can vary greatly at the surface. The phenomenon is in fact controlled by the surface charge.
4.3 Multiple associations
Highly concentrated solutions combine ionic associations and it is therefore possible to form contact ion chains48 of very large size. For concentrated solutions, this results in large clusters, sometimes called prenucleation clusters49,50 if they are formed just before saturation of the electrolyte. In fact, this phenomenon is not necessarily related to the insolubility of the salt. The electrostatic association itself can form these very large polyionic species. This can be understood using a simple model.Let us assume that the formation of these species is linear and that these aggregates are therefore sequences of CIPs. The smallest aggregate is the classical ion pair for which the association constant K° is given by (36) for atomic ions. When larger species are formed, other ions are added in an alternating sequence of cations and anions. Species with an even number of ions are unique. To simplify, we assume that each ion can place itself on either side of the chain in configurations similar to those it would have in a simple pair, but divided into two parts (on the left and right of the chain). Thus, for an even chain of size 2n, the configuration integral of the internal partition functions (35) is K°2n−1 and the formation constant is 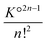 . For aggregates with an odd number of ions 2n + 1, there are two symmetrical possibilities: either with an excess cation or an anion. The two formation constants are the same:
. For aggregates with an odd number of ions 2n + 1, there are two symmetrical possibilities: either with an excess cation or an anion. The two formation constants are the same: 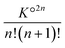 . The total number of cations (or anions) in solution Ctot is expressed as a function of the concentration of free cations (or anions):
. The total number of cations (or anions) in solution Ctot is expressed as a function of the concentration of free cations (or anions):
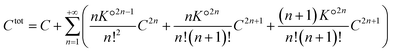 | (40) |
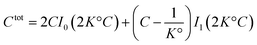 | (41) |
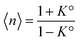 . It diverges at the critical concentration 1/K°. Thus for numerous electrolytes, a second regime with a percolation cluster appears above a critical concentration.
. It diverges at the critical concentration 1/K°. Thus for numerous electrolytes, a second regime with a percolation cluster appears above a critical concentration.
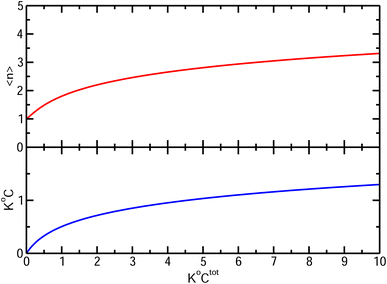 | ||
| Fig. 4 Bottom: Free ion (either cation or anion) concentration C and Top: average cluster size, as functions of K°Ctot. | ||
In this case, this macroscopic species must be treated separately because it is unique, but this does not necessarily mean that a phase separation occurs. It is simply a sign that we have a true mixture: at high concentrations, statistically all the solutes are in contact and a macroscopic species is bound to form. An attractive interaction can accelerate this percolation phenomenon without inducing a phase transition as has recently been seen52 for the solvent phases in liquid–liquid extraction.
5 Conclusion
In this article, we explained how the chemical models used in concentrated, mainly ionic, solutions can be justified. In practice, for weak interactions, these models express an effective attraction between solutes. They can therefore describe macroscopically a whole class of experimental systems as long as the repulsions do not predominate, but the reality of the associations modelled in this way can be problematic. A microscopic analysis shows that, as Onsager suggested, there are no good or bad criteria for defining chemical species in the case of weak interactions, as long as the problem is treated exactly. In fact, the two descriptions are equivalent. The only difference is that a chemical model describes microscopic states more precisely.However, not all chemical models have the same potential. A relevant criterion for defining chemical species is to select the simplest model that minimises the excess free energy and therefore the deviations from ideality. However, this remains a delicate task, particularly for charged systems where electrostatic attraction is long-range. We have demonstrated here the general formulae for calculating the equilibrium constants of the mass action law from atomic models. This involves calculating an internal partition function averaged over the solvent configurations for the solutions. The result may depend on the standard state considered (choice of C°).
When put into action, this project will make it possible to characterise concentrated solutions using biased simulations. In most aqueous solutions, chemical speciation, both in free solutions and at interfaces, is mainly dictated, at least for single ions, by the formation of CIPs. At high concentrations, it is possible to predict a transition to macroscopic aggregation. Above a percolation threshold, the solution is mainly made up of a macroscopic species, sometimes called prenucleation cluster. The situation is then similar to that of micelles, but the aggregated solutes do not necessarily have a well-defined characteristic size.
An important point that has not been addressed is the study of transport phenomena. The ambiguity surrounding the definition of the species can be resolved more easily at the dynamic level, as the species have their own mobility.
Conflicts of interest
There is no conflicts to declare.Acknowledgements
We are grateful to O. Bernard for several useful discussions. The French ANR Agence Nationale de la Recherche grant ANR-18-CE29-0010 is acknowledged.References
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 305 CAS.
- L. Onsager and R. M. Fuoss, J. Phys. Chem., 1932, 36, 2689–2778 CrossRef CAS.
- J. M. G. Barthel, H. Krienke and W. Kunz, Physical Chemistry of Electrolyte Solutions, Springer, 1998 Search PubMed.
- P. J. Camp and G. N. Patey, J. Chem. Phys., 1999, 111, 9000–9008 CrossRef CAS.
- R. Kjellander and D. J. Mitchell, J. Chem. Phys., 1994, 101, 603–626 CrossRef CAS.
- Y. Zhou, S. Yeh and G. Stell, J. Chem. Phys., 1995, 102, 5785–5795 CrossRef CAS.
- A. Villard, O. Bernard and J.-F. Dufrêche, J. Mol. Liq., 2018, 270, 30–39 CrossRef CAS.
- W. Kunz, P. LoNostro and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 1 CrossRef CAS.
- D. G. Leaist and P. A. Lyons, J. Phys. Chem., 1981, 85, 1756–1762 CrossRef CAS.
- T. Cartailler, P. Turq, L. Blum and N. Condamine, J. Phys. Chem., 1992, 96, 6766–6772 CrossRef CAS.
- H. Krienke and J. Barthel, J. Mol. Liq., 1998, 78, 123–128 CrossRef CAS.
- H. Krienke and J. Barthel, J. Mol. Liq., 2000, 87, 191–216 CrossRef CAS.
- N. Bjerrum, Mat.-Fys. Medd.–K. Dan. Vidensk. Selsk., 1926, 7, 1 CAS.
- A. Selmani, B. Siboulet, M. Špadina, Y. Foucaud, G. Dražić, B. Radatović, K. Korade, I. Nemet, D. Kovačević, J.-F. Dufrêche and K. Bohinc, ACS Appl. Nano Mater., 2023, 6, 12711–12725 CrossRef CAS PubMed.
- K. Wang, B. Siboulet, D. Rebiscoul and J.-F. Dufreche, J. Phys. Chem. C, 2021, 125, 20551–20569 CrossRef CAS.
- M. Döpke, J. Lützenkirchen, O. Moultos, B. Siboulet, J.-F. Dufrêche, J. Padding and R. Hartkamp, J. Phys. Chem. C, 2019, 123, 16711–16720 CrossRef.
- S. Hocine, R. Hartkamp, B. Siboulet, M. Duvail, B. Coasne, P. Turq and J.-F. Dufrêche, J. Phys. Chem. C, 2016, 120, 963–973 CrossRef CAS.
- T. Hiemstra, W. Van Riemsdijk and G. Bolt, J. Colloid Interface Sci., 1989, 133, 91–104 CrossRef CAS.
- O. Bernard, J. Mol. Liq., 2023, 390, 123023 CrossRef CAS.
- T. T. Duignan, M. D. Baer and C. J. Mundy, Curr. Opin. Colloid Interface Sci., 2016, 23, 58–65 CrossRef CAS.
- J. J. Molina, J.-F. Dufrêche, M. Salanne, O. Bernard, M. Jardat and P. Turq, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 065103(R) CrossRef.
- J. J. Molina, J.-F. Dufrêche, M. Salanne, O. Bernard and P. Turq, J. Chem. Phys., 2011, 135, 235509 CrossRef.
- P. Turq, L. Blum, O. Bernard and W. Kunz, J. Phys. Chem., 1995, 99, 822–827 CrossRef CAS.
- H. Falkenhagen and W. Ebeling, in Ionic Interactions, ed. S. Petrucci, Academic Press, 1971, pp. 1–60 Search PubMed.
- W. Ebeling, R. Feistel and H. Krienke, J. Mol. Liq., 2022, 346, 117814 CrossRef CAS.
- C. Shi, Y. Jing and Y. Jia, J. Mol. Liq., 2016, 215, 640–646 CrossRef CAS.
- The Collected Works of Lars Onsager, ed. P. C. Hemmer, H. Holden and S. Kjelstrup Ratkje, World Scientific, 1995 Search PubMed.
- G. Ciccotti, P. Turq and F. Lantelme, Chem. Phys., 1984, 88, 333–338 CrossRef CAS.
- W. G. McMillan and J. E. Mayer, J. Chem. Phys., 1945, 13, 276 CrossRef CAS.
- R. Kjellander, A. P. Lyubartsev and S. Marcelja, J. Chem. Phys., 2001, 114, 9565–9577 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 1986 Search PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin and P. A. Kollman, AMBER 10, University of California, San Francisco, 2008 Search PubMed.
- J. W. Caldwell and P. A. Kollman, J. Phys. Chem., 1995, 99, 6208–6219 CrossRef CAS.
- E. C. Meng and P. A. Kollman, J. Phys. Chem., 1996, 100, 11460–11470 CrossRef CAS.
- M. Duvail, A. Villard, T.-N. Nguyen and J.-F. Dufrêche, J. Phys. Chem. B, 2015, 119, 11184–11195 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350 CrossRef CAS.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- A. Grossfield, WHAM: an implementation of the weighted histogram analysis method, 2008, http://membrane.urmc.rochester.edu/content/wham/, version 2.0.2 Search PubMed.
- L. Blum, in Theoretical Chemistry: Advances and Perspectives, ed. H. Eyring and D. Henderson, Academic Press, 1980, vol. 5, pp. 1–66 Search PubMed.
- L. Blum and O. Bernard, J. Stat. Phys., 1995, 79, 569–583 CrossRef.
- L. Blum, M. F. Holovko and I. A. Protsykevych, J. Stat. Phys., 1996, 84, 191–204 CrossRef.
- O. Bernard and L. Blum, J. Chem. Phys., 1996, 104, 4746–4754 CrossRef CAS.
- J.-P. Simonin, O. Bernard and L. Blum, J. Phys. Chem. B, 1998, 102, 4411–4417 CrossRef CAS.
- J.-F. Dufrêche, O. Bernard and P. Turq, J. Mol. Liq., 2002, 96–97, 123–133 CrossRef.
- K. Wang, S. Bertrand and J.-F. Dufrêche, J. Phys. Chem. C, 2023, 127, 22315–22335 CrossRef CAS.
- V. Migliorati, A. Serva, F. M. Terenzio and P. D’Angelo, Inorg. Chem., 2017, 56, 6214–6224 CrossRef CAS.
- A. Coste, A. Poulesquen, O. Diat, J.-F. Dufrêche and M. Duvail, J. Phys. Chem. B, 2019, 123, 5121–5130 CrossRef CAS PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819 CrossRef CAS.
- D. Gebauer and H. Cölfen, Nano Today, 2011, 6, 564–584 CrossRef CAS.
- J. Israelachvili, Intermolecular & Surfaces Forces, Academic Press, 1992 Search PubMed.
- M. Vatin, M. Duvail, P. Guilbaud and J.-F. Dufrêche, J. Phys. Chem. B, 2021, 125, 3409–3418 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |