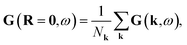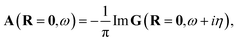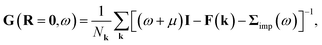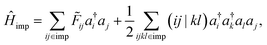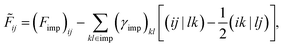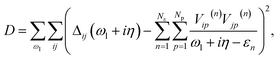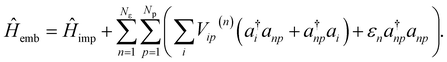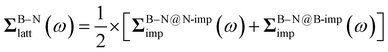DOI:
10.1039/D4FD00068D
(Paper)
Faraday Discuss., 2024,
254, 641-652
Restoring translational symmetry in periodic all-orbital dynamical mean-field theory simulations
Received
28th March 2024
, Accepted 9th April 2024
First published on 30th July 2024
Abstract
Dynamical mean-field theory (DMFT) and its cluster extensions provide an efficient Green’s function formalism to simulate spectral properties of periodic systems at the quantum many-body level. However, traditional cluster DMFT breaks translational invariance in solid-state materials, and the best strategy to capture non-local correlation effects within cluster DMFT remains elusive. In this work, we investigate the use of overlapping atom-centered impurity fragments in recently-developed ab initio all-orbital DMFT, where all local orbitals within the impurity are treated with high-level quantum chemistry impurity solvers. We demonstrate how the translational symmetry of the lattice self-energy can be restored by designing symmetry-adapted embedding problems, which results in an improved description of spectral functions in two-dimensional boron nitride monolayers and graphene at the levels of many-body perturbation theory (GW) and coupled-cluster theory. Furthermore, we study the convergence of self-energy and density of states as the embedding size is systematically expanded in one-shot and self-consistent DMFT calculations.
1. Introduction
Quantum embedding methods1–8 provide an efficient route for many-body simulation of material properties, because of their simultaneous treatment of local electron interactions and large system size (i.e., thermodynamic limit). Among variants of quantum embedding theories, Green’s function-based embedding approaches, such as dynamical mean-field theory (DMFT)2,5,9–15 and self-energy embedding theory (SEET),6,16,17 are particularly suitable for simulating spectral functions and band structures of solids as measured in photoemission spectroscopy experiments. In DMFT, the full system is mapped onto a local impurity problem, which is self-consistently embedded in a non-interacting bath through the hybridization function. By computing the one-particle Green’s function of the impurity using a high-level theory, DMFT captures strong local correlation effects via the many-body self-energy correction.
Despite the success of DMFT in the calculation of correlated electron materials, it remains challenging to achieve systematic convergence towards the full system limit. The main reason is associated with the uncontrolled errors in the construction of impurity orbitals and the effective Hamiltonian within the commonly-used downfolding formalism,18 where a low-energy model with a few strongly correlated orbitals is derived through techniques such as the constrained random phase approximation (cRPA).19 This uncertainty is further complicated by the double counting errors when DFT is combined with DMFT.20 Recently, one of us proposed a full cell DMFT framework to avoid these issues and enable ab initio HF + DMFT and GW + DMFT simulations of solids.5,12 In full cell DMFT, all local orbitals of atoms within a selected unit cell or supercell are treated as the impurity, and bare Coulomb interactions are adopted in the impurity Hamiltonian. Many-body quantum chemistry solvers, such as the coupled-cluster Green’s function (CCGF) approach,21–27 are then employed to solve the large impurity problem.
Nevertheless, the full cell formalism retains certain challenges in traditional cluster extensions of DMFT.28–30 A major issue is that cluster DMFT breaks the translational invariance when a finite number of sites are chosen as the impurity. Within the full cell framework, this issue arises because non-local interactions between atoms within the same cell are treated at a higher level of theory than interactions between atoms belonging to different cells. Such a choice leads to non-equivalent self-energy elements for pairs of atoms that should be equivalent under periodic boundary conditions. As a result, the band degeneracy in the Brillouin zone can be severely disrupted, limiting the understanding of band structures and interpretation of spectral functions. Previously, several reperiodization and center-focused extrapolation schemes have been explored to restore the translational symmetry of the self-energy in DMFT simulations of 1D and 2D Hubbard models.31–33 However, these numerical experiments stay at the level of lattice models, and a strategy to preserve translational invariance within full cell DMFT remains elusive.
In this work, we investigate the use of overlapping atom-centered fragments as the impurity to restore translational symmetry in all-orbital DMFT simulations (we avoid the name “full cell DMFT” since the impurity is no longer confined in a cell). By systematically expanding the size of the impurity around a center atom, we formulate embedding problems that largely preserve the real-space symmetry in the original lattice, using 2D boron nitride monolayer (BN) and graphene as test cases. With G0W0 and CCGF impurity solvers,24,34,35 we show that accurate local and momentum-resolved density of states (DOS) can be obtained by applying a center-focused self-energy correction scheme in HF + DMFT and GW + DMFT calculations, compared against full G0W0 and EOM-CCSD benchmarks.36 We also compare the performance of one-shot and self-consistent DMFT simulations and discuss the challenges in converging towards the full system limit.
2. Method
The all-orbital periodic HF + DMFT and GW + DMFT algorithms were described in detail in ref. 5 and 12. Here, we only summarize the main formalism necessary for the discussion of symmetry-adapted DMFT. Our goal is to compute the lattice interacting Green’s function of the full system| | | G(k,ω) = [g−1(k,ω) − Σ(k,ω)]−1, | (1) |
where g(k, ω) and Σ(k, ω) are the non-interacting Green’s function and the self-energy defined in the k-space. We focus on the description of the HF + DMFT algorithm here, so g(k, ω) is simply the HF Green’s function| | | g(k,ω) = [(ω + μ)I − F(k)]−1, | (2) |
where F(k) is the Fock matrix and μ is the chemical potential. The local interacting Green’s function in real space can be obtained through a Fourier transform| | 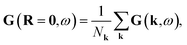 | (3) |
and the spectral function is defined as| | 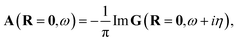 | (4) |
with η as the broadening factor.
The key approximation of DMFT is to approximate the momentum-dependent self-energy Σ(k, ω) with the impurity self-energy Σimp(ω)
which is equivalent to ignoring the non-local inter-site many-body corrections to the mean-field self-energy in real space. Here, the impurity self-energy
Σimp(
ω) is obtained by solving an impurity embedded in a non-interacting bath. The bath orbitals are derived from the discretization of a hybridization function
Δ(
ω), defined as
| | | Δ(ω) = (ω + μ)I − Fimp − Σimp(ω) − G−1(R = 0,ω), | (6) |
which describes the delocalization effects from the impurity–environment interaction. The DMFT equations are solved self-consistently until the impurity Green’s function
Gimp(
ω) and the lattice Green’s function
G(
R =
0,
ω) agree:
The DMFT lattice Green’s function is
| | 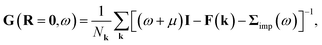 | (8) |
where the impurity self-energy is
| | | Σimp(ω) = ΣHLimp(ω) − ΣHFimp | (9) |
with
ΣHLimp(
ω) being the self-energy computed at a high-level theory (G
0W
0 or CCGF in this work).
We employ the intrinsic atomic orbital plus projected atomic orbital (IAO + PAO) basis4,37 to represent impurity local orbitals. Once an impurity fragment is selected, the impurity Hamiltonian can be written as:
| | 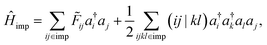 | (10) |
where
i,
j,
k,
l stand for impurity local orbitals and (
ij|
kl) denotes a two-electron repulsion integral (ERI). The HF contribution to the impurity self-energy can be exactly removed from the one-particle impurity Hamiltonian:
| | 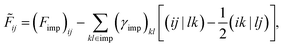 | (11) |
where
γimp is the impurity density matrix, so HF + DMFT is free of double counting.
To obtain the bath parameters, we optimize bath couplings {Vip(n)} and energies {εn} to minimize a cost function over a range of real-frequency points:5
| | 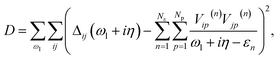 | (12) |
where
Nε is the number of bath energies and
Np is the number of bath orbitals per bath energy, and we use a broadening factor
η = 0.05 a.u. unless specified. The bath degrees of freedom are truncated by only coupling bath orbitals to the valence IAOs. The full impurity-bath problem is defined from the embedding Hamiltonian
| | 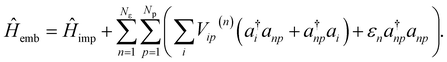 | (13) |
3. Computational details
The focus of this work is to investigate how the choice of DMFT impurity fragments affects translational invariance in the lattice self-energy and Green’s function. Different from previous full cell DMFT, we choose to start from an impurity of a single atom and gradually expand the impurity by adding adjacent atoms. As shown in Fig. 1 for 2D BN, this leads to the following fragment choices: (1) center atom only (impurity = 1 atom); (2) center atom plus nearest neighbors (impurity = 4 atoms); (3) center atom plus nearest and second nearest neighbors (impurity = 10 atoms). We refer to these impurity choices as symmetry-adapted DMFT, in contrast to the full cell DMFT that employs a unit cell of two atoms as the impurity. Because there are two different types of atoms in 2D BN, we formulate and solve two embedding problems (B-centered and N-centered) in each DMFT iteration. The lattice self-energy is then updated through a center-focused scheme in real space33| | | Σatom-Blatt(ω) = ΣB@B-impimp(ω) | (14) |
| | | Σatom-Nlatt(ω) = ΣN@N-impimp(ω) | (15) |
| | 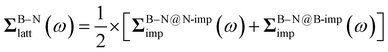 | (16) |
Here, the lattice self-energy within a B or N atom (e.g., Σatom-Blatt(ω)) is approximated by the impurity self-energy obtained from corresponding B or N centered impurity calculations (e.g., ΣB@B-impimp(ω)), while the B–N bond self-energy ΣB–Nlatt(ω) is averaged over two impurity calculations. We note that, the non-local B–N bond self-energy can only be obtained from DMFT simulations with more than a pair of B–N atoms, e.g., “center + 1st” or “center + 1st + 2nd” impurity fragment. In principle, one could also extract longer-range self-energy from large-cluster DMFT calculations, such as the non-local B1–B2 self-energy in 2D BN (B1/B2 denote different B atoms). However, we do not pursue this direction here, as we find such longer-range self-energy contributes negligibly to the final prediction of DOS at the G0W0 level.
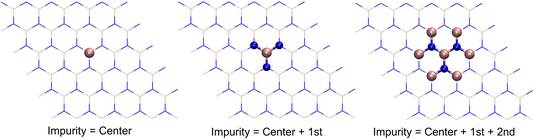 |
| | Fig. 1 Illustration of impurity sizes used in DMFT simulations of 2D BN in this work, i.e., center atom only, center atom plus nearest neighbors (“center + 1st”), as well as center atom plus nearest and second nearest neighbors (“center + 1st + 2nd”). | |
By designing impurity problems that better preserve the real-space symmetry of the original lattice and enforcing the self-energy of all atoms and bonds to be treated on equal footing, we anticipate that the translational symmetry of DMFT self-energy can be largely restored. We note in passing that the strategy to mitigate inequivalent treatments of center and edge sites in quantum embedding has been previously explored by Van Voorhis and co-workers in the bootstrap embedding theory.38,39
We studied 2D boron nitride and graphene using experimental lattice constants: 2.50 Å for 2D BN40 and 2.42 Å for graphene.41 We used a vacuum spacing of 20 Å along the z axis to avoid image interactions between neighboring sheets. All calculations were performed based on the PySCF quantum chemistry package42,43 and the fcDMFT library.44 Norm-conserving GTH-PADE pseudopotentials45,46 and the GTH-DZVP basis set were employed. The minimal basis sets GTH-SZV were used as the pre-defined AOs to construct the IAOs. Γ-Centered 6 × 6 × 1 (2D BN) and 7 × 7 × 1 (graphene) k-point meshes were adopted for the mean-field and DMFT calculations. In DMFT calculations, the numbers of impurity and bath orbitals are (13i, 48b) (“center”, 13 impurity and 48 bath orbitals), (26i, 96b) (“unit cell”), (52i, 144b) (“center + 1st”), (130i, 144b) (“center + 1st + 2nd”), respectively.
4. Results
We first show DOS results of one-shot all-orbital HF + DMFT calculations of 2D BN in Fig. 2, with G0W0@HF as the impurity solver. We use the G0W0 solver here since the full G0W0 DOS can be easily obtained to serve as the benchmark. As shown in Fig. 2a, when the impurity fragment consists of only a B or N atom (i.e., a multiorbital extension of single-site DMFT that ignores all inter-atom self-energy corrections), one-shot HF + DMFT severely underestimates the band gap by 1.44 eV (“center”), despite an improvement over HF (2.97 eV overestimation). As the impurity size is increased, the band gap error of one-shot HF + DMFT is systematically reduced to 0.89 eV (“unit cell”), 0.54 eV (“center + 1st”), and 0.19 eV (“center + 1st + 2nd”), due to the better treatment of non-local correlation and screening effects. We find that, the one-shot full cell DMFT spectrum shape does not agree well with that of full G0W0@HF, especially in the valence part, which is a consequence of breaking translational invariance. This is further revealed by the momentum-resolved DOS in Fig. 2b and c. For example, at the Γ point, the two degenerate valence bands at around −2 eV are artificially split into two bands separated by 1 eV.
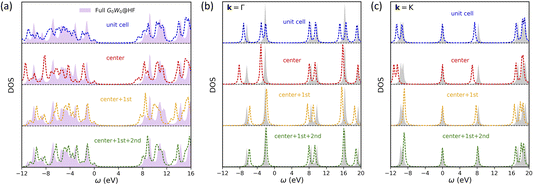 |
| | Fig. 2 One-shot all-orbital HF + DMFT density of states for 2D BN with a G0W0@HF impurity solver. All results are compared against a full G0W0@HF calculation. Four choices of impurity are tested: a BN unit cell, center atom only, center atom plus nearest neighbors, center atom plus nearest and second nearest neighbors. All spectra are shifted so that the valence band maximum is aligned at zero. (a) Local DOS. (b) Momentum-resolved DOS at the Γ point. (c) Momentum-resolved DOS at the K point. | |
On the other hand, the spectrum shape is much improved in symmetry-adapted one-shot HF + DMFT, suggesting that the translational symmetry in lattice self-energy is largely restored. At the Γ point, all three symmetry-adapted DMFT calculations predict correct band degeneracy across a wide energy window. At the K point, only the band degeneracy prediction at around −10 eV is slightly off in “center + 1st” and “center + 1st + 2nd” calculations. Moreover, we note that even at the “center + 1st + 2nd” level with 10 atoms as the impurity, one-shot HF + DMFT does not achieve quantitative agreement with full G0W0@HF. This discrepancy suggests that the self-energy assembly scheme may not be optimal or a larger impurity size is needed within the current HF + DMFT framework.
We further investigate the effect of self-consistency in HF + DMFT simulations of 2D BN, as presented in Fig. 3. We observe that self-consistent DMFT improves the prediction of the band gap for small and medium impurity sizes, reducing the error from 1.44 eV (“center”), 0.89 eV (“unit cell”), and 0.54 eV (“center + 1st”) to 0.52 eV, 0.42 eV, and 0.08 eV, respectively. Furthermore, the DOS predictions in small-impurity calculations (“center” and “unit cell”) are also superior when the self-consistency is enforced, while the improvement in the “center + 1st” HF + DMFT calculation is less significant. By directly comparing the band structures predicted by self-consistent full cell and “center + 1st” HF + DMFT calculations in Fig. 4, we further demonstrate that the description of band degeneracy and shape is improved by restoring the translational symmetry (note that valence bands are misaligned in the full cell DMFT band structure).
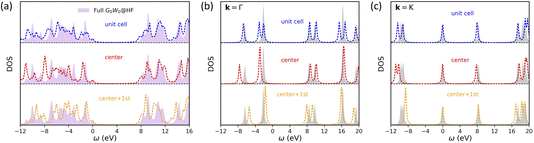 |
| | Fig. 3 Self-consistent all-orbital HF + DMFT density of states for 2D BN with a G0W0@HF impurity solver. (a) Local DOS. (b) Momentum-resolved DOS at the Γ point. (c) Momentum-resolved DOS at the K point. | |
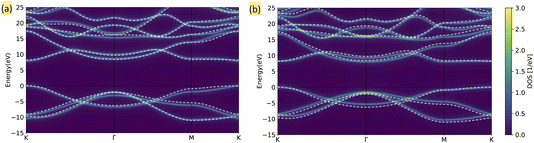 |
| | Fig. 4 Band structure for 2D BN from self-consistent HF + DMFT with G0W0@HF solver. The heat map represents the HF + DMFT result, while the white dashed line represents the full G0W0@HF reference. (a) Full cell impurity. (b) “Center + 1st” impurity. | |
After establishing the accuracy of symmetry-adapted HF + DMFT for 2D BN, we further perform one-shot GW + DMFT calculations with the “center + 1st” impurity. Here, the coupled-cluster Green’s function at the singles and doubles level is employed as the impurity solver (which is equivalent to EOM-CCSD). The local DOS prediction is shown in Fig. 5. We see that symmetry-adapted GW + DMFT predicts perfectly the valence spectrum compared with the periodic EOM-CCSD spectrum of the full system. The one-shot GW + DMFT predicted direct band gaps are 9.54 eV (Γ point) and 6.90 eV (K point), an underestimation of 0.24 eV and 0.58 eV compared to full EOM-CCSD. In contrast, G0W0@HF overestimates the direct band gaps by 0.82 eV and 0.85 eV.
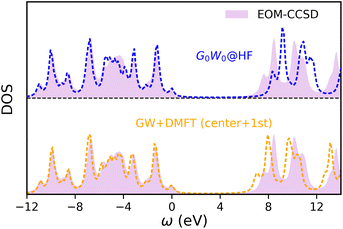 |
| | Fig. 5 Local DOS of 2D BN from a one-shot GW + DMFT calculation with a “center + 1st” impurity fragment, compared with full G0W0 and EOM-CCSD spectra. | |
Next, we apply symmetry-adapted HF + DMFT with the G0W0 impurity solver to study graphene, a 2D semi-metal system (note: there is a small band gap here due to the use of a 7 × 7 × 1 k-mesh). We choose graphene because electron correlation in a semi-metal is typically believed to be more delocalized than that in an insulator (e.g., 2D BN), making it a more challenging system for embedding methods. We find that the breaking of translational invariance in full cell HF + DMFT (i.e., with “unit cell” impurity) is more severe in the case of graphene compared to 2D BN, resulting in unsatisfactory predictions of the local DOS in both one-shot (Fig. 6a) and self-consistent HF + DMFT (Fig. 7a). The violation of band degeneracy in full cell HF + DMFT is more evident at the Γ point (Fig. 6b and 7b), for instance, the degenerate bands at −4 eV and 12 eV are split into multiple non-degenerate peaks.
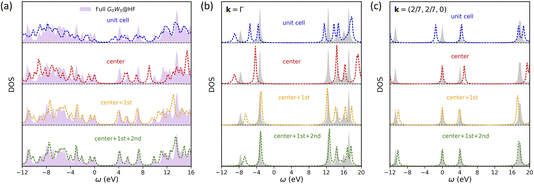 |
| | Fig. 6 One-shot all-orbital HF + DMFT density of states for graphene with the G0W0@HF impurity solver. (a) Local DOS. (b) Momentum-resolved DOS at the Γ point. (c) Momentum-resolved DOS at k = (2/7, 2/7, 0). | |
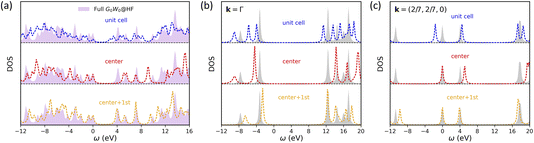 |
| | Fig. 7 Self-consistent all-orbital HF + DMFT density of states for graphene with the G0W0@HF impurity solver. (a) Local DOS. (b) Momentum-resolved DOS at the Γ point. (c) Momentum-resolved DOS at k = (2/7, 2/7, 0). | |
In the meantime, we find systemically improved DOS predictions in symmetry-adapted one-shot HF + DMFT when the impurity size is increased. The band gap error is 0.93 eV (“center”), 0.22 eV (“center + 1st), and 0.05 eV (“center + 1st + 2nd) compared with the full G0W0@HF result. In particular, a near-quantitative prediction is achieved when the “center + 1st + 2nd” impurity is employed in the one-shot HF + DMFT calculation. This better performance of symmetry-adapted HF + DMFT in graphene compared to 2D BN is somewhat unexpected. This may result from the fact that non-local C–C bond self-energy does not require averaging over two impurity calculations in the case of graphene, while such an averaging scheme may introduce extra errors in the case of 2D BN. Moreover, comparing Fig. 6 and 7, we conclude that the impact of self-consistency is limited in HF + DMFT simulations of graphene.
5.
Conclusions
In this work, we investigate a strategy to restore translational symmetry in ab initio all-orbital HF + DMFT and GW + DMFT calculations of periodic systems, such as 2D boron nitride and graphene. By employing overlapping impurity fragments that preserve the real-space symmetry of the original lattice, we demonstrate the possibility of enforcing translational invariance in the DMFT lattice self-energy, leading to improved DOS and band degeneracy compared to previous full cell DMFT. The DOS and band gap predictions can also be systematically improved by expanding the symmetry-adapted impurity fragment sizes. Our results suggest that self-consistency plays a less crucial role than the size and shape of impurity fragments, which is partly due to the weakly correlated nature of the systems tested in this study. We conclude that achieving fast and systematic convergence towards the full system limit, while preserving the translational invariance, remains a challenging task for ab initio all-orbital DMFT. It is interesting to further investigate the strategy for extracting and assembling non-local lattice self-energy from small impurity calculations. Screened Coulomb interactions may be adopted within the current ab initio DMFT framework to accelerate the convergence, e.g., through the recently-developed moment-constrained RPA approach.47 Finally, more numerical investigations are needed to understand how this strategy for restoring translational symmetry would work for systems with stronger electron correlations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Science Foundation (CHE-2337991) and a start-up fund from Yale University. J. L. acknowledges support from the Tony Massini Postdoctoral Fellowship in Data Science from Yale University.
References
- Q. Sun and G. K.-L. Chan, Quantum Embedding Theories, Acc. Chem. Res., 2016, 49, 2705 CrossRef CAS PubMed.
- A. Georges and G. Kotliar, Hubbard Model in Infinite Dimensions, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 6479 CrossRef PubMed.
- G. Knizia and G. K.-L. Chan, Density Matrix Embedding: A Simple Alternative to Dynamical Mean-Field Theory, Phys. Rev. Lett., 2012, 109, 186404 CrossRef PubMed.
- Z. H. Cui, T. Zhu and G. K.-L. Chan, Efficient Implementation of Ab Initio Quantum Embedding in Periodic Systems: Density Matrix Embedding Theory, J. Chem. Theory Comput., 2020, 16, 119 CrossRef PubMed.
- T. Zhu and G. K. L. Chan, Ab Initio Full Cell GW+DMFT for Correlated Materials, Phys. Rev. X, 2021, 11, 021006 CAS.
- A. A. Rusakov, S. Iskakov, L. N. Tran and D. Zgid, Self-energy embedding theory (SEET) for periodic systems, J. Chem. Theory Comput., 2019, 15, 229 CrossRef CAS PubMed.
- H. Ma, N. Sheng, M. Govoni and G. Galli, Quantum Embedding Theory for Strongly Correlated States in Materials, J. Chem. Theory Comput., 2021, 17, 2116 CrossRef CAS PubMed.
- M. Nusspickel and G. H. Booth, Systematic Improvability in Quantum Embedding for Real Materials, Phys. Rev. X, 2022, 12, 011046 CAS.
- A. Georges, G. Kotliar, W. Krauth and M. Rozenberg, Dynamical Mean-Field Theory of Strongly Correlated Fermion Systems and the Limit of Infinite Dimensions, Rev. Mod. Phys., 1996, 68, 13 CrossRef CAS.
- G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet and C. A. Marianetti, Electronic Structure Calculations with Dynamical Mean-Field Theory, Rev. Mod. Phys., 2006, 78, 865 CrossRef CAS.
- D. Zgid and G. K.-L. Chan, Dynamical Mean-Field Theory from a Quantum Chemical Perspective, J. Chem. Phys., 2011, 134, 094115 CrossRef PubMed.
- T. Zhu, Z.-H. Cui and G. K.-L. Chan, Efficient Formulation of Ab Initio Quantum Embedding in Periodic Systems: Dynamical Mean-Field Theory, J. Chem. Theory Comput., 2020, 16, 141 CrossRef PubMed.
- S. Biermann, F. Aryasetiawan and A. Georges, First-Principles Approach to the Electronic Structure of Strongly Correlated Systems: Combining the GW Approximation and Dynamical Mean-Field Theory, Phys. Rev. Lett., 2003, 90, 086402 CrossRef CAS PubMed.
- P. Sun and G. Kotliar, Extended Dynamical Mean-Field Theory and GW Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085120 CrossRef.
- F. Nilsson, L. Boehnke, P. Werner and F. Aryasetiawan, Multitier Self-Consistent GW+EDMFT, Phys. Rev. Mater., 2017, 1, 043803 CrossRef.
- S. Iskakov, C. N. Yeh, E. Gull and D. Zgid, Ab initio self-energy embedding for the photoemission spectra of NiO and MnO, Phys. Rev. B, 2020, 102, 85105 CrossRef CAS.
- C. N. Yeh, S. Iskakov, D. Zgid and E. Gull, Electron correlations in the cubic paramagnetic perovskite Sr(V,Mn) O3: Results from fully self-consistent self-energy embedding calculations, Phys. Rev. B, 2021, 103, 195149 CrossRef CAS.
- J. Karp, A. Hampel and A. J. Millis, Dependence of DFT+DMFT results on the construction of the correlated orbitals, Phys. Rev. B, 2021, 103, 195101 CrossRef CAS.
- F. Aryasetiawan, M. Imada, A. Georges, G. Kotliar, S. Biermann and A. I. Lichtenstein, Frequency-Dependent Local Interactions and Low-Energy Effective Models from Electronic Structure Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195104 CrossRef.
- X. Wang, M. J. Han, L. de’ Medici, H. Park, C. A. Marianetti and A. J. Millis, Covalency, Double-Counting, and the Metal-Insulator Phase Diagram in Transition Metal Oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195136 CrossRef.
- M. Nooijen and J. G. Snijders, Coupled cluster approach to the single-particle Green’s function, Int. J. Quantum Chem., 1992, 44, 55 CrossRef.
- M. Nooijen and J. G. Snijders, Coupled cluster Green’s function method: Working equations and applications, Int. J. Quantum Chem., 1993, 48, 15 CrossRef CAS.
- K. Bhaskaran-Nair, K. Kowalski and W. A. Shelton, Coupled cluster Green function: Model involving single and double excitations, J. Chem. Phys., 2016, 144, 144101 CrossRef PubMed.
- T. Zhu, C. A. Jiménez-Hoyos, J. McClain, T. C. Berkelbach and G. K.-L. Chan, Coupled-Cluster Impurity Solvers for Dynamical Mean-Field Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 115154 CrossRef CAS.
- A. Shee and D. Zgid, Coupled Cluster as an Impurity Solver for Green’s Function Embedding Methods, J. Chem. Theory Comput., 2019, 15, 6010 CrossRef CAS PubMed.
- B. Peng and K. Kowalski, Green’s Function Coupled-Cluster Approach: Simulating Photoelectron Spectra for Realistic Molecular Systems, J. Chem. Theory Comput., 2018, 14, 4335 CrossRef CAS PubMed.
- K. Laughon, J. M. Yu and T. Zhu, Periodic Coupled-Cluster Green’s Function for Photoemission Spectra of Realistic Solids, J. Phys. Chem. Lett., 2022, 13, 9122 CrossRef CAS PubMed.
- A. I. Lichtenstein and M. I. Katsnelson, Antiferromagnetism and d-wave superconductivity in cuprates: A cluster dynamical mean-field theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R9283 CrossRef CAS.
- G. Kotliar, S. Y. Savrasov, G. Pálsson and G. Biroli, Cellular Dynamical Mean Field Approach to Strongly Correlated Systems, Phys. Rev. Lett., 2001, 87, 186401 CrossRef.
- A. Liebsch, H. Ishida and J. Merino, Multisite versus multiorbital Coulomb correlations studied within finite-temperature exact diagonalization dynamical mean-field theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 1 CrossRef.
- G. Biroli, O. Parcollet and G. Kotliar, Cluster dynamical mean-field theories: Causality and classical limit, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 205108 CrossRef.
- M. Capone, M. Civelli, S. S. Kancharla, C. Castellani and G. Kotliar, Cluster-dynamical mean-field theory of the density-driven Mott transition in the one-dimensional Hubbard model, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195105 CrossRef.
- M. Klett, N. Wentzell, T. Schäfer, F. Simkovic, O. Parcollet, S. Andergassen and P. Hansmann, Real-space cluster dynamical mean-field theory: Center-focused extrapolation on the one- and two particle-levels, Phys. Rev. Res., 2020, 2, 033476 CrossRef CAS.
- T. Zhu and G. K. L. Chan, All-Electron Gaussian-Based G0W0 for Valence and Core Excitation Energies of Periodic Systems, J. Chem. Theory Comput., 2021, 17, 727 CrossRef CAS PubMed.
- J. Lei and T. Zhu, Gaussian-based quasiparticle self-consistent GW for periodic systems, J. Chem. Phys., 2022, 157, 214114 CrossRef CAS PubMed.
- J. McClain, Q. Sun, G. K.-L. Chan and T. C. Berkelbach, Gaussian-based coupled-cluster theory for the ground-state and band structure of solids, J. Chem. Theory Comput., 2017, 13, 1209 CrossRef CAS PubMed.
- G. Knizia, Intrinsic Atomic Orbitals: An Unbiased Bridge between Quantum Theory and Chemical Concepts, J. Chem. Theory Comput., 2013, 9, 4834 CrossRef CAS PubMed.
- H. Z. Ye, N. D. Ricke, H. K. Tran and T. Van Voorhis, Bootstrap Embedding for Molecules, J. Chem. Theory Comput., 2019, 15, 4497 CrossRef CAS PubMed.
- O. R. Meitei and T. Van Voorhis, Periodic Bootstrap Embedding, J. Chem. Theory Comput., 2023, 19, 3123 CrossRef CAS PubMed.
- L. H. Li, Y. Chen, G. Behan, H. Zhang, M. Petravic and A. M. Glushenkov, Large-scale mechanical peeling of boron nitride nanosheets by low-energy ball milling, J. Mater. Chem., 2011, 21, 11862 RSC.
- G. Yang, L. Li, W. B. Lee and M. C. Ng, Structure of graphene and its disorders: a review, Sci. Technol. Adv. Mater., 2018, 19, 613 CrossRef CAS PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, PySCF: the Python-Based Simulations of Chemistry Framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z. H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. Smith, C. Sun, S. N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K. L. Chan, Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 24109 CrossRef CAS PubMed.
-
fcDMFT library, 2024, https://github.com/ZhuGroup-Yale/fcdmft Search PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from h to rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- C. J. Scott and G. H. Booth, Rigorous Screened Interactions for Realistic Correlated Electron Systems, Phys. Rev. Lett., 2024, 132, 076401 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Tianyu
Zhu
and
Tianyu
Zhu
 *
*