Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Classification and quantitative characterisation of the excited states of π-conjugated diradicals†
Lujo
Matasović
a,
Hugo
Bronstein
 b,
Richard H.
Friend
b,
Richard H.
Friend
 a and
Felix
Plasser
a and
Felix
Plasser
 *c
*c
aCavendish Laboratory, University of Cambridge, Cambridge CB3 0HF, UK
bYusuf Hamied Department of Chemistry, University of Cambridge, Cambridge CB2 1EW, UK
cDepartment of Chemistry, Loughborough University, Loughborough LE11 3TU, UK. E-mail: f.plasser@lboro.ac.uk; Tel: +44 (0)1509 226946
First published on 26th April 2024
Abstract
Diradicals are of high current interest as emerging materials for next generation optoelectronic applications. To tune their excited-state properties it would be greatly beneficial to have a detailed understanding of the wave functions of the different states involved but this endeavour is hampered by formal and practical barriers. To tackle these challenges, we present a formal analysis as well as concrete results on diradical excited states. We start with a detailed investigation of the available states of a two-orbital two-electron model viewed from both the valence-bond and molecular orbital perspectives. We highlight the presence of diradical and zwitterionic states and illustrate their connections to the states found in closed-shell molecules. Subsequently, we introduce practical protocols for analysing states from realistic multireference computations applying these to the para-quinodimethane (pQDM) molecule. The analysis reveals four different categories of states – diradical, zwitterionic, HOMO–SOMO as well as biexciton – while also providing insight into their energetics and optical properties. Twisting the CH2 groups allows us to interconvert between the closed- and open-shell forms of pQDM illustrating the connection between the states in both forms. More generally, we hope that this work will lay the foundations for a more powerful rational design approach to diradicals for photophysical applications.
1 Introduction
With fully spin-allowed emission, luminescent organic radicals emerged as an attractive platform for optoelectronics.1 The design principles behind these systems are now well established,2–4 leading to the fabrication of near- and infra-red light-emitting diodes with record efficiencies2 and a rapid expansion of available radical structures with exciting properties and applications.5,6 However, despite high photoluminescence yields, fine-tuning additional photophysical properties, such as enhancing the oscillator strengths of low-energy transitions, remains challenging, underscoring the need for developing structures with new photophysical pathways.On the other hand, with a unique combination of magneto-optical properties, π-conjugated diradicals and diradicaloids comprise a fascinating class of chemical systems finding application in domains of electrical conductivity,7–11 non-linear optics,12,13 singlet fission,13–15 optoelectronics16–20 and spintronics.21 As molecules with two (nearly) degenerate frontier orbitals occupied by two unpaired electrons, diradicals have been characterised in detail in terms of their reactivity,22 and significant effort has been invested both into controlling the singlet–triplet gaps of diradicals23–25 and in making them stable.19,26,27
However, unlike for the luminescent mono-radicals, the photophysical properties of these molecules are understood less well. Notably, the possible types of excited states of molecules with a diradical ground state differ significantly from excited states of closed-shell molecules and no comprehensive analysis scheme has been developed. Therefore, the topic of diradical excited state classification remains highly pertinent. It is of high interest to understand energies and optical transition strengths of the states involved as well as to elucidate how the different states of open- and closed-shell molecules are formally connected.
Owing to the significant amount of static correlation, excited state computations on diradicals are challenging, both in terms of producing accurate energies and interpreting the results. The description of diradicals requires advanced approaches, such as multireference and spin-flip methods,28,29 and, indeed, both approaches have been successfully applied to the description of diradical systems.12,13,22,30–33 There has also been substantial interest in quantifying the radical character of organic molecules in a rigorous way; several measures of counting the associated number of unpaired electrons have been proposed, including the single-determinant broken-symmetry approach,13,34 methods based on the occupation numbers of the lowest weakly occupied natural orbitals35,36 as well as the distribution of (effectively) unpaired electrons using one-particle density matrices37–40 and, more recently, fractional occupation number weighted electron densities.41
However, aside from the overall number of unpaired electrons, it remains unclear how to consistently differentiate between different classes of states in a reproducible manner. In particular, the concept of (zwitter)ionic states has remained elusive in practical work despite their importance7,23,42,43 both in closed- and open-shell systems. This gap in our understanding has become particularly significant in light of recent studies describing the photophysics of luminescent diradicals.18–20,44 Several groups have recently demonstrated di- and polyradicals with significant absorption and emission in the near-infrared region, explaining the luminescence with spontaneous excited-state symmetry breaking and/or the population of low-lying zwitterionic states.18,45–47
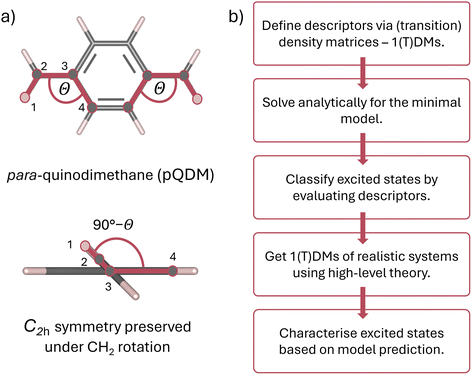
This work proposes a classification framework for the possible states of predominantly open-shell systems. We demonstrate how different types of states can be identified using a set of wave function descriptors based on their associated (transition) density matrices. After briefly describing the underlying methods and defining descriptors of interest, we apply them to the foundational two-orbital two-electron model, predicting the evolution of the excited states' character with varying degree of static correlation. Exemplary results are presented on the paradigmatic pro-aromatic diradicaloid para-quinodimethane (pQDM),48 see Fig. 1a. By twisting its outer CH2 groups, we smoothly convert the pQDM molecule from one of predominantly closed-shell character (where CH2 groups are coplanar to the π plane) to a diradical (where CH2 groups are orthogonal to the π plane). We illustrate how the ground and the excited states change upon increasing the open-shell character of the molecule, allowing for rigorous and intuitive theoretical elucidation of the excited state character of π-conjugated diradicaloids (Fig. 1).
We start this work with the mathematical foundations in Section 2. Practical implications are shown in Section 3, starting with a model system and presenting detailed results on pQDM. The two sections are written in a largely self-contained fashion, so a reader mostly interested in the practical implications is welcome to skip directly to Section 3.
2 Methods
In this section we present the underlying theory; we start by a discussion of the wave functions present in a two-orbital two-electron model (TOTEM) and their interconversions when going from the closed- to open-shell limits. Subsequently, we present the equations for our wave function analysis protocols. We finish with the Computational details.2.1 TOTEM: model wave functions
The main properties of a diradical can be understood most readily when considering a two-orbital two-electron model (TOTEM).7,35,49 Distributing two electrons among four spin-orbitals yields six possible microstates. After spin-adaptation these are grouped as three individual singlets along with one triplet state. For the purpose of the following discussion, we will consider the four states with one spin-up and one spin-down electron (meaning that MS = 0) and write their wave functions in the following form|Ψ0〉 = cos(η)|ϕH![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) H〉 − sin(η)|ϕL H〉 − sin(η)|ϕL![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) L〉 L〉 | (1) |
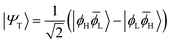 | (2) |
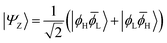 | (3) |
|Ψ1〉 = sin(η)|ϕH![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) H〉 + cos(η)|ϕL H〉 + cos(η)|ϕL![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) L〉 L〉 | (4) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) H〉) and it obtains increased admixture of the LUMO2 configuration when moving to the open-shell case. The two following states are the triplet (ΨT) and zwitterionic singlet (ΨZ). These are the simple HOMO/LUMO states, independent of the mixing angle η. The third singlet state Ψ1 is the orthogonal counterpart to Ψ0. It starts as a LUMO2 configuration at η = 0 and obtains increased HOMO2 character.
H〉) and it obtains increased admixture of the LUMO2 configuration when moving to the open-shell case. The two following states are the triplet (ΨT) and zwitterionic singlet (ΨZ). These are the simple HOMO/LUMO states, independent of the mixing angle η. The third singlet state Ψ1 is the orthogonal counterpart to Ψ0. It starts as a LUMO2 configuration at η = 0 and obtains increased HOMO2 character.
We find the above-presented formulation favourable in terms of its rather simple mathematical description readily providing normalised spin-adapted wave functions and the need of only including one adjustable parameter to tune between closed- and open-shell character. However, it is worth mentioning that alternative formulations exist, where the mixing angle is introduced between frontier orbitals instead of Slater determinants.30,50
Eqn (1)–(4) are written with respect to delocalised symmetry adapted orbitals. For the discussions to follow, it is beneficial to rewrite them in terms of orbitals ϕA and ϕB that are localised on the left and right radical centres, respectively.51 These orbitals are defined as
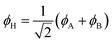 | (5) |
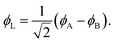 | (6) |
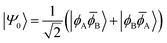 | (7) |
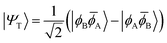 | (8) |
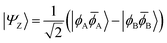 | (9) |
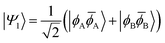 | (10) |
2.2 Wave function analysis
The analysis of the wave functions presented herein relies on previously established methods based on the 1-electron density (1DM) and transition density (1TDM) matrices.56,57 Here, we provide the relevant mathematical details, reserving the review of the main physical implications for the Results and discussion section.The 1TDM between the ground state wave function Ψ0 and excited-state wave function ΨJ is defined as
| D0Jpq = 〈Ψ0|a†paq|ΨJ〉 | (11) |
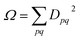 | (12) |
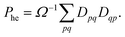 | (13) |
Combining the above rules, we can identify two effective selection rules for optical transition strengths. A state can only have non-vanishing oscillator strength if Ω ≠ 0 and Phe ≠ −1. We will discuss both conditions in the context of realistic calculations below.
To differentiate between diradical and zwitterionic states, we will use the concept of an electron–hole correlation coefficient Rhe describing the mutual distribution of the electron–hole pair.59 The value of Rhe ranges from −1 to +1. Here, Rhe = 0 means that no correlation is present, which is the case for a simple MO-to-MO transition. A positive value means that electron and hole are more likely to be in the same region of space whereas a negative value means that they avoid each other dynamically. To quantify the overall number of unpaired electrons and, hence, diradical character we use the number of unpaired electrons
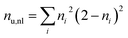 | (14) |
Finally, we will use the promotion number p based on the difference density matrix, as initially defined by Head-Gordon and co-workers.63 This value is computed by constructing the difference density matrix (1DDM) between ground and excited state. The 1DDM is subsequently diagonalised. Separation of the eigenvectors according to their signs provides detachment and attachment densities. The sum over all positive or negative eigenvalues of the 1DDM – denoted as the promotion number p – gives the total number of electrons rearranged during the excitation process. The value of p is 1 for simple one-electron excited states whereas it becomes larger in the case of double excitations60 and orbital relaxation.57,64 Within the present context it is particularly interesting that p is expected to be zero between two states possessing the same density matrices. In particular, the p values between the different diradical and zwitterionic states constructed from two SOMOs are all expected to be zero, and we will evaluate this idea below.
2.3 Computational details
The molecular geometries of pQDM were optimised at the PBE/ANO-S-VDZP65,66 level of theory in the overall spin–triplet configuration. Obtained geometries were then symmetrised to C2h point group. The potential curve of 10 geometries was obtained by rigid rotation of both CH2 groups with respect to the phenyl bridge by 10-degree steps, ranging from θ = 0 to θ = 90° and preserving the point group symmetry.Vertical excitation energies were done in OpenMolcas67 using the complete active space self-consistent field (CASSCF) level of theory with the ANO-S-VDZP basis set.66,68 An active space of 8 electrons in 8 active orbitals (1 × ag, 1 × au, 3 × bg, 3 × bu) was chosen. State averaging was performed over 8 × 1Ag, 6 × 1Au, 6 × 3Ag and 6 × 3Au spin-adapted states. A relatively large number of singlet roots was required to capture the dark and the bright zwitterionic states in the 1Ag and 1Au symmetries, considering that the energies of zwitterionic states tend to be overestimated in CASSCF jobs.55,69,70 Notably, the four relevant orbitals (HOMO, LUMO and two SOMOs) all exhibit bg and bu symmetries (see Fig. S1†). Therefore, the ensuing low-lying transitions are exclusively of A symmetry and we focus on these. A brief discussion of the higher-lying B states is presenting in Table S3.†
Dynamic correlation was treated with multi-state second-order perturbation theory (MS-CASPT2),71 with an IPEA shift72 of 0.25. The problem of intruder states in the perturbative approach was addressed using a regularisation technique introduced by Battaglia et al.73 with a σ2 value of 0.3. Wave function analysis was performed using the libwfa wave-function analysis library interfaced to OpenMolcas,74,75 and the post-processing of the wave function descriptors was done using TheoDORE 3.1.1.76 The input to these analysis routines consisted of CASSCF wave functions mixed via the multi-state procedure but not including explicit PT2 corrections.
The underlying computational research data (input/output files of OpenMolcas and geometries) are provided via a separate repository (DOI: https://doi.org/10.17028/rd.lboro.25379311).
3 Results and Discussion
3.1 Two-orbital two-electron model
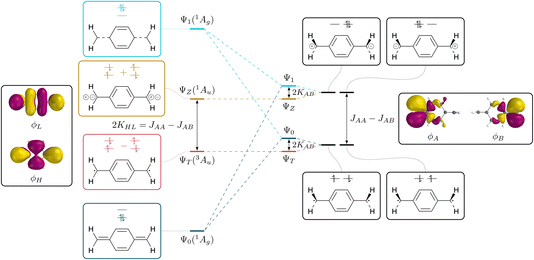
The connection between the states of a closed-shell molecule and a diradical within the two-orbital two-electron model (TOTEM) is shown in Fig. 2. Generally, there are four possible ways of distributing two electrons in two orbitals if one of them is spin-up and the other one spin-down (that is MS = 0) and these are shown on the right. Combining these configurations to spin-adapted states yields three singlets and one triplet component. The character of these states will depend on the energies of the frontier orbitals and the coupling between them. Closed-shell character is obtained for a large orbital energy difference and weak coupling and vice versa for open-shell character.The closed-shell case is illustrated on the left in Fig. 2. The lowest state Ψ0 is a totally symmetric closed-shell singlet with a doubly occupied HOMO. Two HOMO–LUMO singly excited states follow, both of Au symmetry, denoted ΨT and ΨZ marking the diradical triplet and the zwitterionic singlet. As shown in eqn (2) and (3), both states are composed of the same configurations where only the sign differentiates between the singlet and the triplet. The energies of these states have been discussed in detail elsewhere77–79 and are listed in compressed form in Table 1. For the present purposes it is enough to realise that the energy splitting between ΨT and ΨZ is given by twice the exchange integral between HOMO and LUMO (KHL). Within the TOTEM, the next state is produced via the doubly excited LUMO2 configuration (Ψ1), which is totally symmetric and formally has the analogous character to Ψ0 only that HOMO and LUMO are exchanged. We have shown previously that such states are not usually found in practical calculations,60 but that there is usually strong configuration mixing. In any case, it provides the starting point for our discussion.
| State | ΔE (c.s.)b | ΔE (o.s.)b | f | Ω | P he | n u,nl | p | |
|---|---|---|---|---|---|---|---|---|
| a s = sin(2η), c = cos(2η), where η is the mixing angle. b For simplicity, energies are given with respect to a reference state of two non-interacting electrons located on the two orbitals, that is, Eref = hH + hL = hA + hB where hX is the one-electron energy for orbital ϕX. | ||||||||
| Ψ 0 | J HH − Δh | J AB + KAB | — | — | — | 2s4 | — | |
| Ψ T | J HL − KHL | = | J AB − KAB | 0 | 1 | +s | 2 | c |
| Ψ Z | J HL + KHL | = | J AA − KAB | f 0(1 − s) | 1 | −s | 2 | c |
| Ψ 1 | J LL + Δh | J AA + KAB | 0 | s 2 | 1 | 2s4 | 2c | |
To the right of Fig. 2 we present the open-shell case with the configurations expanded into degenerate localised SOMOs. We first note that it is possible to construct four different configurations. In two of them we find the electrons distributed over both orbitals; these are denoted as diradical. In the other two both electrons are simultaneously on one side; these are denoted ionic. The difference in energy between these respective configurations is given by the difference between the on-site Coulomb integral with both electrons on the same side (JAA = JBB) and the inter-site repulsion (JAB). Since JAA is always greater than JAB, the diradical states are seen to be lower in energy. In the next step, we form spin- and spatial symmetry adapted linear combinations of these configurations yielding the four wave functions listed in eqn (7)–(10). This produces the diradical triplet (ΨT) and singlet (Ψ0), as well as the two zwitterionic singlets (ΨZ and Ψ1). These pairs of states are both split in energy by the inter-site exchange integral KAB.
We next proceed with the comparison of the left and right side of Fig. 2 describing the conversion from closed-shell via diradicaloid to diradical. It is noteworthy that the ΨT and ΨZ states remain unaltered along this conversion. They are both the only states of their given symmetry (1Au/3Au) meaning that there is no possibility for mixing with other states. By contrast, the Ψ0 and Ψ1 states (both totally symmetric singlets) mix strongly along this path; they have closed-shell character on the left and open-shell character on the right. In line with basic textbook knowledge,80 one finds that the bonded ground state (Ψ0 on the left) is formed as an even mixture between diradical and ionic resonance structures.
The presented viewpoint is not only relevant to the understanding of diradicals but also sheds new light onto the singlet and triplet states of closed-shell molecules. Following previous discussions,51–55 the HOMO–LUMO triplet states in alternating hydrocarbons can be assigned diradical character whereas the associated singlets are zwitterionic. The singlet–triplet gap can, thus, be identified with the energy difference between the diradical and zwitterionic configurations. It corresponds to the extra energy required to put both electrons into the same orbital (JAA) compared to the energy of two electrons in different orbitals (JAB). Indeed, one finds that 2KHL = JAA − JAB, yielding two interpretations of the singlet–triplet gap.
Having outlined the idealised states present within the TOTEM, we are now interested in finding ways of identifying these states in practical computations. We will be interested in highlighting the four states belonging to the TOTEM as well as finding states involving additional orbitals. As a tool to do so, we will use the wave function descriptors of Section 2. First, we are interested in the evolution of these descriptors for the model wave functions described in eqn (1)–(4). Following the procedures sketched in the Section S1 (ESI),† we can compute the descriptors for varying values of η. Note that within this section we treat η as an independent parameter whereas within the next section η will be effectively determined by the molecular geometry via the torsion angle between the benzene ring and the CH2 groups.
The results are summarised in Table 1 and shown graphically in Fig. 3 and we start the discussion with the energies. Whereas the other descriptors are uniquely defined within our model, there are more variables involved with respect to the energies, as shown in Table 1. Nonetheless, we present qualitative potential energy curves in Fig. 3a (see also ref. 49 and 81). The main point to notice at the closed-shell geometry (η = 0) is that all four states are clearly separated as determined by the HOMO–LUMO gap Δh and the exchange integral KHL. By contrast, at the open-shell geometry (η = 45°), the states form two quasi-degenerate pairs, split only by the smaller inter-site exchange integral KAB.
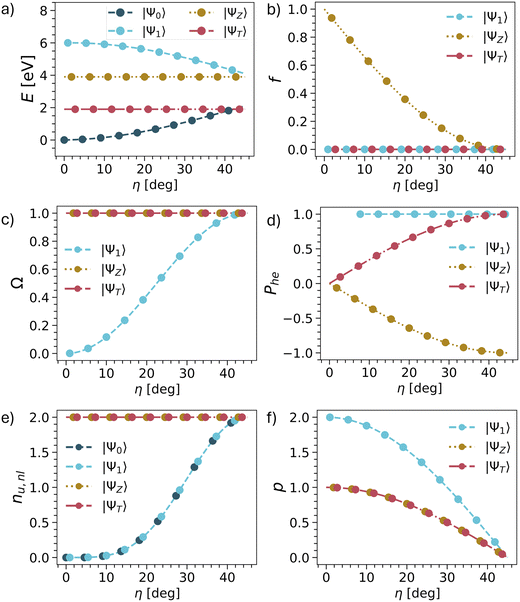 | ||
| Fig. 3 Evolution of energies (a), oscillator strengths (b) and wave function descriptors (c–f) vs. mixing angle η in TOTEM (treating η as an independent parameter). The associated equations are shown in Table 1. | ||
Next, we consider the oscillator strength (Fig. 3b). Here it is worth noting that transitions to the ΨT or Ψ1 are always forbidden due to spin and spatial selection rules, respectively, and only ΨZ is potentially bright. We find that ΨZ starts as a bright state but becomes dark as the ground state obtains open-shell character. We will discuss this phenomenon in more detail below.
We continue with the four wave function descriptors Ω, Phe, nu,nl, p. The purpose of these is to present a “fingerprint” that will allow us to identify the associated states in realistic computations when various states interact. The single excitation character Ω is presented in Fig. 3c. The ΨT and ΨZ states are always singly excited (Ω = 1) with respect to Ψ0, whereas the character of Ψ1 changes from doubly excited (Ω = 0) to singly excited (Ω = 1).
We proceed to the de-excitation character Phe reflecting particle–hole permutation symmetry (Fig. 3d).57 De-excitations reflect the fact that, if the LUMO is partially occupied in the ground state, then it is possible to de-excite from the LUMO into the HOMO along with exciting from the HOMO to the LUMO. At the closed-shell geometry, no de-excitations are possible. Phe vanishes for ΨT and ΨZ while being undefined for Ψ1 due to a division by zero. As η is increased, the de-excitations also increase in magnitude. For the triplet, this goes up to +1, whereas it goes down to −1 for the singlet. In the case of Ψ1, the Phe value is always 1 (but becomes only meaningful at higher η values when Ω is also larger). Reviewing ΨZ, it is crucial to realise that Phe converges to −1 in the open-shell limit. This reflects an antisymmetric 1TDM that, as outlined above, can only produce a vanishing matrix element with a symmetric operator such as the transition dipole moment. In other words, any transition dipole moment that is present through the HOMO/LUMO excitation is cancelled out by the LUMO/HOMO de-excitation. Thus, we find that within the TOTEM, all three states possess vanishing oscillator strengths at the diradical limit. Ψ1 is forbidden by spatial symmetry, ΨT by spin symmetry, and ΨZ by particle–hole permutation symmetry.
The number of unpaired electrons (nu,nl) is shown in Fig. 3e. The states ΨT and ΨZ always possess two unpaired electrons. Ψ0 and Ψ1 convert from being closed-shell (nu,nl = 0) to open-shell (nu,nl = 2). Finally, we proceed to the number of electrons rearranged during the excitation process represented by the promotion number p, as shown in Fig. 3f. The crucial realisation here is that in the open-shell limit all four states possess the same density matrices (singly occupied HOMO, singly occupied LUMO). As a consequence, the difference density between them and, therefore, also p vanishes.
In summary, we can use the following conditions to identify the TOTEM states within the diradical limit: Ω = 1, Phe = ±1, nu,nl = 2, p = 0.
3.2 pQDM – planar geometry
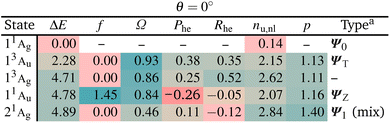
We start with a brief excited state analysis of pQDM at the planar geometry (a torsional angle of θ = 0°). This geometry corresponds to the left-hand side of Fig. 2. In this case, the ground state wave function Ψ0 can largely be described by a single configuration, meaning it corresponds to a textbook closed-shell molecule. We will investigate how much the lowest excited states of this system can indeed be captured by the TOTEM and if any additional π and π* orbitals of the phenyl bridge and subsequent mixing between the states play a role.Table 2 provides the analysis of the first five states of planar pQDM (results on an extended set of states are presented in Table S3†). We show energies, oscillator strengths, and the four descriptors presented in Fig. 3. In addition, we present the electron–hole correlation coefficient (Rhe),59 which is not included in Fig. 3 considering that it is a more complicated quantity not directly amenable to our model. Nonetheless, it will play an important role in differentiating between diradical and zwitterionic states later on. First we note that matching between the TOTEM states and the states actually obtained is readily possible where four out of the first five states (all except T2/13Ag) match the model. As expected, the ground state 11Ag is predominantly the HOMO2 closed-shell configuration (contributing with 88%) with only minor contributions from other configurations, yielding an effective number of unpaired electrons reasonably close to zero (nu,nl = 0.14).
| a Type assignment according to model wave functions, as defined in eqn (1)–(4). |
|---|
|
The lowest singlet and triplet excited states, 13Au and 11Au, lie at 2.28 and 4.71 eV, with 11Au possessing a significant oscillator strength (f = 1.45). They are both predominantly reached via the HOMO–LUMO transition, corresponding to ΨT and ΨZ in our model. Both states are characterised as predominantly singly excited (Ω ≈ 1, p ≈ 1) with two unpaired electrons (nu,nl ≈ 2). In the TOTEM, the Phe values would be zero for a closed-shell ground state. Deviations from zero, that is, Phe = 0.38 for ΨT and Phe = −0.26 for ΨZ, indicate already partial open-shell character for the ground state as also found in ref. 48. Note that in our model, a value of Phe = 0.3 corresponds to a mixing angle of η ≈ 9°, meaning that the planar geometry can be thought of as lying at this value when compared to Fig. 3. The meaning of the correlation coefficient Rhe has been discussed in detail elsewhere.82,83 For the present purposes, it is enough to realise that Rhe would be zero for a single-orbital transition out of a closed-shell ground state. Somewhat enhanced values indicate the contributions of different configurations.
The last state shown, 21Ag, has about 30% of contribution of the LUMO2 configuration and, thus, resembles Ψ1. However, there are also other important configurations involved. The partial doubly excited character, as expected for Ψ1 at the planar geometry, is reflected by a lowered Ω value (0.46) and raised p. As opposed to the TOTEM where Ψ1 is almost perfectly closed-shell, the state obtained here has a number of unpaired electrons of nu,nl = 2.84. This difference highlights that the TOTEM is an insufficient model for the full description of this state. This observation is in line with our previous discussions: it is rarely possible to find a state that is truly a pure LUMO2 configuration.60 There tends to be strong mixing with other configurations.
Reviewing Table 2, we can say that the TOTEM is a reasonable model for describing four out of the five lowest states at this geometry. Next we will be interested in finding out how these states translate to a twisted geometry.
3.3 pQDM – twisted geometry
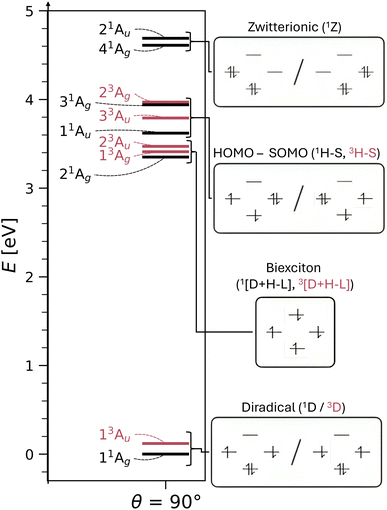
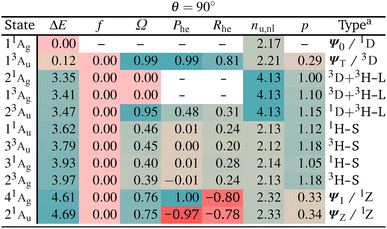
We turn to the excited state analysis of pQDM at the twisted geometry, focusing on the most diradical-like structure, with a torsional angle (θ) of 90°. Whereas it was fairly easy to find the TOTEM states in the planar geometry, it is considerably harder to do so for the twisted geometry, as other configurations play an important role.We start with a discussion of the overall states and major electron configurations. The energies of the first 11 states are shown in Fig. 4 (left) with singlets shown in black and triplets in red. The ground state is of singlet multiplicity with a low-energy triplet just above it. A rather dense set of singlet and triplet states follows between 3 and 4 eV. And finally there are two singlets at ≈4.6 eV.
The dominant orbital configurations are shown in Fig. 4 (right). To describe the character of these states we need to consider four MOs, the two SOMOs deriving from the TOTEM and two additional orbitals (denoted HOMO and LUMO). Note that the HOMO and LUMO from the planar geometry have become the SOMOs located on the CH2 groups, whereas the new HOMO and LUMO comprise additional orbitals, located solely on the phenyl bridge. Within Fig. 4, we use a representation of localised SOMOs (ϕA and ϕB) corresponding to eqn (7)–(10). It should be noted in this context that the actual states printed by OpenMolcas were of the form of eqn (1)–(4) and we transformed them to localised orbitals manually. We find that the two lowest states are singlet and triplet diradical states, i.e., they are the Ψ0 and ΨT states of the TOTEM, and we describe their character as 1D and 3D. The next three states can be viewed as biexciton states: they start from the 3D and 1D states and have an additional HOMO–LUMO triplet excitation. Conceptually, these are similar to the biexciton states in singlet fission systems84 all comprising four open shells.60 The next four states are four HOMO–SOMO states comprised of different spin and spatial symmetry. These HOMO–SOMO states are similar to HOMO–SOMO transitions found in individual radicals with a covalently bound donor group.2,3 Finally, at 4.61 and 4.69 eV, we find the singlet zwitterionic (1Z) states, which represent the missing ΨZ and Ψ1 states of the TOTEM. Notably, these zwitterionic states have no analogues in the triplet manifold, considering that the configurations where all orbitals are doubly occupied are forbidden due to the Pauli principle. States higher up in energy (not shown in Fig. 4) comprise SOMO–LUMO transitions.
The enhanced complexity of the twisted geometry compared to the planar geometry is striking. A number of states of widely varying character are present. Characterising these states is challenging, both from a formal and practical perspective. To get more insight into these states, we provide a detailed analysis of the calculated states in Table 3 presenting results for all states until 4.7 eV (higher energy states are shown in Tables S4 and S5†). Viewing Table 3, it is first noteworthy that, at the fully symmetric twisted geometry, all states are dark. The reasons for this will be discussed in more detail below.
| a Type assignment according to model wave functions, as defined in eqn (1)–(4) as well as using the following abbreviations: diradical (D), zwitterionic (Z), HOMO (H), LUMO (L), SOMO (S). |
|---|
|
Viewing Table 3, it is next of interest what descriptors can be favourably used to identify the TOTEM states. First, we can use the promotion number p, which should converge toward zero for the isolated TOTEM (Fig. 3f). This value is not reached exactly, but the TOTEM states are indeed distinguished by low p-values (p < 0.5), highlighting that there is almost no rearrangement of electron density between the different states (since they all have singly occupied SOMOs). The de-excitation measures (Phe) are also striking. These are 0.99 and 1.00 for the ΨT and Ψ1 states, whereas a value of −0.97 is obtained for ΨZ. These values again illustrate that excitations and de-excitations both occur between the SOMOs.
Moving to the correlation coefficients, we find a value of Rhe = 0.82 for 13Au (when computed with respect to 11Ag). This strongly positive correlation reflects that both states are of the same type, that is, both are diradical. By contrast, strongly negative correlation is obtained for 41Ag and 21Au, in agreement with their zwitterionic character.
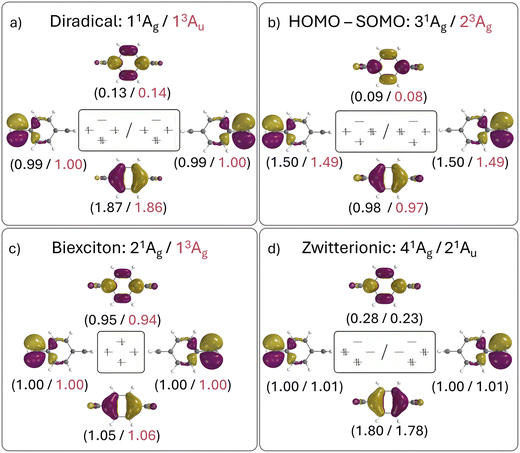
Proceeding to the other types of states shown in Table 3, we note that the biexciton type states are clearly differentiated via their four unpaired electrons (nu,nl = 4.13). Biexcitons are formed as a combination of the quasi-degenerate diradical states (1D, 3D) and the triplet HOMO–LUMO transition (3H–L). Combining two triplets, that is 3D + 3H–L, generally produces a singlet, a triplet, and a quintet. Here, the singlet and triplet are represented in our computations via the 21Ag and 13Ag states. Combining a singlet and a triplet (1D + 3H–L) only produces a triplet and this is found for the 23Au state. Interestingly, within our classification scheme the two 3D + 3H–L states are characterised as doubly excited with respect to the 11Ag ground state (Ω = 0.00), whereas the 1D + 3H–L state comes out as singly excited (Ω = 0.95). Conversely, the promotion numbers, also sometimes used to classify multiply excited character,63,85 are near 1.0 for all the states highlighting the complexities of open-shell wave functions.
Finishing with the HOMO–SOMO states, we note that these possess the simplest wave functions being composed of only a single configuration with two unpaired electrons. For the most part, these states have descriptor values similar to singly excited states of closed-shell molecules:57,60 no de-excitations (Phe = 0.0), only a small amount of correlation (Rhe < 0.3), two unpaired electrons (nu,nl = 2.1), and a promotion number near one (p ≈ 1.1). The only unusual feature is the low Ω values, formally indicating partially doubly excited character. This, however, is mostly a reflection of the open-shell nature of the ground state rather than indicating a special property of the excited state.
The relevant orbital compositions are shown in Fig. 5 using the natural orbital representation. It can be seen that, in all cases, the involved orbitals possess similar shapes (with the SOMOs on the CH2 groups and the HOMO and LUMO on the central benzene ring). Moreover, the occupation numbers largely follow the expectations drawn from the simple orbital diagram. This highlights that a four-electron four-orbital model is sufficient to explain the relevant states. However, it is also noteworthy that there is significant involvement of the LUMO for the diradical (ni > 0.1) and even more for the zwitterion (ni > 0.2) highlighting the importance of additional strong correlation effects. Note that this is also reflected in the trends of the computed numbers of unpaired electrons (nu,nl), as shown in Table 3.
Finally, we comment on the oscillator strengths of the states shown, which are all vanishingly small (f < 0.001). All gerade (g) states are forbidden by spatial selection rules while all triplet states are forbidden by spin selection rules. As outlined above, also a Phe value of −1, as found for the 21Au state, and a Ω value of zero, as found for the 21Ag state, mean that the transition dipole moments must vanish. These considerations highlight the challenges in designing luminescent diradicals, which will require effectively surpassing these various selection rules by mixing states and/or breaking the spatial symmetry.
3.4 pQDM – potential curve
Having provided a detailed discussion of the planar and twisted geometries, we are now interested in investigating how the different states interconvert into each other. In particular, it is of interest whether the model picture of Fig. 3 can be reproduced. For this purpose, we have computed potential energy curves for pQDM along the twisting coordinate. States were chosen, so as to include the minimal set comprising all TOTEM states shown in Table 3, that is 4 × 1Ag, 2 × 1Au, 1 × 3Au. The results for energies, oscillator strengths and wave function descriptors are shown in Fig. 6, highlighting that the results are already quite involved with this minimal set of states. Results of more excited states are presented in Fig. S2–S5.†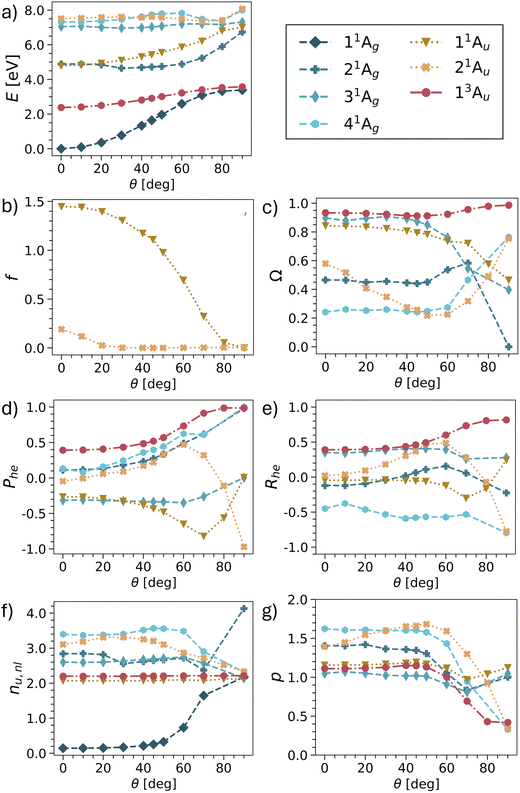 | ||
| Fig. 6 Potential energies (a), oscillator strengths (b), and wave function descriptors (c–g) for pQDM with change of the torsional angle θ (as defined in Fig. 1). | ||
Starting with the energies (Fig. 6a), we find that the lowest two states (11Ag and 13Au) do indeed conform with the expected behaviour for the Ψ0 and ΨT states, that is, they start with a notable energy gap and become quasi-degenerate upon twisting. Note, however, that in the TOTEM the triplet becomes lower in energy according to Hund's rule, whereas in our computations the singlet always remains the lowest state.
Disentangling the properties of the higher states is somewhat more challenging as there are several state crossings involved. We will now proceed in elucidating the development of the remaining two TOTEM states (ΨZ, and Ψ1) along the twisting curve. At the planar geometry (θ = 0°), the 11Au state is the HOMO–LUMO transition and, thus, corresponds to the ΨZ state. In line with Fig. 3, we find that its oscillator strength (Fig. 6b) rapidly goes down and approaches zero with enhanced twisting. As a telltale sign of the ΨZ state, we find its markedly negative Phe values steadily going down until 70°. We also find negative values of the correlation coefficient Rhe, reflecting the zwitterionic character of this state. At around 80°, there is an avoided crossing between the 11Au and 21Au states and, at the fully twisted geometry, the 21Au state obtains the zwitterionic character, as also shown in Table 3. The exchange of wave function character between the two states is particularly visible in Fig. 6d, where the 21Au state continues the lowering of the Phe values. We can understand this change by the fact that, at the fully twisted geometry (θ = 90°), all conjugation is broken, thus penalising the zwitterionic state located on the outer CH2 groups.
As opposed to the three states discussed, no clear identification of the fourth TOTEM state (Ψ1) is possible. As explained in the context of Table 2, the 21Ag state possesses partial LUMO2 (and thus Ψ1) character at θ = 0°. However, other configurations mix considerably. The state with the most pronounced doubly excited character (Ω = 0.24) is 41Ag, also including the LUMO2 configuration, and can therefore be seen to also incorporate part of the Ψ1 character. Following the different descriptors, we find that the 21Ag and 41Ag states together approach the limits for the zwitterionic Ψ1 state, that is, Phe = 1, Rhe = −1, p = 0. At the twisted geometry, we assign 41Ag as the Ψ1 state. However, as opposed to the 1Au states, we cannot name a clear crossover point where the change occurs.
We conclude by noting that all four TOTEM states can indeed be identified in the presented curves. However, Fig. 6 shows that even pQDM, chosen as a supposedly simple model system, goes far beyond the TOTEM in terms of its observed complexity, with a high degree of mixing between the different state characters observed along the potential curve.
4 Conclusions
We presented a chemically intuitive and at the same time mathematically rigorous framework for describing the character of different excited states in π-conjugated diradicals. This encompasses a formal physical description as well as practical tools for characterising these states in realistic computations. Aside from a categorisation of the states, our model provides crucial insight into other properties, most notably energies and optical transition strengths.We discussed the states of open-shell systems within a two-orbital two-electron model (TOTEM), highlighting the differences between diradical and zwitterionic states. We showed how these states emerge within the mathematical treatment but also provided a more intuitive graphical route toward understanding them. Moving to realistic calculations on pQDM, we found that, aside from diradical and zwitterionic states, HOMO–SOMO excitations and biexcitons also played a crucial role in the relevant energy window. All types of states exist in pairs of singlet and triplet states, with the striking exception of the zwitterionic states, which possess no triplet analogue due to the Pauli principle. Subsequently, we highlighted how the states interconvert upon twisting of the CH2 groups. The intensity of the initially bright state drops sharply and, interestingly, at the twisted geometry, all states shown were dark (f < 0.001). We illustrated four effective selection rules responsible for the lack of oscillator strength at this geometry comprising spin, spatial and particle–hole permutation symmetry as well as doubly excited character.
Due to their intricate electronic structure properties, π-conjugated diradicals provide a fascinating playground for tuning optoelectronic properties in an unprecedented fashion. Whereas closed-shell molecules are often largely determined by the energies and shapes of their HOMO and LUMO, there are four orbitals to be tuned in the case of diradicals, the HOMO, LUMO and two SOMOs. The energies of and interactions between these orbitals provide the basis for new types of state characters not readily observed in closed-shell molecules. This enhanced complexity provides new opportunities but also significant challenges for molecular design applications. It is a particularly fascinating question whether it is possible to harness zwitterionic states for luminescence noting that these have no dark spin-triplet analogue. In an ideal world, one would design a molecule with large oscillator strengths as found in the planar closed-shell case while also eliminating the close-lying triplets, thus providing a potent emitter without a triplet loss channel. We hope that the present investigation will lay the groundwork for the rational design of such systems.
Author contributions
Lujo Matasović: investigation, visualization, writing – original draft. Hugo Bronstein: conceptualization, writing – review & editing. Richard Friend: supervision, writing – review & editing. Felix Plasser: conceptualization, formal analysis, methodology, software, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. M. acknowledges support from the Harding Distinguished Postgraduate Programme and Winton Scholarship.References
- Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 CrossRef CAS PubMed.
- X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Nature, 2018, 563, 536–540 CrossRef CAS PubMed.
- A. Abdurahman, T. J. H. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Nat. Mater., 2020, 19, 1224–1229 CrossRef CAS PubMed.
- J. M. Hudson, T. J. H. Hele and E. W. Evans, J. Appl. Phys., 2021, 129, 180901 CrossRef CAS.
- P. Murto and H. Bronstein, J. Mater. Chem. C, 2022, 10, 7368–7403 RSC.
- A. Mizuno, R. Matsuoka, T. Mibu and T. Kusamoto, Chem. Rev., 2024, 124, 1034–1121 CrossRef CAS PubMed.
- T. Stuyver, T. Zeng, Y. Tsuji, P. Geerlings and F. De Proft, Nano Lett., 2018, 18, 7298–7304 CrossRef CAS PubMed.
- L. Li, J. Z. Low, J. Wilhelm, G. Liao, S. Gunasekaran, C. R. Prindle, R. L. Starr, D. Golze, C. Nuckolls, M. L. Steigerwald, F. Evers, L. M. Campos, X. Yin and L. Venkataraman, Nat. Chem., 2022, 14, 1061–1067 CrossRef CAS PubMed.
- K. Yang, X. Zhang, A. Harbuzaru, L. Wang, Y. Wang, C. Koh, H. Guo, Y. Shi, J. Chen, H. Sun, K. Feng, M. C. Ruiz Delgado, H. Y. Woo, R. P. Ortiz and X. Guo, J. Am. Chem. Soc., 2020, 142, 4329–4340 CrossRef CAS PubMed.
- S. Zhang, M. Pink, T. Junghoefer, W. Zhao, S.-N. Hsu, S. Rajca, A. Calzolari, B. W. Boudouris, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2022, 144, 6059–6070 CrossRef CAS PubMed.
- T. Kubo, A. Shimizu, M. Sakamoto, M. Uruichi, K. Yakushi, M. Nakano, D. Shiomi, K. Sato, T. Takui, Y. Morita and K. Nakasuji, Angew. Chem., Int. Ed., 2005, 44, 6564–6568 CrossRef CAS PubMed.
- M. Nakano and B. Champagne, J. Phys. Chem. Lett., 2015, 6, 3236–3256 CrossRef CAS.
- M. Nakano, Chem. Rec., 2017, 17, 27–62 CrossRef CAS PubMed.
- O. Varnavski, N. Abeyasinghe, J. Aragó, J. J. Serrano-Pérez, E. Ortí, J. T. López Navarrete, K. Takimiya, D. Casanova, J. Casado and T. Goodson III, J. Phys. Chem. Lett., 2015, 6, 1375–1384 CrossRef CAS PubMed.
- J. Messelberger, A. Grünwald, P. Pinter, M. M. Hansmann and D. Munz, Chem. Sci., 2018, 9, 6107–6117 RSC.
- G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. Ponce Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Nat. Chem., 2016, 8, 753–759 CrossRef CAS PubMed.
- T. Jousselin-Oba, M. Mamada, J. Marrot, A. Maignan, C. Adachi, A. Yassar and M. Frigoli, J. Am. Chem. Soc., 2019, 141, 9373–9381 CrossRef CAS PubMed.
- A. Punzi, Y. Dai, C. N. Dibenedetto, E. Mesto, E. Schingaro, T. Ullrich, M. Striccoli, D. M. Guldi, F. Negri, G. M. Farinola and D. Blasi, J. Am. Chem. Soc., 2023, 145, 20229–20241 CrossRef CAS PubMed.
- A. Abdurahman, J. Wang, Y. Zhao, P. Li, L. Shen and Q. Peng, Angew. Chem., Int. Ed., 2023, 62, e202300772 CrossRef CAS PubMed.
- A. Abdurahman, L. Shen, J. Wang, M. Niu, P. Li, Q. Peng, J. Wang and G. Lu, Light: Sci. Appl., 2023, 12, 272 CrossRef CAS PubMed.
- T. D. Nguyen, E. Ehrenfreund and Z. V. Vardeny, Science, 2012, 337, 204–209 CrossRef CAS PubMed.
- T. Stuyver, B. Chen, T. Zeng, P. Geerlings, F. De Proft and R. Hoffmann, Do Diradicals Behave like Radicals?, Chem. Rev., 2019, 119, 11291–11351 CrossRef CAS PubMed.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed.
- J. J. Dressler and M. M. Haley, J. Phys. Org. Chem., 2020, 33, e4114 CrossRef CAS.
- J. M. Anglada, J. Poater, I. d. P. R. Moreira and J. M. Bofill, J. Org. Chem., 2023, 88, 8553–8562 CrossRef CAS PubMed.
- X. Hu, W. Wang, D. Wang and Y. Zheng, J. Mater. Chem. C, 2018, 6, 11232–11242 RSC.
- Z. Feng, S. Tang, Y. Su and X. Wang, Chem. Soc. Rev., 2022, 51, 5930–5973 RSC.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- M. Nakano, Top. Curr. Chem., 2017, 375, 47 CrossRef PubMed.
- A. Bajaj and M. E. Ali, J. Phys. Chem. C, 2019, 123, 15186–15194 CrossRef CAS.
- J. Wu and D. Casanova, Electronic Structure Characterization of Diradicaloids with Spin-Flip (SF) Methods, Jenny Stanford Publishing, Singapore, 1st edn, 2022, pp. 83–143 Search PubMed.
- D. Casanova, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1561 CrossRef CAS.
- K. Yamaguchi, Y. Takahara and T. Fueno, Appl. Quantum Chem., 1986, 155–184 CAS.
- V. Bonačić-Koutecký, J. Koutecký and J. Michl, Angew. Chem., Int. Ed. Engl., 1987, 26, 170–189 CrossRef.
- Y. Jung and M. Head-Gordon, ChemPhysChem, 2003, 4, 522–525 CrossRef CAS PubMed.
- K. Takatsuka, T. Fueno and K. Yamaguchi, Theor. Chim. Acta, 1978, 48, 175–183 CrossRef CAS.
- V. N. Staroverov and E. R. Davidson, J. Am. Chem. Soc., 2000, 122, 186–187 CrossRef CAS.
- M. Head-Gordon, Chem. Phys. Lett., 2003, 372, 508–511 CrossRef CAS.
- F. Plasser, H. Pašalić, M. H. Gerzabek, F. Libisch, R. Reiter, J. Burgdörfer, T. Müller, R. Shepard and H. Lischka, Angew. Chem., Int. Ed., 2013, 52, 2581–2584 CrossRef CAS PubMed.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS PubMed.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2014, 114, 429–492 CrossRef CAS PubMed.
- G. Gryn'ova, M. L. Coote and C. Corminbœuf, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2015, 5, 440–459 CrossRef PubMed.
- S. Gorgon, K. Lv, J. Grüne, B. H. Drummond, W. K. Myers, G. Londi, G. Ricci, D. Valverde, C. Tonnelé, P. Murto, A. S. Romanov, D. Casanova, V. Dyakonov, A. Sperlich, D. Beljonne, Y. Olivier, F. Li, R. H. Friend and E. W. Evans, Nature, 2023, 620, 538–544 CrossRef CAS PubMed.
- P. Murto, R. Chowdhury, S. Gorgon, E. Guo, W. Zeng, B. Li, Y. Sun, H. Francis, R. H. Friend and H. Bronstein, Nat. Commun., 2023, 14, 4147 CrossRef CAS PubMed.
- Z. Zhou, K. Yang, L. He, W. Wang, W. Lai, Y. Yang, Y. Dong, S. Xie, L. Yuan and Z. Zeng, J. Am. Chem. Soc., 2024, 146, 6763–6772 CrossRef CAS PubMed.
- C. P. Yu, R. Chowdhury, Y. Fu, P. Ghosh, W. Zeng, T. B. E. Mustafa, J. Grüne, L. E. Walker, D. G. Congrave, X. W. Chua, P. Murto, A. Rao, H. Sirringhaus, F. Plasser, C. P. Grey, R. H. Friend and H. Bronstein, Sci. Adv., 2024, 10(30) DOI:10.1126/sciadv.ado3476.
- Z. Pei, N. L. Magann, M. J. Sowden, R. B. Murphy, M. G. Gardiner, M. S. Sherburn and M. L. Coote, J. Am. Chem. Soc., 2023, 145, 16037–16044 CrossRef CAS PubMed.
- L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11, 92–111 CrossRef CAS.
- Y. L. A. Schmerwitz, A. V. Ivanov, E. O. Jonsson, H. Jonsson and G. Levi, J. Phys. Chem. Lett., 2022, 13, 3990–3999 CrossRef CAS PubMed.
- P. Kimber and F. Plasser, in Classification and Analysis of Molecular Excited States, Elsevier, 2024, pp. 55–83 Search PubMed.
- K. Schulten, I. Ohmine and M. Karplus, J. Chem. Phys., 1976, 64, 4422–4441 CrossRef CAS.
- W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1996, 29, 67–75 CrossRef CAS.
- C. Angeli, J. Comput. Chem., 2009, 30, 1319–1333 CrossRef CAS PubMed.
- S. A. do Monte, R. F. K. Spada, R. L. R. Alves, L. Belcher, R. Shepard, H. Lischka and F. Plasser, J. Phys. Chem. A, 2023, 127, 9842–9852 CrossRef CAS PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- P. Kimber and F. Plasser, Phys. Chem. Chem. Phys., 2020, 22, 6058–6080 RSC.
- S. A. Bäppler, F. Plasser, M. Wormit and A. Dreuw, Phys. Rev. A, 2014, 90, 052521 CrossRef.
- F. Plasser, B. Thomitzni, S. A. Bäppler, J. Wenzel, D. R. Rehn, M. Wormit and A. Dreuw, J. Comput. Chem., 2015, 36, 1609–1620 CrossRef CAS PubMed.
- M. T. do Casal, J. M. Toldo, M. Barbatti and F. Plasser, Chem. Sci., 2023, 14, 4012–4026 RSC.
- S. Matsika, X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. A, 2014, 118, 11943–11955 CrossRef CAS PubMed.
- W. Barford and N. Paiboonvorachat, J. Chem. Phys., 2008, 129, 164716 CrossRef PubMed.
- M. Head-Gordon, A. M. Grana, D. Maurice and C. A. White, J. Phys. Chem., 1995, 99, 14261–14270 CrossRef CAS.
- F. Plasser and A. Dreuw, J. Phys. Chem. A, 2015, 119, 1023–1036 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Pierloot, B. Dumez, P.-O. Widmark and B. O. Roos, Theor. Chim. Acta, 1995, 90, 87–114 CrossRef CAS.
- G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov(Gulak), L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Martí, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, K. Andersson and M. P. Fülscher, Chem. Phys. Lett., 1992, 192, 5–13 CrossRef CAS.
- M. Boggio-Pasqua, M. J. Bearpark, M. Klene and M. A. Robb, J. Chem. Phys., 2004, 120, 7849–7860 CrossRef CAS PubMed.
- K. Andersson, P. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- G. Ghigo, B. O. Roos and P. Åke Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- S. Battaglia, L. Fransén, I. F. Galván and R. Lindh, J. Chem. Theory Comput., 2022, 18, 4814–4825 CrossRef CAS PubMed.
- F. Plasser, S. A. Mewes, A. Dreuw and L. González, J. Chem. Theory Comput., 2017, 13, 5343–5353 CrossRef CAS PubMed.
- F. Plasser, A. I. Krylov and A. Dreuw, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1595 CrossRef CAS.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- X. K. Chen, D. Kim and J. L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS PubMed.
- P. Kimber and F. Plasser, J. Chem. Theory Comput., 2023, 19, 2340–2352 CrossRef CAS PubMed.
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Ltd, 2nd edn, 2007 Search PubMed.
- J. Wen, Z. Havlas and J. Michl, J. Am. Chem. Soc., 2015, 137, 165–172 CrossRef CAS PubMed.
- M. Hoffmann, S. A. Mewes, S. Wieland, C. Popp and A. Dreuw, J. Phys. Chem. Lett., 2019, 10, 6112–6117 CrossRef CAS PubMed.
- S. A. Mewes, F. Plasser and A. Dreuw, J. Phys. Chem. Lett., 2017, 8, 1205–1210 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Theory Comput., 2018, 14, 9–13 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Derivations of the equations used and additional computational results. See DOI: https://doi.org/10.1039/d4fd00055b |
| This journal is © The Royal Society of Chemistry 2024 |