Hydrogen bond types which do not fit accepted definitions

Abstract

There are various interactions that either partially fit or do not fit the currently accepted definitions of the hydrogen bond. However, they possess characteristics of this interaction. It seems that it is partly connected to the fact that these definitions are not precise. The typical 3c–4e (three centres – four electrons) A–H⋯B hydrogen bond is characterized by the single-atom A and B centres that are highly electronegative. On the other hand, non-typical interactions that do not fit the hydrogen bond definitions well are characterised by uncommon proton donors and/or proton acceptors. The cases of multi-centre proton acceptors, π-electron or σ-electron systems are well known – such interactions are designated as A–H⋯π and A–H⋯σ hydrogen bonds, respectively. However, the cases of interactions with the multi-centre proton donors and proton acceptors do not fit the majority of definitions of hydrogen bond. The π⋯H⁺⋯π system in the proton-bound homodimer of acetylene is an example. This system can be classified as a hydrogen bond according to the two-sites hydrogen bond, 2sHB, definition. There are various types of interactions discussed in this review; among them, those that are undoubtedly unclassified as hydrogen bonds, i.e., hydride bonds, and charge inverted hydrogen bonds, CIHBs. Special emphasis is also put here on the proton sponges and other systems such as the [FHF]⁻ anion or [NgHNg]⁺ cation (Ng is the noble gas centre).

---

Sławomir J. Grabowski

Sławomir J. Grabowski received his PhD (1986) at the University of Warsaw, Poland. Currently, he is employed as the Ikerbasque Research Professor at the University of the Basque Country, Spain. He is the author of the book Understanding Hydrogen Bonds: Theoretical and Experimental Views, The Royal Society of Chemistry, UK 2021. His work encompasses the hydrogen bond and other Lewis acid – Lewis base interactions in a gas phase and in crystals. He is a member of the Editorial Boards of Journal of Physical Organic Chemistry (Wiley) and Computational and Theoretical Chemistry (Elsevier).

---

Introduction

Hydrogen bond has been known for over one hundred years as an important interaction that steers the arrangement of chemical species such as molecules or ions.^1–4 It is crucial in numerous chemical, physical and biological processes (e.g., proton transfer reactions⁵ and life processes⁶ including DNA replication).⁷ It seems that in the study of Latimer and Rodebush,⁸ the first definition of the hydrogen bond was proposed despite the latter term not being used. It was stated that “the hydrogen nucleus held between 2 octets constitutes a weak bond”. The term “hydrogen bond” was probably used for the first time by Lewis in his monograph since he stated that “hydrogen, when attached firmly to a pair of electrons, as in the hydrogen–hydrogen or hydrogen–carbon bond … can form a loose attachment to another pair of electrons, thus forming the hydrogen bond”.⁹ It is worth mentioning that Lewis has also referred to earlier ideas of this interaction by Huggins,¹⁰ which were advanced by the studies of Latimer and Rodebush⁸ mentioned above. However, one should also mention the very early studies of Werner,¹¹ Hantzsch¹² and Pfeiffer,¹³ who used such terms as “nebenvalenz” (minor valence) and “innere komplexsalzbildung” to describe intra- and intermolecular hydrogen bonds.

The statement of Lewis⁹ cited here may be treated as the definition of the hydrogen bond; numerous other definitions were proposed in other later studies. Herein, it is worth noting one of the latest definitions^14,15 that is recommended by IUPAC, which states that “the hydrogen bond is an attractive interaction between a hydrogen atom from a molecule or a molecular fragment X–H, in which X is more electronegative than H, and an atom or a group of atoms in the same or a different molecule, in which there is evidence of bond formation”.¹⁴ This definition (named from now on as the IUPAC definition) is very similar to an early one given by Pimentel and McClellan¹⁶ and to the more recent definition given by Jeffrey and Saenger.¹ The X–H⋯Y term is used in the IUPAC definition, and the term A–H⋯B is applied in this review. However, H is designated here as the hydrogen atom while A and B are other centres. If B will mark the boron centre later in the text, it will be noted.

The IUPAC definition follows the traditions of other definitions where three centres are indicated, A–H⋯B, and where the H-atom is attached more strongly to one of them (A is named as the proton donor) and weakly to another one (B is named as the proton acceptor). However, this definition contains unclear terms and it is ambiguous without additional explanations since one does not know what the “evidence of bond formation” means and how the electronegativity of centres is understood (evaluated). Is it in agreement with the Pauling definition of electronegativity,¹⁷ or with any other definition of this phenomenon? Hence, the IUPAC definition is accompanied by two articles where descriptions, as well as lists of criteria, characteristics, and footnotes are included that are often valuable and useful.^14,15 In addition, there are various spectroscopic and crystallographic evidences of the hydrogen bond.^14,15 Some criteria are described in such a way that may be treated as evidences also. It is stated that the “electronegativity of an atom can be very different in different environments”.¹⁴ However, it does not solve the problem since for each case of the interaction, additional detailed analyses are needed to know which centre, A or H, attracts electrons stronger.

The articles accompanying the IUPAC definition provide a useful information on hydrogen bond interactions. They contain the above mentioned lists and additional descriptions, where the energetic, geometric, topological and spectroscopic characteristics are included.^14,15 These articles are at least partly in agreement with other studies where the characteristics of the hydrogen bond were described. These characteristics are briefly presented below since it seems to be useful to refer to numerous important studies concerning the hydrogen bond.

It was assumed that for the A–H⋯B arrangement, the H⋯B distance should be shorter than the corresponding sum of the H and B van der Waals radii, at least approximately.¹⁸ Why? For the shorter H⋯B distances, the hydrogen bond may be classified as the Lewis acid – Lewis base interaction since the electron charge transfer from the B unit to the A–H one is detected. For longer distances, such a transfer is often negligible.¹⁹ It is also claimed that the hydrogen bond is an electrostatic interaction, at least it is partly electrostatic.^4,19 The electrostatic, long-range forces act beyond the sum of H and B van der Waals radii. Thus, this distance criterion is controversial. The same concerns very short H⋯B distances where the covalent contribution is dominant. Desiraju has claimed in an early study that the hydrogen bond is an interaction without borders.²⁰ The latter statement of the lack of borders for the hydrogen bond may be related to numerous characteristics of this interaction. For example, it concerns the strength of the H-bond. Different ranges of the energy of the hydrogen bond interaction are presented in various studies, and a wide range between 0.1 and 60 kcal mol⁻¹ was proposed,^21,22 for example. Weaker interactions correspond to van der Waals forces, while stronger ones to covalent bonds. However, the above-mentioned boundaries for the latter range are not so sharp.^21,22

The determination of the range of the A–H⋯B angle is also problematic. No doubt, the hydrogen bond is a directional interaction. Thus, the A–H⋯B systems tend toward linearity. However, it is difficult to determine the lowest value of the A–H⋯B angle. It is assumed in the study accompanying the IUPAC definition that this angle should be greater than 110°.¹⁵ Sometimes, it is noted that this angle should be greater than 90°. For example, Taylor and Kennard discussed the C–H⋯B interactions (C designates carbon centre). They rejected from the analysis those systems where the C–H⋯B angle is lower than 90°.²³ Some of the other criteria and of other descriptions of the A–H⋯B systems are presented in the next sections.

The A–H bond elongation as a result of the A–H⋯B connection was treated for a long time as a signature of the hydrogen bond,^24,25 in other words as evidence of its formation. This elongation is accompanied by the shift of the corresponding A–H bond stretching mode to lower frequencies, as a so-called red shift. However, various systems were found to possess numerous characteristics of hydrogen bonds, but shortening of the A–H bond was observed as a result of complexation.²⁶ For such systems, the shift of the corresponding A–H stretching mode to higher frequencies occur, as a so-called blue shift. It is worth mentioning that such blue-shifted hydrogen bonds were announced very early.^27–29 However, the increase of the number of studies on such interactions is observed after the appearance of the article of Hobza and Havlas.²⁶ Thus, one can see that there are not any clear evidences of the existence of the hydrogen bond interaction. This is because the energetic or geometrical criteria, such as the hydrogen bond energy, H⋯B distance, and A–H bond elongation, do not have strictly defined ranges.

The classification of hydrogen bonds

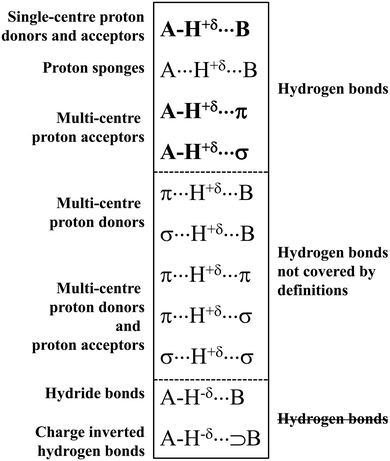
The typical A–H⋯B hydrogen bonds are characterised by A and B centres possessing high values of electronegativity.^1–3 Hence, these arrangements with fluorine, oxygen or nitrogen were usually classified as hydrogen bonds. That is why an early study by Suttor³⁰ on C–H⋯B systems classified as hydrogen bonds was a subject of criticism and controversy.³¹ It was stated that these interactions are not classified as hydrogen bonds because the electronegativity of the carbon centre is not high, and because the H⋯B distances in the crystal structures analysed are close to the sum of the corresponding van der Waals radii. However, a statistical analysis by Taylor and Kennard on the C–H⋯B arrangements²³ that was based on the crystal structures stored in the Cambridge Structural Database, CSD,^32,33 supported the study by Suttor. This statistical analysis²³ proved beyond any doubt that numerous C–H⋯B systems may be classified as hydrogen bond interactions.

Since that time, the situation related to studies on the hydrogen bonds may be considered dynamic because numerous atypical systems were classified as hydrogen bonds. One can mention here a case of multi-centre proton acceptors. It was found, for example, that the π-electron systems may play a role as the proton acceptors. These arrangements are marked as the A–H⋯π hydrogen bonds,⁴ and special attention was put on the C–H⋯π interactions that often occur in crystal structures and that steer the arrangement of chemical species.³⁴ The other interactions are those where σ-electrons act as the Lewis base centre. This class of interactions was classified in 2004 as the A–H⋯σ hydrogen bonds in a theoretical study on the AH₄⁺⋯H₂ and [AH₄⁺(H₂)₄] ⋯H₂ complexes (where A = N, P, As, Sb, Bi).³⁵ Hence, three great sub-classes of hydrogen bonds, A–H⋯B, A–H⋯π and A–H⋯σ,¹⁹ may be specified as being covered by several definitions of hydrogen bonds, especially by the IUPAC definition.^14,15 They are presented in Scheme 1, where other various sub-classes of the hydrogen bond interaction are also specified.

Scheme 1 Three groups of interactions: hydrogen bonds covered by the IUPAC definition; hydrogen bonds not covered by the IUPAC definition, but by the 2sHB definition; and interactions that are not classified as hydrogen bonds because of the nucleophilic H-centre.

Scheme 1 shows that the hydrogen centre is characterized by the positive charge. This is required in numerous definitions of the hydrogen bond interaction – the H-centre acts as the electrophile. The hydrogen is strongly linked with the A-centre, and its weaker interaction with the B-centre is observed. This occurs for the three types of interactions mentioned above, which are covered by the IUPAC definition. The proton sponges,^36,37 marked as A⋯H^+δ⋯B, are also among the classes of interactions that are included by the latter definition. These species may be considered as systems where the proton is inserted between two electron-rich moieties. One can see that the proton sponges follow the definition of Latimer and Rodebush⁸ mentioned above. For the majority of proton sponges, the H-centre is moved closer to one of the neighbouring centres, say A. Only in the case where these are the same atoms (A = B) and the proton is situated in the A⋯A mid-point, two A⋯H contacts are equivalent and it is difficult to classify them as covalent bonds or as intermolecular contacts.

Scheme 1 shows that the H-centre is positively charged (+δ) for the majority of the systems presented. It is justified for the neutral H-bonded complexes, where the electron charge shift from the H-atom to the A-centre occurs. This is because the polarization of the A–H bond is observed with the greater electron charge accumulation of the A–H σ-orbital at the A-centre than at the hydrogen one. The A⋯H^+δ⋯B designation is applied here for the proton sponges and for related systems. This is because “the pure proton” is not located between lone electron pairs or between other electron-rich centres. The electron charge shifts in the proton sponges and related systems lead to the decrease of the positive charge of the proton. For example, for the proton inserted between two fluoride anions, i.e., for the [FHF]⁻ system, the range of the charge of the H-centre is between +0.57 a.u. and +0.60 a.u. for the [FHF]⁻ anion interacting with various Lewis acid species (Natural Bond Orbital, NBO, charges for systems optimized at the MP2/aug-cc-pVTZ level).³⁸

It is worth mentioning here the definition of the hydrogen bond proposed by Weinhold and Klein (referenced hereafter as the WK definition). It states the following: “Hydrogen bond: a fractional chemical bond of coordinative A–H⋯B Lewis acid–base type, associated with the partial intermolecular A–H⋯:B ↔ A:⋯H–B resonance (3-center/4-electron proton-sharing) commonly originating in the 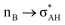donor–acceptor interaction between the lone pair n_B of the Lewis base and the hydride antibond 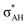of the Lewis acid.”³⁹ One can see that the “range” of this definition is much narrower than that of the IUPAC definition. It does not cover systems with the multi-centre proton acceptors. Thus, only A–H⋯B interactions are covered by the WK definition, and also proton sponges, A⋯H^+δ⋯B, those where the proton located in the A⋯B mid-point may be treated as the systems where resonance forms contribute almost equivalently to the real structure.

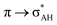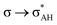The A–H⋯π and A–H⋯σ interactions are not covered by the WK definition,³⁹ but they are by the IUPAC one.^14,15 For these interactions, the main orbital–orbital and interactions (overlaps) are observed, respectively.⁴⁰ For the A–H⋯B hydrogen bond, this is the 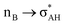overlap, as it was mentioned above.

The other types of interactions presented in Scheme 1 are not covered by the commonly accepted definitions of the hydrogen bond rather. Herein, one can see the group of interactions with the negatively charged hydrogen atom, hydride bonds, A–H^−δ⋯B,^41,42 and the charge inverted hydrogen bonds, CIHBs, marked as A–H^−δ⋯⊃B.^43–45 These systems are not classified as the hydrogen bonds since for the latter interactions, it is commonly accepted that the H-atom is positively charged, i.e., it is the Lewis acid centre.

Another group of interactions is characterized by the multi-centre proton donor.^46,47 The Lewis base site may be a single atom centre or multi-centre π-electron or σ-electron system (Scheme 1).⁴⁸ These interactions are not taken into account in the IUPAC definition. However, a new definition has been proposed²² that covers these interactions. It will be discussed in the next section of this article.

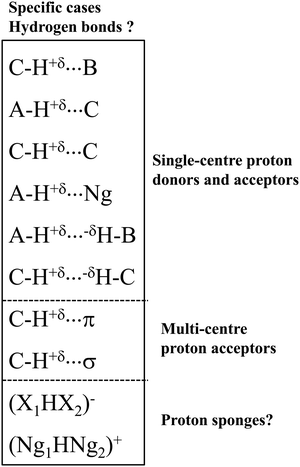
Let us present specific interactions that were often questioned as the hydrogen bonds (Scheme 2). These interactions belong to three groups of the hydrogen bond: (i) the group where a single-centre proton donor and a single-centre proton acceptor occur, (ii) the group with multi-centre proton acceptor, as well as (iii) the proton sponges and systems possessing characteristics of proton sponges.

Scheme 2 Examples of the specific types of hydrogen bonds.

Let us present the first group of these specific interactions. These are hydrogen bonds with the carbon centre as the proton donor or/and as the proton acceptor. The C–H⋯B systems^4,30 were mentioned above; the A–H⋯C interactions^49,50 seem to be less frequently analysed. Finally, the C–H⋯C interactions^49–51 seem to be exotic in comparison with the other types of the hydrogen bond. There are also A–H⋯H–B dihydrogen bonds, DHBs, in this group, where two H-centres characterised by the opposite charges are in a contact.⁵² Special attention should be directed toward the C–H⋯H–C interactions. In such systems, the H⋯H contacts between the hydrogen centres of clearly opposite charges do not frequently occur.

In the second group, the C–H proton-donating bond occurs, and π-electrons³⁴ or σ-electrons⁵³ are the proton acceptors. For such systems with multi-centre proton acceptors, the interactions are rather weak. Additionally, in the case of the C–H proton-donating bonds, they should be very weak. However, there are several cases of medium and strong interactions of these types. For example, for the complex of acetylene with the cyclopentadienyl anion, where the C–H⋯C hydrogen bond occurs, the SAPT/6-311++G(d,p) interaction energy is equal to −9.9 kcal mol⁻¹.⁵⁴

The systems of the third group of interactions presented in Scheme 2 are similar to proton sponges since the proton is inserted here between electron donating moieties. These are (X₁HX₂)⁻ ions (X₁ and X₂ mark halogens).⁵⁵ The (FHF)⁻ system, where the strongest hydrogen bond occurs, is most often analysed.^38,56 The similar (Ng₁HNg₂)⁺ systems (Ng₁ and Ng₂ mark noble gas atoms) also may be classified as hydrogen bonded moieties.⁵⁶ This will be discussed later in this article.

Two-site hydrogen bond definition

The systems with the multi-centre proton donors are presented in Scheme 1 as those which are not classified as the hydrogen bonded species by the majority of known definitions of this interaction. To be more precise – such systems are not taken into account by these definitions. For example, it is stated in the IUPAC definition that the hydrogen atom comes “from a molecule or a molecular fragment”, and it is linked with the single- or multi-centre site of the electron donor.^14,15 Furthermore, what is the situation for the proton between two acetylene molecules where the π⋯H⁺⋯π interaction occurs,^46,47 or for the proton between two fluoride anions in the (FHF)⁻ species?³⁸ How should interactions in the proton sponges be classified?^36,37

It seems that the situation would be clear if the definition is limited to the interaction between the Lewis acid and the Lewis base sites, i.e., between two sites. This is a case of various definitions of the donor–acceptor interactions, particularly for the σ-hole bonds. It is worth mentioning that the σ-hole is characterized by the electron charge depletion. The latter leads to an increase of the electrostatic potential, EP, at the centre considered, say Z, in the direction of the bond to this centre, up to the positive EP values. Such σ-holes possessing positive EP may interact with the electron-rich sites, despite the fact that the centres containing σ-holes are often characterized by the high electronegativity. The corresponding interactions are called σ-hole bonds. The concept of the σ-hole and the definition of the σ-hole bond were proposed by Politzer, Murray and Clark,^57–59 and it states the following: “A σ-hole bond is a noncovalent interaction between a covalently-bonded atom of Groups IV–VII and a negative site, e.g., a lone pair of a Lewis base or an anion.”⁵⁹ This definition, clearly referring to two sites, is accompanied by the explanation concerning the nature of the Lewis acid site. “It involves a region of positive electrostatic potential, labeled a σ-hole, on the extension of one of the covalent bonds to the atom.”⁵⁹ It is interesting that Politzer and co-workers justified that the hydrogen bond is classified as the σ-hole bond.

Taking into account the advantage of the two sites definition of the σ-bond, the following definition was proposed recently for the hydrogen bond.²² The hydrogen bond is a local stabilizing interaction between the proton or the electron charge-deficient region of hydrogen and the electron-rich region attributed to one or more centres. The advantages of the use of this definition, that was labelled as 2sHB (two-sites hydrogen bond), are presented below. This definition indicates that the hydrogen bond is a local and stabilizing interaction. For example, for the water dimer presented in Fig. 1, the H⋯O contact stabilizes this dimer. However, not only are there other atom–atom intermolecular interactions, but they are not as significant (sometimes even negligible) as the H⋯O hydrogen bond.

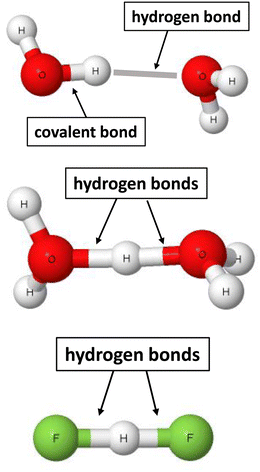Fig. 1 Examples of moieties where hydrogen bonds occur. From the top to the bottom: water dimer, H₅O₂⁺ cation, and the (FHF)⁻ anion.

The 2sHB definition may be applied for intramolecular hydrogen bonds. The latter interactions are often local stabilizing interactions for conformers that correspond to the local energetic minima. The difference between the energy of the conformer with the intramolecular hydrogen bond and the energy of the conformer, where such interaction does not occur, is often treated as the hydrogen bond energy. However, such estimation is rather rough, and other measures of the strength of the intramolecular hydrogen bond are often applied.^60–62

The 2sHB definition indicates that the hydrogen bond occurs between two sites. That is a case for the water dimer, where hydrogen and oxygen atoms are in a contact. There are other pairs of connected hydrogen and oxygen atoms. However, these are covalent bonds, together with the O–H proton-donating bond or the intermolecular H⋯O contacts characterised by long distances, i.e., corresponding to very weak interactions. It is difficult sometimes to classify any interaction as the hydrogen bond or the covalent bond since there is no “sharp” border between them. Hence, for the H₅O₂⁺ cation⁵⁴ and the (FHF)⁻ anion,³⁸ pairs of hydrogen bonds may be indicated, H⋯O and H⋯F, respectively. For the latter anion, the proton is inserted exactly in the mid-point of the distance between fluorine centres. For the H₅O₂⁺ cation, the proton is in the mid-point of the O⋯O distance or nearly so – it depends on the level of calculations performed. Fig. 1 indicates that pairs of H-bonds occur for the H₅O₂⁺ and (FHF)⁻ systems. In the other case, but less probable, these pairs may be classified as covalent bonds. The latter situation seems to be less probable since it would be connected with the divalent character of the hydrogen centre.^17,63

The 2sHB definition states that the electron donor B also may be attributed to multi-centre systems. Fig. 2 presents such a situation for the T-shaped dimer of acetylene⁶⁴ and for the C₄H₅⁺ cation.^46,47

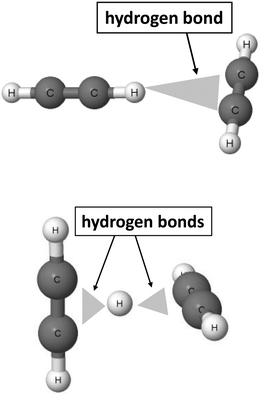Fig. 2 Examples of moieties where hydrogen bonds with multi-centre proton acceptors occur. From the top to the bottom: T-shaped acetylene dimer and C₄H₅⁺ cation.

In the acetylene dimer, the C–H proton-donating bond of one of the molecules is in a contact with the π-electrons of the second molecule. This is exactly the C–H⋯π (H⋯π) hydrogen bond between two sites, the H-centre and the π-electrons of the C≡C bond. The C₄H₅⁺ cation may be treated as a system where the proton is inserted between two acetylene molecules. Thus, two H⋯π contacts (see Fig. 2) may be classified here as the hydrogen bonds. This system is analysed in detail further in this article. Similarly, other examples of hydrogen bonds in terms of the 2sHB definition are presented in the next sections of this article.

It is worth mentioning that the 2sHB definition excludes the hydride bond and charge-inverted bond as the HB interactions. This is because the definition clearly states the electrophile character of the H-centre. These two types of interactions are roughly presented in the next section.

Hydride bond and charge-inverted hydrogen bond

The hydride bond and the charge-inverted hydrogen bond are not classified as hydrogen bonds by the IUPAC and 2sHB definitions (Scheme 1). However, they are discussed in this article since there are definitions that do classify them as hydrogen bonds. Besides, it seems to be interesting and important to systematically arrange and summarize the information concerning these interactions.

The early definition of the hydrogen bond that was introduced by Pimentel and McClellan¹⁶ is one of these definitions that take into account the A–H bond and the B unit that are connected through the H⋯B link, i.e., the A–H⋯B bridge. However, this definition does not specify if the H-atom in this bridge is the Lewis acid or the Lewis base centre. Similarly, the electron donating or accepting properties of the A and B centres also are not specified. This definition states that “A H bond exists between a functional group A–H and an atom or a group of atoms B in the same or a different molecule when

(a) there is evidence of bond formation (association or chelation),

(b) there is evidence that this new bond linking A–H and B specifically involves the hydrogen atom already bonded to A.”¹⁶

One can see that this definition covers those interactions that are covered by other definitions, among them by the IUPAC one. In their definition, Pimentel and McClellan take into account the C–H⋯O or C–H⋯N links and even the A–H⋯π interactions, where aromatic π-electron systems play the role of Lewis bases.¹⁶

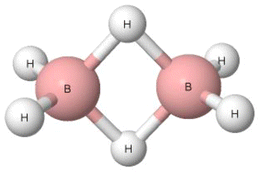
Pimentel and McClellan have classified the B–H–B bridges in diborane (Fig. 3) and in other boranes as hydrogen bonds since they have noted that “to summarize, most of the evidence available is in favor of calling the borane bridge a H bond interaction.”¹⁶ The H-centre in this B–H–B bridge is characterised by the greater electronegativity value than the boron centre, 2.20 and 2.04, respectively, according to the Pauling electronegativity scale.¹⁷ This may suggest that the B–H–B arrangement is not classified as the hydrogen bond. Additionally, the bridge angle is far from linearity. It is lower than 90°, which may also indicate that the B–H–B arrangement is not a hydrogen bond. Diborane and tetramethyldiborane were analysed later. It has been noted that in these two molecules, the boron centres are characterized by tetrahedral arrangements.⁶⁵ In each of these two species, two B–H–B bridges occur. For each bridge, the electron pair is shared between the H atom and two boron centres, forming the three-centre bond, i.e., 3c–2e system. This is different than for the typical hydrogen bonds with the positively charged H-centre that are classified as the 3c–4e systems, at least in terms of the HB definition of Weinhold and Klein.³⁹ However, it was pointed out in several studies that the terminal hydrogen atoms of diborane are negatively charged, while the hydrogen atoms of B–H–B bridges are slightly positively charged, possessing even Lewis acid properties since they form typical hydrogen bonds with the Lewis base centres, including π-electrons of aromatic systems.^66–69 One can see that there are properties of the B–H–B bridges that provide evidence for and against their classification as hydrogen bonds. However, according to the definition of Pimentel and McClellan,¹⁶ these arrangements are classified as hydrogen bonds, similarly as the systems with the negatively charged central hydrogen atom.

Fig. 3 The structure of diborane with two B–H–B links.

The latter systems have been analysed from time to time in early and recent studies. One example is the study on the linear LiH dimer that was analysed theoretically at the HF level in an early study by Jordan.⁷⁰ This dimer was a subject of later investigations, including the study by McDowell where apart from the HF calculations, the MP2 and QCISD methods were applied.⁷¹ However, the wide and systematic theoretical studies with the use of the MP2/6-311++G(d,p) level results on systems with a negatively charged H-centre were performed by Rozas and co-workers.⁷² The A–H⋯Li systems were analysed (A = Li, Be, B), where Li linked with –H, –CH₃ and –F substituents plays the role of the Lewis acid centre, while the A–H bond belongs to the Li–H, H–Be–H, H–Be–F and H–B⁽⁻⁾H₃ species playing a role of the Lewis base units. A few systems with the Be Lewis acid centre were also considered in this study.⁷² These interactions were named as inverse hydrogen bonds. However, the term hydride bond is used here, which was proposed in another study on the systems containing a negatively charged hydrogen.⁴² It is worth mentioning that the interactions analysed by Rozas and co-workers are often strong ones. For example, for the linear arrangements of Li–H⋯Li–H and H–B⁽⁻⁾H₃⋯Li–H systems, the MP2/6-311++G(d,p) interaction energies (ZPE and BSSE corrections included) are equal to −23.1 kcal mol⁻¹ and −45.6 kcal mol⁻¹, respectively.⁷² For the former complex, all atoms are located at the same line. Meanwhile, for the latter complex, the H, B, Li and H atoms are located in the same line, and the three H-atoms bonded to the boron centre and located outside this line form the H⋯Li intermolecular links. For non-linear, fully optimized systems, the interactions are stronger than for linear arrangements.⁷² Additionally, in each non-linear system, two stabilizing contacts, i.e., H⋯Li/Be and F⋯Li/Be, occur. For the complexes analysed in this study,⁷² the Quantum Theory of Atoms in Molecules, QTAIM,⁷³ charges of the hydride hydrogen centres between −0.90 a.u. and −0.74 a.u. are observed. The latter “least negative” value occurs for three H-atoms of the H–B⁽⁻⁾H₃⋯Li–H system, mentioned above here, being in a contact with the Li centre.

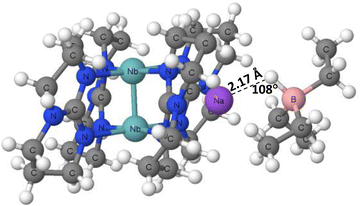
The X-ray crystal structures of tetrakis(μ₂-1,3,4,6,7,8-hexahydropyrimido(1,2-a)pyrimidinato)-diniobium sodium triethylborate (PAWFAU refcode) and tetrakis(μ₂-1,3,4,6,7,8-hexahydropyrimido(1,2-a)pyrimidinato)-diniobium bis(sodium triethylborate) (PAWDUM refcode)⁷⁴ are among the first experimental solid state evidences of the occurrence of hydride bonds. The authors indicated that in these structures, the novel B–H⋯Na⁺ interactions between sodium cations and BEt₃H⁻ anions occur. Thus, these interactions may be classified as the hydride bonds between the H-centres bonded to boron atoms and the sodium cations, H^−δ⋯Na⁺. Fig. 4 shows the fragment of the PAWDUM crystal structure, where such interaction is designated. The distance between the Na⁺ ion and the H-atom bonded to the boron centre is equal to 2.47 Å, and the Na–H–B angle is 107.8°, which is far from linearity.

Fig. 4 The fragment of the PAWDUM crystal structure.

Calculations on similar systems to that one discussed above, where the simple monoatomic cation acts as the Lewis acid, have been performed. The complexes of BeH₂ with the Li⁺, Na⁺ and Mg²⁺ cations were analysed.⁴² The Be-centre is positively charged, while the negatively charged hydridic H-atoms that are attached may act as the Lewis base centres. It was found that the corresponding H^−δ⋯Li⁺, H^−δ⋯Na⁺, and H^−δ⋯Mg²⁺ hydride bonds for these linear complexes are strong interactions since the binding energies are equal to −18.3 kcal mol⁻¹, −11.7 kcal mol⁻¹ and −59.7 kcal mol⁻¹, respectively, for the MP2/aug-cc-pVQZ calculations (BSSE correction included). The formation of these complexes is connected with the electron charge shifts from the BeH₂ species to the Li⁺, Na⁺, and Mg²⁺, cations, 41 mē, 31 mē and 163 mē (mē – millielectron, i.e., 10⁻³ ē), respectively. These are considered to be large shifts (especially for the magnesium cation complex). For example, for the trans-linear conformation of the water dimer linked by the O–H⋯O hydrogen bond, such a shift from the Lewis base to the Lewis acid unit is equal to 13 mē (MP2/6-31+G(d,p) result).⁷⁵ The interaction energy for this water dimer and at the same level of approximation is equal to −4.5 kcal mol⁻¹,⁷⁵ indicating that it is medium in strength as a hydrogen bond.

It is interesting that the cation – beryllium species interactions in complexes discussed here do not possess the characteristics of covalency, at least from the QTAIM approach⁷³ point of view. The Laplacian of the electron density at the bond critical point (BCP), ∇²ρ_BCP, of the cation–hydridic hydrogen bond paths is positive. This indicates that these are not covalent bonds. Besides, the total electron energy density at the BCP, H_BCP, for H^−δ⋯Li⁺ and H^−δ⋯Na⁺ bond paths is also positive. Only for the H^−δ⋯Mg²⁺ bond path, the H_BCP value is negative, showing that the latter interaction may be considered as partly covalent in nature. The decomposition of the energy of interaction for these three systems was also performed,⁴² and it was found that two terms of energy are meaningful: the electrostatic term and delocalization term. The latter term is related to the electron charge shifts resulting from complexation. This term is also related to the covalent character of interaction.^19,63 The results of decomposition show that for the Li⁺⋯HBeH complex, the electrostatic and delocalization terms are almost equal to one another. For the Na⁺⋯HBeH complex, the electrostatic interaction energy is the most important attractive term. For the Mg²⁺⋯HBeH complex, the absolute value of the delocalization term is almost two time greater than the absolute value of the electrostatic term. These results for the three complexes of BeH₂ show that the hydride bonds are rather electrostatic interactions in nature. Only for extremely strong interactions, such as in the Mg²⁺⋯HBeH complex, the partially covalent character is manifested.

The latter results are in line with those which concern halogen–hydride bonds⁷⁶ that are links between the halogen and hydride centres. They may be named as the halogen bonds, if the halogen Lewis acid centre is taken into account, or the hydride bonds, if one considers the negatively charged hydrogen Lewis base centre. The complexes of F₃CCl and F₃SiCl with LiH, BeH₂ and HBeF were analysed theoretically at a few different levels of approximation up to MP2/6-311++G(3df,3pd) and MP2/aug-cc-pVTZ.⁷⁶ In these complexes, the chlorine centre acts as the Lewis acid site through the σ-hole located in the extension of the C–Cl or Si–Cl bond and the hydridic, negatively charged hydrogen is the Lewis base centre. Let us roughly present the MP2/aug-cc-pVTZ results. The complexes of F₃CCl are more strongly linked with the Lewis base units than the corresponding complexes of F₃SiCl. The complexes of LiH are stronger than those of BeH₂ and HBeF. The strongest interaction is observed for the F₃CCl⋯HLi complex since the binding energy is −3.5 kcal mol⁻¹. For the remaining complexes, the absolute value of this energy does not exceed 2.2 kcal mol⁻¹. Thus, these complexes are linked by weak interactions. The QTAIM analysis shows the positive ∇²ρ_BCP and H_BCP values for halogen–hydride bonds in all of the above mentioned complexes. It means that these interactions do not possess the covalent character. The results of the decomposition of the energy of interaction for all systems analysed show that the electrostatic term is the most important attractive one.

The complexes of tetrafluoroethylene and teracyanoethylene with the LiH, NaH, BeH₂ and MgH₂ species were analysed up to the MP2/aug-cc-pVTZ level.⁷⁷ The hydrides act here as the Lewis base units by H-centres, while the inclusion of fluoro- and cyano- substituents into ethylene species makes the double CC bond region electron-poor. This results in the positive electrostatic potential at this bond and consequently the Lewis acid properties. The results show that the species containing the hydridic hydrogen is situated towards the CC bond of the therafluoro- and tetracyanoethylene forming distorted T-shaped conformations.⁷⁷ However, the absolute value of interaction energy for these complexes exceeds 3 kcal mol⁻¹ in a few cases only. Usually, these interactions are weaker.

There are other studies on hydride bonds, also experimental ones. For example, the Si–H⋯Se interaction in 1-mesitylselanyl-8-(dimethylsilyl)naphthalene was analysed⁷⁸ since the X-ray crystal structure was determined. In this study, the X-ray results are accompanied by results of various theoretical approaches. The Si–H⋯Se interaction was classified in this study as the “mixed” chalcogen–hydride bond. Similarly, the “mixed” halogen–hydride bond was discussed in the above-mentioned study.⁷⁶ In the case of the Si–H⋯Se interaction, the negatively charged H-atom is the Lewis base centre, while the selenium centre approximately acts as the Lewis acid through the σ-hole located in the elongation of the C–Se bond.

The Me₃Si–H⋯Y complexes (Y = ICF₃, BrCN, and HCN) have been recently analysed experimentally, which was supported by the theoretical calculations.⁷⁹ Additionally, other systems containing hydridic hydrogen were theoretically analysed.⁷⁹ The authors claimed that such interactions with the hydridic H-centre should have a new name as the name ‘charge-inverted hydrogen bond’ or CIHB, proposed by Jabłoński^43–45 “does not capture the nature of interaction.” However, CIHBs cover the specific class of systems, according to the definition given by Jabłoński, wherein interactions containing the hydridic hydrogen are included but not all. This is roughly described further in this section. In addition, the name hydride bond proposed almost twenty years ago⁴² captures all interactions containing hydridic hydrogen. The names halogen–hydride bonds⁷⁶ and chalcogen–hydride bonds⁷⁸ were also applied for interactions where halogen and chalcogen centres, respectively, act as the electron acceptors.

The charge-inverted hydrogen bond term was proposed in 2009 to account for the interaction between the hydrogen centre possessing the partial negative charge and the centre characterised by the electron vacancy (the electron gap).^43–45 Such interactions are marked as A–H⋯⊃B or A–H^−δ⋯⊃^+δB to indicate the Lewis base and Lewis acid properties of the H and B centres, respectively (X and Y designations were applied in ref. 43 instead of A and B applied here, respectively). The CIHB complexes were analysed⁴³ at the B3LYP/aug-cc-pVTZ and MP2/aug-cc-pVTZ levels, where the Li–H, H–Be–H. Cu–H, H₃Si–H and H₃Ge–H species act as H donors, i.e., as the Lewis base units, while BH₃, AlH₃ and GaH₃ are the Lewis acid units because of the electron vacancy at the B, Al and Ga centres. The great interaction energies were found for the majority of systems analysed. For example, for LiH complexes, the absolute energies of interaction calculated by the MP2 method were over 50 kcal mol⁻¹.

In another study, the CIHB interaction was compared with other interactions, where the hydrogen centre possesses a negative charge.⁴⁴ It was stated that CIHBs are characterized by unique properties since the great values of the deformation energies are observed for both interacting units. Conversely, in the case of other interactions with the hydridic hydrogen centre, one of the interacting units at most is deformed significantly due to the interaction. In the case of CIHBs, the electrostatic and delocalization interaction energy terms are the most important attractive contributions, while the dispersion term is not so significant. Besides, in a case of strong CIHBs, the covalent character of interaction is revealed. For example, the QTAIM parameters indicate that the total electron energy density, H_BCP, is negative. The properties of CIHBs and their various kinds are described and summarized in another review study.⁴⁵

In summary, one can see that the term hydride bond concerns interactions where the negatively charged hydrogen centre is in a contact with the electron acceptor. This system may be designated as A–H^−δ⋯B, where B is the above-mentioned electron acceptor, while the A-centre forms a covalent bond with the hydrogen. The B centre may belong to the neutral species, to an ion (a cation, although the greater anions possessing electron-accepting sites are also possible). Examples of hydride bonds, where the B centre is a monoatomic cation (Li⁺, Na⁺ or Mg²⁺), were discussed in this section. The CIHB interaction concerns the sub-class of hydride bonds, where the B electron accepting centre is characterised by the electron vacancy (the electron gap). For example, the trivalent boron or aluminium centres possess six electrons in the outer shell. Thus, regarding the electron structure, these centres are characterised by the vacant p-orbital.

Hydrogen bonds with multi-centre proton donors

Hydrogen bonds characterized by multi-centre proton acceptors were reported in early studies. One example is the monograph of Pimentel and McClellan, where the π-electron systems, particularly aromatic ones, were considered.¹⁶ Herein, it was mentioned before that the latter interactions with the multi-centre proton acceptors are classified as hydrogen bonds by the majority of contemporary definitions. Scheme 1 includes two types of such interactions, i.e., A–H^+δ⋯π and A–H^+δ⋯σ.

However, the mirror-like interactions (where there are multi-centre proton donors) are not covered by these definitions, among them by the IUPAC definition.^14,15 These interactions are classified as hydrogen bonds by the 2sHB definition. Such interactions, i.e., π⋯H^+δ⋯B (see Scheme 1) were theoretically analysed.⁴⁸ These are systems where the proton is inserted between the acetylene molecule and the F₂O or FHO species. In the latter Lewis base units, one or two H-atoms in the water molecule are replaced by fluorine atoms to make the oxygen centre less electronegative. Consequently, in C₂H₃⁺⋯ F₂O and C₂H₃⁺⋯ FHO complexes, the proton is closer to the acetylene unit than to the oxygen centre due to the electron-withdrawing properties of the fluorine substituents. The binding energies for these complexes calculated at the MP2/6-311++G(3df,3pd) level (BSSE correction included) are equal to −3.9 kcal mol⁻¹ and −13.3 kcal mol⁻¹, respectively. The oxygen centre, the proton and the mid-point of the C≡C bond of acetylene are approximately situated at the same line. In the case of the C₂H₃⁺ unit, the proton is situated in the T-shaped position to the acetylene. It is worth mentioning that the H-centre is not exactly the proton possessing the unit charge, +1 a.u., since electron charge shifts occur for these complexes from the F₂O and FHO Lewis base units to the C₂H₃⁺ cation, 150 and 233 millielectrons, respectively. The H⁺⋯π local interactions in these complexes possess characteristics of covalent bonds; for example, the Laplacian of the electron density at the corresponding bond critical point, BCP, is negative. In the case of the H⁺⋯O local interactions, the total electron energy density, H_BCP, is negative. This indicates the partially covalent interactions in nature since the Laplacian is positive for the BCPs of these contacts.

These results confirm that the proton forms C₂H₃⁺ units with acetylene rather, but it is not connected covalently with the F₂O or FHO species. The results presented above show that these C₂H₃⁺⋯FHO and C₂H₃⁺⋯F₂O complexes are linked by interactions that possess the characteristics of hydrogen bonds. To the knowledge of the author of this article, there are no experimental studies on complexes linked by the π⋯H^+δ⋯B hydrogen bonds. In the case of σ⋯H^+δ⋯B interactions (Scheme 1), it is probable that neither experimental nor theoretical analyses were performed.

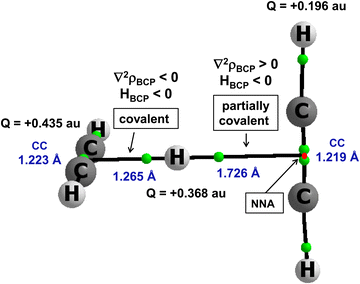
There are other interactions, those with the multi-centre proton donors and with the multi-centre proton acceptors, that are not classified by the majority of definitions as hydrogen bonds. However, they are classified by the 2sHB definition. A notable example is the proton inserted between two π-electron systems, e.g., between two acetylene molecules. This is the C₂H₂⋯H⁺⋯C₂H₂ complex. It was analysed theoretically in an early study,⁴⁶ and its existence was later confirmed experimentally since the protonated acetylene cation C₂H₃⁺ and the proton-bound acetylene dimer cation C₂H₂⋯H⁺⋯C₂H₂ were produced by a pulsed supersonic nozzle/pulsed electrical discharge cluster source.⁴⁷ This complex was also analysed in detail in other more recent theoretical studies.^80–82Fig. 5 presents this complex. It was optimized at the MP2/aug-cc-pVTZ level,⁸⁰ and led to the energetic minimum. Selected geometrical and QTAIM parameters are presented in Fig. 5. Two acetylene molecules are perpendicular one to each other. The proton is inserted between them, closer to one of the acetylene molecules, forming the C₂H₃⁺ unit. However, this is not a “pure” proton since the electron charge shifts occur for this complex. The Natural Bond Orbital, NBO,^25,83 charges are shown in Fig. 5. The H-centre is characterized by a charge of +0.368 a.u., and the whole C₂H₃⁺ unit possesses a charge of about +0.8 a.u., while acetylene molecule that is further from the proton possesses a charge equal to about +0.2 a.u.

Fig. 5 The molecular graph of the C₂H₂⋯H⁺⋯C₂H₂ complex; attractors are designated by big circles, while small green circles correspond to bond critical points, small red points correspond to non-nuclear attractors, and bond paths are designated by continuous black lines.

There are bond paths with the corresponding bond critical points, BCPs, linking the H-centre (the proton) with non-nuclear attractors, NNAs of acetylenes. The BCP of the shorter link indicates the covalent multi-centre bond since the electron density at BCP, ρ_BCP is equal to 0.165 a.u., and the Laplacian of the electron density, ∇²ρ_BCP, and consequently the total electron energy density, H_BCP, are negative. The H⋯CC (mid-point of C≡C bond) distance is equal to 1.265 Å. The H⋯CC distance between the H-centre and the more distant acetylene molecule is equal to 1.726 Å. The characteristics of the corresponding BCP indicate the partially covalent character of this interaction since ρ_BCP is equal to 0.032 a.u., the ∇²ρ_BCP is positive and H_BCP is negative. For this C₂H₂⋯H⁺⋯C₂H₂ complex, the MP2/aug-cc-pVTZ energy of interaction is −20.2 kcal mol^−1 80 if this complex is treated as being composed of two units: C₂H₃⁺ and C₂H₂. In spite of the asymmetric position of the proton in this complex, the potential barrier height for the proton transfer is very low, about 0.04 kcal mol⁻¹. Thus, the proton moves freely between C₂H₂ molecules.

Various other systems containing multi-centre proton donors and proton acceptors were analysed.^{46,80–82,84,85} One notable example is the systems similar to the C₂H₂⋯H⁺⋯C₂H₂ complex discussed above, where a part or all H-atoms of acetylenes are substituted by F or Li atoms.^81,82 The C₂H₄⋯H⁺⋯C₂H₂ (C₂H₅⁺⋯C₂H₂) system was also analysed theoretically as an example of the complex linked by the π⋯H⁺⋯π type of the hydrogen bond.⁴⁶ This interaction possesses similar properties as those that were observed for the C₂H₂⋯H⁺⋯C₂H₂ complex. The proton is closer to the ethylene species than to the acetylene unit. This may be explained by the proton affinity. In the gas phase, the proton affinity of acetylene is 153.3 kcal mol⁻¹ and that of ethylene is 162.6 kcal mol⁻¹.⁸⁶ In such a way, there is the C₂H₅⁺ unit, where the multi-centre covalent bond occurs and there is a weaker interaction of the proton with the acetylene unit.

The C₂H₂⋯H⁺⋯H₂ and H₂⋯H⁺⋯H₂ complexes are examples of systems linked by the π⋯H⁺⋯σ and σ⋯H⁺⋯σ hydrogen bonds, respectively (see Scheme 1), that were analysed theoretically.^84,85 The proton (H-centre) is closer to the acetylene species and to one of the molecular hydrogens for the former complex, and for the latter one, respectively. These complexes are presented in Fig. 6 (results of the MP2/aug-cc-pVQZ calculations). In the C₂H₂⋯H⁺⋯H₂ complex, the distance between the mid-point of the C≡C bond and the proton is equal to 1.130 Å, while the distance between the mid-point of the H₂ molecule and the proton is equal to 1.900 Å. It clearly shows that this complex may be considered as the link between the C₂H₃⁺ proton donor and the molecular hydrogen acting as the proton acceptor. The H⁺⋯σ interaction may be considered as the hydrogen bond according to the 2sHB definition. Similarly, for the H₂⋯H⁺⋯H₂ (H₃⁺⋯H₂) complex, the proton is closer to one of the H₂ molecules. Hence, one of the proton links is the multi-centre covalent bond, while the other one is the hydrogen bond interaction.

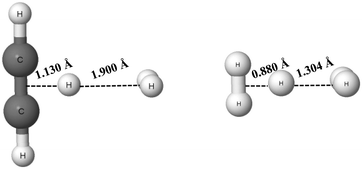Fig. 6 The C₂H₂⋯H⁺⋯H₂ (left) and H₂⋯H⁺⋯H₂ (right) complexes; the distances between the proton and mid-points of neighbouring molecules for both complexes are given.

It is interesting to consider the strength of the hydrogen bonds of the systems presented in Fig. 6. The binding energies calculated at the MP2/aug-cc-pVQZ level for the C₂H₂⋯H⁺⋯H₂ and H₂⋯H⁺⋯H₂ complexes are equal to −8.3 kcal mol⁻¹ and −3.0 kcal mol⁻¹, respectively (BSSE corrections were included here). For the latter complex, the calculation at the MP2/aug-cc-pV5Z level was also performed, but the energetic and geometric results are the same as for the MP2/aug-cc-pVQZ level. These binding energies contain the energies related to geometry deformations resulting from the formation of the complexes. It means that the binding energy is defined as the difference between the energy of the complex and the sum of energies of monomers that were optimized separately (the energetic minima of the isolated monomers are taken into account here). The C₂H₃⁺ and H₂ monomers are considered for the C₂H₂⋯H⁺⋯H₂ complex and the H₃⁺ and H₂ monomers for the H₂⋯H⁺⋯H₂ system.

The decomposition of the energy of interaction^87–89 was performed for these two complexes discussed above, resulting in the following interesting findings. For the C₂H₂⋯H⁺⋯H₂ complex, the repulsive exchange interaction energy term outweighs the absolute value of the electrostatic term. This means that the other attractive interactions are responsible for the stabilization of the complex. Mostly, they are connected with effects of the electron charge shifts. The delocalization interaction energy is related to such shifts, and it is the most important attractive term. Its absolute value is about 50% greater than the absolute value of the electrostatic term. The correlation attractive contribution is approximately equivalent to the electrostatic one.

Similarly, in the case of the H₂⋯H⁺⋯H₂ complex, the electrostatic attractive interaction is completely “cancelled” by the repulsive exchange term. This electrostatic attraction is more important than the correlation attraction. However, the absolute value of the delocalization interaction energy is almost five times greater than the absolute value of the electrostatic term. This shows the great importance of the electron charge shifts to stabilize this complex.

The unique and interesting types of hydrogen bonds discussed in this section were analysed also in terms of the properties of the proton-donating units.⁸⁵ The isolated C₂H₃⁺ and C₂H₅⁺ units, as well as their characteristics, in the complexes were analysed. Let us consider the isolated C₂H₃⁺ unit and its parameters in the C₂H₂⋯H⁺⋯H₂ (C₂H₃⁺⋯H₂) complex. The characteristics discussed below here correspond to the results of the MP2/aug-cc-pVQZ level. The elongation of the π⋯H⁺ distance from 1.117 Å in the C₂H₃⁺ isolated unit to 1.130 Å in the complex that is observed is accompanied by the decrease of the electron density at the corresponding BCP from 0.206 a.u. to 0.202 a.u. (the Laplacian of the electron density at BCP is negative in both cases).

The shift of frequency of the stretching mode related to the C≡C mid-point – proton distance from 2403.8 cm⁻¹ to 2271.4 cm⁻¹ is observed. The increase of the corresponding intensity band from 99.6 km mol⁻¹ to 366.8 km mol⁻¹ occurs. This indicates a red-shift type hydrogen bond. One can see that the π⋯H⁺⋯π, π⋯H⁺⋯σ and σ⋯H⁺⋯σ systems considered here possess characteristics that are typical for hydrogen bonds. This is supported by the energetic, topological, geometrical and spectroscopic results.

Finally, it is worth noting that the systems analysed in this section are also a subject of experimental studies from time to time. The study on the C₂H₂⋯H⁺⋯C₂H₂ complex was mentioned here.⁴⁷ However, one can refer to other systems, as for example, the C₂H₃^+ 47 and C₂H₅^+ 90 cations produced in a pulsed discharge/supersonic beam source. In the latter species, the proton is in a T-shaped position to the acetylene and ethylene molecules, respectively. Hence, both interactions of the proton may be classified as the H⁺⋯π hydrogen bonds, according to the 2sHB definition. The H₂⋯H⁺⋯H₂ (H₃⁺⋯H₂) complex was also produced in a pulsed discharge supersonic nozzle ion source, and the mass-selected photodissociation spectroscopy in the 2000–4500 cm⁻¹ region was applied.⁹¹ The experimental results were supported by theoretical analyses for this complex.

Proton between two electron-donating centres

The IUPAC definition of the hydrogen bond^14,15 was cited earlier here. Briefly speaking, it states that the hydrogen atom that comes from a molecule or a molecular fragment interacts with the centre or with the group of atoms. Numerous other definitions state clearly that the hydrogen atom is covalently bonded, i.e., it is involved in a strong interaction, and it is also involved in a weaker interaction with other centre or centres. Thus, there are problems with systems where the proton is inserted between two electronegative centres or between two electron donating sites. It is difficult to classify them as hydrogen bonds using the above-mentioned definitions. However, they are classified as hydrogen bonds according to the 2sHB definition.²²

The systems discussed in the last section are examples of arrangements that are hydrogen bonds, according to the 2sHB definition, but they are not according to other definitions. In some of these systems, the proton is inserted between two multi-centre sites, i.e., in the π⋯H⁺⋯π, π⋯H⁺⋯σ and σ⋯H⁺⋯σ systems. For some of these systems, the proton is closer to one of the multi-centre sites, and they may be considered as arrangements where the proton interacts stronger with such a close site and weaker with this one that is more distant. However, the above arrangements are characterized by the multi-centre proton donor. Thus, they are classified as hydrogen bonds by the 2sHB definition, but not by other definitions.

A similar problem is connected with systems where the proton is located between two single-centre sites, like in the case of proton sponges,^36,37 for example. However, it seems that the majority of systems classified as proton sponges are asymmetric. Thus, the proton is located closer to one of the nucleophilic sites. Consequently, such systems are defined as hydrogen bonds by the IUPAC and other definitions. The symmetric proton sponges are not so common and their existence was analysed in early⁹² and recent studies.^93,94

Fig. 7 presents the 1-(deutero-dimethylammonio)-8-(dimethylamino)-2,7-dimethoxynaphthalene bromide species that is a fragment of the crystal structure.⁹³ This is the high precision X-ray diffraction measurement (R-factor equal to 2.7% and e.s.d's for CC bonds between 0.001 Å and 0.005 Å) performed at 100 K for the deuterated species. However, the deuteriation concerns only the centre inserted between the nitrogen sites. This means that, instead of the proton, the deuteron is inserted. The N⋯N distance is equal to 2.567 Å with the mid-point proton position. Also, the mid-point location of the deuteron is observed for the deuterated species.⁹³ A similar situation of the mid-point proton position was observed for the protonated 1,6-diazabicyclo[4.4.4]tetradecane, for which the N⋯N distance is equal to 2.526(3) Å.^95,96 In the majority of proton sponges, the application of the 2sHB definition concerns the weaker interaction between the proton and the electron donating site. The stronger interaction usually possesses characteristics of a covalent bond. In the case of the symmetrical proton location, or nearly so, two proton–nucleophile site interactions may be treated as hydrogen bonds according to the 2sHB definition.

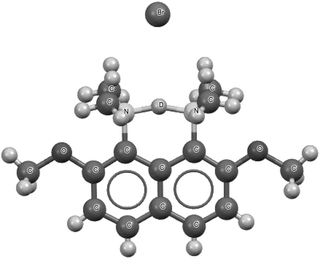Fig. 7 The deuterated 1-(deutero-dimethylammonio)-8-(dimethylamino)-2,7-dimethoxynaphthalene bromide, which is a fragment of the crystal structure.⁹³ The deuteron, D⁺, is located in the centre of the N⋯D⋯N bridge.

There are other systems with the proton located between two nucleophilic sites, the H₅O₂⁺ cation mentioned earlier here is an example (see Fig. 1). There are numerous studies on the latter cation. One example is a study considering its energetic and geometrical parameters in the gas, liquid and solid phases,⁹⁷ as well as high level theoretical extended study.⁹⁸ In general, for this cation, the proton (or rather, the hydrogen atom since it possesses a charge significantly lower than +1 a.u. due to the large electron charge transfers) is located in the mid-point of the O⋯O distance, or nearly so. This cation is often classified as a system linked by the short-strong hydrogen bond, SSHB.⁹⁹ It was assumed that the O–H⋯O SSHBs are characterised by the O⋯O distance ranging from 2.45 Å to 2.65 Å.¹⁰⁰ The absolute value of the interaction energy is greater than 5 kcal mol⁻¹.¹⁰⁰ However, the latter interaction strength concerns the experimental values of hydrogen bridges in liquids. Such absolute values are greater in the gas phase. The value of 12 kcal mol⁻¹ was indicated,¹⁰¹ for example. O⋯O distances lower than 2.45 Å, sometimes close to 2.4 Å, are also observed in crystal structures.⁶³ In the case of the H₅O₂⁺ cation, the O⋯O distance is equal to 2.40–2.41 Å,⁹⁹ and the strong interaction is observed both theoretically and experimentally. For example, the early study shows that the gas-phase bond dissociation enthalpy of this cation into H₃O⁺ and H₂O is approximately equal to 32 kcal mol⁻¹.¹⁰²

Some of the SSHBs may be classified as the low-barrier hydrogen bonds, LBHBs.^103,104 It was explained that for the O–H⋯O systems, the shortening of the O⋯O distance leads to the dropping of the energy barrier height of the proton transfer up to the zero point energy, ZPE, level that occurs for the O⋯O distance at approximately 2.5 Å, i.e., just for LBHBs.¹⁰⁴ Numerous studies show that the proton for the H₅O₂⁺ cation is located in the mid-point of the O⋯O distance or the double-well potential for the proton occurs with the barrier height below the ZPE level (that leads to the free movement of the proton between two energetic minima).⁹⁹ Hence, the O–H⋯O hydrogen bond in the H₅O₂⁺ cation is classified as SSHB and as LBHB.

There are other studies on protonated dimers where the proton is often involved in interactions with two nucleophilic sites. Thus, it is difficult to consider if these interactions are classified as covalent bonds or as hydrogen bonds. One can mention the mass spectrometry study on the protonated acetone dimer,¹⁰⁵ or the infrared photodissociation study on carbon dioxide clusters.¹⁰⁶ One can also mention the theoretical study on the (N₂)₂H⁺, (H₂CO)₂H⁺ and (CH₃OH)₂H⁺ proton-bound homodimers, where the proton is located between two oxygen/nitrogen centres and where it is moved slightly closer to one of them.¹⁰⁷ The calculations at different levels were performed for the above-mentioned complexes, up to the CCSD(T)/6-311++G(3df,3pd) level. The calculation results show that the potential barrier heights for the proton transfer between the oxygen or nitrogen centres are negligible here, about 0.03 kcal mol⁻¹ or even less. Thus, the proton may move “freely” in the large area between the two nucleophilic oxygen or nitrogen sites. For each of these protonated homodimers for both H⁺⋯O/N contacts, the Laplacian of the electron density at the corresponding bond critical point, BCP, is negative. It means that both interactions of the proton possess characteristics of covalent bonds. For the (N₂)₂H⁺ and (N₂)₂D⁺ systems, the infrared spectra over the range of 700–4000 cm⁻¹ using the method of mass-selected photodissociation spectroscopy with argon tagging was performed.¹⁰⁸ The results show that the systems are linear with the shared proton/deuteron.

Special attention should be paid on the (FHF)⁻ anion mentioned earlier that possesses D_∞h symmetry in the gas phase. This symmetry is disturbed in numerous crystal structures since the H-atom is moved from the mid-point of the F⋯F distance. The linearity of the anion is also disturbed since F–H–F angles lower than 180° are often observed.³⁸ This anion is an interesting species where the problem of the divalent hydrogen atom appears in various studies from time to time, including the early studies of Pauling, who explained that the H-atom possessing one electron cannot form two strong bonds with fluorine centres.¹⁰⁹ However, Pauling stated that the ionic structure is possible. Thus, one may consider the (FHF)⁻ anion as a linkage of the H⁺F⁻ ionic structure with the F⁻ anion. Conversely, Pauling explains in his monograph¹⁷ that this anion is an effect of two covalent bonds of the hydrogen with the fluorine centres.

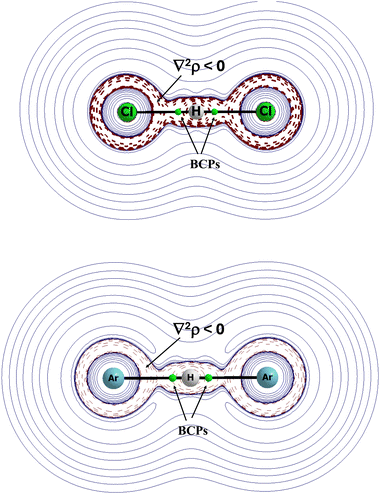
The (XHX)⁻ anions were compared with the (NgHNg)⁺ cations (X and Ng designate halogen and noble gas centres, respectively) since the calculations on these systems were performed up to the CCSD(T)/aug-cc-pVTZ level.⁵⁶ The results indicate similarities between cations and anions. In both cases, the proton is located in the mid-point of the X⋯X and Ng⋯Ng distance. These anions and cations are linear. This is strange, but it seems that the greater electronegativity values of halogens than such values of noble gases does not dramatically influence the differences between the properties of anions and cations. Let us compare the (FHF)⁻ and (NeHNe)⁺ species. The F⋯H and Ne⋯H distances in these ions are equal one to each other at 1.140 Å. The charges of the H-centre for the (FHF)⁻ and (NeHNe)⁺ ions are equal to +0.54 a.u. and +0.66 a.u., respectively. It means that a greater electron charge shifts occur for halogen species than for the noble gas ones. However, these shifts for the (NeHNe)⁺ species are not meaningless. It is worth noting that the electron charge shifts increase with the increase of the atomic numbers of the halogen and noble gas elements. For example, for the (ClHCl)⁻ and (ArHAr)⁺ pair, the H-atom charge is +0.25 a.u. and +0.35 a.u, respectively. It is interesting that for all cations and anions analysed (X = F, Cl, Br, I and Ng = Ne, Ar, Kr, Xe),⁵⁶ the Laplacian of the electron density at the X/Ng⋯H BCP is negative. It means, according to the QTAIM approach,⁷³ that these interactions are covalent in nature. In other words, in these complexes, in anions and in cations, the hydrogen atom may be treated as divalent. One can see that the X⋯H interactions do not differ significantly from the Ng⋯H ones. Both are very strong.

The latter statement is confirmed by the values of the electron density at the BCPs. For the (XHX)⁻ systems, they are located in the range between 0.176 a.u. for the (FHF)⁻ anion and 0.089 a.u. for (IHI)⁻. In the case of noble gas cations, this range is between 0.134 a.u. for the (NeHNe)⁺ cation and 0.097 a.u. for the (XeHXe)⁺ cation.

Fig. 8 presents the maps of the Laplacian of electron density for two complexes, (ClHCl)⁻ and (ArHAr)⁺. In both complexes, the Cl⋯H and Ar⋯H bond paths with the corresponding BCPs lie in areas of the negative values of the Laplacian of electron density. It means that these interactions possess characteristics of covalent bonds, and that they are characterised by the meaningful electron charge shifts.

Fig. 8 The Laplacian of the electron density, ∇²ρ, for the (ClHCl)⁻ anion (top) and for the (ArHAr)⁺ cation (bottom). The areas with the broken lines correspond to the negative values of ∇²ρ, small green circles correspond to bond critical points, and black lines between attractors correspond to bond paths.

There are various experimental studies on (XHX)⁻ and (NgHNg)⁺ ions. The statistical analysis on the (FHF)⁻ anion under the influence of environments of crystal structures was mentioned earlier here.³⁸ There are other studies where the (FHF)⁻ anion and its other halogen analogues, (XHX)⁻ anions, were analysed both experimentally and theoretically.^110,111 The same concerns the (NgHNg)⁺ cations, numerous theoretical and experimental studies on such systems were performed. For example, IR spectra for the (ArHAr)⁺, (KrHKr)⁺ and (XeHXe)⁺ anions were obtained earlier^112,113 or later on the (KrHKr)⁺, (XeHXe)⁺ and (KrHXe)⁺ ions.¹¹⁴ One can mention numerous other theoretical and experimental studies on the (XHX)⁻ and (NgHNg)⁺ ions. It was justified in this section that these ions possess numerous characteristics of hydrogen bond interactions. Thus, they are classified as hydrogen bonds according to the 2sHB definition.

A–H⋯σ hydrogen bonds

The complexes linked by the A–H⋯σ hydrogen bonds are described in this section. It is true that such interactions are classified as hydrogen bonds by the IUPAC, and especially by the 2sHB definition. Thus, they are maybe not so strange systems that deserve to be described in this article. However, the interactions with the σ-electrons as the proton acceptors are often hardly accepted as hydrogen bonds, or they are not known as hydrogen bonds for researchers. Thus, this is the reason they are described here.

Let us firstly consider complexes where the molecular hydrogen acts as the Lewis base through the σ-bond. The A–H⋯H₂ systems were analysed experimentally in early studies. For example, measurements of the dipole moment and vibrational predissociation lifetimes for the F–H⋯H₂ complex in the gas phase were performed. The T-shaped structure of this complex was determined from rotational constants.¹¹⁵ The T-shaped structure of the latter complex and of their isotope analogues, F–H⋯D₂ and F–H⋯DH solvated in helium nanodroplets, was confirmed by the high-resolution infrared spectra.^116–118

The study on the OCH⁺⋯H₂ complex is very interesting since the C–H⋯σ interaction was detected here.⁵³ However, in the description of the results, this interaction was not described and classified as the hydrogen bond.⁵³ Similarly, the complexes of hydrogen fluoride with molecular hydrogen, as well as their isotope analogues, were not classified as hydrogen bond interactions.^115–118

Infrared vibrational predissociation spectra measurements were performed for the above-mentioned OCH⁺⋯H₂ complex.⁵³ It is important that the most extensive vibrational bands come from excitation of the C–H and H₂ stretching vibrations that reveal the rotational structure composed of sub-bands corresponding to the T-shaped minimum energy structure. The QCISD(T)/6-311G(2df,2pd) calculations were also performed for this complex, showing that the latter T-shaped energy minimum conformer is by 4.1 kcal mol⁻¹ lower in energy than the sum of energies of the isolated OCH⁺ and H₂ monomers.⁵³ The experimental spectra of the OCH⁺⋯H₂ complex show the H–H and C–H stretching vibrations of 4060 cm⁻¹ and 2840 cm⁻¹, respectively. These vibrations for the isolated H₂ and OCH⁺ species are equal to 4161 cm⁻¹ and 3089 cm⁻¹, respectively. Thus, the decrease of the C–H stretching frequency corresponding to the elongation of the C–H bond is observed, which is typical for the red-shifted hydrogen bonds. The authors of this study explain that the H–H stretching decrease in the complex compared to the isolated molecular hydrogen is related to the transfer of the electron charge density from the H₂ molecule to the OCH⁺ cation.⁵³ Such a transfer is typical for the hydrogen bonds as a sub-class of the Lewis acid–Lewis base interactions.^19,63

Let us describe the theoretical studies on A–H⋯H₂ systems. For example, the NH₄⁺⋯H₂ complex was analysed theoretically since the MP2/aug-cc-pVTZ calculations were performed for this complex.¹¹⁹ The binding energy for this complex is equal to −2.5 kcal mol⁻¹. This is the T-shaped structure since the molecular hydrogen is perpendicular to the N–H bond of the NH₄⁺ cation. The calculations on NH₄⁺⋯(H₂)_n (n = 1–8) clusters were also performed in this study. It was found that for the NH₄⁺⋯(H₂)₄ cluster, each H₂ molecule is perpendicular to the single N–H bond of the NH₄⁺ cation.¹¹⁹ However, N–H⋯σ arrangements in the latter study were not analysed in terms of the hydrogen bond interaction.

The MP2/aug-cc-pVTZ calculations also have been performed on the AH₄⁺⋯H₂ and AH₄⁺⋯(H₂)₅ (A = N, P, As, Sb, Bi) complexes.³⁵ In these clusters, one hydrogen molecule and four hydrogen molecules, respectively, are perpendicular to the A–H bonds, and it was justified that they are linked with AH₄⁺ ions by A–H⋯σ hydrogen bonds. The decomposition of the energy of interaction for the above-mentioned clusters, where the whole systems are considered as consisting of one molecular hydrogen unit and the remaining part of the system, shows that the energetic terms related to the electron charge shifts are the most important attractive ones, followed by electrostatic and dispersion terms.³⁵ This is probably the first study,³⁵ where the A–H⋯σ interactions that link complexes were classified as hydrogen bonds.

The MP2/6-311++G(3df,3pd) calculations were also performed for the T-shaped F–H⋯H₂ complex⁸⁴ that was previously a subject of experimental studies.^115–118 It was pointed out in this study that the link of this complex possesses characteristics typical for the hydrogen bond interaction.^84,120 The binding energy is equal to −0.8 kcal mol⁻¹. In the case of HF and H₂ units of this complex, the elongation of both σ-bonds by about 0.002 Å is observed as a result of complexation. These elongations are related to the electron charge shift from the H₂ molecule to the HF Lewis acid unit. This shift corresponds to the σ(H₂) → σ*(HF) orbital–orbital overlap. The A–H⋯H₂ interactions were further classified as hydrogen bonds by IUPAC definition,^14,15 and this was pointed out particularly in the description of characteristics of the hydrogen bond.

It is worth mentioning that other σ-bonds are considered as proton acceptors in hydrogen bond interactions. One can mention the A–H⋯C–C interactions of hydrogen fluoride with cyclopropane.^121,122 The latter unit, due to its molecular structure, is characterised by the accumulation of the electron density at the C–C bonds. As a consequence, they possess properties similar to the double CC bonds. Thus, the proton donor, as HF for example, is directed approximately perpendicularly to the CC bond of cyclopropane.

The MP2/aug-cc-pVTZ calculations were performed on complexes of an isomer of diborane, B₂H₄(4), with simple Lewis acid units: HF, HNC, HCl, HCN, HCCH and H₂; the diborane acts as the Lewis base through the B–B single σ-bond in these complexes.¹²³

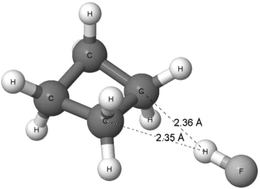
A more extended study on the A–H⋯σ interactions was performed recently¹²⁴ since ωB97XD/aug-cc-pVTZ calculations were performed on complexes of dihydrogen, cyclopropane, cyclobutane and cyclopentane, with such proton-donating units as hydrogen fluoride, hydrogen chloride, water, hydrogen cyanide and acetylene. The complexes’ conformers corresponding to the energetic minima are characterized by the H–F, H–Cl, H–O or H–C bond of the Lewis acid unit directed perpendicularly, or nearly so, to the H–H bond of molecular hydrogen or to the C–C bond of cycloalkane. In other words, at first glance, the structures of these complexes indicate the existence of the A–H⋯σ interactions. Fig. 9 presents the complex of cyclobutane with hydrogen fluoride. The H⋯C distances are lower than the corresponding sum of the van der Waals radii (1.1 Å + 1.7 Å = 2.8 Å according to the Bondi radii¹²⁵). It suggests that this is an attractive F–H⋯σ interaction between the units in the complex. The distance between the H-atom of the HF molecule and the mid-point of the CC bond of cyclobutane is equal to 1.93 Å.

Fig. 9 The complex of cyclobutane with hydrogen fluoride. The H⋯C distances are indicated.

The complexes mentioned above exhibit similar properties of other interactions to those of the interaction in the C₄H₈⋯HF complex. The strongest interaction is observed for the complex of cyclopropane with hydrogen fluoride, where the interaction energy is equal to −5.0 kcal mol⁻¹. For the other complexes, the absolute value of the energy of interaction is lower than 3 kcal mol⁻¹. Thus, these are rather weak interactions. The QTAIM approach⁷³ indicates the occurrence of the A–H⋯σ hydrogen bond for complexes of molecular hydrogen and of cyclopropane because the bond paths exist here between the H-centre of the Lewis acid unit and the critical point of the H–H or C–C bond of the Lewis base species. For the complexes of cyclobutane and cyclopentane, there are similar bond paths between the Lewis acid and Lewis base units. However, sometimes the H-centre of the Lewis acid is linked by the bond path with the C-attractor of the Lewis base.¹²⁴ Thus, one can see that the existence of hydrogen bonds where the C–C σ-bonds play a role of the proton acceptors is confirmed here. Other theoretical tools were used in this study¹²⁴ to analyse the latter type of hydrogen bonds, including the NBO approach,^25,83 and the decomposition of the energy of interactions.^126,127

It is worth mentioning that Cambridge Structural Database^32,33 searches were performed to find hydrogen bonds where simple derivatives of cyclopropane, cyclobutane, and cyclopentane play a role as Lewis base centres through their CC σ-bonds.¹²⁴ Only about forty accurately solved crystal structures were found where such types of hydrogen bonds may occur. This is the experimental evidence of the existence of the A–H⋯σ(CC) hydrogen bonds.

Conclusions and perspectives

Three sub-classes of hydrogen bonds were discussed in the three last sections of this article: hydrogen bonds with multi-centre proton donating bonds, the arrangements where between two electronegative sites the proton is inserted, the proton sponges belong to this sub-class, and the hydrogen bonds where the σ-electrons play a role of the proton acceptor. All these interactions are classified as hydrogen bonds according to the 2sHB definition. The other definitions of the hydrogen bond do not take into account those systems where the multi-centre proton donor occurs.

The hydride bond and the charge-inverted hydrogen bond (the latter interaction is a sub-class of the former one) are also described, although these interactions are not classified as hydrogen bonds since the hydrogens located in the centre of the corresponding systems are negatively charged. However, these interactions are still classified as hydrogen bonds by a few definitions; the definition of Pimentel and McClellan¹⁶ is an example.

One can see that the 2sHB definition is very simple and convenient to apply in the identification of various kinds of hydrogen bonds. It seems that the definitions based on the specification of two interacting sites are very useful. One can refer to the definition of the σ-hole bond that was discussed earlier here.⁵⁹ The definition of the halogen bond proposed by Politzer, Murray and Clark is another example. It is stated in this definition that “A halogen bond is a highly directional, electrostatically-driven noncovalent interaction between a region of positive electrostatic potential on the outer side of the halogen X in a molecule R–X and a negative site B, such as a lone pair of a Lewis base or the π-electrons of an unsaturated system.”⁵⁷ The IUPAC definition of the halogen bond¹²⁸ also considers two sites, electrophilic and nucleophilic regions of centres that are in a contact. It is beyond the scope of this article to discuss the various definitions of the halogen bond. However, one can see that a trend regarding the definitions of various interactions is to consider two sites being in a contact, similarly as in the case of the 2sHB definition.

The two sites definition also may be generalised for a broader range of interactions. Thus, one can state that the Lewis acid–Lewis base interaction occurs between two sites if one of them acts as the electron donor and the other one as the electron acceptor. For such interactions, the electron charge shift is observed from the Lewis base unit to the Lewis acid unit. If the Lewis acid site is an element of the specific group of the periodic system, one can thus specify triel, tetrel, pnicogen, chalcogen, halogen and aerogen bonds for the 13, 14, 15, 16, 17 and 18 groups, respectively. Other interactions also may be mentioned here. However, it is convenient to mark various kinds of interactions in a simple way, presenting a pair of atoms in contact, where at the left and right sites, the Lewis acid and Lewis base centres are given, respectively.¹²⁹ For example, for the hydrogen bond in the water dimer, this is the H⋯O designation.

Coming back to the hydrogen bond interaction and to the perspectives, can we expect new kinds of interactions that require modification of the 2sHB definition or other definitions of the hydrogen bond? It is unlikely if one looks at Scheme 1, as all interactions presented there are covered by the 2sHB definition, except for the hydride bond and the charge-inverted hydrogen bond, where the H-centre is negatively charged. One can expect further progress in investigations on the latter interactions. The number of sub-classes of the hydride bond probably will increase in the future.

Interactions with multi-centre proton-donating bonds seem to be a large sub-class of hydrogen bonds. However, the number of studies on such interactions is very poor, with mostly theoretical calculations and only a few experimental studies. Thus, additional research is very much needed here. The additional research is also needed in the case of systems where the proton is inserted between two electronegative centres. This situation was described in this article. Sometimes, the proton is located in the mid-point of the distance between such centres. This topic is strongly related to SSHBs and LBHBs, which were also discussed in this article. One can see that there is a lot of space for further interesting research on interactions, including the hydrogen bond.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer, Berlin, 1991.
2. G. J. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997.
3. S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, New York, 1997.
4. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New York, 1999.
5. L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105, 3513–3560.
6. J.-M. Lehn, Supramolecular Chemistry, Verlag-Chemie, Weinheim, 1995.
7. J. Poater, M. Swart, C. F. Guerra and F. M. Bickelhaupt, Chem. Commun., 2011, 47, 7326–7328.
8. M. W. Latimer and W. H. Rodebush, J. Am. Chem. Soc., 1920, 42, 1419–1433.
9. G. N. Lewis, Valence and the Structure of Atoms and Molecules, American Chemical Society Monograph Series, The Chemical Catalog Company, Inc., New York, U.S.A., 1923.
10. Latimer and Rodebush wrote in their study (ref. 8): “Mr Huggins of this laboratory in some work as yet unpublished, has used the idea of a hydrogen kernel held between two atoms as a theory in regard to certain organic compounds.”.
11. A. Werner, Liebigs Ann., 1902, 322, 251–297.
12. A. Hantzsch, Berichte, 1910, 43, 3049–3076.
13. Z. Pfeiffer, Berichte, 1914, 47, 1580–1595.
14. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1636.
15. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
16. G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, W.H. Freeman and Company, San Francisco and London, 1960.
17. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, New York, 3rd edn, 1960.
18. W. C. Hamilton and J. A. Ibers, Hydrogen Bonding in Solids, W.A. Benjamin, New York, 1968.
19. S. J. Grabowski, Phys. Chem. Chem. Phys., 2017, 19, 29742–29759.
20. G. R. Desiraju, Acc. Chem. Res., 2002, 35, 565–573.
21. I. G. Kaplan, Theory of molecular interaction, Elsevier, Amsterdam, Oxford, 1986.
22. S. J. Grabowski, Understanding Hydrogen Bonds: Theoretical and Experimental Views, The Royal Society of Chemistry, United Kingdom, Cambridge, 2021.
23. R. Taylor and O. Kennard, J. Am. Chem. Soc., 1982, 104, 5063–5070.
24. T. Steiner, J. Chem. Soc., Perkin Trans. 2, 1995, 1315–1319.
25. F. Weinhold and C. Landis, Valency and Bonding, A Natural Bond Orbital Donor – Acceptor Perspective, Cambridge University Press, Cambridge, 2005.
26. P. Hobza and Z. Havlas, Chem. Rev., 2000, 100, 4253–4264.
27. S. Pinchas, Anal. Chem., 1955, 27, 2–6.
28. S. Pinchas, Anal. Chem., 1957, 29, 334–339.
29. W. G. Schneider and H. J. Bernstein, Trans. Faraday Soc., 1956, 52, 13–18.
30. D. J. Suttor, J. Chem. Soc., 1963, 1105–1110.
31. J. Donohue, in Structural Chemistry and Molecular Biology, ed. A. Rich and N. Davidson, W. H. Freeman, San Francisco, 1968, pp.459–463.
32. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171–179.
33. R. Wong, F. H. Allen and P. Willett, J. Appl. Crystallogr., 2010, 43, 811–824.
34. M. Nishio, M. Hirota and Y. Umezawa, The CH/π Interaction, Evidence, Nature, and Consequences, Wiley-VCH, 1998.
35. J. J. Szymczak, S. J. Grabowski, S. Roszak and J. Leszczynski, Chem. Phys. Lett., 2004, 393, 81–86.
36. R. W. Alder, Chem. Rev., 1989, 89, 1215–1223.
37. H. A. Staab and T. Saupe, Angew. Chem., Int. Ed. Engl., 1988, 27, 865–879.
38. S. J. Grabowski, Crystals, 2016, 6, 3.
39. F. Weinhold and R. A. Klein, Mol. Phys., 2012, 110, 565–579.
40. S. J. Grabowski, J. Phys. Org. Chem., 2013, 26, 452–459.
41. I. Alkorta, I. Rozas and J. Elguero, Chem. Soc. Rev., 1998, 27, 163–170.
42. S. J. Grabowski, W. A. Sokalski and J. Leszczynski, Chem. Phys. Lett., 2006, 422, 334–339.
43. M. Jabloński, Chem. Phys. Lett., 2009, 477, 374–376.
44. M. Jabloński, Chem. Phys., 2014, 433, 76–84.
45. M. Jabloński, Struct. Chem., 2020, 31, 61–80.
46. S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2004, 108, 1806–1812.
47. G. E. Douberly, A. M. Ricks, B. W. Ticknow, W. C. McKee, P. v R. Schleyer and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1897–1906.
48. S. J. Grabowski, J. Phys. Chem. A, 2007, 111, 13537–13543.
49. A. J. Arduengo, III, S. F. Gamper, M. Tamm, J. C. Calabrese, F. Davidson and H. A. Craig, J. Am. Chem. Soc., 1995, 117, 572–573.
50. M. Jabłoński and M. Palusiak, Phys. Chem. Chem. Phys., 2009, 11, 5711–5719.
51. S. J. Grabowski, CrystEngComm, 2023, 25, 4550–4561.
52. V. I. Bakhmutov, Dihydrogen bonds, principles, experiments, and applications, John Wiley & Sons, 2008.
53. E. J. Bieske, S. A. Nizkorodov, F. R. Bennett and J. P. Maier, J. Chem. Phys., 1995, 102, 5152–5164.
54. S. J. Grabowski and P. Lipkowski, J. Phys. Chem. A, 2011, 115, 4765–4773.
55. G. A. Landrum, N. Goldberg and R. Hoffmann, J. Chem. Soc., Dalton Trans., 1997, 19, 3605–3613.
56. S. J. Grabowski, J. M. Ugalde, D. M. Andrada and G. Frenking, Chem. – Eur. J., 2016, 22, 1317–1328.
57. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
58. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294.
59. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
60. J. N. Woodford, J. Phys. Chem. A, 2007, 111, 8519–8530.
61. M. Jabloński, Molecules, 2020, 25, 5512.
62. S. J. Grabowski, Crystals, 2021, 11, 5.
63. S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625.
64. S. Scheiner and S. J. Grabowski, J. Mol. Struct., 2002, 615, 209–218.
65. R. J. Gillespie and I. Hargittai, The VSEPR Model of Molecular Geometry; Allyn & Bacon: Boston, MA, USA, 1991. reprinted: R.J. Gillespie and I. Hargittai, The VSEPR Model of Molecular Geometry, Dover Publications, Inc., Mineola, NY, USA, 2012.
66. S. X. Tian, H.-B. Li, Y. Bai and J. Yang, J. Phys. Chem. A, 2008, 112, 8121–8128.
67. A. Zabardasti, A. Kakanejadifard, A.-A. Hoseini and M. Solimannejad, Dalton Trans., 2010, 39, 5918–5922.
68. A. Zabardasti, M. Joshaghani, S. Nadri, H. Goudarziafshar and M. Solehnassaj, Struct. Chem., 2012, 23, 1497–1502.
69. B. Saha, H. Sharma and P. K. Bhattacharyya, Int. J. Quantum Chem., 2019, 119, e25998.
70. K. D. Jordan, Chem. Phys. Lett., 1976, 40, 441–446.
71. S. A. C. McDowell, J. Comput. Chem., 2003, 24, 1201–1207.
72. I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1997, 101, 4236–4244.
73. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Oxford University Press, New York, 1990.
74. F. A. Cotton, J. H. Matonic and C. A. Murillo, J. Am. Chem. Soc., 1998, 120, 6047–6052.
75. Y. Gu, T. Kar and S. Scheiner, J. Am. Chem. Soc., 1999, 121, 9411–9422.
76. P. Lipkowski, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 10296–10302.
77. I. Alkorta, F. Blanco and J. Elguero, J. Phys. Chem. A, 2008, 112, 6753–6759.
78. H. Keil, R. Herbst-Irmer, S. Rathjen, C. Girschik, T. Muller and D. Stalke, Inorg. Chem., 2022, 61, 6319–6325.
79. S. Civiš, M. Lamanec, V. Špirko, J. Kubišta, M. Špetko and P. Hobza, J. Am. Chem. Soc., 2023, 145, 8550–8559.
80. S. J. Grabowski and F. Ruipérez, ChemPhysChem, 2017, 18, 2409–2417.
81. M. Aarabi, S. Gholami and S. J. Grabowski, Molecules, 2021, 26, 6939.
82. S. Gholami, M. Aarabi and S. J. Grabowski, ChemPhysChem, 2022, 23, e202200273.
83. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
84. S. J. Grabowski, W. A. Sokalski and J. Leszczynski, Chem. Phys. Lett., 2006, 432, 33–39.
85. S. J. Grabowski, Chem. Phys. Lett., 2007, 436, 63–67.
86. E. P. Hunter and S. G. Lias, ‘Proton Affinity Evaluation,’ NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg, MD, 2009, https://webbook.nist.gov.
87. W. A. Sokalski, S. Roszak and K. Pecul, Chem. Phys. Lett., 1988, 153, 153–159.
88. W. A. Sokalski and S. Roszak, J. Mol. Struct., 1991, 234, 387–400.
89. R. W. Gora,EDS v2.1.2 package, Wroclaw, Poland, Jackson, MS, 1998–2003.
90. A. M. Ricks, G. E. Douberly, P. v R. Schleyer and M. A. Duncan, Chem. Phys. Lett., 2009, 480, 17–20.
91. T. C. Cheng, B. Bandyopadyay, Y. Wang, S. Carter, B. J. Braams, J. M. Bowman and M. A. Duncan, J. Phys. Chem. Lett., 2010, 1, 758–762.
92. A. L. Llamas-Saiz, C. Foces-Foces and J. Elguero, J. Mol. Struct., 1994, 328, 297–323.
93. V. A. Ozeryanskii, A. F. Pozharskii, A. J. Bieńko, W. Sawka-Dobrowolska and L. Sobczyk, J. Phys. Chem. A, 2005, 109, 1637–1642.
94. A. Jezierska and J. Panek, J. Mol. Model., 2020, 26, 37.
95. R. W. Alder, A. G. Orpen and R. B. Sessions, J. Chem. Soc., Chem. Commun., 1983, 999–1000.
96. R. W. Alder, R. E. Moss and R. B. Sessions, J. Chem. Soc., Chem. Commun., 1983, 1000–1002.
97. D. Stasko, S. P. Hoffmann, K.-C. Kim, N. L. P. Fackler, A. S. Larsen, T. Drovetskaya, F. S. Tham, C. A. Reed, C. E. F. Rickard, P. D. W. Boyd and E. S. Stoyanov, J. Am. Chem. Soc., 2002, 124, 13869–13876.
98. G. Pitsevich, A. Malevich, E. Kozlovskaya, E. Mahnach, I. Doroshenko, V. Pogorelov, L. G. M. Pettersson, V. Sablinskas and V. Balevicius, J. Phys. Chem. A, 2017, 121, 2151–2165.
99. E. S. Stoyanov and C. A. Reed, J. Phys. Chem. A, 2006, 110, 12992–13002.
100. A. S. Mildvan, M. A. Massiah, T. K. Harris, G. T. Marks, D. H. T. Harrison, C. Viragh, P. M. Reddy and I. M. Kovach, J. Mol. Struct., 2002, 615, 163–175.
101. J. Chen, M. A. McAllister, J. K. Lee and K. N. Houk, J. Org. Chem., 1998, 163, 4611–4619.
102. N. F. Dalleska, K. Honma and P. B. Armentrout, J. Am. Chem. Soc., 1993, 115, 12125–12131.
103. A. Warshel and A. Papazyan, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13665–13670.
104. W. W. Cleland, P. A. Frey and J. A. Gerlt, J. Biol. Chem., 1998, 273, 25529–25532.
105. K. Norrman, T. I. Sølling and T. B. McMahon, J. Mass Spectrom., 2005, 40, 1076–1087.
106. G. E. Douberly, A. M. Ricks, B. W. Ticknor and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 950–959.
107. S. J. Grabowski and J. M. Ugalde, Chem. Phys. Lett., 2010, 493, 37–44.
108. A. M. Ricks, G. E. Douberly and M. A. Duncan, J. Chem. Phys., 2009, 131, 104312.
109. L. Pauling, J. Am. Chem. Soc., 1931, 53, 1367–1400.
110. H. Gómez, G. Meloni, J. Madrid and D. M. Neumark, J. Chem. Phys., 2003, 119, 872–879.
111. S. A. Pyaleva, H. Elgabarty, D. Sebastiani and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2017, 19, 26107–26120.
112. H. Kunttu, J. Seetula, M. Räsänen and V. A. Apkarian, J. Chem. Phys., 1992, 96, 5630–5635.
113. H. Kunttu and J. Seetula, Chem. Phys., 1994, 189, 273–292.
114. M. Tsuge, J. Kalonowski, R. B. Gerber and Y.-P. Lee, J. Phys. Chem. A, 2015, 119, 2651–2660.
115. K. W. Jucks and R. E. Miller, J. Chem. Phys., 1987, 87, 5629–5633.
116. D. T. Moore and R. E. Miller, J. Chem. Phys., 2003, 118, 9629–9636.
117. D. T. Moore and R. E. Miller, J. Phys. Chem. A, 2003, 107, 10805–10812.
118. D. T. Moore and R. E. Miller, J. Phys. Chem. A, 2004, 108, 1930–1937.
119. J. Urban, S. Roszak and J. Leszczynski, Chem. Phys. Lett., 2001, 346, 512–518.
120. It is worth to point out that ref. 84 is cited incorrectly by ref. 14 (IUPAC HB definition) where it is stated “It has also been shown that the σ-bonding electrons of H₂ could act as hydrogen bond acceptors, though the authors of the paper had suggested that it be classified as van der Waals interaction despite the similarity with the hydrogen bonding.” However, in ref. 84 it is clearly described that in a case of the F–H⋯H2 complex and other complexes analysed in this study, the interactions that link complexes “possess some of the characteristics typical for H-bond interactions.”.
121. I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1997, 101, 9457–9463.
122. A. Galano, J. R. Alvarez-Idaboy and A. Vivier-Bunge, Theor. Chem. Acc., 2007, 118, 597–606 and references therein.
123. I. Alkorta, I. Soteras, J. Elguero and J. E. Del Bene, Phys. Chem. Chem. Phys., 2011, 13, 14026–14032.
124. S. J. Grabowski, ChemPhysChem, 2019, 20, 564–574.
125. J. Bondi, J. Phys. Chem., 1964, 68, 441–451.
126. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
127. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759.
128. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
129. S. J. Grabowski, Molecules, 2021, 26, 4939.

---