The peptide bond rupture mechanism in the serine proteases: an in silico study based on sequential scale models

Abstract

Given the importance of serine proteases for biochemical processes, we have studied the peptide bond rupture mechanism using three sequential scale models as representations of the KLK5 enzyme (a protein overexpressed in ovarian cancer). The first model contains the basic functional groups of the residues that conform to the catalytic triad present in serine proteases; the second model contains some additional residues and, finally, the last representation includes all atoms of the KLK5 protein together with 10.000 explicit water molecules. This separation into three scale models allows us to separate the intrinsic reactivity of the catalytic triad from the process taking place in the enzyme. The methodologies employed in this work include full DFT calculations with a dielectric continuum in the first two models and a multi-level setup with a Quantum Mechanics/Molecular Mechanics (QM/MM) partition in the whole protein system. Our results show that the peptide-bond rupture mechanism is a stepwise process involving two proton transfer reactions. The rate-determining step is the second proton transfer from the imidazole group to the amidic nitrogen of the substrate. In addition, we find that the simplest model does not provide accurate results compared to the full protein system. This can be attributed to the electronic stabilization conferred by the residues around the reaction site. Interestingly, the energy profile obtained with the second scale model with additional residues shows the same trends as the full system and could therefore be considered an appropriate model system. It could be used for studying the peptide bond rupture mechanism in case full QM/MM calculations cannot be performed, or as a rapid tool for screening purposes.

---

Introduction

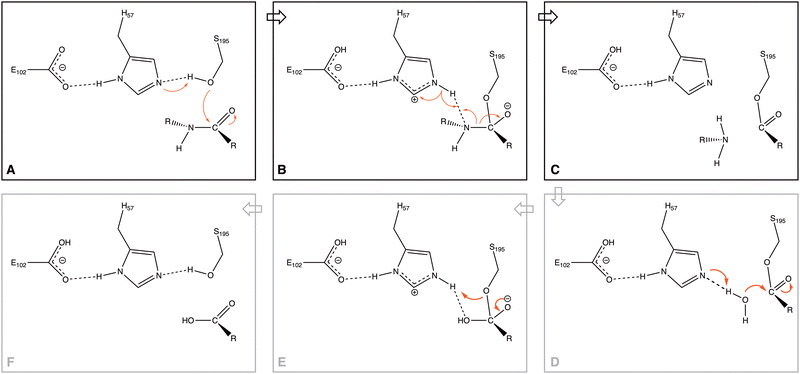
Serine proteases (SP) have recently become one of the most studied families of enzymes¹ because of the key role these enzymes play: cleaving peptide bonds in proteins. They play a vital role in blood-clotting cascades, digestion of dietary proteins, several pathways of development and differentiation of cells,² and in several pathologies and immunologic cells, such as the granules of mast cells, neutrophils, lymphocytes, and cytotoxic T cells.³ At the same time, proteases have been used in environmental applications⁴ and biocatalysts.⁵

Three principal residues constitute the active site of serine proteases (Ser, Asp, and His), the so-called catalytic triad.^6–10 They form part of a network of hydrogen bonds within the protein, which originates at the Asp residue and ends with the Ser residue.¹¹ The role that these residues and the H-bond network play in the reaction mechanism (one of the primary aims of biochemical studies^12,13) was analyzed in experimental studies on peptide bond ruptures in serine proteases; they observed the formation of one particular pose of the triad (Fig. 1A), which plays a role in the proposed mechanism.^14,15

Fig. 1 The proposed reaction mechanism of serine proteases, with shown in panel A the catalytic triad of Asp, His, and Ser. Note that here we only study the process of breaking of the peptide bond (panels A–C).

One member of the protein serine family (trypsin) was studied by a combination of molecular dynamics (MD) and multi-level Quantum Mechanics/Molecular Mechanics (QM/MM) by Kato and co-workers.¹⁶ They described the possible peptide bond rupture mechanism and observed an intermediate in the reaction pathway, which is stabilized by an oxyanion hole. Note that in this study the effect of additional residues and the vibrational frequencies to confirm the reaction path were neglected; for this reason, it is necessary to propose a sequential scale model study, which focuses on the importance of these additional residues. In particular, determining whether it is sufficient to include only these or, alternatively, the full protein environment is necessary.

Here, we are proposing three sequential scale models for the study of the peptide bond rupture mechanism in serine proteases, based on the kallikrein-related peptidase 5 (KLK5), a protein overexpressed in ovarian cancer.^17,18 It plays a key role in stratum conium desquamation,^19,20 and has been related to the carcinogenesis process, and possesses the ability to act as a novel cancer biomarker.^21,22 The goal of this work is three-fold: first, we aim to study the reaction mechanism of the peptide bond rupture taking place in the active site of KLK5, including confirmation of the stationary points through vibrational frequency analysis. Second, we compare the reaction paths obtained with three representations of KLK5, going from a small set of active site residues, through an extended representation of the active site, and finally a real model based on the full protein. This comparison will highlight the role of the protein environment in the peptide bond rupture mechanism. Third, through an energy decomposition analysis we investigate the chemical origins of the barriers involved.

Methodology

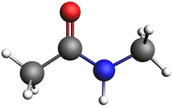
Given the above scenario, we decided to use KLK5 as representative serine protease to obtain the reaction path of the peptide bond rupture. We started by downloading the crystallographic data of this protein from the protein data bank (PDB code: 2PSX)²³ and chose as the substrate a simple peptide model (Fig. 2), in which the NH–CO peptide bond is accompanied by two methyl groups on each side.

Fig. 2 Structure of the substrate used in the peptide bond breaking process. Grey spheres depict carbon atoms, white spheres represent hydrogen atoms, red spheres represent oxygen atoms and blue spheres represent nitrogen atoms.

To locate the active sites in the protein, specifically the catalytic triad, we performed an in silico molecular coupling, using the Molegro Virtual Docker suite (MVD)²⁴ with the MolDock²⁵ score function.

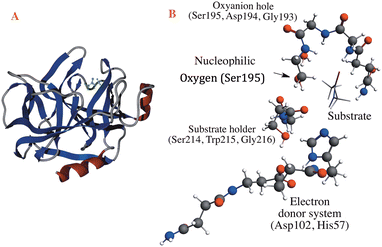
The reaction mechanism of the peptide bond rupture is described using three different scale models as representations of KLK5 for the hydrolysis of the substrate (Fig. 2). The first model, m1, consists of 47 atoms (including the substrate, see Fig. 3) and contains the minimum number of components of the catalytic triad: the nucleophilic oxygen (acting as the oxygen of Ser), the cis-urocanic acid²⁶ as the electron donor system (simulating the behavior of Asp and His) and two amine groups as an oxyanion hole. This model includes a dielectric continuum solvent model for the simulation of the enzyme environment (methanol was chosen as the solvent, to represent the hydrophilic active site cavity). The same dielectric continuum solvent model was used in the second representation of KLK5 with 78 atoms (see Fig. 4). This second scale model, m2, has more realistic residues for the catalytic triad and, additionally, contains some residues of KLK5 (His57, Asp102, Gly193, Asp194, and Ser195) that were proposed as relevant for the reaction mechanism. Finally, we use a “real” system based on the atoms extracted from the PDB file mentioned above (m3 model, Fig. 5). This model contains 13968 atoms, and is divided in two regions: the QM region (treated with the S12g/TZ2P²⁷ method), consisting of 127 atoms and with the principal residues from the catalytic triad (His57, Asp102, Gly193, Asp194, and Ser195) plus the binding residues that are involved in appropriately positioning the substrate in the active site (Gln192, Ser214, Trp215, and Gly216) and the MM region (treated with the AMBER force field²⁸), which consists of the rest of residues together with 10.000 molecules of water.

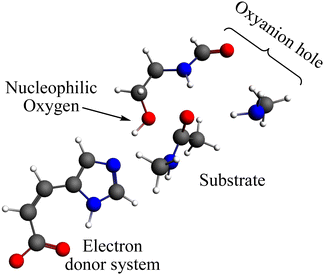Fig. 3 Representation of the m1 model; grey spheres depict carbon atoms, white spheres represent hydrogen atoms, red spheres represent oxygen atoms and blue spheres represent nitrogen atoms.

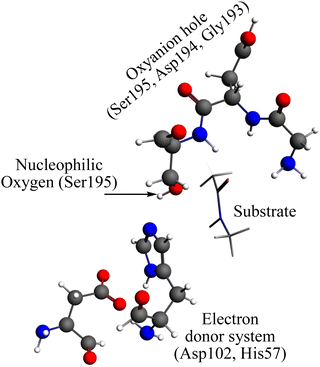Fig. 4 Representation of the m2 model. Grey spheres depict carbon atoms, white spheres represent hydrogen atoms, red spheres represent oxygen atoms, and blue spheres represent nitrogen atoms.

Fig. 5 Representation of the m3 model. (a) Full system with the secondary structure of KLK5 and the substrate depicted in green. (b) QM region of the m3 model, in which the grey spheres depict carbon atoms, white spheres represent hydrogen atoms, red spheres represent oxygen atoms and blue spheres represent nitrogen atoms.

All geometry optimizations of stationary points (reactants, transition states, intermediates, and products) were performed with DFT at the S12g/TZ2P²⁷ level, using the QUILD²⁹ program (models m1 and m2) and the NEWQMMM code (model m3) from the Amsterdam Density Functional (ADF)³⁰ package. In the NEWQMMM calculations, the cut-off between QM and MM was chosen at sensible positions, thereby avoiding the rupture of complex bonds (aromatic, double bonds, etc.). Solvent effects were included with the COSMO³¹ approach for the first two models considering methanol as the solvent. In contrast, explicit water molecules were included in the m3 model. Thermal and entropy effects were not considered to enable a fair comparison with the m3 model.

Moreover, to analyze in detail the interactions between the protein and the substrate along the reaction path, we carried out an energy decomposition analysis of all stationary points, considering the factorization of the whole interaction energy (ΔE_int) as follows:

ΔE = ΔE_prep + ΔE_int (1)

ΔE_int = ΔE_elstat + ΔE_oi + ΔE_Pauli + ΔE_Disp (2)

where, ΔE, the dissociation energy of the protein–substrate complex, is split into preparation energy ΔE_prep, which contains the energy required to distort the initial free fragments (protein and substrate) to the geometry they have in the considered stationary point and the solvation energy, and interaction energy ΔE_int. The latter is in turn decomposed into ΔE_elstat, the classical electrostatic interaction, ΔE_oi, the orbital interaction energy, the dispersion energy, ΔE_Disp, and the Pauli repulsion (ΔE_Pauli).^32,33

Results and discussion

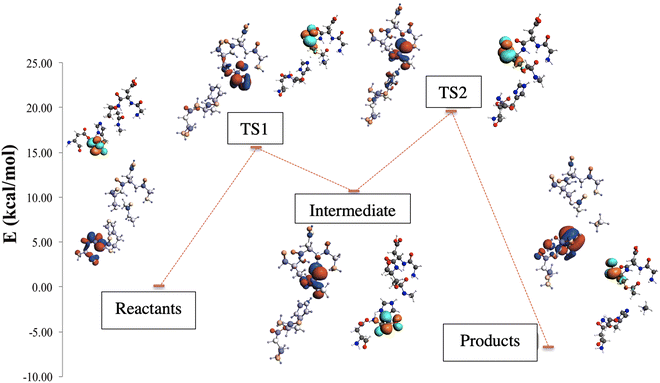
Through the observed in silico molecular couplings, we located the active site of KLK5 (Fig. 6) consisting of the catalytic triad (His57, Asp102, and Ser195). By performing a hydrophobic surface analysis, we found a hydrophobic area surrounding the cavity formed by the three main residues. At the same time, this active site presents a higher hydrophilic behavior than the rest of the nearby surfaces. As anticipated from the literature,^34,35 we found that the peptide bond rupture in KLK5 occurs in two steps (see panels A–C of Fig. 1). First, a proton transfer between the nucleophilic oxygen and the nitrogen of imidazole takes place (panels A and B, Fig. 1). Then, the same proton is transferred from the imidazole ring to the amidic nitrogen from the substrate (panels B and C, Fig. 1), ending in the peptide bond rupture.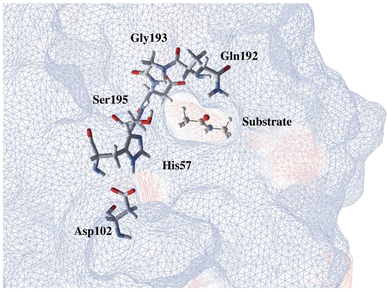

Fig. 6 Proposed substrate into the active site of KLK5. The blue lines depict a hydrophobic surface and the red lines represent a hydrophilic surface.

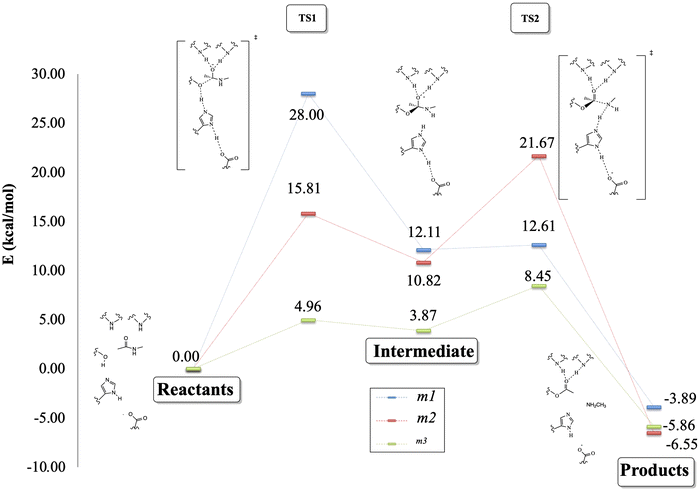
Fig. 7 depicts the reaction paths obtained for each proposed model. In all cases, we found two transition states (TSs) and an intermediate, which is stabilized by the oxyanion hole. The first proton transfer, from the nucleophilic oxygen to the nitrogen of imidazole, has an activation barrier of 28.0 kcal mol⁻¹ for the m1 model; this value is reduced to 15.5 kcal mol⁻¹ for m2 and 5.0 kcal mol⁻¹ for m3, showing the stabilization conferred by the surrounded functional groups in the m2 model and the total residues in the m3 system, which are not present in m1.

Fig. 7 Proposed reaction mechanism (kcal mol⁻¹) for the peptide bond rupture. In blue is shown the reaction path for the m1 model, in red are shown the results for m2 and in green are shown the results obtained for m3.

Concerning the intermediate, we observe similar behavior to that of TS1, with stabilization due to the surrounding functional groups acting on the oxyanion hole, as discussed widely by Warshel and co-workers.^36–38 They concluded that the oxyanion hole plays a key role in charge stabilization, distributing the electronic density in the functional groups around the reaction site.^34–36 For this stationary point, we observed energy differences of 6.9 kcal mol⁻¹ between m3 and m2, and a higher difference, by a factor of almost three, between the energies of m3 and m1.

On the other hand, the TS2 corresponding to the second proton transfer has a much lower energy (12.6 kcal mol⁻¹) than TS1 in the m1 model. In contrast, models m2 and m3 yield higher energy for TS2 than TS1. As a whole, the rate-determining step according to the m1 model is the first proton transfer with an overall energy barrier of 28.0 kcal mol⁻¹. In contrast, for m2 and m3, the rate-determining step is the second proton transfer with energy barriers of 21.7 (m2) and 8.5 (m3) kcal mol⁻¹. From a qualitative point of view, the m2 model provides results closer to the “real model” m3. The proposed oxyanion hole for m2 can simulate the behavior of the protein electronic environment in the proton transfer between the nitrogen of the imidazole and the nitrogen of the substrate better than the functional groups of the m1 model.

Finally, the relative energy of the products obtained through the three models is very similar, varying only by 2.9 kcal mol⁻¹ between m1 and m3, and 2.0 kcal mol⁻¹ between m1 and m2, being in all the cases exothermic reactions. Although the m2 and m3 models differ by about 10 kcal mol⁻¹ in the energy barriers, the qualitative trends given by these two models are the same, whereas those of the m1 model clearly disagree when compared to m3.

For the above reasons, the m2 model has been selected to perform a more detailed study into the electronic density behavior of the highest occupied molecular orbital (HOMO) along the reaction path (see Fig. 8). The MO plots show that the HOMO electronic density in the reactants is localized on the electron donor system site. When the first proton transfer occurs in the TS1, the electronic density goes to the substrate site and the nucleophilic oxygen. In the intermediate, the HOMO is located in part at the substrate but mainly in the oxyanion hole site. As expected, the HOMO follows the negatively charged fragment generated during the proton transfer process. In the second proton transfer process, crossing TS2, the HOMO electronic density begins to migrate to the electron donor system, but mainly remains at the substrate site. Finally, when the peptide bond rupture is done, in the products, the lobes of the HOMO move to the electron donor system, as depicted in Fig. 8.

Fig. 8 Frontier molecular orbitals across the reaction path for the m2 model. The highest occupied molecular orbitals are depicted in blue and red surfaces and the lowest unoccupied molecular orbitals are drawn in magenta and orange surfaces (isosurface value: 0.03 a.u.), for positive or negative each one, respectively. The atoms are colored from red to the blue, indicating the partial charge form negative to positive, respectively.

Table 1 shows the energy decomposition analysis (EDA) across the reaction path, computed through eqn (1) and (2), respectively, and considering as the baseline the reactant energies. Note that the fragments were defined in each path step considering the main involved functional groups. The preparation energy (ΔΔE_prep) plays a key role in the rate-determining step selection. It contributes mostly to the higher energy of TS2 compared to TS1, leading to this second step being rate-determining (see Table 1); the solvation energy contributes most to this. On the other hand, the orbital interactions are essential to stabilize stationary points, being higher in the case of the transition states and lower in the reactants and products. The ΔΔE_Pauli, stabilizes the intermediate. In other words, if the Pauli repulsion decreases in a stationary point, a stable state is promoted. Finally, the classical electrostatic interaction ΔΔE_elstat is lower in the transition states and higher at the minima (reactants, intermediate and products).

Table 1 Energy decomposition analysis (kcal mol⁻¹) for each stationary point along the reaction path of m2; all values referred to reactants; fragments considered are the substrate and the m2 model of KLK5^a

	ΔΔEPauli	ΔΔEelstat	ΔΔEoi	ΔΔEdisp	ΔΔEint	ΔΔEprep	ΔΔE
a The ΔE is the dissociation energy, which is split into the preparation energy ΔEprep and the interaction energy ΔEint; the latter in turn is split into the classical electrostatic interaction ΔEelstat, the orbital interaction energy ΔEoi, the dispersion energy ΔEdisp, and the Pauli repulsion ΔEPauli.
React	0.00	0.00	0.00	0.00	0.00	0.00	0.00
TS1	−82.92	−28.29	117.89	0.10	6.78	9.03	15.81
Inter	−160.92	4.81	158.13	0.72	2.74	8.08	10.82
TS2	−265.75	1.99	263.04	−0.33	−1.05	22.72	21.67
Product	−213.31	65.83	131.17	5.60	−10.71	4.16	−6.55

---

Conclusions

The results obtained in this study provide new insights into the key role played by the choice of model systems. These could be based either on the full system, or in contrast, based on simplified models. The choice of how to represent the enzyme has a large effect on the barriers, specifically for systems that involve proton transfer steps in combination with stabilization via oxyanion holes.

The rupture of peptide bonds can be modelled with a minimal set of residues, obtaining qualitative results of the reaction path. Moreover, in the small models, transition states can be characterized through the frequencies and finding the imaginary frequency that promotes the formation and rupture of peptide bonds. Due to the computational requirements, calculation of the frequencies of the full system, which consists of thousands of atoms, is prohibitive. Therefore, we suggest characterizing the transition states with smaller models.

However, the rate-determining step of the reaction cannot be determined by using small model systems, such as in the case with the smallest model proposed in this work, m1. Not surprisingly, the functional groups around the reaction site are essential in a quantitative study of the reaction mechanism of an enzyme. At the same time, we find that the energy needed to break the peptide bond presents a small variation of ca. 2 kcal mol⁻¹ between the m1 and m2 models, and the difference with the last m3 model is only 1 kcal mol⁻¹.

Moreover, through an energy decomposition analysis study we observed that the component which contributes most to the rate-determining step is the preparation energy ΔE_prep (and within that, the solvation energy). The interaction energy between the fragments is overall almost zero due to the opposite effects of Pauli repulsion, ΔE_Pauli, which has a stabilizing effect along the reaction path, and orbital interactions, ΔE_oi, which has a destabilizing effect on it.

To conclude, we show that with medium-sized models like m2 it is possible to provide qualitatively meaningful results, albeit with an overestimation of the barriers. Model m2 can be therefore be used for rapid screening studies on the peptide bond rupture in this kind of protein that is overexpressed in ovarian cancer and used in some environmental applications, which demonstrates the importance of proposing a minimally sufficient model to simulate a reaction mechanism in biological systems.

Author contributions

Conceptualization: J. Robles and M. Solà. Formal analysis: M. Swart. Investigation: E. Díaz-Cervantes. Methodology: E. Díaz-Cervantes and M. Swart. Supervision: M. Solà, J. Robles, and M. Swart. Validation: M. Swart. Writing original draft: E. Díaz-Cervantes. Writing – review & editing: M. Solà, J. Robles, M. Swart, and E. Díaz-Cervantes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Laboratorio Nacional de Caracterización de Propiedades Fisicoquímicas y Estructura Molecular (UG-UAA-CONACYT, Project: 123732) for the computing time provided at the PIPILA cluster, AEI/MCIU (projects PID2020-114548GB-I00 and PID2020-113711GB-I00), the Generalitat de Catalunya (projects 2021SGR00623 and 2021SGR00487), and FEDER (UNGI10-4E-801) for financial support.

References

1. E. Burchacka, P. Pieta and A. Lupicka-Stowik, Recent advances in fungal serine protease inhibitors, Biomed. Pharmacother., 2022, 146, 112523.
2. P. Vandenabeele, S. Orrenius and B. Zhivotovsky, Serine proteases and calpains fulfill important supporting roles in the apoptotic tragedy of the cellular opera, Cell Death Differ., 2005, 12, 1219–1224.
3. R. J. Parkes, Microbiology - A case of bacterial immortality?, Nature, 2000, 407, 844–845.
4. X. Li, Q. Zhang, Z. Xu, G. Jiang, L. Gan, Y. Tian and B. Shi, High-expression and characterization of a novel serine protease from Ornithinibacillus caprae L9T with eco-friendly applications, Environ. Sci. Pollut. Res., 2022, 29, 35996–36012.
5. M. Naeem, S. Manzoor, M. Abid, M. Tareen, M. Asad, S. Mushtaq, N. Ehsan, D. Amna, B. Xu and A. Hazafa, Fungal Proteases as Emerging Biocatalysts to Meet the Current Challenges and Recent Developments in Biomedical Therapies: An Updated Review, J. Fungi, 2022, 8, 109.
6. A. R. Fersht, The charge relay system in chymotrypsin and chymotrypsinogen, J. Mol. Biol., 1973, 74, 137–149.
7. A. Warshel, Energetics of enzyme catalysis, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 5250–5254.
8. R. D. Gandour, On the importance of orientation in general base catalysis by carboxylate, Bioorg. Chem., 1981, 10, 169–176.
9. L. Polgár, The catalytic triad of serine peptidases, Cell. Mol. Life Sci., 2005, 62, 2161–2172.
10. E. Erez, D. Fass and E. Bibi, How intramembrane proteases bury hydrolytic reactions in the membrane, Nature, 2009, 459, 371–378.
11. V. Daggett, S. Schröder and P. Kollman, Catalytic Pathway of Serine Proteases: Classical and Quantum Mechanical Calculations, J. Am. Chem. Soc., 1991, 113, 8926–8935.
12. L. Hedstrom, Serine Protease Mechanism and Specificity, Chem. Rev., 2002, 102, 4501–4523.
13. A. R. Fersht, Structure and Mechanism in Protein Science. A guide to Enzyme Catalysis and Protein Folding, Feeman and Company, New York, 2nd edn, 1999.
14. A. A. Kossiakoff and S. A. Spencer, Neutron diffraction identifies His 57 as the catalytic base in trypsin, Nature, 1980, 288, 414–416.
15. D. E. Metzler, Biochemistry: The Chemical Reactions of Living, Academic Press, 2nd edn, 2003, vol. 2.
16. T. Ishida and S. Kato, Theoretical Perspectives on the Reaction Mechanism of Serine Proteases: The reaction Free Energy Profiles of the Acylation Process, J. Am. Chem. Soc., 2003, 125, 12035–12048.
17. G. M. Yousef, C. V. Obiezu, K. Jung, C. Stephan, A. Scorilas and E. P. Diamandis, Differential expression of kallikrein gene 5 in cancerous and normal testicular tissues, Urology, 2002, 60, 714–718.
18. J. Bayani, M. Paliouras, C. Planque, S. J. C. Shan, C. Graham, J. A. Squire and E. P. Diamandis, Impact of cytogenetic and genomic aberrations of the kallikrein locus in ovarian cancer, Mol. Oncol., 2008, 2, 250–260.
19. I. E. Ekholm, M. Brattsand and T. Egelrud, Stratum corneum tryptic enzyme in normal epidermis: a missing link in the desquamation process?, J. Invest. Dermatol., 2000, 114, 56–63.
20. C. A. Borgoño, I. P. Michael, N. Komatsu, A. Jayakumar, R. Kapadia, G. L. Clayman, G. Sotiropoulou and E. P. Diamandis, A potential Role for Multiple Tissue Kallikrein Serine Proteases in Epidermal Desquamation, J. Biol. Chem., 2007, 282, 3640–3652.
21. J. Dorn, V. Magdolen, A. Gkazepis, T. Gerte, A. Harlozinska, P. Sedlaczek, E. P. Diamandis, T. Schuster, N. Harbeck, M. Kierchle and M. Schmitt, Circulating biomarker tissue kallikrein-related peptidase KLK5 impacts ovarian cancer patients’ survival, Ann. Oncol., 2011, 22, 1783–1790.
22. E. Bandiera, L. Zanotti, E. Bignotti, C. Romani, R. Tassi, P. Todeschini, G. Tognon, M. Ragnoli, A. D. Santin, M. Gion, S. Pecorelli and A. Ravaggi, Human kallikrein 5: an interesting novel biomarker in ovarian cancer patients that elicits humoral response, Int. J. Gynecol. Cancer, 2009, 19, 1015–1021.
23. M. Debela, P. Goettig, V. Magdolen, R. Huber, N. M. Schechter and W. Bode, Structural basis of the zinc inhibition of human tissue kallikrein 5, J. Mol. Biol., 2007, 373, 1017–1031.
24. R. Thomsen and M. H. Christensen, MolDock: a new technique for high-accuracy molecular docking, J. Med. Chem., 2006, 49, 3315–3321.
25. J. Yang and C. Chen, GEMDOCK: a generic evolutionary method for molecular docking, Proteins, 2004, 55, 288–304.
26. E. L. Ash, J. L. Sudmeier, E. C. De Fabo and W. W. Bachovchin, A low-barrier hydrogen bond in the catalytic triad of serine proteases? Theory versus experiment, Science, 1997, 278, 1128–1132.
27. M. Swart, A new family of hybrid density functionals, Chem. Phys. Lett., 2013, 580, 166–171.
28. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, J. K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
29. M. Swart and M. Bickelhaupt, QUILD: QUantum-regions interconnected by local descriptions, J. Comput. Chem., 2008, 29, 724–734.
30. E. J. Baerends, et al., ADF 2012, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2012.
31. A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., 1993, 2, 799–805.
32. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 45, 1–10.
33. T. Ziegler and A. Rauk, A theoretical study of the ethylene-metal bond in complexes between copper(1 +), silver(1 +), gold(1 +), platinum(0) or platinum(2 +) and ethylene, based on the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1558–1565.
34. P. Langan and J. C.-H. Chen, Seeing the chemistry in biology with neutron crystallography, Phys. Chem. Chem. Phys., 2013, 15, 13705.
35. A. J. Beveridge, A theoretical study of the active sites of papain and S195C rat trypsin: Implications for the low reactivity of mutant serine proteinases, Protein Sci., 1996, 5, 1355–1365.
36. S. C. L. Kamerlin, A. T. Chu and A. Warshel, On Catalytic Preorganization in Oxyanion Holes: Highlighting the Problems with the Gas-Phase Modeling of Oxyanion Holes and Illustrating the Need for Complete Enzyme Models, J. Org. Chem., 2010, 75, 6391–6401.
37. A. Warshel, Computer modeling of Chemical Reactions in Enzymes and Solutions, J. Wiley & Sons, New York, 1991.
38. A. Warshel, Theoretical correlation of structure and energetics in the catalytic reaction of trypsin, J. Am. Chem. Soc., 1986, 108, 6569–6579.

---