Carbon dioxide hydrogenation over the carbon-terminated niobium carbide (111) surface: a density functional theory study

Abstract

Carbon dioxide (CO₂) hydrogenation is an energetic process which could be made more efficient through the use of effective catalysts, for example transition metal carbides. Here, we have employed calculations based on the density functional theory (DFT) to evaluate the reaction processes of CO₂ hydrogenation to methane (CH₄), carbon monoxide (CO), methanol (CH₃OH), formaldehyde (CH₂O), and formic acid (HCOOH) over the carbon-terminated niobium carbide (111) surface. First, we have studied the adsorption geometries and energies of 25 different surface-adsorbed species, followed by calculations of all of the elementary steps in the CO₂ hydrogenation process. The theoretical findings indicate that the NbC (111) surface has higher catalytic activity towards CO₂ methanation, releasing 4.902 eV in energy. CO represents the second-most preferred product, followed by CH₃OH, CH₂O, and HCOOH, all of which have exothermic reaction energies of 4.107, 2.435, 1.090, and 0.163 eV, respectively. Except for the mechanism that goes through HCOOH to produce CH₂O, all favourable hydrogenation reactions lead to desired compounds through the creation of the dihydroxycarbene (HOCOH) intermediate. Along these routes, CH₃* hydrogenation to CH₄* has the highest endothermic reaction energy of 3.105 eV, while CO production from HCO dehydrogenation causes the highest exothermic reaction energy of −3.049 eV. The surface-adsorbed CO₂ hydrogenation intermediates have minimal effect on the electronic structure and interact only weakly with the surface. Our results are consistent with experimental observations.

---

1. Introduction

Recent years have seen a significant increase in interest in the remarkable physical and chemical features of transition metal carbides (TMCs).^1,2 They are carbon-containing close-packed metals exhibiting a remarkable mix of properties, combining the good electric and thermal conductance of transition metals, coupled with the toughness and structural coordination of covalent solids, and the high melting temperatures of ionic solids.^3–5 TMCs have been proposed as viable alternatives for valuable metals as a result of their intrinsic advantages of abundance, high reactivity, endurance, and affordability. Owing to their three distinct types of bonding: metallic, ionic, and covalent they are promising materials for a broad spectrum of technical applications of economic value.^6,7 The discovery in a seminal study by Levy and Boudart⁸ of platinum-like behaviour in TMCs equivalent to that of Pt-group metals attracted significant interest in their potential use in a broad variety of catalytic processes, e.g. the water–gas shift,^9–11 CO hydrogenation¹² and CO₂ hydrogenation^12–20 reactions.

Carbon dioxide is one of the Earth's most significant pollutants and a potent active greenhouse gas, and rising CO₂ levels have been linked to global warming and other negative effects on the environment.^13,19,21 As a result, substantial research has been conducted into the alleviation of its adverse effects and the transformation of CO₂ into useful products, particularly in the context of producing sustainable energy.^22–24 However, the stability of CO₂ and the high adsorption energy restricts the number of potential viable catalysts.^13,20,25 A high activation barrier in C–O bond breaking requires highly efficacious catalysts.

Previous studies have been carried out to gain insight into CO₂ adsorbtion and conversion into usable hydrocarbon alternatives at low-index TMC surfaces,^13,15,20,22 where niobium carbide has been shown to be a substantial generator of CO and the key product of CH₄.¹⁵ As such, NbC has been the topic of a number of experiments to investigate and customise its various characteristics.^26,27 Two often-researched NbC crystalline surfaces are the (100) plane, containing both metal and carbon atoms, and the (111) surface, which is terminated by either metal or carbon atoms that alternate in each layer.⁷ The (111) surface of NbC has been shown to be more active towards gas adsorption than the (100) surface, owing to the higher electronic density of states around the Fermi level at the (111) surface.^7,28–31

Our previous study has investigated CO₂ hydrogenation at the niobium-terminated NbC (111) surface,³² where we found that the most likely products are CH₄ and CO. In contrast to the carbon-terminated (111) surfaces of TMCs at the top of the TM group, like the TiC (111) surface which proved to be unstable,³³ the carbon-terminated NbC surface was found to be important in a number of studies.^5,7,20,34 However, although an experimental study on CO₂ hydrogenation at the NbC (111) surface has been carried out by Prosoff and coworkers,¹⁵ who found that CO and CH₄ are the main products, theoretical investigations of these processes, providing further detail on the reaction mechanism and formed intermediates, are still lacking. In this work, we have therefore carried out a comprehensive computational investigation of the network of reactions involved in CO₂ hydrogenation at the carbon-terminated NbC (111) surface.

Identifying the mechanism of CO₂ hydrogenation and the energetics of the elementary steps is important if we are to gain a better understanding of the formation and scission of the bonds which can aid in the development of active catalysts for the conversion of CO₂ into methane (CH₄), carbon monoxide (CO), methanol (CH₃OH), formaldehyde (CH₂O), and formic acid (HCOOH) during the hydrogenation mechanism. We have used calculations based on the density functional theory (DFT) with periodic surface models to elucidate the CO₂ hydrogenation intermediates and elementary steps on the carbon-terminated NbC (111), where we have focused on the geometric and energetic properties of the adsorbed species, as well as an in-depth examination of the electronic characteristics of the CO₂ hydrogenation products on the C-terminated NbC (111) surface, which is critical for the development of more effective TMC catalysts. In agreement with experiment,¹⁵ we found that CH₄ and CO are indeed the predominant products of CO₂ hydrogenation at the C-terminated NbC (111) surface.

2. Computational details

Method

The Vienna Ab Initio Simulation Package (VASP)^35,36 has been used to perform the computations. The Perdew–Burke–Ernzerhof (PBE) variant of the extended gradient estimation within the projector augmented wave (PAW) approach has been used for the total energy calculations.^37–39 As recommended by Grimme, the DFT-D3⁴⁰ inclusion of the dispersion interactions was also taken into consideration in order to enhance the accuracy of the energy characterization of each system. Plane waves featuring a cut-off energy of 600 eV were used to extend the Kohn–Sham orbitals in the bulk and slab calculations. Monkhorst-Pack grids⁴¹ with meshes of 11 × 11 × 11 and 4 × 4 × 1 points were used to sample the Brillouin domain of the bulk and NbC (111) surface, respectively. The remaining forces and energies were adjusted until they fell below 0.01 eV Å⁻¹ and 10⁻⁵ eV, respectively. Interference between the simulation system and its images was avoided by creating a vacuum space larger than 20 Å between the surface slabs. DFT-D3 is the primary methodology used for these types of calculations in the field of heterogeneous catalysis, with similar set-ups having been reported widely in the literature, thus enabling direct comparison of our results with previous work.^32,42,43 Solvent effects were not included in our calculations. Although these may affect the adsorption characteristics of the various molecules at the surface, they would not alter significantly the relative energies of the adsorbed intermediates and thus would not affect the trends identified in this work.

Model

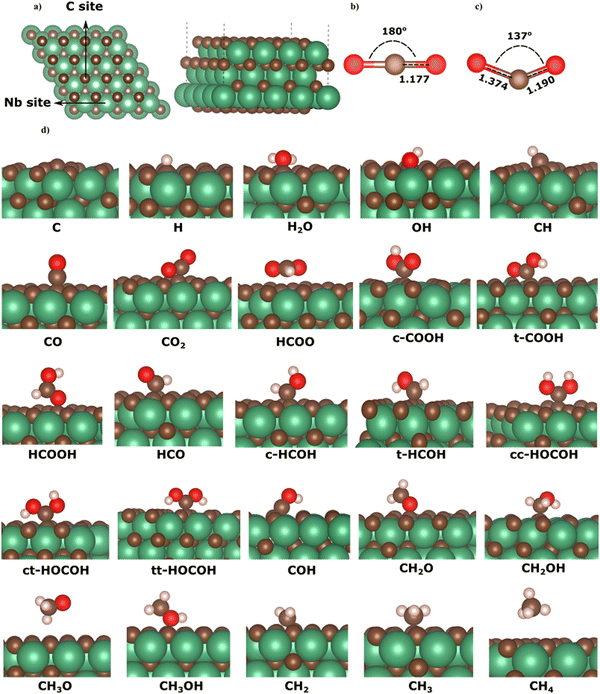
The NbC (111) surface has a hexagonal close-packed (hcp) composition terminated by either Nb or carbon atoms, which comprise the alternating layers. Other than the carbon-terminated NbC (111) surface, previous investigations in the literature have shown that carbon-terminated TMC (111) surfaces were unsustainable.^5,7,20,34 Here, we have solely focused on the C-terminated NbC (111) surface, as this termination may play an essential role in the conversion of CO₂ (see Fig. 1a). The calculated lattice constant of a₀ = 4.53 Å is in excellent agreement with the results of previous numerical (a₀ = 4.51, 4.488 Å)³ and empirical (a₀ = 4.469 Å)⁴⁴ studies. To model the surface, a supercell of 112 atoms was used, consisting of seven atomic layers, four of which were kept frozen at their bulk optimised positions to mimic the bulk material. To determine the most stable and favourable adsorption geometry, each adsorbate was initially put in numerous surface sites before full geometry optimisation. The adsorption energy of each adsorbate (E_ads) can be determined as follows:

E_ads = E_A+slab − E_A − E_slab (1)

where E_A+slab, E_A, and E_slab represent the total energies of, respectively, the system with relaxed adsorbates on the NbC (111) plane, the isolated adsorbates, and the bare NbC (111) slab. Additionally, using equation (2), changes in the charge densities have been determined as the difference between the charge density of the molecule + NbC (111) complex and the charge density of the separate molecule and surface entities in the same geometry as the complex:

ρ = ρ_{Molecule+NbC(111)} − ρ_NbC(111) − ρ_Molecule (2)

where ρ_{Molecule+NbC(111)}, ρ_NbC(111), and ρ_Molecule are the overall charges of the relaxed molecule on the NbC (111) slab, the isolated NbC (111), and isolated molecule, respectively.

Fig. 1 (a) The NbC (111) plane, and the isolated CO₂ molecule (b) prior to, and (c) following adsorption, and (d) adsorption structures with minimum energy for all intermediates on the NbC (111) plane.

The methodology employed in this study has already been validated in previous studies reported in the literature.^32,45

3. Results

3.1 Adsorption configurations and energies on NbC (111) plane

Here, we describe the adsorption on the C-terminated NbC (111) plane of all potential intermediates during the hydrogenation reactions of CO₂. Numerous preliminary configurations of the molecules situated above the NbC (111) plane at different positions were constructed. The most suitable adsorption site was selected following thorough structural optimization of both the NbC (111) plane and the intermediates. Fig. 1 shows the geometries of the lowest energy adsorptions of all intermediates on the NbC (111) plane. Table 1 likewise provides geometry and energy data, where binding between the species and the surface is denoted by the * sign, whereas the chemical bonds in each intermediate following adsorption are depicted without markings.

Table 1 Lowest energy adsorption data of all intermediate species within the CO₂ hydrogenation process at the NbC (111) plane. Intermediates-surface bonds are denoted by a * while chemical linkages within each intermediate following adsorption are indicated as unmarked

Species	E ads (eV)	Bond length (Å)	Species	E ads (eV)	Bond length (Å)
H	−5.130, −3.52^45	d*H–C = 1.10	t-HCOH	−6.342, −5.35^45	d*C–C = 1.39
					d O–C = 1.31
					d C–H = 1.10
					d O–H = 1.00
C	−11.757	d*C–C = 1.35	cc-HOCOH	−4.824	d*C–C = 1.39
	−7.61^45				d O–C = 1.34
					d O–H = 0.98
H2O	−1.226, −0.997,^32 −1.33^10	d*C–O = 1.48	ct-HOCOH	−5.302	d*C–C = 1.40
		d H–O = 1.01			d O–C = 1.32
		d H–O = 1.04			d O–H = 0.98, 1.01
OH	−5.304, −5.52,^45 −5.427^32	d*C–O = 1.31	tt-HOCOH	−5.561	d*C–C = 1.42
		d H–O = 0.98			d O–C = 1.31
					d O–H = 1.00
CH	−9.442,	d*C–C = 1.22	COH	−7.347, −4.88^45	d*C–C = 1.26
	−7.29,^45	d C–H = 1.08			d O–C = 1.27
	−7.404^32				d O–H = 1.01
CO	−4.008, −2.48^45	d*C–C = 1.32	CH2O	−1.908, −2.63^45	d*O–C = 1.36
		d O–C = 1.17			d O–C = 1.28
					d C–H = 1.09
CO2	−0.358, −0.27^10	d*C–C = 1.44	CH2OH	−4.219, −3.293,^32 −3.09^45	d*C–C = 1.50
		d*C–O = 1.62			d O–C = 1.40
		d O–C = 1.19, 1.37			d O–H = 0.99
					d C–H = 1.11, 1.12
HCOO	−0.469, −5.222^32	d O–C = 1.25	CH3O	−0.261	d O–C = 1.33
		d C–H = 1.17			d C–H = 1.13, 1.12
c-COOH	−4.155, −4.105^32	d*C–C = 1.48	CH3OH	−1.614, −0.72,^45 −0.959^32	d*O–C = 1.46
		d O–C = 1.22, 1.36			d O–H = 1.00
		d O–H = 0.98			d O–C = 1.49
					d C–H = 1.09
t-COOH	−4.408, −3.959^32	d*C–C = 1.42	CH2	−7.418,	d*C–C = 1.36
		d O–C = 1.27, 1.32		−5.797,^32	d C–H = 1.10
		d O–H = 0.98		−5.81^45
HCOOH	−1.539, −1.642^32	d*C–O = 1.41	CH3	−4.528, −3.58,^45 −3.721^32	d*C–C = 1.49
		d O–C = 1.28, 1.31			d H–C = 1.10
		d O–H = 0.98
		d C–H = 1.10
HCO	−4.214, −3.74,^45 −4.240^32	d*C–C = 1.48	CH4	−0.161, −0.298,^32 −0.17^45	d H–C = 1.10
		d O–C = 1.22
		d C–H = 1.11
c-HCOH	−6.232	d*C–C = 1.38
		d O–C = 1.33
		d O–H = 0.98
		d C–H = 1.10

---

CO₂. To evaluate the adsorption mechanism, we deposited CO₂ onto a relaxed NbC (111) slab. A C–C connection is formed between the CO₂ and the surface as it approaches a surface C atom. Furthermore, with a bond length of 1.62 Å, one of the oxygen atoms of the CO₂ binds to the surface C atom. As the C–O bond lengths change from 1.177 Å to 1.190 Å and 1.374 Å, the CO₂ adsorption leads to an alteration of its original arrangement, including a change to the O–C–O angle which reduces from 180° to 137°, which indicates activation of the CO₂ molecule on the surface. Fig. 1a–c shows the NbC (111) slab and CO₂ prior to and following attachment. CO₂ hydrogenation on this plane is more likely than on the Nb-terminated plane, where the adsorption energy was large (−1.863 eV),³² as shown by the calculated adsorption energy of −0.358 eV, which is in agreement with the results of the study by Liu et al. on the C-terminated Mo₂C (001) surface with an adsorption energy of −0.27 eV for CO₂.¹⁰ As such, the C-terminated NbC (111) could be an effective catalyst for CO₂ hydrogenation processes.

For each intermediate in the CO₂ hydrogenation reaction network, we have reported the geometries and energies of adsorption in the next section.

C. With an adsorption energy of −11.757 eV and a C–C bond length of 1.35 Å, C is strongly adsorbed on the NbC (111), in agreement with the study on the Mo₂C (100) and Mo₂C (110) surfaces where large adsorption energies of −7.61 and −7.71 eV, respectively, were obtained for the carbon atom.⁴⁵

H. Hydrogen forms an H–C connection with a bond length of 1.10 Å to the NbC (111) surface, where it tends to adsorb directly on top of a surface C atom with an adsorption energy of −5.130 eV. This large adsorption energy is in line with the findings of Silveri et al., who demonstrated that metal sites are less suitable for the attachment of the hydrogen atom.³⁴ The NbC surface, however, is more electron-rich than the TMCs containing smaller d orbitals, like TiC, with a narrower spatial expansion. As a result, it is more appealing for adsorption, and the adsorption energy is larger than TiC.²⁸ Large adsorption energies for H atoms at TMC surfaces were also seen in the work by Qi et al., obtaining −3.52 and −3.26 eV for the Mo₂C (100) and Mo₂C (110) surfaces, respectively.⁴⁵

H₂O. Water adsorbes with an energy of −1.226 eV, and it prefers to adsorb at a bridging site through its O atom (consistent with the literature¹⁰).

OH. The large adsorption energy of −5.304 eV is achieved when the molecule adsorbs at a bridging site, where its oxygen atom links to a carbon atom on the surface, in agreement with the literature.^10,45

CH. With an adsorption energy of −9.442 eV, CH tends to adsorb virtually on top of a C atom on the NbC (111) surface at a bond distance of 1.22 Å. The large adsorption energy is in accord with CH adsorption on Mo₂C surfaces (−7.29 and −7.11 eV).⁴⁵

CO. CO attaches to the NbC (111) plane through its C atom sited on top of the carbon atom of the surface, with a C–C bond length and adsorption energy of 1.32 Å and −4.008 eV, respectively. During the adsorption phase, the C–O bond length increases by around 0.03 Å.

HCOO. This molecule binds to the bridging site, almost above an underlying Nb atom, with a short distance between the C atom of HCOO and the C atom of the NbC (111) plane of approximately 2.01 Å. The adsorption energy of HCOO is −0.469 and no chemical bond is formed.

Cis-COOH and trans-COOH. C–C bonds with lengths of 1.48 Å and 1.42 Å were formed, respectively, when these molecules approach the surface. The c-COOH attaches directly on top of a surface C atom, but the t-COOH is inclined toward the bridging site in such a manner that the O atom of the t-COOH interacts with the underlying Nb atoms. c-COOH and t-COOH have adsorption energies of −4.155 eV and −4.408 eV, respectively.

HCOOH. Adsorption occurs on top of a surface C atom through an O–C bond with a bond length of 1.41 Å, and an adsorption energy of −1.539 eV. Due to the adsorption, the C–O bond lengths in the HCOOH molecule change, one decreasing by 3.7% and the other increasing by 5.8%.

HCO. With a C–C bond length of 1.48 Å and adsorption energy of −4.214 eV, HCO attaches to the surface through a surface C atom of NbC (111), with the molecule slightly inclined to the bridging site.

Cis-HCOH and trans-HCOH. These molecules adsorb in such a manner that the C atoms of c-HCOH and t-HCOH form a C–C bond to a C atom of the NbC (111) surface, with bond lengths of 1.38 Å and 1.39 Å for the cis and trans conformers, respectively. With an adsorption energy of −6.342 eV, the t-HCOH is attached directly above the surface C atom, while the c-HCOH molecule shifts to the bridging site with an adsorption energy of −6.232 eV, in accord with the 5.35 eV released for these molecules on the molybdenum carbide surface.⁴⁵

Cc-HOCOH, ct-HOCOH and tt-HOCOH. These dihydroxycarbene molecules are adsorbed on surface C atoms, with C–C bond lengths of 1.39 Å, 1.40 Å and 1.42 Å, and adsorption energies of −4.824 eV, −5.302 eV and −5.561 eV for cc-HOCOH, ct-HOCOH and tt-HOCOH, respectively.

COH. With an adsorption energy of −7.347 eV and a bond length of 1.26 Å, COH attaches to the surface through its C atom by forming a C–C bond.

CH₂O. This molecule attaches to a surface C atom through its O atom with a C–O bond length of 1.36 Å and adsorption energy of −1.908 eV.

CH₂OH. With an adsorption energy of −4.219 eV, this molecule attaches to a surface C site on NbC (111) via its C atom with a C–C bond length of 1.50 Å. Following adsorption, the original C–O bond length increases by 2.9%.

CH₃O. CH₃O adsorbs to the surface through its H atom, where the minimum distance between the molecule and the NbC (111) surface is around 2.20 Å, with an adsorption energy of −0.261 eV.

CH₃OH. At an inclination of 77.5° to the surface, this molecule adsorbs above the C atom with an O–C bond length of 1.46 Å and an adsorption energy of −1.614 eV.

CH₂. Here, the C atom is attached at the bridging site, at a C–C distance of 1.36 Å to the NbC (111) surface and an adsorption energy of −7.418 eV.

CH₃. CH₃ adsorbs to the surface through C–C bonding at 1.49 Å with and adsorption energy of −4.528 eV.

CH₄. The long interaction distance of 3.17 Å and small adsorption energy of −0.161 eV indicates physical adsorption of CH₄ at the surface.

The calculated adsorption energies of the intermediates on the C-terminated NbC (111) surface show highly localized, strong interaction between the adsorbates and the surface. All adsorption geometries where the intermediates adsorb on the surface via their carbon atoms are energetically preferred over those structures that attach to the surface via their oxygen atoms. These results indicate the formation of C–C bonds between the adsorbates and surface, in accord with the large energies released, when these species adsorb on the molybdenum carbide surface via attachment to a surface carbon atom.⁴⁵

3.2. Reaction networks in the CO₂ hydrogenation process

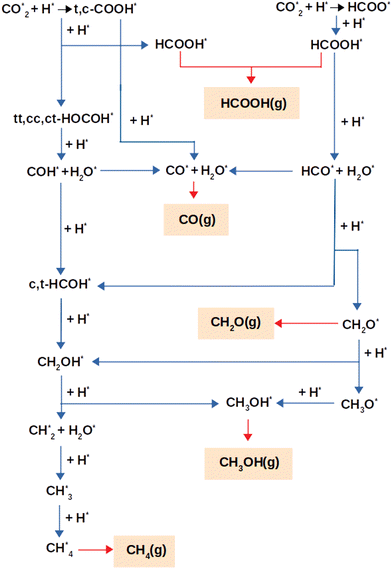
Fig. 2 depicts the reaction pathways that result in the production of the products, e.g. CO, HCOOH, CH₂O, CH₃OH, and CH₄, that were considered for this study. Mechanisms via HCOO or (trans,cis)-COOH intermediates act as the foundation for the overall reaction network. In the next section, the reaction pathways are discussed, using the optimum adsorption geometries for all intermediates.

Fig. 2 Possible CO₂ hydrogenation reaction mechanisms on the NbC (111) surface.

3.3. Chemical reactions

We have studied the possible processes of CO₂ hydrogenation over the NbC (111) plane, which are discussed in detail in this section. Table 2 shows the predicted reaction energies for all elementary steps in the hydrogenation at the NbC (111) surface.

Table 2 Possible elementary steps and their related energies

Elementary reactions	ΔE (eV)	Elementary reactions	ΔE (eV)
CO2 (g) → CO2*	−0.358	c-COOH* + H* → cc-HOCOH*	0.676
CO2* + H* → HCOO*	4.334	t-COOH* + H* → tt-HOCOH*	0.082
CO2* + H* → c-COOH*	0.369	c-COOH* + H* → ct-HOCOH*	−0.038
CO2* + H* → t-COOH*	−0.005	t-COOH* + H* → ct-HOCOH*	0.336
HCOO* + H* → HCOOH*	−2.080	cc-HOCOH* → tt-HOCOH*	−0.968
c-COOH* + H* → CO* + H2O*	−0.930	ct-HOCOH* → tt-HOCOH*	−0.254
t-COOH* + H* → CO* + H2O*	-0.556	tt-HOCOH* + H* → COH* + H2O*	1.205
c-COOH* + H* → HCOOH*	1.886	ct-HOCOH* + H* → COH* + H2O*	0.951
t-COOH* + H* → HCOOH*	2.259	cc-HOCOH* + H* → COH* + H2O*	0.237
HCOOH* + H* → HCO* + H2O*	0.234	COH* → CO* + H*	−1.843
HCOOH* → HCOOH (g)	1.539	COH* + H* → t-HCOH*	1.116
HCO* + H* → t-HCOH*	−0.090	COH* + H* → c-HCOH*	1.429
HCO* + H* → c-HCOH*	0.223	t-HCOH* + H* → CH2OH*	2.711
HCO* → CO* + H*	−3.049	c-HCOH* + H* → CH2OH*	2.398
CO* → CO (g)	4.008	CH2OH* + H* → CH2* + H2O*	−0.357
HCO* + H* → CH2O*	2.068	CH2* + H* → CH3*	1.830
CH2O* → CH2O (g)	1.908	CH3* + H* → CH4*	3.105
CH2O* + H* → CH3O*	4.857	CH4* → CH4(g)	0.161
CH2O* + H* → CH2OH*	0.553	CH3OH* → CH3OH (g)	1.641
CH3O* + H* → CH3OH*	−2.338	H2O* → H2O (g)	1.226
CH2OH* + H* → CH3OH*	1.967

---

Formate, HCOO*, or carboxyl species, trans-COOH* (t-COOH*) and/or cis-COOH* (c-COOH*) were formed as a consequence of the initial step of CO₂ hydrogenation via the reactions:

CO₂* + H* → HCOO* (3)

CO₂* + H* → (t,c)-COOH* (4)

The generation of HCOO* and c-COOH* are endothermic processes, with reaction energies of 4.334 and 0.369 eV, respectively, whereas the generation of t-COOH* is an exothermic process with an energy of −0.005 eV. Through the HCOO* + H* → HCOOH* reaction, HCOO* can gradually hydrogenate to formic acid (HCOOH), with an exothermic energy of −2.080 eV, whereas the combination of hydrogen atoms with carboxyl species (c-COOH* and t-COOH*) also forms HCOOH*. Such processes (c,t-COOH* + H* → HCOOH*) are endothermic, with cis and trans conformers requiring energies of 1.886 eV and 2.259 eV, respectively. Dihydroxycarbenes (cc-HOCOH*, ct-HOCOH*, and tt-HOCOH*) are formed through the hydrogenation of carboxyl species (c-COOH and t-COOH) via basic reactions of c,t-COOH* + H* → (ct, cc, tt)-HOCOH*. The production of tt-HOCOH* and cc-HOCOH* from t-COOH* and c-COOH* conformers is an endothermic process, with reaction energies of 0.676 eV and 0.082 eV, respectively. The production of the ct-HOCOH* conformer from t-COOH* results in the release of a reaction energy of 0.336 eV, whereas the synthesis of the ct-HOCOH* conformer from c-COOH* releases 0.038 eV of energy. Exothermic reactions of ct-HOCOH* → tt-HOCOH* and cc-HOCOH* → tt-HOCOH* with reaction energies of −0.254 and −0.968 eV, respectively, result in the converstion of ct-HOCOH and cc-HOCOH to tt-HOCOH.

This network of reactions results in additional products using two different hydrogenation mechanisms, one through HCOOH* and the other through a HOCOH*. Detailed descriptions of these mechanisms are shown below.

3.3.1. Product formation through formic acid. Fig. 3 shows the reaction profiles and associated energy values of several possible routes for the hydrogenation of CO₂ and following intermediates to HCOOH, CO, CH₂O, CH₃OH, and CH₄ over the NbC (111) surface. The reaction pathways leading to various products are discussed in further detail in the following sections.

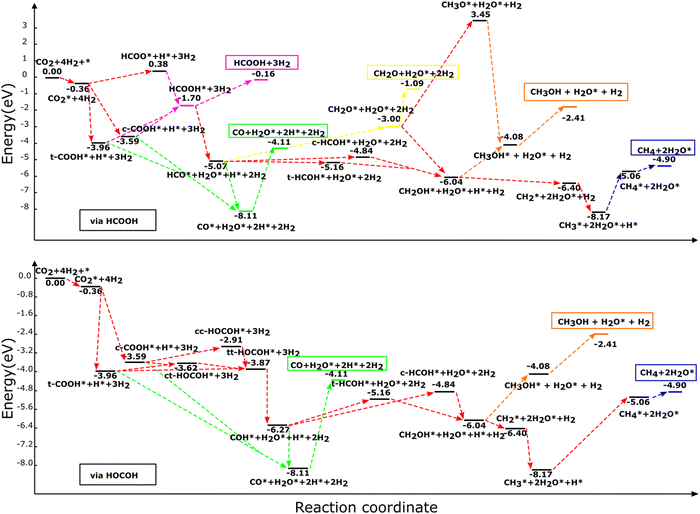Fig. 3 Reaction profile for the hydrogenation of CO₂ and all intermediates to HCOOH, CO, CH₂O, CH₃OH, and CH₄ molecules via (a) HCOOH and (b) HOCOH on the NbC (111) plane. The illustrated profiles are associated with the total free energy of the catalyst, CO₂, and four H₂ molecules in the gas phase.⁴⁶

3.3.1.1. Formic acid formation. HCOOH may be formed in any one of three ways, as was stated already. Initially, CO₂ is hydrogenated to generate HCOO* which subsequently receives another H to produce HCOOH. The other process goes through hydrogenation of CO₂ to t-COOH* or c-COOH* with the production of HCOOH* as an end product of further hydrogenation of (t,c)-COOH*. The hydrogenation of CO₂ to generate HCOO* requires 4.33 eV, whereas the synthesis of HCOOH from the HCOO* product is an exothermic reaction. Thus, the generation of HCOOH through the (t,c)-COOH* intermediate is thermodynamically more advantageous than the HCOO* pathway (see Table 2).
3.3.1.2 Carbon monoxide formation via formic acid. The (t,c)-COOH* and the HCOOH* pathways are the two main routes by which carbon monoxide is produced. In the first, CO is formed through the degradation of (t,c)-COOH* using the chemical mechanism of (t,c)-COOH* + H* → CO* + H₂O*, which are exothermic processes with reaction energies of −0.556 and −0.930 eV, for the trans and cis conformers, respectively.

Breakdown of HCOOH* to HCO* (HCOOH* + H* → HCO* + H₂O*) leads to an endothermic reaction energy of 0.234 eV, which is followed by HCO* dehydrogenation (HCO* → CO* + H*) to produce CO with a reaction energy of −3.049 eV. In consequence, the general reactions for CO production using HCOOH may be written as:

CO₂* → (t,c)-COOH* → CO* (5)

CO₂* → t-COOH* → HCOOH* → HCO* → CO* (6)

3.3.1.3 Formaldehyde formation via formic acid. The sole pathway to obtain CH₂O from CO₂ is via HCO*, where HCO* accepts hydrogen to generate CH₂O. Formaldehyde (CH₂O*) or (c,t)-HCOH* may be formed via the hydrogenation of HCO*, with an endothermic energy of 2.068 eV for HCO* + H* → CH₂O*. As a result, the following are the main reactions involved in producing CH₂O:

CO₂* → HCOO*, (t,c)-COOH* → HCOOH* → HCO* → CH₂O* (7)

3.3.1.4. Methanol formation via formic acid. It has been suggested previously that with reaction energies of 0.223 eV and −0.090 eV, respectively, for the cis and trans conformers, hydrogenation of HCO* may result in the creation of (c,t)-HCOH* through the reaction HCO* + H* → (c,t)-HCOH*. HCO* hydrogenation should therefore generate the t-HCOH* conformer more often, since it is an exothermic reaction.

Additional hydrogenation of (c,t)-HCOH* or CH₂O* may lead to the formation of CH₃OH. t-HCOH* and CH₂O* are hydrogenated, but the former occurs through the t-HCOH* + H* → CH₂OH* mechanism, whereas the latter is achieved through CH₂O* via CH₂O* + H* → CH₂OH*. In order to produce CH₂OH*, a total of 2.711 eV and 0.553 eV of energy is required for the two separate processes. CH₂OH* is more likely to be generated via CH₂O* hydrogenation than through t-HCOH*, because the hydrogenation of CH₂O* to CH₂OH* is more efficient in terms of energy than the hydrogenation of t-HCOH*. Continuing the hydrogenation of CH₂OH* results in the formation of CH₃OH* (CH₂OH* + H* → CH₃OH*), distinguished by its endothermic nature with an energy of 1.967 eV. Hydrogenation of CH₂O* may also produce methoxy (CH₃O*), in addition to CH₂OH*. However, whereas this mechanism happens via CH₂O* + H* → CH₃O* and consumes a significant amount of energy (4.857 eV), the following hydrogenation stage leads to CH₃OH* via CH₃O* + H* → CH₃OH* which releases just 2.338 eV of reaction energy. Although it is energetically possible to produce CH₃OH using CH₃O, the recommended method is to go through CH₂OH* hydrogenation to produce CH₃OH* owing to the less endothermic reaction involved. For CH₃OH* synthesis, the suggested sequence of steps is as follows:

CO₂*→ HCOO*, (t,c)-COOH* → HCOOH* → HCO* → CH₂O*, (c,t)-HCOH* → CH₂OH* → CH₃OH* (8)

3.3.1.5. Methane formation via formic acid. Only dissociation of CH₂OH* (CH₂OH* + H* → CH₂* + H₂O*) results in the synthesis of CH₂*, and the end products CH₃* and CH₄*. Reactions CH₂* + H* → CH₃ and CH₃* + H* → CH₄* may generate CH₄* by hydrogenating CH₂* and CH₃* with reaction energies of 1.830 eV and 3.105 eV for the production of CH₃* and CH₄*, respectively. The following is an ordinary sequence, indicating some reactions that contribute to the synthesis of CH₄* from HCOOH*:

CO₂* → HCOO*, (t,c)-COOH* → HCOOH* → HCO* → CH₂O*, (c,t)-HCOH* → CH₂OH* → CH₂* → CH₃* → CH₄* (9)

3.3.2. Product formation via dihydroxycarbene. It has already been mentioned that the hydrogenation of (t,c)-COOH* may generate CO, CH₃OH, and CH₄. As a result of the exothermic nature of the transformation of cc-HOCOH* and ct-HOCOH* to tt-HOCOH* ((cc,ct)-HOCOH* + H* → tt-HOCOH*), with respective energies of −0.968 eV and −0.254 eV, the tt-HOCOH* species is likely to be dominant on the surface.
3.3.2.1. Carbon monoxide formation via dihydroxycarbene. From the direct breakdown of (t,c)-COOH*, CO* may be produced, although it can also be produced via COH*. The first route was described in detail in Section 3.3.1.2, where the processes were found to be exothermic with energies of −0.556 eV via the cis and −0.930 eV via the trans conformer. In the second route, COH* and H₂O* are formed via the breakdown of the most suitable HOCOH* conformers (tt-HOCOH*) via the reaction tt-HOCOH* + H* → COH* + H₂O* with a reaction energy of 1.205 eV. Further breakdown of COH* (COH* → CO* + H*) leads to the generation of CO*. CO* tends to be created through the COH* route with the exothermic mechanism of creating CO* from COH* with a reaction energy of −1.843 eV. As a consequence, the reactions for CO production using HOCOH* could be written as:

CO₂* → (t,c)-COOH* → CO* (10)

CO₂* → (t,c)-COOH* → (cc,ct,tt)-HOCOH* → COH* → CO* (11)

3.3.2.2. Methanol production from dihydroxycarbene. Trans-HCOH* or cis-HCOH* is formed after addition of a hydrogen atom via COH* + H* → t-HCOH* and COH* + H* → c-HCOH* with endothermic energies of 1.116 eV and 1.429 eV, respectively. Further hydrogenation of (t,c)-HCOH* results in the formation of CH₂OH* via the process (t,c)-HCOH* + H* → CH₂OH*. CH₃OH* is then generated through additional hydrogenation of CH₂OH*. The creation of CH₂OH* from (t,c)-HCOH* and the generation of CH₃OH* from CH₂OH* are endothermic processes with reaction energies of 2.711 eV, 2.398 eV and 1.967 eV. Based on the relative energies, we suggest that the following route is the most likely to lead to the generation of CH₃OH*:

CO₂* → (t,c)-COOH* → (cc,ct,tt)-HOCOH* → COH* → (t,c)-HCOH* → CH₂OH* → CH₃OH* (12)

3.3.2.3. Methane formation via dihydroxycarbene. Decomposition of CH₂OH* into either HOCOH or HCOOH results in the production of CH₂* and its further hydrogenation. As a result, the following route is suggested to generate CH₄* via HOCOH*:

CO₂* → (t,c)-COOH* → (cc,ct,tt)-HOCOH* → COH* → (t,c)-HCOH* → CH₂OH* → CH₂* → CH₃* → CH₄* (13)

3.4. Electronic properties from CO₂ adsorption

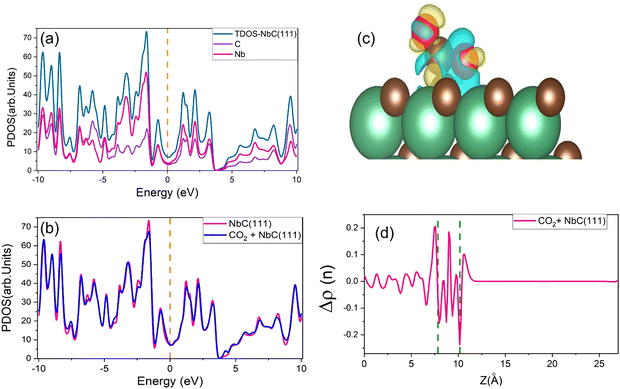
Charge densities and total densities of state (TDOS) are calculated to gain more detailed insight into the CO₂ adsorption at the NbC (111) surface. The density of states is large around the Fermi level, as seen in Fig. 4a, and there is no energy gap at this level. A partly filled d band and potentially occupied s orbital in NbC may contribute to the metal characteristics of the compound, which is consistent with previous observations.^3,4 The TDOS behaves in a manner comparable to the behavior of the DOS of the Nb atoms, and both above and below the Fermi level, the participation of Nb atoms in the TDOS is much greater than that of the C atoms, because the electronic structure of NbC is defined by surface states formed of Nb 4d orbitals at about E_F.^47,48 However, Fig. 4b demonstrates that whenever a CO₂ molecule is adsorbed on the NbC (111) surface, there is no substantial variation in the TDOS, apart from a slight increase at the Fermi level.

Fig. 4 (a) The PDOS for the NbC (111) surface, (b) the TDOS of NbC (111) prior to and after adsorption of CO₂, (c) view of the charge density differences, with the C and O atoms illustrated in brown and red (isovalue = ±0.002) and, (d) the planar average charge density. The Fermi level is set at zero.

Next, we have used equation (2) to determine the charge density difference caused by CO₂ adsorption by considering separately the charge density of CO₂ + NbC (111), the bare slab, and the isolated CO₂. Fig. 4c depicts the rearrangement of charge density in the system following CO₂ adsorption, where yellow indicates a positive charge difference and blue indicates a negative charge difference. CO₂ is seen to have accumulated negative charge upon adsorption at the surface. We have also used the planar mean charge density differential Δρ(z)²³ to investigate the charge rearrangement of CO₂ following adsorption on NbC (111), as shown below:

Δρ(z) = Δρ(z)_{Molecule+NbC(111)} − Δρ(z)_NbC(111) − Δρ(z)_Molecule (14)

where Δρ(z)_{Molecule+NbC(111)}, Δρ(z)_NbC(111), and Δρ(z)_Molecule represent the planar mean charge densities of the relaxed Molecule + NbC(111) system, bare NbC (111) slab, and the isolated CO₂ molecule, respectively. The dashed zone in Fig. 4d represents the site of CO₂ on the NbC (111) surface. The negative (positive) values of Δρ(z) zones indicate the charge density increase (depletion) sites following the adsorption of CO₂.

3.4.1 Electronic properties of the products. TDOS and charge densities for CH₄, CO, CH₂O, and CH₃OH products are shown in Fig. 5 to better explain the desorption mechanism. Whether present or absent from the surface, the TDOS for CH₄ and CO adopt a similar pattern, as seen in Fig. 5a and b, particularly near the Fermi level. As seen in Fig. 5c and d, the TDOS for CH₃OH and CH₂O shift somewhat towards positive energies and diverge from the NbC (111) TDOS when the adsorbates are present. From the data presented here, it can be concluded that modest variations in charge transmission happen throughout the adsorption process. Given the nature of their bonding to the surface, the TDOS of the adsorption arrangements for CH₃OH and CH₂O deviate further from the TDOS of the bare slab than those for CH₄ and CO. In contrast to the CH₄ and CO molecules adsorbing on the surface using their carbon atoms, the CH₃OH and CH₂O compounds connect to the surface using their oxygen atoms, causing the NbC (111) TDOS to deviate by a small amount from those of the bare surface.

Fig. 5 The TDOS, the planar average charge densities, and charge density differences for (a) CH₄ (isovalue = ±0.00005), (b) CO (isovalue = ±0.001), (c) CH₃OH (isovalue = ±0.002) and, (d) CH₂O (isovalue = ±0.002). The Fermi level is set at zero.

4. Conclusion

In this investigation, we have calculated the energetics of the interaction of 25 reactant, intermediate and product species at the carbon-terminated NbC (111) surface and we have evaluated their reactions in the CO₂ hydrogenation process, where it has been shown that methane has the maximum capacity for hydrogen of all the investigated products.

CH₂O generation is expected to be produced predominantly from HCOOH rather than other intermediates, because the endothermic reaction energies for the production of CH₄, CH₃OH and CO via HCOOH are rather high, and the route through HCOOH is thus not practical for the synthesis of CH₃OH, CH₄ or CO. The suggested pathways for each product have been collected in Fig. 6 to allow direct comparison. According to our findings, 4.902 eV in energy is generated during CO₂ hydrogenation to methane over the C-terminated NbC (111) surface through the route:

CO₂* → t-COOH* → tt-HOCOH* → COH* → t-HCOH* → CH₂OH* → CH₂* → CH₃* → CH₄* → CH₄ (g) (15)

Fig. 6a shows the desorption of CH₄ into the gas phase as a result of this reaction. The second strongly exothermic CO₂ hydrogenation mechanism, releasing an energy of 4.107 eV, is the route to CO generation (Fig. 6b):

CO₂* → t-COOH* → tt-HOCOH* → COH* → CO* → CO (g) (16)

and

CO₂* → t-COOH* → CO* → CO (g) (17)

The obtained results are in agreement with experiments, which have suggested that CH₄ and CO are the main products of CO₂ hydrogenation over transition metal carbides.^15,45

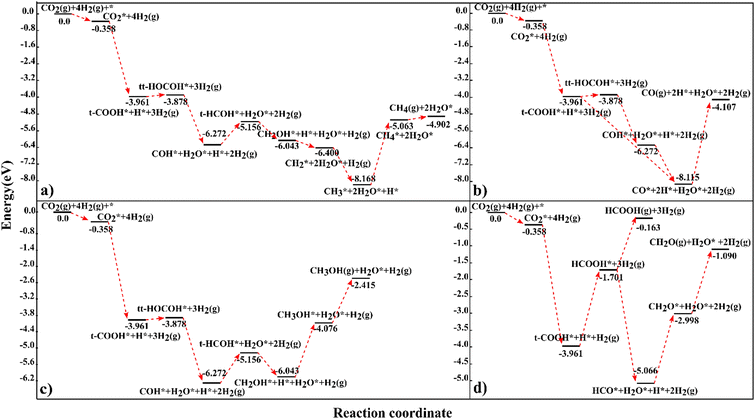Fig. 6 The preferred reaction profiles for CO₂ hydrogenation to (a) CH₄, (b) CO, (c) CH₃OH, and (d) CH₂O and HCOOH on the NbC (111) plane. The illustrated profiles are compared to the summation of the total free energies of the catalyst, CO₂, and four H₂ in the gas phase.⁴⁶

CH₃OH is the third possible product with an exothermic energy of 2.415 eV, through the preferred route (Fig. 6c):

CO₂* → t-COOH* → tt-HOCOH* → COH* → t-HCOH* → CH₂OH* → CH₃OH* → CH₃OH(g) (18)

Fig. 6d shows that CH₂O and HCOOH production, releasing energies of 1.090 and 0.163 eV, respectively, are the least likely products of CO₂ hydrogenation based on the routes:

CO₂* → t-COOH* → HCOOH* → HCO* → CH₂O* → CH₂O(g) (19)

and

CO₂* → t-COOH* → HCOOH* → HCOOH (g) (20)

In conclusion, we have used DFT calculations to investigate a comprehensive network of reaction pathways for CO₂ hydrogenation to CH₄, CO, CH₃OH, CH₂O and HCOOH over the carbon-terminated NbC (111) surface. By evaluating the predicted reaction energies, we can conclude that the most abundant products should be CH₄ and CO, followed to a lesser extent by CH₃OH, CH₂O, and HCOOH, which findings are in excellent agreement with experimental findings.

The calculated adsorption energies of the intermediates on the surface show highly localized strong interactions between the adsorbates and the surface, which lead to an overall exothermic reaction pathway that provides sufficient energy to overcome the desorption energy required to release the products from the surface. Furthermore, where there is co-adsorption of the hydrogen and the intermediates at the surface, the hydrogenation step energies indicate that the presence of hydrogen on the surface makes the intermediates more reactive, which as a result readily undergo further surface-mediated reactions to form CH₄, CO and the other products.

The carbon-terminated (111) surfaces of TMCs are generally less stable than the metal-terminated planes. However, Quesne et al.⁵ calculated the energies of both carbon- and metal-terminated surfaces across the TMC series, where the carbon-terminated (111) surfaces of NbC, TaC, MoC and WC were found to be preferred over the metal-terminated surfaces. The carbon-terminated NbC (111) was also found to be important in a number of other studies,^5,7,20,34 whereas our results also indicate that the carbon-terminated NbC (111) surface remains stable during the adsorption of CO₂. Furthermore, the results from this study indicate that CO₂ adsorption on the carbon-terminated NbC (111) surface at E_ads = −0.358 eV is weaker than at the metal-terminated NbC (111) with E_ads = −1.863 eV (calculated in our previous study³²). We have also found a larger exothermic reaction energy for CO₂ methanation on the carbon-terminated surface, releasing 4.902 eV, than the same process at the metal-terminated surface, releasing 2.747 eV, as calculated in our previous work.³² Overall, the results suggest that the carbon-terminated surface should be a promising catalyst for CO₂ hydrogenation, allowing an energetically favourable hydrogenation process.

From our calculations, we can make a number of secondary observations. For example, it is much more advantageous to produce CO immediately from either t-COOH or COH* degradation through the tt-HOCOH route. Furthermore, the majority of CH₄, CO, and CH₃OH is generated by t-COOH* via the tt-HOCOH route, whereas the majority of CH₂O originates from HCO* via the HCOOH reaction. Along these routes, HCO* fragmentation has the highest exothermic reaction energy of −3.049 eV, whereas CH₃* hydrogenation to CH₄* requires the highest endothermic reaction energy of 3.105 eV.

It is worth mentioning that in this study we have only investigated the thermodynamics of the reactions, without considering the kinetics and activation energies. The proposed mechanisms were suggested based on the comparative reaction energies of the different pathways, which identified the energetically favoured reaction mechanism. The inclusion of transition states in the catalytic pathways would provide further insight, for example allowing us to identify the rate-determining step, but it would not invalidate the thermodynamically favourable reaction pathway.

We have also assessed the electronic features of the system of CO₂ and the intermediates formed as a result of its hydrogenation over the C-terminated NbC (111) surface, which have indicated that the adsorbates have little effect on the surface.

This work has led to detailed understanding of some of the fundamental steps in the CO₂ catalytic hydrogenation mechanism at the C-terminated NbC (111) surface which results in the production of C1 type surface species. Since the field of CO₂ hydrogenation still requires significant advances in the understanding of reaction mechanisms for C–C coupling, for synthesis of higher alcohols and higher hydrocarbons, further potential pathways leading to the production of other useful compounds have yet to be explored. However, we consider that the results of this work may assist experiment in the development of effective catalysts based on transition metal carbides.

Data availability statement

The data that support the findings of this study are available on request from the corresponding author.

Conflicts of interest

There are no competing interest to declare.

Acknowledgements

S. S. T thanks the Iran National Science Foundation (INSF) Grant No. 97020912 for the financial support of this investigation. The authors are also grateful to the Research Affairs Division of the Amirkabir University of Technology (AUT), Tehran, Iran, for their financial support. This work has used the computational facilities of the Advanced Research Computing at Cardiff (ARCCA) Division, Cardiff University, and HPC Wales. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431), this work has also used the ARCHER2 UK National Supercomputing Service (http://archer2.ac.uk).

References

1. B. I. Sharma, J. Maibam, R. Paul, R. Thapa and R. B. Singh, Indian J. Phys., 2010, 84, 671–674.
2. J. A. Rodriguez, J. Evans, L. Feria, A. B. Vidal, P. Liu, K. Nakamura and F. Illas, J. Catal., 2013, 307, 162–169.
3. F. Viñes, C. Sousa, P. Liu, J. Rodriguez and F. Illas, J. Chem. Phys., 2005, 122, 174709.
4. K. Kobayashi, Jpn. J. Appl. Phys., 2000, 39, 4311.
5. M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2018, 20, 6905–6916.
6. H. W. Hugosson, O. Eriksson, U. Jansson and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 134108.
7. H. H. Hwu and J. G. Chen, Chem. Rev., 2005, 105, 185–212.
8. A. Vojvodic, C. Ruberto and B. I. Lundqvist, J. Phys.: Condens. Matter, 2010, 22, 375504.
9. F. Viñes, J. A. Rodriguez, P. Liu and F. Illas, J. Catal., 2008, 260, 103–112.
10. P. Liu and J. A. Rodriguez, J. Phys. Chem. B, 2006, 110, 19418–19425.
11. N. M. Schweitzer, J. A. Schaidle, O. K. Ezekoye, X. Pan, S. Linic and L. T. Thompson, J. Am. Chem. Soc., 2011, 133, 2378–2381.
12. P. M. Patterson, T. K. Das and B. H. Davis, Appl. Catal., A, 2003, 251, 449–455.
13. C. Kunkel, F. Vines and F. Illas, Energy Environ. Sci., 2016, 9, 141–144.
14. S. Posada-Pérez, F. Vines, P. J. Ramirez, A. B. Vidal, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2014, 16, 14912–14921.
15. M. D. Porosoff, S. Kattel, W. Li, P. Liu and J. G. Chen, Chem. Commun., 2015, 51, 6988–6991.
16. S. Posada-Pérez, F. Viñes, P. J. Ramirez, A. B. Vidal, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2014, 16, 14912–14921.
17. M. D. Porosoff, X. Yang, J. A. Boscoboinik and J. G. Chen, Angew. Chem., 2014, 126, 6823–6827.
18. Q. Zhang, L. Pastor-Pérez, W. Jin, S. Gu and T. R. Reina, Appl. Catal., B, 2019, 244, 889–898.
19. S. Posada-Pérez, P. J. Ramírez, R. A. Gutiérrez, D. J. Stacchiola, F. Viñes, P. Liu, F. Illas and J. A. Rodriguez, Catal. Sci. Technol., 2016, 6, 6766–6777.
20. M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760.
21. Z. Ou, C. Qin, J. Niu, L. Zhang and J. Ran, Int. J. Hydrogen Energy, 2019, 44, 819–834.
22. S. Posada-Pérez, P. J. Ramírez, J. Evans, F. Viñes, P. Liu, F. Illas and J. A. Rodriguez, J. Am. Chem. Soc., 2016, 138, 8269–8278.
23. N. Y. Dzade and N. H. d Leeuw, Catalysts, 2021, 11, 127.
24. S. S. Tafreshi, A. Z. Moshfegh and N. H. de Leeuw, J. Phys. Chem. C, 2019, 123, 22191–22201.
25. X. Liu, C. Kunkel, P. Ramírez de la Piscina, N. Homs, F. Viñes and F. Illas, ACS Catal., 2017, 7, 4323–4335.
26. K. Edamoto, E. Shiobara, T. Anazawa, M. Hatta, E. Miyazaki, H. Kato and S. Otani, J. Chem. Phys., 1992, 96, 842–847.
27. K. Edamoto, E. Miyazaki and H. Kato, Vacuum, 1990, 41, 547–549.
28. S. Tokumitsu, T. Anazawa, K. Ozawa, R. Sekine, E. Miyazaki, K. Edamoto, H. Kato and S. Otani, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4516.
29. K. Edamoto, Y. Abe, T. Ikeda, N. Ito, E. Miyazaki, H. Kato and S. Otani, Surf. Sci., 1990, 237, 241–247.
30. K. Edamoto, S. Maehama, E. Miyazaki and H. Kato, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 7461–7465.
31. K. Ozawa, S. Ishikawa, E. Miyazaki, K. Edamoto, H. Kato and S. Otani, Surf. Sci., 1997, 375, 250–256.
32. S. Sarabadani Tafreshi, M. Ranjbar, N. Taghizade, S. F. K. S. Panahi, M. Jamaati and N. H. de Leeuw, ChemPhysChem, 2022, 23, e202100781.
33. K. E. Tan, M. W. Finnis, A. P. Horsfield and A. P. Sutton, Surf. Sci., 1996, 348, 49–54.
34. F. Silveri, M. G. Quesne, A. Roldan, N. H. De Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2019, 21, 5335–5343.
35. A. S. Botana and M. R. Norman, Phys. Rev. Mater., 2019, 3, 044001.
36. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
37. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891.
38. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
40. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
41. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
42. S. S. Tafreshi, A. Roldan and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2015, 17, 21533–21546.
43. S. Sarabadani Tafreshi, S. F. K. S. Panahi, N. Taghizade, M. Jamaati, M. Ranjbar and N. H. de Leeuw, Catalysts, 2022, 12, 1275.
44. https://icsd.products.fiz-karlsruhe.de .
45. K.-Z. Qi, G.-C. Wang and W.-J. Zheng, Surf. Sci., 2013, 614, 53–63.
46. R. A. Angnes, mechaSVG, GitHub repository, 2020 DOI:10.5281/zenodo.3970267.
47. K. Ozawa, S. Ishikawa, S. Tokumitsu, R. Sekine, E. Miyazaki, K. Edamoto, H. Kato and S. Otani, Surf. Sci., 1996, 364, L612–L616.
48. K. Ozawa, S. Ishikawa, K. Edamoto, H. Kato and S. Otani, Surf. Sci., 1999, 419, 226–235.

---