Interfacially-adsorbed particles enhance the self-propulsion of oil droplets in aqueous surfactant

Abstract

Understanding the chemo-mechanical mechanisms that direct the motion of self-propulsive colloids is important for the development of active materials and exploration of dynamic, collective phenomena. Here, we demonstrate that the adsorption of solid particles on the surface of solubilizing oil droplets can significantly enhance the droplets’ self-propulsion speeds. We investigate the relationship between the self-propulsion of bromodecane oil droplets containing silica particles of varying concentration in Triton X-100 surfactant, noting up to order of magnitude increases in propulsion speeds. Using fluorescently labeled silica, we observe packing of the particles at the oil–water interfaces of the rear pole of the moving droplets. For bromodecane oil droplets in Triton X-100, the highest droplet speeds were achieved at approximately 40% particle surface coverage of the droplet interface. We find particle-assisted propulsion enhancement in ionic surfactants and different oil droplet compositions as well, demonstrating the breadth of this effect. While a precise mechanism for the propulsion enhancement remains unclear, the simple addition of silica particles to droplet oil–water interfaces provides a straightforward route to tune active droplet dynamics.

---

Introduction

Understanding and developing chemo-mechanical mechanisms to direct the motion of colloids is a growing interest area in the field of active matter.^1,2 An important consideration when designing chemotactic active colloids is the mechanism by which asymmetric forces will be generated and applied to direct the particle motion. Perhaps the most common approach is to create Janus particles wherein the asymmetry is permanently built into the particle, such as having sides of differing surface chemistry or anisotropic shape.³ However, isotropic colloids, such as spherical liquid droplets, can also propel when exposed to chemical gradients in the surroundings.⁴ In the case of active droplets, motion is typically driven by interfacial tension gradients and Marangoni flows induced by interfacial reactions^5,6 or by micelle-mediated solubilization, a process wherein the droplet contents are transferred into the continuous micellar phase.⁷ It has been proposed that the solubilizate-surfactant interactions and the “filling” of the surfactant micelles correspond to increased interfacial tensions at the droplet surface, and thus droplets propel towards regions of “empty” micelles.^2,8,9 For an isotropic droplet to move via chemotaxis, asymmetry in the chemical gradient across the droplet surface must be maintained, such as by feedback processes involving advective transport dominating over diffusion (e.g. high Péclet number),¹⁰ an externally applied chemical gradient^9,11 or the presence of another nearby droplet that modifies the chemical gradient symmetry.^8,12 Exploring mechanisms by which to impose asymmetry into active colloids is an important step towards controlling properties such as propulsion speed, sensitivity, directionality, and energy efficiency.

In this work, we explore the effect of particles adsorbed at droplet oil–water interfaces on the self-propulsive behaviors of solubilizing oil droplets in nonionic and ionic surfactant solutions. It is well known that particles can adsorb to liquid–liquid interfaces, such as in Pickering emulsions.^13,14 We demonstrate that interfacial adsorption of particles can lead to significant increases in droplet speed, often by over an order magnitude, compared to self-propulsion of solubilizing droplets without particles. We visualized fluorescently-labeled silica particles during the droplet propulsion and determined that the particles pack together to create a cap on the rear pole of the droplet. The degree of surface coverage by this particle cap influenced the droplet speed in a non-monotonic fashion. Bromodecane droplets in Triton X-100 surfactant exhibited the highest speed enhancement when silica particles covered roughly 40% of the droplet surface. Droplets which solubilize but do not self-propel, such as bromooctane in 0.5 wt% Triton X-100, can also be induced to rapidly swim via the addition of surface-active particles. The simple addition of particles to droplet surfaces thus expands our ability to not only tune droplet propulsion speeds, but also broadens the chemical compositions which can be used to create active droplets. These advances may inspire new design approaches for active colloidal swimmers.

Experimental

Materials

Fumed silica particles were generously provided by Wacker Chemie (products HDK S13, HDK H13L, HDK H20RH). The S13 silica had no surface modification, H13L had 50% surface coverage of dimethylsiloxy groups, and H20RH silica had 75% surface coverage of long (∼16 carbons on average) saturated hydrocarbon chains. These fumed silica particles are amorphous aggregates with sizes ranging from 100–500 nm with primary particles of 5–50 nm as reported by the supplier. Other chemicals used include aminopropyl triethoxysilane (APTES) (TCI, 96%), 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC) (Chem Impex Int’l, 99.8%), 2-morpholinoethanesulfonic acid (MES) (Chem Impex Int'l, 99.8%), N-hydroxysuccinimide (NHS) (Chem Impex Int’l, 99.5%), Fluorescein sodium salt (Fluka), bromooctane (Alfa Aesar, 98%), bromodecane (Frontier Scientific, 98%), bromododecane (Alfa Aesar, 98%), bromohexadecane (TCI, 96%), brominated vegetable oil (Spectrum), Triton X-100 (TX) (Alfa Aesar), sodium dodecyl sulfate (SDS) (Sigma Aldrich, 99%), cetyltrimethylammonium bromide (CTAB) (Sigma Aldrich). All chemicals were used as received without further purification.

Preparation of oil-in-water emulsions

Silica particles were first dispersed in oil using a probe sonicator (QSonica Q700). These dispersions were immediately used to fabricate droplets. Unless specified otherwise, droplets were made with a volume ratio of 1 : 10 oil to surfactant solution and were emulsified using a Vortex Genie 2 at its maximum setting (3200 rpm) for 3–5 seconds in 1-dram glass vials. Given that bulk emulsification was used, the droplets had a resultant dispersity in size as well as particle concentration in each droplet.

Brightfield and fluorescence microscopy

To visualize the droplets, 0.5 μL of droplets were pipetted into a glass-bottom dish containing surfactant solution. Droplets were gently agitated to disperse them randomly within the dish. Videos of the droplet motion were taken using a Nikon Ti–U inverted microscope and an Andor Zyla 4.2P camera. Typically, several videos for each set of sample conditions were taken and analyzed to provide sufficient statistical data on droplet speeds and particle surface coverages. Fluorescence images were collected with excitation (AT480/30x) and emission (AT535/40m) filters.

Analysis of droplet speed

The videos for speed analysis were taken with a 6× magnification, 1024 × 1024 resolution, and 30 fps using an Andor Zyla 4.2P camera. Instantaneous droplet speed was analyzed with a MATLAB program as reported previously.^8,15 An average speed was assigned to a sample by averaging the maximum speeds of all the droplets captured within a video. We report the average of the maximum speed and the standard deviation of the maximum speed as seen in Fig. 1 and 5. For the data presented in Fig. 3, each data point represents the maximum speed attained for a single droplet while it was imaged such that we could correlate that speed directly with a particle surface coverage value. Please note that we did not attempt to account for drift velocity due to convection in any of our reported speed measurements. In our experience, drift velocity is less than 10 μm s⁻¹ which is much slower than the self-propelled droplets that can move upwards of 200 μm s⁻¹.

Fig. 1 Silica particles affect the self-propulsion of oil droplets in surfactant solution. (a) 1-Bromodecane oil droplets without particles and with 0.5 wt% H13L silica were dispersed in 0.1 wt% TX and the droplet trajectories were analyzed. Shown are the droplet trajectories over a 60 second period. Droplets without particles were not active, and droplets with particles swam much faster, reaching peak speeds of about 50 μm s⁻¹. Scale, 1 mm. (b) The speed of bromodecane droplets was investigated for various aqueous TX concentrations and H13L particle concentrations. The speed of a droplet was defined as the maximum speed reached during the droplet's lifetime in the video frame. Data shown represent the average and standard deviation for a sample size of at least 10 droplets per experimental condition. The inset shows an optical micrograph of a droplet at 2 wt% particle concentration in 0.1 wt% TX where the packing of the nanoscale particles at the droplet surface become visible, showing high surface coverage. When higher concentrations of TX surfactant are used, we do not often see such fully packed surfaces and the droplets may experience significant motion even at 2 wt% particles. Scale, 50 μm.

Particle surface functionalization with fluorescein to create fluorescently labeled particles

Functionalization of S13 with APTES. In a 25 mL round bottom flask, 250 mg of dry S13 particles were dispersed in 10 mL of acetone. 100 μL of 30 wt% ammonium hydroxide in water was then added, followed by 300 μL of APTES. The flask was then sealed with a septum and sonicated in a bath sonicator (Branson 1510) for 1 hour. The solution was then diluted with acetone to a volume of 30 mL and centrifuged at 7100 RCF for 10 minutes. The supernatant was decanted and the particles were re-dispersed in acetone through sonication and centrifuged again at 7100 RCF for 10 minutes to pellet the particles. The supernatant was discarded, and the nanoparticle pellet was collected and dried overnight. The particles were redispersed in 25 mL of MES buffer (0.5 M, pH 5) for use in the following step. Carbodiimide coupling of fluorescein and amine terminated S13. 125 mL of MES buffer (0.5 M, pH 5) was added to a 250 mL flask, followed by 342.1 mg of fluorescein sodium salt, 165.9 mg of EDC, and 246 mg of NHS. The solution was stirred at room temperature for 30 minutes, and then the 25 mL MES solution of amine-functionalized S13 particles was added. The flask was sealed using a septum, covered in foil, and left to react at room temperature for 24 hours while stirring. The solution was then diluted with acetone and excess reagents were removed similarly to the previous step by using centrifugation, washing, and drying. The particles were dispersed in 10 mL of hexane for use in the following step. Making florescent particles hydrophobic. The 10 mL of fluorescein-functionalized particles were added to a 25 mL round bottom flask followed by 200 μL of diethylamine and 1.5 mL of hexadecyltriethoxysilane. The flask was sealed with a septum and left to react for 24 hours while stirring and covered with foil. The solution was then diluted with acetone and excess reagents were removed similarly to the previous steps by using centrifugation, washing, and drying, ultimately producing hydrophobic, fluorescent fumed silica.

Thermogravimetric analysis (TGA) of dry, functionalized silica particles

The weight loss of functionalized silica particles was monitored by TGA (Discovery Series TGA Q5500).^16,17 TGA traces taken for particles produced after each functionalization step are shown in Fig. S1 (ESI†). The silica particles were heated in air from 25 °C to 120 °C at 10 °C min⁻¹ and held in isotherm for 10 minutes to remove residual solvent. Particles are then heated to 800 °C at 20 °C min⁻¹. The normalized weight loss was then calculated from mass change between 120 °C and 800 °C.

Analysis of particle surface coverage on droplets

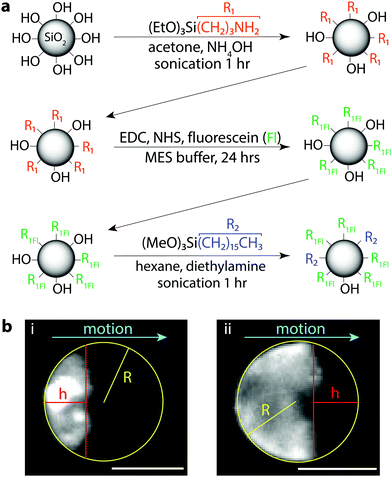
Surface coverage of droplets coated with fluorescent silica nanoparticles were determined from fluorescence images of the droplets. We approximated the particle coverage as a symmetric, spherical cap of particles. From the images, droplet radius and cap radius are measured to calculate the approximate surface coverage of droplets, as shown in Fig. 2. There is notable error inherent within this approximation, given that the particles are not distributed evenly throughout the cap or cap edges, the surface aggregates can become rough or non-spherical due to particle packing, and some distortion in the images is created due to droplet motion during the image exposure, which was necessarily long (30–60 ms) to capture sufficient fluorescence intensity.

Fig. 2 Fluorescence visualization of particles at droplet interfaces. (a) Schematic describing the preparation of fluorescent, hydrophobic fumed silica. (b) The particle surface coverage of a droplet was estimated using fluorescence micrographs. Fluorescence images of two different droplets, both prepared with 1 wt% fluorescent particles in bromodecane with 0.5 wt% TX, are shown as examples. Overlaid diagrams illustrate how particle surface coverage was estimated by assuming a spherical cap, where h is the height of the cap and R is the radius of the droplet (and cap). For (i), estimated fractional surface coverage = h/2R = 32%, and for (ii) fractional surface coverage = 1 − h/2R = 70%. Scale, 50 μm.

Results and discussion

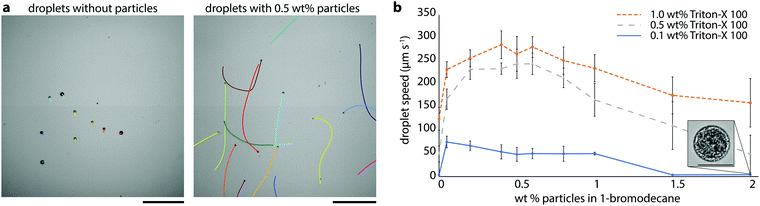
To test whether particles at droplet interfaces might influence self-propulsion of solubilizing oil droplets, we began by examining the effect of partially hydrophobic silica particles on the swimming speeds of 1-bromodecane droplets in aqueous Triton X-100 (hereafter, TX). TX is a nonionic surfactant which has previously been shown to generate active oil droplets via micelle-mediated solubilization.⁸ Bromodecane was chosen because it is an oil with low water solubility, such that solubilization is expected to be micelle-mediated,⁸ and it is denser than water such that the droplets sink to the bottom substrate, lending to ease of experimentation. We chose partially hydrophobized fumed silica particles (H13L produced by Wacker Chemie, 150–500 nm, 50% coverage with dimethylsiloxy groups and 50% residual surface silanols) to favor particle wetting by both oil and water and enhance interfacial activity; these particles are, however, still preferentially dispersible in the oil phase. We prepared polydisperse bromodecane droplets with and without 0.5 wt% H13L particles in 0.1 wt% TX by vortex mixing and examined the droplet dynamics using optical microscopy and droplet tracking analysis (refer to Methods section for details). Droplets were polydisperse but typical diameters of droplets that were analyzed fell in the range of 20–100 μm. The bromodecane droplets without particles moved slowly, no more than 3 μm s⁻¹ (Fig. 1a, left). However, droplets with the silica particles were self-propelled and moved significantly faster, on the order of 50 μm s⁻¹, rapidly careening through the imaging chamber (Fig. 1b and Video S1, ESI†). Qualitatively, it was evident from these initial experiments that the particles had a notable effect on the droplet dynamics.

In order to quantify the relationship between particle concentration, surfactant concentration, and droplet speed, we conducted a series of experiments with aqueous TX surfactant concentrations between 0.1 wt% and 1 wt% and H13L particle concentrations in bromodecane between 0 wt% and 2 wt%. For each sample, we used a standardized procedure in which a small number of droplets (typically less than 20 droplets in 0.5 μL of solution) were extracted from the emulsion sample vial and added to a glass-bottom dish containing 1 mL the same surfactant concentration in which the droplets were prepared. The solution was gently agitated to randomly disperse the droplets, and videos of the droplets were collected over 60 seconds. Droplet trajectories and instantaneous speeds were analyzed using Matlab image analysis.^8,15 Given that the droplets often swam in curved trajectories and exhibited variation in instantaneous speed that was dependent on the path, we used the maximum speed each droplet reached during the video as the basis for comparison. Averages and standard deviations for the resultant maximum speeds for each set of experimental conditions are given in Fig. 1b and Table S1 (ESI†). Droplets exhibited faster speeds in higher surfactant concentrations for a given particle concentration. These trends with surfactant concentration are consistent with a solubilization-driven, micelle-mediated propulsion mechanism.² Higher particle concentration, however, did not always correlate to faster speeds, and instead there was a maximum in droplet speed at intermediate particle concentrations (Fig. 1b). The particle concentration yielding the fastest speeds varied slightly as a function of TX concentration with the droplet speed peaking at around 0.2 wt% to 0.5 wt% H13L particles. At lower particle concentrations, we could not see the particles clearly within the droplets, but at higher particle concentrations, we observed large irregular particle aggregates on the droplets’ surfaces (Fig. 1b inset). We suspected that the particle concentration in the droplet was correlated with the number of particles at the droplet interface and the total displaced oil–water interfacial area, which was, in turn, affecting the droplet speeds.

To directly correlate the particle concentrations to droplet interfacial coverage and speeds, we needed to be able to directly visualize the particles at the droplet surface, such as with fluorescence. We aimed to modify the fumed silica particles with a fluorescent dye, fluorescein, while still retaining a particle surface activity similar to that of the H13L (Fig. 2a). Starting from pristine hydrophilic fumed silica, we functionalized the silanol surface with aminopropyl triethoxysilane (APTES) and then coupled the surface amine with the carboxylic acid of fluorescein sodium salt via carbodiimide coupling chemistry using 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide (EDC) and N-hydroxysuccinimide (NHS). At this stage, the particles were still hydrophilic and dispersed easily in water, so we further functionalized remaining surface silanol groups with hexadecyltrimethoxysilane to render the particles more hydrophobic. After functionalization, the particles were fluorescent and dispersible in the bromodecane. Please refer to the Methods section for specific reaction details and particle surface analysis.

To test if the hydrophobized fluorescent silica could be used for particle visualization, the particles were dispersed into bromodecane at 2 wt% and emulsions were prepared by vortex mixing the bromodecane/particle mixture in 0.5 wt% TX. Immediately upon placing the droplets into fresh surfactant solution for imaging, the droplets were non-mobile and most of the fluorescent particles were dispersed inside the droplets. Over a short time, particles that were circulating inside the droplets began to accumulate at the droplet surface and aggregate, eventually being pushed towards the rear pole of the droplet as the droplet started to propel quickly forward (Fig. 2b and Video S2, ESI†). Using the fluorescent particles, we could visualize the degree of droplet interfacial coverage once the droplets reached a steady-state speed, which we approximated from the micrographs as the surface area of a spherical cap (Fig. 2b). This is a rough estimate, as the particles were not perfectly packed at the interface, the edges of the particle cap were not straight, and we could not visualize the 3D surface coverage around all sides of the droplet simultaneously. There was also some image blur in the fluorescence micrographs because the droplets were moving during the camera exposure time, which was necessarily long (30–60 ms) in order to capture sufficient light intensity to visualize the fluorescent particles.

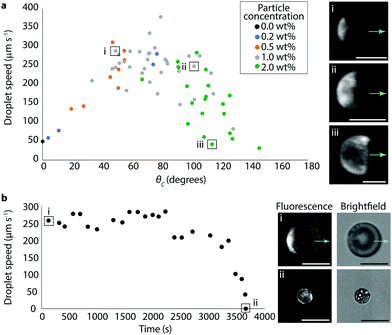
Despite the approximations necessary to quantify surface coverage, we could still visualize the particles sufficiently to correlate the particle coverage with droplet behavior. Bromodecane droplets with fluorescent particle concentrations in the range of 0.2–2 wt% were prepared in 0.5 wt% TX and videos of the droplets under both brightfield and fluorescence were collected (see Video S3 as an example of a fluorescence video, ESI†). From these videos, both speed and surface coverage were measured for individual droplets; surface coverages were converted to cap coverage angle, θ_c, where θ_c = 0° is an uncovered droplet and θ_c = 180° is a fully covered droplet. The speed of the droplets as a function of the coverage angle and particle concentration is shown in Fig. 3a. Droplet speed showed a non-monotonic dependence on particle coverage with the propulsion speed lowest at small (θ_c ≈ 0°) and large (θ_c ≈ 180°) surface coverages. The maximum speed attained was in the range of about 300 μm s⁻¹ at approximately 40% surface coverage, with θ_c just below 90°. Particle concentrations correlated roughly with surface coverage, as expected based on the data in Fig. 1b, although there was still notable variation likely due to dispersity in the numbers of particles within each droplet resultant from the preparation method. The fact that there exists significant variation in surface coverage as a function of initial particle concentration in the bromodecane also explains the relatively large error bars of Fig. 1b.

Fig. 3 Degree of droplet surface covered by particles affects droplet speed. The scatterplot shows the relationship between bromodecane droplet speed and surface coverage with particles in 0.5 wt% TX. Surface coverage is plotted as coverage cap angle θ_c, where θ_c = 0° corresponds to no particle coverage and θ_c = 180° corresponds to complete coverage. Each datapoint represents a single droplet's surface coverage and highest speed reached during imaging. The color coding of the datapoints represents the initial concentration of particles used when preparing the droplet. Black = 0.0 wt%, blue = 0.2 wt%, orange = 0.5 wt%, grey = 1.0 wt%, and green = 2.0 wt% fluorescent particles in bromodecane. The initial particle concentration showed a general correlation with droplet surface coverage, where higher particle concentrations were more likely to produce droplets with higher surface coverages. Fluorescence micrographs of three exemplary droplets are shown and the arrows represent direction of droplet motion. Scale, 50 μm. (b) The scatterplot shows the evolution of a single bromodecane droplet's speed over its lifetime of about an hour in 0.5 wt% TX. The droplet started with fast speeds and moderate particle coverage (θ_c ≈ 50°). Over time, the particle coverage increased while the droplet volume decreased due to solubilization, until eventually the droplet motion ceased with θ_c ≈ 180°. Fluorescence and brightfield micrographs are given at right. The arrows represent the direction of droplet motion. Scale, 100 μm.

The evolution of droplet speed as a single droplet solubilizes over time in 0.5 wt% TX is shown in Fig. 3b. With moderate starting surface coverage (θ_c ≈ 50°), the droplet initially propelled at ∼250 μm s⁻¹ and maintained a similar speed for about 30 minutes, at which point the speed began to decrease until eventually the droplet was nonactive and completely coated with particles. The surface area of the initial particle patch was estimated to be approximately 11 600 μm² and the surface area of the final, fully-covered droplet was estimated to be approximately 10 200 μm²; this indicates that the vast majority of particles are irreversibly adsorbed such that as the droplet volume shrinks, the total surface coverage by particles stays constant and the percent surface coverage increases. A small decrease in particle-covered surface area might be attributed to adsorbed particles jamming more tightly. Using the trajectory from Fig. 3b, we estimate that this droplet had a cruising range of about 0.8 meter over its lifetime of an hour. Droplets with different starting surface coverages or droplet volumes would have different cruising ranges.

We consider the following framework to conceptually rationalize the trends observed in the data of Fig. 3. The measured propulsion speed is around 300 μm s⁻¹ for a half-coated droplet, which, upon using a droplet radius a_drop = 50 μm and kinematic viscosity of 1 μm² s⁻¹, gives a Reynolds number Re = 1.5 × 10⁻². Thus, the droplet motion is in the creeping flow, or low Reynolds number, regime. The oil undergoes solubilization into the aqueous solution, through the formation of oil-filled micelles that are stabilized via uptake of surfactant monomer adsorbed at the oil–water interface. We assume that the flux j_m of oil filled micelles into the aqueous solution is constant. A mass balance on the oil in the drop shows that 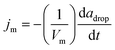, where a_drop is the radius of the oil drop, V_m is the volume of an oil filled micelle, and t is time. The rate of change of the drop radius is small, O (0.01 μm s⁻¹), compared to the propulsion velocity observed in experiments, O (100 μm s⁻¹); hence, the drop radius is assumed to be essentially constant during propulsion. The solubilization consumes adsorbed surfactant at a rate dj_m, where d is the number of surfactant monomers per oil filled micelle, or aggregation number. Replenishment of surfactant at the oil–water interface occurs via adsorption of monomers from the bulk solution. The bulk concentration of surfactant monomer is expected to remain uniform and equal to the critical micelle concentration (C_CMC) during the solubilization process, as a result of an abundance of empty micelles that, via rapid dissociation, rectify the deficit in bulk surfactant concentration due to adsorption.¹⁸

The concentration of adsorbed surfactant may vary along the droplet surface via surface diffusion and advection with the local interfacial fluid flow. Such variation will lead to gradients in surface tension along the oil–water interface that, in turn, drive Marangoni stresses, potentially causing droplet propulsion. The droplets propel with the particle-uncoated portion of their surface facing forward (Fig. 2b and Fig. 3). We therefore expect that there is a gradient of adsorbed surfactant along the droplet interface, where the adsorbed surfactant concentration is highest at the front of the drop and lowest towards the rear. The surface tension therefore follows the opposite trend: highest at the back and lowest at the front. Thus, Marangoni stresses drive an interfacial flow toward the back of the droplet (i.e., the interface is “pulled” backward by the higher interfacial tension at the rear of the drop).

The relative importance of surface diffusion to advection is characterized by a Péclet number Pe = Ua/D_s, where U is the propulsion speed of the drop, and D_s is the surface diffusion coefficient. Using a typical speed U = 100 μm s⁻¹, drop size a_drop = 50 μm, and D_s = 150 μm² s⁻¹ yields Pe = 33. (We have assumed, in the absence of better information, that the surface diffusion coefficient of surfactant monomer is equal to the bulk diffusion coefficient.¹⁹) Hence, advection dominates diffusion. In this regime, it has recently been predicted that droplets in a micellar solution (with bulk surfactant concentration above the C_CMC) can spontaneously self-propel due to a Marangoni instability,¹⁸ resulting from the nonlinear dependence of the advective interfacial flux of surfactant on the interfacial velocity and surfactant concentration. A similar self-propulsion mechanism for a solid particle coated by enzymes that are mobilized by diffusiophoretic flows, generated by a concentration gradient in the product species of the enzymatic reaction, has also recently been proposed.²⁰

Indeed, the particle-free (0 wt%) bromodecane droplets in Fig. 1 do exhibit self-propulsion at the higher surfactant concentrations, which we believe is due to a Marangoni instability as reported by many researchers.^7,21 However, it is important to note that even stationary droplets, such as the particle-free bromodecane in 0.1 wt% TX, still generate fluid pumping from top to bottom, as visualized using side-oriented transmission optical microscopy (Video S4, ESI†). Here, the asymmetry that induces the interfacial flows is imposed by the presence of the substrate, where there is a sustained, higher concentration of oil and higher interfacial tension at the droplet bottom (Fig. 4a). The solubilized oil gradients are axially symmetric so there is no net lateral Marangoni force and the droplet does not translate (i.e. is not self-propelled). The vertical Marangoni force is counterbalanced by gravity. While these “top to bottom” flows do not generate lateral force, they can lead to, and are necessary for, the initial packing of the silica particles along the droplet surface which we believe is the first step in inducing particle-enhanced propulsion.

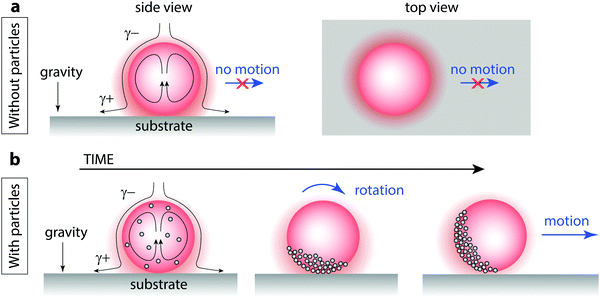Fig. 4 Spontaneous polarization of particles on solubilizing oil droplet interfaces leads to enhanced self-propulsion. (a) An oil droplet that solubilizes but does not self-propel can still experience an interfacial tension gradient from top to bottom where the asymmetry is imposed by the substrate. Solubilized oil builds up near the solid surface, generating Marangoni flows that advect oil-free surfactant from above (side view). The droplet does not move laterally because the oil solubilization is axially symmetric about the vector perpendicular to the surface (top view). γ+ indicates an elevated interfacial tension and γ− indicates a lowered interfacial tension. See Video S4 (ESI†). (b) When particles are introduced, advection of the interfacially-adsorbed particles creates a cap. Once the cap rotates, droplets move laterally; droplets move most quickly when the particle cap is oriented perpendicular to the substrate. See Videos S5 and S6 (ESI†).

We propose that the addition of particles leads to an enhancement in self-propulsion by breaking the symmetry of the interfacial Marangoni flow that is otherwise axially symmetric about the vector perpendicular to the substrate (Fig. 4b). Interfacial flows, present even in stationary solubilizing droplets, serve to advect interfacially-adsorbed particles and pack them to form a cap. In this cap region, it is still unclear precisely how the particles are affecting the interfacial tension gradients, but it appears that an inhomogeneous distribution of particles within the cap can lead to spontaneous cap rotation; once the cap rotates, now the Marangoni force has a lateral component that drives the droplet to propel sideways (Video S5, ESI†). A droplet with a particle cap that is axially symmetric about the vector perpendicular to the surface still pumps fluid from top to bottom at a rate similar to the non-coated drop and remains stationary; the tilting of the particle cap relative to the substrate appears key to lateral motion, as observed with side-view transmission optical microscopy (Video S6, ESI†). Future research will be necessary to fully understand the role of particles in inducing the cap rotation and enhanced lateral propulsion.

To explore the generality of this particle-assisted propulsion, we examined the swimming behaviors of bromodecane in several different surfactants and surfactant concentrations. Bromodecane droplets containing 1 wt% fluorescent particles were emulsified in anionic sodium dodecyl sulfate (SDS), cationic cetyl trimethyl ammonium bromide (CTAB), and nonionic TX of varying concentration. Individual droplets within each sample were tracked and characterized to determine their maximum speed and particle coverage. Only droplets that had between 30% and 50% surface coverage were included in the data shown in Fig. 5 and Tables S2, S3 (ESI†) to account for possible differences in particle surface activity under the varying surfactant conditions.²² Without particles, bromodecane droplets had slow swimming speeds in all concentrations of the ionic surfactants, SDS and CTAB, (<20 μm s⁻¹), although the bromodecane was solubilizing at a noticeable rate (0.03 and 0.06 μm min⁻¹ respectively, Table S4, ESI†). Inclusion of particles increased the droplet speed by over an order of magnitude for many conditions (Video S7, ESI†), and the enhancement increased at higher SDS and CTAB concentrations. Addition of 0.25 M NaCl to 1 wt% and 5 wt% SDS or 1 wt% and 2.5 wt% CTAB marginally increased droplet speeds without particles and also increased solubilization rates slightly, potentially due to screening of the electrostatic repulsion between the charged micelles and interface (Tables S2 and S4, ESI†). Addition of salt in the presence of particles, however, led to significantly faster droplet speeds in 1 wt% SDS-particles-salt (345.9 ± 74.4 μm s⁻¹) and in 1 wt% CTAB-particles-salt (251.6 ± 42.9 μm s⁻¹). Adding salt did not significantly influence the speed of droplets in nonionic surfactant TX-stabilized droplets with or without particles. These results suggest that salt affects the propulsion via surfactant-salt interactions or surfactant-particle-salt interactions, rather than just interactions between the salt and particles alone. In the case of SDS and CTAB, addition of salt may also cause a change in the CMC,^23,24 and salt also may also allow the particles to pack together more tightly by screening charge on the fumed silica resulting from ionic surfactant-particle association.²⁵

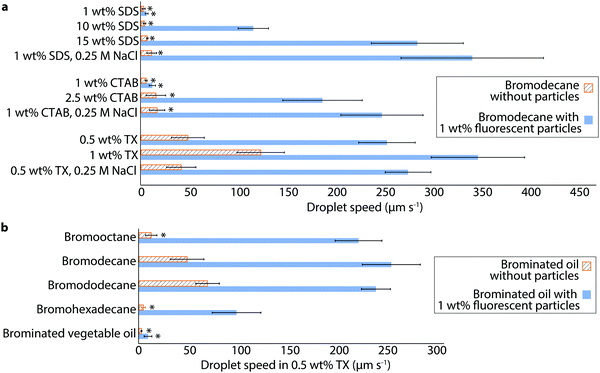Fig. 5 Enhanced self-propulsion of oil droplets of varying oil and surfactant chemistry. (a) Speeds of bromodecane droplets with and without 1 wt% fluorescent silica particles were measured in different concentrations of SDS, CTAB, and TX surfactant, with and without NaCl. The asterisk (*) indicates that the droplets were noticeably drifting rather than self-propelling, as distinguished by the droplets all moving in the same direction. The speeds of droplets prepared with ionic surfactants, SDS and CTAB, were sensitive to the addition of 0.25 M NaCl, whereas droplets in nonionic TX were not. (b) Speeds of various brominated oils with and without 1 wt% fluorescent silica particles were measured in 0.5 wt% TX. See Table S4 (ESI†) for solubilization rates. All oils, except for brominated vegetable oil which had indetectable solubilization, showed significant enhancement in self-propulsion speed due to the surface adsorption of silica particles. Each bar shows the average and standard deviation of a minimum of 5 droplet measurements. The data plotted in (a and b) is tabulated in Tables S2 and S3 (ESI†). Only droplets with 30–50% surface coverage of particles were included in this data to account for possible differences in particle surface adsorption with variation in oil or surfactant.

Given that the oil droplets are propelled by interfacial tension gradients resultant from oil-surfactant interactions, we wondered to what extent oil droplets of varying chemistry and solubilization rates would be influenced by particles. We measured the speeds of 1-bromooctane, 1-bromodecane, 1-bromododecane, 1-bromohexadecane, and brominated vegetable oil droplets with and without 1 wt% fluorescent particles in 0.5 wt% TX (Fig. 5b and Table S3, ESI†). Again, we only consider here droplets with particle surface coverage in the range of 30–50%. All oils except the brominated vegetable oil exhibited enhanced propulsion speeds with particles present. Without particles, the solubilization rates of these oils are 0.41, 0.24, 0.13, <0.01, and <0.01 μm min⁻¹, respectively, where the bromohexadecane and brominated vegetable oil did not solubilize to a measurable extent within one hour (Table S4, ESI†). We do believe, however, that the bromohexadecane still solubilizes, albeit at a slow rate, given previous reports of measurable solubilization of hexadecane in TX.²⁶ Brominated vegetable oil is quite viscous containing molecules of high molecular weight and is thus expected to solubilize even more slowly than the bromohexadecane; brominated vegetable oil droplets do not even form a particle cap. This observation is consistent with the idea that solubilization and the generation of oil gradients is a requirement for sustaining interfacial Marangoni flow that initially packs the particles at the droplet interface and leads to propulsion; while particles can significantly enhance the speed of droplets that undergo some degree of solubilization, particles alone cannot generate propulsion in the absence of solubilization.

Conclusion

In summary, we have demonstrated that adsorption of silica nanoparticles at the interface of a solubilizing oil droplet in surfactant solution can significantly accelerate the droplets’ self-propulsion speed. The polarization of the particles across the droplet surface arises spontaneously to form a cap, and using fluorescent particle visualization, we correlated the degree of particle surface coverage on bromodecane droplets to the droplet speed in TX surfactant. Slowest speeds were found at the lowest and highest surface coverages and the fastest speeds were achieved at intermediate surface coverages of about 40%. The particle-assisted propulsion acceleration was further demonstrated in nonionic, anionic, and cationic surfactants and a range of oils with varying solubilization rates. Future work will include development of fluid mechanical models to understand the role of interfacially adsorbed particles on the droplet behaviors. Approaches by which to modulate the distribution of solubilization and interfacial flow across droplet interfaces, such as by addition of particles, may provide a facile route to tuning active colloid speeds and dynamics. Further exploration involving stimuli-responsive particles²⁷ or droplets containing multiple oils²⁸ with particles at droplet-internal oil–oil interfaces²⁹ may provide new opportunities for tuning the behaviors of swimming droplets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge financial support from the American Chemical Society Petroleum Research Fund (Grant 59833-DNI10), the Army Research Office (Grant W911NF-18-1-0414), and from the Charles E. Kaufman Foundation of the Pittsburgh Foundation (Grant 1031373-438639). We thank Pepijn Moerman for the Matlab code which we used in tracking droplet speeds.

References

1. K. K. Dey and A. Sen, Chemically Propelled Molecules and Machines, J. Am. Chem. Soc., 2017, 139(23), 7666–7676.
2. C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Swimming Droplets, Annu. Rev. Condens. Matter Phys., 2016, 7(1), 171–193.
3. A. M. Pourrahimi and M. Pumera, Multifunctional and Self-propelled Spherical Janus nano/micromotors: Recent Advances, Nanoscale, 2018, 10(35), 16398–16415.
4. S. Lach, S. M. Yoon and B. A. Grzybowski, Tactic, Reactive, and Functional Droplets Outside of Equilibrium, Chem. Soc. Rev., 2016, 45(17), 4766–4796.
5. T. Toyota, N. Maru, M. M. Hanczyc, T. Ikegami and T. Sugawara, Self-propelled Oil Droplets Consuming “Fuel” Surfactant, J. Am. Chem. Soc., 2009, 131(14), 5012–5013.
6. M. M. Hanczyc, T. Toyota, T. Ikegami, N. Packard and T. Sugawara, Fatty Acid Chemistry At The Oil-water Interface: Self-propelled Oil Droplets, J. Am. Chem. Soc., 2007, 129(30), 9386–9391.
7. Z. Izri, M. N. Van Der Linden, S. Michelin and O. Dauchot, Self-propulsion Of Pure water droplets By Spontaneous Marangoni-stress-Driven Motion, Phys. Rev. Lett., 2014, 113(24), 1–5.
8. C. H. Meredith, P. G. Moerman, J. Groenewold, Y. J. Chiu, W. K. Kegel and A. van Blaaderen, et al., Predator–prey Interactions Between Droplets Driven By Non-reciprocal Oil Exchange, Nat. Chem., 2020, 12(12), 1136–1142,  DOI:10.1038/s41557-020-00575-0.
9. C. Jin, C. Kru-ger and C. C. Maass, Chemotaxis And Autochemotaxis Of Self-propelling Droplet Swimmers, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(20), 5089–5094.
10. S. Michelin, E. Lauga and D. Bartolo, Spontaneous Autophoretic Motion Of Isotropic Particles, Phys. Fluids, 2013, 25(6), 061701.
11. I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, Maze Solving By Chemotactic Droplets, J. Am. Chem. Soc., 2010, 132(4), 1198–1199.
12. P. G. Moerman, H. W. Moyses, E. B. Van Der Wee, D. G. Grier, A Van Blaaderen and W. K. Kegel, et al., Solute-mediated Interactions Between Active Droplets, Phys. Rev. E, 2017, 96, 032607.
13. B. P. Binks and T. S. Horozov, Colloidal Particles At Liquid Interfaces, Cambridge University Press, 2006.
14. B. P. Binks, Colloidal Particles At A Range Of Fluid-Fluid Interfaces, Langmuir, 2017, 33(28), 6947–6963.
15. J. C. Crocker and D. G. Grier, Methods Of Digital Video Microscopy For Colloidal Studies, J. Colloid Interface Sci., 1996, 179(1), 298–310.
16. F. M. Wisser, M. Abele, M. Gasthauer, K. Müller, N. Moszner and G. Kickelbick, Detection Of Surface Silanol Groups On Pristine And Functionalized Silica Mixed Oxides And Zirconia, J. Colloid Interface Sci., 2012, 374(1), 77–82,  DOI:10.1016/j.jcis.2012.01.015.
17. R. Mueller, H. K. Kammler, K. Wegner and S. E. Pratsinis, OH Surface Density Of SiO₂ And TiO₂ By Thermogravimetric Analysis, Langmuir, 2003, 19(1), 160–165.
18. M. Morozov, Adsorption Inhibition By Swollen Micelles May Cause Multistability In Active Droplets, Soft Matter, 2020, 16(24), 5624–5632.
19. X. W. Fang, S. Zhao, S. Z. Mao, J. Y. Yu and Y. R. Du, Mixed micelles of cationic-nonionic surfactants: NMR self-diffusion studies of Triton X-100 and cetyltrimethylammonium bromide in aqueous solution, Colloid Polym. Sci., 2003, 281(5), 455–460.
20. M. De Corato, I. Pagonabarraga, L. K. E. A. Abdelmohsen, S. Sánchez and M. Arroyo, Spontaneous polarization and locomotion of an active particle with surface-mobile enzymes, Phys. Rev. Fluids, 2020, 5(12), 1–11.
21. B. V. Hokmabad, R. Dey, M. Jalaal, D. Mohanty, M. Almukambetova and K. A. Baldwin, et al., Emergence of Bimodal Motility in Active Droplets, Phys. Rev. X, 2021, 11(1), 11043,  DOI:10.1103/PhysRevX.11.011043.
22. H. Katepalli and A. Bose, Response of Surfactant Stabilized Oil-in-Water Emulsions to the Addition of Particles in an Aqueous Suspension, Langmuir, 2014, 30, 12736–12742.
23. T. D. Gurkov, D. T. Dimitrova, K. G. Marinova, C. Bilke-Crause, C. Gerber and I. B. Ivanov, Ionic Surfactants On Fluid Interfaces: Determination Of The Adsorption; Role Of The Salt And The Type Of The Hydrophobic Phase, Colloids Surf., A, 2005, 261(1–3), 29–38.
24. S. Mahbub, M. R. Molla, M. Saha, I. Shahriar, M. A. Hoque and M. A. Halim, et al., Conductometric And Molecular Dynamics Studies Of The Aggregation Behavior Of Sodium Dodecyl Sulfate (SDS) And Cetyltrimethylammonium Bromide (CTAB) In Aqueous And Electrolytes Solution, J. Mol. Liq., 2019, 283, 263–275,  DOI:10.1016/j.molliq.2019.03.045.
25. H. Wang, V. Singh and S. H. Behrens, Image Charge Effects On The Formation Of Pickering Emulsions, J. Phys. Chem. Lett., 2012, 3(20), 2986–2990.
26. H. Zhong, L. Yang, G. Zeng, M. L. Brusseau, Y. Wang and Y. Li, et al., Aggregate-based sub-CMC solubilization of hexadecane by surfactants, RSC Adv., 2015, 5(95), 78142–78149.
27. J. Tang, P. J. Quinlan and K. C. Tam, Stimuli-responsive Pickering Emulsions: Recent Advances And Potential Applications, Soft. Matter., 2015, 11(18), 3512–3529,  10.1039/C5SM00247H.
28. R. V. Balaj and L. D. Zarzar, Reconfigurable Complex Emulsions: Design, Properties, And Applications. Chem, Phys. Rev., 2020, 1(1), 011301.
29. S. I. Cheon, L. Batista Capaverde Silva, R. Ditzler and L. D. Zarzar, Particle Stabilization of Oil–Fluorocarbon Interfaces and Effects on Multiphase Oil-in-Water Complex Emulsion Morphology and Reconfigurability, Langmuir, 2020, 36, 7083–7090.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02234a

---