Unprecedented neptunyl(V) cation-directed structural variations in Np2Ox compounds†
Zhong-Fei
Xu‡
ab,
Wen-Jing
Zhang‡
ab,
Ping
Zhang
b and
Shu-Xian
Hu
 *ab
*ab
aDepartment of Physics, University of Science and Technology Beijing, Beijing 100083, China. E-mail: hushuxian@csrc.ac.cn
bBeijing Computational Science Research Center, Beijing, 100193, China
First published on 30th August 2021
Abstract
Studies on transuranic oxides provide a particularly valuable insight into chemical bonding in actinide compounds, in which subtle differences between metal ions and oxygen atoms are of fundamental importance for the stability of these compounds as well as their existence. In the case of neptunium, it is still mainly limited to specific Np oxide compounds without periodicity in the formation of stable structures or different oxidation states. Here, we report a systematic global minimum search of Np2Ox (x = 1–7) clusters and the computational study of their electronic structures and chemical bonding. These studies suggest that Np(V) ion could play the structure-directing role, and thus the mixed-valent Np(III/V) in Np2O4 is predicted accessible. In comparison with lower oxidation state Np analogues, significant 5f-orbital covalent interactions with Np(V)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding are observed, which shows that these model neptunium oxides can provide new understandings into the behavior of 5f-electrons in chemical bonding and structural design.
O bonding are observed, which shows that these model neptunium oxides can provide new understandings into the behavior of 5f-electrons in chemical bonding and structural design.
1. Introduction
Nanoscience sometimes produces results that are more mystifying than in any other discipline. Acceptably, neptunium is one of the most complex and fascinating chemical elements in the periodic table.1 Changes in neptunium dioxide (NpO2) particle size from bulk to nanoparticles (NPs) could have a dramatic effect on NpO2 properties. In different solution environments, Np has been known to exist and even co-exist in several oxidation states, from Np(III) to Np(VII).1c,2 Among those oxidation states, the pentavalent neputonium within the NpO2+ cation is the most widely concerned neptunium species both in nuclear reprocessing technology and under environmentally relevant conditions.2,3 Recently, it was repeatedly found that neptunium oxide NPs are produced during nuclear waste processing under oxidizing conditions, and formed in interfacial processes between neptunium of different initial oxidation states and various mineral surfaces, and found as bonded to mineral or organic colloids in the groundwater.4 All these results indicate the high importance of neptunium oxide NPs in the context of the environmental behavior of neptunium. A complete understanding of neptunium oxides at a fundamental level is therefore essential if one is to design future nuclear waste remediation and separation cycles, as well as to develop advanced fuel cycles. Quantum chemistry methods can be used to study radioactive neptunium safely via the geometry structure and the electronic structure of such NPs.5Small neptunium oxide clusters can be prepared by laser ablation of neptunium metal in the presence of an oxygen-saturated atmosphere. In the presence of oxygen gas, neptunium oxide clusters such as NpO2 and Np2O5 have already been generated and detected.6 Several experimental studies have already been applied to study the structural, energetic, vibrational, electronic, and magnetic properties of neptunium oxide clusters.3a,7 For example, the photoionization spectra of NpOx were measured and strongly size-dependent ionization potentials were observed.8 For the NpO2 molecule, the electron–spin resonance and optical spectroscopy in neon and argon matrices revealed that its ground state is a 2Δ state, and the molecular bond length and vibrational frequency have been predicted to be 1.761 Å and 942 cm−1,9 respectively. Accompanying these experimental results, several theoretical calculations were also performed to explore the ground-state electronic structures of neptunium oxide clusters,10 however, most of those studies were mostly focused on the monomer neptunium oxide clusters.11 In this paper, we systematically study the atomic and electronic structures of neutral dimer Np oxide clusters, which provide more conclusive properties of Np materials with a systematic oxidation state than the monomer species.
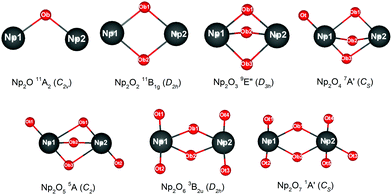
2. Results and discussion
2.1. Electronic structure and oxidation state in new neptunium complexes
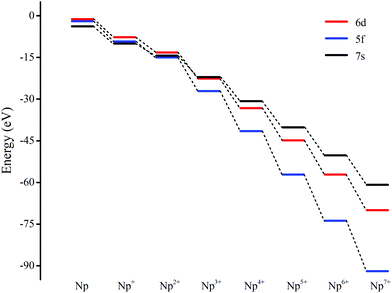
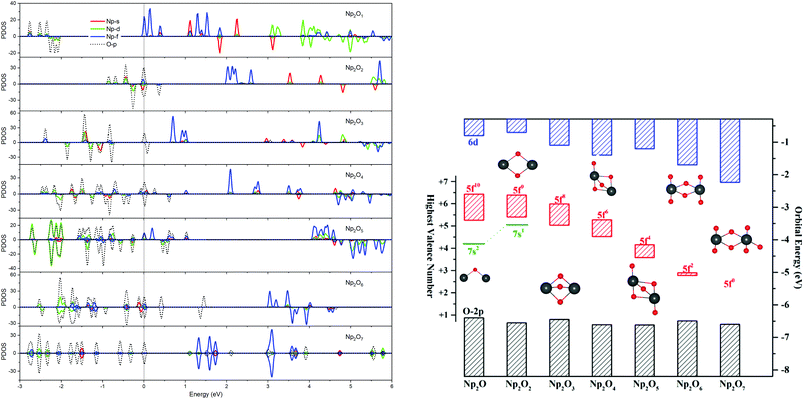
The most intriguing question concerning Np2Ox nanoparticles is the potential presence of various oxidation states of neptunium. Global minimum searching by using particle-swarm optimization methodologies based Crystal Structure Analysis in Particle Swarm Optimization (CALYPSO) code12 combined with full geometry optimization performed at DFT levels (GGA+U and PBE/TZ2P)13 were firstly carried out and followed by DLPNOCCSD(T)14 energy corrections to predict the ground-state structures corresponding to each potential energy profiles. Based on the most stable structure, which is shown in Fig. 1, the electronic structure, and chemical bonding analyses were further explored. The series of Np2Ox molecules are fascinating for at least three reasons: (1) each lowest-energy structure appears to be the primary product of the reaction between two Np atoms and the oxygen atoms. (2) They are the simplest examples of a series of complexes with fully distributed oxidation states of Np, e.g. Np(I), Np(II) or Np(VII) is a highly unusual oxidation state of Np.15 (3) One more interesting aspects of this work are the apparent production of several fundamental new molecules of Np, including the Np(II) complex Np2O2 in addition to the mix-valent Np(V/III) complex Np2O4, and the heptavalent Np oxide Np2O7. To address some of these matters, we have delved more deeply into the electronic structure of and bonding in these Np2Ox complexes.The ground electron configuration of an Np atom is [Rn]7s26d15f4. As known, neptunium could exhibit six oxidation states in molecular complexes, from +2 to +7, with +5 being the most common in aqueous media, although the accessibility of divalent oxidation state requires skillful efforts. An Np(I) complex could, in principle, retain its two metal-based electrons in an s2f4, an s1f5, or an s1d1f4 configuration. The relative energies of the 7s, 6d, and 5f orbitals in a low-valent early-actinide complex will be sensitive to the ligands present. For example, the ligand field provided by three substituted cyclopentadienyl ligands causes U(II) complexes [U[(Ad,MeArO)3mes]− to have an f4 configuration,16 in contrast to the 5f36d1 configuration for the U2+ ion in [U(Cp′′)3]− (Cp′′ = C5H3-(SiMe3)2) complex.17 In both of these cases, the ligand field is strong enough and isotropic enough to destabilize the 7s orbitals well above the 6d orbitals, and the 5f orbitals are still as high in energy as 6d orbitals to be used to host the metal-based electron. A further complication in determining the electronic structures of the low-valent early actinides is expected to arise because when valence orbitals’ energy levels of low-valent Np are in a narrow range and are not fully filled, there is usually obvious destruction of the Aufbau principle in any DFT method. For example, in the case of low oxidation state Np, placing the added electrons in the f0 orbital will result in the unoccupied f±3 orbital below the f0 orbital. Contrary to expectations, if the electron is placed in the f±3 orbital, the unoccupied f0 orbital is below the f±3 orbital.18 To avoid these problems and to give a quantitative description in the 7s, 6d and 5f orbital energies, we have used the approximation of “smearing” in which the electrons that lie around the Fermi level and that are close in energy are smeared out over the orbitals, which are fractional occupations and mainly depends on the major quantum and angular momentum. The calculated energies of 5f, 6d and 7s atomic orbitals of Np(0) to Np(VII) are displayed in Scheme 1, which shows regular periodic trends in the valence orbitals of Npn+ as n proceeds from 0 to 7. In Np(0) and Np(I), in essence, the three orbitals are almost degenerate with the 6d being the highest energy level. Thus, our calculation of the s1f5 state for the Np(I) molecule Np2O is reasonable. Starting from Np(II), the 5f level has declined below of 7s level and still degenerated to the 7s level, where the 6d orbitals retain higher energy than the 7s orbitals. Thus, Np has the electronic configuration of s1f4 or f5 in Np2O2.19 At Np(III), the 6d and 7s switched energetic levels, however, their energies are still near-degenerated, both being higher than 5f levels. Consequently, Np2O3 has the Np (f4) configuration. As Np oxidation proceeds through the series, the valence orbitals drop in energy with the dropping in the range of 5f > 6d > 7s. This decreasing extent in the energy for different angular momentum enlarges the range of 7s, 6d, and 5f energy levels, and makes the 5f orbitals much inert for the higher oxidation state. Thereofore, more electron-transfer from neptunium to the ligand becomes more difficult, thus making the unpaired electrons largely located on the nonbonding 5f AOs with increasing formal charge, with the number of electrons decreasing.
For instance, our calculations indicate that the ground state electronic configuration of the Np2+ ion in Np2O2 is 5f47s1,28 which differs from the Np2+ 5f46d1 electronic configuration in the [Np(Cp′′)3]− complex,17 in contrast to the 5f36d1 configuration for the U2+ ion in [U(Cp′′)3]−,20 or the configuration of 5f6 state for Pu2+ in the [Pu(Cp′′)3]−.21 This is ascribed to the short Np–O bond length arouses strong interaction to destabilize the 6d orbital above the 7s orbitals. As traversing the series of oxidation states, the Np 5f orbitals gradually decrease in energy levels and become less chemically accessible, thereby the 5fn+1 configuration for trivalent Np has been presumed to have more stability. Thus, the predicted Np3+ ion with a 5f4 electron configuration in Np2O3 is reasonable. Remarkably, Np2O4 consists of a 5f2 electronic configuration of one of the neptunium centers as well as a 5f4 electronic configuration of the other neptunium, being capable of indicating the formation of the first mixed-valent Np3+/Np5+ oxide compound. The reason for the formation of such an electronic structure is that Np5+ with double-degenerated f2 configuration has extreme stability over that of Np4+ with triple-degenerate f3 configuration, due to the lower energy levels of Np5+ with 5f orbitals having stronger covalence with O 2p orbitals, which is necessary for forming Np(V)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O multiple bonds. Therefore, Np2O5 has a (5fNp1)2–(5fNp2)2 valence configuration with two pentavalent Np, which could be considered as the fifth oxygen atom consequently oxidizing the Np2(III) atom in Np2O4 into Np2(V). This mechanism is evocative of the stabilization of Np(V). The ground state Np2O6 is a triplet 3B2u state with the electronic structure of 5f1–5f1 on Np atoms, thus each Np has a hexavalent oxidation state. For Np2O7, the lowest stable isomer is a closed-shell singlet 1A′ with the valence electronic structure of 5f0 on Np, thus a compound featuring heptavalent Np has been predicted. In addition, the series of Np2Ox considered currently is in a neutral state and the valent state of the Np2Ox compound indeed significantly affect the electronic structure of the Np atom, which will be discussed in our further works.
O multiple bonds. Therefore, Np2O5 has a (5fNp1)2–(5fNp2)2 valence configuration with two pentavalent Np, which could be considered as the fifth oxygen atom consequently oxidizing the Np2(III) atom in Np2O4 into Np2(V). This mechanism is evocative of the stabilization of Np(V). The ground state Np2O6 is a triplet 3B2u state with the electronic structure of 5f1–5f1 on Np atoms, thus each Np has a hexavalent oxidation state. For Np2O7, the lowest stable isomer is a closed-shell singlet 1A′ with the valence electronic structure of 5f0 on Np, thus a compound featuring heptavalent Np has been predicted. In addition, the series of Np2Ox considered currently is in a neutral state and the valent state of the Np2Ox compound indeed significantly affect the electronic structure of the Np atom, which will be discussed in our further works.
The effective charge analyses (Table S10†) show that the charge value on Np in Np2Ox compounds increases gradually, implying that the increased oxidation state along with the increased number of oxygen atoms, agrees well with the decreasing spin population values in this series. As detailed in Table 1, the 5f population for both Np in Np2O is 5.45|e|, which generally decreases when x increases and becomes 5.14|e| in Np2O2 (f5), 4.16|e| in Np2O3 (f4), 2.53|e| (f2) and 3.92|e| (f4) for Np2O4, 2.23|e| for Np2O5 (f2), and 1.15|e| for Np2O6 (f1) and 0.00|e| in Np2O7 (f0). This is a piece of evidence that the oxidation state of Np has increased from +I to +VII, as expected. Obviously, Np atoms in Np2O4 exhibits two oxidation states, +V in Np1 and +III in Np2, ascribed to the stable Np(V) electronic state. In addition, the trend of Bader charges on Np in Np2Ox compounds exhibit a decreasingly enlarging trend, from 0.63|e| in Np2O to 2.79|e| in Np2O7, and not linearly correlated with the oxidation state of Np, which is because a very high OS metal cation in compounds would spontaneously oxidize its ligands by self-reduction. The stabilities of the various oxidation states of Np along the series are shown in Fig. 2, where the formal oxidation states, are plotted together with the corresponding values for the HOMO–LUMO gaps.
 | ||
| Fig. 2 The formal oxidation state of Np along with the series together with the corresponding values for the HOMO–LUMO gaps of Np2Ox (x = 1 to 7). | ||
| Species | 2S+1Λ (symm.) | Elec. conf. | OS | Geometry | BO | Q Np | S Np |
|---|---|---|---|---|---|---|---|
| Np2O | 11A2(C2v) | f5s1–f5s1 | I–I | Np–O = 2.063 | 1.51 | 0.63 | 5.45 |
| Np1–Np2 = 3.481 | |||||||
| Np1–O–Np2 = 105.7 | |||||||
| Np2O2 | 11B1g(D2h) | f4f5s1 | II–II | Np–O = 2.086 | 0.77 | 1.20 | 5.14 |
| Np1–Np2 = 3.260 O1–O2 = 2.603 Np1–O–Np2 = 101.5 | |||||||
| Np2O3 | 9E′′(D3h) | f4–f4 | III–III | Np–O = 2.105 Np1–Np2 = 2.943 O–O = 2.603 | 0.55 | 1.75 | 4.16 |
| Np1–O–Np2 = 86.6 | |||||||
| Np2O4 | 7A′(Cs) | f2–f4 | V–III | Np1–O = 1.811, 1.972, 2.255, 2.255 | 0.72 | 2.39 | 2.35 |
| Np2–O = 1.997, 2.276, 1.997 Np1–Np2 = 2.994 | 1.77 | 3.92 | |||||
| Ot–Np1–Ot = 179.0 | |||||||
| Np2O5 | 5A(C2) | f2–f2 | V–V | Np–O = 1.802, 2.103, 2.444, 1.899 | 0.31 | 2.42 | 2.23 |
| Np1–Np2 = 3.105 | |||||||
| Ot–Np–Ot = 179.0 | |||||||
| Np2O6 | 3B2u(D2h) | f1–f1 | VI–VI | Np–O = 2.100, 2.100, 1.792, 1.792 | 1.02 | 2.62 | 1.15 |
| Np1–Np2 = 3.323 Ot–Np–Ot = 174.9 | |||||||
| Np2O7 | 1A′(Cs) | f0–f0 | VII–VII | Np1–O = 1.787, 1.787, 2.013, 1.961 | 0.13 | 2.79 | 0.00 |
| Np2–O = 1.797, 1.797, 1.846, 2.236, 2.324 | 2.74 | ||||||
| Np1–Np2 = 3.493 | |||||||
| Ot–Np1–Ot = 171.1 | |||||||
| Ot–Np2–Ot = 166.4 |
2.2. f–f bond in Np2O3
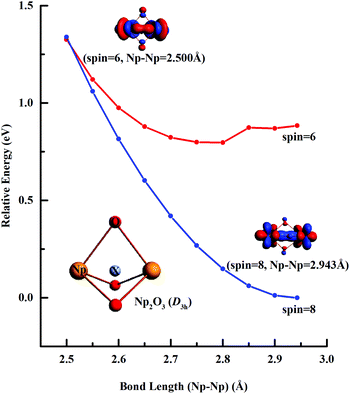
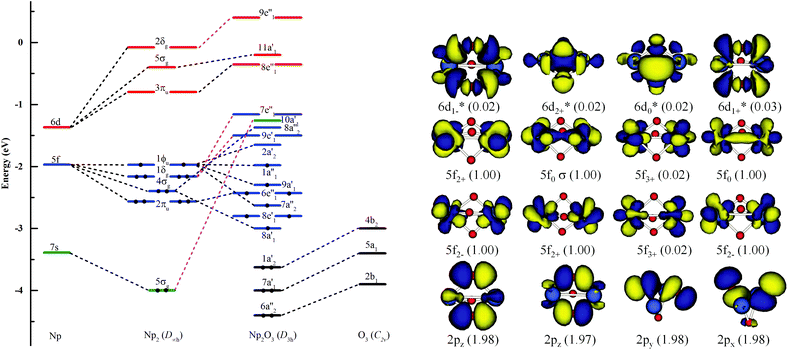
Fig. 3 illustrates the linear synchronous transit (LST) potential energy surfaces of Np2O3 species upon converting a 9E′′ to the 7E′′ state as a function of the distance (Rn) from two Np centers (Np-core yellow and O-cores red) with Rn = R0 − 0.05n (n = 1–9). The starting point with R0 = 2.943 pm corresponds to the D3h structure, and the reduced ending point with R9 = 2.500 pm, corresponds to the D3h structure. Along both the potential energy surfaces, energies increase sharply before R0 and also gradually increase after R0, indicating that R0 = 2.943 is the local minimum. The nonet state is generally lower in energy than the septet, while the 7E′′ structure with proposed f–f bonding is only slightly lower energy at R9 = 2.500 about 0.013 eV compared to the 9E′′ one. Therefore, the 7E′′ structure is significantly less stable than the 9E′′ one, giving the 9E′′ without the f–f bond for the ground state of Np2O3. The intrinsic bonding mechanism in Np2O3 between Np and O atoms has been revealed by analyzing the Kohn–Sham molecular orbitals of Np2O3 and their MO energy levels with correlation to the atomic orbitals (AOs).As illustrated in Fig. 4, the fragment molecular orbital (FMO) analysis of the Np2O3 (D3h) 9E′′ ground state can be interpreted base on the orbital interactions between Np2 and O3 fragments. For O3 ligands, the O 2p-based π* MOs 2b1, 5a1 and 4b2 play as electron acceptors when inserted into Np2, and transformed into group orbitals 7a′1 + 6a′′2 + 1a′2 of the Np2O3. According to the frontier occupied MOs shown in Fig. 3, the splitting of Np valence orbitals upon interacting with O 2p is consistent with the conventional crystal-field theory. Without spin–orbit coupling, firstly, the 7s orbitals as doubly-occupied orbitals are σg in a D2h field in Np2 dimer species that is considerably further destabilized by the strong interaction with the O 2p orbitals to be unoccupied 10a′1 orbital. Similarly, Np 5f orbitals are split as ϕu (fϕ) ∼ δu (fδ) ≪ πu (fπ) < σu (fσ) in Np2 species, where the strong destabilization of the fσ, fδ and fπ orbitals from the f-manifold is an indication of their strong interaction with the unfilled O 2p orbitals. Several MOs with the low orbital energies shown in the plot reflect the strong bonding interaction between the central Np 5f hybrid orbitals and O 2p orbitals; the σu of Np2 overlaps with the corresponding two O 2pz orbitals, forming 8a′1 bonding orbitals and 8a′′2 anti-bonding orbital of Np2O3. The πu group orbitals of Np2 transform into 8e′ and 6e′′ orbitals of Np2O3. The δu group orbitals of Np2 were destabilized by the corresponding 2p orbitals of O3 π*, forming 9e′ and 7e′′1 anti-bonding orbitals. The ϕu group orbitals of Np2 possess as non-bonding orbitals (7a′′2, 9a′1, 1a′′1 and 2a′2) of Np2O3. Consequently, the strong fδ/dδ–π* orbital interactions play a key role in stabilizing the complex. In addition, we chose the localized equivalent molecular orbital picture of Np2O3 (Fig. 4) based on CASSCF calculations to sketch the correlated and spin–orbit coupled valence electronic structure of ligated Np–O3–Np. Inspection of the CASSCF wave function shows that Np2O3 is mainly single-configurational, with a 96% dominant configurational ((O2p)8(Np5f)8) weight and 1% weight for the configuration-((O2p)8(Np5f)6(Np6d)2). Since, the most stable spin state of the Np2O3 complex is the nonet state, among the eight unpaired electrons, which are localized on Np 5f orbitals, we observe the presence of two half-a-bond (Fig. 5) and the singly occupied σ-type orbitals containing significant contributions from both Np 5fz3 orbitals. The Np–Np interactions are characterized by a BOMayer of 0.55 from PBE calculations (comparable to 6.89 for the Np![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Np double bond in Np2), which substantiates the Np–Np single bond character. Each Np forms a strong σ-bond to the central O36− unit through the covalent overlaps of hybridized Np (5f6d) orbitals with O(2s2p) hybrids. Each Np–O bond of dominant π-character can be described as three-center two electrons (3c–2e) bonds that possess some σ-admixture. The large electronegativity difference between Np (1.36) and O (3.44) (Pauling units) leads to bond-pair polarization toward O, especially for the π-type pairs, which are strongly localized on O and lead to its effective negative charge.
Np double bond in Np2), which substantiates the Np–Np single bond character. Each Np forms a strong σ-bond to the central O36− unit through the covalent overlaps of hybridized Np (5f6d) orbitals with O(2s2p) hybrids. Each Np–O bond of dominant π-character can be described as three-center two electrons (3c–2e) bonds that possess some σ-admixture. The large electronegativity difference between Np (1.36) and O (3.44) (Pauling units) leads to bond-pair polarization toward O, especially for the π-type pairs, which are strongly localized on O and lead to its effective negative charge.
2.3. Mixed-valent in Np2O4
The mixed-valence has been encountered in a number of scientific areas,22 and it has been considered relying on ligand field theory and qualitatively related to the extent of delocalization of the valence shell electrons. Especially in the transition-metal-containing compounds, the ligand field affects the local spin of metal atoms. The Np2O4 is a mixed-valent compound that could be ensured by structural and electronic structures that support the delocalization of 5f electrons in Np3+/Np5+, however, it depends less on the ligand field. Firstly, Np(V) cation Np(III) has a quasi-tetrahedral type with the three Np–O single bonds of ca. 2.000 Å, while Np(V) exists in a [O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Np(V)
Np(V)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]+ fragment, where Np(V) presents an octahedral coordination type, e.g. O
O]+ fragment, where Np(V) presents an octahedral coordination type, e.g. O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Np bond lengths of 1.811 Å and 1.972 Å, and the bond angle Ot1–Np1–Ob3 of 178.3 deg. as well as the bond angle Ot1–Np1–Ob1/Ob2 of 105.4 deg., known as an Np(V) structural feature. In addition, Np–Ob distances are shorter at the Np(V) site than at the Np(III). Thus, this mixed-valent cluster could be classified into a class II system,22a which has three bridging Ob between two Np ions of differing valences. In this bonding feature, two Np atoms are at a very close distance of 2.994 Å, which is of unprecedented structure and the oxidation state of Np. This structure identifies the stable geometry of anion compounds Hf2O4− and Zr2O4−,23 where the C3v isomer has typical M–O and M
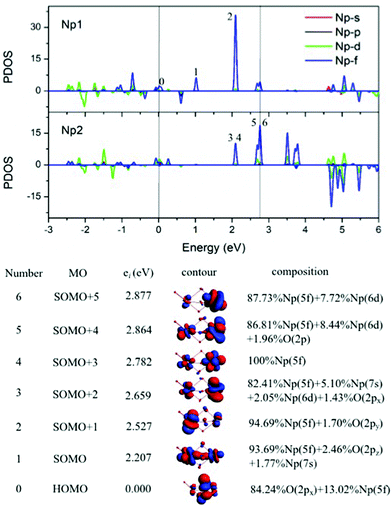
Np bond lengths of 1.811 Å and 1.972 Å, and the bond angle Ot1–Np1–Ob3 of 178.3 deg. as well as the bond angle Ot1–Np1–Ob1/Ob2 of 105.4 deg., known as an Np(V) structural feature. In addition, Np–Ob distances are shorter at the Np(V) site than at the Np(III). Thus, this mixed-valent cluster could be classified into a class II system,22a which has three bridging Ob between two Np ions of differing valences. In this bonding feature, two Np atoms are at a very close distance of 2.994 Å, which is of unprecedented structure and the oxidation state of Np. This structure identifies the stable geometry of anion compounds Hf2O4− and Zr2O4−,23 where the C3v isomer has typical M–O and M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching modes in IR spectra. Secondly, the atomic free valence and spin and orbital populations (Table 1) indicate two unpaired 5f-electrons on Np(V) atom and four unpaired 5f-electrons on Np(III). We also chose the localized singly occupied molecular orbital (SOMO, Fig. 5) pictures to sketch the correlated oxidation states in Np2O4. That the lowest two SOMOs are from Np(V) atom and the rest four are from Np(III), reflects that the higher oxidation state of Np has lower valence orbitals, due to the enlarging difference of spin-polarization of Np(V) and Np(III). Thirdly, with the formation of Np(V), the bond angle transfers from bent to linear, which is largely ascribed to the 5f-participant in the chemical bonding of Np–O.24 Such as one of the Np
O stretching modes in IR spectra. Secondly, the atomic free valence and spin and orbital populations (Table 1) indicate two unpaired 5f-electrons on Np(V) atom and four unpaired 5f-electrons on Np(III). We also chose the localized singly occupied molecular orbital (SOMO, Fig. 5) pictures to sketch the correlated oxidation states in Np2O4. That the lowest two SOMOs are from Np(V) atom and the rest four are from Np(III), reflects that the higher oxidation state of Np has lower valence orbitals, due to the enlarging difference of spin-polarization of Np(V) and Np(III). Thirdly, with the formation of Np(V), the bond angle transfers from bent to linear, which is largely ascribed to the 5f-participant in the chemical bonding of Np–O.24 Such as one of the Np![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding MO in 4A was composed of 24.85% of Np1 5f orbitals into the bonding, 6.05% larger in contribution compared to 18.80% of Np1 5f orbitals in the counterpart MO in 4C. This phenomenon has been found as the unique feature for f-orbitals that the participation of f orbitals in chemical bonding could direct the structure of a compound.24b As is known, the most stable oxidation state is Np(V) and several neptunium oxidation states could exist simultaneously in the solution, thus we could provide evidence for the co-existence of two different cations (Np3+, Np5+) in Np2O4 compounds.
O bonding MO in 4A was composed of 24.85% of Np1 5f orbitals into the bonding, 6.05% larger in contribution compared to 18.80% of Np1 5f orbitals in the counterpart MO in 4C. This phenomenon has been found as the unique feature for f-orbitals that the participation of f orbitals in chemical bonding could direct the structure of a compound.24b As is known, the most stable oxidation state is Np(V) and several neptunium oxidation states could exist simultaneously in the solution, thus we could provide evidence for the co-existence of two different cations (Np3+, Np5+) in Np2O4 compounds.
2.4. Heptavalent Np in Np2O7
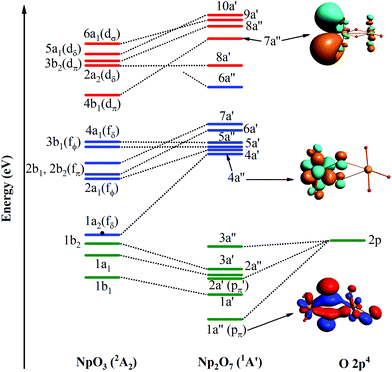
In the ground 1A′ state for Np2O7, Np1 is bounded by three-terminal oxygen atoms with the Np1–Oyl bond length of 1.787 Å, by one actinyl oxygen with the Np1–Ot bond length of 1.961 Å and by one bridging oxygen with the Np1–Ob bond length of 2.013 Å, while the Np2 is bounded by three-terminal oxygen atoms with the Np2–Ot bond length of 1.797, 1.797, 1.846 Å and by one bridging oxygen with the Np2–Ob bond length of 2.236 Å. Different from the structure of U2O7,25 each Np has four effectively coordinated oxygen atoms, consisting of two Np–Ob single bonds and three Np![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bonds, which is ascribed to hexavalent U in U2O7 and heptavalent Np in Np2O7. As the investigation on the electronic structure of NpO3 and the NpO3+ cation,11c we have known that Np is hexavalent in NpO3 and heptavalent in NpO3+ cation. Thus, this Np2O7 structure could be understood as two quasi-planar NpO3+ cations connected by an O2− anion, that is oxygen further oxides two Np(VI)O3 into Np(VII) with the formation of Np2O7. As noted in Fig. 6, the MO diagram for Np2O7 in correlated to the MOs of one Np1 based NpO3 fragment and one O fragment shows that the upper paired electrons reside in the O 2p-based MOs. For example, the O 2p-based 1a′′ and 2a′ MOs are completely filled and these two MOs represent strong bonding interactions between Np 5f AOs and O 2p AOs, resulting in Np1 5f- and 6d-based antibonding orbitals (4a′′ and 7a′′), destabilized into a virtual band. Meanwhile, the occupied MOs are bonding orbitals with adiabatic polarization of O 2p orbitals toward the Np 5f shell, as shown from the electronic structure of MO 1a′′ of Np2O7 in Fig. 6. In addition, the bonding between Np and the oxide within the NpO3 fragment has significant 5f orbitals mixed into the bonding, suggesting that 5f orbitals participate in chemical bonding in the high Np compounds. Taking the Np1–O bonding orbital HOMO 3a′ as an example, that is mainly composed of 24.4% of the 5f orbitals and 76.7% of the 2p orbitals into the bonding. For Np2O7, the lowest 14 unoccupied MOs are mainly Np 5f character, where seven of them localized on Np1 5f orbitals are shown in Fig. 6. These wavefunction analyses clearly indicate that the Np center has an (s0f0d0) configuration. Thus, Np has been determined as possessing an oxidation state of +VII, and the Np2O7 can be therefore classified as an Np(VII) species, expanding the database for heptavalent Np compounds from a monomer molecular Np(VII) complex, e.g. NpO3(NO3)2− or NpO4−,11a,26 to a dimer molecule, which could be considered as an example for the existence of heptavalent Np in nano-particles between the molecule and solid-state Np(VII) compounds, e.g. [Co(NH3)6]NpO5 and Na5NpO6.27
O double bonds, which is ascribed to hexavalent U in U2O7 and heptavalent Np in Np2O7. As the investigation on the electronic structure of NpO3 and the NpO3+ cation,11c we have known that Np is hexavalent in NpO3 and heptavalent in NpO3+ cation. Thus, this Np2O7 structure could be understood as two quasi-planar NpO3+ cations connected by an O2− anion, that is oxygen further oxides two Np(VI)O3 into Np(VII) with the formation of Np2O7. As noted in Fig. 6, the MO diagram for Np2O7 in correlated to the MOs of one Np1 based NpO3 fragment and one O fragment shows that the upper paired electrons reside in the O 2p-based MOs. For example, the O 2p-based 1a′′ and 2a′ MOs are completely filled and these two MOs represent strong bonding interactions between Np 5f AOs and O 2p AOs, resulting in Np1 5f- and 6d-based antibonding orbitals (4a′′ and 7a′′), destabilized into a virtual band. Meanwhile, the occupied MOs are bonding orbitals with adiabatic polarization of O 2p orbitals toward the Np 5f shell, as shown from the electronic structure of MO 1a′′ of Np2O7 in Fig. 6. In addition, the bonding between Np and the oxide within the NpO3 fragment has significant 5f orbitals mixed into the bonding, suggesting that 5f orbitals participate in chemical bonding in the high Np compounds. Taking the Np1–O bonding orbital HOMO 3a′ as an example, that is mainly composed of 24.4% of the 5f orbitals and 76.7% of the 2p orbitals into the bonding. For Np2O7, the lowest 14 unoccupied MOs are mainly Np 5f character, where seven of them localized on Np1 5f orbitals are shown in Fig. 6. These wavefunction analyses clearly indicate that the Np center has an (s0f0d0) configuration. Thus, Np has been determined as possessing an oxidation state of +VII, and the Np2O7 can be therefore classified as an Np(VII) species, expanding the database for heptavalent Np compounds from a monomer molecular Np(VII) complex, e.g. NpO3(NO3)2− or NpO4−,11a,26 to a dimer molecule, which could be considered as an example for the existence of heptavalent Np in nano-particles between the molecule and solid-state Np(VII) compounds, e.g. [Co(NH3)6]NpO5 and Na5NpO6.27
 | ||
| Fig. 6 Frontier canonical Kohn–Sham valence MO envelopes of Np2O7 with dominant AO contributions. The value of contour envelopes is 0.05 a.u. | ||
3. Conclusion
We have investigated the geometry and electronic structures of the Np2Ox (x = 1–7) species to explore how the Np oxidation state, as well as chemical bonding between Npn+ and O, directs the structural stability in this series. This work is intended to give several contributions in charting future directions in the neptunium chemistry with the formation of a specific oxidation state. In general, Np2Ox provides an approach that the chemistry of radioactive Np complexes could be successfully studied via the combination of global-minimum search technology and relativistic quantum chemistry methods. The Np oxidation state traversing from +I to +VII shows the increased 5f-contribution to the Np–O bonding. The significant difference of Np(V) from lower oxidation states Np implies that the formation of Np(V) is extremely stable arising from the participation of 5f orbitals in chemical bonding and the ONpO linearity. Thus, the fact that mixed-valent Np2(III/V)O4 occurs between Np(III)2O3 and Np(V)2O5 is not surprising. The presently proposed Np2(VII)O7 complex with the previously reported Np(VII) compounds demonstrates that Np(VII) oxidation state is plausible in both oxides, whose stability comes from the significant interactions between O 2p orbitals and both, the Np 6d and 5f atomic orbitals. Although without spectroscopic studies on these systems, this complete computational study in both aspects of structural conformation and electronic structure corroboration, is able to provide theoretically fundamental understanding in neptunium even to the extent of early actinide elements and provide some guidance for actinide chemistry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by grants from the National Natural Science Foundation of China (No. 21976014 and U1930402) and the Science Challenge Project of China (No. TZ2018004). We are very grateful to the Tianhe2-JK for generous grants of computer time.References
- (a) J. Ibers, Nat. Chem., 2010, 2, 996–996 CrossRef CAS PubMed; (b) Z. Zheng and P. C. Burns, Recent development in clusters of rare earths and actinides: chemistry and materials, Springer, 2017 CrossRef; (c) P. L. Arnold, M. S. Dutkiewicz and O. Walter, Chem. Rev., 2017, 117, 11460–11475 CrossRef CAS PubMed.
- G. Tian, J. Xu and L. Rao, Angew. Chem., 2005, 117, 6356–6359 CrossRef.
- (a) S. E. Gilson, P. Li, J. E. Szymanowski, J. White, D. Ray, L. Gagliardi, O. K. Farha and P. C. Burns, J. Am. Chem. Soc., 2019, 141, 11842–11846 CrossRef CAS PubMed; (b) K. E. Roberts, T. J. Wolery, C. E. Atkins-Duffin, T. G. Prussin, P. G. Allen, J. J. Bucher, D. K. Shuh, R. J. Finch and S. G. Prussin, Radiochim. Acta, 2003, 91, 87–92 CrossRef CAS.
- R. Husar, R. Hübner, C. Hennig, P. M. Martin, M. Chollet, S. Weiss, T. Stumpf, H. Zänker and A. Ikeda-Ohno, Chem. Commun., 2015, 51, 1301–1304 RSC.
- (a) P. J. Hay and R. L. Martin, Los Alamos Sci., 2000, 26, 382–391 CAS; (b) J. Autschbach, N. Govind, R. Atta-Fynn, E. J. Bylaska, J. W. Weare and W. A. de Jong, Computational methods in lanthanide and actinide chemistry, 2015, pp. 299–342 Search PubMed; (c) T. Saue and L. Visscher, Computational methods in lanthanide and actinide chemistry, 2015, pp. 55–87 Search PubMed.
- L. Zhang, E. A. Dzik, G. E. Sigmon, J. E. S. Szymanowski, A. Navrotsky and P. C. Burns, J. Nucl. Mater., 2018, 501, 398–403 CrossRef CAS.
- (a) R. Copping, V. Mougel, C. Den Auwer, C. Berthon, P. Moisy and M. Mazzanti, Dalton Trans., 2012, 41, 10900–10902 RSC; (b) S. M. Cornet, L. J. L. Häller, M. J. Sarsfield, D. Collison, M. Helliwell, I. May and N. Kaltsoyannis, Chem. Commun., 2009, 917–919 RSC.
- B. W. Veal, D. J. Lam and H. Diamond, Physica B+C, 1977, 86–88, 1193–1194 CrossRef.
- A. Kovács and R. J. M. Konings, J. Phys. Chem. A, 2011, 115, 6646–6656 CrossRef PubMed.
- (a) Y. Yang, H. Liu and P. Zhang, J. Chem. Phys., 2016, 144, 184304 CrossRef PubMed; (b) R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125–4143 CrossRef CAS PubMed; (c) C. Zhang, S.-X. Hu, H.-T. Liu, Y. Yang and P. Zhang, J. Phys. Chem. A, 2018, 122, 4085–4091 CrossRef CAS PubMed.
- (a) J. K. Gibson, W. A. de Jong, P. D. Dau and Y. Gong, J. Phys. Chem. A, 2017, 121, 9156–9162 CrossRef CAS PubMed; (b) P. D. Dau, R. Maurice, E. Renault and J. K. Gibson, Inorg. Chem., 2016, 55, 9830–9837 CrossRef CAS PubMed; (c) A. Kovács, Struct. Chem., 2020, 31, 1247–1271 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed; (b) E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed; (c) B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS.
- Y. Guo, C. Riplinger, D. G. Liakos, U. Becker, M. Saitow and F. Neese, J. Chem. Phys., 2020, 152, 024116 CrossRef CAS PubMed.
- L. Maria, J. Marçalo and J. K. Gibson, Encyclopedia of Inorganic and Bioinorganic Chemistry, 2011, pp. 1–13 Search PubMed.
- D. P. Halter, C. T. Palumbo, J. W. Ziller, M. Gembicky, A. L. Rheingold, W. J. Evans and K. Meyer, J. Am. Chem. Soc., 2018, 140, 2587–2594 CrossRef CAS PubMed.
- J. Su, C. J. Windorff, E. R. Batista, W. J. Evans, A. J. Gaunt, M. T. Janicke, S. A. Kozimor, B. L. Scott, D. H. Woen and P. Yang, J. Am. Chem. Soc., 2018, 140, 7425–7428 CrossRef CAS PubMed.
- C. E. Kefalidis, L. Castro, A. Yahia, L. Perrin and L. Maron, in Computational Methods in Lanthanide and Actinide Chemistry, John Wiley & Sons Ltd Chichester, UK, 2015, pp. 343–373 Search PubMed.
- X. Cao and M. Dolg, Mol. Phys., 2003, 101, 961–969 CrossRef CAS.
- F. S. Guo, N. Tsoureas, G. Z. Huang, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2020, 59, 2299–2303 CrossRef CAS PubMed.
- C. J. Windorff, G. P. Chen, J. N. Cross, W. J. Evans, F. Furche, A. J. Gaunt, M. T. Janicke, S. A. Kozimor and B. L. Scott, J. Am. Chem. Soc., 2017, 139, 3970–3973 CrossRef CAS PubMed.
- (a) M. B. Robin and P. Day, in Advances in inorganic chemistry and radiochemistry, Elsevier, 1968, vol. 10, pp. 247–422 Search PubMed; (b) S. K. Cary, S. S. Galley, M. L. Marsh, D. L. Hobart, R. E. Baumbach, J. N. Cross, J. T. Stritzinger, M. J. Polinski, L. Maron and T. E. Albrecht-Schmitt, Nat. Chem., 2017, 9, 856–861 CrossRef CAS PubMed; (c) L. Chen, T. Zheng, S. Bao, L. Zhang, H. K. Liu, L. Zheng, J. Wang, Y. Wang, J. Diwu and Z. Chai, Chem. – Eur. J., 2016, 22, 11954–11957 CrossRef CAS PubMed; (d) V. Dugaev, Inorg. Mater., 2000, 36, 524–526 CrossRef CAS; (e) E. Epifano, M. Naji, D. Manara, A. Scheinost, C. Hennig, J. Lechelle, R. Konings, C. Guéneau, D. Prieur and T. Vitova, Commun. Chem., 2019, 2, 1–11 CrossRef; (f) P. Riseborough and J. M. Lawrence, Rep. Prog. Phys., 2016, 79, 084501 CrossRef CAS PubMed; (g) D. Schweinfurth, Y. Rechkemmer, S. Hohloch, N. Deibel, I. Peremykin, J. Fiedler, R. Marx, P. Neugebauer, J. van Slageren and B. Sarkar, Chem. – Eur. J., 2014, 20, 3475–3486 CrossRef CAS PubMed.
- S. Li and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 2665–2683 CrossRef CAS PubMed.
- (a) E. Lu, S. Sajjad, V. E. Berryman, A. J. Wooles, N. Kaltsoyannis and S. T. Liddle, Nat. Commun., 2019, 10, 1–10 CrossRef PubMed; (b) S.-X. Hu, P. Zhang, E. Lu and P. Zhang, Inorg. Chem., 2020, 59, 18068–18077 CrossRef CAS PubMed.
- S. O. Odoh, J. Shamblin, C. A. Colla, S. Hickam, H. L. Lobeck, R. A. K. Lopez, T. Olds, J. E. S. Szymanowski, G. E. Sigmon, J. Neuefeind, W. H. Casey, M. Lang, L. Gagliardi and P. C. Burns, Inorg. Chem., 2016, 55, 3541–3546 CrossRef CAS PubMed.
- P. D. Dau, R. Maurice, E. Renault and J. K. Gibson, Inorg. Chem., 2016, 55, 9830–9837 CrossRef CAS PubMed.
- (a) V. Spitsyn, A. Gelman, N. Krot, M. Mefodiyeva, F. Zakharova, Y. A. Komkov, V. Shilov and I. Smirnova, J. Inorg. Nucl. Chem., 1969, 31, 2733–2745 CrossRef CAS; (b) A. L. Smith, A. Hen, P. E. Raison, E. Colineau, J.-C. Griveau, N. Magnani, J.-P. Sanchez, R. J. Konings, R. Caciuffo and A. K. Cheetham, Inorg. Chem., 2015, 54, 4556–4564 CrossRef CAS PubMed.
- P. Zhang, W.-L. Zou, P. Zhang and S.-X. Hu, Eur. J. Inorg. Chem., 2021 DOI:10.1002/ejic.202100444.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr03408a |
| ‡ These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |