Stratification of polymer–colloid mixtures via fast nonequilibrium evaporation†
Kyoungmun
Lee
 and
Siyoung Q.
Choi
and
Siyoung Q.
Choi
 *
*
Department of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Korea. E-mail: sqchoi@kaist.ac.kr
First published on 25th September 2020
Abstract
In drying liquid films of polymer–colloid mixtures, stratification in which polymers are placed on top of larger colloids is studied. It is often presumed that the formation of segregated polymer–colloid layers is solely due to the proportion in size at fast evaporation as in binary colloid mixtures. By comparing experiments with a theoretical model, we found that the transition in viscosity near the drying interface was another important parameter for controlling the formation of stratified layers in polymer–colloid mixtures. At high evaporation rates, increased polymer concentrations near the surface lead to a phase transition from a semidilute to concentrated regime, in which colloidal particles are kinetically arrested. Stratification only occurs if the formation of a stratified layer precedes the evolution to the concentrated regime near the drying interfaces. Otherwise, the colloids will be trapped by the polymers in the concentrated regime before forming a segregated layer. Also, no stratification is observed if the initial polymer concentration is too low to form a sufficiently high polymer concentration gradient within a short period of time. Our findings are relevant for developing solution-cast polymer composites for painting, antifouling and antireflective coatings.
1. Introduction
Solution-cast polymer composite films composed of polymer matrices containing colloidal particles have been widely studied for many applications, including paints,1 coatings,2,3 and cosmetics,4,5 because they provide highly tuned macroscopic properties relative to the pure polymer,6 through a simple manufacturing process. The controlled properties of the dried films are largely dependent on the spatial distribution of the polymer and colloid,7–10 which is strongly influenced by the solvent evaporation process.11,12 In particular, stratified layers consisting of a polymer layer on a colloidal layer have exhibited highly improved antifouling performance,13,14 and photoactive properties.15Several previous studies have demonstrated ways of controlling the segregated layers of polymer–colloid mixtures in an equilibrium state.16–18 However, relatively little is known about how polymer–colloid mixtures can be stratified during the simple, fast and inexpensive nonequilibrium solvent evaporation process. Although solvent casting is one of the simplest manufacturing methods, from coffee ring stains19 to many industrial applications,1–5 the inherent nonequilibrium nature of drying has made it difficult to clarify the underlying mechanism.
As a solvent evaporates, the spatial distribution of the solutes in liquid films is determined by two competing factors: diffusion20 and receding drying interfaces. Solutes tend to distribute uniformly in drying films with a diffusion constant D, while a nonuniform concentration gradient is developed by the downward velocity of the interface vev. Which of the two phenomena dominates can be quantified by the dimensionless Péclet number Pe = vevz0/D, where z0 is the initial film thickness. If Pe > 1, the solutes cannot diffuse uniformly within the time of evaporation, and they accumulate near the top of the film. On the other hand, the drying film shows almost uniform distribution if Pe < 1.
In binary colloid mixtures, it was recently shown that stratifications with smaller colloids placed on large colloids can be realized if Pe is larger than 1.21–24 This occurs when the concentration gradient of both the large and smaller particles increases near the liquid/air interface. Fortini et al.22 proposed that the inverted stratification was caused by an imbalance in the osmotic pressure between the larger and smaller colloids. Zhou et al.23 suggested that the stratification phenomenon could be explained quantitatively using a diffusion model, with cross-interaction between the colloids. Sear and Warren24 argued that diffusiophoretic motion induced by the concentration gradient of the smaller components can exclude the larger colloids from the drying interfaces.
In a way similar to binary colloid mixtures, it has been proposed that a polymer–colloid mixture can yield the same stratified layers if the Pe values of both the polymer and colloid are larger than 1.24,25 However, these results have only been demonstrated by simulation and modelling studies, and few experimental studies have been performed on polymer–colloid stratification. Although polymers and colloids can show similar behaviors at very dilute concentrations,26,27 they might behave much differently at the high concentrations that any drying solution must experience for complete drying.28,29 The obvious difference is viscosity. It rapidly increases at relatively low concentrations in the polymer solution, slowing the motions of the species.29–31 In contrast, the viscosity of the colloidal suspension increases relatively slowly.32 Thus, the growth in viscosity near the interface, which can kinetically arrest larger colloids,33–35 needs to be considered differently for polymer and colloidal systems, but no appropriate studies have been performed yet.
In this work, we experimentally show that the formation of stratified layers, where a small polymer layer is placed on larger colloids, can be predicted using two competing time scales: the time at which the colloid begins to stratify (ts*) and the time at which the colloid is arrested by the transitions of viscosity near the interface (tc*).
We consider that the colloid starts to be arrested near the drying interfaces when the polymer concentration reaches a concentrated regime where the polymer chains are densely packed.31 The stratification can be observed only if ts* precedes tc*, or tc*/ts* > 1. Otherwise, the viscosity near the drying interface rapidly grows within a very short time and the colloids are kinetically trapped before a sufficient downward velocity away from the surface of large colloids is generated. In addition, when the initial polymer concentration is too low, no stratification can occur either because the concentration gradient of the polymer, or the additional migration velocity of the larger colloid, is not enough until the evaporation ends.
For the predictive analysis of ts* and tc*, we propose a simple model modified from a previous work.24 We observed quite excellent agreement in the final film morphology of the model prediction and experimental studies. Our comprehensive study predicts the spatial distribution of polymers and colloids in the final dried film, based on the experimental system and drying conditions.
2. Results and discussion
2.1 Structure of dried films of polymer–colloid
Mixtures of an aqueous polystyrene (PS) suspension with a mean diameter dc = 1 μm, and poly(ethylene glycol) (PEG) or poly(vinyl alcohol) (PVA) were used as a model system for stratification. The molecular weights of the polymers of PEG Mn (number average molecular weight) 6000 g mol−1, PEG Mn 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, PVA Mw (weight average molecular weight) 6000 g mol−1, and PVA Mw 13
000 g mol−1, PVA Mw (weight average molecular weight) 6000 g mol−1, and PVA Mw 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–23
000–23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (PVA Mw 18
000 g mol−1 (PVA Mw 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) were chosen to meet the condition of radius of colloid (Rcolloid) ≫ radius of polymer (Rpolymer). Before drying, the film solutions contained an initial volume fraction of ϕi,p = 0.01 or 0.04 for the polymer and ϕi,c = 0.67 × ϕi,p for the colloid, respectively. The volume ratio between polymer and colloid was selected to show a clear difference of stratified layer and non-stratified layer in the final dried films. The mixture solutions were deposited on glass substrates as z0 = 1.25 mm. The evaporation was performed at an ambient temperature and a relative humidity of 23%, resulting in an initial polymer Péclet number Pei,p > 1 (Fig. S1, ESI†). All of the experimental systems are summarized in Table 1. When the evaporation was completed, the final film morphologies were analyzed with the help of scanning electronic microscopy (SEM) and ImageJ analysis.
000) were chosen to meet the condition of radius of colloid (Rcolloid) ≫ radius of polymer (Rpolymer). Before drying, the film solutions contained an initial volume fraction of ϕi,p = 0.01 or 0.04 for the polymer and ϕi,c = 0.67 × ϕi,p for the colloid, respectively. The volume ratio between polymer and colloid was selected to show a clear difference of stratified layer and non-stratified layer in the final dried films. The mixture solutions were deposited on glass substrates as z0 = 1.25 mm. The evaporation was performed at an ambient temperature and a relative humidity of 23%, resulting in an initial polymer Péclet number Pei,p > 1 (Fig. S1, ESI†). All of the experimental systems are summarized in Table 1. When the evaporation was completed, the final film morphologies were analyzed with the help of scanning electronic microscopy (SEM) and ImageJ analysis.
| Colloid | Polymer | R g (nm) | ϕ i,p | Pei | Stratification | t c*/ts* | t c* | t s* | |
|---|---|---|---|---|---|---|---|---|---|
Colloid was fixed as PS to exclude gravitational effect during drying (ρPS ≈ ρwater). A total of 8 systems were experimentally studied under ϕi,p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,c = 3 ϕi,c = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, z0 = 1.25 mm and 23% relative humidity conditions.a See ESI. 2, z0 = 1.25 mm and 23% relative humidity conditions.a See ESI. |
|||||||||
| PS (r = 500 nm) | PEG | M n 6000 | 3.6 | 0.01 | 4 | X | 1.012 | 0.928 | 0.917 |
| 0.04 | 7 | O | 1.153 | 0.670 | 0.581 | ||||
| PEG |
M
n 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7.4 | 0.01 | 9 | X | 0.976 | 0.841 | 0.862 | |
| 0.04 | 22 | X | 0.818 | 0.243 | 0.297 | ||||
| PVA | M w 6000 | 3.5 | 0.01 | 4 | X | 0.994 | 0.873 | 0.878 | |
| 0.04 | 9 | O | 0.911 | 0.400 | 0.439 | ||||
| PVA |
M
w 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6.8 | 0.01 | 8 | X | 0.882 | 0.707 | 0.802 | |
| 0.04 | 24 | X | 0.466 | 0.118 | 0.253 | ||||
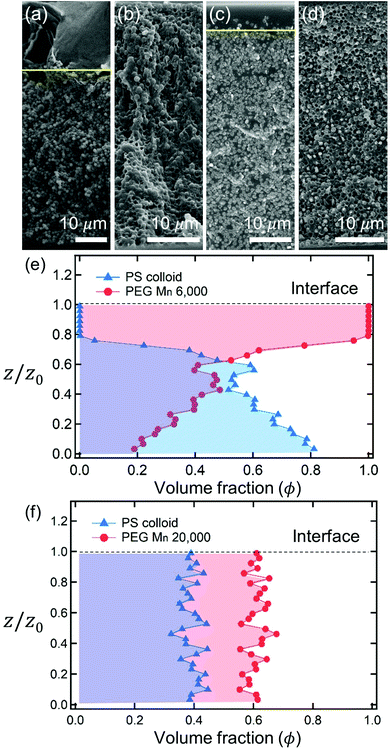
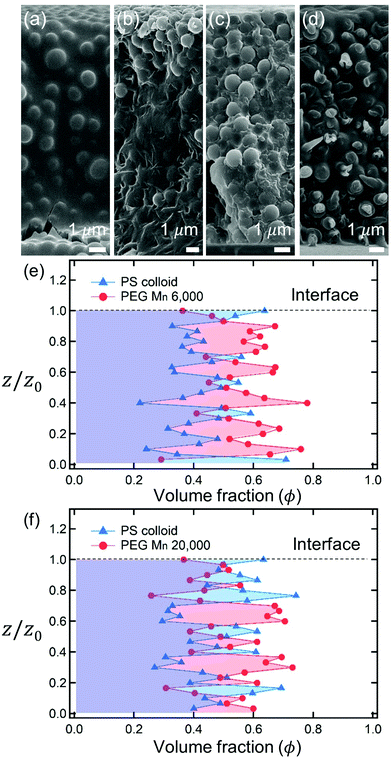
After complete drying, the polymers were enriched at the top of the films for PEG Mn 6000 g mol−1 (ϕi,p = 0.04) [Fig. 1(a)] and PVA Mw 6000 g mol−1 (ϕi,p = 0.04) [Fig. 1(c)] while the other 6 dried films shown in Fig. 1(b, d) and 2(a–d) were not segregated, but randomly distributed. Although the stratified layers in Fig. 1(a and c) also showed different degrees of stratification, there was a clear difference between the stratified layers [Fig. 1(e)] and non-stratified layers [Fig. 1(f), 2(e and f)].
2.2 Modified theoretical model of dynamic stratification
As the solvent evaporated at Pe > 1 for both polymer and colloid, the descending air/water interface zinterface compressed the polymer and colloid, and they accumulated near the drying interface. From previous studies,24,36 the transition of the polymer concentration in a drying film ϕp(z,t) can be written as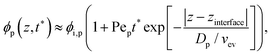 | (1) |
| zinterface(t*) = z0 − vevt = (1 − t*)z0 | (2) |
| ϕp(zinterface − rcolloid,tc*) = ϕp**. | (3) |
Meanwhile, increasing the concentration gradients of the small polymers can also create the diffusiophoretic drift velocity of larger colloids vdiffusiophoresis37,38
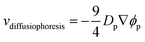 | (4) |
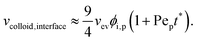 | (5) |
| vcolloid,interface(ts*) = vev. | (6) |
The final morphologies of the drying polymer–colloid mixtures are determined by the two competing time scales ts* and tc*. There are three regimes for the predictive analysis of the stratification of polymer–colloid mixtures. The first is tc*/ts* > 1, where the downward motion of the colloidal particles appears before ϕp(zinterface − rcolloid,tc*) = ϕp**. The second is tc*/ts* < 1, where the polymer volume fraction reaches ϕp** before the evolution of vcolloid,interface(ts*) = vev. The third is ts* ≈ 1, where ts* reaches the time at which evaporation ends (t* = 1), even though ts* precedes tc*.
2.3 Comparison of experimental results and the theoretical model
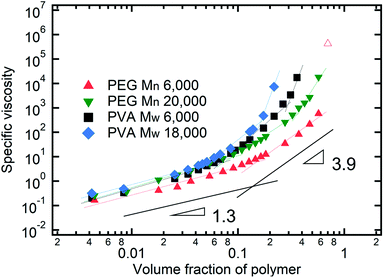
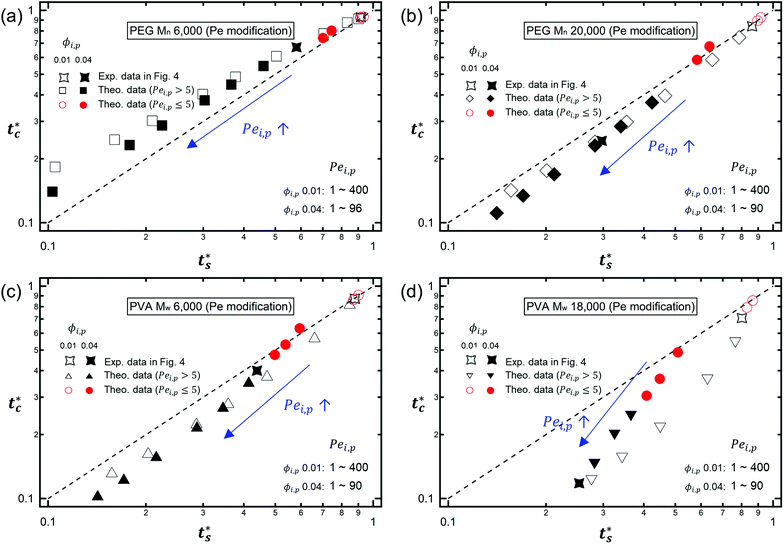
As described above, the prediction of polymer–colloid stratification can be estimated using the competition between tc* and ts*. For the time dependent volume fraction of the polymer in the drying films, evaporation rates were determined by measuring mass reduction (Fig. S2, ESI†). To calculate the time dependent (or concentration dependent) polymer diffusion coefficient, the average volume fractions of polymer in the drying film were used to estimate Dp (see Fig. S4, ESI†). Here, the self-diffusion coefficient of the polymer is used rather than the collective diffusion coefficient due to the slow polymer diffusion caused by the presence of colloids as the concentration increases (Fig. S3, ESI†). The transition of the volume fraction of semidilute entangled ϕe to the concentrated regime ϕ** in good solvent was determined by the specific viscosity ηsp slope transition29,30,40 shown in Fig. 3. From the slope transition of semidilute unentangled (ηsp ∼ ϕ1.3p) to semidilute entangled (ηsp ∼ ϕ3.9p), ϕe of the polymer in good solvent was measured. Similarly, ϕ** can be estimated using the slope transition point between the semidilute entangled regime (ηsp ∼ ϕ3.9p) and the concentrated regime (ηsp ∼ ϕαp, where α > 3.9).In drying films of polymer–colloid mixtures, the final film morphology can be predicted using the three regimes in the (ts*, tc*) plane. Regime 1 with tc*/ts* > 1 indicates clearly stratified layers in the dried films. Regime 2 represents nonsegregated layers, because tc* appears before ts*. Regime 3 also shows nonstratified layers in the final morphology of the complete dried polymer–colloid mixtures, since ts* appears very close to 1 (ts* ≈ 1).
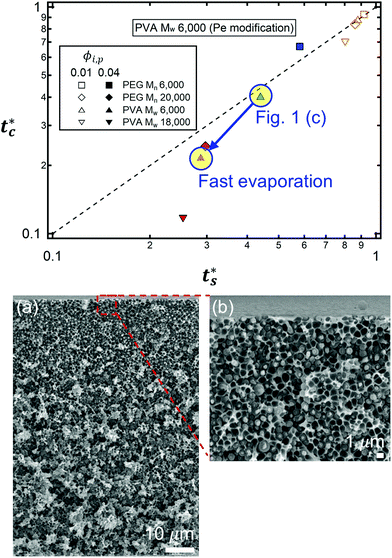
The theoretical predictions based on eqn (3) and (6) and the experimental stratification results from 8 different systems are presented in Fig. 4. There is good agreement between the model prediction and experimental results.
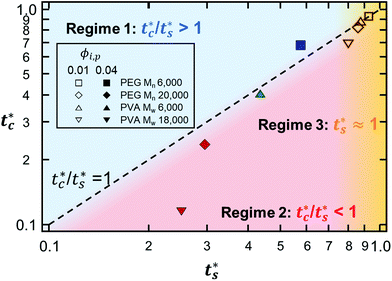 | ||
| Fig. 4 State diagram on the (ts*, tc*) plane. The dotted line corresponds to tc*/ts* = 1. Theoretical predictions of 8 different systems are denoted as symbols in the diagram, and the experimental results are represented by colors. Blue indicates regime 1 (tc*/ts* > 1) where a stratified layer is expected and red shows regime 2 (tc*/ts* < 1). Orange designates regime 3 (ts* ≈ 1) (Fig. S5, ESI†). The green indicates the intermediate state where a stratified layer is observed in experiments while it belongs to regime 2 in model prediction. All data points show overall agreement with one exception, the filled green triangle, which also appears close to tc*/ts* = 1. | ||
However, the model prediction does not show excellent agreement with experimental studies, especially for the PVA Mw 6000 (ϕi,p = 0.04) system, which appears to be closest to tc*/ts* = 1. This might be due to the air/water interfacial activity of PVA Mw 6000 (Fig. S6, ESI†), which can lead to a smaller ts* under real drying conditions, but it cannot bring tc* forward since tc* is related to z = zinterface − rcolloid, not z = zinterface. To reduce the interfacial activity effect of PVA Mw 6000 (ϕi,p = 0.04) on stratification, we moved the point to deviate from tc*/ts* = 1 in our theoretical model by changing vev. As it deviates from tc*/ts* = 1, the theoretical prediction becomes consistent with the experimental result for PVA Mw 6000 (ϕi,p = 0.04) (Fig. 5).
2.4 Conditions for polymer–colloid stratification
To analyze the general conditions for polymer–colloid stratification, we represented tc* and ts* in another experimental parameter. As mentioned above, the polymer-on-top structure can be formed when the two conditions, both ts* < 1 and tc*/ts* > 1, are satisfied. From eqn (3) and (6), tc* and ts* are (see ESI†)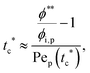 | (7) |
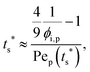 | (8) |
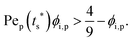 | (9) |
The second requirement for stratified layers in polymer–colloid mixtures, tc*/ts* > 1, can be expressed as
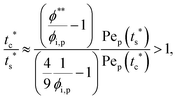 | (10) |
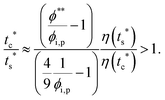 | (11) |
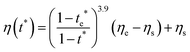 | (12) |
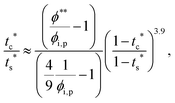 | (13) |
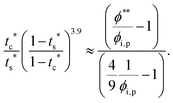 | (14) |
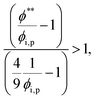 | (15) |
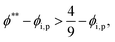 | (16) |
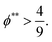 | (17) |
It is interesting to note that the predicted stratification of the polymer–colloid mixtures does not depend on the drying rate vev, or Pe, as long as Pe ≫ 1. This tendency can also be seen in Fig. 6, which shows the theoretical predictions of the 8 systems above, with vev values changed. Ignoring the data points of Pei,p ≤ 5, which fail to follow the aforementioned assumption that Pe ≫ 1, all the other points belong to the same regime once the polymer type and initial volume fraction are determined. This is quite plausible since the increase in polymer concentration near the drying interface accelerates both tc* and ts* in a similar order. Thus, it might be hard to create stratified layers in polymer–colloid mixtures only by varying the evaporation rate vev, or Pe. Altering other properties that can increase tc*/ts* to larger than 1, such as utilizing the interfacial activity of the polymer [PVA Mw 6000 ϕi,p 0.04 in Fig. 1(c) and 4] or the gravitational velocity from the density difference shown in Fig. S7 (ESI†), could be another solution to achieve stratified layers in polymer–colloid mixtures.
Our experimental and modelling studies on polymer–colloid stratification show different results to the previous simulation study by Cheng and Grest,42 which demonstrated the kinetic arresting of nanoparticles in the polymer-enriched surface layer with strong polymer–nanoparticle interactions. The difference might come from the size ratio of polymer and colloid. In our studies, we chose systems having size ratios of Rcolloid/Rpolymer of 150 and 70. Stratification can occur in the systems having a size ratio of 150 while it cannot occur in the systems having a size ratio of 70 since tc*/ts* becomes smaller than 1 as the size ratio decreases. This implies that a non-stratified layer would be observed if the size ratio decreased to 5 as in the work of Cheng and Grest.42
In addition, in several simulation studies,43,44 it was shown that the stratification phenomena could be controlled by changing the drying rate vev, or Pe, in binary colloidal mixtures. This discrepancy may come from the differences in fundamental characteristics between polymer and colloid. However, all of the stratification results in polymer–colloid mixtures that can be predicted by our modified model shown in Fig. 6 were not confirmed experimentally. Our modified model is very simple with several assumptions. These assumptions and simplicity might be another cause of the inconsistent results between binary colloids and polymer–colloid mixtures in controlling stratification by changing the drying rate vev or Pe. There might be some missing points in our simplified model, which could be clarified by further studies.
3. Conclusion
In summary, we demonstrated that dynamic stratification of polymer–colloid mixtures can be achieved by controlling viscosity near the drying interface, which results from increasing polymer concentration. When the polymer–colloid solution evaporates, the polymer starts to increase in solution viscosity near the air/water interface within a relatively very short time, unlike colloidal suspensions. Since the transition in viscosity due to the polymer can cause the kinetic arrest of colloidal particles, which hinders the diffusiophoretic downward motion of colloids, stratified layers are only observed if the formation of a stratified layer precedes the transition in viscosity near the liquid/air interfaces.Our model calculations for tc* and ts*, inspired by a previous study,24 show that the segregation of polymer–colloid mixtures can only occur under the condition of tc*/ts* > 1, unless the solute fraction of the polymer is sufficiently low. The requirement for stratification, tc*/ts* > 1, implies that the stratification of polymer–colloid mixtures may not rely on the drying rate if Pe ≫ 1, since both tc* and ts* vary in a similar order as vev changes. Our model calculations are further supported by the consistency between the model prediction and final experimental film morphologies.
In other words, for the stratified layers in polymer–colloid mixtures, a polymer volume fraction that is not too low is necessary. If the polymer volume fraction is too low, it takes a fairly long time to create a sufficiently high concentration gradient of polymer that can induce diffusiophoretic motion of colloidal particles in the drying solution. In addition, both Pep and ϕ** should be sufficiently high to achieve a stratified layer in drying polymer–colloid mixtures. For a large Pep, the evaporation rate should be fast or the polymer size should be large at the constant initial film height. However, since a larger molecular weight of polymer leads to a lower ϕ**, it is better to use a lower molecular weight of polymer and fast evaporation rate to satisfy larger values in both Pep and ϕ**, which are the prerequisites for stratification in polymer–colloid mixtures.
In more general terms, the consistent results of the experiments and model prediction may shed light on methods of controlling surface enrichment in general solution–cast polymer composites. The ability to predict morphology in a simple nonequilibrium solvent evaporation process is highly desirable for preparing materials whose surface properties are crucial to performance, such as antireflective or organic photovoltaics. Our insights on how polymer concentration affects colloidal dynamics and stratification can be exploited to control segregated layers in solution-cast polymer–colloid mixtures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (Grants NRF-2015R1C1A1A01054180, and NRF-2019R1F1A1059587).Notes and references
- H. M. van der Kooij and J. Sprakel, Soft Matter, 2015, 11, 6353 RSC.
- A. Beaugendre, S. Degoutin, S. Bellayer, C. Pierlot, S. Du-quesne, M. Casetta and M. Jimenez, Prog. Org. Coat., 2017, 110, 210 CrossRef CAS.
- J. C. Padget, J. Coat. Technol., 1994, 66, 89 CAS.
- A. G. Márquez, T. Hidalgo, H. Lana, D. Cunha, M. J. Blanco-Prieto, C. Álvarez-Lorenzo, C. Boissiére, C. Sánchez, C. Serre and P. Horcajada, J. Mater. Chem. B, 2016, 4, 7031 RSC.
- S. A. Wissing and R. H. Müller, Int. J. Cosmet. Sci., 2001, 23, 233 CrossRef CAS.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194 CrossRef CAS.
- B. J. Anderson and C. F. Zukoski, Macromolecules, 2008, 41, 9326 CrossRef CAS.
- B. J. Anderson and C. F. Zukoski, Macromolecules, 2009, 42, 8370 CrossRef CAS.
- J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cas-sagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Polymer, 2010, 51, 3321 CrossRef CAS.
- P. Cassagnau, Polymer, 2008, 49, 2183 CrossRef CAS.
- S. K. Kumar, V. Ganesan and R. A. Riggleman, J. Chem. Phys., 2017, 147, 020901 CrossRef.
- N. Jouault, D. Zhao and S. K. Kumar, Macromolecules, 2014, 47, 5246 CrossRef CAS.
- D. M. Yebra, S. Kiil and K. Dam-Johansen, Prog. Org. Coat., 2004, 50, 75 CrossRef CAS.
- I. Banerjee, R. C. Pangule and R. S. Kane, Adv. Mater., 2011, 23, 690 CrossRef CAS.
- J. J. van Franeker, D. Westhoff, M. Turbiez, M. M. Wienk, V. Schmidt and R. A. J. Janssen, Adv. Funct. Mater., 2015, 25, 855 CrossRef CAS.
- R. S. Krishnan, M. E. Mackay, P. M. Duxbury, A. Pastor, C. J. Hawker, B. V. Horn, S. Asokan and M. S. Wong, Nano Lett., 2006, 7, 484 CrossRef.
- Q. Wei, T. Nishizawa, K. Tajima and K. Hashimoto, Adv. Mater., 2008, 20, 2211 CrossRef CAS.
- E. S. McGarrity, A. L. Frischknecht and M. E. Mackay, J. Chem. Phys., 2008, 128, 154904 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827 CrossRef CAS.
- R. Brown, Philos. Mag., 1828, 4, 161 CrossRef.
- M. P. Howard, A. Nikoubashman and A. Z. Panagiotopoulos, Langmuir, 2017, 33, 3685 CrossRef CAS.
- A. Fortini, I. Martín-Fabiani, J. L. De La Haye, P.-Y. Dugas, M. Lansalot, F. D’Agosto, E. Bourgeat-Lami, J. L. Keddie and R. P. Sear, Phys. Rev. Lett., 2016, 116, 118301 CrossRef.
- J. Zhou, Y. Jiang and M. Doi, Phys. Rev. Lett., 2017, 118, 108002 CrossRef.
- R. P. Sear and P. B. Warren, Phys. Rev. E, 2017, 96, 62602 CrossRef.
- M. P. Howard, A. Nikoubashman and A. Z. Panagiotopoulos, Langmuir, 2017, 33, 11390 CrossRef CAS.
- P. J. Flory and T. G. J. Fox, J. Am. Chem. Soc., 1951, 73, 1909 CrossRef.
- S. Matsuoka and M. K. Cowman, Polymer, 2002, 43, 3447 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1979 Search PubMed.
- R. H. Colby, Rheol. Acta, 2010, 49, 425 CrossRef CAS.
- Y. Takahashi, Y. Isono, I. Noda and M. Nagasawa, Macromolecules, 1985, 18, 1002 CrossRef CAS.
- W. W. Graessley, Polymer, 1980, 21, 258 CrossRef CAS.
- I. M. Krieger and T. J. Dougherty, Trans. Soc. Rheol., 1959, 3, 137 CAS.
- D. Langevin and F. Rondelez, Polymer, 1978, 19, 875 CrossRef CAS.
- C.-Y. Chou, B. C. Eng and M. Robert, J. Chem. Phys., 2006, 124, 044902 CrossRef.
- R. P. Sear, J. Chem. Phys., 2018, 148, 134909 CrossRef.
- A. I. Fedorchenko and A. A. Chernov, Int. J. Heat Mass Transfer, 2003, 46, 915 CrossRef CAS.
- J. L. Anderson, M. E. Lowell and D. C. Prieve, J. Fluid Mech., 1982, 117, 107 CrossRef CAS.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61 CrossRef.
- T. Okuzono, K. Ozawa and M. Doi, Phys. Rev. Lett., 2006, 97, 136103 CrossRef.
- M. Rubinstein and R. H. Colby, In Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- Y. Tang, G. S. Grest and S. Cheng, Langmuir, 2018, 34, 7161 CrossRef CAS.
- S. Cheng and G. S. Grest, ACS Macro Lett., 2016, 5, 694 CrossRef CAS.
- R. Tatsumi, T. Iwao, O. Koike, Y. Yamaguchi and Y. Tsuji, Appl. Phys. Lett., 2018, 112, 053702 CrossRef.
- Y. Tang, G. S. Grests and S. Cheng, J. Chem. Phys., 2019, 150, 224901 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01504k |
| This journal is © The Royal Society of Chemistry 2020 |