Ligand density quantification on colloidal inorganic nanoparticles

Abstract

Colloidal inorganic nanoparticles are being used in an increasingly large number of applications ranging from biological imaging to television displays. In all cases, nanoparticle surface chemistry can significantly impact particle physical properties, processing, and performance. The first step in leveraging this tunability is to develop analytical approaches to describe surface chemical features. Some of the most basic descriptors of particle surface chemistry include the quantity, identity, and arrangement of ligands appended to the particle core. Here, we review approaches to quantify molecular ligand densities on nanoparticle surfaces and consider fundamental barriers to the accuracy of this analysis including parameters such as dispersity in colloidal nanoparticle samples, particle–ligand interactions, and currently available analytical techniques. Techniques reviewed include widely studied methods such as optical, atomic, vibrational, and nuclear magnetic resonance spectroscopies as well as emerging or niche approaches including electrospray-differential mobility analysis, pH-based methods, and X-ray photoelectron spectroscopy. Collectively, these studies elucidate surface chemistry architectures that accelerate both fundamental understanding of nanoscale physical phenomena and the implementation of these materials in a wide range of technologies.

---

Ashley M. Smith

Ashley M. Smith was born and raised in New Kensington, Pennsylvania, USA. She earned her B.A. in chemistry from Washington and Jefferson College in 2011, where she performed undergraduate research under the direction of Patricia A. Brletic. Ashley is now a Ph. D. student at the University of Pittsburgh in the lab of Prof. Jill E. Millstone. Her research focuses on using NMR-based methods to study metal nanoparticle ligands.

Kathryn A. Johnston

Kathryn A. Johnston was born in Pittsburgh, Pennsylvania, USA. She earned her B.S. in chemistry from Villanova University in 2012, where she performed undergraduate research under the direction of Deanna L. Zubris. She is now a Ph. D. student at the University of Pittsburgh in the lab of Prof. Jill E. Millstone, where her research investigates the ligand chemistry of silver nanoparticles and its impact on gene expression in bacteria exposed to these materials.

Scott E. Crawford

Scott E. Crawford was born in Clinton, Pennsylvania, USA. He obtained a B.S. in chemistry and economics at the University of Pittsburgh in 2013, where he conducted research under the direction of Sachin S. Velankar. Currently, he is a Pittsburgh Quantum Institute fellow pursuing a Ph. D. in chemistry at the University of Pittsburgh under the supervision of Prof. Jill E. Millstone. His research involves developing methods to systematically control metal nanomaterial surface chemistry and studying the impact of that surface chemistry on nanomaterial optoelectronic and catalytic properties.

Lauren E. Marbella

Lauren E. Marbella earned her B.S. in biochemistry from Duquesne University in 2009, where she performed undergraduate research in the laboratory of Partha Basu. She earned her M.S. at the University of Pittsburgh under the direction of Megan M. Spence, studying peptide translocation in lipid membranes using solid state NMR. She completed her Ph.D. in chemistry at the University of Pittsburgh in 2016 under the direction of Prof. Jill Millstone, investigating the formation and final characteristics of metal nanoparticles using magnetic resonance techniques. She is currently a postdoctoral researcher at the University of Cambridge in the laboratory of Clare Grey.

Jill E. Millstone

Jill E. Millstone is an Associate Professor of Chemistry at the University of Pittsburgh with affiliated appointments in the Departments of Chemical Engineering and Mechanical Engineering and Materials Science. Before joining the University of Pittsburgh, she completed her Ph. D. at Northwestern University and post-doctoral research at the University of California, Berkeley. Since 2011, she has received awards including the NSF CAREER Award, the ACS Unilever Award and the Cottrell Research Scholar Award. In addition, she serves on the editorial advisory board of ACS Nano. Her group studies the chemical mechanisms underpinning metal nanoparticle synthesis, surface chemistry, and optoelectronic behaviors.

---

1. Introduction

Nanoparticles (NPs) demonstrate a myriad of new and potentially useful properties that deviate from those observed in their bulk or molecular counterparts. A key component of these structure–function relationships is the surface chemistry of the NPs. Surface chemistry is defined by both the crystallographic features of the particle surface as well as the ligands appended to it. Here, ligands refer to species adsorbed to the NP surface and can range from monoatomic ions to large macromolecules. Ligands can be used to control the growth of the particle,^1–3 to provide stability to particles once formed,^4–6 and also to direct their functionality.^7–12 For example, ligands may influence charge transfer in NP-based devices¹³ or targeting in biological systems.¹⁴ On extended solid surfaces, correlations between surface ligand architectures and the function of the material have been well-documented,^15–17 in no small part because of the thorough characterization of the ligand architecture itself.^18–21 However, the study and use of ligand arrangements on colloidal inorganic NPs present unique (and sometimes deceptively mundane) challenges including polydispersity in NP samples, determination of NP surface area, and purification of particle conjugates from unbound ligands.

The analytical methods used to assess NP ligand architectures depend on the questions one asks about the ligand shell structure. Three fundamental aspects of this structure are the identity of the constituent ligands, the quantity of each ligand type, and the spatial arrangement of those ligands, both with respect to each other and to the NP core. Therefore, a crucial first step towards understanding and leveraging NP surface chemistry is to describe each of these architectural features, the most basic of which is the quantity of ligands appended to the NP surface. Ligand quantification studies may be used in a variety of ways including to assess as-synthesized particle ligand densities, ligand densities after post-synthetic modification (e.g. ligand exchange), or following particle exposure to, or operation in, various environments.^22,23 Ligand identification and quantification then provides a robust foundation from which to study additional features of the NP ligand shell including aspects of its arrangement and dynamics,^24,25 as well as NP efficacy in downstream applications, including drug delivery^26,27 and heterogeneous catalysis.^28,29

Here, we review techniques that determine NP ligand density, focusing on methods that yield a quantitative ligand analysis (i.e. an absolute ligand density as opposed to relative ligand ratios). In section 2, we outline characteristics of both the NP and the ligand that inherently influence particle ligand densities as well as the analytical methods used to evaluate them. We then discuss the implementation of these approaches in detail, with the discussion divided into sections based on the analytical approach. Thermogravimetric analysis, the first widely implemented technique for ligand quantification, is discussed in section 3. Subsequently, we highlight various spectroscopic methods, including optical (section 4), atomic (section 5), nuclear magnetic resonance (section 6), and vibrational (section 7) spectroscopies. We also include brief reviews of niche or emerging techniques including electrospray-differential mobility analysis (section 8), pH-based methods (section 9), and X-ray photoelectron spectroscopy (section 10). We have summarized the ligand density results of the highlighted studies in a referenced table (Table 1). In order to facilitate comparisons between methods, we report all ligand densities in units of ligands per nm², using information contained in the specific reports to make unit conversions when necessary.

Table 1 Compilation of ligand densities (in units of ligands per nm²) reported in the papers discussed in the text

Particle type	Ligand identity	Reported NP size (nm)^a	Packing density (ligands per nm^2)	Quantification technique	Source
a For all reported sizes where a standard deviation is not given in the table, a standard deviation was not reported in the original text. For NP size ranges, a size range (as opposed to a standard deviation) was reported in the original text. b In addition to a terminal thiol, this DNA sequence also includes a C6 alkane spacer moiety before and after the ssDNA sequence. c In addition to a terminal thiol, this DNA sequence also includes a hexyloxy spacer moiety between the thiol group and the ssDNA sequence. d The size reported for this NP is an edge length of Au nanocages.
Ag	MUA	4.5 ± 1.3	6.4	TGA	88
	1 kDa PEGSH	25.4 ± 2.1	2.11 ± 0.06	NMR	130
Au	MPA	5	6.7	ICP-OES	120
	MPA	13.2 ± 1.4	6.26 ± 0.59	ICP-MS	119
	Thioctic acid	11.6 ± 1.0	1.72	XPS	155
	DDT	5.6	4.67	TGA	77
	MUA/DPPBA	1.8 ± 0.4	5.50 ± 0.88	NMR	25
	MUA	2.4 ± 0.5	14	pH	150
	MUA	12.6 ± 1.2	4.97	XPS	154
	MUA	13 ± 1	4.5 ± 0.1	NMR	54
	MUA	13.8 ± 0.9	4.68 ± 0.05	UV-vis	52
	Tetradecanethiol	2.0 ± 0.8	5.81 ± 0.14	TGA	66
	Tetradecanethiol	3.9 ± 0.5	4.35	TGA	71
	EG4-SH	3.4	4.17	TGA	75
	HS(CH2)11-(EG)6-OH	1.3 ± 0.3	3.8 ± 0.7	XPS	153
	1 kDa PEGSH	60	1.4	IR	23
	2 kDa PEGSH	5.7 ± 2	2.38	TGA	67
	2 kDa PEGSH	4.9 ± 1.0	7.04 ± 2.97	TGA	68
	2 kDa PEGSH	11.7 ± 1.4	2.25 ± 0.01	TGA	64
	2.1 kDa PEGSH	15 ± 1.8	3.93	TGA	63
	5 kDa PEGSH	2.8 ± 1	2.88	TGA	79
	1 kDa NH2PEGSH	16.9 ± 0.26	0.36 ± 0.05	TGA	74
	3 kDa PEGNH2	50^d	2.21 ± 0.18	UV-vis	98
	0.6 kDa TA-PEG-Mal	10	0.83 ± 0.06	UV-vis	110
	740 Da HCO2-PEGSH	4.1 ± 0.8	1.33	pH	149
	3.4 kDa FITC-PEGSH	27.6 ± 2.1	5.56	TGA	76
	2 kDa PS-SH	4.4 ± 1.2	3.45	TGA	70
	7 kDa PNIPAM	5.2	0.83	TGA	73
	4.7 kDa cumyl-NIPAM	2.2 ± 0.8	2.2	TGA	72
	HS-DNA (10 bp)	20	0.69	ES-DMA	146
	HS-DNA (12 bp)^b	15.7 ± 1.2	0.21 ± 0.01	PL	97
	HS-DNA (25 bp)	10	0.21 ± 0.04	PL	101
	HS-DNA (25 bp)	15	0.23	PL	100
	HS-DNA (32 bp)^c	15.7 ± 1.6	0.17 ± 0.01	PL	102
	BSA	20	0.13 ± 0.01	PL	109
	BSA	30	0.03	ES-DMA	148
	Tiopronin	3.9 ± 1.7	3.83	TGA	81
	MBI	13	3.44 ± 0.03	Raman	144
	MBI	13	3.80 ± 0.05	Raman	61
	1-Pyrenebutanethioic acid S-butyl ester	12.5 ± 1.5	4.08 ± 0.17	PL	108
	MMC	5.3 ± 2.1	0.86	UV-vis	51
	Calix[4]arene enantiometers	4.7 ± 1.3	1.10	UV-vis	112
	Calix[6]arene derivatives	4.2 ± 0.9	0.42 ± 0.03	UV-vis	113
	Calix[8]arene phosphinoxides	4.3 ± 0.8	0.44	UV-vis	114
CdS	Thiophenol	2.4 ± 0.1	1.37 ± 0.34	NMR	126
CdSe	Oleate	3.5 ± 0.1	4.6 ± 0.4	NMR	139
	Oleate	4.2	4.1	NMR	22
	Oleate/tetradecanoate	3.3 ± 0.2	2.9 ± 0.5	NMR	57
	Oleate/tetradecanoate	3.5	4.2 ± 0.7	NMR	131
	1 kDa LA-PEG-CHO	6.2	1.66 ± 0.09	UV-vis	111
	TOPO/TOPSe	3.7 ± 0.4	3.72	NMR	143
	CH3-TP	3.7	4.1 ± 2.7	NMR	24
Fe3O4	350 Da SiPEG	30–40	0.79	TGA	87
	Glycine	14	1.27	TGA	85
InP	TOPO	4.7	3	NMR	138
PbS	Oleate/tetradecanoate	3.1	4.3 ± 0.5	NMR	131
PbSe	Oleate	3–7	4.2	NMR	123
	Oleate	4.9	3.18	NMR	22
	Oleate/tetradecanoate	3.7	3.1 ± 0.5	NMR	131
Pd	1-Octyne	2.5 ± 0.3	7.69	TGA	29
	DDT	2.2 ± 0.7	3.49	TGA	91
	DDT	3.4 ± 1.0	4.57	TGA	28
	Butylphenyl	2.2 ± 0.4	4.76	TGA	89
Pt	Chlorophenyl	1.9 ± 0.3	12.50	TGA	94
	Butylphenyl	2.9 ± 0.5	17.24	TGA	95
Ru	1-Octynyl	2.6 ± 0.2	6.67	TGA	93
SiO2	2 kDa PNIPAM	54.3 ± 3.7	0.58	TGA	82
	Alanine	7	2.02 ± 0.13	TGA	84
	Lysine	7	2.3 ± 0.2	TGA	83
SiO2@Au	pMA-PEG2000-Fl	90 nm core, 17 nm shell	0.28 ± 0.13	Raman	145
ZnO	DDA	3.6 ± 0.4	1.2 ± 0.2	NMR	142

---

2. General considerations for ligand quantification

An ideal method to quantify ligands on a NP surface would be to isolate an individual NP and count ligands directly bound to that structure only. However, since techniques have not yet been developed to characterize particles in such detail, all current analytical methods for determining particle ligand densities involve analysis of the bulk colloid in some way. Below, we outline general considerations when quantifying ligands on a NP surface, including characteristics of the NP core (section 2.1) and ligand shell (section 2.2).

2.1 Core considerations

Measurements of NP concentration and core morphology strongly influence the accuracy of ligand density determination because both parameters are needed to determine the total surface area of the particle sample. This total surface area is then used to extract ligand density values.

2.1.1 Particle concentration and surface area calculation. In order to determine particle ligand densities, the general approach is to divide the total amount of ligands measured by the total amount of particle surface area measured. This method of ligand density determination is necessary because single particle ligand counting is not yet feasible (vide supra). Therefore, although we focus here on quantification of NP ligands, quantification of particle ligand densities also critically depends on the measurement of total particle surface area. Surface area can be determined directly using methods such as gas sorption approaches^30–34 or may be determined indirectly by calculating surface area from NP core concentrations and average particle dimensions (where dimensions may be determined by techniques including transmission electron microscopy (TEM), scanning electron microscopy (SEM), or dynamic light scattering (DLS)).

However, whether particle surface area is measured directly or indirectly, particle concentration must also be determined in order to quantify per particle ligand densities. There are multiple methods to measure NP core concentrations. Two of the most common approaches are absorption spectroscopy and atomic spectroscopies such as inductively coupled plasma mass spectrometry/atomic emission spectroscopy (ICP-MS/AES). For absorption spectroscopy measurements, absorbance of the NP sample at a specific wavelength is recorded. Then, using the particle molar extinction coefficient at this wavelength, the particle concentration can be determined.^35–38 Absorption spectroscopy, especially in the solution phase, has several advantages including the ability to perform measurements in situ (e.g. assessing NP concentration as a function of ligand exchange or modification reactions). However, because each NP has an extinction coefficient (at a given wavelength) that varies as a function of NP size, shape, and surface chemistry, dispersity in these parameters influences the calculated NP concentration when using a single average extinction coefficient. Polte and co-workers have conducted a detailed study of these dispersity-induced errors, including particle size variation, NP surface modification, and metal oxidation state.³⁹

Unlike absorption measurements, ICP-MS/AES measures the total number of atoms of interest in the NP sample. Then, the atom concentrations are combined with experimentally determined NP sizes and shapes to derive the total surface area of the sample. Therefore, ICP-MS/AES approaches have the same shortcomings introduced by NP dispersity as discussed above.^40–43 However, ICP-MS/AES measures atom concentration directly and is unparalleled in atom detection sensitivity regardless of NP size, surface chemistry, or oxidation state (detection limits vary depending on instrument, experimental conditions, and analyte of interest but can range as low as parts-per-trillion for Au detected with high resolution ICP-MS).⁴⁴

Taken together, each particle surface area determination approach ultimately assumes an average particle size and shape and determines a total particle surface area from those values. As a result, the error in calculated ligand density is fundamentally limited by the dispersity of the particle sample in terms of both size and shape, regardless of the method selected (see ESI† for sample calculation methodology).

2.1.2 Core morphology. Even if single particle ligand counting was possible, different surface features can be exhibited within a single particle and each unique surface will likely have a distinct ligand density for any given ligand of interest. NP properties that may produce this heterogeneity include core composition, size, and shape. Particle size and shape influence parameters such as the population of exposed crystal facets and surface radii of curvature, which can influence inter-ligand interactions. Composition also influences the population of exposed Miller planes (and corresponding surface atom densities) for any given particle, and ligands may arrange differently depending on these features.^45,46 Further, in multi-element NPs (e.g. alloyed or metal chalcogenide NPs), ligand binding and arrangements will vary depending on which atoms are present at the NP surface and the affinity of the ligand for each atom (or site) type.^47–49 It is important to note that in the ligand quantification approaches discussed here, facet- or atom-specific ligand quantification is not resolved, although recent nuclear magnetic resonance (NMR) studies have shown promise for determining these details.⁵⁰

Finally, NP core properties not only influence intrinsic ligand binding motifs, they also impact the selection of analytical approaches for evaluating those motifs. For example, in certain absorption spectroscopy techniques, ligand-dependent shifts in particle optical features such as localized surface plasmon resonances (LSPRs) are exploited.^51,52 For these techniques, particles must be of both a composition and a size that exhibit spectroscopically discernible LSPRs, among other factors. Likewise, the composition of the NPs may impact the use of techniques such as ICP-MS/AES, where challenges including spectral interferences between analyte elements can occur.

2.2 Ligand property considerations

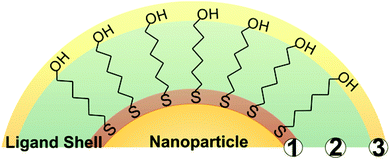
While a wide variety of chemical moieties may act as NP ligands, organic small molecules are some of the most common and are the most widely studied with respect to quantification. These ligands have three key regions (Fig. 1). First is the particle binding moiety (e.g. –SH, –PR₃, –NH₂) which is directly appended to the NP surface. The density of ligands on the surface of a NP is fundamentally limited by the space this functional group occupies.^53–55 The second region is the intra-molecular portion, and there is a wide array of chemical functionalities that can be present at this site. Interactions between adjacent intra-molecular regions (i.e. inter-molecular interactions) can also influence ligand density limits via factors such as steric effects and noncovalent interactions. Last, there is the solvent-facing portion of the molecule. Each region, and/or all regions in concert, may influence not only the fundamental limits on the physical space occupied by the ligands but also the dynamics of these ligands in ligand exchange equilibria,^56,57 surface ligand migration (i.e. translational motion),^58,59 and ligand conformation with respect to the surface (e.g. tilt, cant, or intra-ligand conformers).^60–62

Fig. 1 Scheme representing three key regions of small molecule capping ligands: 1. the particle binding moiety, 2. an intra-molecular region, and 3. a terminal group. N. B. Components in regions 2 and 3 can also interact with the NP surface under certain conditions (vide infra).

All of these dynamic factors can play key roles in the accuracy of any given ligand quantification approach. For example, in preparing NP-ligand conjugates for quantification analysis (and typically, for subsequent applications), the conjugates must be washed thoroughly in order to remove any unbound or non-specifically bound ligands from solution. However, if the ligands are not strongly associated with the particle, such as trisodium citrate on AuNPs,¹⁵ the on-particle ligand density will be modified during the purification steps, and accurate ligand quantification may not be possible with current capabilities.

These ligand dynamics also impact variation in ligand density from sample to sample as a function of several factors. First, variability can occur from ligand dissociation during particle washing procedures as mentioned above. Second, ligand adsorption is a dynamic process, and therefore depending on how long the sample is exposed to excess ligand, some variability is expected. Consequently, it is helpful to analyze ligand density by conducting both a binding isotherm study as well as a time-based quantification study at constant ligand excess, in order to assess whether consistent ligand loading values are achieved during the functionalization procedure selected. In this report, standard errors or deviations in ligand density values are included for all cases where they are available from the original report.

3. Thermogravimetric analysis (TGA)

One of the earliest and most common methods used to assess NP ligand density is TGA.^63–76 In a typical experiment, the sample is thoroughly dried and its dry mass recorded. Then, the sample is heated (rates range from 5–20 °C per minute), and its change in mass is recorded as a function of temperature. The temperature of mass loss is related to ligand identity. After heating, the percentage of mass loss within a ligand-specific temperature range can be correlated with the number of ligands appended to the particle. The corresponding NP concentration is typically determined from the remaining mass after heating.

Early studies of TGA-based NP ligand quantification were reported by Murray and co-workers. The authors examined various thiolated ligands appended to small, pseudospherical AuNPs (d = 1.5–5.2 nm).^77–80 Throughout these studies, the authors found that ligand density varied only slightly depending on particle size and ligand identity. For example, the studies found that dodecanethiol (DDT) ligand densities were approximately 4.6 ligands per nm² for both 2.8 nm and 5.2 nm diameter AuNPs.⁷⁷ Larger ligands such as α-methoxy-ω-mercapto-poly(ethylene glycol) (PEGSH, molecular weight (MW) = 5 kDa) on similarly sized NPs (d = 2.8 ± 1 nm) produced lower ligand densities (2.88 ligands per nm²),⁷⁹ demonstrating that larger ligands may pack less densely on AuNP surfaces, even when the surface has a high radius of curvature.

The authors extended their studies to more diverse ligands, including the thiol-terminated, biologically relevant molecule tiopronin. Tiopronin (MW = 163 Da) is smaller than PEGSH but sterically bulkier than DDT and exhibits a ligand density of 2.68 ligands per nm² on 3.1 ± 1.2 nm diameter AuNPs. Interestingly, this tiopronin ligand density is markedly lower than for either the polymeric ligand or the alkanethiol. In this case, the decreased ligand density was attributed to the steric bulk directly surrounding the NP binding moiety.⁸¹ Taken together, these studies indicate that for a given particle binding moiety (and NP surface), the steric bulk directly at this molecular region is the limiting factor in determining ligand surface coverage, independent of both the size of the remainder of the molecule (e.g. the case of PEGSH) and the particle radius of curvature.

Thiol-terminated PEG ligands (range of MWs = 2.1–51.4 kDa) on AuNPs (d = 15–170 nm) were also studied using TGA by Holmes and co-workers.⁶³ The authors observed a decrease in surface ligand density as polymer MW increases, consistent with other studies of thiol-terminated polymeric ligands (Fig. 2). Colvin and co-workers also investigated the ligand density of various thiolated PEG molecules using TGA, and importantly, compared those results with ligand density values obtained by two other methods: analytical ultracentrifugation (AU) and total organic carbon analysis (TOC). The authors found that ligand loading densities were similar for all three methods with values that deviated by less than 22% across a variety of PEGSH MWs (MW = 1–20 kDa) and particle diameters (d = 5, 10, 15, or 20 nm).⁶⁴

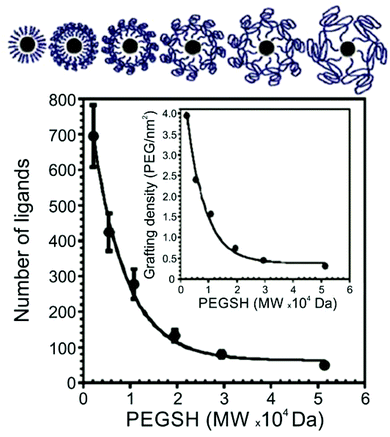Fig. 2 Number of PEGSH ligands on 15 nm AuNPs as a function of PEGSH molecular weight, showing that ligand density decreases as ligand chain length increases; inset plots “grafting” (i.e. ligand) density as a function of PEGSH molecular weight. Modified figure from ref. 63 with permission from The Royal Society of Chemistry.

While AuNP–ligand conjugates are the most thoroughly studied NPs using TGA, TGA has also been used to study ligand densities on other particle types, including silica,^82–84 magnetite,^85–87 Ag,⁸⁸ Pd,^{28,29,89–92} Ru,⁹³ and Pt.^94–96 These studies have been conducted primarily in conjunction with catalysis or biomedical studies that draw connections between NP ligand density and particle performance in a given application. For example, Shon and co-workers investigated the correlation between ligand density and catalytic activity of PdNPs in the isomerization of allyl alcohols to their carbonyl analogues. Using a variety of alkanethiol and thiosulfate ligands, the authors found that NPs with lower ligand densities exhibited enhanced catalytic activity.^28,91,92 Various other reports also correlate ligand densities on Pd and Pt NPs to catalytic figures of merit, including activity.^29,89,94,95

For biological investigations, Davis and co-workers have found that lymph node uptake of magnetite NPs (d = 40–50 nm) was influenced by the ligand density of pendant PEG molecules (PEG terminally substituted by trimethoxysilane, SiPEG; MW = 350, 550, 750, or 1000 Da).⁸⁶ By comparing different ligand densities with various MWs of SiPEG, the authors found that the biodistribution of these particles could be tuned for optimized lymph node uptake. The highest uptake was observed for magnetite particles capped with 750 Da SiPEG with a maximum loading of 0.8 μmol per m² (0.48 ligands per nm²), although improved lymph node uptake was observed in nearly all cases with the addition of SiPEG compared to the un-PEGylated magnetite NPs.⁸⁶

The above studies demonstrate that TGA is an effective technique for ligand quantification for a wide range of both ligand and particle types. However, it is important to note that this method is limited in the characterization of multicomponent ligand shells (i.e. particle ligand shells that contain more than one ligand type), since often it is not possible to distinguish between ligand removal temperatures, especially for ligands with similar masses.

4. Optical spectroscopy

Ligand quantification using optical spectroscopy includes both absorption and photoluminescence (PL) measurements. These techniques frequently exploit optically active indicators, such as fluorescein, which are used to label ligands appended to the particle surface. Typically, these labelled ligands are released for measurement by digesting the particle. The optical signal from the labelled ligands is then compared to a calibration curve prepared from standards to determine unknown ligand concentrations. Colorimetric or fluorescence assays may also be used to quantify the concentration of free ligand before and after the introduction of particles, where the change in concentration after particle introduction is attributed to ligands attaching to the particle surface. For plasmonic particles, techniques have been developed to correlate changes in the LSPR to ligand densities. Additionally, if optically active ligands are used, techniques such as time-correlated single photon counting (TCSPC) or measurements of ligand excimer PL can be used to measure the amount of ligand present in a sample. Following quantification of ligand concentrations by the above methods, the corresponding NP concentration is typically determined using either atomic or absorption spectroscopy.

4.1 Photoluminescence (PL) spectroscopy

A variety of PL techniques have been developed to quantify ligand density and functionality. These methods require ligands that are inherently fluorescent, ligands that are labelled with a fluorophore, or the addition of a fluorescent indicator. Both steady-state and time-resolved techniques have been used.

4.1.1 Fluorescently-labelled ligands. In 2000, Mirkin and Letsinger used PL spectroscopy to quantify oligonucleotide loading on AuNPs (d = 15.7 ± 1.2 nm) and established relationships between various ligand properties and the extent of DNA hybridization on the NP surface.⁹⁷ Specifically, the authors used fluorescein to label individual thiolated oligonucleotides (12 base pair (bp) single-stranded DNA (ssDNA) with a hexanethiol spacer before and after the DNA sequence) and then exploited the quenching properties of AuNPs as a signal mediator. AuNPs and other metals are known to quench the emission of nearby luminophores through decay pathways such as nanosurface energy transfer (NSET), in which conduction electrons in the metal interact with the luminophore dipole.^98,99 Therefore, in these experiments, no PL was observed from the fluorophore-labelled ligands when appended to the NPs. After incubating the AuNPs in 2-mercaptoethanol, the thiolated ssDNA was displaced, and after separation from remaining AuNPs via centrifugation, PL from the displaced oligonucleotides was measured at 520 nm. The concentration of released ssDNA was determined by comparing this PL signal to a standard calibration curve and used to calculate a ligand density of 0.21 ± 0.01 ligands per nm².⁹⁷ Using similar methods, the authors also showed that only 4% of particle-bound ssDNA hybridized with a complementary strand when the oligonucleotide sequences were directly appended to the AuNP via a terminal thiol linkage. However, hybridization efficiency increased to 44% if a 20 base pair “spacer” sequence was added between the thiol and the DNA sequence of interest.⁹⁷

This general method of quantification via the release of fluorescently-labelled ligands has been slightly modified to study a variety of particle morphologies and ligand types.^98,100–105 Mirkin and co-workers expanded their initial studies to quantify ligand density on different sizes of AuNPs (d = 10–250 nm) and investigated how parameters such as salt concentration and post-conjugation treatments (e.g. sonication) impacted final DNA density on the NPs.^100–102 In these studies, dithiothreitol (DTT) was used to displace the fluorescein-labelled ligand shell (Fig. 3). The ligand density decreased with AuNP size from 0.20 ± 0.04 ligands per nm² for 10 nm AuNPs to 0.06 ± 0.01 ligands per nm² for planar Au.¹⁰¹ The same group used these quantitative values to establish surface ligand-dependent particle properties. For example, the authors observed a positive correlation between AuNP cellular uptake and oligonucleotide loading density.¹⁰³ Liu and co-workers have also used fluorescence-based techniques to analyse DNA loading on AuNPs (d = 50 nm) in different salt concentrations and in a 2% PEG solution (MW = 20 kDa), where the PEG in solution does not adsorb to the particles but is thought to improve particle stability.¹⁰⁴

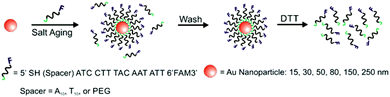Fig. 3 Scheme illustrating the quantitative analysis of oligonucleotide-functionalized AuNPs of various core diameters. Here, AuNPs are functionalized with fluorescein-labelled oligonucleotides in the presence of salt, purified, and then exposed to DTT, which removes the ligands from the NP surface. The released ligands are then quantified using photoluminescence spectroscopy. Adapted with permission from ref. 100. Copyright 2006 American Chemical Society.

In addition to total ligand density, fluorophore labelling has also been used to quantify the density of functional groups available for modification. For example, Fiammengo and co-workers quantified the number of “modifiable” amino groups on AuNPs (d = 29–41 nm) capped by different fractions of amine- and carboxylic acid-terminated PEGSH (MW = 600 Da or 3 kDa). The amine-functionalized ligands were post-synthetically labelled with 5(6)-carboxylfluorescein NHS ester, displaced using DTT, and then quantified using PL spectroscopy.¹⁰⁵ While this technique does not provide a full quantitative description of ligands on the AuNP surface, it instead reports on the number of amino groups that are available for functionalization, as not all of the amino groups were able to be fluorescently labelled.

4.1.2 “Turn on” fluorescent indicators. Another class of PL-based methods use “turn on” fluorescent indicators to quantify ligand density and/or functionality. In these techniques, an indicator is used that only shows luminescence in the presence of specific analytes. For example, Perry and Heinz used fluorescamine, which exhibits PL in the presence of primary amines, to investigate peptide loadings on silica particles as part of a wider study on silica NP surface chemistry.¹⁰⁶ The fluorescamine assay also has been used by Weller and co-workers, who quantified the number of accessible amino groups on 3-sulfanylpropyltrimethoxysilane-capped AuNPs (d = 2.2 ± 0.5 nm) after the NPs underwent silane polycondensation with 3-aminopropyldimethylethoxysilane.¹⁰⁷

4.1.3 Optically active ligands. Similarly, certain ligands may exhibit unique PL properties that are dependent upon their chemical environment. For instance, Katz and co-workers investigated the ligand density of 1-pyrenebutanethioic acid S-butyl ester and thiocarbonic acid O-(4-pyren-1-ylbutyl) S-butyl ester ligands on AuNPs (d = 12.5 ± 1.5 nm) and exploited the fact that, when appended to the NP surface, the hydrophobic pyrene moieties aggregate, which leads to an approximately 25 to 35-fold increase in the excimer emission band area.¹⁰⁸ In these experiments, known concentrations of citrate-stabilized AuNPs were titrated into a solution that contained a known concentration of either the thiocarbonate or thioester ligands. The fluorescence area between 360 and 600 nm was measured following each AuNP addition, and the titration continued until the fluorescence area reached a maximum, indicating saturation of the AuNP surface. This experiment was repeated at several different ligand concentrations, and a linear plot of the AuNP concentration at the saturation point versus the corresponding ligand concentration was obtained. The slope of the line corresponds to the number of ligands per saturated AuNP, and a ligand footprint of 24.5 ± 1.0 Ų (4.08 ± 0.17 ligands per nm²) was determined.¹⁰⁸

An additional method using optically active ligands exploits differences in the luminescent lifetime between the ligand luminopores when they are on or off a particle surface. Franzen and co-workers used TCSPC to determine the number of [Ru(bipy)₂bipy-C₆H₁₂S]²⁺(RCBS)-labelled bovine serum albumin (BSA) ligands on AuNPs (d = 20 nm).¹⁰⁹ Emission from RCBS is partially quenched when appended to AuNPs, resulting in a shorter lifetime. The AuNPs were incubated in an excess of the RCBS-labelled BSA ligands (500 : 1 ligand : AuNP ratio), and a biexponential lifetime was observed. From these data, two distinct lifetimes could be extracted, consistent with RCBS on and off particle. The coefficients of the fit for each lifetime corresponded to the relative ratios of each species in solution, and, in combination with the measured quantum yields, the concentration of the RCBS on and off particle could be determined. This method was validated using a second PL technique, in which a known concentration of the AuNPs was incubated in rhodamine B isothiocyanate-labelled BSA and then the particle–ligand conjugates were removed via centrifugation. The fluorescence of the BSA was measured before and after AuNP introduction and compared to a standard curve; the decrease in fluorescence (and therefore ligand concentration) was attributed to the BSA appended to the NP.¹⁰⁹

4.2 Absorption spectroscopy

Ligand quantification using absorption spectroscopy typically requires the use of indicators, labels, or particles that produce optical signals that quantitatively correlate with ligand loading values.

4.2.1 Ligands tagged with optically active labels. Absorption spectroscopy methods may monitor the absorbance of the ligand, the particle, or an external indicator to assess ligand density. Mattoussi and co-workers monitored the absorbance of a ligand by synthesizing a modular molecule consisting of a thioctic acid anchoring unit, a PEG chain, and a maleimide terminal group (TA-PEG-Mal). This ligand was then appended to AuNPs (d = 10 or 15 nm).¹¹⁰ The pendant maleimide was coupled to a peptide and Cy5 dye in a two-step reaction. Following particle purification, the Cy5 concentration was measured at 649 nm; extinction from non-Cy5 coupled AuNPs was subtracted as a blank. Footprints of 1.20 ± 0.08 and 1.27 ± 0.10 nm² (0.83 ± 0.06 and 0.79 ± 0.06 ligands per nm²) were measured for the 10 and 15 nm AuNPs, respectively. However, the authors point out that these values underestimate ligand concentration because they are based on the assumption that both coupling steps were 100% efficient.¹¹⁰ The same group used an analogous technique to investigate the loading of aldehyde-terminated ligands (lactic acid-PEG-CHO) on CdSe@ZnS semiconductor NPs (d = 6.2 and 6.8 nm) by conjugating 2-hydrazinopyridine to the aldehyde, which forms a chromophore with distinct absorption at 350 nm. In these experiments, the authors found that the ligand density was relatively insensitive to core size but that the ligand density decreases with increased ligand denticity.¹¹¹

4.2.2 Plasmonic NPs. For plasmonic AuNPs, the LSPR can also be used to monitor ligand loading. Katz and co-workers have reported a number of such studies. In 2008, the authors found that titrating 5,11,17,23-tetrakis-mercaptomethyl-25,26,27,28-tetrapropoxylcalix[4]arene (MMC) into a known concentration of tetraoctylammonium bromide (TOAB)-capped AuNPs (d = 5.3 ± 2.1 nm) produced a linear red-shift in the LSPR.⁵¹ Upon saturation of the AuNP surface with MMC, the LSPR ceased to shift in response to additional ligand. The ligand concentration at the saturation point and the AuNP concentration are both known, providing a quantitative assessment of ligand footprint, which was 116 Ų (0.86 ligands per nm²).⁵¹ The same group has also used this technique to quantify calix[4]arene enantiomers (1.10 ligands per nm²),¹¹² calix[6]arenes (0.42 ± 0.03 ligands per nm²),¹¹³ and calix[8]arenes (0.44 ligands per nm²).¹¹⁴ Similarly, Weinstock and co-workers observed a consistent blue shift in the LSPR as function of 11-mercaptoundecanoic acid (MUA) addition to a solution of AuNPs (d = 13.8 ± 0.9) originally terminated by the inorganic cluster α-AlW₁₁O₃₉⁹⁻. Upon saturation of the AuNP surface with MUA, no further change in the LSPR wavelength was noted, and the concentration of ligand added at this saturation point was used to determine the ligand footprint (Fig. 4).⁵²

Fig. 4 Ligand exchange of the α-AlW₁₁O₃₉⁹⁻ cluster-capped AuNPs with MUA. (A) Absorption spectra of the AuNP LSPR during the ligand exchange, and (B) plot of the change in LSPR absorbance at the initial λ_max of 526 nm as a function of added MUA concentration. Adapted with permission from ref. 52. Copyright 2012 American Chemical Society.

4.2.3 Optically active indicators. Finally, the absorbance of an external indicator can also be used to study ligand loading. Liang and co-workers quantified the conjugation of the therapeutic peptide p12 and a targeting peptide onto tiopronin-capped AuNPs (d = 2 nm) using the colorimetric bicinchoninic acid assay and observed 65% and 90% conjugation efficiency for the therapeutic and targeting peptides, respectively.¹¹⁵ Similar techniques have been used to quantify peptide¹¹⁶ and ssDNA¹¹⁷ loadings on AuNPs. In these studies, the free ligand concentration was monitored by UV absorption before and after AuNP incubation, which demonstrates that dye-free, absorption-based ligand quantification is also possible.

Xia and Chen used a ninhydrin assay as part of their investigation of α-amino-ω-mercapto-poly(ethylene glycol) (NH₂PEGSH) density as a function of polymer molecular weight (MW = 3, 5, or 20 kDa) on various sizes of Au pseudospherical NPs, nanorods, and nanocages (Fig. 5). Ninhydrin reacts with primary amines to produce a dark purple colour with an absorbance peak at 565 nm.⁹⁸ A known concentration of the AuNPs was incubated in a known concentration of NH₂PEGSH. Aliquots of the free NH₂PEGSH were removed before and after this incubation step and were mixed with ninhydrin. The change in absorbance before and after particle incubation was measured at 565 nm and compared to a standard curve, which allowed the change in NH₂PEGSH concentration (i.e. the concentration of ligands on particle) to be quantified. This method indicated that the ligand densities ranged from 2.21 to 0.21 ligands per nm² for 3 kDa and 20 kDa NH₂PEGSH, respectively, on 50 nm Au nanocages.⁹⁸ The authors compared this method to several other techniques, where the ninhydrin assay consistently indicated higher ligand loadings compared to other approaches including a fluorescamine assay (see section 4.1.2; 2.21 ligands per nm²versus 1.64 ligands per nm² for 50 nm Au nanocages). While the fluorescamine assay had a lower detection limit (∼250 nM versus 500 nM), it was more sensitive to discrepancies in sample preparation (e.g. whether or not all AuNPs had sedimented prior to measurement). Consequently, the authors recommended the ninhydrin assay as a more robust technique for quantification.

Fig. 5 Scheme demonstrating 4 different techniques for the quantitative characterization of NH₂PEGSH on AuNPs: (i) a fluorescamine photoluminesence assay, (ii) a ninhydrin-based absorption spectroscopy method, (iii) fluorescein labelling of terminal amines on the appended ligand, and (iv) Cu²⁺ labelling of terminal amines, an ICP-MS method. Techniques (i) and (ii) quantify ligand density, whereas (iii) and (iv) quantify the amino groups available for functionalization. Adapted with permission from ref. 98. Copyright 2012 American Chemical Society.

Chan and co-workers have used an external indicator to investigate the impact of PEGSH grafting on both the serum protein absorption and subsequent macrophage uptake of AuNPs. Here, they incubated AuNPs (d = 15, 30, 60, or 90 nm) in various concentrations of PEGSH (MW = 5 kDa) and assumed all particle-bound thiol groups were unavailable for further reaction. After incubation, the remaining thiol content was quantified using 5,5′-dithiobis(2-nitrobenzoic acid), which reacts with thiols in a stoichiometric fashion to produce an absorption band at 412 nm.¹¹⁸ The intensity of this band can then be monitored and compared to a standard curve in order to extract a quantitative value of unreacted thiol, which can be used to infer a quantity of thiols that had been adsorbed to NP surfaces.

Despite broad use, it is important to note that these optical spectroscopy methods can be limited because either the particle core or the ligands must be spectroscopically active or modified to be so post-synthetically. Such modifications can have undesired consequences for the ligand architecture. For example, changes can occur in ligand density due to an increase in ligand size as a result of fluorophore labelling. Further, when labelling is used, the efficiency of the labelling reaction is typically not 100%. Finally, absorption or luminescence from metal or semiconductor NPs may interfere with ligand-based PL or absorption measurements and therefore the ligand of interest must be extensively purified or spectroscopically distinct from the NP core optical features.

5. Atomic spectroscopy

ICP is an atomic spectroscopy method that uses high temperature plasma to decompose an analyte into its constituent atoms, and these atomized products can be subsequently analysed by either a MS or AES detector. ICP is most commonly used in the quantitative analysis of transition metals. However, it can also be used to detect lighter elements such as sulphur^119,120 or phosphorus^121,122 under certain conditions, which allows NP concentration and ligand concentration to be determined simultaneously in some cases.

For example, Lämmerhofer and co-workers used ICP-MS to quantify gold : sulphur ratios for AuNPs with various diameters between 13.2 ± 1.4 and 26.2 ± 4.4 nm.¹¹⁹ They demonstrated a linear relationship between ligand density and ligand chain length with various mercaptoalkanoic acids (MAAs) and examined NP ligand density with thiolated oligo EGs. The authors report average ligand densities of 4.96 ± 0.27 and 4.29 ± 0.45 ligands per nm² for shorter (MW = 282 Da) and longer oligo ethylene glycols (EGs, MW = 459 Da), respectively, and these values are consistent with other ligand densities reported for oligo EGs appended to AuNPs. While atmospheric interferences (e.g. oxygen or nitrogen with sulphur) can be a challenge for sulphur atom concentration quantification using ICP-MS, Lämmerhofer used an internal standard as well as spike recovery experiments to validate their sulphur detection approach. Here, spike recovery experiments involve adding a known amount of the compound of interest to standards that already contain this compound. The sample is then analysed, and the standard concentration is subtracted from the total sulphur concentration in order to confirm that the added amount is retained.¹¹⁹ Further, since Au concentrations can be much higher than sulphur concentrations for large AuNPs, this method incorporates operating parameters that reduce the Au signal to as little as 0.1% to prevent it from overloading the detector. By reducing the amount of Au signal reaching the detector, this method can simultaneously measure both the sulphur signal from the thiolated ligands and the Au signal from the NPs.

ICP-AES has also been used to quantify ligand densities. Hackley and co-workers examined the gold : sulphur ratio for a variety of particle sizes, observing that packing density is largely independent of particle size (d = 5–100 nm). Working without an internal standard in this case, Hackley cautions that the particles and ligands must be sufficiently concentrated to ensure that the sulphur is present at a significant percentage of the total sample mass for accurate quantification.¹²⁰ Weiss and co-workers have applied similar techniques to study phosphorus-containing ligands on CdSe NPs.^121,122 Importantly, by observing the number of ligands post-purification in conjunction with NMR data, Weiss was able to establish particle binding equilibria for these ligands (vide infra).¹²¹

While not demonstrated yet, it is straightforward to envision expanding these atomic spectroscopy methods to examine mixed-moiety ligand shells, provided that each ligand contains spectroscopically distinct elements.

6. Nuclear magnetic resonance (NMR) spectroscopy

Given the distinct advantages of NMR spectroscopy for small molecule characterization, significant efforts have been devoted to developing NMR approaches for ligand density determination. A common method to study ligand densities using NMR involves the addition of an internal standard. With this method, a known concentration of a molecule that has NMR resonances distinct from the ligands of interest is added to the NP solution. The internal standard peak is then integrated along with the ligand peak of interest, and the concentration of the ligand can be determined by one of two methods. The first method uses comparison to a calibration curve, which is generated by plotting the ratio of the integrated ligand peak divided by the integrated internal standard peak against the known ligand concentrations.⁵⁴ The alternative approach involves quantification based on the number of ¹H nuclei contributing to the internal standard peak and the ligand peak of interest and does not necessarily require a calibration curve. Here, a known concentration of internal standard is added to the unknown sample. The concentration of the unknown sample can be determined by comparing the integral of an internal standard peak to the integral value from the sample ligand peak of interest, both of which must correspond to a known number of protons.¹²³ In these experiments, NMR offers the advantage of being able to analyse multi-component ligand shells under various conditions. Further, unlike many of the other methods discussed, NMR has the additional capability to probe ligand dynamics and arrangement in addition to ligand quantities in real time. Here, we primarily focus on ligand densities but discuss additional findings from NMR, if reported.

The expanded capabilities of NMR come with several technical considerations that strongly influence spectral interpretation. The major consideration for analysing the NMR spectra of molecules appended to a colloidal surface are related to how that surface and core material may change the observed NMR features of the appended ligands. Specifically, ligands bound to NP surfaces typically exhibit broader NMR linewidths and/or differences in chemical shift compared to the ligands free in solution. These changes in NMR signals can necessitate reassignment of the particle-bound spectra (e.g. using 2D NMR analysis such as homonuclear correlation spectroscopy (COSY) and/or heteronuclear single quantum correlation (HSQC) to determine the segment of the ligand that corresponds to the new NMR resonances upon NP binding) and often result in lower (in some cases, prohibitively low) signal to noise ratios. The physical underpinnings of this line broadening vary depending on the system, but they can generally be attributed to either inhomogeneous line broadening (e.g. chemical shift distribution),^124,125 homogeneous line broadening (e.g. dipolar coupling due to ligand packing¹²⁶ or electron-nuclear coupling¹²⁷), or a combination of both.^128,129

Unfortunately, this line broadening can obscure quantification in some cases. For example, when ligands bind to NPs with a high population of free carriers (e.g. metal NPs or doped semiconductor NPs), the NMR resonances from nuclei on the ligand that are in proximity to the carriers are attenuated by ligand–carrier spin interactions. The degree of attenuation is related to the distance between the nuclei and free carriers, and thus inaccurate quantification can occur if all nuclei corresponding to a particular resonance are not accounted for in a given peak integration.

Regardless of whether the analysis is performed on or off particle, the NP concentration for these methods is typically determined by either absorption or atomic spectroscopy methods.

6.1 “Off particle” NMR analysis

To avoid the adverse effects associated with line broadening and chemical shift changes, ligands can be removed from the NPs for routine, quantitative NMR analysis. In the case of metal NPs, which have a high concentration of conduction electrons, ligands must be removed from the particle surface to achieve accurate quantification. In other systems, quantification of unbound species may be employed as a matter of convenience to provide higher resolution spectra and avoid spectral reassignment. In addition, when monitoring dynamic processes, such as ligand exchange, the species of interest may be released from the particle surface during the reaction. Here, we will discuss literature examples from each of these scenarios in which off particle species were analysed.

In our laboratory, we have shown that a combination of TEM for AuNP sizing, ICP-MS for Au quantification, and ¹H NMR for ligand quantification can reveal physical processes underpinning the formation and properties (e.g. final ligand density) of both single and mixed ligand shells on metal NPs. Here, we use acetonitrile (ACN) as an internal standard and use a calibration curve to perform quantitative analysis of ligand shells (Fig. 6). The accuracy of this method was verified by synthesizing a molecule that was detectable by both our method using ¹H NMR as well as ICP-AES (using a Se tag). Both NMR and ICP-AES were in statistical agreement, indicating that the NMR quantification approach is reliable for metal NPs.⁵⁴ In this work, we found that PEGSH (MW = 1 kDa) is easily displaced by incoming mercaptoalkanoic acids (MAAs) and is amenable to post-synthetic modification. In contrast, more densely packed monolayers (e.g. if the original ligand shell is composed of MAAs) are not readily modified, exhibiting exchange efficiencies as low as 2% with other thiolated ligands, likely due to inter-ligand interactions (e.g. van der Waals forces) between neighbouring alkyl chains. This NMR-based approach can be applied to a wide range of particle and ligand types, limited only by chemical resolution in the NMR spectrum.^25,130

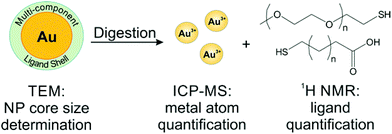Fig. 6 Scheme of a typical off particle NMR analysis. Here, NP conjugates are digested for quantification by ICP-MS, while the released ligands are quantified by ¹H NMR. Adapted with permission from ref. 54. Copyright 2015 American Chemical Society.

This work was preceded by studies of semiconductor NP systems. For example, Owen and co-workers have used a ferrocene internal standard to quantitatively study the displacement of cadmium carboxylate from CdSe NPs.¹³¹ In this study, the original particles remained intact, but the as-synthesized ligands (carboxylate complexes) were displaced using one of several different reagents (such as N,N,N′,N′-tetramethylethylene-1,2-diamine (TMEDA)). Serial precipitation and centrifugation of the NPs (to which TMEDA had been added) were performed, followed by collection of the supernatant, which was then dried under vacuum. The concentration of free carboxylate ligands that had been displaced from the NPs by TMEDA was determined. Similar experiments quantified the species displaced during ligand exchange on CdS, PbSe, and PbS NPs. From the quantitative NMR analysis, the authors demonstrated that the composition changes due to metal-carboxylate displacement could be correlated to optoelectronic features of semiconductor NPs, including specific absorption transitions as well as PL quantum yield.¹³¹ Likewise, Weiss and co-workers have used ferrocene as the internal standard for the quantification of 4-hexylphenyldithiocarbamate (C6-PTC) on CdS NPs.¹³² The NPs were originally functionalized with oleate and underwent a ligand exchange with C6-PTC. The number of C6-PTC ligands bound to the particles was obtained by quantifying bound and unbound oleate (based on the differences in peak shape and chemical shift) and also determining the stoichiometry of the ligand exchange, where one bound C6-PTC displaces at least two oleate ligands.¹³²

Even in semiconductor NP systems, line broadening upon particle attachment can be extreme, making on particle quantification approaches prohibitively time consuming. In order to overcome this barrier, Weiss and co-workers demonstrated that CdSe NP ligand densities could be quantified by ¹H NMR using an alternative external standard approach, in which only unbound species are observed.²⁴ To measure ligand densities of methylthiophenolate (CH₃-TP) on CdSe NPs, the authors compared NMR spectra from the NP sample and a sample of CH₃-TP that did not contain NPs. The NMR response of the sample was compared to the NMR signal obtained from mixing the CdSe NPs with the same amount of CH₃-TP as in the external standard. Here, an assumption is made that any ligands that attach to the NP surface will be shifted and dramatically dephased and thus too broad to distinguish from the spectral baseline. Therefore, since both the reference and the sample contain the same quantity of ligands, the signal from the ligand + NP sample comes only from the unbound ligands free in solution, and it was inferred that the remaining quantity has adsorbed to the particle surface. Using this approach, the measured difference in NMR signal between the NP-free sample and the NP-containing sample is proportional to the number of bound CH₃-TP ligands. From this study, typical ligand densities ranged from 1.4–7.6 ligands per nm² for CdSe NPs with a variety of diameters between 2.26–4.74 nm.²⁴

6.2 “On particle” NMR analysis

On particle ligand quantification is feasible in NP systems with low free charge carrier densities (e.g. intrinsic semiconductors), because line broadening is likely the result of factors such as ligand packing,¹²⁶ chemical shift distributions from faceting on the particle surface,¹³³ and slow tumbling^134,135 rather than a result of coupling to free carriers. Therefore, all species contributing to a specific resonance can be accounted for. However, on particle approaches, even where physically possible, can be significantly more expensive than their off particle analogues in terms of time and material due to lower signal to noise ratios and in some cases, the need for additional spectral assignment.^136,137 Despite these challenges, on particle NMR analyses of ligand shells is attractive because of the potential to not only characterize ligand quantity but also to elucidate features such as ligand arrangement and binding affinity on the particle surface all within a single experiment.

Early work developing on particle NMR quantification was performed on intrinsic semiconductor NPs. Here, Pines and co-workers used the internal standard method without a calibration curve for the quantification of thiophenol on CdS NPs exhibiting different core sizes (d = 1.18 ± 0.1–1.92 ± 0.1 nm).¹²⁶ Using dichloromethane (DCM) as the internal standard, the authors found that as the size of the NPs increases, the number and percent coverage of thiophenol ligands decreases, indicating that larger NPs have less dense ligand shells. Interestingly, the authors noticed that as particle size was reduced, ¹H NMR lines were broadened, contrary to what is expected given the faster tumbling rate of the smaller NPs. Detailed models of selective spin–spin relaxation (T₂) measurements showed that the increase in linewidth was most likely the result of tightly bundled thiophenol islands on the surface of the CdS NPs, providing not only quantitative information on the NP ligand shell but also information on the ligand arrangement as a function of NP size.¹²⁶ The insight provided by NMR allowed the authors to correlate ligand shell morphology in terms of packing arrangement with ligand density – parameters that influence the resulting NP physical behaviour.

More recent work exploring on particle NMR ligand quantification was conducted by Hens and co-workers, analysing both InP¹³⁸ and PbSe¹²³ NPs with dibromomethane as the internal standard. When PbSe NPs (d = 3–7 nm) are capped with oleate, an average ligand density of 4.2 oleate per nm² was determined.¹²³ The authors have also studied oleate densities using Quantas software that is derived from the pulse-length-based concentration determination (PULCON) method, where the software adds an artificial peak of standard intensity.^22,139 This simulated peak can then be integrated along with the ligand peaks to determine the ligand concentration. The authors analysed the impact of washing with NP nonsolvents on oleate ligand densities on CdSe and PbSe NPs. They found that the ligand density decreases as a consequence of increased methanol washing steps, from an initial 4.1 oleate per nm² to 3.2 oleate per nm² and 3.18 oleate per nm² to 1.16 oleate per nm² for CdSe and PbSe NPs, respectively.²² The ligand density for PbSe NPs obtained with the Quantas approach is lower than that found using the internal standard approach (further interpretation likely requires additional information about the particle dispersity). Finally, Hens and co-workers also used the Quantas approach to determine the ligand density of oleate on the surface of the CdSe NPs (d = 3.5 ± 0.1 nm) to be 4.6 ± 0.4 oleate per nm² in the absence of additional methanol washing steps.¹³⁹ The ligand densities for CdSe NPs without additional methanol washing steps are comparable, which is expected given the synthetic similarities between the studies.

In order to understand the relationship between optical properties and surface chemistry in semiconducting NPs, Owen and co-workers again used ferrocene as an internal standard to determine ligand density on CdSe NPs before and after ligand exchange.⁵⁷ Here, ferrocene was used to provide distinct resolution between proton chemical shifts of the standard versus the ligands of interest, due to the deshielding effects noted for many metal-containing compounds.¹⁴⁰ In this report, the particle concentration was measured using the absorbance and molar extinction coefficient of the NPs. The authors found that the original carboxylate-terminated CdSe NPs undergo a quantitative (>99%) ligand exchange with tri-n-butylphosphine (Bu₃P). After replacement of carboxylate with Bu₃P, the CdSe NPs are then replaced by various n-alkylamines, and an aliquot of n-alkylamine-capped NPs was placed into deuterated medium for analysis following washing to remove unbound ligands. The resulting ligand shells were more dense than the Bu₃P ligand shells,⁵⁷ leading the authors to conclude that n-alkylamine ligands provide higher surface coverage than Bu₃P. This increase in amine ligand density was then correlated to higher NP quantum yields.

Apart from metal chalcogenide particles, on particle NMR-based ligand quantification has also been used to analyse ligand shells on a variety of other NP cores, including silica¹⁴¹ and metal oxides.¹⁴² For example, Mayer and co-workers determined the density of dodecylamine (DDA) ligands on the surface of zinc oxide (ZnO) NPs using trimethoxybenzene as an internal standard, where NP concentration was determined with ICP-AES.¹⁴² The authors found that there were both “strongly” and “weakly” bound DDA populations present on the surface of the NPs and were able to quantify the contributions of each type of ligand to the overall ligand density. The average density of the strongly bound ligands was 1.0 ± 0.3 DDA per nm², while the average density of both the strongly and weakly bound ligands was higher at 1.9 ± 0.4 DDA per nm². Interestingly, these ligand densities are much lower than anticipated based on the estimated maximum surface coverage on an extended flat surface of ZnO (Fig. 7). Particle surface coverage could be increased by annealing the NPs to remove surface hydroxide ligands, which may block surface sites and make them unavailable for DDA binding. Indeed, after annealing, the average strongly bound ligand density increased to 3.5 ± 0.3 DDA per nm².¹⁴²

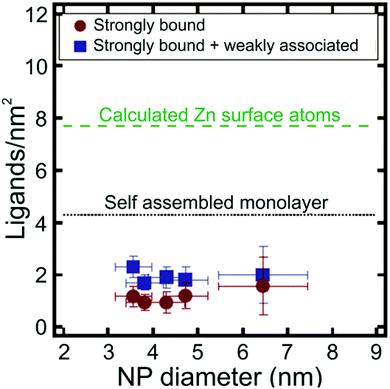Fig. 7 Ligands per nm² as a function of NP diameter for ZnO NPs. Particle ligand densities are lower than predicted for a self-assembled monolayer (SAM) of DDA ligands on a flat ZnO surface. Adapted with permission from ref. 142. Copyright 2014 American Chemical Society.

In addition to solution phase NMR techniques, solid state NMR has also been used to quantify NP ligand densities. For example, Griffin and co-workers measured the number of trioctylphosphine oxide (TOPO) and trioctylphosphine selenide (TOPSe) ligands on CdSe NPs (d = 3.7 ± 0.4 nm) using a ³¹P spin counting method by comparing to a known amount of gallium phosphide.¹⁴³ In this work, the authors used a combination of isotropic ³¹P chemical shift and ³¹P–⁷⁷Se rotational echo double resonance (REDOR) techniques in magic-angle spinning experiments to distinguish between TOPO and TOPSe ligands, which are bound to Cd atoms on the surface of the NPs. Quantitative analysis assumed the CdSe NPs to be stoichiometric in the Cd and Se composition and found an average of 150–170 ligands per particle (3.72 ligands per nm²). From a combination of synthetic manipulation of growth conditions and computational modelling, the authors established that all the Cd sites on the particle surface are passivated, while no binding occurs at the Se sites. This observation was supported by spin echo measurements that were consistent with an average P–P distance of 8–10 Å, indicating capping of alternate sites on the particle surface.

In summary, NMR quantification overcomes many of the limitations imposed in the previously discussed methods, such as the ability to simultaneously identify multiple ligand types while avoiding the need for post-synthetic modification of the ligand itself, as is often the case for optical spectroscopy methods. Further, NMR techniques are amenable to a variety of experimental conditions (e.g. temperature or solvent), can assess ligand arrangement and dynamics, as well as have the potential to perform quantification studies in situ. However, there are drawbacks to the approach, including potential challenges of spectral peak assignment, and depending on sample concentration, long experiment times due to the inherently low sensitivity of NMR.

7. Vibrational spectroscopy

Another method that has been explored for NP ligand quantification is vibrational spectroscopy, which includes Raman and attenuated total reflectance-Fourier transform infrared (ATR-FTIR) spectroscopies. For both of these spectroscopies, ligand signal must be calibrated before concentrations can be determined. Analogous to the NMR methods discussed above, an internal standard can be added to samples in a surface-enhanced Raman spectroscopy (SERS) measurement to extract quantitative ligand values. In the work discussed here, NP concentrations are typically found by measuring the absorbance at a certain wavelength and then converting to concentration using the molar extinction coefficient.

7.1 Raman spectroscopy

Zhang and co-workers used an isotope-encoded surface-enhanced Raman spectroscopy internal reference (IESIR) method to quantify mercaptobenzimidazole (MBI) on the surface of AuNPs.¹⁴⁴ In this method, the internal standard used was of identical structure but different isotopic substitution than the ligand of interest. Using this identical structure helps to eliminate quantification errors arising from matrix interferences or variations in SERS substrate activity. First, a calibration curve was prepared with varying ratios of MBI-d₀ and MBI-d₄. Next, AuNP samples were incubated in a known amount of MBI-d₀. The AuNP samples were centrifuged to remove the MBI-capped AuNPs, and MBI-d₄ was added to the supernatant, which was used to measure the SERS spectra. The data was fit to a Langmuir isotherm, which gave a maximum MBI packing density of 571 ± 4.6 pmol per cm² (3.44 ± 0.03 ligands per nm²).¹⁴⁴ Zhang and co-workers subsequently extended their analysis to various solution pH values, which changed the form of the MBI ligand on the AuNPs (thione at low pH versus thiolate at higher pH).⁶¹ The change in the MBI form altered the binding constants and packing density, with a higher density at low pH and a lower density at high pH.

Halas and co-workers have used SERS to quantify p-mercaptoaniline-PEG-fluorescein (pMA-PEG-Fl) on silica@Au nanoshells.¹⁴⁵ The authors first constructed a Langmuir isotherm to calibrate the SERS response of pMA molecules adsorbed on the Au nanoshells by taking SERS spectra at various pMA concentrations. A binding constant of 9.48 × 10³ ± 884 M⁻¹ was found, representing the affinity of the pMA for the nanoshell surface. Then, the packing density of pMA-PEG-Fl could be determined by referencing this calibration. The packing density of pMA-PEG2000-Fl is 46.7 ± 20.8 pmol per cm² (0.28 ± 0.13 ligands per nm²), and the packing density of pMA-PEG5000-Fl is 15.3 ± 7.9 pmol per cm² (0.09 ± 0.05 ligands per nm²).¹⁴⁵

7.2 Infrared spectroscopy

ATR-FTIR spectroscopy has also been used to quantify NP ligand density. Hackley and co-workers used ATR-FTIR to quantify PEGSH and MPA on AuNPs and subsequently confirmed their method via comparison to ES-DMA measurements (vide infra).²³ The authors generated calibration curves by plotting the intensity of IR absorbance versus the concentration of free ligand to quantify the maximum surface density of PEGSH with different molecular weights (MW = 1, 5, or 20 kDa). The ligand density of PEGSH was found to be inversely proportional to the molecular weight. In addition, since IR allows multiple ligands to be distinguished, the authors studied the effects of the addition of a secondary ligand either simultaneously (co-loading) or sequentially (backfilling) on PEGSH surface density. When MPA was added at the same time as PEGSH, the amount of PEGSH that was adsorbed to the AuNPs was reduced. When BSA was added to an already existing PEGSH monolayer, there was a decrease in the amount of PEGSH adsorbed if the molecular weight of the PEGSH was small (here, 5 kDa or less). However, if the molecular weight of the PEGSH was larger (20 kDa), the amount of PEGSH adsorbed remained the same.²³

Similar to the optical methods, vibrational spectroscopy methods require spectroscopically active molecules to be effective. However, like NMR (vide supra), as long as those molecules have spectroscopically distinct features, vibrational spectroscopy can simultaneously quantify multiple ligand types.

8. Electrospray-differential mobility analysis (ES-DMA)

Electrospray-differential mobility analysis (ES-DMA) aerosolizes and then separates NPs based on their electrical mobility. The electrical mobility of the particles is dependent on both particle charge and size and results from the particle acceleration that occurs in an electric field in the differential mobility analyser, balanced by a drag force. Particles with larger or more ligands appended to them have a higher drag force than particles with smaller or fewer ligands on the surface. The applied voltage in the DMA is varied with time in order to scan the particle size distribution, which is then detected by a condensation particle counter. By comparing the particle sizes before and after the introduction of ligands, the ligand density can be determined. An advantage of this technique is that no specific labelling is needed, and the surface coating thickness can be determined relatively easily. However, a disadvantage is that in order to convert the surface coating thickness to ligand coverage, the conformation of the ligands must be known a priori. In these measurements, NP size instead of concentration is used to determine ligand density as described above.

Zachariah and co-workers have used ES-DMA to find the ligand density of ssDNA on AuNPs (d = 20 nm).¹⁴⁶ The authors first measured the surface coating thickness and then converted to surface coverage based on the known random coil conformation of poly-T ssDNA ligands. Depending on the length of the ssDNA, the model for DNA packing, and the concentration of salt, the surface coverage ranges from 2.0 × 10¹² to 6.9 × 10¹³ ligands per cm² (0.02 to 0.69 ligands per nm²), with the shorter strands having the higher surface coverage, consistent with the ligand densities found in other studies of ssDNA on AuNPs in the presence of salt.¹⁴⁶ Hackley and co-workers have also used ES-DMA to quantify the competitive adsorption of PEGSH (MW = 5 kDa) and mercaptopropionic acid (MPA) on AuNPs (d = 30 or 60 nm).^23,147 The authors found that as the amount of MPA added to the NPs increased, the surface density of PEGSH decreased.

In an attempt to avoid the need for a priori knowledge of ligand conformation mentioned above, Zachariah and co-workers modified their technique by coupling an aerosol particle mass analyser (APM) to the ES-DMA system to study AuNPs (d = 30 nm) capped with BSA.¹⁴⁸ First, the size distribution of citrate-capped AuNPs was measured, and then NPs with a selected mobility were analysed with the APM to determine their mass distribution. This analysis was repeated for the BSA-functionalized AuNPs. The mass difference between these two types of NPs was then used to calculate the ligand coverage. At the highest amount of BSA added to the AuNPs, the coverage was determined to be 3 mg per m² (0.03 ligands per nm²).¹⁴⁸ However, although this modified technique does not require knowledge of the ligand conformation to determine ligand density, there is another limitation in that the mass of the ligand on the NP before functionalization (in this case citrate) is neglected, and the particles are assumed to be “bare.”

While a wide range of molecules can be analysed without specialized modification, this technique remains limited by the approximation of ligand conformation unless APM is used. Further, neglecting initial ligand mass on the NP sample when using APM can lead to overestimations of the mass of the original NPs, which yields a ligand density that is lower than the true value.

9. pH titrations

Another approach for ligand quantification uses pH titration.^149,150 In this process, acid or base is titrated into a known amount of NPs. The pH change is monitored, and based on the equivalence point, the ligand concentration can be extracted. Of course, this technique requires that the particles are not sensitive to aggregation caused by changes in pH and that the ligand has some well-known pH response. For these studies, ICP-AES is used to determine the corresponding AuNP concentration.

Latham and Williams demonstrated this method on AuNPs by titrating a potassium hydroxide solution into a known amount of carboxylic acid-terminated PEGSH-capped AuNPs (MW = 700 Da, d = 4.1 ± 0.8 nm).¹⁴⁹ In contrast to unbound ligand, where a sharp transition occurs, the transition for AuNP-bound ligands was longer and occurred at more basic pH values. With the known particle concentration, the equivalence point of the titration corresponded to the quantity of ligands on the particle. However, the authors cautioned that the particle mass was estimated without taking the mass of the ligands bound to the particle into account and therefore the ligands per particle may actually be a 10–15% underestimation.¹⁴⁹ Parak and co-workers presented a similar method for quantifying MAAs and an amphiphilic polymer on AuNPs. The authors also observed a broadening of the pH curve and shift in the pK_a of the bound MAA ligands relative to the free ligand. The authors emphasized that the pH data also provides information regarding colloidal stability of the NP solutions.¹⁵⁰

While using pH titrations to quantify particle ligand density is relatively simple, the main disadvantage is that it can only be used with ligands that have a pH-sensitive component.

10. X-ray photoelectron spectroscopy (XPS)

XPS measurements have long been commonplace for studying the elemental composition of flat surfaces and have been applied to NP films as well.^151,152 Therefore, it seems expected that the technique would also be explored for quantification of NP ligand shells. However, because XPS is a surface-sensitive technique, the use of XPS for NP ligand density determination is nuanced. In a recent report, Hamers and co-workers used XPS to quantify the density of ω-(1-mercaptoundec-11-yl)hexa(ethylene glycol) carboxylic acid (HS-(CH₂)₁₁(EG)₆-COOH) ligands on AuNPs (d = 1.3–6.3 nm). By dropcasting their samples onto silicon wafers, the authors found an average ligand density of 3.9 ± 0.2 ligands per nm². Further, they found that the radius of curvature of small (d < 2 nm) NPs must be taken into account for dropcast samples.¹⁵³ Several additional studies have also demonstrated the use of dropcast samples for an XPS quantification approach.^154–156

Another method for XPS ligand quantification was demonstrated by Alivisatos and co-workers examining phosphorous-containing ligands on CdSe NPs.¹⁵⁷ By analysing only a single monolayer of NPs and accounting for the escape depths of the electrons for the different elements, they established NP size dependent (range, d = 0.9–3.0 nm) surface coverages of between 30–60% TOPO ligands on CdSe NPs, with higher coverages on smaller NPs.¹⁵⁷ However, the article implies several caveats to XPS for ligand quantification. First, the authors demonstrate that a monolayer of particles is needed to extract accurate ligand quantities. The authors also note that in order to form the monolayer, some portion of the original ligand may be displaced with substrate-binding moieties and therefore the method might systematically underestimate total ligand quantities.

Taking all factors together, XPS is a particularly complex approach for ligand quantification. In addition to particle curvature and substrate coverage densities, the technique, by definition, does not probe the core concentration directly (i.e. electron escape depth is much shorter than the particle diameter in many cases). It is also important to note that because of the surface bias, the signal to noise ratio for core and surface elements will be different, especially in the case where the ligand moieties facilitate adsorption of adventitious carbon.

11. Summary and outlook

Given the diversity of techniques used and systems studied, how does one select a method to quantify ligand density in their NP systems and evaluate the meaning of the resulting values? For example, do different ligand quantification techniques agree with one another? If not, are there systematic deviations between methods? For example, compare results for a well-studied system such as PEGSH-terminated AuNPs (MW = 1–2 kDa, NP diameters above 6 nm). While TGA and NMR techniques agree that ligand densities are approximately 2.5 ligands per nm², other quantification approaches such as absorption spectroscopy give much smaller values. Likewise, absorption spectroscopy also finds lower ligand densities when examining other systems such as DNA appended to AuNPs (d = 15–20 nm), indicating that absorption spectroscopy may systematically underestimate ligand densities. However, despite some discrepancies, careful sample preparation and measurements seem to facilitate general agreement in ligand densities between methods when the NP systems are comparable (Table 1). Therefore, method selection is primarily driven by particle properties. For example, one must evaluate experimental constraints such as whether the ligand and/or NP is optically active or whether the NMR chemical shifts of the ligand are spectroscopically discernible.

Collectively, these studies also make it clear that important barriers remain for the determination and accuracy of ligand quantification approaches both with respect to total ligand density and surface-specific ligand densities within a single given particle. The major obstacles include dispersity in NP size and shape as well as NP concentration determination. As these challenges are met, methods that can not only quantify NP ligands but also determine their arrangement and ultimately their dynamics will be needed. Motivation to address these challenges is clear: even for the information already in hand, strong correlations between surface chemistry and particle behaviour are observed. We expect that the studies summarized here will be both a foundation and springboard to selectively, reproducibly, and effectively use surface chemistry to control the formation and properties of colloidal NPs.

Acknowledgements

This work was supported by a National Science Foundation CAREER Award (CHE-1253143), the Research Corporation for Science Advancement, and the University of Pittsburgh.

Notes and references

1. A. Puzder, A. J. Williamson, N. Zaitseva, G. Galli, L. Manna and A. P. Alivisatos, Nano Lett., 2004, 4, 2361–2365.
2. J. Zeng, Y. Zheng, M. Rycenga, J. Tao, Z.-Y. Li, Q. Zhang, Y. Zhu and Y. Xia, J. Am. Chem. Soc., 2010, 132, 8552–8553.
3. M. Grzelczak, J. Perez-Juste, P. Mulvaney and L. M. Liz-Marzan, Chem. Soc. Rev., 2008, 37, 1783–1791.
4. Y. Li and M. A. El-Sayed, J. Phys. Chem. B, 2001, 105, 8938–8943.
5. L. S. Ott and R. G. Finke, Coord. Chem. Rev., 2007, 251, 1075–1100.
6. J. Israelachvili, Intermolecular and Surface Forces, Elsevier, Burlington, MA, 3rd edn, 2011.
7. M. A. Boles, D. Ling, T. Hyeon and D. V. Talapin, Nat. Mater., 2016, 15, 141–153.
8. E. A. McArthur, A. J. Morris-Cohen, K. E. Knowles and E. A. Weiss, J. Phys. Chem. B, 2010, 114, 14514–14520.
9. A. Verma and F. Stellacci, Small, 2010, 6, 12–21.
10. A. Albanese, P. S. Tang and W. C. Chan, Annu. Rev. Biomed. Eng., 2012, 14, 1–16.
11. Z. V. Feng, I. L. Gunsolus, T. A. Qiu, K. R. Hurley, L. H. Nyberg, H. Frew, K. P. Johnson, A. M. Vartanian, L. M. Jacob and S. E. Lohse, Chem. Sci., 2015, 6, 5186–5196.
12. A. M. Alkilany, P. K. Nagaria, C. R. Hexel, T. J. Shaw, C. J. Murphy and M. D. Wyatt, Small, 2009, 5, 701–708.
13. J.-S. Lee, M. I. Bodnarchuk, E. V. Shevchenko and D. V. Talapin, J. Am. Chem. Soc., 2010, 132, 6382–6391.
14. W. W. Yu, E. Chang, R. Drezek and V. L. Colvin, Biochem. Biophys. Res. Commun., 2006, 348, 781–786.
15. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170.
16. K. L. Prime and G. M. Whitesides, Science, 1991, 252, 1164–1167.
17. P. E. Laibinis, G. M. Whitesides, D. L. Allara, Y. T. Tao, A. N. Parikh and R. G. Nuzzo, J. Am. Chem. Soc., 1991, 113, 7152–7167.
18. A. Ulman, Chem. Rev., 1996, 96, 1533–1554.
19. H. Sellers, A. Ulman, Y. Shnidman and J. E. Eilers, J. Am. Chem. Soc., 1993, 115, 9389–9401.
20. R. K. Smith, P. A. Lewis and P. S. Weiss, Prog. Surf. Sci., 2004, 75, 1–68.
21. H. Häkkinen, Nat. Chem., 2012, 4, 443–455.
22. A. Hassinen, I. Moreels, K. De Nolf, P. F. Smet, J. C. Martins and Z. Hens, J. Am. Chem. Soc., 2012, 134, 20705–20712.
23. D.-H. Tsai, M. Davila-Morris, F. W. DelRio, S. Guha, M. R. Zachariah and V. A. Hackley, Langmuir, 2011, 27, 9302–9313.
24. V. A. Amin, K. O. Aruda, B. Lau, A. M. Rasmussen, K. Edme and E. A. Weiss, J. Phys. Chem. C, 2015, 119, 19423–19429.
25. S. E. Crawford, C. M. Andolina, A. M. Smith, L. E. Marbella, K. A. Johnston, P. J. Straney, M. J. Hartmann and J. E. Millstone, J. Am. Chem. Soc., 2015, 137, 14423–14429.
26. J. V. Jokerst, T. Lobovkina, R. N. Zare and S. S. Gambhir, Nanomedicine, 2011, 6, 715–728.
27. T.-L. Cheng, K.-H. Chuang, B.-M. Chen and S. R. Roffler, Bioconjugate Chem., 2012, 23, 881–899.
28. D. J. Gavia and Y.-S. Shon, Langmuir, 2012, 28, 14502–14508.
29. G. He, Y. Song, X. Kang and S. Chen, Electrochim. Acta, 2013, 94, 98–103.
30. G. Ren, D. Hu, E. W. C. Cheng, M. A. Vargas-Reus, P. Reip and R. P. Allaker, Int. J. Antimicrob. Agents, 2009, 33, 587–590.
31. A. J. Esswein, M. J. McMurdo, P. N. Ross, A. T. Bell and T. D. Tilley, J. Phys. Chem. C, 2009, 113, 15068–15072.
32. H.-F. Lin, S.-C. Liao and S.-W. Hung, J. Photochem. Photobiol., A, 2005, 174, 82–87.
33. Y. Xing, J. Phys. Chem. B, 2004, 108, 19255–19259.
34. S. Trasatti and O. Petrii, Pure Appl. Chem., 1991, 63, 711–734.
35. W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221.
36. X. Liu, M. Atwater, J. Wang and Q. Huo, Colloids Surf., B, 2007, 58, 3–7.
37. E. Chang, N. Thekkek, W. W. Yu, V. L. Colvin and R. Drezek, Small, 2006, 2, 1412–1417.
38. B. Ballou, B. C. Lagerholm, L. A. Ernst, M. P. Bruchez and A. S. Waggoner, Bioconjugate Chem., 2004, 15, 79–86.
39. T. Hendel, M. Wuithschick, F. Kettemann, A. Birnbaum, K. Rademann and J. Polte, Anal. Chem., 2014, 86, 11115–11124.
40. A. Scheffer, C. Engelhard, M. Sperling and W. Buscher, Anal. Bioanal. Chem., 2008, 390, 249–252.
41. D. M. Mitrano, A. Barber, A. Bednar, P. Westerhoff, C. P. Higgins and J. F. Ranville, J. Anal. At. Spectrom., 2012, 27, 1131–1142.
42. M. O. Oyewumi, R. A. Yokel, M. Jay, T. Coakley and R. J. Mumper, J. Controlled Release, 2004, 95, 613–626.
43. I. Moreels, K. Lambert, D. De Muynck, F. Vanhaecke, D. Poelman, J. C. Martins, G. Allan and Z. Hens, Chem. Mater., 2007, 19, 6101–6106.
44. U. Gießmann and U. Greb, Fresenius’ J. Anal. Chem., 1994, 350, 186–193.
45. J. Y. Rempel, B. L. Trout, M. G. Bawendi and K. F. Jensen, J. Phys. Chem. B, 2006, 110, 18007–18016.
46. K. Liu, N. Zhao and E. Kumacheva, Chem. Soc. Rev., 2011, 40, 656–671.
47. P. Liu and J. K. Norskov, Phys. Chem. Chem. Phys., 2001, 3, 3814–3818.
48. J. S. Owen, J. Park, P.-E. Trudeau and A. P. Alivisatos, J. Am. Chem. Soc., 2008, 130, 12279–12281.
49. J. Jasieniak and P. Mulvaney, J. Am. Chem. Soc., 2007, 129, 2841–2848.
50. X. Liu, M. Yu, H. Kim, M. Mameli and F. Stellacci, Nat. Commun., 2012, 3, 1182.
51. J.-M. Ha, A. Katz, A. B. Drapailo and V. I. Kalchenko, J. Phys. Chem. C, 2009, 113, 1137–1142.
52. Y. Wang, O. Zeiri, A. Neyman, F. Stellacci and I. A. Weinstock, ACS Nano, 2012, 6, 629–640.
53. T. Djebaili, J. Richardi, S. Abel and M. Marchi, J. Phys. Chem. C, 2015, 119, 21146–21154.
54. A. M. Smith, L. E. Marbella, K. A. Johnston, M. J. Hartmann, S. E. Crawford, L. M. Kozycz, D. S. Seferos and J. E. Millstone, Anal. Chem., 2015, 87, 2771–2778.
55. T. Djebaili, J. Richardi, S. Abel and M. Marchi, J. Phys. Chem. C, 2013, 117, 17791–17800.
56. M. J. Hostetler, A. C. Templeton and R. W. Murray, Langmuir, 1999, 15, 3782–3789.
57. N. C. Anderson and J. S. Owen, Chem. Mater., 2013, 25, 69–76.
58. C. Wang, H. Zhang, J. Zhang, N. Lv, M. Li, H. Sun and B. Yang, J. Phys. Chem. C, 2008, 112, 6330–6336.
59. P. Ionita, A. Volkov, G. Jeschke and V. Chechik, Anal. Chem., 2008, 80, 95–106.
60. Z. Wu and R. Jin, Nano Lett., 2010, 10, 2568–2573.
61. S. M. Ansar, R. Haputhanthri, B. Edmonds, D. Liu, L. Yu, A. Sygula and D. Zhang, J. Phys. Chem. C, 2011, 115, 653–660.
62. M. S. Yavuz, Y. Cheng, J. Chen, C. M. Cobley, Q. Zhang, M. Rycenga, J. Xie, C. Kim, K. H. Song, A. G. Schwartz, L. V. Wang and Y. Xia, Nat. Mater., 2009, 8, 935–939.
63. K. Rahme, L. Chen, R. G. Hobbs, M. A. Morris, C. O'Driscoll and J. D. Holmes, RSC Adv., 2013, 3, 6085–6094.
64. D. N. Benoit, H. Zhu, M. H. Lilierose, R. A. Verm, N. Ali, A. N. Morrison, J. D. Fortner, C. Avendano and V. L. Colvin, Anal. Chem., 2012, 84, 9238–9245.
65. G. H. Woehrle, L. O. Brown and J. E. Hutchison, J. Am. Chem. Soc., 2005, 127, 2172–2183.
66. A. Badia, S. Singh, L. Demers, L. Cuccia, G. R. Brown and R. B. Lennox, Chem. – Eur. J, 1996, 2, 359–363.
67. T. L. Doane, Y. Cheng, A. Babar, R. J. Hill and C. Burda, J. Am. Chem. Soc., 2010, 132, 15624–15631.
68. M. Maccarini, G. Briganti, S. Rucareanu, X.-D. Lui, R. Sinibaldi, M. Sztucki and R. B. Lennox, J. Phys. Chem. C, 2010, 114, 6937–6943.
69. S. Takae, Y. Akiyama, H. Otsuka, T. Nakamura, Y. Nagasaki and K. Kataoka, Biomacromolecules, 2005, 6, 818–824.
70. M. K. Corbierre, N. S. Cameron and R. B. Lennox, Langmuir, 2004, 20, 2867–2873.
71. M. K. Corbierre, N. S. Cameron, M. Sutton, K. Laaziri and R. B. Lennox, Langmuir, 2005, 21, 6063–6072.
72. J. Shan, M. Nuopponen, H. Jiang, E. Kauppinen and H. Tenhu, Macromolecules, 2003, 36, 4526–4533.
73. M. Liang, I.-C. Lin, M. R. Whittaker, R. F. Minchin, M. J. Monteiro and I. Toth, ACS Nano, 2009, 4, 403–413.
74. M. Uz, V. Bulmus and S. Alsoy Altinkaya, Langmuir, 2016, 32, 5997–6009.
75. M. Zheng, Z. Li and X. Huang, Langmuir, 2004, 20, 4226–4235.
76. K. Sebby and E. Mansfield, Anal. Bioanal. Chem., 2015, 407, 2913–2922.
77. M. J. Hostetler, J. E. Wingate, C.-J. Zhong, J. E. Harris, R. W. Vachet, M. R. Clark, J. D. Londono, S. J. Green, J. J. Stokes, G. D. Wignall, G. L. Glish, M. D. Porter, N. D. Evans and R. W. Murray, Langmuir, 1998, 14, 17–30.
78. Y.-S. Shon, S. M. Gross, B. Dawson, M. Porter and R. W. Murray, Langmuir, 2000, 16, 6555–6561.
79. W. P. Wuelfing, S. M. Gross, D. T. Miles and R. W. Murray, J. Am. Chem. Soc., 1998, 120, 12696–12697.
80. R. H. Terrill, T. A. Postlethwaite, C.-H. Chen, C.-D. Poon, A. Terzis, A. Chen, J. E. Hutchison, M. R. Clark, G. Wignall, J. D. Londono, R. Superfine, M. Falvo, C. S. Johnson, E. T. Samulski and R. W. Murray, J. Am. Chem. Soc., 1995, 117, 12537–12548.
81. A. C. Templeton, S. Chen, S. M. Gross and R. W. Murray, Langmuir, 1999, 15, 66–76.
82. I.-C. Lin, M. Liang, T.-Y. Liu, Z. Jia, M. J. Monteiro and I. Toth, Bioorg. Med. Chem., 2012, 20, 6862–6869.
83. C. Guo and G. P. Holland, J. Phys. Chem. C, 2014, 118, 25792–25801.
84. C. Guo and G. P. Holland, J. Phys. Chem. C, 2015, 119, 25663–25672.
85. S. P. Schwaminger, P. F. García, G. K. Merck, F. A. Bodensteiner, S. Heissler, S. Günther and S. Berensmeier, J. Phys. Chem. C, 2015, 119, 23032–23041.
86. L. Illum, A. E. Church, M. D. Butterworth, A. Arien, J. Whetstone and S. S. Davis, Pharm. Res., 2001, 18, 640–645.
87. M. D. Butterworth, L. Illum and S. S. Davis, Colloids Surf., A, 2001, 179, 93–102.
88. B. M. Amoli, S. Gumfekar, A. Hu, Y. N. Zhou and B. Zhao, J. Mater. Chem., 2012, 22, 20048–20056.
89. Z.-Y. Zhou, X. Kang, Y. Song and S. Chen, Chem. Commun., 2011, 47, 6075–6077.
90. M. Cargnello, N. L. Wieder, P. Canton, T. Montini, G. Giambastiani, A. Benedetti, R. J. Gorte and P. Fornasiero, Chem. Mater., 2011, 23, 3961–3969.
91. E. Sadeghmoghaddam, K. Gaïeb and Y.-S. Shon, Appl. Catal., A, 2011, 405, 137–141.
92. E. Sadeghmoghaddam, C. Lam, D. Choi and Y.-S. Shon, J. Mater. Chem., 2011, 21, 307–312.
93. W. Chen, N. B. Zuckerman, X. Kang, D. Ghosh, J. P. Konopelski and S. Chen, J. Phys. Chem. C, 2010, 114, 18146–18152.
94. Z.-Y. Zhou, X. Kang, Y. Song and S. Chen, Chem. Commun., 2012, 48, 3391–3393.
95. Z.-Y. Zhou, J. Ren, X. Kang, Y. Song, S.-G. Sun and S. Chen, Phys. Chem. Chem. Phys., 2012, 14, 1412–1417.
96. F. Mirkhalaf, J. Paprotny and D. J. Schiffrin, J. Am. Chem. Soc., 2006, 128, 7400–7401.
97. L. M. Demers, C. A. Mirkin, R. C. Mucic, R. A. Reynolds, R. L. Letsinger, R. Elghanian and G. Viswanadham, Anal. Chem., 2000, 72, 5535–5541.
98. X. Xia, M. Yang, Y. Wang, Y. Zheng, Q. Li, J. Chen and Y. Xia, ACS Nano, 2012, 6, 512–522.
99. C. S. Yun, A. Javier, T. Jennings, M. Fisher, S. Hira, S. Peterson, B. Hopkins, N. O. Reich and G. F. Strouse, J. Am. Chem. Soc., 2005, 127, 3115–3119.
100. S. J. Hurst, A. K. R. Lytton-Jean and C. A. Mirkin, Anal. Chem., 2006, 78, 8313–8318.
101. H. D. Hill, J. E. Millstone, M. J. Banholzer and C. A. Mirkin, ACS Nano, 2009, 3, 418–424.
102. Z. Li, R. Jin, C. A. Mirkin and R. L. Letsinger, Nucleic Acids Res., 2002, 30, 1558–1562.
103. D. A. Giljohann, D. S. Seferos, P. C. Patel, J. E. Millstone, N. L. Rosi and C. A. Mirkin, Nano Lett., 2007, 7, 3818–3821.
104. X. Zhang, M. R. Servos and J. Liu, J. Am. Chem. Soc., 2012, 134, 9910–9913.
105. L. Maus, J. P. Spatz and R. Fiammengo, Langmuir, 2009, 25, 7910–7917.
106. S. V. Patwardhan, F. S. Emami, R. J. Berry, S. E. Jones, R. R. Naik, O. Deschaume, H. Heinz and C. C. Perry, J. Am. Chem. Soc., 2012, 134, 6244–6256.
107. A. Schroedter and H. Weller, Angew. Chem., Int. Ed., 2002, 41, 3218–3221.
108. M. M. Y. Chen and A. Katz, Langmuir, 2002, 18, 2413–2420.
109. H. Xie, A. G. Tkachenko, W. R. Glomm, J. A. Ryan, M. K. Brennaman, J. M. Papanikolas, S. Franzen and D. L. Feldheim, Anal. Chem., 2003, 75, 5797–5805.
110. E. Oh, K. Susumu, J. Blanco-Canosa, I. Medintz, P. Dawson and H. Mattoussi, Small, 2010, 6, 1273–1278.
111. N. Zhan, G. Palui, J.-P. Merkl and H. Mattoussi, J. Am. Chem. Soc., 2016, 138, 3190–3201.
112. J.-M. Ha, A. Solovyov and A. Katz, Langmuir, 2009, 25, 153–158.
113. J.-M. Ha, A. Solovyov and A. Katz, Langmuir, 2009, 25, 10548–10553.
114. J.-M. Ha, A. Solovyov and A. Katz, J. Phys. Chem. C, 2010, 114, 16060–16070.
115. A. Kumar, H. Ma, X. Zhang, K. Huang, S. Jin, J. Liu, T. Wei, W. Cao, G. Zou and X.-J. Liang, Biomaterials, 2012, 33, 1180–1189.
116. R. Lévy, N. T. K. Thanh, R. C. Doty, I. Hussain, R. J. Nichols, D. J. Schiffrin, M. Brust and D. G. Fernig, J. Am. Chem. Soc., 2004, 126, 10076–10084.
117. A. Kira, H. Kim and K. Yasuda, Langmuir, 2009, 25, 1285–1288.
118. C. D. Walkey, J. B. Olsen, H. Guo, A. Emili and W. C. Chan, J. Am. Chem. Soc., 2012, 134, 2139–2147.
119. H. Hinterwirth, S. Kappel, T. Waitz, T. Prohaska, W. Lindner and M. Lämmerhofer, ACS Nano, 2013, 7, 1129–1136.
120. S. Elzey, D.-H. Tsai, S. Rabb, L. Yu, M. Winchester and V. Hackley, Anal. Bioanal. Chem., 2012, 403, 145–149.
121. M. D. Donakowski, J. M. Godbe, R. Sknepnek, K. E. Knowles, M. Olvera de la Cruz and E. A. Weiss, J. Phys. Chem. C, 2010, 114, 22526–22534.
122. A. J. Morris-Cohen, M. D. Donakowski, K. E. Knowles and E. A. Weiss, J. Phys. Chem. C, 2010, 114, 897–906.
123. I. Moreels, B. Fritzinger, J. C. Martins and Z. Hens, J. Am. Chem. Soc., 2008, 130, 15081–15086.
124. A. Badia, L. Demers, L. Dickinson, F. Morin, R. Lennox and L. Reven, J. Am. Chem. Soc., 1997, 119, 11104–11105.
125. C. I. Ratcliffe, K. Yu, J. A. Ripmeester, M. B. Zaman, C. Badarau and S. Singh, Phys. Chem. Chem. Phys., 2006, 8, 3510–3519.
126. J. R. Sachleben, E. W. Wooten, L. Emsley, A. Pines, V. L. Colvin and A. P. Alivisatos, Chem. Phys. Lett., 1992, 198, 431–436.
127. B. S. Zelakiewicz, T. Yonezawa and Y. Tong, J. Am. Chem. Soc., 2004, 126, 8112–8113.
128. R. Sharma, G. P. Holland, V. C. Solomon, H. Zimmermann, S. Schiffenhaus, S. A. Amin, D. A. Buttry and J. L. Yarger, J. Phys. Chem. C, 2009, 113, 16387–16393.
129. J. Trébosc, J. W. Wiench, S. Huh, V. S. Y. Lin and M. Pruski, J. Am. Chem. Soc., 2005, 127, 3057–3068.
130. K. A. Johnston, A. M. Smith, L. E. Marbella and J. E. Millstone, Langmuir, 2016, 32, 3820–3826.
131. N. C. Anderson, M. P. Hendricks, J. J. Choi and J. S. Owen, J. Am. Chem. Soc., 2013, 135, 18536–18548.
132. R. D. Harris, V. A. Amin, B. Lau and E. A. Weiss, ACS Nano, 2016, 10, 1395–1403.
133. Z. Hens, I. Moreels and J. C. Martins, ChemPhysChem, 2005, 6, 2578–2584.
134. Z. Hens and J. C. Martins, Chem. Mater., 2013, 25, 1211–1221.
135. R. Vatassery, J. A. Hinke, A. Sanchez-Diaz, R. Hue, K. R. Mann, D. A. Blank and W. L. Gladfelter, J. Phys. Chem. C, 2013, 117, 10708–10715.
136. G. F. Pauli, B. U. Jaki and D. C. Lankin, J. Nat. Prod., 2005, 68, 133–149.
137. M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons Ltd, West Sussex, England, 2nd edn, 2008.
138. I. Moreels, J. C. Martins and Z. Hens, ChemPhysChem, 2006, 7, 1028–1031.
139. B. Fritzinger, R. K. Capek, K. Lambert, J. C. Martins and Z. Hens, J. Am. Chem. Soc., 2010, 132, 10195–10201.
140. M. D. Rausch and V. Mark, J. Org. Chem., 1963, 28, 3225–3228.
141. S. E. Lehman, Y. Tataurova, P. S. Mueller, S. V. S. Mariappan and S. C. Larsen, J. Phys. Chem. C, 2014, 118, 29943–29951.
142. C. N. Valdez, A. M. Schimpf, D. R. Gamelin and J. M. Mayer, ACS Nano, 2014, 8, 9463–9470.
143. L. R. Becerra, C. B. Murray, R. G. Griffin and M. G. Bawendi, J. Chem. Phys., 1994, 100, 3297–3300.
144. D. Zhang and S. M. Ansar, Anal. Chem., 2010, 82, 5910–5914.
145. C. S. Levin, S. W. Bishnoi, N. K. Grady and N. J. Halas, Anal. Chem., 2006, 78, 3277–3281.
146. L. F. Pease, D.-H. Tsai, R. A. Zangmeister, M. R. Zachariah and M. J. Tarlov, J. Phys. Chem. C, 2007, 111, 17155–17157.
147. D.-H. Tsai, F. W. DelRio, R. I. MacCuspie, T. J. Cho, M. R. Zachariah and V. A. Hackley, Langmuir, 2010, 26, 10325–10333.
148. S. Guha, X. Ma, M. J. Tarlov and M. R. Zachariah, Anal. Chem., 2012, 84, 6308–6311.
149. A. H. Latham and M. E. Williams, Langmuir, 2006, 22, 4319–4326.
150. G. Charron, D. Hühn, A. Perrier, L. Cordier, C. J. Pickett, T. Nann and W. J. Parak, Langmuir, 2012, 28, 15141–15149.
151. Y. Joseph, I. Besnard, M. Rosenberger, B. Guse, H.-G. Nothofer, J. M. Wessels, U. Wild, A. Knop-Gericke, D. Su and R. Schlögl, J. Phys. Chem. B, 2003, 107, 7406–7413.
152. H. Zhang and B. Yang, Thin Solid Films, 2002, 418, 169–174.
153. M. D. Torelli, R. A. Putans, Y. Tan, S. E. Lohse, C. J. Murphy and R. J. Hamers, ACS Appl. Mater. Interfaces, 2015, 7, 1720–1725.
154. M. R. Ivanov and A. J. Haes, Anal. Chem., 2012, 84, 1320–1326.
155. A. A. Volkert, V. Subramaniam, M. R. Ivanov, A. M. Goodman and A. J. Haes, ACS Nano, 2011, 5, 4570–4580.
156. S. D. Techane, L. J. Gamble and D. G. Castner, J. Phys. Chem. C, 2011, 115, 9432–9441.
157. J. E. B. Katari, V. L. Colvin and A. P. Alivisatos, J. Phys. Chem., 1994, 98, 4109–4117.

---

Footnotes

† Electronic supplementary information (ESI) available: Flow charts depicting the process for ligand density determination. See DOI: 10.1039/c6an02206e

‡ These authors contributed equally to this work.

---