Open Access Article
Open Access ArticleIs C50 a superaromat? Evidence from electronic structure and ring current calculations†
Ana Sanz
Matías
*a,
Remco W. A.
Havenith
bc,
Manuel
Alcamí
de and
Arnout
Ceulemans
*a
aDepartment of Chemistry, University of Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: ana.sanzmatias@chem.kuleuven.be; arnout.ceulemans@chem.kuleuven.be; Fax: +32-16-327992
bTheoretical Chemistry, Zernike Institute for Advanced Materials and Stratingh Institute for Chemistry, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: r.w.a.havenith@rug.nl; Tel: +31-50-3637754
cGhent Quantum Chemistry Group, Department of Inorganic and Physical Chemistry, Ghent University, Krijgslaan 281 (S3), B-9000 Gent, Belgium
dDepartamento de Química, Módulo-13, Universidad Autónoma de Madrid, Cantoblanco, 28049 Madrid, Spain. E-mail: manuel.alcami@uam.es; Tel: +34-91-4973857
eInstituto Madrileño de Estudios Avanzados en Nanociencias (IMDEA-Nanociencia), Cantoblanco 28049 Madrid, Spain. E-mail: manuel.alcami@imdea.org
First published on 28th September 2015
Abstract
The fullerene-50 is a ‘magic number’ cage according to the 2(N + 1)2 rule. For the three lowest isomers of C50 with trigonal and pentagonal symmetries, we calculate the sphericity index, the spherical parentage of the occupied π-orbitals, and the current density in an applied magnetic field. The minimal energy isomer, with D3 symmetry, comes closest to a spherical aromat or a superaromat. In the D5h bond-stretch isomers the electronic structure shows larger deviations from the ideal spherical shells, with hybridisation or even reversal of spherical parentages. It is shown that relative stabilities of fullerene cages do not correlate well with aromaticity, unlike the magnetic properties which are very sensitive indicators of spherical aromaticity. Superaromatic diamagnetism in the D3 cage is characterized by global diatropic currents, which encircle the whole cage. The breakdown of sphericity in the D5h cages gives rise to local paratropic countercurrents.
1 Introduction
Orbital levels of globular molecules can be associated with scalar or tensor spherical harmonic functions on the basis of a common nodal structure.1,2 Spherical aromaticity arises whenever the occupied frontier orbitals correspond to a closed parent spherical shell. For scalar harmonics these magic electron counts fulfill the 2(N + 1)2 rule.3 In contrast to 2D Hückel aromats, 3D spherical aromats or superaromats are particularly hard to find, since in fact they have to obey three requirements: (i) the overall shape of the molecule has to be close to a hollow sphere, (ii) the electron count has to fulfill the magic rule, and (iii) the projection of the orbitals on the spherical harmonics must yield complete spherical shells.4Fullerenes are hollow carbon cages formed by hexagons and pentagons which, in spite of allowing closure, bring strain to the structure.5–7 Although a plethora of fullerene cages is mathematically possible, only a few have been detected experimentally.8 In view of their approximate globular shape fullerenes could be expected to be promising targets for spherical aromaticity. However, the two most prominent peaks in the mass spectra of evaporated graphite correspond to C60 and C70,9 neither of which holds a magic electron count.10,11 The exceptional stability of icosahedral C60 has been attributed to it being the first leapfrog cage with isolated pentagons.7 The frontier orbitals of leapfrog cages are based on entangled spherical shells,12,13 which is exactly the opposite of the spherical shell model. Likewise C70 represents the first case of a cylindrical fullerene with isolated pentagons.14 It too corresponds to a severe symmetry breaking of the spherical model.
Another intense peak in the mass spectrum corresponds to C50. This is a magic electron count which fulfils the 2(N + 1)2 rule with N = 4. Despite theoretical research has already been carried out on its isomers,15–18 little attention has been paid to what is mentioned as a cause of their different stability: spherical aromaticity.19 This paper will be devoted, through a distinct approach, to a detailed examination of the electronic structure of 50-fullerenes, with special attention to the role of spherical aromaticity.
1.1 Isomers of C50
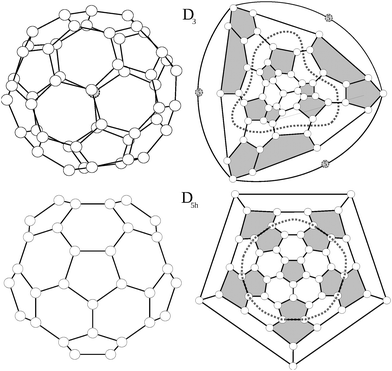
Among the 271 possible isomers of C50, high level calculations invariably point to the extra stability of only two C50 isomers, with D3 and D5h symmetry.15–18 Interestingly, these are the only isomers without triplets of directly fused pentagons. They are shown in Fig. 1, together with their Schlegel diagrams.For the D3 isomer a modified Schlegel diagram was adopted to obtain a better visualization of the symmetry. Since the main rotational axis of the molecule, C3, crosses through the top and bottom carbon atoms instead of being centred in a hexagon, a standard Schlegel projection in a hexagon will not offer a suitable representation of the trigonal symmetry. Instead we erase the bottom carbon atom (atom 5 in Fig. 1, situated in the center of three fused hexagons) and replace it by a triangle linking its three surrounding atoms. Consequently, when the Schlegel projection is performed through this triangle, the symmetry of the structure is preserved. The D3 isomer consists of six isolated pentagon–pentagon pairs which are arranged in a trigonal way. Top and bottom of the trigonal axis are occupied by a carbon atom lying in the centre of three adjacent hexagons, and linked to three pentagon–pentagon pairs.
The D5h structure on the other hand is a regular pentagonal prism, with five isolated pentagon–pentagon pairs arranged around the equator, and a top and bottom isolated pentagon. For the D5h structure, Lu et al.17 found two stable bond-stretch isomers,20 denoted hereafter as A and B, with different bond lengths within the same connectivity. Both isomers differ in their frontier orbitals: while in the most stable one (A) the HOMO corresponds to an orbital of a1′ symmetry and the LUMO to an orbital of a2′ symmetry, for the B isomer the HOMO and LUMO orbitals are exchanged (HOMO a2′ and LUMO a1′). As we will discuss later these different electronic distributions yield very different structures and values of aromaticity.
According to previous calculations15,18 the D3 structure is the most stable, despite the presence of six adjacent pentagons (AP) as compared to only five AP's in the D5h isomer. This represents an exception to the Pentagon Adjacency Penalty Rule (PAPR),21,22 which states that the most stable fullerene isomer corresponds to the one with the lowest number of adjacent pentagons and for every extra AP a destabilization of the system between 0.8–0.9 eV is expected.
So far experimental isolation of 50-fullerenes has been limited to the preparation of the chloro-derivative, decachlorofullerene[50] C50Cl10.23 It was demonstrated by a variety of techniques that this derivative most likely has a D5h structure, with the ten chlorine atoms attached to the equatorial pentagon–pentagon fusions.24 This compound was nicknamed ‘saturnene’ in view of the chlorine ring around its equator. In contrast the ground state of unsubstituted C50 has not yet been characterized experimentally.
2 Methodology
D 3, D5h (A) and D5h (B) symmetry structures were generated with CaGe25 software and optimized using density functional theory (DFT). In particular, the B3LYP functional26,27 and the 6-31G* basis set were chosen. These calculations were carried out using the GAUSSIAN program.28 Isomerization between the A and B states was further investigated with MOLPRO.29 A Hückel calculation was performed in order to obtain energy level diagrams and π bond orders.30 For a given fullerene, keeping to a minimum the sum of squares of the distance from each atom to a least squares sphere yields S, the least squares sphericity parameter:31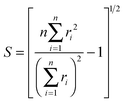 | (1) |
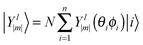 | (2) |
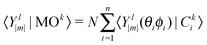 | (3) |
Nucleus independent chemical shifts (NICS, ppm)32 were computed at the centre of the cage using the GIAO method. Current density maps were calculated at the BLYP/6-31G* level using the ipsocentric choice of origin as implemented in GAMESS-UK33 and SYSMO.34 Diatropic and paratropic currents are represented, respectively, by anticlockwise and clockwise circulations.
3 Results
3.1 Ground state of C50
A summary of the optimization calculations results can be found in Table 1. In excellent agreement with the literature, D3 is the most stable isomer followed by D5h (B) and D5h (A), 2.23 and 5.58 kcal mol−1 higher in energy. The D3 HOMO–LUMO gap is also significantly higher, indicative of a larger aromaticity.4 The different sphericity is due to the distribution of adjacent pentagon pairs (6 and 5, respectively) on the structures and has been pointed previously as the reason for the energy difference between these isomers.18 However, the higher sphericity of the atomic framework is not a warranty of a neat closed spherical shell electronic structure.| Isomer | AP | E rel | Gap | S | NICS |
|---|---|---|---|---|---|
| D 3 | 6 | 0 | 2.27 | 0.024 | −40.3 |
| D 5h (A) | 5 | 5.58 | 1.27 | 0.037 | −32.5 |
| D 5h (B) | 5 | 2.23 | 1.37 | 0.051 | −2.7 |
The difference in geometry between D5h A and B isomers is most pronounced on the equatorial belt. The calculated length of C–C bonds for the equatorial pentagon–pentagon fusions is 1.396 Å for the A isomer, versus 1.478 Å for the B isomer. As noted by Lu et al., in the A isomer the pentaphenyl belt has a quinoid-like valence-bond structure, while in the B isomer it is a sequence of aromatic benzenes,17 as shown in Fig. 2. Accordingly the two bonding schemes can be characterized as a Fries structure for A, and a Clar structure for B.
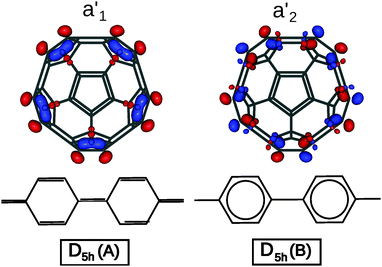 | ||
| Fig. 2 Bond alternation in the equatorial belts for the A (Fries) and B (Clar) isomers of C50, and orbital pictures of the frontier molecular orbitals (A isomer: a1′ HOMO, a2′ LUMO). | ||
While the two bond-stretch isomers are close in energy, their HOMO and LUMO are interchanged: for A, the HOMO has a1′ orbital symmetry and the LUMO a2′, while for B it is the opposite (HOMO a2′ and LUMO a1′). These MOs are mainly concentrated along the equator of the molecule. The a1′ orbital is bonding on the C–C bonds at the pentagon–pentagon fusions, and thus will be occupied in the Fries structure. In contrast the a2′ is antibonding and thus will favor single bonds on these sites, yielding a chain of isolated aromatic sextets which is typical for a Clar structure. Since the two structures are close both in energy and in geometry, we have investigated whether electron correlation effects could stabilize an intermediate resonant structure.
First it should be noted that both D5h isomers A and B have, as shown by a CASSCF(18,12) 6-31G calculation, an undoubtedly monodeterminantal wavefunction. The obtained energy difference between them (3.06 kcal mol−1, Table S9, ESI†) is in agreement with the DFT results, which yield a 3.35 kcal mol−1 gap (Table 1). In order to explore the possibility of the above mentioned resonant isomer lying lower in energy than A and B, further calculations are performed on intermediate structures. The ground state singlet and a state average calculation including the GS and first excited state singlet are carried out using CASSCF(6,6) with a 6-31G basis set. The intermediate coordinates are obtained through linear combinations (interpolation) of A and B leading to the interconversion of A and B. While no energy well is observed, there seems to be an avoided crossing at 0.6 B + 0.4 A (Fig. S1, ESI†), a coordinate in which both A and B electronic structures coexist in a resonant structure. The barrier between B and A amounts to 33 kcal mol−1.
The Hückel calculation for the D5h graph, with all nearest neighbour interactions equal, invariably yields the ground state of the B isomer. However by changing the orbital occupation numbers of the frontier orbitals, one can study the bonding scheme in the A isomer as well. The Hückel π bond order of C–C bonds in equatorial pentagon–pentagon fusions clearly reproduces the DFT results: in the A isomer this bond order is 0.528 in agreement with the proposed Fries structure, while for B it is 0.385, showing a preponderant Clar structure.
3.2 Spherical parentages
Spherical parentages of occupied molecular π-orbitals have been calculated on the basis of the Hückel eigenvectors, which only take into account the connectivity of the cage. As an example in Table 2 we report the results of overlap calculations between the nine highest occupied Hückel MOs (HMOs 17–25) and the g-type spherical harmonics. As can be seen the g-parentage of these orbitals is never lower than 81%. A global survey of the overlap percentages between HMOs and spherical harmonics is provided in Table 3.| MO | gz4 | gz3x | gz3y | gz2(x2−y2) | gz2xy | gzx3 | gzy3 | gx4+y4 | gxy(x2−y2) | ∑ (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.08 | 89.75 | 0.00 | 0.00 | 0.05 | 89.88 |
| 18 | 0.00 | 0.08 | 0.90 | 66.80 | 3.08 | 0.00 | 0.11 | 25.79 | 1.22 | 97.97 |
| 19 | 0.00 | 2.48 | 0.07 | 3.08 | 65.66 | 0.01 | 0.02 | 1.21 | 25.84 | 98.36 |
| 20 | 96.85 | 0.01 | 0.34 | 0.00 | 0.00 | 0.00 | 0.06 | 0.00 | 0.00 | 97.25 |
| 21 | 0.00 | 0.02 | 0.01 | 4.47 | 18.48 | 0.06 | 0.00 | 12.44 | 51.16 | 86.63 |
| 22 | 0.00 | 0.00 | 0.04 | 18.47 | 4.46 | 0.03 | 0.00 | 51.20 | 12.44 | 86.62 |
| 23 | 0.07 | 18.65 | 47.60 | 0.14 | 0.31 | 0.00 | 14.51 | 0.26 | 0.13 | 81.66 |
| 24 | 0.06 | 35.71 | 30.63 | 0.20 | 0.49 | 0.00 | 13.99 | 0.32 | 0.26 | 81.64 |
| 25 | 0.03 | 23.35 | 0.43 | 0.09 | 0.42 | 0.00 | 64.12 | 0.06 | 0.21 | 88.70 |
| ∑ (%) | 97.01 | 80.31 | 80.00 | 93.24 | 92.97 | 89.87 | 92.81 | 91.28 | 91.30 |
| l | HMO | D 3 | D 5h (A) | D 5h (B) |
|---|---|---|---|---|
| 0 (s) | 1 | 100 | 100 | 100 |
| 1 (p) | 2–4 | ∼99.7 | ∼99.8 | ∼99.8 |
| 2 (d) | 5–9 | >95 | >97 | >97 |
| 3 (f) | 10–16 | >91 | >92 | >92 |
| 4 (g) | 17–24 | >81 | >81 | >81 |
| 4 (g) | HOMO | 88 (a1) | 92.2 (a1′) | 0 (a2′) |
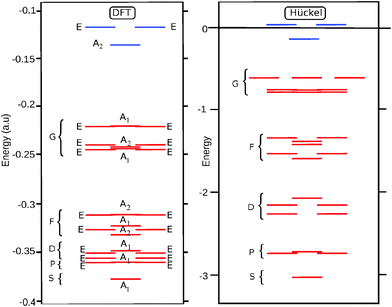
For the D3 cage the valence orbital shell shows a close match with the particle on a sphere model: the 25 occupied orbitals correspond to a closed spherical shell up to l = 4. This is confirmed by the energy diagram in Fig. 3. Since the symmetry and shape of the Hückel and DFT MOs are similar, the spherical shell structure is also retrieved in the DFT orbital ordering.
For D5h, on the other hand, the results show a large difference between the A and B isomers. The Hückel result for the D5h cage yields a HOMO with a2′ symmetry, which corresponds to the HOMO of the B-isomer. For this orbital the sign of the eigenvector in the equator alternates ten times when going around, indicating that it has an l = 5 parentage. Indeed the overlap of this HOMO with the l = 4 g-harmonics is exactly zero, as the g-orbitals do not subduce an a2′ symmetry:
| Γl=4(D5h) = a1′ + e1′ + e2′ + e1′′ + e2′′ | (4) |
As a result the B isomer is found to be characterized by a pseudo-spherical shell, in which one of the g-orbitals is replaced by a h-orbital. The ground state of the B isomer thus is not a spherical aromat, and consequently, the filling rule for spherical shells does not apply. In contrast, in the A isomer the HOMO has a1′ symmetry, and can be identified as the LUMO of the Hückel calculation. This orbital has a close resemblance to the z4 harmonic function of the g-shell. By occupying this orbital instead of the a2′ HOMO, the occupation of the g-shell is completed, and the sphericity of the electronic structure is nicely restored. The results of overlap calculations thus indicate that for the D3 and D5h (A) C50 isomers the projection of the occupied π-orbitals on the spherical harmonics yields complete spherical shells, while for the D5h (B) isomer it does not. However, as we pointed out in the introduction while the mapping on closed spherical shells is a criterion for spherical aromaticity, it is not sufficient. The degree of distortion of sphericity is equally important. Ring current density plots provide a way to investigate this further.
3.3 Ring currents
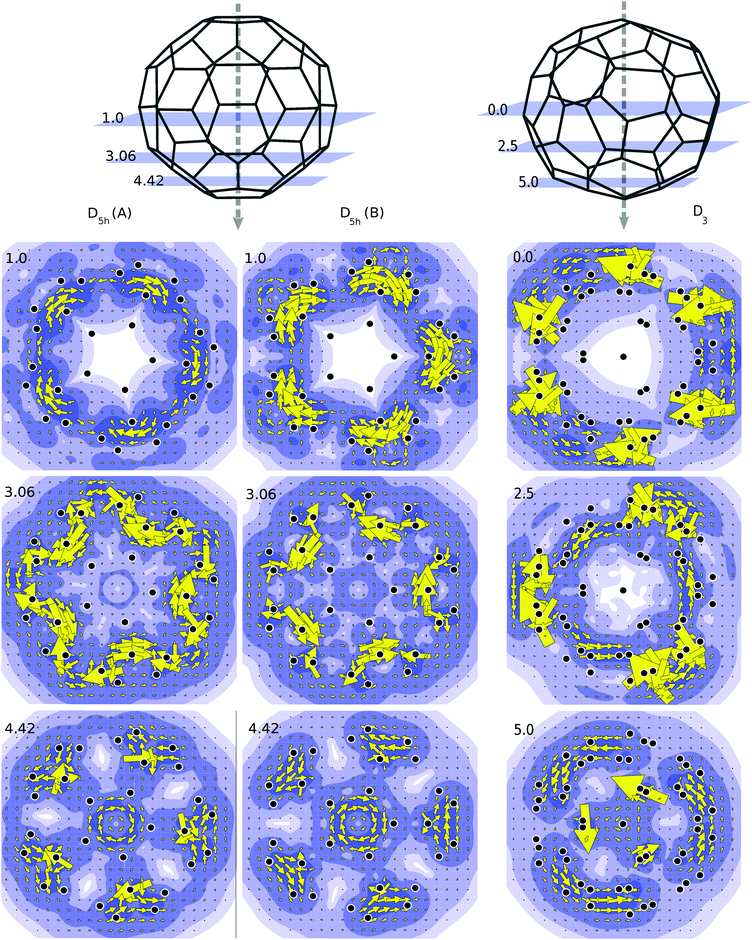
Annulenes which satisfy Hückel's rule display a diatropic ring current when subjected to a magnetic field which is oriented perpendicular to the plane of the molecule. The diatropic ring current is mainly due to the diamagnetic response of the π-electron cloud.35 Likewise in true spherical aromats one expects that application of a magnetic field would induce a global diatropic rotation of the electron cloud about the axial direction of the magnetic field.36 To study this effect we have applied a magnetic field along the principal rotational axis of the C50-isomers, and made plots of the current densities in perpendicular planes at various latitudes. Current density plots showing the contribution from the π orbitals for the C50 isomers are presented in Fig. 4. When the projection plane is next to an atom, current density may be higher than average, hence the large arrows that appear occasionally in the plots. As shown in Fig. 4 the current plots for the D3 isomer are the ones that are most consistent with a global diatropic circulation. This is especially clear for the plots in the planes at 5.0 and 2.5 a.u., which avoid direct atomic contact. Due to the large HOMO–LUMO gap, the coefficients of the transitions are small, i.e., the total currents seem to be composed of many allowed transitions, each with a small contribution.The case for the D5h geometry is less clear cut and the two isomers behave differently. For the D5h (A) isomer currents are still diatropic on the poles and tropics, but near the equator paratropic counter currents are observed. The B isomer shows analogous characteristics but the paratropic aspects are more pronounced in line with the incomplete filling of the spherical g-shell. In both cases, the centered paratropic current that appears at 4.42 a.u. (Fig. 4) corresponds to the bottom pentagon of the cage. Since the projection plane is parallel to it, the plot obtained is comparable to those of annulenes. Thus it is not a global current but a local one, not representative of the character of the molecule as a whole.
A more detailed understanding can be obtained by analyzing the separate excitations to virtual orbitals that contribute to the magnetic response. Both D5h isomers are characterized by a small HOMO–LUMO gap. The corresponding excitations have the symmetry of the z-component of the magnetic dipole operator:
| a1′ × a2′ = A2′ = Γ(Rz) | (5) |
The matrix element in this operator appears to be strong since both levels share an l = 5 parentage.
As we have already indicated the a2′ orbital has no g-character, but its Hückel projection overlaps to almost 99% with the a2′ component of the l = 5 shell. The relevant h-orbital is expressed as:
sin5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsin θsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5ϕ ∼ 5x4y − 10x2y3 + y5 5ϕ ∼ 5x4y − 10x2y3 + y5 | (6) |
The remaining a1′ orbital shows a strong overlap with the g-shell, 92.2% according to Table 3, nevertheless it also overlaps to a significant extent of 26% with the a1′ component of the l = 5 shell. The corresponding function is given by:
sin5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5ϕ ∼ 5xy4 − 10x3y2 + x5 5ϕ ∼ 5xy4 − 10x3y2 + x5 | (7) |
The large simultaneous overlaps with equisymmetric l = 4 and l = 5 parent harmonics indicate that we have arrived at a point in the spectrum where orthogonality of the projected spherical harmonics breaks down as a result of the finite size of the atomic basis set. The affiliation of the HOMO and the LUMO to two complementary components of the h-shell explains the large paratropic contribution of this excitation, since the mixing of both by the magnetic dipole operator will create a large orbital moment along the z-axis.
As for the D5h A isomer, it is clear that the weak surrounding diatropic current is generated by small contributions of many different excitations from the π molecular orbitals below the HOMO (from the MOs 142–149 to the LUMO and above). However, besides the main HOMO–LUMO excitation, other transitions seem to be also highly contributing to the global paratropic picture, such as 146 → 151, 147 → 151 (mainly) and 150 → 156.
4 Discussion
Our results show that, as compared to 2D cylindrical aromats, spherical analogues show more extensive hybridization between spherical shells. The reason is that point group symmetries are often too low to discriminate between spherical parentages. This effect becomes more pronounced in the frontier orbital region. As an example total symmetry in the D5h point group was unable to distinguish l = 4 and l = 5 components. This would imply that one should direct the search for superaromats to clusters with high symmetries. The highest point groups are the tetrahedral, octahedral and icosahedral groups, but these give rise to atomic orbit counts that are divisors of the group orders 24, 48, and 120 respectively, and these counts are mostly not commensurate with magic numbers such as 32, 50 or 72.Compatibility between magic counts and symmetry numbers thus would require a different strategy, by adjusting electron counts through doping with hetero-atoms. A successful example is the endohedral U@C28 metallo-fullerene, where the carbon cage has tetrahedral symmetry and attains the magic electron count of 32 by doping with four electrons from uranium.37
The link between fullerene stability and magic electron counts is not well established either. The most stable fullerenes C60 and C70 are not aromats. Clearly the stability of the neutral fullerenes is dictated more by the frequency of occurrence of stable motifs, i.e. the fact that pentagons are isolated as in C60 and C70 or the absence of pentagon triplets as in C50, rather than by electron count. Nevertheless the higher aromatic character of some isomer can affect the expected stability by taking only into account the distribution of motifs. For the three analysed structures of C50 the D3 isomer complies best with a spherical aromat. It has a higher degree of sphericity and a neat closed shell spherical parentage. According to DFT calculations it is slightly more stable than the D5h isomers, even though the PAPR rule would predict it to be around 20 kcal mol−1 less stable. Therefore a most favourable electronic structure (i.e. enhanced aromaticity) can stabilize some isomers of neutral fullerenes and favour structures with a worst distribution of structural motifs.
These effects should be more evident for negatively charged fullerenes, and in these systems electronic effects can determine the stability instead of strain. For instance in the case of endohedral metallo fullerenes, where stability is mainly dictated by the charge transfer to the carbon cage and the most stable isomers correspond to the most stable negatively charged carbon cages, the structure observed experimentally does not fulfil in many cases the isolated pentagon rule.38 The stability of these isomers has been directly related to the electronic structure of the π shell39 and with maximum aromaticity.40
Of the two D5h isomers, the A isomer fulfils the criteria for spherical aromaticity, while the B isomer is an anti-aromat as far as spherical parentage is concerned. While the relative stabilities do not typically correlate with aromaticity, the magnetic properties are very sensitive to the spherical shell nature of the cages. The aromaticity of the D3 isomer is confirmed by a substantial diamagnetic NICS value, and a global diatropic ring current. The NICS values of the D5h isomers also reflect their spherical shell character (Table 1). The main difference between A and B isomers lies in the currents surrounding the equator, since the cap current density plots look quite similar (diatropic except for the apical pentagons, which are paratropic). The current density maps however indicate paratropic currents even for the A isomer, which is more aromatic. The reason is the strong hybridization between the spherical shells in the frontier orbital region, made possible by the prismatic symmetry of these isomers.
5 Conclusions
Spherical aromaticity appears to remain an elusive concept. Our investigation of fullerenes with a magic number of 50 electrons has confirmed that although the distribution of the pentagons dominates the fullerene energy landscape, enhanced spherical aromaticity of some isomers can compensate the destabilization due to the presence of an extra pair of adjacent pentagons. It can also lead to a breakdown of the spherical filling rule, as we have demonstrated for the case of the D5h (B) isomer, or to strong hybridization of spherical components, due to symmetry breaking, as was found in the D5h (A) isomer. Nonetheless the quest for spherical aromats should continue, preferably by considering high-symmetry cages in combination with doping to achieve a magic electron count.Acknowledgements
A.S.M. would like to thank Mutua Madrileña for a predoctoral scholarship, and Yang Wang for helpful discussions and providing useful programs. R.W.A.H. acknowledges the Zernike Institute for Advanced Materials for financial support. MA acknowledges support from MICINN project CTQ2013-43698-P and CAM project NANOFRONTMAG-CM ref. S2013/MIT-2850. A.C. is indebted to the FWO-Vlaanderen for financial support.References
- M. Reiher and A. Hirsch, Chem. – Eur. J., 2003, 9, 5442–5452 CrossRef CAS PubMed.
- Z. Chen and R. B. King, Chem. Rev., 2005, 105, 3613–3642 CrossRef CAS PubMed.
- A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2000, 39, 3915–3917 CrossRef CAS.
- M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1184 CrossRef.
- E. Albertazzi, C. Domene, P. W. Fowler, T. Heine, G. Seifert, C. Van Alsenoy and F. Zerbetto, Phys. Chem. Chem. Phys., 1999, 1, 2913–2918 RSC.
- T. G. Schmalz, W. A. Seitz, D. J. Klein and G. E. Hite, J. Am. Chem. Soc., 1988, 110, 1113–1127 CrossRef CAS.
- H. W. Kroto, Nature, 1987, 329, 529–531 CrossRef CAS.
- P. W. Fowler and D. E. Manolopoulos, An atlas of fullerenes, Clarendon Press, 1995 Search PubMed.
- D. E. Manolopoulos, J. C. May and S. E. Down, Chem. Phys. Lett., 1991, 181, 105–111 CrossRef CAS.
- R. Hoffmann and M. Gouterman, J. Chem. Phys., 1962, 36, 2189–2195 CrossRef CAS.
- A. Ceulemans and P. W. Fowler, J. Chem. Soc., Faraday Trans., 1992, 88, 2797–2798 RSC.
- A. Ceulemans, S. Compernolle and E. Lijnen, Phys. Chem. Chem. Phys., 2004, 6, 238–241 RSC.
- P. W. Fowler and A. Ceulemans, J. Phys. Chem., 1995, 99, 508–510 CrossRef CAS.
- K. Hedberg, L. Hedberg, M. Bühl, D. S. Bethune, C. A. Brown and R. D. Johnson, J. Am. Chem. Soc., 1997, 119, 5314–5320 CrossRef CAS.
- W. G. Xu, Y. Wang and Q. S. Li, J. Mol. Struct.: THEOCHEM, 2000, 531, 119–125 CrossRef CAS.
- L. Zhechkov, T. Heine and G. Seifert, J. Phys. Chem. A, 2004, 108, 11733–11739 CrossRef CAS.
- X. Lu, Z. Chen, W. Thiel, P. v. R. Schleyer, R. Huang and L. Zheng, J. Am. Chem. Soc., 2004, 126, 14871–14878 CrossRef CAS PubMed.
- S. Díaz-Tendero, M. Alcamí and F. Martín, Chem. Phys. Lett., 2005, 407, 153–158 CrossRef.
- X. Lu and Z. Chen, Chem. Rev., 2005, 105, 3643–3696 CrossRef CAS PubMed.
- S. J. Austin, J. Baker, P. W. Fowler and D. E. Manolopoulos, J. Chem. Soc., Perkin Trans. 2, 1994, 2319–2323 RSC.
- E. Albertazzi, C. Domene, P. W. Fowler, T. Heine, G. Seifert, C. Van Alsenoy and F. Zerbetto, Phys. Chem. Chem. Phys., 1999, 1, 2913–2918 RSC.
- E. E. B. Campbell, P. W. Fowler, D. Mitchell and F. Zerbetto, Chem. Phys. Lett., 1996, 250, 544–548 CrossRef CAS.
- S.-Y. Xie, F. Gao, X. Lu, R.-B. Huang, C.-R. Wang, X. Zhang, M.-L. Liu, S.-L. Deng and L.-S. Zheng, Science, 2004, 304, 699 CrossRef CAS PubMed.
- Z. Chen, Angew. Chem., Int. Ed., 2004, 43, 4690–4691 CAS.
- G. Brinkmann and A. W. M. Dress, J. Algorithm., 1997, 23, 345–358 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012 Search PubMed.
- Programs to generate and analyse Hückel orbitals and energies in fullerenes have been provided by Y. Wang.
- Y. Wang, M. Alcamí and F. Martín, in Handbook of Nanophysics: Clusters and Fullerenes, ed. K. Sattler, CRC Press, 2010 Search PubMed.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS.
- M. F. Guest, I. J. Bush, H. J. J. van Dam, P. Sherwood, J. M. H. Thomas, J. van Lenthe, R. W. A. Havenith and J. Kendrick, The GAMESS-UK electronic structure package: algorithms, developments and applications.
- P. Lazzeretti and R. Zanasi, SYSMO package, 1980, University of Modena, with additional routines for evaluation and plotting of current density by E. Steiner, P. W. Fowler, R. W. A. Havenith and A. Soncini.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846 CrossRef CAS PubMed.
- T. Guo, M. D. Diener, Y. Chai, M. J. Alford, R. E. Haufler, S. M. McClure, T. Ohno, J. H. Weaver, G. E. Scuseria and R. E. Smalley, Science, 1992, 257, 1661–1664 CAS.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- Y. Wang, S. Díaz-Tendero, M. Alcamí and F. Martín, Nat. Chem. Search PubMed , in press.
- M. García-Borràs, S. Osuna, M. Swart, J. M. Luis and M. Solà, Angew. Chem., Int. Ed., 2013, 52, 9275–9278 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: CASSF(18,12) calculation results for C50D5h; detailed results of spherical parentages for C50D3 and D5h. See DOI: 10.1039/c5cp04970a |
| This journal is © the Owner Societies 2016 |