 Open Access Article
Open Access ArticleSpatiotemporal evolution of heterogeneous structures in agarose gels revealed by particle tracking†
Naoya
Yanagisawa‡
 a,
Takemi
Hara‡
a,
Takemi
Hara‡
 a and
Miho
Yanagisawa
a and
Miho
Yanagisawa
 *abc
*abc
aKomaba Institute for Science, Graduate School of Arts and Sciences, The University of Tokyo, 3-8-1 Komaba, Meguro, Tokyo 153-8902, Japan. E-mail: myanagisawa@g.ecc.u-tokyo.ac.jp
bGraduate School of Science, The University of Tokyo, Hongo 7-3-1, Bunkyo, Tokyo 113-0033, Japan
cCenter for Complex Systems Biology, Universal Biology Institute, The University of Tokyo, Komaba 3-8-1, Meguro, Tokyo 153-8902, Japan
First published on 3rd December 2024
Abstract
Upon decreasing the temperature, agarose solution exhibited gelation and phase separation, forming a cloudy gel consisting of agarose-rich and agarose-poor phases. Both phenomena contribute to the formation of a heterogeneous gel structure, but the primary influence of both processes on this heterogeneity remains unclear. In this study, we defined the specific gelation and phase separation temperatures of an agarose solution and examined the resulting gel structures with and without phase separation. Microscopic observation and colloid diffusion analysis revealed that phase separation leads to inhomogeneities several micrometers in size. Furthermore, we found that the distributions of colloidal diffusion coefficients and particle displacements strongly reflected the heterogeneity primarily induced by phase separation and gelation. Our findings contribute to the physicochemical understanding of the heterogeneous structures of various (bio) polymer gels associated with the phase separation of polymers.
1. Introduction
The phase separation and gelation of polymer solutions are among the most representative phase transition phenomena in the fields of polymer science and soft matter physics. In the case of phase separation, polymer solutions with an upper or lower critical solution temperature (UCST or LCST) transition from one phase to two coexisting phases below (or above) the critical temperature. When gelation (polymerization) of a polymer occurs simultaneously with phase separation, spatial fluctuations in the polymer density led to the formation of gels with large holes, i.e., porous gels. Examples of porous gels comprising synthetic polymers with LCST-type phase separation include poly(N-isopropyl acrylamide) gels1–3 and tetra-polyethylene glycol (PEG) gels.4 These porous gels have been used for various applications such as gas adsorption, chromatography, and separation.5–7 To regulate the pore size and understand the structural transition, the coupled dynamics of the phase separation and gelation of polymers have been studied extensively.Agarose gel, a polysaccharide gel, is subject to phase separation with decreasing temperature.8–11 The structure of agarose gels formed by fast quenching from a high temperature of >80 °C (in a homogeneous liquid phase) to a low temperature of <25 °C has been studied using various methods such as light scattering structural analysis,10–14 electron- or fluorescence microscopy observations,10,15,16 and rheological measurements.12,17–19 These reports revealed that lowering the temperature leads to helical formation between agarose molecules and dehydration of agarose, which induce gelation and phase separation, respectively.12 At low concentrations (≪0.1 wt%), where macroscopic gelation does not occur, aggregated agarose colloids are formed; this is called the gel fluid phase.12,19 At high concentrations (≥0.1 wt%), simultaneous gelation and phase separation of agarose produce a porous gel. At deeper quenching depths, gelation halts the development of density fluctuations associated with phase separation.8,9 On the other hand, when the quenching depth was shallow, the gelation did not abruptly halt the development of density fluctuations, resulting in a gel with larger pores (i.e., a heterogeneous structure). However, the spatiotemporal evolution of the heterogeneous structure of agarose gels, which is strongly influenced by phase separation, is not fully understood.
Understanding the roles of phase separation and gelation is crucial for analyzing heterogeneity. When the temperature is maintained between the phase separation temperature (Tp) and the gelation temperature (Tg > Tp), we can study heterogeneity primarily due to gelation. Inhomogeneities strongly affected by phase separation can be analyzed using rapid cooling below Tp and slow cooling at a controlled rate. In both methods, phase separation and gelation occur simultaneously; however, slow cooling allows phase separation to take precedence. Therefore, by rapidly cooling to Tg (fast quenching) and gradually cooling below Tp (slow quenching), we can identify the main influences of these processes on heterogeneity.
In this study, we investigate the spatiotemporal development of heterogeneous structures in agarose gels prepared using fast quenching to Tg and slow quenching below Tp. Rheological measurements and image analysis of the 0.5 g/100 mL agarose solution revealed that gelation occurred below 40 °C and that micrometer-sized heterogeneous structures formed due to phase separation below 35 °C. Next, we analyzed the diffusion behavior of colloids added to an agarose solution upon decreasing the temperature. This technique, known as micro-rheology, offers higher spatial resolution than macro-rheology and allows us to investigate the local mechanical properties at the microscale.20–23 Thus, this method is suitable for examining spatially heterogeneous gel structures. By mapping the diffusion coefficient below the phase separation temperature, we confirmed the characteristic size of the heterogeneous structure, which coincided with the size determined by image analysis. Furthermore, the probability distribution of the colloid's migration distance above the phase separation temperature successfully captured the heterogeneous structure derived from gelation. The findings of this study contribute to the understanding and control of the physicochemical properties of various (bio) polymer gels with phase separation and aggregation.
2. Experimental
2.1. Materials
Agarose was purchased from Sigma-Aldrich (MO, USA; Agarose, type IV, Lot no. 043K1302), and the nominal molecular weight determined by gel permeation chromatography was 2.9 × 105 g mol−1. Distilled water (Invitrogen, CA, USA; Catalog no. 10977-023) was used as the solvent. Polystyrene colloids with a diameter of 0.5 μm and a density of 1.06 g cm−3 purchased from Thermo Fisher Scientific (MA, USA; G500, Lot no. 252203) were used. Colloids of the same size have been used in a previous study using particle tracking,20 and they are comparable in size to or slightly larger than the mesh size of the agarose gel.9 The surfaces of the colloids are coated with a fluorescent dye, Firefli™ Fluorescent Green, which increases their hydrophilicity compared to standard polystyrene colloids. Similar fluorescent polystyrene colloids, using a different fluorescent dye, have been used to measure colloidal diffusion in agarose gels without significantly affecting the gel's structure or the diffusion measurements.20,24,252.2. Sample preparation
Agarose is dissolved in distilled water at a temperature of 80 °C for more than 1 h. Colloids were added at a volume fraction of 0.003, which is comparable to that reported previously (0.000626 to 0.1527). The average number density of colloids is greater than one per square of 20 μm sides. To prevent evaporation, the agarose solution was sandwiched between two coverslips (Matsunami, Osaka, Japan, S1111) using a frame-seal spacer (Bio-Rad, No. SLF0201, 9 × 9 mm, height 3 mm). The agarose concentration is fixed to be 0.5 g/100 mL, and the gelation temperature Tg is approximately 40 °C.10,282.3. Microscopic observation and diffusion analysis of colloids
The agarose sample was observed under a microscope (Olympus, BX85, Tokyo, Japan) using a 40× objective lens (UPlanFLN, Olympus). Under this microscope, colloids with a diameter of 500 nm appeared as black dots measuring 2 × 2 pixels (approximately 0.6 μm). The diffusion of these colloids in the agarose solution was recorded using a high-speed camera (HAS-D71, DITECT, Tokyo, Japan) at frame rates of 500 frames s−1. The spatial resolution of the colloidal diffusion is approximately 0.3 μm. A Peltier temperature control stage (10021; Linkam Scientific Inst., Tadworth, UK) was used to regulate the temperature of the agarose solution. The temperature is regulated in two ways: (i) slow quenching from 80 to 25 °C with 0.3 °C min−1, or (ii) fast quenching from 80 °C to a certain quenching temperature Tq with 20 °C min−1. The obtained images were analyzed using the Fiji software (NIH, USA) and the Python program to obtain the value of each colloidal displacement.2.4. Viscosity measurement
To estimate the value of Tg, we measure the steady shear viscosity η of agarose solutions at a constant temperature T using a rotational viscometer (ViscoQC300L, Anton Paar Co.) with a cone-and-plate measuring system of 24 mm diameter with a cone angle of 3° (CP52). A CP40 cone (diameter: 48 mm, angle: 0.8°) was used to measure the lower viscosity (1–15 mPa s). The measurable shear rate ranges of CP52 and CP40 are approximately 0.1–500 s−1 and 1–2000 s−1, respectively. Samples were changed each time when viscosity measurements were carried out at steady-state temperatures in the range of 30–60 °C. In addition, the sample temperature was controlled using a heat bath for gentle quenching (i), as in the colloid diffusion experiment. The obtained η is fitted by the following power law: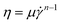 | (1) |
3. Results and discussion
3.1. Estimation of the gelation point via slow quenching
To investigate the heterogeneous structure of agarose gels below the gelation temperature Tg, we first estimated the value of Tg using macroscopic viscosity measurements. A cone–plate rotational viscometer was used to measure the agarose solution viscosity η (see Experimental sections 2.3 and 2.4). Fig. 1(a) shows the shear rate dependence of η at different temperatures T for an agarose concentration of 0.5 g/100 mL. It shows that a decrease in T from 60 to 30 °C increases the value of η at a constant
dependence of η at different temperatures T for an agarose concentration of 0.5 g/100 mL. It shows that a decrease in T from 60 to 30 °C increases the value of η at a constant  and the slope of η against
and the slope of η against  . By fitting this curve to eqn (1), we derive the viscosity coefficient μ and the viscosity index n and plot them against T in Fig. 1(b and c). μ follows an exponential law (or Arrhenius law) at a high T (see the exponential fitting line shown as a dotted line in Fig. 1(b)), but deviates at a low T due to the gelation as reported previously.12 Similarly, n remains almost constant at high T but decreases at low T as shown in Fig. 1(c). The temperature at which the temperature dependence of these μ and n changes (indicated as red arrows in Fig. 1(b and c)) is used here as Tg. The estimated Tg is approximately 40 °C for the 0.5 g/100 mL agarose. This Tg value is close to the previously reported value, approximately 38–40 °C,10,16,29 and lower than that of approximately 45 °C for the 1.0 g/100 mL agarose (see Fig. S1 in ESI†). We also examined the temperature dependence of μ (see Fig. S2, ESI†) using the Vogel–Fulcher equation, commonly applied in glass transition studies, to estimate the Vogel temperature at which μ diverges. However, we could not accurately determine this value due to the narrow μ range of approximately 1 to 10 kPa. The value of n at T ≥ 40 °C is approximately 0.8 (Fig. 1(c)), suggesting that the agarose solution is not a Newtonian solution with n = 1 due to the entanglement of the agarose molecules, etc.30
. By fitting this curve to eqn (1), we derive the viscosity coefficient μ and the viscosity index n and plot them against T in Fig. 1(b and c). μ follows an exponential law (or Arrhenius law) at a high T (see the exponential fitting line shown as a dotted line in Fig. 1(b)), but deviates at a low T due to the gelation as reported previously.12 Similarly, n remains almost constant at high T but decreases at low T as shown in Fig. 1(c). The temperature at which the temperature dependence of these μ and n changes (indicated as red arrows in Fig. 1(b and c)) is used here as Tg. The estimated Tg is approximately 40 °C for the 0.5 g/100 mL agarose. This Tg value is close to the previously reported value, approximately 38–40 °C,10,16,29 and lower than that of approximately 45 °C for the 1.0 g/100 mL agarose (see Fig. S1 in ESI†). We also examined the temperature dependence of μ (see Fig. S2, ESI†) using the Vogel–Fulcher equation, commonly applied in glass transition studies, to estimate the Vogel temperature at which μ diverges. However, we could not accurately determine this value due to the narrow μ range of approximately 1 to 10 kPa. The value of n at T ≥ 40 °C is approximately 0.8 (Fig. 1(c)), suggesting that the agarose solution is not a Newtonian solution with n = 1 due to the entanglement of the agarose molecules, etc.30
 | ||
Fig. 1 Temperature dependence of solution viscosity for 0.5 g/100 mL agarose. (a) Shear rate  dependence of solution viscosity η. The error bars are standard errors (SEs) in the time variation of viscosity at the constant dependence of solution viscosity η. The error bars are standard errors (SEs) in the time variation of viscosity at the constant  . Solid lines indicate the fitting with the power law, eqn (1). The fitting derives (b) the viscosity coefficient μ (b) and index n (c). Error bars indicate conditions with a fitting error R2 > 0.9, and closed points indicate conditions with a maximum R2. The red arrows in (b) and (c) indicate a temperature of 40 °C, where the temperature dependencies of μ and n change during the cooling process. The dotted and broken lines in (b) and (c) show the exponential fitting and the average value for T ≥ 40 °C, respectively. . Solid lines indicate the fitting with the power law, eqn (1). The fitting derives (b) the viscosity coefficient μ (b) and index n (c). Error bars indicate conditions with a fitting error R2 > 0.9, and closed points indicate conditions with a maximum R2. The red arrows in (b) and (c) indicate a temperature of 40 °C, where the temperature dependencies of μ and n change during the cooling process. The dotted and broken lines in (b) and (c) show the exponential fitting and the average value for T ≥ 40 °C, respectively. | ||
3.2. Image analysis of the heterogeneous gel structure
When the temperature of 0.5 g/100 mL agarose was lowered below Tg approximately 40 °C, the solution became more viscoelastic and appeared opaque. We observed the non-uniformity caused by temperature quenching under a microscope. Unlike the slow quenching from 80 to 25 °C with 0.3 °C min−1 mentioned above, here the solution temperature T was rapidly quenched from 80 °C to several quenching temperatures, Tq (22, 25, 28, 31, 34, and 37 °C), below Tg = 40 °C (see Experimental sections 2.3 and 2.4 for details). Typical images are shown in Fig. 2(a). The larger heterogeneous structure of several micrometers was observed at Tq = 34 °C rather than at Tq = 22 °C. If we interpret this heterogeneous structure as originating from the phase separation of agarose, this suggests that at low Tq, gelation proceeds rapidly and maintains the size growth of the heterogeneous structure via phase separation. Because this heterogeneous structure was not observed at Tq > 35 °C, we estimated the phase separation temperature Tp to be 35 °C.Fourier transform of the images under several Tq conditions was performed to obtain the characteristic length scales of the heterogeneous structures. The results are shown in Fig. 2(b), where the intensity (radial profile) obtained by integrating the Fourier transform is plotted against the wavenumber k, where the color indicates Tq. Since an increase at low k (<0.2) was observed for all samples regardless of Tq, this can be attributed to uneven illumination. Here, we focus on the peak shift at approximately k = 1, as indicated by the arrows in Fig. 2(b). We derive the k value corresponding to this peak and plot the characteristic length (= 2π/k) against Tq (Fig. 2(c)). It shows that the characteristic length is >4 μm for Tq > 25 °C and becomes smaller with decreasing Tq. This supports our hypothesis that rapid gelation at low temperatures inhibits the growth of heterogeneous structures via phase separation.
3.3. Colloidal diffusion analysis
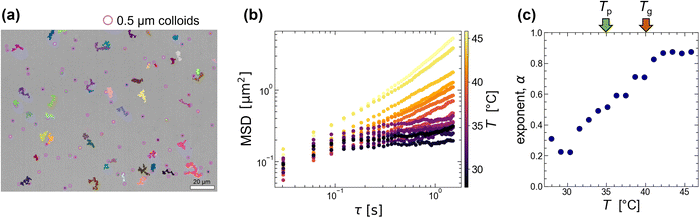
From the image analysis (Fig. 2), we found that the 0.5 g/100 mL agarose solution forms a heterogeneous structure with a few μm scale below Tp = 35 °C (<Tg = 40 °C). To confirm this size scale from a difference in the local viscosity, we add colloids with a diameter of 0.5 μm (smaller than the characteristic length shown in Fig. 2(c)) to the agarose solution and analyzed the thermal diffusion at different T. Fig. 3(a) is an example of microscopic image of agarose gels with colloids at Tg = 40 °C, where the pink circles with a diameter of 2.5 μm and the other lines indicate the positions of colloids and their trajectories for 40 s, respectively. This shows that only a few colloids exhibit large migration distances; alternatively, the viscoelasticity is spatially inhomogeneous.Before considering the spatial heterogeneity, we analyzed the averaged mean square displacement (MSD) of several colloids at different T during the slow quenching from 80 to 25 °C with 0.3 °C min−1. In Fig. 3(b), the horizontal axis represents the delay time τ, and the vertical axis represents the MSD. The color represents the temperature T. Both logarithmic plots show that the MSD curves at a high T > Tg (= 40 °C) are almost linear against τ, while the MSD curves approach a certain value for a long time scale of τ > 0.5 s at a low T < Tg. To get the overall picture, we fit the curves with a power law MSD ∼ τα for the whole-time scale and plot the exponent α versus T in Fig. 3(c). As T is lowered below Tg = 40 °C (shown as a red arrow), α decreases drastically from approximately 0.9 to 0.2, but no obvious change was observed around Tp (shown as a green arrow). A similar trend was observed for 1.0 g/100 mL agarose, where α decreased monotonically from over 1 to 0.2 below approximately 50 °C near the Tg (Fig. S3, ESI†). The reason why α is greater than 1 at high temperatures might be due to that thermophoretic particles drift along the unintended temperature gradient. These results indicate that the spatially averaged diffusion of colloids captures the viscoelastic changes upon gelation but cannot capture the viscoelastic changes upon phase separation below Tp.
To visualize the spatial heterogeneity below Tg, we analyzed each colloidal diffusion and mapped the diffusion coefficient D (Fig. 4). D was obtained by fitting the MSD of a single colloid for τ ∼ 1 s (i.e., D = MSD/4τ) and averaging over three MSDs of the same colloid. To discuss spatial inhomogeneity rather than the absolute value of the apparent diffusion coefficient, α is fixed at 1 for the fitting. Although the value of D is spatially constant in the case of the lattice size of 30 μm (Fig. 4(a)), a spatially inhomogeneous distribution of D was observed for the case of the lattice size below 10 μm (Fig. 4(b)). This is consistent with the heterogeneous size of 4–7 μm below Tg suggested by FFT image analysis (Fig. 2(c)). When the lattice size is reduced below this value, the number of white lattices (i.e., the colloid-free region) increases. Adding more colloids can reduce the number of white lattices; however, artifacts caused by the colloids on the gel structure become more noticeable.
Next, we analyzed the histograms of the time-averaged D obtained from the MSD of each colloid (Fig. 5). The temperature was controlled in two ways: (a) slow quenching from 80 to 25 °C (<Tp (= 35 °C)) with 0.3 °C min−1 or (b) fast quenching from 80 to 40 °C (∼Tg) and then maintained to be 40 °C. For T ≥ 40 °C (= Tg), the histogram has a single peak. The width of the distribution at 40 °C was wider than that at 58 °C, suggesting increased heterogeneity due to gelation. The peak position shifts to lower values with time at Tg (Fig. 5(b)), and the shift increases as T decreases (Fig. 5(a)). This is consistent with the increase in viscosity at lower T values (Fig. 1). As T decreases further below Tp (= 35 °C), the distribution changes from a single peak to a double peak shape (Fig. 5(a)). Unlike the other peaks, the large D peak becomes slightly higher at lower T and approaches ∼1 μm2 s−1. Because this D value corresponds to the D of colloids in water, the two observed peaks below Tg may reflect the large and smaller D values of the solvent-rich and agarose-rich phases after phase separation. To highlight the impact of gelation over phase separation, we analyzed the MSD after fast quenching below Tp (Fig. S4, ESI†). The α value at 34 °C decreased from 0.4 to less than 0.1 after 10 min of quenching, indicating that gelation was enhanced compared to that of slow quenching (Fig. S4(c), ESI†). Accompanied by this, single-peak distributions of D were observed (Fig. S5, ESI†). A comparison of Fig. 5 and Fig. S5 (ESI†) reveals that accelerated gelation at low temperatures obscures the larger D peak, which reflects colloidal diffusion in the agarose-poor phase. Thus, the double-peak distribution of D observed during the slow quenching process may strongly reflect the structural heterogeneity caused by phase separation rather than gelation. Using smaller colloids or reducing the τ of the MSD may result in a double-peak distribution of D, reflecting slight inhomogeneity due to gelation even after the fast quenching.
Finally, we analyze the probability that the colloids have a displacement 〈Δx〉 at a lag time of τ = 0.5 s (shorter than that of 1 s in Fig. 5). The van Hove correlation function (VHF) distribution is shown in Fig. 6. The temperature control conditions in Fig. 6 are identical to those in Fig. 5. The ensemble-averaged VHF at high T (≫Tg = 40 °C) and at low T (<Tp = 35 °C) can be fitted with a single Gaussian distribution. The derived variance σ2 is plotted as gray dots in Fig. 6(b), showing that the variance becomes smaller for lower T. Interestingly, the VHF at intermediate T (i.e., Tp ≤ T ≤ Tg) has a shoulder at around 〈Δx〉 approximately 0.8 μm for both temperature conditions. To qualitatively analyze these distributions, we fit them with a double Gaussian and plot the σ2 against T or time in Fig. 6(b and d), where the large and small σ2 are plotted as orange and blue dots, respectively. This double Gaussian distribution of VHF after the quenching to Tg was also observed for 〈Δx〉 at τ = 1.0 s (Fig. S6, ESI†). The temperature at which the single Gaussian splits into double Gaussian was near Tg = 40 °C (Fig. 6(a)) and the larger σ2 of the double Gaussian (shown in orange) vanished at low temperatures around Tp = 35 °C.
Similar phenomena were observed for 1.0 g/100 mL agarose (see Fig. S7 and S8, ESI†). The double Gaussian of the VHF was observed at intermediate T (i.e., Tp ≤ T ≤ Tg) with τ = 0.5 and 1.0 s. In addition, the double Gaussian distribution at Tg was maintained for more than 1 day (see Fig. S7, ESI†). From these results, we conclude that the double Gaussian of the VHF observed at intermediate T (i.e., Tp ≤ T ≤ Tg) in Fig. 6(a) strongly reflects heterogeneity resulting from gelation rather than phase separation,31 unlike the double Gaussian of D strongly reflecting phase separation (Fig. 5(a)). This is consistent with the fact that gelation due to network formation always exhibits heterogeneity in the gel structure at the microscale (polymer-rich and polymer-poor phases). Below Tp, the density fluctuation progressed with time and the spatial size of the μm-sized inhomogeneity increased (Fig. 2(c)). In contrast, the large σ2 of 〈x〉 became smaller and then vanished at low temperatures (Fig. 6(b)). The progression of gelation or phase separation at low temperatures may have reduced the microscale heterogeneity around the individual colloids. Another possible reason is that the colloids were unable to escape the fine-meshed polymer gel below Tp. It has been reported that when a 0.4 wt% agarose solution is quickly quenched from 80 °C to room temperature, the VHF of 0.5 μm particles with τ < 0.1 s appears to be exponential due to the heterogeneous structure upon gelation.20 By analyzing the VHF over shorter time intervals, it may be possible to characterize the heterogeneous structure during gelation more clearly, possibly as an exponential distribution.
4. Conclusion
Upon decreasing the temperature, agarose solution exhibited gelation and phase separation, forming an opaque gel composed of agarose-rich and agarose-poor phases. Although both phenomena have been reported to contribute to the formation of a heterogeneous gel structure, the primary influence of each process on this heterogeneity has remained unclear. By estimating the gelation temperature Tg using a rheometer and observing the gel with a microscope, we showed that the gel undergoes phase separation below the phase separation temperature Tp, forming heterogeneous structures with sizes of several micrometers. To investigate the heterogeneous structure, we added colloids with sizes comparable to the gel mesh size into the agarose solution and measured colloidal diffusion upon decreasing the temperature. The diffusion coefficient D obtained from the time-averaged MSD showed a double-peak distribution only under conditions where phase separation rather than gelation prevailed. On the other hand, the displacement distribution of colloids showed a double Gaussian distribution when gelation rather than phase separation prevailed. These results strongly suggest that both analyses carried out on the same colloidal diffusion can effectively capture the primary influence of both phase separation and gelation processes on the heterogeneous gel structure. In addition, by adjusting the colloid size and mean squared displacement (MSD) lag time, we can tailor their observation system to the specific size of the structure. Moreover, this method is much easier to execute than direct observation techniques using fluorescent labeling or electron microscopy. We believe that these analytical methods can be applied to different materials and that our results contribute to the physicochemical understanding of the heterogeneous structures of different (bio)polymer gels, which may be related to phase separation.Author contributions
M. Y. designed the research, T. H. and N. Y. performed experiments, and all authors analyzed and interpreted data. M. Y. and N. Y. wrote the manuscript. All authors read and approved the final manuscript.Data availability
The data that support the findings of this study are available from the corresponding author, M. Y., upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially funded by the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant numbers 22H01188, 24H02287 (M. Y.)) and the Japan Science and Technology Agency (JST) (grant numbers FOREST, JPMJFR213Y (M. Y.); CREST, JPMJCR22E1 (M. Y.)).References
- I. Bischofberger and V. Trappe, Sci. Rep., 2015, 5, 15520 CrossRef.
- C. Wang and T. Hashimoto, Macromolecules, 2023, 56, 6354–6374 CrossRef CAS.
- F. Tanaka, Y. Katsumoto, S. Nakano and R. Kita, React. Funct. Polym., 2013, 73, 894–897 CrossRef CAS.
- S. Ishikawa, Y. Iwanaga, T. Uneyama, X. Li, H. Hojo, I. Fujinaga, T. Katashima, T. Saito, Y. Okada, U. I. Chung, N. Sakumichi and T. Sakai, Nat. Mater., 2023, 22, 1564–1570 CrossRef CAS.
- J. L. Wu, F. Xu, S. M. Li, P. W. Ma, X. C. Zhang, Q. H. Liu, R. W. Fu and D. C. Wu, Adv. Mater., 2019, 31, 1802922 CrossRef.
- K. Nakanishi and N. Tanaka, Acc. Chem. Res., 2007, 40, 863–873 CrossRef CAS.
- X. Y. Yang, L. H. Chen, Y. Li, J. C. Rooke, C. Sanchez and B. L. Su, Chem. Soc. Rev., 2017, 46, 481–558 RSC.
- P. Aymard, D. R. Martin, K. Plucknett, T. J. Foster, A. H. Clark and I. T. Norton, Biopolymers, 2001, 59, 131–144 CrossRef CAS.
- J. Narayanan, J.-Y. Xiong and X.-Y. Liu, J. Phys.:Conf. Ser., 2006, 28, 83 CrossRef CAS.
- T. Morita, T. Narita, S. Mukai, M. Yanagisawa and M. Tokita, AIP Adv., 2013, 3, 042128 CrossRef.
- M. Matsuo, T. Tanaka and L. Ma, Polymer, 2002, 43, 5299–5309 CrossRef CAS.
- M. Ghebremedhin, S. Seiffert and T. A. Vilgis, Curr. Res. Food Sci., 2021, 4, 436–448 CrossRef CAS PubMed.
- T. Fujii, T. Yano, H. Kumagai and O. Miyawaki, Food Sci. Technol. Res., 2000, 6, 94–98 CrossRef CAS.
- N. Fatin-Rouge, K. J. Wilkinson and J. Buffle, J. Phys. Chem. B, 2006, 110, 20133–20142 CrossRef CAS.
- D. Lynam, C. Peterson, R. Maloney, D. Shahriari, A. Garrison, S. Saleh, S. Mehrotra, C. Chan and J. Sakamoto, Carbohydr. Polym., 2014, 103, 377–384 CrossRef CAS PubMed.
- N. Russ, B. I. Zielbauer, K. Koynov and T. A. Vilgis, Biomacromolecules, 2013, 14, 4116–4124 CrossRef CAS PubMed.
- V. Normand, D. L. Lootens, E. Amici, K. P. Plucknett and P. Aymard, Biomacromolecules, 2000, 1, 730–738 CrossRef CAS.
- L. Martikainen, K. Bertula, M. Turunen and O. Ikkala, Macromolecules, 2020, 53, 9983–9992 CrossRef CAS.
- N. Ichinose and H. Ura, Sci. Rep., 2020, 10, 2620 CrossRef CAS PubMed.
- M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud'homme, M. Beck and D. A. Weitz, Phys. Rev. E, 2001, 64, 061506 CrossRef CAS.
- T. Moschakis, A. Lazaridou and C. G. Biliaderis, J. Colloid Interface Sci., 2012, 375, 50–59 CrossRef CAS PubMed.
- J. Yonemoto, Y. Maki, I. Koh, K. Furusawa and M. Annaka, Biomacromolecules, 2021, 22, 3819–3826 CrossRef CAS PubMed.
- P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449–1455 RSC.
- N. Fatin-Rouge, K. Starchev and J. Buffle, Biophys. J., 2004, 86, 2710–2719 CrossRef CAS PubMed.
- A. Pluen, P. A. Netti, R. K. Jain and D. A. Berk, Biophys. J., 1999, 77, 542–552 CrossRef CAS.
- T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001 CrossRef PubMed.
- Y. Maki and M. Annaka, Food Hydrocolloids, 2020, 101, 105525 CrossRef CAS.
- M. Tokita, M. Uwataki, Y. Yamashita, T. Hara and M. Yanagisawa, Soft Matter, 2023, 19, 7379–7387 RSC.
- K. Lahrech, A. Safouane and J. Peyrellasse, Phys. A, 2005, 358, 205–211 CrossRef CAS.
- L. Zhang, L. Che, W. Zhou and X. D. Chen, Int. J. Food Eng., 2012, 8, 10 Search PubMed.
- K. J.-A. Martens, J. Van Duynhoven and J. Hohlbein, Langmuir, 2020, 36(20), 5502–5509 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01122h |
| ‡ H. T. and N. Y. contributed equally to this paper. |
| This journal is © The Royal Society of Chemistry 2025 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–64
000–64