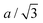Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strain and collapse during lithiation of layered transition metal oxides: a unified picture†
Thibaut
Jousseaume
 a,
Jean-François
Colin
b,
Marion
Chandesris
a,
Jean-François
Colin
b,
Marion
Chandesris
 b,
Sandrine
Lyonnard
a and
Samuel
Tardif
b,
Sandrine
Lyonnard
a and
Samuel
Tardif
 *a
*a
aUniv. Grenoble Alpes, CEA IRIG, 17 Av. des Martyrs, 38000 Grenoble, France. E-mail: samuel.tardif@cea.fr
bUniv. Grenoble Alpes, CEA LITEN, 17 Av. des Martyrs, 38000 Grenoble, France
First published on 28th February 2024
Abstract
Developing long-life, high-energy density materials such as the Ni-rich LiNixMnyCozO2 (NMCxyz) is needed to manufacture advanced Li-ion batteries. However, these compounds suffer from a capacity fade upon cycling, attributed to the H2–H3 phase transition and to the associated volume changes. Here, by applying operando XRD we show that the usually blamed H2-H3 transition is actually not taking place in Ni-rich layered transition metal oxides, except for the 100% nickel composition LNO. We find a universal mechanism instead, that only depends on the lithium content, irrespective of nickel content, applied charge rate or phase diagram of the bulk material. We discover that strain appears when the structure collapses, below 40% lithium in the layers. Below this critical lithium content, exponentially growing strain and large lattice distortions occur, which may favor irreversible cracks. Since lithium loss upon cycling induces a shift towards lower lithium content in positive active material, the consequences of repeated and irreversible stress are expected to be exacerbated on the long-term. Therefore, unifying structure, crystalline strain and cracks, our results reveal that the lithium content window is the main driver of degradation in layered transition metal oxides, rather than the potential window.
Broader contextThe automotive industry aims at improving the performance of electric batteries in terms of fast charging, stored energy capacity and lifetime to meet the needs of their customers. Layered transition metal (TM) oxides such as LiNixMnyCozO2 (NMCxyz) with high nickel content (Ni-rich) have a better energy density than those with medium nickel content. However, they exhibit accelerated capacity loss during cycling, which limits their use. In this paper we identify the cause of the larger degradation of Ni-rich NMCs compared to their Ni-poor counterparts. The identification of this mechanism was made possible by unifying the lithium intercalation mechanism of various Ni-rich NMCs under different kinetic conditions. Based on this mechanism, we show that these degradation are indeed common to all layered TM oxides, and that they escalate in the case of Ni-rich NMCs due to the chemical destabilisation of the material when it is lithium depleted during the charge. When the material has a low lithium concentration indeed, it suffers from heterogeneous distortion of the crystalline structure, leading to the appearance of stresses and cracks in the crystals. Hence, we show that lithium loss triggers a variety of degradations in layered TM oxides. |
1 Introduction
Current Li-ion battery materials provide moderate energy densities. This remains an issue for electrical mobility applications, where the tremendous characteristics of oil must be surpassed.1 Increasing the nickel content x in the widely known layered transition metal (TM) oxides LiNixMnyCozO2 (NMCxyz) can improve the battery capacity, for instance from LiNi0.6Mn0.2Co0.2O2 (NMC622), to LiNi0.8Mn0.1Co0.1O2 (NMC811), and even to 100% of nickel with LiNiO2 (LNO). Indeed, more lithium can be extracted in the electrochemical stability window of carbonate electrolytes when the nickel content is higher. Nevertheless, high nickel content NMCs present a reduced lifetime, which has been ascribed to particle cracks, surface reconstruction, oxygen leaks or heterogeneous behaviour.2–6 Knowing how to limit these deleterious effects is thus key to develop long lifetime batteries.The very (de)lithiation mechanism in the NMC materials is still debated in the literature. Contradictory conclusions hinder the elucidation of the fading mechanism, which can be material-dependent. Often, a discontinuous lattice parameter evolution was reported for Ni-rich NMC, with three hexagonal phases H1, H2 and H3 in charge, characterised by the lattice parameter c as cH2 > cH1 > cH3.7–12 However, other studies found a continuous lattice parameter evolution, that describes the material with a single hexagonal structure all along the process, after the first delithiation.13–16 Moreover, the effect of the nickel content on the lithiation mechanism is not entirely grasped as well. For instance, Ryu et al.3 reported that NMCs with 90% and 95% nickel content undergo a phase transformation, whereas 60% and 80% nickel contents do not, in contrast with the single phase mechanism proposed by Li et al.17 in NMC from 30% to 90% nickel content.
Such differences could be due to errors in the determination of the structural evolution that can stem from several factors: the experimental setup that is used, the cell dedicated to the measurement, or the technique itself. For example, coin cells with a polyimide window, such as the one used by Ryu et al.,3 are reported to have a reaction rate under the window that is slower than elsewhere in the cell.18 Several other experimental conditions could influence the miscellaneous results mentioned above, such as defects in the material, cell pressure, low angular resolution, separator, cycling potential window, electrode characteristics, or choice of electrolyte.9,19–21 In addition, the applied charge rate (C-rate) is often study-dependent, but its effect on the material is usually ignored, even though it is bound to the chemical potential.22 For instance, it has been shown that new thermodynamically metastable phases appear when the charge rate is increased because their nucleation energy is reached.23 Recently, Wu et al.24 reported the same structural evolution of NMC622 at different C-rates, but with a non-standard electrolyte, and with lower resolution of transfer momentum than standard X-ray diffraction. Since the NMC phase diagram is reported to be influenced by the C-rate,25 a detailed study of the lithiation mechanism accounting for the charge rate is needed, in representative conditions and with high angular resolution to distinguish phase transformation from heterogeneities that are known to take place in NMC electrodes, especially in large cells.26–28
Here, the crystalline structure of several Ni-rich NMCs is investigated using both laboratory and high resolution synchrotron operando X-ray diffraction under varied C-rate conditions to evidence the effects of nickel content and applied current on the lithiation. We propose a unified structural model of Ni-rich layered oxides based on the correlated observation and quantification of lattice parameters and strain evolutions during lithiation. This universal model introduces a critical lithium content controlling the evolution of crystalline strain in the materials, and establishes the general conditions for materials irreversible damages on long-term cycling. The key role of lithium loss in battery aging is underlined, suggesting an identical degradation process for layered TM oxides.
2 Materials and method
2.1 Materials
We investigated NMC622, NMC811 and LNO in full cell in single layer format pouch cells. The NMC622 and NMC811 positive electrodes were manufactured at LITEN (Univ. Grenoble Alpes, CEA). The slurry was made of 96% respective active material (Targay), 2.5% polymer binder (PVDF5130, Solvay), and 1.5% additive conductor (1% of Super C65, Imerys and 0.5% of VGCF, Showa Denko), in mass ratio. Those electrodes were stacked with negative electrodes, manufactured at LITEN with a slurry composed of 95% of graphite (Imerys), 2% of thickener (CMC, Ashland), and 3% of binder (SBR, BASF) in mass ratio, coated on a 10 μm-thick copper foil. The LNO electrodes were provided by BASF and composed of 94% of active material, 3% of polymer binder (PVDF5130, Solvay), and 3% of additive conductor (C65 Carbon black, TIMCAL) in mass ratio. The LNO electrode was stacked with the following negative electrode provided by BASF: a 10 μm copper foil coated by 94% of graphite (Imerys), 2% of thickener (CMC, Dow), and 4% additives conductor (2% C45 Carbon black, Imerys and 2% SBR, Zeon). The loadings were 12 and 10.4 mg cm−2 respectively for NMC622 and NMC811 electrodes balanced with 7 mg cm−2 graphite anodes, and about 4.4 mg cm−2 for LNO electrodes on a 20 μm-thick aluminium foil balanced with 3.5 mg cm−2 graphite anodes. The electrodes were assembled with a 25 μm-thick separator (Celgard), and sealed in pouch cells in water free (<1 ppm) argon atmosphere. The surface of the positive and negative electrodes are respectively 10.24 cm2 and 12.25 cm2. The electrolyte was 1 M LiPF6 in ethylene carbonate (EC), propylene carbonate (PC) and dimethyl carbonate (DMC) in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 volume ratio.
3 volume ratio.
2.2 Electrochemical cycling
Each pouch cell was subjected to conditioning cycles at 45 °C before being probed by the synchrotron X-ray beam. The conditioning cycles followed: 5 min at C/20 (C/n is the current needed to charge the cell in n hours), a 12 hours rest period, 4 hours of charge at C/20, ∼8 hours at C/10, two discharges and one charge at C/10, and finally a storage at state of charge (SOC) 10% before being measured. During the operando X-ray diffraction measurement (XRD), a VSP potentiostat (Biologic) monitored the cell cycling under room temperature (20 ± 2 °C) in galvanostatic conditions. The same cycling protocol was used for the pouch cells measured between C/5 and 2C: charge at C/n until 4.2 V with a voltage hold until the current reaches C/200 or after 1 h 30 min of hold. The discharges were performed at C/n from 4.2 V to 2.5 V with a voltage hold at 2.5 V with the same charge ending conditions.2.3 Operando laboratory X-ray diffraction
Operando laboratory X-ray diffraction (L-XRD) was performed in a Bruker D8 advance diffractometer with a Cu anticathode to follow the slow charge, i.e. without kinetic limitations. The active materials were the same as for the pouch cells. They were milled with carbon black in 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mass ratios in a water-free (<0.5 ppm) and oxygen-free (<2 ppm) atmosphere. The mixture was then measured during its first charge in the Leriche cell29 mounted in half cell configuration with LP100 electrolyte (1 M LiPF6 in EC
30 mass ratios in a water-free (<0.5 ppm) and oxygen-free (<2 ppm) atmosphere. The mixture was then measured during its first charge in the Leriche cell29 mounted in half cell configuration with LP100 electrolyte (1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC
PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC in 1
DMC in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratios). The diffraction patterns were recorded in reflection geometry (Bragg–Brentano), using a beryllium window as a current collector. The XRD patterns were measured operando in the [15°,79°] range as the cell was charged at C/100, each pattern required about 1 h of measurement. The same setup was used to collect diffraction patterns of pristine NMC622 and NMC811. LNO pristine diffraction pattern was measured with the setup used for higher charge rates (see following). The pristine patterns were analysed with the FullProf package to perform the full Rietveld refinement.30
3 ratios). The diffraction patterns were recorded in reflection geometry (Bragg–Brentano), using a beryllium window as a current collector. The XRD patterns were measured operando in the [15°,79°] range as the cell was charged at C/100, each pattern required about 1 h of measurement. The same setup was used to collect diffraction patterns of pristine NMC622 and NMC811. LNO pristine diffraction pattern was measured with the setup used for higher charge rates (see following). The pristine patterns were analysed with the FullProf package to perform the full Rietveld refinement.30
2.4 Operando synchrotron X-ray diffraction
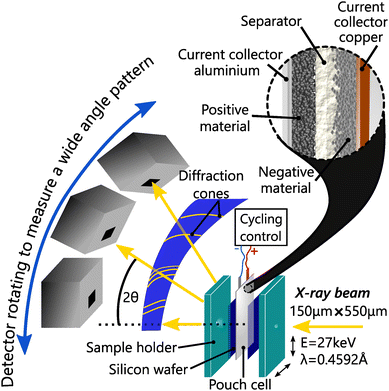
To study the impact of C-rate, better time resolution was obtained using operando synchrotron X-ray diffraction (S-XRD) on BM32 beamline at the European synchrotron radiation facility. The X-ray beam energy was set to 27 keV, and had a size of about 550 μm × 150 μm and a flux of about 5 × 1010 ph s−1. The pouch cells were measured with the setup shown in Fig. 1 in transmission geometry (Debye–Scherrer).To ensure reproducible conditions, two silicon windows on both sides of the cell applied the pressure homogeneously, in particular at the measurement points. The pouch cells and the silicon windows were held together using a bespoke sample holder, which was tightened with a torque wrench to a constant nominal value. The diffraction patterns were calibrated and integrated from images recorded by a moveable 2D CdTe detector with the use of the pyFAI-multigeometry module.31 This setup enabled a good angular resolution (7.8 × 10−3) over the 2θ range [2°, 30°], an adapted temporal resolution of 1 min 30 s for fast charge, and high statistics. Le Bail refinement was applied to every full patterns measured in operando conditions, including L-XRD measurements, to allow high precision in the structure solving using the software Jana2006.32 The same procedure was applied to partial patterns to allow fast and accurate refinement. Whether analysing the L-XRD or S-XRD data, the anisotropic strain along [001] is fitted when it does not vanish.
3 Results and discussion
3.1 Pristine materials characterisation
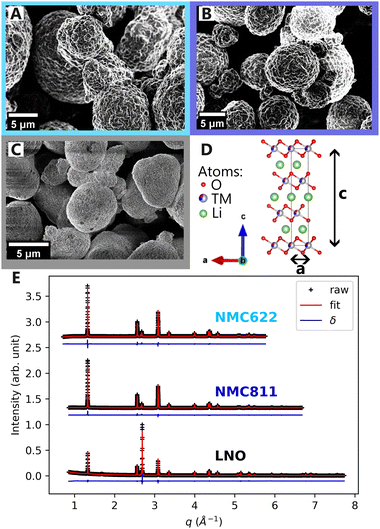
Scanning electron microscopy (SEM) images of NMC622, NMC811 and LNO pristine powders in Fig. 2A–C, reveal comparable particle morphologies. Despite distinct nickel contents, they all present primary particle size of 100 nm–1 μm, and secondary particle size of around ten microns (ESI† Section S1). They also share an identical atomic arrangement, as evidenced by Rietveld refinements of the pristine materials indexed on the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m hexagonal space group (Fig. 2D and E). The refined parameters in Table 1 indicate that the higher nickel content is, the lower the c and the higher the a parameters are. Therefore, despite minor differences in lattice parameters, the three materials are very alike at the pristine state.
m hexagonal space group (Fig. 2D and E). The refined parameters in Table 1 indicate that the higher nickel content is, the lower the c and the higher the a parameters are. Therefore, despite minor differences in lattice parameters, the three materials are very alike at the pristine state.
| NMC622 | NMC811 | LNO | |
|---|---|---|---|
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
| a | 2.8703 | 2.8727 | 2.8747 |
| c | 14.2255 | 14.2127 | 14.1775 |
| d TM–O | 1.9732 | 1.9708 | 1.9719 |
3.2 Structural characterisation close to thermodynamic equilibrium
According to the current knowledge, the structure of NMCxyz depends on the nickel content x, the voltage V and the C-rate Cr, and so does the strain. Then, if (f,g) are functions giving respectively the structure X and the strain ε of NMC xyz, then X = f(x,V,Cr) and ε = g(x,V,Cr). We will progressively show in this article that structure and strain can be simplified as functions of one variable only, the lithium content, featuring the unified structural model. The delithiation of NMC622, NMC811 and LNO was first investigated at very slow charge rate to picture the mechanism close to thermodynamic equilibrium. To this end, operando X-ray diffraction in a laboratory diffractometer (L-XRD) was performed using the Leriche cell.29Operando XRD is particularly suited to characterise time-resolved phase transitions in crystalline materials as it betrays the presence of a phase at a given moment. A change in the structure is reflected by a change in the number, positions or shape of the peaks, making it possible to monitor the evolution of the structure. Here, the 003 and 101 diffraction peaks of NMC622 and NMC811 (Fig. S2A and B respectively, ESI†) are shifting continuously, whereas those of LNO are splitting or shifting discontinuously, indicating a delithiation mechanism of NMC622 and NMC811 different from LNO. Le Bail refinements confirm that LNO is transforming into four different phases through three phase transformations (Fig. 3C and D) as reported in other studies,33–35 whereas NMC622 and NMC811 are following a solid-solution mechanism (Fig. 3A and B).Interestingly, we observe that all peaks broaden at the beginning of the charge, while at the end of charge the broadening is specific to the 〈00l〉 peaks (Fig. S3D, ESI)†. This effect deserves a detailed analysis, as peak broadening generally carries key additional information on crystalline materials organisation. Indeed as we show in ESI† Section S3, we were able to model the recorded broadenings using the hypothesis of a 1st order phase transition. However as we will extensively discuss in the following sections, it can also be interpreted with a more convincing scenario using a different structural framework, that is a single-phase solid-solution mechanism featuring anisotropic strain.
3.3 Charge rate impact
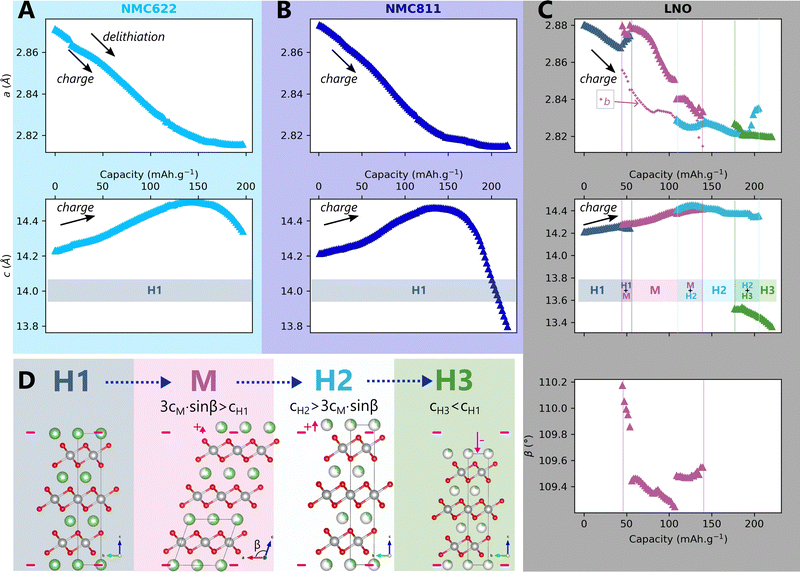
The impact of charge rate on the delithiation mechanisms was investigated by synchrotron XRD (S-XRD) using pouch cells cycled from C/5 to 2C between 2.5 V and 4.2 V in full cell configuration. A special attention was granted to the setup to be as non-intrusive as possible (Fig. 1). We also reduced the dose absorbed by raster scanning the cells during the cycling and by using a moderate photon flux to limit beam damage in the electrodes. It is necessary to consider it when analysing the impact of C-rate on the phase diagram since beam damage is reported to trigger artificial phase transitions in batteries.36 In the following, the structure evolution of the material is measured as function of the lithium content cLi. Note that cLi is only obtained from electrochemical data, and does not assume any theoretical value of capacity (see ESI† Section S4).The startling match of lattice parameters evolution as a function of cLi (Fig. 4) shows that the structural behaviour of the three nickel stoichiometries is not influenced by the applied C-rate. The data recorded before the constant current steps (Fig. S8, ESI†), and the full pattern (‘FP’) refinement procedure confirm it. The biphasic boundaries of LNO phase transformations are not significantly affected neither. Indeed, the expected enlarging of biphasic zones due to the increase of heterogeneous lithiation states caused by the diffusion hindrance is only measured for the H1 → M transition (Fig. 4C), in the limits of the analysis performed here, and cannot be extended to every transitions. Note that the technique employed here averages the material structure over the electrode depth. The use of S-XRD on a single crystal with a micro beam is needed to elucidate whether C-rate affects the two phases coexistence at the crystal scale in LNO, which is beyond the scope of this work. The structure evolution at C/100 is nearly identical (Fig. S5, ESI†), but with a shift in cLi due to a biased estimation of the lithium content in the in situ cell as mentioned in ESI† Section S5. As a result, the structural evolution of the three materials under charge is not changed across at least two orders of magnitude of C-rates. At this point we can write that the structure X is given by X = f(x,V).
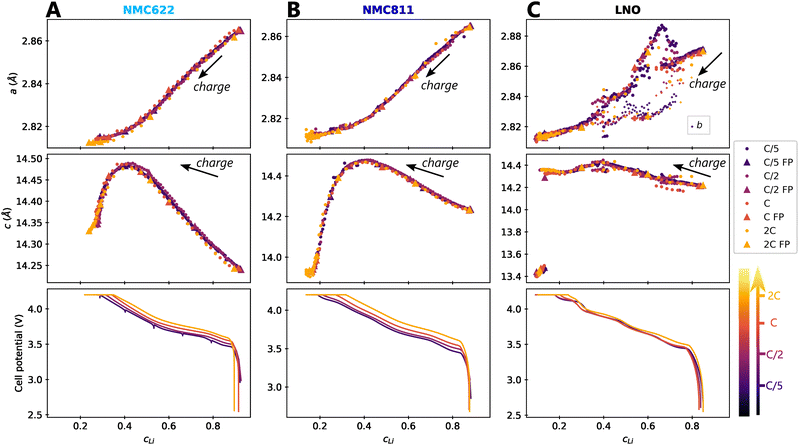 | ||
Fig. 4 Impact of C-rate on structural evolutions during cycling. Structural evolution and potential curves of (A) NMC622, (B) NMC811 and (C) LNO as a function of lithium content cLi for increasing C-rates from darker to lighter colors. 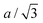 and b lattice parameter of M phase are plotted for LNO, but its four phases are not distinguished. The potential spikes of the C/5 curve of NMC622 are rest periods and have no incidence on the present results. The label “FP” stands for parameters refined from the Full Pattern, accounting for every diffraction peaks. A part of refined parameters during the H2–H3 transition were removed due to a bias in the fit making the results less reliable. The full dataset is provided in Fig. S6 (ESI†). and b lattice parameter of M phase are plotted for LNO, but its four phases are not distinguished. The potential spikes of the C/5 curve of NMC622 are rest periods and have no incidence on the present results. The label “FP” stands for parameters refined from the Full Pattern, accounting for every diffraction peaks. A part of refined parameters during the H2–H3 transition were removed due to a bias in the fit making the results less reliable. The full dataset is provided in Fig. S6 (ESI†). | ||
3.4 Nickel content effect
We find that the structural behaviour of NMC622, NMC811 and LNO during charge and discharge can be described using a common framework of typical atomic distances rather than the standard crystallographic classification based on specific crystalline lattices and symmetries. Indeed, we only need the distance between neighbouring TM atoms dTM and the inter-layer (IL) distance dIL to build a single structural model accounting for the evolutions of the various materials (Fig. 5A and Fig. S13A, ESI†). This finding is strongly supported by characteristic features common to the NMCs calculated with the derivatives of dIL and dTMvs. cLi. Note that the derivatives of LNO's parameters are discontinuous because 1st order phase transitions are inherently discontinuous. Three key lithium contents can be highlighted (Fig. 5B). (1) A same cLi value of 0.4 where the two NMCs and LNO reach their maximum of dIL. The existence of dIL maximum is related to the competition between the O–O repulsion and the structure collapse. According to the literature, the structure collapse origin could be related to more covalent Ni–O bonds, as evidenced from the decreasing Ni–O distance,16,34 which in turn weakens the repulsion of neighbouring O layers.35 (2) No matter the materials, the plateau value of dTM is at cLi ≃ 0.32; and (3) the maximum value of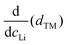 is found at a same lithium content, cLi ≃ 0.62 (Fig. S13B, ESI†). The existence of the characteristic lithium contents is strengthened by both their existence in discharge (Fig. S13D, ESI†), and their existence when these materials are charged at C/100 (ESI† Section S10). Therefore, we suspect these features to be common to all NMCxyz with x ≥ 0.33, as supported by simulations of Min et al.37 Additionally, the position of the dIL maximum is also in agreement with the mobility and hopping rates of lithium in NMC811 since both are decreasing from cLi ≃ 0.413 from the moment the galleries gap height is reduced, hindering lithium diffusion.
is found at a same lithium content, cLi ≃ 0.62 (Fig. S13B, ESI†). The existence of the characteristic lithium contents is strengthened by both their existence in discharge (Fig. S13D, ESI†), and their existence when these materials are charged at C/100 (ESI† Section S10). Therefore, we suspect these features to be common to all NMCxyz with x ≥ 0.33, as supported by simulations of Min et al.37 Additionally, the position of the dIL maximum is also in agreement with the mobility and hopping rates of lithium in NMC811 since both are decreasing from cLi ≃ 0.413 from the moment the galleries gap height is reduced, hindering lithium diffusion.
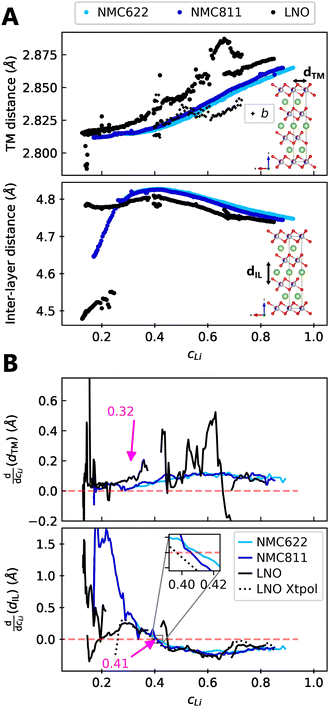 | ||
| Fig. 5 Crystallographic distances evolutions in function of lithium concentration. (A) TM and inter-layer (IL) distances (respectively a and c/3 for hexagonal symmetry) from refined lattice parameters of NMC622, NMC811 and LNO charged at C/5 and measured by S-XRD. (B) Derivatives of centered rolling mean of dTM and dIL by lithium content cLi for NMC622, NMC811 and LNO. The black dotted line is the derivative of the LNO interpolation curve of c parameter defined in Fig. S10 (ESI†). The red dashed line stands for the zero. The same trend is observed at C/100 in Fig. S3 (ESI†), although the calculation of cLi is less reliable with the cell used at C/100. | ||
The similarity of layered TM oxides is further supported by the NMC811 dIL evolution above 4.2 V (Fig. S9, ESI†). dIL in NMC811 tends toward that of LNO, though limited by its distinct chemical composition. Moreover, dTM and dIL in LNO evolve as in the other NMCs, even though it undergoes phase transformations, confirming their resemblance. Therefore within this frame, X ≃ f(cLi), greatly simplifying the structure of NMCxyz.
3.5 Strain analysis
We now show that strain ε can also be described by a single variable cLi. Peak broadening, as observed earlier at slow charge rate, can indicate a certain evolution of strain present in the structure during cycling. This strain could be either isotropic, meaning that the material is identically stressed in all directions in space, or anisotropic, when the strain develops in one particular direction of space. Generally, distinguishing isotropic from anisotropic strain in solid-state materials lies in a careful examination of the various hypothesis behind each potential cause and physical process. In the present case, isotropic strain analysis may be ambiguous, or even impractical, because of the possible confusion between heterogeneous lithiation state of particles and particles under stress, when assuming an isotropic space distribution. Because the strain represents a scale of heterogeneity of lattice parameters with respect to its averaged value, identical modifications of the XRD patterns would arise from an isotropic strain or a multi-alike-phases material, making impossible to differentiate the two situations (see ESI† Section S13). Here, we naturally face such burden, since heterogeneous lithiation states are intrinsic to polycrystalline NMCs.26,27,38 Moreover, extended exposure of the material to the X-ray beam might artificially broaden the Bragg peaks, although the exposure has been limited in this work.36 These two reasons prevent the analysis of isotropic strain to be properly performed. Alternatively, anisotropic strain analysis could be applied since it does not affect every diffraction peaks. In the specific case of NMC materials, however, while extracting the features of anisotropic strain using powder XRD data turned out to be possible, it appeared not possible to ascribe broadening effects to one or the other cause. In fact, as we now discuss in more details, local hererogeneities and anisotropic strain may be bound and both trigger the same aftereffects on the XRD patterns.Firstly, let us discuss how lithiation heterogeneties can create anisotropic features in NMCs. Those are particularly insidious because they stem from a local heterogeneity of lithium concentration homogeneously distributed at the crystal scale. This lithium heterogeneity represents a heterogeneous lithium concentration within the galleries of a single crystal. This is not modelled by the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group since the latter assumes a homogeneous distribution of the lithium in the layers. Due to the larger variation of the lattice parameter c compared to a, the crystalline concentration heterogeneity naturally induces anisotropic effects.
m space group since the latter assumes a homogeneous distribution of the lithium in the layers. Due to the larger variation of the lattice parameter c compared to a, the crystalline concentration heterogeneity naturally induces anisotropic effects.
Let us consider fa and fc, two functions describing a(cLi) and c(cLi), obtained by smoothing the experimental results at C/5, as shown in Fig. 6A and B. The strain ε represents the heterogeneity of lattice parameters as compared to the equilibrium value, here simplified by the averaged value. Considering this, we can roughly estimate the endured strain along ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) , εa associated with a local heterogeneity ΔcLi, of cLi, according to eqn (1):
, εa associated with a local heterogeneity ΔcLi, of cLi, according to eqn (1):
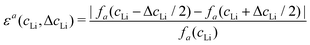 | (1) |
![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) , εc, and both are plotted in Fig. 6C and D respectively, for various amplitude of ΔcLi. Therefore, eqn (1) gives strain as a function of two variables, cLi and ΔcLi.
, εc, and both are plotted in Fig. 6C and D respectively, for various amplitude of ΔcLi. Therefore, eqn (1) gives strain as a function of two variables, cLi and ΔcLi.
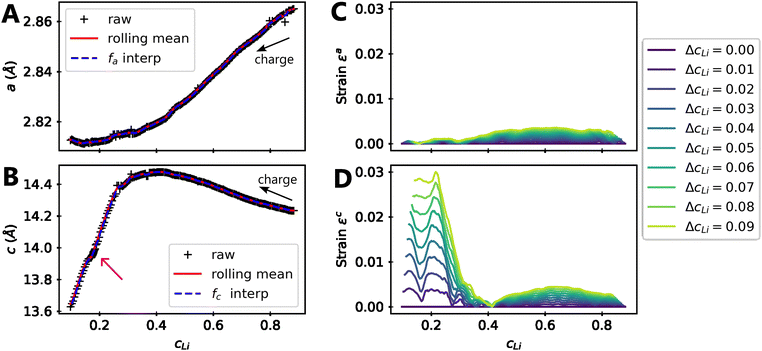 | ||
Fig. 6 Modelling of strain due to local heterogeneities. Refined (A) a and (B) c lattice parameters of NMC811 charged to 4.64 V in black markers, the rolling mean of the refined data in plain red, which is used to build the functions fa and fc in dashed blue. The magenta arrow indicates a constant voltage step at 4.2 V, before charging until 4.64 V. The strain is evaluated using eqn (1) along ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) direction in (C) and direction in (C) and ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) in (D) for increasing local heterogeneities of cLi, ΔcLi. in (D) for increasing local heterogeneities of cLi, ΔcLi. | ||
Although a weak strain is present in both ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) and
and ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) directions for cLi in the range [0.4,1], its intensity decreases below cLi = 0.4 along direction
directions for cLi in the range [0.4,1], its intensity decreases below cLi = 0.4 along direction ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) , while that along direction
, while that along direction ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) increases until reaching a value about 30 times higher. This is typically reflecting the appearance of an anisotropic strain, since the strain is significantly more pronounced in a direction with respect to the other. These effects can be measured by XRD since the heterogeneity can be interpreted as lattice domains of the same crystal with distinct lattice parameters. Accordingly, the warping of the Bragg diffraction peaks caused by the lattice parameter evolution has been simulated and compared to the experimental data to validate the direct impact of local heterogeneities on the shape of diffraction peaks (ESI† Section S16 and Fig. S20). This analysis confirms the similar modification of both simulated and experimental Bragg peaks below cLi = 0.4. It reveals that the local heterogeneity ΔcLi varies, and increases further below cLi = 0.4. It suggests also that ΔcLi is a function of cLi only in early cycling, implying that ε is function of one variable only as shown later.
increases until reaching a value about 30 times higher. This is typically reflecting the appearance of an anisotropic strain, since the strain is significantly more pronounced in a direction with respect to the other. These effects can be measured by XRD since the heterogeneity can be interpreted as lattice domains of the same crystal with distinct lattice parameters. Accordingly, the warping of the Bragg diffraction peaks caused by the lattice parameter evolution has been simulated and compared to the experimental data to validate the direct impact of local heterogeneities on the shape of diffraction peaks (ESI† Section S16 and Fig. S20). This analysis confirms the similar modification of both simulated and experimental Bragg peaks below cLi = 0.4. It reveals that the local heterogeneity ΔcLi varies, and increases further below cLi = 0.4. It suggests also that ΔcLi is a function of cLi only in early cycling, implying that ε is function of one variable only as shown later.
Secondly, now that the possible effect of local lithiation heterogeneities on local strain has been quantified, we refine the XRD data obtained across the various nickel content NMCs and at several charge rates, using anisotropic strain description. This second analysis method is based on the refinement of diffraction peaks distortion which proceeds from the lattice distance deviations. We observed a larger broadening of 003 compared to 101 Bragg reflection at the end of charge (Fig. S2 and S3D, ESI†). Other 〈hkl〉 reflections having larger l component with respect to h and k have the same broadening at higher q values. This behaviour is typical of anisotropic strain oriented in the ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) direction, and is coherent with the large shrinkage of c in the NMCs and LNO. The unidirectionnal feature is confirmed by the anisotropic strain parameter obtained from Le Bail refinement at C/100 which is null at the beginning of charge and becomes positive at the same time for the three NMCs (Fig. S17, ESI†). For LNO, the anisotropy is correlated to the H3 phase only, and seems to be absent in the other phases, suggesting a special mechanism bound to H3.
direction, and is coherent with the large shrinkage of c in the NMCs and LNO. The unidirectionnal feature is confirmed by the anisotropic strain parameter obtained from Le Bail refinement at C/100 which is null at the beginning of charge and becomes positive at the same time for the three NMCs (Fig. S17, ESI†). For LNO, the anisotropy is correlated to the H3 phase only, and seems to be absent in the other phases, suggesting a special mechanism bound to H3.
The Le Bail refinement of anisotropic strain in the three materials at different cycling conditions in function of the lithium content is reported in Fig. 7. In this representation, all data point fall on a master curve with a specific exponential-growing trend at small cLi. First of all, it means that faster kinetics does not induce stronger directional strain, since the anisotropic strain starts to increase from cLi below 0.4–0.45 for the three materials, irrespective of the charge rate. Additionally, it indicates that the extent of anisotropic strain is not related to the material itself, but only to the amount of lithium filling the layers. It is unexpected to observe that neither the charge rate nor the NMC nickel stoichiometry impact the strain intensity, suggesting that its nature is exactly the same in the three layered TM oxides, independently of the crystalline structure. Furthermore, the anisotropic strain increases when NMC811 is overcharged until 4.65 V (blue star in Fig. 7). It confirms that the strain intensity is not related to the material itself, but only to the amount of lithium extracted, since its value tends toward that of LNO at a similar cLi. Finally, a similar analysis during discharge shows that the anisotropic strain appears and vanishes at the same cLi for the three materials during delithiation or lithiation (Fig. S18, ESI†). Thus, the anisotropic strain is reversible in layered TM oxides, at least in early cycles. It shows that strain depends only on cLi, i.e. ε = g(cLi), implying that either ΔcLi is not bound to ε, or that ΔcLi is directly bound to cLi. That is why ε = g(cLi,ΔcLi) = g(cLi) in early cycling when the structure is still preserved.
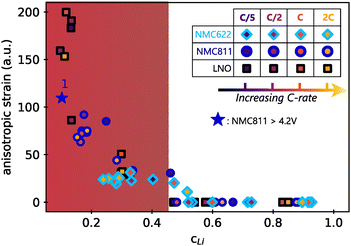 | ||
| Fig. 7 Anisotropic strain in function of lithium content cLi. Values were obtained by refining the full patterns with Le Bail method. The filling colors of markers indicate the charge rate associated with each of the three materials investigated. Same shape of markers are used for all LNO phases for better clarity. The blue star is the anisotropic strain of NMC811 during overcharge (see Fig. S9, ESI†). The anisotropic strain exponentially grows below a critical cLi value ∼0.4 (red zone). | ||
The similarity of the strain estimated from local lithiation heterogeneities compared to what is experimentally obtained from XRD patterns refinements (Fig. 7vs.Fig. 6D), is striking. Therefore, these results show that a local heterogeneity can induce effects that have the same consequences as an anisotropic strain created from other causes, such as from defects. It also suggests that strain is directly bound to the structure function f as given by eqn (1). Furthermore, whether the cause is anisotropic strain or a local lithiation heterogeneity, both strongly indicate a critical lithium content of 0.4 for Ni-rich layered TM oxides below which the structure is under exponential distortion from the very first cycles.
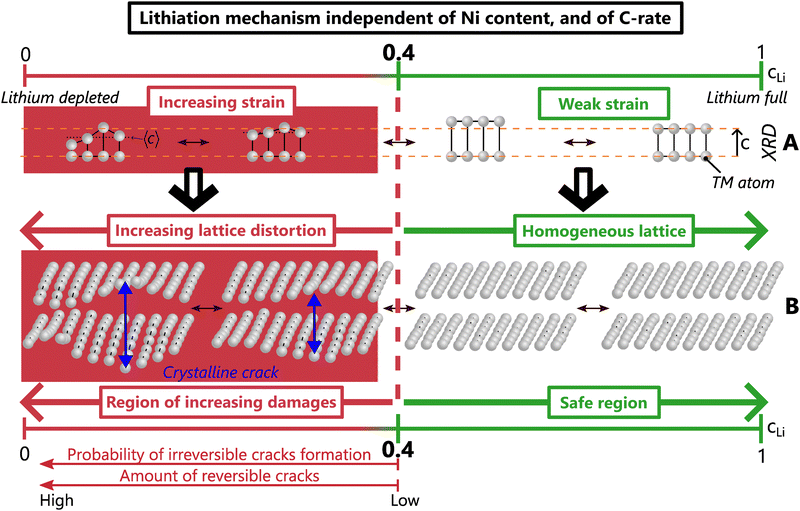
The existence of a critical lithium content reveals the underlying mechanism of layered TM oxides structures. Interestingly, the anisotropic strain appears when dIL reaches its maximum (Fig. 5) and begins to decrease. Both shrinkage of the TM layers – which is still much debated in the community – and strain do appear in concert with a lithium depletion below cLi = 0.4. Therefore, the two phenomena may find their cause in the same origin since they occur at the same time. Further investigation by X-ray absorption spectroscopy or by NMR may enable to clarify underlying mechanisms but are beyond the scope of this study. Importantly, the observation of a dIL maximum can be seen in previously reported results in Ni-rich NCA (accompanied by cracks), LiCoO2 and many sodiated layered TM oxides at a comparable cLi or cNa, i.e. 0.4 for most and 0.45 for LCO.39–43 This suggests that such a lithium (and likely sodium) threshold exists in many layered TM oxides. Changing the chemical composition may shift the absolute value of the cLi threshold, but not the very nature of the structural mechanism. This model describes the structure as X = f(cLi), and strain as ε = g(cLi, ΔcLi) in the general case, and ε = g(cLi) in early cycling. These common structure and strain features driven by the lithium content attest of a single mechanism shared by layered TM oxides.
3.6 Potential impact on degradation
The existence of anisotropic strain in the layered TM oxides could potentially favour stress-induced ageing of the materials. Strain creates stress as a function of the Young modulus, which in turn can lead to defects formation. In fact, Ni-rich layered TM oxides exhibit cracks induced by stress in primary and/or secondary particles, which are reported to be a major cause of degradation.9,44 Since the strain describes lattice imperfections at the crystal level, it could favour crystalline cracks apparition. By crystalline cracks, here we intend cracks that nucleate and spread inside a single crystal, as opposed to those developed between primary particles of polycrystalline particles. Our results suggest that crystalline cracks are favoured below 40% lithium content in layered TM oxides, which corresponds to about 85% SOC for NMC622, but only 65% SOC for LNO. Previous studies reported cracks in single crystal NCA or NMC at high SOC,3,10,45–47 the origin of which was often attributed to H2 → H3 transition or ageing. Based on the cLi -driven master curve of strain, we infer that crystalline cracks appearance is instead correlated to very low lithium content, below the critical lithium value. Firstly, similar crystalline cracks also appear in NMC622 or NMC333 only when they are overcharged,11,48,49i.e., when their lithium content is low. Secondly, crystalline cracks can be observed during the first cycles, which rules out a pure ageing effect but agrees with early developed strain-trigerred mechanism.10,45,50Note that cracks at particle scale are different in nature from crystalline cracks. They are probably related to both volume changes3,51 and inter-crystal strain50,52 occuring at high SOC. The inter-crystal strain cannot be directly measured by XRD, but can be followed indirectly. A qualitative analysis based on our data (ESI† Section S17) suggests that the C-rate affects the inter-crystal strain only at high cLi, when the solid lithium diffusion is low.13,39,53,54
In the literature, crystalline cracks are reportedly either nucleated from the surface or at edge dislocations within the crystal structure.47,49 Both can be explained using the anisotropic strain evolution that we evidenced. Defects, such as Ni/Li antisites or stacking faults as described by the “crack incubation at dislocation core”,49 essentially distort the crystal along the ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) direction, hence inducing anisotropic strain. Those cracks are exacerbated by higher cutoff voltages, corroborating the increase of the anisotropic strain intensity when the lithium content is the lowest, such as the overcharged NMC811 in Fig. 6. Yet faster charge rates seem to provoke the appearance of crystalline cracks in some studies,47,55 whereas our results support a crystalline strain independent of C-rate. It is likely due to the longer diffusion length of single crystals compared to the aggregated (but small) crystals of polycrystalline NMCs used in our study. Furthermore, larger heterogeneties are induced if the crystallographic orientation of the interface is not optimised56,57 which favour crystalline cracks.47,55 Therefore, it is possible that crystalline cracks start to appear below cLi = 0.4 in layered TM oxides, and are reversible as long as they are still in the “incubation” stage, before crack propagation.
direction, hence inducing anisotropic strain. Those cracks are exacerbated by higher cutoff voltages, corroborating the increase of the anisotropic strain intensity when the lithium content is the lowest, such as the overcharged NMC811 in Fig. 6. Yet faster charge rates seem to provoke the appearance of crystalline cracks in some studies,47,55 whereas our results support a crystalline strain independent of C-rate. It is likely due to the longer diffusion length of single crystals compared to the aggregated (but small) crystals of polycrystalline NMCs used in our study. Furthermore, larger heterogeneties are induced if the crystallographic orientation of the interface is not optimised56,57 which favour crystalline cracks.47,55 Therefore, it is possible that crystalline cracks start to appear below cLi = 0.4 in layered TM oxides, and are reversible as long as they are still in the “incubation” stage, before crack propagation.
We propose that local lithiation heterogeneities, anisotropic strain, defects present at the pristine state and crystalline cracks are actually closely bound to each other. Defects present before the first delithiation have been observed in NCA and LiCoO2,58,59 as well as defects appearing or spreading during the charge in a Ni-rich NMC or in a Li-rich layered oxide, respectively.60,61 Those could alter the local equilibrium potential and as a consequence, the lithium pathway, which suggests that a mechano-chemical equilibrium potential drives the lithium insertion at very local scale, as proposed for LiCoO2.62 The mechano-chemical potential can favour local lithium concentration heterogeneities, which would induce a local warping of the lattice, and finally anisotropic strain. The distorted lattice could easily trigger crystalline cracks, that in turn affect the local mechano-chemical equilibrium potential. Thus, it is proposed that lithiation heterogeneities and anisotropic strain act in concert, and finally lead to the creation of crystalline cracks. Hence we suggest a single mechanism unifying both structure, local lithium distribution heterogeneities, strain and cracks at crystal scale in layered TM oxides. This mechanism is driven by the lithium content, irrespective of the nickel content, the charge rate, the phase diagram and likely of the poly/single crystalline nature (Fig. 8). When cLi exceeds 0.4, weak strain and homogeneous lattice constitute the safe zone where crack nucleation is very unlikely. In contrast, below cLi = 0.4, the increasing strain induces more and more lattice distortions, and a higher probability of forming crystalline cracks, that cause considerable damage to the material.
Our results highlight the key role of lithium loss in the layered TM oxides degradation not only because it limits the capacity of the battery, but also because it directly exacerbates material degradation. Due to lithium loss, the lithium content range in the positive active materials during operation is gradually shifting to lower values, further and further below the critical content. This shift intensifies the material strain and irreversible cracks, and consequently favours TM dissolution, oxygen leak or structure reconstruction into rocksalt or spinel type,63 likely due to parasitic reactions with electrolyte at high voltage, further promoting lithium loss. Thereby, lithium loss turns into a vicious circle in which the greater the lithium loss, the larger the irreversible degradations, and reciprocally. In this regard, lithium loss could be considered as the dominant factor of degradation since it triggers many others. Its impact may be mitigated either by lithium regeneration, or by shifting to a lower cLi value the critical content. The first could be realised with pre-formation of the solid electrolyte interphase which consumes a large amount of lithium. The second can be achieved by lattice doping or coating to stabilise the emptied layered structure, such as with Zr, Mo, Nb or other materials that showed increased capacity and less cracks appearance.64,65 Other strategies exist to alleviate inter-granular cracks at particle scale such as a protective surface layer, an optimised crystallographic orientation, or the building of a gradient of TM atoms inside secondary particles of layered TM oxides.56,66–70
4. Conclusions
In conclusion, combined laboratory and synchrotron operando structural studies of Ni-rich NMCs confirmed that phase transitions occur only in LNO, in contrast to the solid solution mechanism for NMC622 and NMC811 during the entire (de)lithiation. Nevertheless, by adopting a non-standard perspective to analyse the crystallographic data, we correlate the materials structure and degradation beyond the standard definition of phase transformation. LNO and NMCs show identical local structural and strain evolutions, which enables us to propose a unified model of the structure of layered TM oxides, irrespective of the nickel content, the charge rate, or the crystalline nature. This model is likely shared with many layered oxides. In this model, lithium extraction below a critical lithium content 0.4 triggers exponential lattice distortion, which is shown to be closely bound to the increase of anisotropic strain and local lithiation heterogeneities. Lithium loss is revealed as the main culprit in NMC fatigue by shifting the working window far below the critical content and triggers stress-induced parasitic reactions. As a consequence, battery manufacturers should envision to mark out the accessible lithium content range depending on the layered TM oxide used, for example using potential derivatives (Fig. S24, ESI†), to preserve materials from degradation upon cycling.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The “CEA Battery FOCUS” program is acknowledged for the funding of the PhD program of T. J. Beamtime at the ESRF was granted within the Battery Pilot Hub MA4929 “Multi-scale Multi-techniques investigations of Li-ion batteries: towards a European Battery Hub” and proposal IH-CH-1577. Funding from French ANR PIA3 Equipex + project MAGNIFIX under grant agreement ANR-21-ESRE-0011, and ANR PEPR PIA4 project DIADEM-ESRF under grant agreement 22-PEXD-0011 are acknowledged, as well EU H2020 Research and Innovation Program project BIG-MAP under grant agreement No. 957189. Olivier Ulrich, Jean-Sébastien Micha and Olivier Geaymond (BM32 beamline staff) are thanked for their help in the preparation of the experiments. Morgane Herbomel and Yvan Reynier are thanked for the manufacturing of electrodes and Daniel Tomasi is thanked for the preparation of the pouch cells at CEA-LITEN.References
- A. Manthiram, ACS Cent. Sci., 2017, 3, 1063–1069 CrossRef CAS PubMed
.
- S. Li, Z. Jiang, J. Han, Z. Xu, C. Wang, H. Huang, C. Yu, S.-J. Lee, P. Pianetta, H. Ohldag, J. Qiu, J.-S. Lee, F. Lin, K. Zhao and Y. Liu, Nat. Commun., 2020, 11, 4433 CrossRef CAS PubMed
.
- H.-H. Ryu, K.-J. Park, C. S. Yoon and Y.-K. Sun, Chem. Mater., 2018, 30, 1155–1163 CrossRef CAS
.
- C. Xu, K. Märker, J. Lee, A. Mahadevegowda, P. J. Reeves, S. J. Day, M. F. Groh, S. P. Emge, C. Ducati, B. L. Mehdi, C. C. Tang and C. P. Grey, Nat. Mater., 2021, 20, 84–92 CrossRef CAS PubMed
.
- Y. Mao, X. Wang, S. Xia, K. Zhang, C. Wei, S. Bak, Z. Shadike, X. Liu, Y. Yang, R. Xu, P. Pianetta, S. Ermon, E. Stavitski, K. Zhao, Z. Xu, F. Lin, X.-Q. Yang, E. Hu and Y. Liu, Adv. Funct. Mater., 2019, 29, 1900247 CrossRef
.
- K.-Y. Park, Y. Zhu, C. G. Torres-Castanedo, H. J. Jung, N. S. Luu, O. Kahvecioglu, Y. Yoo, J.-W. T. Seo, J. R. Downing, H.-D. Lim, M. J. Bedzyk, C. Wolverton and M. C. Hersam, Adv. Mater., 2022, 34, 2106402 CrossRef CAS PubMed
.
- S. Zheng, C. Hong, X. Guan, Y. Xiang, X. Liu, G.-L. Xu, R. Liu, G. Zhong, F. Zheng, Y. Li, X. Zhang, Y. Ren, Z. Chen, K. Amine and Y. Yang, J. Power Sources, 2019, 412, 336–343 CrossRef CAS
.
- W.-S. Yoon, K. Y. Chung, J. McBreen and X.-Q. Yang, Electrochem. Commun., 2006, 8, 1257–1262 CrossRef CAS
.
- C. D. Quilty, D. C. Bock, S. Yan, K. J. Takeuchi, E. S. Takeuchi and A. C. Marschilok, J. Phys. Chem. C, 2020, 124, 8119–8128 CrossRef CAS
.
- G. W. Nam, N.-Y. Park, K.-J. Park, J. Yang, J. Liu, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2019, 4, 2995–3001 CrossRef CAS
.
- G. Qian, Y. Zhang, L. Li, R. Zhang, J. Xu, Z. Cheng, S. Xie, H. Wang, Q. Rao, Y. He, Y. Shen, L. Chen, M. Tang and Z.-F. Ma, Energy Storage Mater., 2020, 27, 140–149 CrossRef
.
- S. Liu, P. J. West, H. Zhong, J. Bai, E. Stavitski, D. Leshchev, A. C. Marschilok, E. S. Takeuchi, D. C. Bock and K. J. Takeuchi, Chem. Mater., 2023, 35, 8857–8871 CrossRef CAS
.
- K. Märker, P. J. Reeves, C. Xu, K. J. Griffith and C. P. Grey, Chem. Mater., 2019, 31, 2545–2554 CrossRef
.
- A. Jetybayeva, N. Schön, J. Oh, J. Kim, H. Kim, G. Park, Y.-G. Lee, R.-A. Eichel, K. Kleiner, F. Hausen and S. Hong, ACS Appl. Energy Mater., 2022, 5, 1731–1742 CrossRef CAS
.
- J. Li, L. E. Downie, L. Ma, W. Qiu and J. R. Dahn, J. Electrochem. Soc., 2015, 162, A1401–A1408 CrossRef CAS
.
- P.-Y. Liao, J.-G. Duh, J.-F. Lee and H.-S. Sheu, Electrochim. Acta, 2007, 53, 1850–1857 CrossRef CAS
.
- W. Li, H. Y. Asl, Q. Xie and A. Manthiram, J. Am. Chem. Soc., 2019, 141, 5097–5101 CrossRef CAS PubMed
.
- O. J. Borkiewicz, K. M. Wiaderek, P. J. Chupas and K. W. Chapman, J. Phys. Chem. Lett., 2015, 6, 2081–2085 CrossRef CAS PubMed
.
- Y. Zhang, L. Tao, C. Xie, D. Wang, Y. Zou, R. Chen, Y. Wang, C. Jia and S. Wang, Adv. Mater., 2020, 32, 1905923 CrossRef CAS PubMed
.
- T. Danner, M. Singh, S. Hein, J. Kaiser, H. Hahn and A. Latz, J. Power Sources, 2016, 334, 191–201 CrossRef CAS
.
- T. Hirai, I. Yoshimatsu and J. Ichi Yamaki, J. Electrochem. Soc., 1994, 141, 611–614 CrossRef CAS
.
- S. Tardif, N. Dufour, J.-F. Colin, G. Gébel, M. Burghammer, A. Johannes, S. Lyonnard and M. Chandesris, J. Mater. Chem. A, 2021, 9, 4281–4290 RSC
.
- Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, J. Am. Chem. Soc., 2013, 135, 5497–5500 CrossRef CAS PubMed
.
- X. Wu, B. Song, P.-H. Chien, S. M. Everett, K. Zhao, J. Liu and Z. Du, Adv. Sci., 2021, 8, 2102318 CrossRef CAS PubMed
.
- Y.-N. Zhou, J.-L. Yue, E. Hu, H. Li, L. Gu, K.-W. Nam, S.-M. Bak, X. Yu, J. Liu, J. Bai, E. Dooryhee, Z.-W. Fu and X.-Q. Yang, Adv. Energy Mater., 2016, 6, 1600597 CrossRef
.
- J. Park, H. Zhao, S. D. Kang, K. Lim, C.-C. Chen, Y.-S. Yu, R. D. Braatz, D. A. Shapiro, J. Hong, M. F. Toney, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2021, 20, 991–999 CrossRef CAS PubMed
.
- W. E. Gent, Y. Li, S. Ahn, J. Lim, Y. Liu, A. M. Wise, C. B. Gopal, D. N. Mueller, R. Davis, J. N. Weker, J.-H. Park, S.-K. Doo and W. C. Chueh, Adv. Mater., 2016, 28, 6631–6638 CrossRef CAS PubMed
.
- A. Vamvakeros, D. Matras, T. E. Ashton, A. A. Coelho, H. Dong, D. Bauer, Y. Odarchenko, S. W. T. Price, K. T. Butler, O. Gutowski, A.-C. Dippel, M. V. Zimmerman, J. A. Darr, S. D. M. Jacques and A. M. Beale, Small
Methods, 2021, 5, 2100512 CrossRef CAS PubMed
.
- J. B. Leriche, S. Hamelet, J. Shu, M. Morcrette, C. Masquelier, G. Ouvrard, M. Zerrouki, P. Soudan, S. Belin, E. Elkaïm and F. Baudelet, J. Electrochem. Soc., 2010, 157, A606 CrossRef CAS
.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef
.
- J. Kieffer, V. Valls, N. Blanc and C. Hennig, J. Synchrotron Radiat., 2020, 27, 558–566 CrossRef CAS PubMed
.
- V. Petrícek, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345–352 CrossRef
.
- H. Li, N. Zhang, J. Li and J. R. Dahn, J. Electrochem. Soc., 2018, 165, A2985–A2993 CrossRef CAS
.
- L. De Biasi, A. Schiele, M. Roca-Ayats, G. Garcia, T. Brezesinski, P. Hartmann and J. Janek, ChemSusChem, 2019, 12, 2240–2250 CrossRef CAS PubMed
.
- H. Li, W. Hua, X. Liu-Théato, Q. Fu, M. Desmau, A. Missyul, M. Knapp, H. Ehrenberg and S. Indris, Chem. Mater., 2021, 33, 9546–9559 CrossRef CAS
.
- T. Jousseaume, J.-F. Colin, M. Chandesris, S. Lyonnard and S. Tardif, ACS Energy Lett., 2023, 8, 3323–3329 CrossRef CAS PubMed
.
- K. Min, K. Kim, C. Jung, S.-W. Seo, Y. Y. Song, H. S. Lee, J. Shin and E. Cho, J. Power Sources, 2016, 315, 111–119 CrossRef CAS
.
- L. Nowack, D. Grolimund, V. Samson, F. Marone and V. Wood, Sci. Rep., 2016, 6 Search PubMed
.
- A. Grenier, P. J. Reeves, H. Liu, I. D. Seymour, K. Märker, K. M. Wiaderek, P. J. Chupas, C. P. Grey and K. W. Chapman, J. Am. Chem. Soc., 2020, 142, 7001–7011 CrossRef CAS PubMed
.
- H. Li, A. Liu, N. Zhang, Y. Wang, S. Yin, H. Wu and J. R. Dahn, Chem. Mater., 2019, 31, 7574–7583 CrossRef CAS
.
- G. G. Amatucci, J. M. Tarascon and L. C. Klein, J. Electrochem. Soc., 1996, 143, 1114 CrossRef CAS
.
- Y. Biecher, A. Baux, F. Fauth, C. Delmas, G. R. Goward and D. Carlier, Chem. Mater., 2022, 34, 6431–6439 CrossRef CAS
.
- X. Li, Y. Wang, D. Wu, L. Liu, S.-H. Bo and G. Ceder, Chem. Mater., 2016, 28, 6575–6583 CrossRef CAS
.
- C. Xu, P. J. Reeves, Q. Jacquet and C. P. Grey, Adv. Energy Mater., 2021, 11, 2003404 CrossRef CAS
.
- J.-H. Kim, S. J. Kim, T. Yuk, J. Kim, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2018, 3, 3002–3007 CrossRef CAS
.
- A. K. C. Estandarte, J. Diao, A. V. Llewellyn, A. Jnawali, T. M. M. Heenan, S. R. Daemi, J. J. Bailey, S. Cipiccia, D. Batey, X. Shi, C. Rau, D. J. L. Brett, R. Jervis, I. K. Robinson and P. R. Shearing, ACS Nano, 2021, 15, 1321–1330 CrossRef CAS PubMed
.
- H.-H. Ryu, B. Namkoong, J.-H. Kim, I. Belharouak, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2021, 6, 2726–2734 CrossRef CAS
.
- P. Yan, J. Zheng, T. Chen, L. Luo, Y. Jiang, K. Wang, M. Sui, J.-G. Zhang, S. Zhang and C. Wang, Nat. Commun., 2018, 9, 2437 CrossRef PubMed
.
- P. Yan, J. Zheng, M. Gu, J. Xiao, J.-G. Zhang and C.-M. Wang, Nat. Commun., 2017, 8, 14101 CrossRef CAS PubMed
.
- L. Romano Brandt, J.-J. Marie, T. Moxham, D. P. Förstermann, E. Salvati, C. Besnard, C. Papadaki, Z. Wang, P. G. Bruce and A. M. Korsunsky, Energy Environ. Sci., 2020, 13, 3556–3566 RSC
.
- A. O. Kondrakov, A. Schmidt, J. Xu, H. Geßwein, R. Mönig, P. Hartmann, H. Sommer, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2017, 121, 3286–3294 CrossRef CAS
.
- R. Xu and K. Zhao, J. Mech. Phys. Solids, 2018, 121, 258–280 CrossRef CAS
.
- V. Charbonneau, A. Lasia and G. Brisard, J. Electroanal. Chem., 2020, 875, 113944 CrossRef CAS
.
- S.-L. Wu, W. Zhang, X. Song, A. K. Shukla, G. Liu, V. Battaglia and V. Srinivasan, J. Electrochem. Soc., 2012, 159, A438 CrossRef CAS
.
- Y. Bi, J. Tao, Y. Wu, L. Li, Y. Xu, E. Hu, B. Wu, J. Hu, C. Wang, J.-G. Zhang, Y. Qi and J. Xiao, Science, 2020, 370, 1313–1317 CrossRef CAS PubMed
.
- Z. Xu, Z. Jiang, C. Kuai, R. Xu, C. Qin, Y. Zhang, M. M. Rahman, C. Wei, D. Nordlund, C.-J. Sun, X. Xiao, X.-W. Du, K. Zhao, P. Yan, Y. Liu and F. Lin, Nat. Commun., 2020, 11, 83 CrossRef CAS PubMed
.
- Y. Lu, T. Zhu, E. McShane, B. D. McCloskey and G. Chen, Small, 2022, 18, 2105833 CrossRef CAS PubMed
.
- S. Ahmed, A. Pokle, S. Schweidler, A. Beyer, M. Bianchini, F. Walther, A. Mazilkin, P. Hartmann, T. Brezesinski, J. Janek and K. Volz, ACS Nano, 2019, 13, 10694–10704 CrossRef CAS PubMed
.
- H. Gabrisch, R. Yazami and B. Fultz, Electrochem. Solid-State Lett., 2002, 5, A111 CrossRef CAS
.
- S. Li, Z. Yao, J. Zheng, M. Fu, J. Cen, S. Hwang, H. Jin, A. Orlov, L. Gu, S. Wang, Z. Chen and D. Su, Angew. Chem., Int. Ed., 2020, 59, 22092–22099 CrossRef CAS PubMed
.
- A. Singer, M. Zhang, S. Hy, D. Cela, C. Fang, T. A. Wynn, B. Qiu, Y. Xia, Z. Liu, A. Ulvestad, N. Hua, J. Wingert, H. Liu, M. Sprung, A. V. Zozulya, E. Maxey, R. Harder, Y. S. Meng and O. G. Shpyrko, Nat. Energy, 2018, 3, 641–647 CrossRef CAS
.
- Z. Xu, D. Hou, D. J. Kautz, W. Liu, R. Xu, X. Xiao and F. Lin, Adv. Mater., 2020, 32, 2003417 CrossRef CAS PubMed
.
- H. Zhang, F. Omenya, P. Yan, L. Luo, M. S. Whittingham, C. Wang and G. Zhou, ACS Energy Lett., 2017, 2, 2607–2615 CrossRef CAS
.
- F. A. Susai, D. Kovacheva, A. Chakraborty, T. Kravchuk, R. Ravikumar, M. Talianker, J. Grinblat, L. Burstein, Y. Kauffmann, D. T. Major, B. Markovsky and D. Aurbach, ACS Appl. Energy Mater., 2019, 2, 4521–4534 CrossRef CAS
.
- F. Xin, A. Goel, X. Chen, H. Zhou, J. Bai, S. Liu, F. Wang, G. Zhou and M. S. Whittingham, Chem. Mater., 2022, 34, 7858–7866 CrossRef CAS
.
- S. Tan, Z. Shadike, J. Li, X. Wang, Y. Yang, R. Lin, A. Cresce, J. Hu, A. Hunt, I. Waluyo, L. Ma, F. Monaco, P. Cloetens, J. Xiao, Y. Liu, X.-Q. Yang, K. Xu and E. Hu, Nat. Energy, 2022, 7, 484–494 CrossRef CAS
.
- D. Ren, E. Padgett, Y. Yang, L. Shen, Y. Shen, B. D. A. Levin, Y. Yu, F. J. DiSalvo, D. A. Muller and H. D. Abruña, ACS Appl. Mater. Interfaces, 2019, 11, 41178–41187 CrossRef CAS PubMed
.
- S. Natarajan, S. B. Moodakare, P. Haridoss and R. Gopalan, ACS Appl. Mater. Interfaces, 2020, 12, 34959–34970 CrossRef CAS PubMed
.
- K.-J. Park, M.-J. Choi, F. Maglia, S.-J. Kim, K.-H. Kim, C. S. Yoon and Y.-K. Sun, Adv. Energy Mater., 2018, 8, 1703612 CrossRef
.
- C. S. Yoon, K.-J. Park, U.-H. Kim, K. H. Kang, H.-H. Ryu and Y.-K. Sun, Chem. Mater., 2017, 29, 10436–10445 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee04115h |
| This journal is © The Royal Society of Chemistry 2024 |