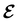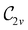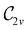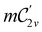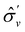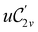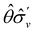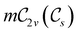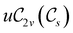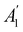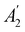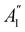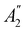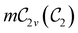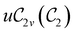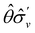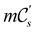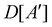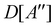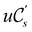Open Access Article
Open Access ArticleSymmetry and reactivity of π-systems in electric and magnetic fields: a perspective from conceptual DFT†
Meilani
Wibowo-Teale
 *a,
Bang C.
Huynh
*a,
Bang C.
Huynh
 *a,
Andrew M.
Wibowo-Teale
*a,
Andrew M.
Wibowo-Teale
 a,
Frank
De Proft
a,
Frank
De Proft
 b and
Paul
Geerlings
b and
Paul
Geerlings
 *b
*b
aSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK. E-mail: meilani.wibowo@nottingham.ac.uk; bang.huynh@nottingham.ac.uk
bResearch group of General Chemistry (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, B-1050 Brussels, Belgium. E-mail: pgeerlin@vub.be
First published on 30th April 2024
Abstract
The extension of conceptual density-functional theory (conceptual DFT) to include external electromagnetic fields in chemical systems is utilised to investigate the effects of strong magnetic fields on the electronic charge distribution and its consequences on the reactivity of π-systems. Formaldehyde, H2CO, is considered as a prototypical example and current-density-functional theory (current-DFT) calculations are used to evaluate the electric dipole moment together with two principal local conceptual DFT descriptors, the electron density and the Fukui functions, which provide insight into how H2CO behaves chemically in a magnetic field. In particular, the symmetry properties of these quantities are analysed on the basis of group, representation, and corepresentation theories using a recently developed automatic program for symbolic symmetry analysis, QSYM2. This allows us to leverage the simple symmetry constraints on the macroscopic electric dipole moment components to make profound predictions on the more nuanced symmetry transformation properties of the microscopic frontier molecular orbitals (MOs), electron densities, and Fukui functions. This is especially useful for complex-valued MOs in magnetic fields whose detailed symmetry analyses lead us to define the new concepts of modular and phasal symmetry breaking. Through these concepts, the deep connection between the vanishing constraints on the electric dipole moment components and the symmetry of electron densities and Fukui functions can be formalised, and the inability of the magnetic field in all three principal orientations considered to induce asymmetry with respect to the molecular plane of H2CO can be understood from a molecular perspective. Furthermore, the detailed forms of the Fukui functions reveal a remarkable reversal in the direction of the dipole moment along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the presence of a parallel or perpendicular magnetic field, the origin of which can be attributed to the mixing between the frontier MOs due to their subduced symmetries in magnetic fields. The findings in this work are also discussed in the wider context of a long-standing debate on the possibility to create enantioselectivity by external fields.
O bond in the presence of a parallel or perpendicular magnetic field, the origin of which can be attributed to the mixing between the frontier MOs due to their subduced symmetries in magnetic fields. The findings in this work are also discussed in the wider context of a long-standing debate on the possibility to create enantioselectivity by external fields.
1 Introduction
Physicists and chemists have always been interested in the properties of atoms and molecules under particular, sometimes extreme, conditions. In recent years, growing interest in the influence of external factors such as electric fields (described by Shaik as ‘novel effectors of chemical change’),1,2 mechanical forces,3,4 and (very high) pressure5,6 on chemical reactivity has prompted the study of ‘new chemistries’ that may arise in these conditions. This ‘evolution’ in fact illustrates the rising interest of both experimentalists and theoreticians in extending the portfolio of reaction conditions to enable unprecedented chemical transformations for the synthesis of novel materials. Remarkably, the experimental discovery of new reaction conditions and the theoretical development of computational methods to describe the behaviours of atoms and molecules under these conditions often proceed hand-in-hand. Ongoing studies on the chemical effects of external electric fields,7 recent investigations in the domain of mechanochemistry on how mechanical forces influence chemical structures and reactivity,8 and advanced developments in organic synthesis and materials design under very high pressure9,10 are some striking examples.Of these extreme conditions, the effects of strong magnetic fields on chemistry have unfortunately not been widely examined, not least because the magnetic fields that can be generated and sustained for a reasonable amount of time on Earth do not exceed 50 T.11 However, the astrophysical discoveries of much stronger magnetic fields on the surfaces of white dwarfs (ca. 102 T)12–15 and neutron stars (ca. 109 T)16 have since inspired a number of theoretical studies on the chemistry of atoms and small molecules in strong magnetic fields. Starting in the 1990s, these studies were mainly carried out to examine the energetics and spectra of very light atoms, revealing important changes in the electronic configurations of ground and excited states with increasing magnetic field strength.17,18 Specifically, electron pairs are gradually uncoupled such that states with more unpaired β-electrons and higher angular momenta become stabilised by spin- and orbital-Zeeman interactions.
Focussing on the chemical relevance of these trends, we recently analysed several atomic properties in strong magnetic fields19 calculated using current-density-functional theory (current-DFT).20–23 In particular, we utilised the framework of conceptual density-functional theory (conceptual DFT) to extract chemically relevant concepts from the results of density-functional theory (DFT) calculations. This was possible thanks to the recent extensions of the conventional formulations of both conceptual DFT24–30 and a wide variety of quantum-chemical methods20–22,31–35 to include arbitrary strength magnetic fields19,36,37 in a non-perturbative manner using London atomic orbitals (LAOs)38 [also known as gauge-including atomic orbitals (GIAOs)]. This in turn enabled detailed considerations of the variations of atomic electronegativity and hardness with magnetic field.
The observed deviations in these trends across the periodic table compared to their expected behaviour in the absence of a field shed light on the dramatic changes in chemical reactivity that are expected to occur under these extreme conditions.19 For example, Lange et al.33 showed how the 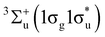 state of H2 becomes the ground state in strong magnetic fields on the order of 105 T. This state, which is purely repulsive in the absence of a magnetic field, exhibits binding with a preferential orientation of the H2 molecule perpendicular to the applied field. This discovery inspired the work on atomic properties in ref. 19, which in turn led us to investigate the effects of strong magnetic fields on electronic charge distributions and molecular structures for diatomics and small polyatomics that are slightly more complex than H2 in ref. 36. Through detailed calculations, significant changes to the physical properties of these systems were found, most notably the reversal of bond polarity in hydrogen halides at high field strengths, in line with the simplistic predictions using the atom-based quantities from conceptual DFT in ref. 19.
state of H2 becomes the ground state in strong magnetic fields on the order of 105 T. This state, which is purely repulsive in the absence of a magnetic field, exhibits binding with a preferential orientation of the H2 molecule perpendicular to the applied field. This discovery inspired the work on atomic properties in ref. 19, which in turn led us to investigate the effects of strong magnetic fields on electronic charge distributions and molecular structures for diatomics and small polyatomics that are slightly more complex than H2 in ref. 36. Through detailed calculations, significant changes to the physical properties of these systems were found, most notably the reversal of bond polarity in hydrogen halides at high field strengths, in line with the simplistic predictions using the atom-based quantities from conceptual DFT in ref. 19.
Of course, predictions based on atomic data cannot capture additional effects caused by the overall orientation of the structure relative to the external field. Molecular symmetry was thus identified as an essential consideration to rationalise the changes in the dipole moment as a function of the applied field. However, whilst the theoretical apparatus for a general treatment of molecular symmetry in external electromagnetic fields has long been understood,39–43 few practical implementations are available. Fortunately, a new program, QSYM2, has recently been developed to meet this need.44 Along with capabilities to determine molecular, orbital, and wavefunction symmetries in external fields, QSYM2 can be directly applied to analyse the symmetry of electron densities and density-related functions, which is helpful in the interpretation of conceptual DFT results.
The chemistry in strong magnetic fields that has been investigated for diatomics33,36 and small polyatomics36 displays many intriguing features. However, in the systems studied thus far using a combination of electron density with several global conceptual DFT descriptors such as electronegativity45 and hardness,46 only σ-bonds are present. It is therefore interesting to examine how strong magnetic fields may alter the reactivity of π-systems. In the present work, we examine the reactivity of formaldehyde, H2CO, a prototypical π-system containing a reactive C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, in the presence of electric and magnetic fields. Specifically, we investigate the symmetry of its Fukui functions47 to gain insight into the effects of external fields on the enantioselectivity of the system towards attacking nucleophiles. Fukui functions are a type of local conceptual DFT descriptor that describes intricate variations in the electron density that occur during chemical reactions. They have been demonstrated to be capable of providing theoretical understanding of several selectivity aspects of chemical reactions, albeit without any external fields applied.24,48 This choice of the prototypical π-system also facilitates a direct comparison with a recent study on chemical reactivity in the presence of electric fields in ref. 49.
O bond, in the presence of electric and magnetic fields. Specifically, we investigate the symmetry of its Fukui functions47 to gain insight into the effects of external fields on the enantioselectivity of the system towards attacking nucleophiles. Fukui functions are a type of local conceptual DFT descriptor that describes intricate variations in the electron density that occur during chemical reactions. They have been demonstrated to be capable of providing theoretical understanding of several selectivity aspects of chemical reactions, albeit without any external fields applied.24,48 This choice of the prototypical π-system also facilitates a direct comparison with a recent study on chemical reactivity in the presence of electric fields in ref. 49.
This article is organised as follows. In Section 2, we outline the essentials of current-DFT and conceptual DFT required for this study, followed by a detailed discussion of symmetry in the presence of external electric and magnetic fields. In Section 3, we briefly describe the computational details of our work. The reactivity of H2CO in the presence of electric and magnetic fields is then presented and discussed from the perspective of symmetry in Section 4. In particular, simple arguments from group theory are first employed to predict the symmetry of electric dipole moments in external fields. The result from this is then used to predict the more intricate symmetries of electron densities, molecular orbitals (MOs), and Fukui functions which are subsequently verified by detailed analyses using QSYM2.44 The insight obtained demonstrates how control of enantioselectivity using external magnetic fields is not possible—this observation is in fact consistent with earlier studies50–55 and the detailed symmetry information of the associated Fukui functions offers a simple, yet illuminating, molecular perspective. Finally, conclusions and directions for future work are summarised in Section 5. A short summary of the classification of chirality based on group theory is given in Appendix A, followed by a selection of relevant character tables in Appendix B.
2 Theory
2.1 Density-functional theory in external fields
In this section, we review several aspects of DFT that are important for external-field quantum chemistry and thus pertinent to the calculations done in this work.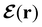 and magnetic field B(r) = ∇ × A(r), where A(r) denotes a magnetic vector potential. Both
and magnetic field B(r) = ∇ × A(r), where A(r) denotes a magnetic vector potential. Both 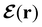 and B(r) are in general position-dependent, but, in this article, we restrict ourselves to considering only uniform fields, so that we can drop the position argument and simply write
and B(r) are in general position-dependent, but, in this article, we restrict ourselves to considering only uniform fields, so that we can drop the position argument and simply write 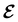 and B. The electronic Hamiltonian describing this molecular system is then given by
and B. The electronic Hamiltonian describing this molecular system is then given by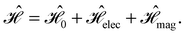 | (1) |
The first contribution is the zero-field Hamiltonian and has the form
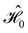 on the multiplicative external potential vext which is dictated by the geometric arrangement of the nuclei:
on the multiplicative external potential vext which is dictated by the geometric arrangement of the nuclei: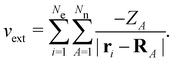 | (2) |
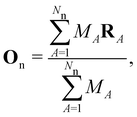 | (3) |
The second contribution describes the interaction between the system and the external electric field:56
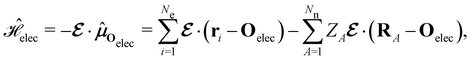 | (4) |
is the electric dipole moment operator relative to a chosen origin Oelec. In a neutral system, the choice of this origin bears no consequences to
 . In a charged system, changing the position of this origin only introduces a constant term to
. In a charged system, changing the position of this origin only introduces a constant term to  . Therefore, without any loss of generality, we choose Oelec = 0, i.e. at the origin of the Cartesian coordinate system, and subsequently drop the subscript Oelec.
. Therefore, without any loss of generality, we choose Oelec = 0, i.e. at the origin of the Cartesian coordinate system, and subsequently drop the subscript Oelec.
Finally, the third contribution gives the non-relativistic interaction of the electrons with the external magnetic field:
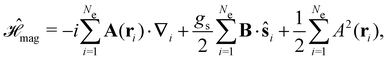 | (5) |
2.1.2.1 Electric fields. The non-perturbative inclusion of a strong external electric field is rather simple to handle since, as eqn (4) shows, the effect of the electric field on the system is linear in the field strength. If the system is described by a normalised Ne-electron wavefunction Ψ(x1,…,xNe) where xi ≡ (ri, si) is the composite spatial–spin coordinate of the ith electron, then its interaction energy with the electric field is given by
where μ = 〈Ψ|
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) |Ψ〉 is the electric dipole moment of the system. If the electron density of the system,24,58
|Ψ〉 is the electric dipole moment of the system. If the electron density of the system,24,58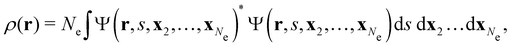 | (6) |
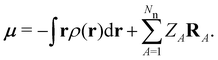 | (7) |
2.1.2.2. Magnetic fields. The non-perturbative inclusion of a strong external magnetic field is more involved. This is because the magnetic vector potential A(r) is only uniquely defined up to an arbitrary gradient:22
| A(r) → A(r) + ∇f(r) ≡ A′(r), |
| B′(r) = ∇ × A′(r) = ∇ × [A(r) + ∇f(r)] = ∇ × A(r) = B(r), |
| ∇ · A(r) = 0. |
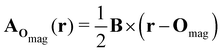 | (8) |
which leaves B unchanged and which respects the Coulomb gauge by satisfying the Laplace's equation: ∇2fΔOmag(r) = 0.
However, the inconsequential arbitrariness in the choice of gauge via the origin Omag means that quantum-chemical calculation results for physical properties such as electron densities and electric dipole moments must be gauge-independent. One way to ensure this is to include additional field-independent atomic-orbital (AO) basis functions so that gauge independence can be achieved in the complete-basis-set limit.59 A second, more economical way is to employ field-dependent AO basis functions, such as LAOs,38 which have been shown to yield gauge-origin-invariant computational results for physical properties even with minimal numbers of AO functions.38,59–61 Each LAO ωμ(r; Rμ) centred at position Rμ is a product of a conventional Gaussian AO φμ(r; Rμ) with the London phase factor exp[−iAOmag(Rμ) · r]:
| ωμ(r; Rμ) = φμ(r; Rμ)exp[−iAOmag(Rμ) · r]. | (9) |
The use of LAOs in electronic-structure calculations requires that conventional methods applicable at zero magnetic field be modified, not least because the presence of London phase factors means that wavefunctions are now in general complex-valued. This means that any formulations or implementations that assume real quantities and that do not take into account complex conjugation properly will not be valid at finite magnetic fields. To address this, efficient algorithms for evaluating molecular integrals over LAOs have been devised31,32,62,63—the availability of LAO integrals have since enabled a wide range of ab initio electronic-structure methods such as Hartree–Fock (HF),32 current-DFT,20–23 configuration interaction (CI),33 and coupled-cluster (CC)34 to be used for non-perturbative calculations in strong-magnetic-field regimes where |B| ∼ B0 = ħe−1a0−2 ≈ 2.3505 × 105 T.
| jm(r) = jp(r) + gs∇ × m(r), |
is the paramagnetic current density which describes currents induced by orbital effects, and the second term is the spin-current density which describes currents due to the spin-Zeeman interaction [the second term in eqn (5)]. Here, the magnetisationm(r) of the system is given by
where ŝs acts only on the spin coordinate s. This idea was first put forth by Vignale and Rasolt20,21 and then further refined by Tellgren et al.22,23 to result in a formal theory that takes (ρ, jm) as basic densities and (u, A) as basic potentials where
Here, u is the modified scalar potential that is required to ensure the Legendre–Fenchel conjugation between the concave extrinsic energy functional
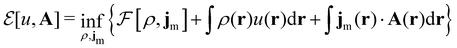 | (10) |
characteristic of conventional DFT.58
To put the theory into practical use, Vignale and Rasolt20,21 proceeded in the same way as in Kohn and Sham67 theory to decompose the intrinsic energy functional 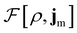 , for which the closed form is unknown, into more manageable contributions:
, for which the closed form is unknown, into more manageable contributions:
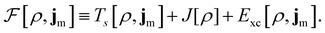 | (11) |
The first term,
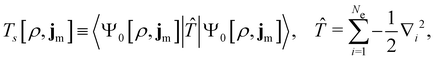 | (12) |
is the usual Coulomb interaction energy, and the last term, Exc[ρ, jm], is the unknown exchange–correlation energy that must be approximated.
By definition, the non-interacting ground-state wavefunction Ψ0[ρ, jm] in eqn (12) is a single Slater determinant:
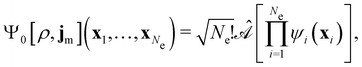 | (13) |
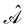 is the antisymmetriser acting on the composite spatial–spin coordinates xi in terms of which the spin–orbitals ψi are written. The corresponding kinetic energy, electron density, paramagnetic current density, and magnetisation are given explicitly in terms of the spin–orbitals by
is the antisymmetriser acting on the composite spatial–spin coordinates xi in terms of which the spin–orbitals ψi are written. The corresponding kinetic energy, electron density, paramagnetic current density, and magnetisation are given explicitly in terms of the spin–orbitals by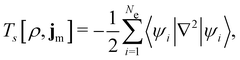 | (14a) |
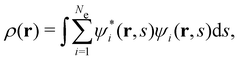 | (14b) |
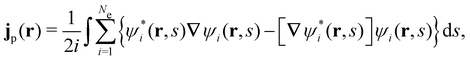 | (14c) |
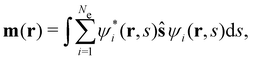 | (14d) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ψi(x) = εiψi(x), i = 1,…, Ne, ψi(x) = εiψi(x), i = 1,…, Ne, |
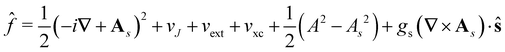 | (15) |
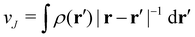 is the well-known Hartree potential, vxc = δExc[ρ, jm]/δρ the exchange–correlation scalar potential, As = A + Axc the effective vector potential, and Axc = δExc[ρ, jm]/δjm the exchange–correlation vector potential. Clearly, to ensure accurate and meaningful calculations, the unknown exchange–correlation energy Exc[ρ, jm] above must be approximated in an appropriate manner. However, in practice, constructing approximations for Exc as functionals of the magnetisation current density jm (and also the electron density ρ) is difficult,22,68 and so the spin-resolved formulation due to Vignale and Rasolt,21 using only jp, shall be used instead.
is the well-known Hartree potential, vxc = δExc[ρ, jm]/δρ the exchange–correlation scalar potential, As = A + Axc the effective vector potential, and Axc = δExc[ρ, jm]/δjm the exchange–correlation vector potential. Clearly, to ensure accurate and meaningful calculations, the unknown exchange–correlation energy Exc[ρ, jm] above must be approximated in an appropriate manner. However, in practice, constructing approximations for Exc as functionals of the magnetisation current density jm (and also the electron density ρ) is difficult,22,68 and so the spin-resolved formulation due to Vignale and Rasolt,21 using only jp, shall be used instead.
The practical calculations of current-DFT using vorticity-based corrections to local density approximation (LDA) and generalised gradient approximation (GGA) levels are known to yield rather poor accuracy.69–71 However, introducing the current dependence via the kinetic energy density at the meta-GGA level has been shown to provide good-quality results compared to higher-level correlated approaches.72 Therefore, in the present work, we shall utilise the explicit current dependence at the meta-GGA level via a modification of the (gauge-dependent) kinetic energy density,
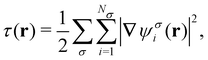 | (16) |
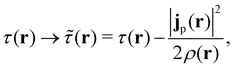 | (17) |
We also use the regularised form of the strongly constrained and appropriately normed (SCAN) semi-local density functional of Sun et al.,78 denoted r2SCAN, as proposed by Furness et al.79 The r2SCAN functional is based on the dimensionless kinetic energy density,
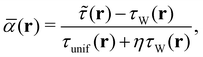 | (18) |
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) (r) the everywhere positive kinetic energy density which is modified for use in a magnetic field and has the same form as eqn (17). A simple regularisation using the parameter η = 10−3 has been defined in ref. 79 to guarantee that the r2SCAN functional avoids the numerical instabilities suffered by the original SCAN functional.79,80
(r) the everywhere positive kinetic energy density which is modified for use in a magnetic field and has the same form as eqn (17). A simple regularisation using the parameter η = 10−3 has been defined in ref. 79 to guarantee that the r2SCAN functional avoids the numerical instabilities suffered by the original SCAN functional.79,80
The global hybrid exchange–correlation functionals based on r2SCAN have been recently developed.81 They are constructed as
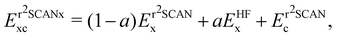 | (19) |
| ΔE ≈ ΔE(1) + ΔE(2) | (20a) |
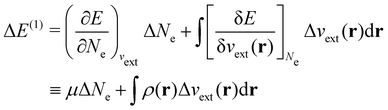 | (20b) |
 | (20c) |
In our previous studies on incorporating external magnetic fields into the framework of conceptual DFT,19,36 the two most important quantities are the first- and second-order responses of the energy functional E with respect to the number of electrons Ne at a constant external potential vext. The first of these, the electronic chemical potential,45
where I and A denote the first ionization potential and the electron affinity, respectively. The second of these,
has been identified with Pearson's chemical hardness46,90 and can, once again in its finite-difference form, be written as the difference between I and A:
It is worth noting that both μ and η are global in nature, i.e. they are independent of position. On the other hand, the electron density,
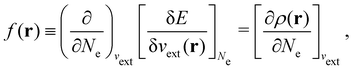 | (21a) |
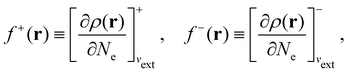 | (21b) |
The Fukui functions are generalisations of the vital rôle played by the frontier MOs in Fukui's reactivity theory.92–94 This is clearly seen in the analytical forms of the Fukui functions where they can be shown to be equal to the sum of the frontier MO density and a non-trivial correction term involving the relaxation of all MOs upon adding or subtracting one electron to or from the system.93,94 The remaining second-order derivative in eqn (20), [δ2E/δvext(r)δvext(r′)]Ne, identifiable as the linear response function χ(r, r′),24,95 is more involved due to its non-local nature and is therefore not considered in the present study. However, it may open up new avenues for future investigations in view of the recent interest in its chemical content.96
An external uniform magnetic field B can be included in the Fukui functions most easily via a finite-difference approximation along the lines of our previous work on electronegativity and hardness.19 In the particular case of f+(r), which is especially relevant for the study of nucleophilic attacks,25 subtracting the density for the neutral system, ρNe(r; B), from the corresponding density of the anionic system, ρNe+1(r; B), yields the following working equation:
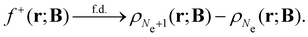 | (22a) |
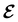 , included in this work for comparative purposes, are computed in a completely analogous way:49
, included in this work for comparative purposes, are computed in a completely analogous way:49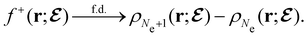 | (22b) |
We conclude this section with a comment that the formalism of incorporating electric and magnetic fields in conceptual DFT may be useful in the development of perturbed reactivity descriptors in which the intrinsic conceptual DFT reactivity descriptors of one reactant (say, A) can incorporate properties of another reactant (say, B). Though conceptually well developed by Pantoja-Hernández, Franco-Pérez, Miranda-Quintana, Gázquez, and Ayers,97–99 the practical evaluation is demanding. This may however be simplified, in a first approximation, by concentrating on the effects on reactant A caused by the electric and/or magnetic fields generated by reactant B in the non-perturbative way in our approach presented above, which may lead to an identification of the parameters introduced in ref. 97–99.
2.2 Symmetry analysis
In this section, we give formal descriptions for the concepts of symmetry that we will utilise extensively to gain insight into the reactivity of π-systems in external fields. of the system is defined as the group consisting of all unitary transformations û that commute with
of the system is defined as the group consisting of all unitary transformations û that commute with 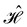 :36
:36Such unitary transformations are called unitary symmetry operations of the system. The additive form of the Hamiltonian in eqn (1) means that
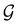 is the intersection of
is the intersection of 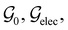 and
and 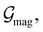 which are the unitary symmetry groups of
which are the unitary symmetry groups of 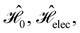 and
and 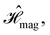 respectively. In this work, the elements in these groups are further restricted to be point transformations acting on the configuration space in which physical systems such as atoms, molecules, and fields are described.100 Then,
respectively. In this work, the elements in these groups are further restricted to be point transformations acting on the configuration space in which physical systems such as atoms, molecules, and fields are described.100 Then, 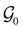 is also commonly referred to as the point group of the zero-field molecular system and
is also commonly referred to as the point group of the zero-field molecular system and 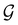 the point group of the molecular system in external fields.
the point group of the molecular system in external fields.
When magnetic phenomena are considered,40,41,101–103 antiunitary symmetry operations â that commute with 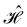 ,
,
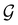 is no longer the largest symmetry group of the electronic Hamiltonian
is no longer the largest symmetry group of the electronic Hamiltonian 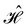 . Instead, there exists a supergroup of
. Instead, there exists a supergroup of 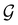 , denoted
, denoted 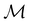 and called the magnetic symmetry group of the system, which contains all unitary symmetry operations in
and called the magnetic symmetry group of the system, which contains all unitary symmetry operations in 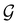 alongside other antiunitary symmetry operations not present in
alongside other antiunitary symmetry operations not present in 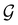 . In fact,
. In fact, 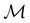 must admit
must admit 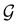 as a normal subgroup of index 2, so that we can write
as a normal subgroup of index 2, so that we can write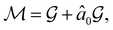 | (23) |
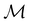 but once chosen must be fixed.40 The left coset
but once chosen must be fixed.40 The left coset 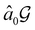 contains all antiunitary elements of
contains all antiunitary elements of 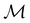 , and
, and 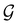 is called the unitary halving subgroup of
is called the unitary halving subgroup of 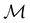 .
.
One antiunitary operation that plays an important part in the symmetry characterisation of systems in the presence of magnetic fields is that of time reversal, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) . With respect to
. With respect to ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) , magnetic symmetry groups can be classified into two kinds:40,104,105
, magnetic symmetry groups can be classified into two kinds:40,104,105
(i) grey groups—those containing ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) :
:
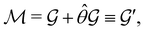 | (24) |
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) and the last equality defines the notation
and the last equality defines the notation 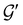 for the grey group that admits
for the grey group that admits 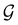 as its unitary halving subgroup, and
as its unitary halving subgroup, and
(ii) black-and-white groups—those not containing ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) :
:
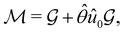 | (25) |
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) û0, with û0 a unitary operation not in
û0, with û0 a unitary operation not in 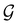 .
.
Clearly, in the absence of an external magnetic field, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) is a symmetry operation of the electronic Hamiltonian in eqn (1), so the system's magnetic symmetry group must be a grey group. In contrast, when an external magnetic field is applied,
is a symmetry operation of the electronic Hamiltonian in eqn (1), so the system's magnetic symmetry group must be a grey group. In contrast, when an external magnetic field is applied, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ceases to be a symmetry operation because the time-odd nature of the magnetic field vector39,40 gives rise to terms in the electronic Hamiltonian [eqn (5)] that do not commute with
ceases to be a symmetry operation because the time-odd nature of the magnetic field vector39,40 gives rise to terms in the electronic Hamiltonian [eqn (5)] that do not commute with ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) (cf. Appendix A of ref. 36). Therefore, if the system possesses any antiunitary symmetry operations at all, then its magnetic symmetry group must be a black-and-white group; otherwise, it only has a unitary symmetry group (see the B = B
(cf. Appendix A of ref. 36). Therefore, if the system possesses any antiunitary symmetry operations at all, then its magnetic symmetry group must be a black-and-white group; otherwise, it only has a unitary symmetry group (see the B = B![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) case in Table S1 in the ESI† for an example).
case in Table S1 in the ESI† for an example).
For any magnetic group 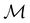 , it is useful to consider a unitary group
, it is useful to consider a unitary group 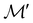 isomorphic to
isomorphic to 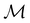 . In cases where
. In cases where 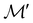 is easily identifiable with a subgroup of the full rotation-inversion group in three dimensions O(3) and can thus be given a Schönflies symbol, the magnetic group
is easily identifiable with a subgroup of the full rotation-inversion group in three dimensions O(3) and can thus be given a Schönflies symbol, the magnetic group 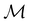 can be written as
can be written as 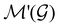 .41,105 When this is not easy or possible, however, the antiunitary coset form with respect to the unitary symmetry group
.41,105 When this is not easy or possible, however, the antiunitary coset form with respect to the unitary symmetry group 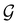 and a representative antiunitary operation â0 can always be employed to uniquely denote
and a representative antiunitary operation â0 can always be employed to uniquely denote 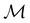 , as done in eqn (23)–(25). This is because a Schönflies symbol can always be assigned to
, as done in eqn (23)–(25). This is because a Schönflies symbol can always be assigned to 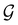 , which is guaranteed to be a subgroup of the zero-field molecular point group
, which is guaranteed to be a subgroup of the zero-field molecular point group 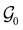 .
.
2.3 Orbit-based symmetry analysis
In this section, we briefly describe the symmetry analysis framework that is utilised to provide insight into the conceptual DFT quantities (Section 2.1.4) computed in this work. We also explain the various types of information that can be gained from the different choices of groups used in the analysis and highlight several subtleties related to magnetic symmetry.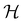 (which, as we shall see in Section 2.3.2, could be one of the symmetry groups of the system being studied, or a non-symmetry group altogether). Formally, this means identifying the subspace W⊆V spanned by the orbit‡ of w generated by
(which, as we shall see in Section 2.3.2, could be one of the symmetry groups of the system being studied, or a non-symmetry group altogether). Formally, this means identifying the subspace W⊆V spanned by the orbit‡ of w generated by 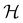 :
: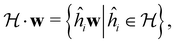 | (26) |
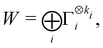 | (27) |
 if
if  is a unitary group, or known irreducible corepresentations if
is a unitary group, or known irreducible corepresentations if 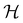 is a magnetic group,40,104,106–108 and ki their multiplicities. The mathematical details of this procedure are described in Section 2.4 of ref. 44 and will not be repeated here. There is one important technical detail that we wish to highlight, however. To simplify the way each operation ĥi acts on w to form the orbit in eqn (26), we shall set both the centre of mass of the nuclear framework [eqn (3)] and the gauge origin of the magnetic vector potential [eqn (8)] to coincide with the origin of the Cartesian coordinate system. The invariance of physical quantities with respect to these origins ensures that this particular choice that we make does not alter the results and conclusions of our work in any way.
is a magnetic group,40,104,106–108 and ki their multiplicities. The mathematical details of this procedure are described in Section 2.4 of ref. 44 and will not be repeated here. There is one important technical detail that we wish to highlight, however. To simplify the way each operation ĥi acts on w to form the orbit in eqn (26), we shall set both the centre of mass of the nuclear framework [eqn (3)] and the gauge origin of the magnetic vector potential [eqn (8)] to coincide with the origin of the Cartesian coordinate system. The invariance of physical quantities with respect to these origins ensures that this particular choice that we make does not alter the results and conclusions of our work in any way.
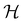 is chosen as one of the symmetry groups of the system. In particular, if
is chosen as one of the symmetry groups of the system. In particular, if 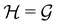 , then the decomposition in eqn (27) is called the unitary symmetry of w, and if
, then the decomposition in eqn (27) is called the unitary symmetry of w, and if 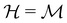 , this decomposition is instead called the magnetic symmetry of w.
, this decomposition is instead called the magnetic symmetry of w.
It is also possible to take 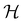 to be a group that is not a symmetry group of the system. In such cases, the decomposition in eqn (27), although still well-defined, no longer describes the symmetry of w in the strictest sense, because
to be a group that is not a symmetry group of the system. In such cases, the decomposition in eqn (27), although still well-defined, no longer describes the symmetry of w in the strictest sense, because 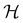 contains operations that do not commute with the system's electronic Hamiltonian—we shall henceforth refer to this as non-symmetry analysis. However, when
contains operations that do not commute with the system's electronic Hamiltonian—we shall henceforth refer to this as non-symmetry analysis. However, when 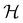 has definitive relations to the actual symmetry groups of the system, the transformation properties of w with respect to
has definitive relations to the actual symmetry groups of the system, the transformation properties of w with respect to 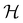 can provide helpful information. For example, if a system in the presence of some external field has unitary symmetry point group
can provide helpful information. For example, if a system in the presence of some external field has unitary symmetry point group 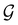 , then, by choosing
, then, by choosing 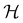 as the zero-field point group
as the zero-field point group 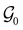 , which must be a supergroup of
, which must be a supergroup of 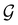 , the behaviours of w with respect to
, the behaviours of w with respect to 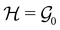 provide a way to quantify if and how the introduction of external fields alters the symmetry of w. See Section 4.2.2 for examples.
provide a way to quantify if and how the introduction of external fields alters the symmetry of w. See Section 4.2.2 for examples.
2.3.3.1 Corepresentation theory. The formal and technically correct way to analyse symmetry with respect to any magnetic group
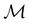 is to respect the antiunitarity of half of the elements in
is to respect the antiunitarity of half of the elements in 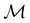 and make use of Wigner's corepresentation theory106 to derive the irreducible corepresentations of
and make use of Wigner's corepresentation theory106 to derive the irreducible corepresentations of 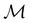 to be used in the decomposition of eqn (27). The comprehensive formulations of this theory40,106,107 and its corresponding character theory108,109 show that every irreducible corepresentation of
to be used in the decomposition of eqn (27). The comprehensive formulations of this theory40,106,107 and its corresponding character theory108,109 show that every irreducible corepresentation of 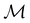 [eqn (23)] must be induced by one or two irreducible representations of the unitary halving subgroup
[eqn (23)] must be induced by one or two irreducible representations of the unitary halving subgroup 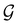 in one of three ways. This thus gives rise to only three possible kinds of irreducible corepresentations:
in one of three ways. This thus gives rise to only three possible kinds of irreducible corepresentations:
(i) D[Δ] is an irreducible corepresentation of the first kind of 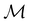 that is induced once by the irreducible representation Δ of
that is induced once by the irreducible representation Δ of 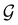 .
.
(ii) D[2Δ] is an irreducible corepresentation of the second kind of 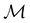 that is induced twice by the irreducible representation Δ of
that is induced twice by the irreducible representation Δ of 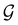 .
.
(iii) D[Δ1⊕Δ2] is an irreducible corepresentation of the third kind of 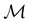 that is induced by two inequivalent irreducible representations Δ1 and Δ2 of
that is induced by two inequivalent irreducible representations Δ1 and Δ2 of 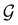 .
.
A striking consequence of this is that the character table of 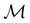 can be derived entirely from the character table of
can be derived entirely from the character table of 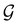 , and that the character table of
, and that the character table of 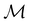 contains only the unitary elements of
contains only the unitary elements of 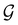 and no antiunitary elements in the coset
and no antiunitary elements in the coset  —this is in fact implemented in QSYM2.44 This makes sense because characters of antiunitary elements are not invariant with respect to a unitary transformation of basis unless the unitary transformation is also real (and thus orthogonal),40,108 and so cannot be tabulated in any sensible way. Furthermore, Corollaries 1 and 2 of Theorem 10 in ref. 108 ensure that the multiplicities ki in eqn (27) can be deduced using only the character of W under
—this is in fact implemented in QSYM2.44 This makes sense because characters of antiunitary elements are not invariant with respect to a unitary transformation of basis unless the unitary transformation is also real (and thus orthogonal),40,108 and so cannot be tabulated in any sensible way. Furthermore, Corollaries 1 and 2 of Theorem 10 in ref. 108 ensure that the multiplicities ki in eqn (27) can be deduced using only the character of W under  . It should be noted, however, that the character table of
. It should be noted, however, that the character table of  is not necessarily identical to that of
is not necessarily identical to that of  because the conjugacy class structure of
because the conjugacy class structure of 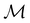 differs from that of
differs from that of 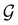 .108,109
.108,109
2.3.3.2 Magnetic symmetry via representations. Several authors40,110 have suggested that corepresentation theory is not always necessary to treat all physical problems associated with magnetic groups. This is in fact the case if w is real-valued and the linear space V that contains w is restricted to be over real numbers only—let us denote this
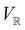 . The antiunitary operations of
. The antiunitary operations of 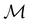 then act on
then act on 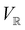 linearly, and so their characters remain invariant upon any change of basis on
linearly, and so their characters remain invariant upon any change of basis on 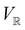 . Representation theory can thus be applied to
. Representation theory can thus be applied to 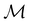 and a meaningful character table for the irreducible representations of
and a meaningful character table for the irreducible representations of 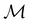 on
on 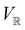 can be constructed. The irreducible representations of
can be constructed. The irreducible representations of 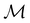 on
on 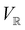 are in fact equivalent to those of
are in fact equivalent to those of 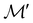 on V when restricted to
on V when restricted to 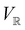 , where
, where 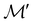 is a unitary group isomorphic to
is a unitary group isomorphic to 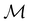 (Section 2.2.1).
(Section 2.2.1).
The advantage of this procedure is that the transformation behaviours of w are also classifiable under the antiunitary operations in 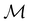 , which can impose additional constraints beside those arising from the unitary operations. As will be illustrated in Sections 4.1 and 4.2.1.2, these additional constraints are often necessary to correctly predict the symmetry properties of real-valued quantities.
, which can impose additional constraints beside those arising from the unitary operations. As will be illustrated in Sections 4.1 and 4.2.1.2, these additional constraints are often necessary to correctly predict the symmetry properties of real-valued quantities.
However, we must caution that, if w is non-real and V a complex linear space, using the irreducible representations of the unitary group 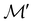 on V in eqn (27) to characterise the space W spanned by the orbit
on V in eqn (27) to characterise the space W spanned by the orbit  in which antiunitarity of actions is preserved can produce ill-defined or misleading symmetry classifications. This is once again due to the fact that characters of antiunitary operations are not necessarily invariant on complex linear spaces.40,108 One important consequence of this is that it is not possible to classify a non-real w as even or odd under time reversal
in which antiunitarity of actions is preserved can produce ill-defined or misleading symmetry classifications. This is once again due to the fact that characters of antiunitary operations are not necessarily invariant on complex linear spaces.40,108 One important consequence of this is that it is not possible to classify a non-real w as even or odd under time reversal ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) , since w is either not an eigenfunction of
, since w is either not an eigenfunction of ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) (e.g. |1/2,+1/2〉 and |1/2,−1/2〉 spinors), or if w is an eigenfunction of
(e.g. |1/2,+1/2〉 and |1/2,−1/2〉 spinors), or if w is an eigenfunction of ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) with eigenvalue λ, then scaling w by any non-real scalar also introduces a phase factor to λ, as demonstrated by Uhlmann.111
with eigenvalue λ, then scaling w by any non-real scalar also introduces a phase factor to λ, as demonstrated by Uhlmann.111
3 Computational details
The structure of H2CO was optimised at the cTPSS/cc-pVTZ level of theory whereby the geometrical alignment of H2CO is depicted in Fig. 1 in which the molecule lies in the yz-plane with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond aligned with the z-axis. For the optimised geometry, the calculations of electric dipole moments, electron densities, MOs, and Fukui functions were carried out using current-DFT with the cTPSS and r2SCAN0 functionals, described in Section 2.1.3, employing two different basis sets, 6-31G**112,113 and cc-pVTZ,114 in seven cases: at zero field, in the presence of a uniform electric field with strength
O bond aligned with the z-axis. For the optimised geometry, the calculations of electric dipole moments, electron densities, MOs, and Fukui functions were carried out using current-DFT with the cTPSS and r2SCAN0 functionals, described in Section 2.1.3, employing two different basis sets, 6-31G**112,113 and cc-pVTZ,114 in seven cases: at zero field, in the presence of a uniform electric field with strength 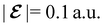 along three Cartesian x-, y-, and z-directions, and in the presence of a uniform magnetic field with strength |B| = 1.0B0 along three Cartesian x-, y-, and z-directions. All calculations were performed using QUEST.115 Since the calculation of the Fukui function f+(r) also involves the calculation of the electron density of the anionic species [eqn (22)], which is known to be unbound, the basis sets were chosen without the inclusion of diffuse functions to minimise the escaping tendency of the added electron.116 The symmetry assignments for the resulting electric dipole moments, electron densities, MOs, and Fukui functions were then determined by the QSYM2 program (v0.8.0).44
along three Cartesian x-, y-, and z-directions, and in the presence of a uniform magnetic field with strength |B| = 1.0B0 along three Cartesian x-, y-, and z-directions. All calculations were performed using QUEST.115 Since the calculation of the Fukui function f+(r) also involves the calculation of the electron density of the anionic species [eqn (22)], which is known to be unbound, the basis sets were chosen without the inclusion of diffuse functions to minimise the escaping tendency of the added electron.116 The symmetry assignments for the resulting electric dipole moments, electron densities, MOs, and Fukui functions were then determined by the QSYM2 program (v0.8.0).44
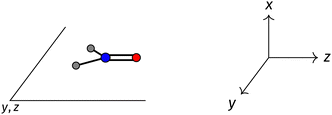 | ||
Fig. 1 Geometrical arrangement of H2CO in all calculations. The molecule lies in the yz-plane with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond aligned with the z-axis. H: grey, C: blue, O: red. O bond aligned with the z-axis. H: grey, C: blue, O: red. | ||
4 Results and discussion
In this section, we present calculation results and their symmetry analysis for formaldehyde, H2CO. We start in Section 4.1 by examining the constraints imposed by the unitary and magnetic symmetries of the system on its electric dipole moment components in various external field arrangements. This provides a preliminary understanding of the molecule's reactivity which we then explore further via the symmetries of its electron density and MOs in Section 4.2, and then its Fukui functions in Section 4.3. Ultimately, we explore from a molecular perspective the reasons that allow or forbid an external field to induce asymmetry between the two faces of H2CO.4.1 Symmetry of electric dipole moments
In Table 1, we present the symmetry constraints on the electric dipole moments of H2CO in various external electric and magnetic field orientations. In particular, for every field orientation, we show both the unitary symmetry group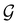 and the magnetic symmetry group
and the magnetic symmetry group 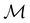 of the molecule-plus-field system alongside the electric dipole moment components that are allowed to be non-vanishing by the respective groups. As we shall see in Sections 4.2 and 4.3, the allowed dipole moment components will be of importance in the discussion of how external fields affect the overall symmetry and shape of the electron density and the Fukui functions. In the following discussion, we shall refer to fields applied along the x-axis as ‘perpendicular’ due to their orthogonality to the molecular plane of H2CO (Fig. 1), fields along the y-axis as ‘in-plane’, and fields along the z-axis as ‘parallel’ due to their collinearity with the important C
of the molecule-plus-field system alongside the electric dipole moment components that are allowed to be non-vanishing by the respective groups. As we shall see in Sections 4.2 and 4.3, the allowed dipole moment components will be of importance in the discussion of how external fields affect the overall symmetry and shape of the electron density and the Fukui functions. In the following discussion, we shall refer to fields applied along the x-axis as ‘perpendicular’ due to their orthogonality to the molecular plane of H2CO (Fig. 1), fields along the y-axis as ‘in-plane’, and fields along the z-axis as ‘parallel’ due to their collinearity with the important C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond.
O bond.
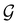 gives the unitary symmetry group of the molecule-plus-field system and
gives the unitary symmetry group of the molecule-plus-field system and 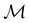 the magnetic symmetry group (cf. Section 2.2.1). In the absence of an external magnetic field,
the magnetic symmetry group (cf. Section 2.2.1). In the absence of an external magnetic field, 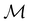 is a grey group as denoted by the dash [eqn (24)]. All symmetry analysis was performed in the QSYM2 program (v0.8.0).44 Character tables for all groups as generated by QSYM2 are given in Appendix B
is a grey group as denoted by the dash [eqn (24)]. All symmetry analysis was performed in the QSYM2 program (v0.8.0).44 Character tables for all groups as generated by QSYM2 are given in Appendix B
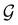 of the system descends from
of the system descends from 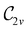 to
to 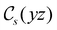 in the perpendicular orientation, to
in the perpendicular orientation, to 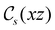 in the in-plane orientation, and to
in the in-plane orientation, and to 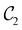 in the parallel orientation. Note that even though both perpendicular and in-plane magnetic fields give rise to the
in the parallel orientation. Note that even though both perpendicular and in-plane magnetic fields give rise to the 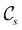 unitary symmetry group, the mirror plane with which this group is defined is different in the two cases: σyz in the perpendicular case and σxz in the in-plane case. Consequently, in both cases, the two electric dipole components that lie in the mirror plane of the system are allowed to be non-zero by the respective unitary symmetry groups: μy and μz by
unitary symmetry group, the mirror plane with which this group is defined is different in the two cases: σyz in the perpendicular case and σxz in the in-plane case. Consequently, in both cases, the two electric dipole components that lie in the mirror plane of the system are allowed to be non-zero by the respective unitary symmetry groups: μy and μz by 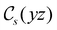 in the perpendicular case and μx and μz by
in the perpendicular case and μx and μz by 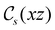 in the in-plane case. Likewise, in the parallel case, only μz is allowed to be non-zero by
in the in-plane case. Likewise, in the parallel case, only μz is allowed to be non-zero by 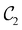 . All three deductions stem from the fact that these electric dipole moment components are totally symmetric in the respective unitary symmetry groups.
. All three deductions stem from the fact that these electric dipole moment components are totally symmetric in the respective unitary symmetry groups.
However, the above constraints placed by unitary symmetry groups on the dipole components turn out to be too loose. By including time reversal in our consideration of symmetry operations, we find that, in all three magnetic-field orientations, the system also admits magnetic black-and-white symmetry groups 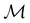 (Section 2.2.1) that are isomorphic to
(Section 2.2.1) that are isomorphic to 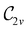 and that contain the corresponding unitary symmetry groups
and that contain the corresponding unitary symmetry groups 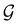 as halving subgroups. In the perpendicular and in-plane cases, the
as halving subgroups. In the perpendicular and in-plane cases, the 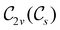 magnetic group additionally constrains μy and μx, respectively, to vanish—these components are highlighted in red in Table 1. Therefore, in all three cases, the only electric dipole component that is allowed to be non-zero by symmetry is μz, which is a more stringent requirement than that imposed by the unitary symmetry groups.
magnetic group additionally constrains μy and μx, respectively, to vanish—these components are highlighted in red in Table 1. Therefore, in all three cases, the only electric dipole component that is allowed to be non-zero by symmetry is μz, which is a more stringent requirement than that imposed by the unitary symmetry groups.
The further restrictions on μy and μx in the perpendicular and in-plane cases by 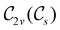 are in fact due to the antiunitary operations in the group. First, we note that μ is a real vector in
are in fact due to the antiunitary operations in the group. First, we note that μ is a real vector in 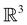 , and so, as explained in Section 2.3.3.2, representation theory can be used to characterise the symmetry transformation of μ with respect to
, and so, as explained in Section 2.3.3.2, representation theory can be used to characterise the symmetry transformation of μ with respect to 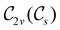 , remembering that μ is a time-even polar vector and therefore remains invariant under the action of time reversal. Then, the character table of
, remembering that μ is a time-even polar vector and therefore remains invariant under the action of time reversal. Then, the character table of 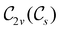 treated as a unitary group (Table 5 in Appendix B) can be consulted to deduce how the components of μ transform. For instance, consider the perpendicular case where
treated as a unitary group (Table 5 in Appendix B) can be consulted to deduce how the components of μ transform. For instance, consider the perpendicular case where ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) h ≡
h ≡ ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yzh and
yzh and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) v ≡
v ≡ ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xzv. We find that μx transforms as
xzv. We find that μx transforms as 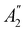 , μy as
, μy as 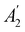 , and μz as
, and μz as 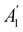 . The origin for the vanishing requirement of μy becomes clear: while μy remains invariant under both unitary elements in the group, it is inverted under
. The origin for the vanishing requirement of μy becomes clear: while μy remains invariant under both unitary elements in the group, it is inverted under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2 and
Ĉ2 and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) v and therefore must be zero. The same argument can be used to rationalise the vanishing requirement of μx in the in-plane case.
v and therefore must be zero. The same argument can be used to rationalise the vanishing requirement of μx in the in-plane case.
 and
and  for both perpendicular and in-plane electric fields, respectively, which is in line with the computational results reported in a previous study by Clarys et al.49
for both perpendicular and in-plane electric fields, respectively, which is in line with the computational results reported in a previous study by Clarys et al.49
The reason for the lack of additional constraints on μ by the magnetic group  in the absence of external magnetic fields is straightforward. Since
in the absence of external magnetic fields is straightforward. Since  is now a magnetic grey group [cf. Section 2.2.1 and eqn (24)], the time-reversal operator
is now a magnetic grey group [cf. Section 2.2.1 and eqn (24)], the time-reversal operator ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) belongs to
belongs to  , and so every antiunitary element of
, and so every antiunitary element of  can be written as
can be written as ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) û where û is in fact an element of the unitary halving subgroup
û where û is in fact an element of the unitary halving subgroup  . Then, since μ is a real-valued time-even vector on
. Then, since μ is a real-valued time-even vector on 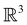 , it is guaranteed to remain invariant under
, it is guaranteed to remain invariant under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) :
: ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) μ = μ. Consequently, the action of
μ = μ. Consequently, the action of ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) û on μ is identical to that of û, and so the antiunitary half of
û on μ is identical to that of û, and so the antiunitary half of 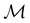 (i.e.
(i.e.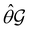 ) transforms μ in exactly the same manner as
) transforms μ in exactly the same manner as 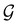 does. No new constraints on μ can thus be introduced by
does. No new constraints on μ can thus be introduced by 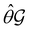 in addition to those already imposed by
in addition to those already imposed by 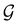 .
.
We must now highlight a remarkable difference between the symmetry effects of electric and magnetic fields which has implications for the discussions in Sections 4.2 and 4.3 on the differences in reactivity in the two types of field. The x-component of the dipole moment, whose presence is an indicator of the symmetry breaking of the electron density with respect to the molecular plane, is, as intuitively expected, non-zero for a perpendicular electric field (and zero in the other electric-field orientations). However, in the presence of a magnetic field, this component is required to vanish by the full magnetic symmetry group in all three magnetic-field orientations, thereby preserving the symmetry of the electron density with respect to the molecular plane.
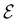 is set at 0.1 a.u. and the magnetic field strength B at 1.0B0
is set at 0.1 a.u. and the magnetic field strength B at 1.0B0
A close inspection of Table 2 reveals several interesting features. When a perpendicular electric field is applied, the z-component of the electric dipole only changes by a small amount from its zero-field counterpart (from −0.9485 a.u. to −0.9088 a.u.), as intuitively expected. On the other hand, the newly induced x-component shows a much greater gain (from 0 to +1.0645 a.u.).
If a parallel electric field is applied instead, a large change is observed for the only non-zero z-component, which is even accompanied by a sign inversion (from −0.9485 a.u. to +1.5262 a.u.). This is in accordance with the orientation of the uniform electric field where the positively charged plate from which the electric field lines emerge is on the carbon side: the electron density in H2CO is attracted towards the carbon side to such an extent that causes the original dipole moment to be inverted.
Interestingly, in the presence of an in-plane electric field, no reversal in the direction of μz is observed but the change is quite large despite the field being still perpendicular to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (from −0.9485 a.u. to −0.3133 a.u.). This is most likely due to the presence of the hydrogen atoms and the C–H σ-bonds that allow the electron density to be shifted along the y-direction towards one of the hydrogen atoms via the σ-framework of the molecule. Some electron density is thus drawn away from the oxygen end towards the carbon and hydrogen end causing the observed reduction of μz.
O bond (from −0.9485 a.u. to −0.3133 a.u.). This is most likely due to the presence of the hydrogen atoms and the C–H σ-bonds that allow the electron density to be shifted along the y-direction towards one of the hydrogen atoms via the σ-framework of the molecule. Some electron density is thus drawn away from the oxygen end towards the carbon and hydrogen end causing the observed reduction of μz.
The magnetic field cases are much more intricate. For the perpendicular-field orientation, the only surviving electric dipole component (μz as imposed by symmetry) also exhibits a sign change (from −0.9485 a.u. to +0.5307 a.u.), as is also the case in the parallel-field orientation (from −0.9485 a.u. to +1.0228 a.u.). These sign reversals are analogous to those we observed in hydrogen halides, H2O, and NH3 in a previous study.36 As will be seen in Section 4.2.3.3, they can be traced back to large shifts in polarity of the frontier MOs facilitated by a field-induced reduction in symmetry.
In view of its importance in the reactivity discussion in Section 4.3, we provide a similar analysis for formyl fluoride, HFCO, in Section S2.1 of the ESI.† Again, all computed results for electric dipole moments reflect the expected symmetry, now starting from a 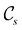 unitary symmetry at zero field with two non-zero dipole moment components μy and μz. Note also the additional vanishing constraints imposed by the magnetic groups on μx in both the in-plane and parallel magnetic-field cases.
unitary symmetry at zero field with two non-zero dipole moment components μy and μz. Note also the additional vanishing constraints imposed by the magnetic groups on μx in both the in-plane and parallel magnetic-field cases.
4.2 Symmetry of electron densities and molecular orbitals
4.2.1.1 Unitary symmetry of electron densities. The calculated electric dipole moments serve as a preliminary indicator on the distortion of the electron density ρ(r) caused by the external field, in some cases with a concomitant change in symmetry. In the Kohn–Sham-like formulation of current-DFT used in this work [eqn (14)], ρ(r) is written as a sum of squared moduli of the occupied MOs [eqn (14b)]. As all unitary symmetry groups
 considered in this study are Abelian (Table 1 and Appendix B), they only admit non-degenerate irreducible representations. Hence, in the absence of any symmetry breaking in
considered in this study are Abelian (Table 1 and Appendix B), they only admit non-degenerate irreducible representations. Hence, in the absence of any symmetry breaking in  in the occupied spin–orbitals [i.e. none of the spin–orbitals contributing to eqn (14b) and their symmetry-equivalent partners in
in the occupied spin–orbitals [i.e. none of the spin–orbitals contributing to eqn (14b) and their symmetry-equivalent partners in  span more than one irreducible representation of
span more than one irreducible representation of  ],117 the corresponding ρ(r) must transform according to the totally symmetric irreducible representation of
],117 the corresponding ρ(r) must transform according to the totally symmetric irreducible representation of 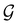 . Formally, if ψi(x) is a spin–orbital spanning the non-degenerate irreducible representation Γi of
. Formally, if ψi(x) is a spin–orbital spanning the non-degenerate irreducible representation Γi of 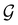 , then
, thenwhere χΓi(ĝ) is the character of ĝ in the irreducible representation χΓi. From eqn (14b), we then have:
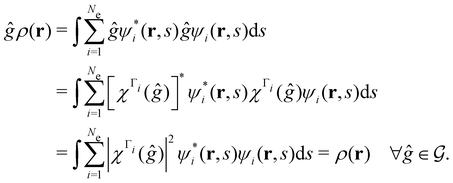 | (28) |
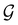 , effectively considering only cases where the Kohn–Sham Slater determinants [eqn (13)] and their MOs conserve unitary symmetry.
, effectively considering only cases where the Kohn–Sham Slater determinants [eqn (13)] and their MOs conserve unitary symmetry.
4.2.1.2 Magnetic symmetry of electron densities. However, as
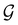 only describes unitary symmetry, it is not necessarily able to provide the full symmetry information of the system, especially when magnetic fields are present (cf. Section 4.1.1). We must therefore also consider how the electron density ρ(r) transforms under the magnetic symmetry group
only describes unitary symmetry, it is not necessarily able to provide the full symmetry information of the system, especially when magnetic fields are present (cf. Section 4.1.1). We must therefore also consider how the electron density ρ(r) transforms under the magnetic symmetry group 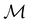 of the system. As ρ(r) is everywhere real-valued, and as the containing linear space for ρ(r) is well known to be the Banach space
of the system. As ρ(r) is everywhere real-valued, and as the containing linear space for ρ(r) is well known to be the Banach space 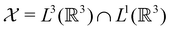 58 which is a real linear space, representation theory can be used to classify the symmetry of ρ(r) using the irreducible representations of
58 which is a real linear space, representation theory can be used to classify the symmetry of ρ(r) using the irreducible representations of 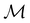 on
on 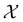 , as explained in Section 2.3.3.2.
, as explained in Section 2.3.3.2.
Let us first consider 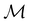 to be a magnetic grey group, which is applicable in the absence of external magnetic fields. Using the fact that ρ(r) is totally symmetric with respect to
to be a magnetic grey group, which is applicable in the absence of external magnetic fields. Using the fact that ρ(r) is totally symmetric with respect to 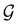 and that ρ(r) is invariant under time reversal, we conclude that ρ(r) must also transform as the totally symmetric irreducible representation of
and that ρ(r) is invariant under time reversal, we conclude that ρ(r) must also transform as the totally symmetric irreducible representation of 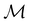 on
on 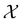 , since
, since ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ûρ(r) = ûρ(r) = ρ(r) for any û in
ûρ(r) = ûρ(r) = ρ(r) for any û in 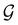 . For instance, consider the perpendicular-electric-field case where the magnetic symmetry group is
. For instance, consider the perpendicular-electric-field case where the magnetic symmetry group is 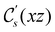 whose character table of irreducible representations is given in Table 7: the only irreducible representation that has +1 characters under all unitary operations as well as time reversal is +A′, which is totally symmetric in
whose character table of irreducible representations is given in Table 7: the only irreducible representation that has +1 characters under all unitary operations as well as time reversal is +A′, which is totally symmetric in 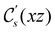 .
.
On the other hand, if  is a magnetic black-and-white group, which is the case in the presence of external magnetic fields, then there is no a priori requirement that ρ(r) must transform as the totally symmetric irreducible representation of
is a magnetic black-and-white group, which is the case in the presence of external magnetic fields, then there is no a priori requirement that ρ(r) must transform as the totally symmetric irreducible representation of  . This is because even though ρ(r) is invariant under
. This is because even though ρ(r) is invariant under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) , there is no guarantee that it is also invariant under â0 =
, there is no guarantee that it is also invariant under â0 = ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) û0 for û0 a unitary operation not in
û0 for û0 a unitary operation not in  [see eqn (25)]. By extension, there is no guarantee that ρ(r) is invariant under any other antiunitary element â =
[see eqn (25)]. By extension, there is no guarantee that ρ(r) is invariant under any other antiunitary element â = ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) û of
û of  either, where û is also a unitary operation not in
either, where û is also a unitary operation not in 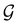 . To express this difficulty formally, from eqn (6), we have:
. To express this difficulty formally, from eqn (6), we have:
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) , and that ρ(r) is invariant under
, and that ρ(r) is invariant under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) . But since û is not a unitary symmetry operation of the system and thus does not commute with
. But since û is not a unitary symmetry operation of the system and thus does not commute with 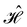 , it is not possible to comment on how Ψ transforms under û without further analysis, thus precluding any a priori knowledge of how ρ(r) transforms under the whole of
, it is not possible to comment on how Ψ transforms under û without further analysis, thus precluding any a priori knowledge of how ρ(r) transforms under the whole of 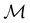 . For example, consider the perpendicular-magnetic-field case where the magnetic symmetry group is
. For example, consider the perpendicular-magnetic-field case where the magnetic symmetry group is 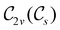 whose character table of irreducible representations is given in Table 5: both
whose character table of irreducible representations is given in Table 5: both 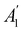 and
and 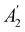 have +1 characters under all unitary operations, but there is insufficient information on how ρ(r) is transformed by the antiunitary elements in the group to deduce which of these two irreducible representations actually describes the symmetry of ρ(r). Fortunately, in Section 4.2.2.2, we will illustrate how arguments based on symmetry constraints imposed on electric dipole moments can provide the unknown transformation information.
have +1 characters under all unitary operations, but there is insufficient information on how ρ(r) is transformed by the antiunitary elements in the group to deduce which of these two irreducible representations actually describes the symmetry of ρ(r). Fortunately, in Section 4.2.2.2, we will illustrate how arguments based on symmetry constraints imposed on electric dipole moments can provide the unknown transformation information.
4.2.1.3 Magnetic symmetry of molecular orbitals. Unfortunately, it is also not possible to use the same argument based on group Abelianity and spin–orbital non-degeneracy as in Section 4.2.1.1 to ascertain the representation spanned by ρ(r) in a magnetic black-and-white group. Firstly, this argument requires that the spin–orbitals ψi(x) contributing to ρ(r) be classifiable as a representation of
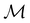 , but since ψi(x) are in general complex-valued in the presence of magnetic fields [eqn (9)], representation theory cannot be applied to assign meaningful unitary symmetries for ψi(x). Essentially, as explained in Section 2.3.3.2, this boils down to the fact that ψi(x) do not have well-defined characters under antiunitary operations.
, but since ψi(x) are in general complex-valued in the presence of magnetic fields [eqn (9)], representation theory cannot be applied to assign meaningful unitary symmetries for ψi(x). Essentially, as explained in Section 2.3.3.2, this boils down to the fact that ψi(x) do not have well-defined characters under antiunitary operations.
However, more importantly, if we consider each spin–orbital ψi(x) as a function on the one-electron Hilbert space 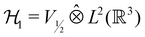 where V1/2 is the two-dimensional space spanned by the spinors |1/2,+1/2〉 ≡ |α〉 and |1/2,−1/2〉 ≡ |β〉 which describes the symmetry of electron spins,118 then, on
where V1/2 is the two-dimensional space spanned by the spinors |1/2,+1/2〉 ≡ |α〉 and |1/2,−1/2〉 ≡ |β〉 which describes the symmetry of electron spins,118 then, on 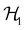 , the action of
, the action of ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) is given in terms of the 1/2-spinors by119
is given in terms of the 1/2-spinors by119
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) |α〉 = +|β〉, |α〉 = +|β〉, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) |β〉 = −|α〉. |β〉 = −|α〉. |
where ωμ and ων are LAOs [eqn (9)] and
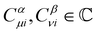 , the time-reversal partner
, the time-reversal partner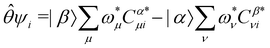 | (29) |
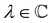 such that
such that ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ψi = λψi. This means that the space spanned by the orbit
ψi = λψi. This means that the space spanned by the orbit 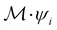 must always be at least two-dimensional because the antiunitary elements in
must always be at least two-dimensional because the antiunitary elements in 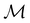 are always guaranteed to generate at least one linearly independent partner when acting on ψi. The simple line of reasoning in eqn (28) thus no longer applies.
are always guaranteed to generate at least one linearly independent partner when acting on ψi. The simple line of reasoning in eqn (28) thus no longer applies.
The above difficulties highlight an important implication: the antiunitarity of certain symmetry operations in the presence of magnetic fields complicates the magnetic symmetry of spin–orbitals and prevents them from being easily related to the unitary symmetry of electron densities. Fortunately, QSYM2 is capable of analysing explicitly the unitary symmetry of ρ(r) under 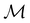 without having to involve the symmetries of the constituent spin–orbitals,44 thus sidestepping the difficulties described above. Throughout the rest of this section, therefore, we will focus mainly on density symmetries as proxies for how external fields affect the distribution of electrons in the system. Then, we will examine how the a posteriori knowledge of density symmetries obtained via QSYM2 sheds light on the more complicated spin–orbital magnetic symmetries.
without having to involve the symmetries of the constituent spin–orbitals,44 thus sidestepping the difficulties described above. Throughout the rest of this section, therefore, we will focus mainly on density symmetries as proxies for how external fields affect the distribution of electrons in the system. Then, we will examine how the a posteriori knowledge of density symmetries obtained via QSYM2 sheds light on the more complicated spin–orbital magnetic symmetries.
Before moving on to the results, we make one final remark that the action of time reversal defined in eqn (29) is one that involves spin explicitly. This means that, since every spin–orbital ψi is by definition a one-electron wavefunction, the space spanned by ψi and its time-reversal partner ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ψi must be characterised by the projective, or double-valued, irreducible corepresentations of
ψi must be characterised by the projective, or double-valued, irreducible corepresentations of 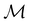 .100,120 However, this does not add much insight to the discussion in this article, and so we will instead neglect the action of
.100,120 However, this does not add much insight to the discussion in this article, and so we will instead neglect the action of ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) on the spin coordinate, effectively treating
on the spin coordinate, effectively treating ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) as though it were the conventional complex conjugation operation and therefore ignoring spin–orbit coupling.121 This is reasonable as long as the pertinent spin–orbitals are spin–collinear, which is indeed the case in all calculations in this work. It is then possible to use only the single-valued irreducible corepresentations of
as though it were the conventional complex conjugation operation and therefore ignoring spin–orbit coupling.121 This is reasonable as long as the pertinent spin–orbitals are spin–collinear, which is indeed the case in all calculations in this work. It is then possible to use only the single-valued irreducible corepresentations of 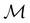 to describe the symmetry of spin–orbitals (cf. Section 4.2.3).
to describe the symmetry of spin–orbitals (cf. Section 4.2.3).
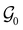 of the system, any symmetry breaking of the dipole moment with respect to
of the system, any symmetry breaking of the dipole moment with respect to 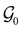 induced by external fields must manifest in the first term via the electron density ρ(r). Conversely, eqn (7) also allows one to deduce the symmetry of the electron density from the symmetry of the dipole moment. The discussion in Section 4.1 shall therefore allow us to predict several aspects of the density symmetry that cannot be ascertained by the general considerations in Section 4.2.1—these will then be confirmed by explicit analyses provided by QSYM2.
induced by external fields must manifest in the first term via the electron density ρ(r). Conversely, eqn (7) also allows one to deduce the symmetry of the electron density from the symmetry of the dipole moment. The discussion in Section 4.1 shall therefore allow us to predict several aspects of the density symmetry that cannot be ascertained by the general considerations in Section 4.2.1—these will then be confirmed by explicit analyses provided by QSYM2.
4.2.2.1 Densities in electric fields. Let us commence the analysis with the more intuitive cases in the absence of external fields and presence of external electric fields where both unitary and magnetic groups give rise to the same constraints on the dipole moment components (Table 1). Fig. 2 shows the electron densities of the neutral H2CO molecule in the presence of an external electric field in the three orientations discussed earlier (Table 1), alongside the density at zero field for comparison. The electron densities are presented as contours in the vertical plane perpendicular to the molecular plane containing the C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, and also in the horizontal plane of the molecule.
O bond, and also in the horizontal plane of the molecule.
Compared to the zero-field case [Fig. 2(a)], Fig. 2(b) reveals that the presence of a perpendicular electric field along the positive x-direction 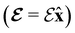 shifts the ρ(r) contours towards the negative x-direction below the molecular plane in the view shown, especially in the valence region, thus breaking symmetry with respect to this plane. This is as expected from the non-zero μx component allowed by both the unitary symmetry group
shifts the ρ(r) contours towards the negative x-direction below the molecular plane in the view shown, especially in the valence region, thus breaking symmetry with respect to this plane. This is as expected from the non-zero μx component allowed by both the unitary symmetry group 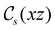 and the magnetic symmetry group
and the magnetic symmetry group 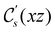 (Tables 1 and 2).
(Tables 1 and 2).
In fact, the symmetry breaking of ρ(r) due to the perpendicular electric field can be quantified by performing a non-symmetry analysis (Section 2.3.2) in the zero-field point group 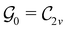 using QSYM2: it is found that the perpendicular electric field causes ρ(r) to break symmetry in
using QSYM2: it is found that the perpendicular electric field causes ρ(r) to break symmetry in 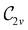 and transform as A1⊕B1. This reducible representation has a character of 0 under
and transform as A1⊕B1. This reducible representation has a character of 0 under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz which implies that ρ(r) no longer has a definitive symmetry with respect to this reflection operation. This is consistent with the observation that the electron density regions above and below the molecular plane have become asymmetrical due to the distortion induced by the perpendicular electric field.
yz which implies that ρ(r) no longer has a definitive symmetry with respect to this reflection operation. This is consistent with the observation that the electron density regions above and below the molecular plane have become asymmetrical due to the distortion induced by the perpendicular electric field.
On the other hand, in the in-plane and parallel orientations of the external electric field shown in Fig. 2(c) and (d), respectively, the symmetry of ρ(r) with respect to the molecular plane is preserved, which is expected from the vanishing constraints imposed on μx by both unitary and magnetic symmetry groups (Table 1). This is also confirmed by the non-symmetry analysis in 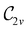 : in the in-plane case, ρ(r) transforms as A1⊕B2 which is a two-dimensional reducible representation with a character of +2 under
: in the in-plane case, ρ(r) transforms as A1⊕B2 which is a two-dimensional reducible representation with a character of +2 under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz, thus indicating that ρ(r) is symmetric under this reflection;§ likewise, in the parallel case, ρ(r) transforms as A1 and is therefore also symmetric under
yz, thus indicating that ρ(r) is symmetric under this reflection;§ likewise, in the parallel case, ρ(r) transforms as A1 and is therefore also symmetric under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz. We note that the symmetry breaking observed in the in-plane case is now with respect to a different mirror plane—the σxz plane—of the molecule, as shown in Fig. 2(g), in accordance with the non-zero μy component allowed by symmetry (Tables 1 and 2).
yz. We note that the symmetry breaking observed in the in-plane case is now with respect to a different mirror plane—the σxz plane—of the molecule, as shown in Fig. 2(g), in accordance with the non-zero μy component allowed by symmetry (Tables 1 and 2).
We caution in passing that the fact that ρ(r) is guaranteed to be totally symmetric in the unitary symmetry group 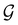 as well as the magnetic grey group
as well as the magnetic grey group 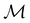 does not necessarily reveal anything about its symmetry with respect to the molecular plane. This can be seen most clearly in the perpendicular-field case where the symmetry groups are
does not necessarily reveal anything about its symmetry with respect to the molecular plane. This can be seen most clearly in the perpendicular-field case where the symmetry groups are 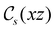 and
and 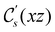 , neither of which contains any
, neither of which contains any ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz-related operations. This is why to examine the transformation of ρ(r) under
yz-related operations. This is why to examine the transformation of ρ(r) under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz, a non-symmetry analysis in the zero-field unitary group
yz, a non-symmetry analysis in the zero-field unitary group 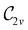 was required.
was required.
It is also noteworthy that, in the in-plane and parallel cases, the density shift towards the carbon atom region is responsible for the inversion of the dipole moment along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (that is, μz) as discussed in Section 4.1.3. In fact, Fig. 2(g) and (h) show that the presence of the hydrogen atoms creates additional ‘sinks’ towards which the electron density can be driven by the applied electric field that lies in the molecular plane. This is clearly not possible if the electric field is applied perpendicular to the molecule instead, as is evident by the nearly identical sideways distribution of the electron density between the zero-field case [Fig. 2(e)] and the perpendicular case [Fig. 2(f)].
O bond (that is, μz) as discussed in Section 4.1.3. In fact, Fig. 2(g) and (h) show that the presence of the hydrogen atoms creates additional ‘sinks’ towards which the electron density can be driven by the applied electric field that lies in the molecular plane. This is clearly not possible if the electric field is applied perpendicular to the molecule instead, as is evident by the nearly identical sideways distribution of the electron density between the zero-field case [Fig. 2(e)] and the perpendicular case [Fig. 2(f)].
4.2.2.2 Densities in magnetic fields. We proceed next to the cases of external magnetic fields where magnetic symmetry can impose additional constraints on some dipole moment components (Table 1); Fig. 3 shows the electron density contours in these cases (alongside the zero-field electron density contours for comparison). From the vanishing constraints on both μx and μy in all three magnetic-field orientations (Table 1), it is unsurprising that all densities in Fig. 3 transform as A1 in the non-symmetry group
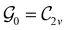 and are therefore symmetric with respect to both
and are therefore symmetric with respect to both ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz and
yz and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xz. In other words, applying an external magnetic field along any of the Cartesian axes to H2CO does not cause the electron density ρ(r) to break any of its original reflection symmetries.
xz. In other words, applying an external magnetic field along any of the Cartesian axes to H2CO does not cause the electron density ρ(r) to break any of its original reflection symmetries.
The origin of the observed symmetry preservation for ρ(r) can be traced back to the presence of symmetry elements in the corresponding magnetic black-and-white symmetry groups that involve ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz and
yz and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xz [i.e.
xz [i.e.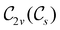 ,
, 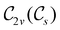 , and
, and 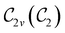 ], be they with or without an accompanying time-reversal operation. These symmetry elements constrain both μx and μy to vanish, thus requiring ρ(r) to be symmetric accordingly. It turns out that ρ(r) is also totally symmetric in each of the magnetic symmetry groups in the three magnetic-field cases considered (Fig. 3).
], be they with or without an accompanying time-reversal operation. These symmetry elements constrain both μx and μy to vanish, thus requiring ρ(r) to be symmetric accordingly. It turns out that ρ(r) is also totally symmetric in each of the magnetic symmetry groups in the three magnetic-field cases considered (Fig. 3).
We must however emphasise that the fact that ρ(r) transforms as the totally symmetric irreducible representation under the above three magnetic black-and-white groups  is a conclusion that has been obtained from an explicit symmetry analysis of the calculated result for ρ(r) using QSYM2, instead of one that could have been predicted by simply considering the mathematical definition of ρ(r), because of the reasons outlined in Section 4.2.1.2. This conclusion regarding the electron density on the microscopic level is in fact consistent with what one would expect based on the constraints imposed by the magnetic groups on the electric dipole moment, which is the simplest non-scalar tensor describing static properties of materials on the macroscopic level.40 We must also highlight the fortuitous isomorphism between the three magnetic groups
is a conclusion that has been obtained from an explicit symmetry analysis of the calculated result for ρ(r) using QSYM2, instead of one that could have been predicted by simply considering the mathematical definition of ρ(r), because of the reasons outlined in Section 4.2.1.2. This conclusion regarding the electron density on the microscopic level is in fact consistent with what one would expect based on the constraints imposed by the magnetic groups on the electric dipole moment, which is the simplest non-scalar tensor describing static properties of materials on the macroscopic level.40 We must also highlight the fortuitous isomorphism between the three magnetic groups  and the zero-field point group
and the zero-field point group 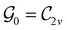 : total symmetry of ρ(r) with respect to any of these
: total symmetry of ρ(r) with respect to any of these  also implies total symmetry with respect to
also implies total symmetry with respect to  because of the invariance of ρ(r) under time reversal.
because of the invariance of ρ(r) under time reversal.
The contour plots in Fig. 3 also provide insight into the behaviour of the z-components of the electric dipole moment in various magnetic-field orientations (Table 2). Fig. 3(d) shows a pronounced shift of the electron density towards the carbon region in the xz-plane when the magnetic field is applied parallel to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, thus accounting for the drastic μz inversion from −0.9485 a.u. to +1.0228 a.u. (Table 2). Similarly, Fig. 3(f) shows a rather more subtle shift of the electron density towards the carbon region in the yz-plane when the magnetic field is applied perpendicular to the molecule, which is responsible for the corresponding μz inversion from −0.9485 a.u. to +0.5307 a.u. (Table 2). In the next section, the symmetry of frontier MOs will be used to shed even more light on these inversions.
O bond, thus accounting for the drastic μz inversion from −0.9485 a.u. to +1.0228 a.u. (Table 2). Similarly, Fig. 3(f) shows a rather more subtle shift of the electron density towards the carbon region in the yz-plane when the magnetic field is applied perpendicular to the molecule, which is responsible for the corresponding μz inversion from −0.9485 a.u. to +0.5307 a.u. (Table 2). In the next section, the symmetry of frontier MOs will be used to shed even more light on these inversions.
 , unitary symmetry group
, unitary symmetry group  , and magnetic symmetry group
, and magnetic symmetry group  are also shown. We note in particular that magnetic symmetries in
are also shown. We note in particular that magnetic symmetries in  are given in terms of its single-valued irreducible corepresentations since time reversal is taken to act only on spatial coordinates (therefore ignoring spin) and is thus identical to the conventional complex conjugation (cf. the last paragraph of Section 4.2.1.3).
are given in terms of its single-valued irreducible corepresentations since time reversal is taken to act only on spatial coordinates (therefore ignoring spin) and is thus identical to the conventional complex conjugation (cf. the last paragraph of Section 4.2.1.3).
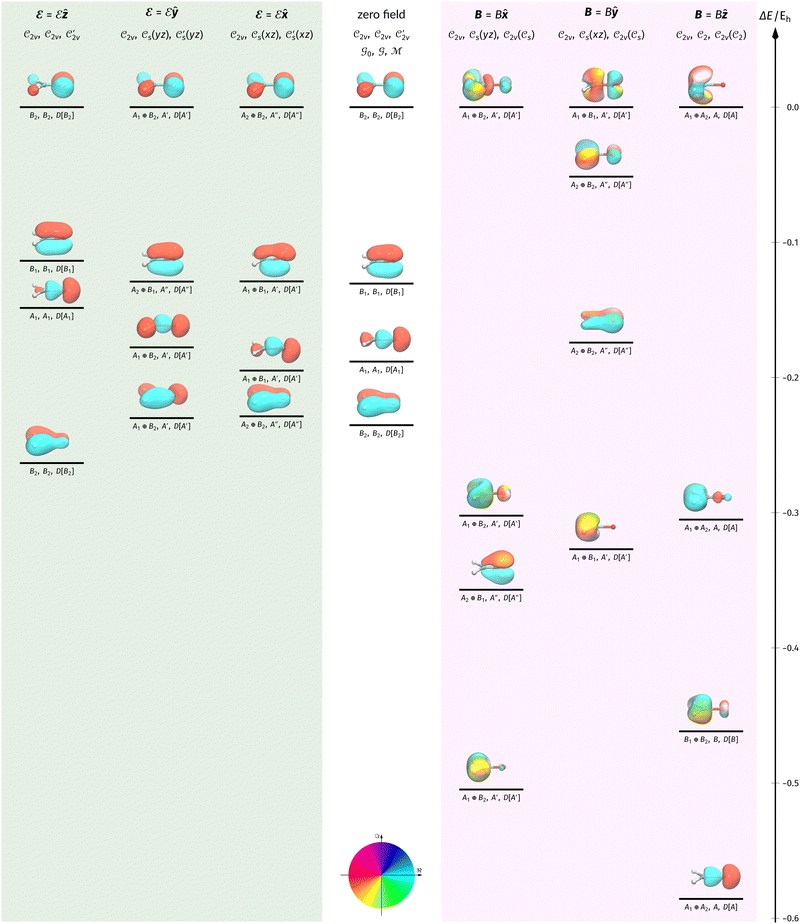 | ||
Fig. 4 Isosurfaces and relative energies of frontier MOs in the α-spin space of H2CO in various external-field configurations. The isosurface for MO ψ(r) is plotted at |ψ(r)| = 0.1, and the colour at each point r on the isosurface indicates the phase angle argψ(r) ∈ (−π,π] at that point according to the accompanying colour wheel shown at the bottom of the table.123 The orbital energies are given relative to that of the highest occupied MO (HOMO) in each case, so that ΔE = E − EHOMO. The symmetries of each MO are specified in the corresponding non-symmetry zero-field group  , unitary symmetry group , unitary symmetry group  , and magnetic symmetry group , and magnetic symmetry group  . Magnetic symmetries in . Magnetic symmetries in  are given in terms of its single-valued irreducible corepresentations since time reversal is taken to act only on spatial coordinates (therefore ignoring spin) and is thus identical to the conventional complex conjugation (cf. the last paragraph of Section 4.2.1.3). are given in terms of its single-valued irreducible corepresentations since time reversal is taken to act only on spatial coordinates (therefore ignoring spin) and is thus identical to the conventional complex conjugation (cf. the last paragraph of Section 4.2.1.3). | ||
4.2.3.1 Modular symmetry breaking in electric fields. The MOs in the electric-field cases provide straightforward and intuitive ‘references' that form the basis for our subsequent discussion on the more complicated MOs in the presence of magnetic fields. Applying an electric field perpendicular to the C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in either the x- or y-direction (i.e. perpendicular and in-plane cases) indeed breaks the symmetry of the frontier MOs, as is evident by the fact that they all span reducible representations in the non-symmetry zero-field group
O bond in either the x- or y-direction (i.e. perpendicular and in-plane cases) indeed breaks the symmetry of the frontier MOs, as is evident by the fact that they all span reducible representations in the non-symmetry zero-field group 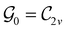 . For example, an electric field along the x-direction causes the frontier MOs to span either A1⊕B1 or A2⊕B2 in
. For example, an electric field along the x-direction causes the frontier MOs to span either A1⊕B1 or A2⊕B2 in 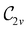 , both of which have a character of 0 under
, both of which have a character of 0 under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz (cf.Table 3) and therefore have no definitive symmetry with respect to this reflection. This is consistent with the expectation that the perpendicular electric field along the x-direction distorts the shape of the electron density and breaks the symmetry of the MO moduli |ψ(r)| with respect to the molecular plane. Likewise, applying an electric field along the y-direction causes the frontier MOs to span either A1⊕B2 or A2⊕B1 in
yz (cf.Table 3) and therefore have no definitive symmetry with respect to this reflection. This is consistent with the expectation that the perpendicular electric field along the x-direction distorts the shape of the electron density and breaks the symmetry of the MO moduli |ψ(r)| with respect to the molecular plane. Likewise, applying an electric field along the y-direction causes the frontier MOs to span either A1⊕B2 or A2⊕B1 in 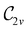 , both of which are symmetry-broken under
, both of which are symmetry-broken under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xz, once again on account of the MO moduli |ψ(r)|.
xz, once again on account of the MO moduli |ψ(r)|.
Since the MOs in the presence of electric fields remain entirely real-valued, the nature of the observed symmetry breaking of these MOs with respect to the non-symmetry zero-field group 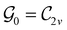 in the perpendicular and in-plane cases is the same as that of the electron densities discussed in Section 4.2.2.1. In both cases, symmetry breaking arises primarily from the distortion of the shape, or more formally, the modulus |·|, of the quantity of interest driven by the external field. We will therefore refer to this type of symmetry breaking as modular symmetry breaking. In fact, the symmetry elements of
in the perpendicular and in-plane cases is the same as that of the electron densities discussed in Section 4.2.2.1. In both cases, symmetry breaking arises primarily from the distortion of the shape, or more formally, the modulus |·|, of the quantity of interest driven by the external field. We will therefore refer to this type of symmetry breaking as modular symmetry breaking. In fact, the symmetry elements of 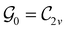 under which the electron densities and MOs undergo modular symmetry breaking as an external electric field is introduced are those elements that do not belong to the unitary symmetry group
under which the electron densities and MOs undergo modular symmetry breaking as an external electric field is introduced are those elements that do not belong to the unitary symmetry group  of the molecule-plus-field system.
of the molecule-plus-field system.
4.2.3.2 Phasal symmetry breaking in magnetic fields. The situation is remarkably different for magnetic fields. Applying a magnetic field perpendicular to the C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in either the x- or y-direction (i.e. perpendicular and in-plane cases) no longer distorts the shapes of the MOs either along or perpendicular to the applied direction, yet the MOs still exhibit symmetry breaking in the non-symmetry zero-field group
O bond in either the x- or y-direction (i.e. perpendicular and in-plane cases) no longer distorts the shapes of the MOs either along or perpendicular to the applied direction, yet the MOs still exhibit symmetry breaking in the non-symmetry zero-field group  . For example, when the magnetic field is applied in the y-direction, the HOMO has A1⊕B1 symmetry in
. For example, when the magnetic field is applied in the y-direction, the HOMO has A1⊕B1 symmetry in  . Once again, from Table 3, this representation conserves symmetry under
. Once again, from Table 3, this representation conserves symmetry under ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xz but not
xz but not ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz. A careful examination of the isosurface plot of this HOMO [enlarged and reproduced in Fig. 5(a)] in conjunction with the colour wheel in Fig. 4 suggests that the observed
yz. A careful examination of the isosurface plot of this HOMO [enlarged and reproduced in Fig. 5(a)] in conjunction with the colour wheel in Fig. 4 suggests that the observed ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz-symmetry breaking is caused by the phase rather than shape of the MO. This is because there is not a single multiplicative phase relation for every point between the top and bottom halves of the MO (i.e. it is not possible to say that the top half is the bottom half multiplied by a fixed scalar factor like +1 or −1), hence the symmetry breaking under spatial unitary transformations in
yz-symmetry breaking is caused by the phase rather than shape of the MO. This is because there is not a single multiplicative phase relation for every point between the top and bottom halves of the MO (i.e. it is not possible to say that the top half is the bottom half multiplied by a fixed scalar factor like +1 or −1), hence the symmetry breaking under spatial unitary transformations in 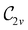 . We shall therefore term this phenomenon phasal symmetry breaking to signify its difference in nature to the modular symmetry breaking observed in the presence of an electric field.
. We shall therefore term this phenomenon phasal symmetry breaking to signify its difference in nature to the modular symmetry breaking observed in the presence of an electric field.
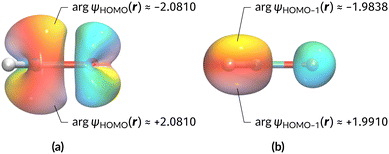 | ||
| Fig. 5 Enlarged side views of the isosurface plots at |ψ(r)| = 0.1 for (a) the HOMO and (b) the HOMO−1 in the in-plane magnetic field case (B = Bŷ). For each MO ψ(r), the phase angles in radians at two example points on the isosurface that are related by the σyz mirror plane are shown. These plots demonstrate the two types of phasal symmetry breaking in a magnetic field. Note that the isosurfaces in this figure are viewed directly down the y-axis so that the σyz-relationship between the top and bottom faces of the molecule can be easily identified. This view is slightly different from that adopted for the MO isosurface plots in Fig. 4. | ||
It turns out that there are two ways in which MO phases can break spatial symmetry. The first way is demonstrated by the HOMO in the B = Bŷ case shown in Fig. 5(a) where it can be seen that any two points on the isosurface that are related by the σyz mirror plane are also complex conjugates of each other. This implies that, even though ψHOMO and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yzψHOMO are linearly independent and thus symmetry-broken in
yzψHOMO are linearly independent and thus symmetry-broken in  , incorporating the antilinear effect of the time-reversal operator
, incorporating the antilinear effect of the time-reversal operator ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) via its complex-conjugation action (see the last paragraph of Section 4.2.1.3) restores symmetry since we now have
via its complex-conjugation action (see the last paragraph of Section 4.2.1.3) restores symmetry since we now have ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yzψHOMO = ψHOMO. In other words, ψHOMO has a character of +1 under
yzψHOMO = ψHOMO. In other words, ψHOMO has a character of +1 under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz, which is unexpected because characters under antiunitary symmetry operations are in general not well-defined (Section 2.3.3.2). The same argument can be made for
yz, which is unexpected because characters under antiunitary symmetry operations are in general not well-defined (Section 2.3.3.2). The same argument can be made for ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2, the remaining antiunitary element of the magnetic group
Ĉ2, the remaining antiunitary element of the magnetic group  , to arrive at the equality
, to arrive at the equality ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2ψHOMO = ψHOMO, thus allowing ψHOMO to be (rather fortuitously) classifiable as the irreducible representation
Ĉ2ψHOMO = ψHOMO, thus allowing ψHOMO to be (rather fortuitously) classifiable as the irreducible representation 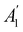 of this group (Table 5), as verified by QSYM2, even though ψHOMO itself is a complex-valued quantity, in an apparent contradiction to the points raised in Section 2.3.3.2. Here, the HOMO phases break spatial unitary symmetry in
of this group (Table 5), as verified by QSYM2, even though ψHOMO itself is a complex-valued quantity, in an apparent contradiction to the points raised in Section 2.3.3.2. Here, the HOMO phases break spatial unitary symmetry in 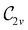 but conserve magnetic antiunitary symmetry in
but conserve magnetic antiunitary symmetry in 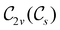 .
.
However, this behaviour is not general. Fig. 5(b) shows the HOMO−1 in the B = Bŷ case where σyz-related points on the isosurface are no longer complex conjugates of each other. This means that ψHOMO−1 and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yzψHOMO−1 are non-identical, and the difference is simply too great to be attributed to mere numerical imprecision. Consequently, ψHOMO−1 has no well-defined symmetry under
yzψHOMO−1 are non-identical, and the difference is simply too great to be attributed to mere numerical imprecision. Consequently, ψHOMO−1 has no well-defined symmetry under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz (as well as
yz (as well as ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2 by a similar argument) and is therefore not classifiable using any of the irreducible representations of
Ĉ2 by a similar argument) and is therefore not classifiable using any of the irreducible representations of 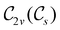 in Table 5. This is as expected by virtue of the discussion in Section 2.3.3.2. The phases of the HOMO−1 now break both spatial unitary symmetry in
in Table 5. This is as expected by virtue of the discussion in Section 2.3.3.2. The phases of the HOMO−1 now break both spatial unitary symmetry in 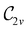 and magnetic antiunitary symmetry in
and magnetic antiunitary symmetry in 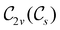 .
.
To reliably quantify the symmetry of complex-valued MOs in magnetic groups, we must appeal to corepresentation theory (Section 2.3.3.1). As such, the magnetic symmetries of the MOs in Fig. 4 are given in terms of the irreducible corepresentations of their respective magnetic groups  —these have been computed by QSYM2 using Corollaries 1 and 2 of Theorem 10 in ref. 108. To understand how these magnetic symmetry assignments can be interpreted, we shall consider again the HOMO and HOMO−1 in the B = Bŷ case. First, note that the HOMO has A′ symmetry in the
—these have been computed by QSYM2 using Corollaries 1 and 2 of Theorem 10 in ref. 108. To understand how these magnetic symmetry assignments can be interpreted, we shall consider again the HOMO and HOMO−1 in the B = Bŷ case. First, note that the HOMO has A′ symmetry in the 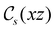 unitary symmetry group and D[A′] symmetry in the
unitary symmetry group and D[A′] symmetry in the 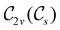 magnetic symmetry group. The unitary symmetry A′ of the HOMO means that the orbit [eqn (26)]
magnetic symmetry group. The unitary symmetry A′ of the HOMO means that the orbit [eqn (26)]
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xzψHOMO = ψHOMO. The magnetic symmetry D[A′] of the HOMO then means that the orbit
xzψHOMO = ψHOMO. The magnetic symmetry D[A′] of the HOMO then means that the orbitalso spans the same one-dimensional space, which is akin to saying that the antiunitary operations
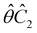 and
and 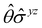 do not add any extra degrees of linear independence to
do not add any extra degrees of linear independence to  . This is expected as we have identified earlier that
. This is expected as we have identified earlier that 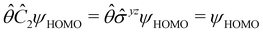 .
.
Let us turn our attention next to the HOMO−1 which has A′′ unitary symmetry in 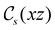 and D[A′′ ] magnetic symmetry in
and D[A′′ ] magnetic symmetry in 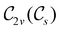 . The unitary symmetry suggests that the orbit
. The unitary symmetry suggests that the orbit
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) xzψHOMO−1= −ψHOMO−1. The magnetic symmetry then indicates that, just as in the HOMO case, the antiunitary operations
xzψHOMO−1= −ψHOMO−1. The magnetic symmetry then indicates that, just as in the HOMO case, the antiunitary operations ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2 and
Ĉ2 and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz do not add any extra degrees of linear independence either. Therefore, even though we have stated earlier that ψHOMO−1 has no definitive symmetries under
yz do not add any extra degrees of linear independence either. Therefore, even though we have stated earlier that ψHOMO−1 has no definitive symmetries under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2 and
Ĉ2 and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz, the computed magnetic symmetry reveals that there still exist linear relations between ψHOMO−1,
yz, the computed magnetic symmetry reveals that there still exist linear relations between ψHOMO−1, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2ψHOMO−1, and
Ĉ2ψHOMO−1, and ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yzψHOMO−1, so that the orbit
yzψHOMO−1, so that the orbitalso spans the same one-dimensional space.
4.2.3.3 Physical interpretations of modular and phasal symmetry breaking. The above detailed analysis of two types of symmetry breaking exhibited by the MOs brings to light possible reasons why certain erroneous conclusions could be drawn by an incomplete consideration of symmetry. Ultimately, it is important to recognise that orbital symmetry breaking does not necessarily translate faithfully to density symmetry breaking, especially if the former is a sole consequence of complex phases that only arises from antiunitary actions, which is what has been observed thus far for the frontier MOs in the three magnetic-field orientations considered (Fig. 4). In fact, if we were to disregard all phases in these complex-valued MOs and consider only the real-valued moduli |ψi(r)|, we would find that |ψi(r)| transform as the totally symmetric irreducible representations in the three magnetic groups
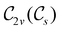 ,
, 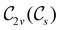 , and
, and 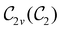 , and also in the non-symmetry zero-field group
, and also in the non-symmetry zero-field group 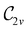 . As such, from eqn (14b), the density itself must also be similarly totally symmetric in these groups, as indicated in Fig. 3.
. As such, from eqn (14b), the density itself must also be similarly totally symmetric in these groups, as indicated in Fig. 3.
We conclude this discussion with a final remark: the reversal in the z-component of the electric dipole moment observed for the perpendicular and parallel magnetic fields (Table 2) that we explained briefly using the shapes of the electron densities at the end of Section 4.2.2.2 can be rationalised in greater depth with the MO plots in Fig. 4. In the perpendicular-field case (B = B![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ), the HOMO, HOMO−1, and HOMO−3 all show pronounced shifts towards the CH2 moiety in the molecule. The same can be observed for the HOMO, HOMO−1, and HOMO−2 in the parallel-field case (B = Bẑ). One possible explanation for these drastic shifts can be attributed to strong interactions between frontier MOs facilitated by the external magnetic field, in much the same way as that described in Section 3.3.2 of ref. 44: MOs that have different symmetries and cannot interact at zero field are subduced to the same symmetry when a magnetic field is introduced and can thus mix with one another via the Kohn–Sham-like operator [eqn (15)] resulting in the observed electron density transfers.
), the HOMO, HOMO−1, and HOMO−3 all show pronounced shifts towards the CH2 moiety in the molecule. The same can be observed for the HOMO, HOMO−1, and HOMO−2 in the parallel-field case (B = Bẑ). One possible explanation for these drastic shifts can be attributed to strong interactions between frontier MOs facilitated by the external magnetic field, in much the same way as that described in Section 3.3.2 of ref. 44: MOs that have different symmetries and cannot interact at zero field are subduced to the same symmetry when a magnetic field is introduced and can thus mix with one another via the Kohn–Sham-like operator [eqn (15)] resulting in the observed electron density transfers.
4.3 Fukui functions and their symmetry
We note that the anionic densities exhibit more pronounced responses to external electric fields, which is compatible with the higher polarisability expected for negatively charged ions. This is demonstrated most clearly in Fig. S1(b) (ESI†) for the perpendicular electric field where the symmetry breaking with respect to the molecular plane is now much more prominent than that exhibited by the neutral density [Fig. 2(b)]. The density difference plots in Fig. S2(a)–(f) in the ESI† further highlight these trends. Likewise, Fig. S1(g) (ESI†) shows a slightly more significant shift of the anionic density towards the carbon end of the molecule in a parallel magnetic field compared to the neutral density [Fig. 3(d)], while still preserving the symmetry with respect to the molecular plane. The corresponding difference plots in Fig. S2(i) and (l) (ESI†) are however less conclusive.
It follows immediately from the above considerations that the symmetry of the Fukui function for nucleophilic attack calculated for H2CO must be the same as that reported for the electron density in Section 4.2.2 and Fig. 2 and 3. This is in fact confirmed by the explicit symmetry analyses of the computed f+(r) using QSYM2, as shown in Fig. 6.
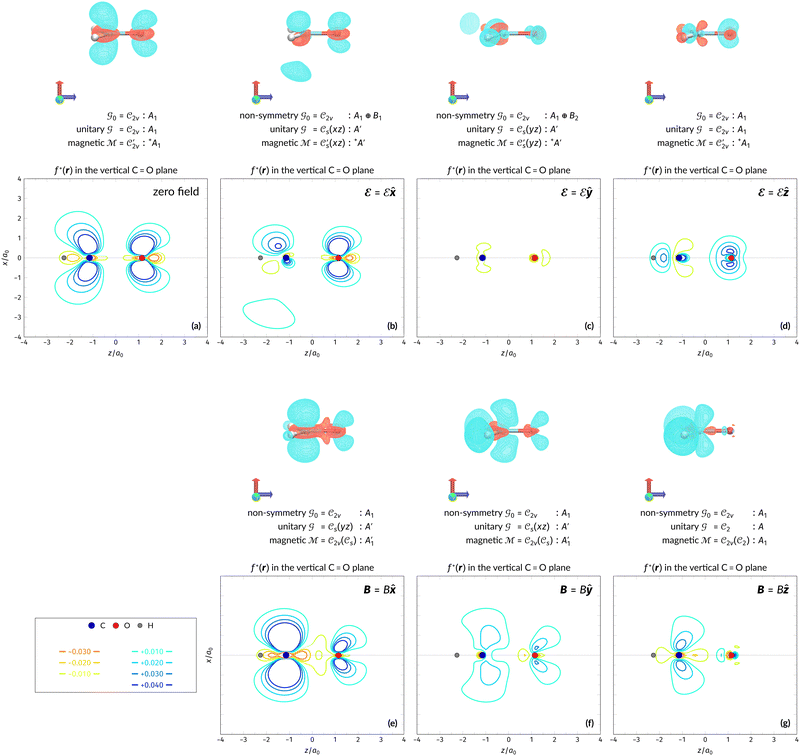 | ||
Fig. 6 Contour plots of the Fukui function for nucleophilic attack, f+(r), of H2CO in various external-field configurations. Above each plot are the three-dimensional isosurface of the corresponding Fukui function at isovalue f+(r) = 0.01 and the representations spanned by f+(r) and its symmetry partners in various groups as determined by QSYM2 (see also Appendix B for relevant character tables). Magnetic symmetries in 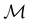 are given in terms of its irreducible representations since Fukui functions are real-valued (cf. Section 2.3.3.2). Positive regions (blue) indicate sites in the system that are favourable for nucleophilic attack. All Fukui functions were calculated using the finite-difference approach [eqn (22)] at the r2SCAN0/cc-pVTZ level. The electric field strength are given in terms of its irreducible representations since Fukui functions are real-valued (cf. Section 2.3.3.2). Positive regions (blue) indicate sites in the system that are favourable for nucleophilic attack. All Fukui functions were calculated using the finite-difference approach [eqn (22)] at the r2SCAN0/cc-pVTZ level. The electric field strength 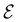 is set at 0.1 a.u. and the magnetic field strength B at 1.0B0. is set at 0.1 a.u. and the magnetic field strength B at 1.0B0. | ||
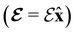 breaks this symmetry of f+(r) [Fig. 6(b)] and would, in principle, lead to enantioselectivity with all else being equal. Of course, the experimental conditions to achieve this would be extremely intricate and demanding if any enantiomeric excess were to be realised at all (cf. ref. 49). Remarkably, the distortion due to the perpendicular electric field at the oxygen atom is much smaller than that at the carbon atom—this difference can be traced back to the much higher sensitivity of the anionic density at the carbon side than the oxygen side [Fig. S1(b), ESI†]. Consequently, the regioselectivity of the carbon atom as the preferred site for nucleophilic attack over the oxygen atom is reduced when compared to the zero-field case.
breaks this symmetry of f+(r) [Fig. 6(b)] and would, in principle, lead to enantioselectivity with all else being equal. Of course, the experimental conditions to achieve this would be extremely intricate and demanding if any enantiomeric excess were to be realised at all (cf. ref. 49). Remarkably, the distortion due to the perpendicular electric field at the oxygen atom is much smaller than that at the carbon atom—this difference can be traced back to the much higher sensitivity of the anionic density at the carbon side than the oxygen side [Fig. S1(b), ESI†]. Consequently, the regioselectivity of the carbon atom as the preferred site for nucleophilic attack over the oxygen atom is reduced when compared to the zero-field case.
On the other hand, with a parallel electric field [Fig. 6(d)], the oxygen atom appears to be more reactive towards nucleophiles, which is in line with the largest dipole moment inversion observed across all cases considered in this work (Section 4.1.3). However, the spatially diminished Fukui function in the xz-plane means that the overall propensity for a nucleophilic attack in this plane is substantially lowered. In fact, the Fukui function for the parallel-electric-field case in Fig. 6(d) is reminiscent of the reactivity arising from a σ-type charge distribution, as opposed to the reactivities due to π-type charge distributions exhibited by all other external-field configurations [except the case of 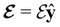 in Fig. 6(c) where the field has essentially driven the reactive sites away from the vertical C
in Fig. 6(c) where the field has essentially driven the reactive sites away from the vertical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O plane].
O plane].
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in either the x- or y-direction does not destroy the symmetry of f+(r) with respect to the molecular plane, so that the probability for a nucleophilic attack from either above or below the molecular plane remains identical. Likewise, applying a magnetic field parallel to the C
O bond in either the x- or y-direction does not destroy the symmetry of f+(r) with respect to the molecular plane, so that the probability for a nucleophilic attack from either above or below the molecular plane remains identical. Likewise, applying a magnetic field parallel to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond retains the symmetry of f+(r) with respect to the molecular plane but causes the region around the carbon atom that is prone to be attacked by nucleophiles to become more compact, thus lowering the overall reactivity of the molecule towards nucleophiles in the xz-plane.
O bond retains the symmetry of f+(r) with respect to the molecular plane but causes the region around the carbon atom that is prone to be attacked by nucleophiles to become more compact, thus lowering the overall reactivity of the molecule towards nucleophiles in the xz-plane.
In all three cases, the carbon atom remains more electrophilic than the oxygen atom despite the dipole moment inversion (Section 4.1.3). This is because the dipole moment inversion exhibited by the neutral system, which is accounted for by the charge shift in the occupied frontier MOs (Section 4.2.3.3), must be counteracted by the charge redistribution in the anion so as to retain carbon as the preferential site for nucleophilic attack. This argument is in accordance with the fundamental rôle of the possible differences in polarisation between the anion and the neutral system previously noted by some of the authors when the molecule is subject to an external electric field.49
It is also interesting to note that the Fukui functions in Fig. 6(e)–(g) suggest that the external magnetic fields significantly alter the Bürgi–Dunitz trajectory124 that is adopted by a nucleophile attacking the reactive carbon atom: the approach angle of ca. 107° at zero field is reduced to ca. 90° in perpendicular and in-plane magnetic fields, and then to ca. 75° in a parallel magnetic field. This might have profound consequences for nucleophilic addition reactions that rely on steric control, but a detailed investigation of this effect is beyond the scope of the current article and will therefore be tackled in a future study.
4.4 A remark on the rôles of external fields in asymmetric induction
The detailed symmetry analyses of the electron density and the associated conceptual DFT descriptors (e.g. the Fukui functions) can be put in a broader perspective of the long-standing issue on the possibility of creating enantioselective conditions in chemical synthesis by using magnetic fields or combinations of electric and magnetic fields. The issue dates back to the early work more than a century ago by Louis Pasteur who thought that, since a static magnetic field can induce optical rotation (the so-called Faraday effect), it should also be able to induce chirality (which he termed ‘dissymmetry’) in chemical reactions in much the same way as optically active molecules can.50,125 Unfortunately, this idea was quickly debunked by rigorous symmetry arguments, the most notable of which was put forth by Pierre Curie in 1894 positing that neither a static electric field nor a static magnetic field can result in ‘une reaction dissymetrique' due to the presence of a plane of symmetry.51 These arguments were later refined in the 1970s where time-reversal symmetry and kinetic effects were also taken into account by De Gennes,52,126 Mead et al.,53 and Rhodes and Dougherty,54 and then put into a concise language of symmetry transformations by Barron127 that we summarise in Appendix A. On this basis, it bears no surprise that the results of a paper by Zadel et al. in 1994 claiming ‘absolute asymmetric synthesis in a static magnetic field’128 turned out to be irreproducible. As a well-known case of scientific fraud by one of the authors, the paper was retracted soon after.55Though related to these classical studies, the examinations carried out in this work are fundamentally different. In the first instance, we investigate in detail the evolution in shapes and phases of electron densities, frontier MOs, and Fukui functions in an archetypical π-electron system under the influence of a magnetic field, which, to the best of our knowledge, has never been extensively done. We focus in particular on the symmetry properties of these quantum-chemical quantities, especially on whether the external field preserves or breaks their symmetry with respect to the molecular plane. In our mechanistic point of view concerning the direction of the attacking nucleophile on the carbonyl group, we adopt a molecular perspective, which is to be differentiated from the question whether a magnetic field bears left-right asymmetry. The conclusions from our studies however coincide with those obtained from the more abstract lines of reasoning mentioned above.
In fact, in all three orientations of the external magnetic field, the full magnetic group  of the system always contains either a reflection in the molecular plane
of the system always contains either a reflection in the molecular plane ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz or a time-reversed reflection in the molecular plane
yz or a time-reversed reflection in the molecular plane 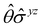 , even with one of the hydrogen atoms in H2CO replaced by a fluorine atom to give a prochiral carbon centre in HFCO (cf. Section S2 of the ESI†). This means that the system is either non-chiral or falsely chiral (see Appendix A for a discussion of these terms), leading invariably to molecular-plane-symmetric electron densities and Fukui functions and precluding any enantioselectivity. It should be noted that only when time-reversal symmetry is included is the symmetry conservation with respect to the molecular plane correctly accounted for in all three considered orientations of the magnetic field. Remarkably, an electric field perpendicular to the molecular plane is able to induce asymmetry with respect to this plane, which is a consequence of the difference in symmetry properties between electric and magnetic fields.
, even with one of the hydrogen atoms in H2CO replaced by a fluorine atom to give a prochiral carbon centre in HFCO (cf. Section S2 of the ESI†). This means that the system is either non-chiral or falsely chiral (see Appendix A for a discussion of these terms), leading invariably to molecular-plane-symmetric electron densities and Fukui functions and precluding any enantioselectivity. It should be noted that only when time-reversal symmetry is included is the symmetry conservation with respect to the molecular plane correctly accounted for in all three considered orientations of the magnetic field. Remarkably, an electric field perpendicular to the molecular plane is able to induce asymmetry with respect to this plane, which is a consequence of the difference in symmetry properties between electric and magnetic fields.
5 Conclusion
In this article, the influence of strong external magnetic fields on the electronic charge distribution and their consequences on the reactivity of π-systems were investigated, focussing on the nucleophilic attack on formaldehyde, H2CO, as a prototype. This was motivated by the extension of conceptual DFT to include new variables, such as electromagnetic fields and pressure, so as to cope with the increasing variation in experimental reaction conditions. This work concentrated on two local conceptual DFT descriptors, the electron density and especially its derivatives with respect to the number of electrons, the Fukui functions, to gain insight into the reactivity of the π-system in H2CO. In particular, these descriptors were used to interpret the influence of an external magnetic field on the electronic structure of the system, and also to determine how this is different from when an electric field is applied instead. To this end, results from current-DFT calculations were examined through the lenses of representation and corepresentation theories using a recently developed automatic program for symbolic symmetry analysis, QSYM2, that can handle MOs, electron densities, and density-derived quantities such as Fukui functions in a variety of unitary and magnetic groups.The detailed symmetry analysis results for electron densities, frontier MOs, and Fukui functions agree with the preliminary predictions based on a careful consideration of the constraints that unitary and magnetic symmetries can impose on the components of the electric dipole moment. The variation of the electron density and the Fukui functions upon applying an external magnetic field showed a strong dependence on the field orientation which, except in the parallel-field case, was different from that observed when an electric field is applied instead. This difference was satisfactorily rationalised by the symmetry considerations that were detailed at length in this article. Specifically, the electron density reflects the symmetry of the dipole moment, and since all three principal magnetic-field orientations considered in this work preserve the reflection symmetry of the system with respect to the molecular plane, be it as a unitary operation or a time-reversed one, the dipole moment component perpendicular to this plane must always vanish, thus forcing the electron density and all density-related quantities to remain symmetric with respect to this plane.
An analysis of the shapes and reduced symmetries of the frontier MOs provided a rationale for the pronounced reversals in direction of the dipole moment along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in both perpendicular- and parallel-magnetic-field orientations. Moreover, magnetic fields induce phasal symmetry breaking in complex-valued MOs, which however is not carried over to the electron density where, in the three magnetic-field orientations considered, all modular symmetries with respect to the zero-field unitary symmetry group of the molecule are conserved. A corepresentation-theoretic analysis in the full magnetic symmetry group accounted for this peculiar behaviour.
O bond in both perpendicular- and parallel-magnetic-field orientations. Moreover, magnetic fields induce phasal symmetry breaking in complex-valued MOs, which however is not carried over to the electron density where, in the three magnetic-field orientations considered, all modular symmetries with respect to the zero-field unitary symmetry group of the molecule are conserved. A corepresentation-theoretic analysis in the full magnetic symmetry group accounted for this peculiar behaviour.
Finally, in the finite-difference approach, the Fukui function for nucleophilic attack was computed from the densities of the system and its corresponding anion at the same geometry, shedding light on how the molecule responds to an incoming nucleophile. In all magnetic-field cases where the shape of the Fukui function remained of π-type, the carbon atom remained more electrophilic than the oxygen atom. On the other hand, in the parallel electric-field case where the shape of the Fukui function became σ-type, the oxygen atom became more reactive towards nucleophilic attack than the carbon atom, but the overall reactivity of the molecule towards a nucleophile is strongly reduced. Furthermore, whilst a perpendicular electric field was able to induce asymmetry in the reactivity of H2CO with respect to the molecular plane, this turns out to be not possible with any of the three magnetic-field orientations. This finding, supported by a series of analogous calculations on the prochiral formyl fluoride molecule, HFCO, was put into the context of a long-standing debate on the possibility of enantioselective synthesis under the influence of electromagnetic fields.
Conflicts of interest
There are no conflicts to declare.Appendix
A Group-theoretical classification of chirality
The traditional concept of chirality, which posits that chiral objects are those that are non-superimposable on their mirror images, turns out to be insufficient when less ‘tangible’ systems are considered, such as those with external electric and magnetic fields.125,127 Recognising this, Barron127,129 introduced a more rigorous classification of chirality that also takes into account the action of time reversal. In what follows, we shall restate Barron's chirality classification using the symmetry groups introduced in Section 2.2.1.A system is said to be non-chiral if its unitary symmetry group  contains improper rotations. Since every improper rotation can be written as a product of a reflection and a proper rotation, this is consistent with the traditional description of non-chirality that a system and its mirror image are superimposable, possibly with the aid of a suitable rotation (Fig. 7, left panel). An example of a non-chiral system is a uniform magnetic field B in free space: the unitary symmetry group of this system is
contains improper rotations. Since every improper rotation can be written as a product of a reflection and a proper rotation, this is consistent with the traditional description of non-chirality that a system and its mirror image are superimposable, possibly with the aid of a suitable rotation (Fig. 7, left panel). An example of a non-chiral system is a uniform magnetic field B in free space: the unitary symmetry group of this system is  which contains a
which contains a ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) h reflection and infinitely many improper rotations about the S∞ axis parallel to B.42,43
h reflection and infinitely many improper rotations about the S∞ axis parallel to B.42,43
On the other hand, a system is said to be falsely chiral if its unitary symmetry group  contains only proper rotations, but it admits a magnetic symmetry group
contains only proper rotations, but it admits a magnetic symmetry group 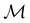 containing improper rotations composited with time reversal. Falsely chiral systems are so named because any lack of consideration of time reversal would lead to the wrong conclusion that they are chiral. Once again, as every improper rotation can be written as a product of a reflection and a proper rotation, this is consistent with Barron's definition of false chirality that a system and its mirror image are non-superimposable by any proper rotations, but superimposable by a suitable combination of time reversal with a proper rotation (Fig. 7, middle panel). A typical illustration of false chirality consists of a collinear arrangement of a uniform magnetic field B and a uniform electric field
containing improper rotations composited with time reversal. Falsely chiral systems are so named because any lack of consideration of time reversal would lead to the wrong conclusion that they are chiral. Once again, as every improper rotation can be written as a product of a reflection and a proper rotation, this is consistent with Barron's definition of false chirality that a system and its mirror image are non-superimposable by any proper rotations, but superimposable by a suitable combination of time reversal with a proper rotation (Fig. 7, middle panel). A typical illustration of false chirality consists of a collinear arrangement of a uniform magnetic field B and a uniform electric field 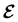 :125 the unitary symmetry group is
:125 the unitary symmetry group is 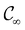 which contains only proper rotations, but the magnetic symmetry group is
which contains only proper rotations, but the magnetic symmetry group is 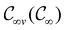 which contains infinitely many
which contains infinitely many ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) v operations.
v operations.
Finally, a system is truly chiral if its unitary symmetry group 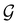 contains only proper rotations and the antiunitary coset of its magnetic symmetry group
contains only proper rotations and the antiunitary coset of its magnetic symmetry group 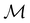 , if any, contains only proper rotations composited with time reversal. This ensures that the system and its mirror image cannot be interconverted by any proper rotations, with or without the composition with time reversal (Fig. 7, right panel). This is exemplified by a collinear arrangement of a uniform magnetic field B and the propagation k of an arbitrarily polarised light beam:125 the full magnetic symmetry group is
, if any, contains only proper rotations composited with time reversal. This ensures that the system and its mirror image cannot be interconverted by any proper rotations, with or without the composition with time reversal (Fig. 7, right panel). This is exemplified by a collinear arrangement of a uniform magnetic field B and the propagation k of an arbitrarily polarised light beam:125 the full magnetic symmetry group is 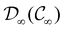 which contains only proper rotations and time-reversed proper rotations.
which contains only proper rotations and time-reversed proper rotations.
B Character tables for select groups
Tables 3–9 show the character tables for the relevant unitary and magnetic groups in this article.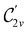 . (a) Character table of irreducible corepresentations for the magnetic grey group
. (a) Character table of irreducible corepresentations for the magnetic grey group 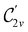 . The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group
. The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group 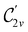 treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under
treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
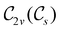 . (a) Character table of irreducible corepresentations for the magnetic black-and-white group
. (a) Character table of irreducible corepresentations for the magnetic black-and-white group 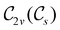 . The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group
. The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group 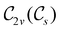 treated as a unitary group. Since
treated as a unitary group. Since ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Ĉ2 is antiunitary, the principal rotation of this group becomes Ê and all irreducible representations are therefore labelled with A according to Mulliken's conventions.130,131 In addition, single and double dashes are used to denote their parity with respect to
Ĉ2 is antiunitary, the principal rotation of this group becomes Ê and all irreducible representations are therefore labelled with A according to Mulliken's conventions.130,131 In addition, single and double dashes are used to denote their parity with respect to ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) h
h
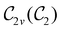 . (a) Character table of irreducible corepresentations for the magnetic black-and-white group
. (a) Character table of irreducible corepresentations for the magnetic black-and-white group 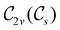 . The irreducible corepresentation type gives the classification in Section. 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group
. The irreducible corepresentation type gives the classification in Section. 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group 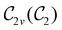 treated as a unitary group. Since Ĉ2 is unitary, it is assigned as the principal rotation of this group, and all irreducible representations are therefore labelled with A or B according to their parity under Ĉ2, as per Mulliken's conventions130,131
treated as a unitary group. Since Ĉ2 is unitary, it is assigned as the principal rotation of this group, and all irreducible representations are therefore labelled with A or B according to their parity under Ĉ2, as per Mulliken's conventions130,131
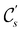 . (a) Character table of irreducible corepresentations for the magnetic grey group
. (a) Character table of irreducible corepresentations for the magnetic grey group 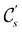 . The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group
. The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group 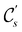 treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under
treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
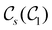 . (a) Character table of irreducible corepresentations for the magnetic black-and-white group
. (a) Character table of irreducible corepresentations for the magnetic black-and-white group 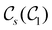 . The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group
. The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic black-and-white group 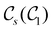 treated as a unitary group
treated as a unitary group
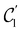 . (a) Character table of irreducible corepresentations for the magnetic grey group
. (a) Character table of irreducible corepresentations for the magnetic grey group 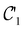 . The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group
. The irreducible corepresentation type gives the classification in Section 2.3.3.1. (b) Character table of irreducible representations over a real linear space for the magnetic grey group 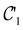 treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under
treated as a unitary group. The +/− presuperscripts give the parity of the irreducible representations under ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
Acknowledgements
MW-T, BCH, and AMW-T acknowledge financial support from the European Research Council under the European Union's H2020 research and innovation program/ERC Consolidator Grant topDFT [grant number 772259]. FDP and PG are thankful to the Vrije Universiteit Brussel for a long term grant of a Strategic Research Program.Notes and references
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642 CrossRef CAS PubMed.
- M. Rahm, R. Cammi, N. W. Ashcroft and R. Hoffmann, J. Am. Chem. Soc., 2019, 141, 10253–10271 CrossRef CAS PubMed.
- Effects of Electric Fields on Structure and Reactivity, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, 2021 Search PubMed.
- T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137–14180 CrossRef CAS PubMed.
- D. Margetic, High Pressure Organic Synthesis, De Gruyter, Inc., 2019 Search PubMed.
- M. Xu, Y. Li and Y. Ma, Chem. Sci., 2022, 13, 329–344 RSC.
- S. Hahn, K. Kim, K. Kim, X. Hu, T. Painter, I. Dixon, S. Kim, K. R. Bhattarai, S. Noguchi, J. Jaroszynski and D. C. Larbalestier, Nature, 2019, 570, 496–499 CrossRef CAS PubMed.
- H. Ruder, Atoms in Strong Magnetic Fields, Limited, Springer London, 1994 Search PubMed.
- P. Schmelcher, Atoms and Molecules in Strong External Fields, Springer, New York, 2002 Search PubMed.
- J. R. P. Angel and J. D. Landstreet, Astrophys. J., 1974, 191, 457–464 CrossRef CAS.
- J. R. P. Angel, Astrophys. J., 1977, 216, 1 CrossRef CAS.
- L.-D. Kong, S. Zhang, S.-N. Zhang, L. Ji, V. Doroshenko, A. Santangelo, Y.-P. Chen, F.-J. Lu, M.-Y. Ge, P.-J. Wang, L. Tao, J.-L. Qu, T.-P. Li, C.-Z. Liu, J.-Y. Liao, Z. Chang, J.-Q. Peng and Q.-C. Shui, Astrophys. J., Lett., 2022, 933, L3 CrossRef CAS.
- O.-A. Al-Hujaj and P. Schmelcher, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 023411 CrossRef.
- M. V. Ivanov and P. Schmelcher, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 3558–3568 CrossRef CAS.
- R. Francotte, T. J. P. Irons, A. M. Teale, F. De Proft and P. Geerlings, Chem. Sci., 2022, 13, 5311–5324 RSC.
- G. Vignale and M. Rasolt, Phys. Rev. Lett., 1987, 59, 2360–2363 CrossRef CAS PubMed.
- G. Vignale and M. Rasolt, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10685–10696 CrossRef PubMed.
- E. I. Tellgren, S. Kvaal, E. Sagvolden, U. Ekström, A. M. Teale and T. Helgaker, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 062506 CrossRef.
- E. I. Tellgren, A. Laestadius, T. Helgaker, S. Kvaal and A. M. Teale, J. Chem. Phys., 2018, 148, 024101 CrossRef PubMed.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989 Search PubMed.
- R. G. Parr and W. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701–728 CrossRef CAS PubMed.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quantum Chem., 2005, 101, 520–534 CrossRef CAS.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Theor. Chem. Acc., 2020, 139, 36 Search PubMed.
- S. Liu, Conceptual Density Functional Theory, Wiley & Sons, Limited, John, 2022 Search PubMed.
- T. J. P. Irons, J. Zemen and A. M. Teale, J. Chem. Theory Comput., 2017, 13, 3636–3649 CrossRef CAS PubMed.
- E. I. Tellgren, A. Soncini and T. Helgaker, J. Chem. Phys., 2008, 129, 154114 CrossRef PubMed.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331 CrossRef CAS PubMed.
- S. Stopkowicz, J. Gauss, K. K. Lange, E. I. Tellgren and T. Helgaker, J. Chem. Phys., 2015, 143, 074110 CrossRef PubMed.
- F. Hampe and S. Stopkowicz, J. Chem. Phys., 2017, 146, 154105 CrossRef PubMed.
- T. J. P. Irons, B. C. Huynh, A. M. Teale, F. De Proft and P. Geerlings, Mol. Phys., 2022, e2145245 CrossRef.
- P. Geerlings and F. De Proft, J. Comput. Chem., 2023, 44, 442–455 CrossRef CAS PubMed.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- R. R. Birss, Symmetry and Magnetism, North-Holland Pub. Co., Amsterdam, 1966 Search PubMed.
- C. J. Bradley and B. L. Davies, Rev. Mod. Phys., 1968, 40, 359–379 CrossRef.
- S. Pelloni and P. Lazzeretti, Int. J. Quantum Chem., 2010, 111, 356–367 CrossRef.
- A. J. Ceulemans, Group Theory Applied to Chemistry, Springer, Netherlands, 2013 Search PubMed.
- A. Pausch, M. Gebele and W. Klopper, J. Chem. Phys., 2021, 155, 201101 CrossRef CAS PubMed.
- B. C. Huynh, M. Wibowo-Teale and A. M. Wibowo-Teale, J. Chem. Theory Comput., 2024, 20, 114–133 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- T. Fievez, N. Sablon, F. De Proft, P. W. Ayers and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 1065–1072 CrossRef CAS PubMed.
- T. Clarys, T. Stuyver, F. De Proft and P. Geerlings, Phys. Chem. Chem. Phys., 2021, 23, 990–1005 RSC.
- M. Avalos, R. Babiano, P. Cintas, J. L. Jiménez, J. C. Palacios and L. D. Barron, Chem. Rev., 1998, 98, 2391–2404 CrossRef CAS PubMed.
- P. Curie, J. Phys. Theor. Appl., 1894, 3, 393–415 CrossRef.
- P.-G. De Gennes, C. R. Acad. Sci. Paris, 1970, 891 Search PubMed.
- C. A. Mead, A. Moscowitz, H. Wynberg and F. Meuwese, Tetrahedron Lett., 1977, 18, 1063–1064 CrossRef.
- W. Rhodes and R. C. Dougherty, J. Am. Chem. Soc., 1978, 100, 6247–6248 CrossRef CAS.
- P. Gölitz, Angew. Chem., Int. Ed. Engl., 1994, 33, 1457 CrossRef.
- M. Aschi, R. Spezia, A. Di Nola and A. Amadei, Chem. Phys. Lett., 2001, 344, 374–380 CrossRef CAS.
- J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance, John Wiley & Sons, Inc., Hoboken, New Jersey, 2007 Search PubMed.
- E. H. Lieb, Int. J. Quantum Chem., 1983, 24, 243–277 CrossRef CAS.
- R. Ditchfield, J. Chem. Phys., 1972, 56, 5688–5691 CrossRef CAS.
- H. F. Hameka, Rev. Mod. Phys., 1962, 34, 87–101 CrossRef CAS.
- T. Helgaker and P. Jørgensen, J. Chem. Phys., 1991, 95, 2595–2601 CrossRef CAS.
- M. Honda, K. Sato and S. Obara, J. Chem. Phys., 1991, 94, 3790–3804 CrossRef CAS.
- R. D. Reynolds and T. Shiozaki, Phys. Chem. Chem. Phys., 2015, 17, 14280–14283 RSC.
- A. K. Rajagopal and J. Callaway, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 1912–1919 CrossRef CAS.
- O. Gunnarsson and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 4274–4298 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- K. Capelle and E. K. U. Gross, Phys. Rev. Lett., 1997, 78, 1872–1875 CrossRef CAS.
- A. M. Lee, N. C. Handy and S. M. Colwell, J. Chem. Phys., 1995, 103, 10095–10109 CrossRef CAS.
- W. Zhu and S. B. Trickey, J. Chem. Phys., 2006, 125, 94317 CrossRef PubMed.
- E. I. Tellgren, A. M. Teale, J. W. Furness, K. K. Lange, U. Ekström and T. Helgaker, J. Chem. Phys., 2014, 140, 034101 CrossRef CAS PubMed.
- J. W. Furness, J. Verbeke, E. I. Tellgren, S. Stopkowicz, U. Ekström, T. Helgaker and A. M. Teale, J. Chem. Theory Comput., 2015, 11, 4169 CrossRef CAS PubMed.
- J. F. Dobson, J. Chem. Phys., 1993, 98, 8870–8872 CrossRef CAS.
- A. D. Becke, Can. J. Chem., 1996, 74, 995 CrossRef CAS.
- J. E. Bates and F. Furche, J. Chem. Phys., 2012, 137, 164105 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- E. Sagvolden, U. Ekström and E. I. Tellgren, Mol. Phys., 2013, 111, 1295–1302 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101 CrossRef PubMed.
- M. Bursch, H. Neugebauer, S. Ehlert and S. Grimme, J. Chem. Phys., 2022, 156, 134105 CrossRef CAS PubMed.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2019, 21, 7378–7388 RSC.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Chem. Sci., 2020, 11, 1431–1439 RSC.
- M. Alonso, T. Bettens, J. Eeckhoudt, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2024, 26, 21–35 RSC.
- A. Borgoo, D. J. Tozer, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2009, 11, 2862–2868 RSC.
- P. Geerlings, D. J. Tozer and F. De Proft, in Chemical Reactivity in Confined Systems, ed. P. K. Chattaraj and D. Chakraborty, John Wiley & Sons Ltd, 2021, ch. 3 Search PubMed.
- J. Eeckhoudt, T. Bettens, P. Geerlings, R. Cammi, B. Chen, M. Alonso and F. De Proft, Chem. Sci., 2022, 13, 9329–9350 RSC.
- R. P. Iczkowski and J. L. Margrave, J. Am. Chem. Soc., 1961, 83, 3547–3551 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- R. G. Pearson, Chemical Hardness, Wiley-VCH Verlag GmbH, 2005 Search PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- W. Yang, R. G. Parr and R. Pucci, J. Chem. Phys., 1984, 81, 2862–2863 CrossRef CAS.
- W. Yang, A. J. Cohen, F. De Proft and P. Geerlings, J. Chem. Phys., 2012, 136, 144110 CrossRef PubMed.
- P. Geerlings, S. Fias, Z. Boisdenghien and F. De Proft, Chem. Soc. Rev., 2014, 43, 4989 RSC.
- P. Geerlings, C. Van Alsenoy and F. De Proft, Theor. Chem. Acc., 2023, 143, 3 Search PubMed.
- R. A. Miranda-Quintana and P. W. Ayers, Phys. Chem. Chem. Phys., 2016, 18, 15070–15080 RSC.
- R. A. Miranda-Quintana, Theor. Chem. Acc., 2017, 136, 76 Search PubMed.
- M. A. Pantoja-Hernández, M. Franco-Pérez, R. A. Miranda-Quintana and J. L. Gázquez, Mol. Phys., 2023, e2199105 CrossRef.
- S. L. Altmann, Rotations, Quaternions, and Double Groups, Dover Publications, Mineola, NY, 2005 Search PubMed.
- J. O. Dimmock and R. G. Wheeler, Phys. Rev., 1962, 127, 391–404 CrossRef CAS.
- P. Lazzeretti, E. Rossi and R. Zanasi, Int. J. Quantum Chem., 1984, 25, 929–940 CrossRef CAS.
- T. A. Keith and R. F. W. Bader, J. Chem. Phys., 1993, 99, 3669–3682 CrossRef CAS.
- A. P. Cracknell, Prog. Theor. Phys., 1965, 33, 812–827 CrossRef.
- A. P. Cracknell, Prog. Theor. Phys., 1966, 35, 196–213 CrossRef.
- E. Wigner, Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra, Academic Press, London, 1959 Search PubMed.
- J. O. Dimmock, J. Math. Phys., 1963, 4, 1307–1311 CrossRef.
- J. D. Newmarch and R. M. Golding, J. Math. Phys., 1982, 23, 695–704 CrossRef.
- J. D. Newmarch, J. Math. Phys., 1983, 24, 742–756 CrossRef.
- K. C. Erb and J. Hlinka, Phase Trans., 2020, 93, 1–42 CrossRef CAS.
- A. Uhlmann, Sci. China Phys. Mech. Amp Astron., 2016, 59, 630301 CrossRef.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- QUEST, a Rapid Development Platform for QUantum Electronic Structure Techniques, 2022, https://quest.codes, accessed November 14, 2023.
- D. J. Tozer and F. De Proft, J. Chem. Phys., 2007, 127, 034108 CrossRef PubMed.
- B. C. Huynh and A. J. W. Thom, J. Chem. Theory Comput., 2019, 16, 904–930 CrossRef PubMed.
- B. C. Hall, Quantum Theory for Mathematicians, Springer London, Limited, New York, NY, 2013 Search PubMed.
- G. E. Stedman and P. H. Butler, J. Phys. Math. Gen., 1980, 13, 3125–3140 CrossRef.
- A. P. Cracknell and K. C. Wong, Aust. J. Phys., 1967, 20, 173 CrossRef.
- M. J. Lax, Symmetry Principles in Solid State and Molecular Physics, Dover Publications, Mineola, N.Y, 2001 Search PubMed.
- L. C. Grove, Groups and Characters, Wiley, New York, 1997 Search PubMed.
- R. Al-Saadon, T. Shiozaki and G. Knizia, J. Phys. Chem. A, 2019, 123, 3223–3228 CrossRef CAS PubMed.
- H. Bürgi, J. Dunitz, J. Lehn and G. Wipff, Tetrahedron, 1974, 30, 1563–1572 CrossRef.
- L. D. Barron, Isr. J. Chem., 2021, 61, 517–529 CrossRef CAS.
- P. G. De Gennes, Ferroelectrics, 1982, 40, 125–129 CrossRef.
- L. D. Barron, Chem. Phys. Lett., 1986, 123, 423–427 CrossRef CAS.
- G. Zadel, C. Eisenbraun, G.-J. Wolff and E. Breitmaier, Angew. Chem., Int. Ed. Engl., 1994, 33, 454–456 CrossRef.
- L. D. Barron, Mol. Phys., 1981, 43, 1395–1406 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1997–2011 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1956, 24, 1118 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00799a |
| ‡ This is a group-theoretic concept describing a set of symmetry-related objects that must not be confused with orbitals, which are one-electron wavefunctions. |
§ Formally, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz belongs to the kernel122 of the A1⊕B2 representation. yz belongs to the kernel122 of the A1⊕B2 representation. |
| This journal is © the Owner Societies 2024 |

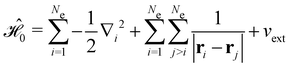
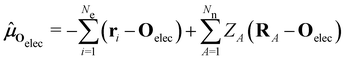
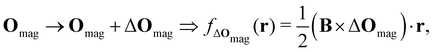
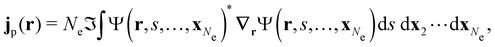
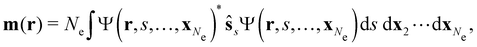
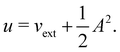
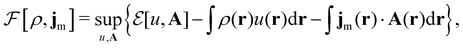
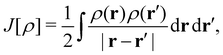
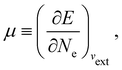
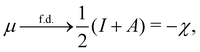
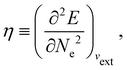
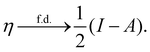
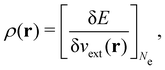
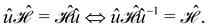
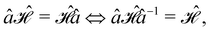
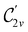
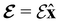
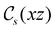
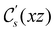
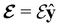
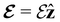
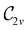
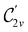
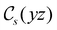
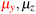
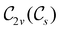
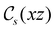
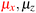
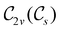
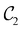
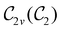
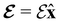
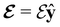
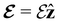
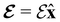
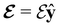
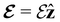
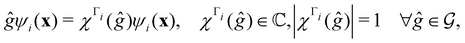
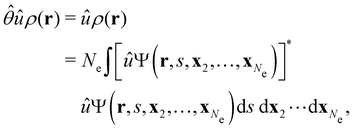
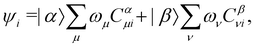
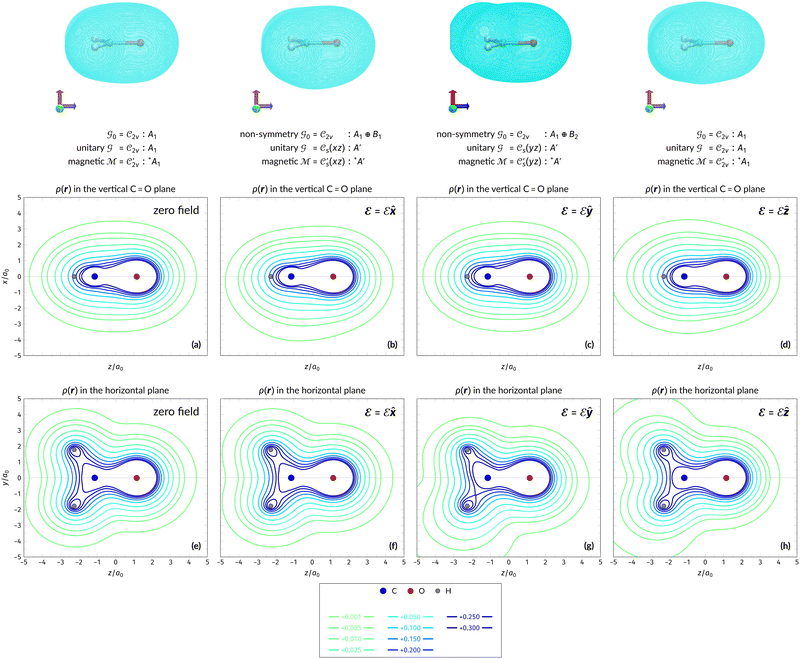
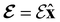
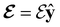
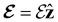
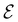
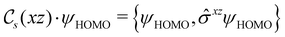
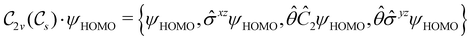
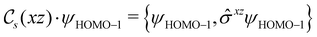
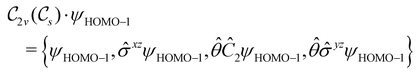
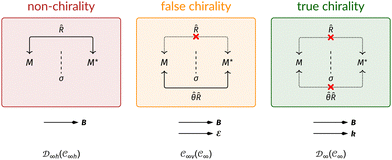
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)