Structural design strategies for superionic sodium halide solid electrolytes†
Seungho
Yu
 *ab,
Kwangnam
Kim
*ab,
Kwangnam
Kim
 c,
Brandon C.
Wood
c,
Hun-Gi
Jung
c,
Brandon C.
Wood
c,
Hun-Gi
Jung
 ab and
Kyung Yoon
Chung
ab and
Kyung Yoon
Chung
 ab
ab
aEnergy Storage Research Center, Korea Institute of Science and Technology, 5, Hwarang-ro 14-gil, Seongbuk-gu, Seoul 02792, Republic of Korea. E-mail: shyu@kist.re.kr
bDivision of Energy & Environment Technology, KIST School, Korea University of Science and Technology, Seoul 02792, Republic of Korea
cMaterials Science Division, Lawrence Livermore National Laboratory, 94550, Livermore, USA
First published on 5th November 2022
Abstract
Sodium all-solid-state batteries (ASSBs) with superionic solid electrolytes (SEs) show substantial potential for large-scale energy-storage applications. Recently, lithium halide SEs have attracted attention owing to their potential compatibility with high-voltage cathode materials and high ionic conductivity. Although sodium halide SEs are believed to exhibit good electrochemical stability, very few compounds have been reported. This study provides design principles for superionic sodium halide SEs through systematic theoretical investigations of Na3MX6 (X = Cl, Br, and I). The Na3MX6 structures depend on the types and sizes of M and X: Na3MCl6 and Na3MBr6 prefer the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases, whereas Na3MI6 prefers the C2/m phase. The Na3MI6C2/m phase is found to exhibit reasonably high ionic conductivity (∼10−4 S cm−1) and anion mixing with Br further improve Na-ion migration, leading to an even higher ionic conductivity (∼10−3 S cm−1) for Na3MBr3I3. The material design principles in this study provide fundamental guidelines for the development of superionic Na halide SEs for high-voltage Na ASSBs.
phases, whereas Na3MI6 prefers the C2/m phase. The Na3MI6C2/m phase is found to exhibit reasonably high ionic conductivity (∼10−4 S cm−1) and anion mixing with Br further improve Na-ion migration, leading to an even higher ionic conductivity (∼10−3 S cm−1) for Na3MBr3I3. The material design principles in this study provide fundamental guidelines for the development of superionic Na halide SEs for high-voltage Na ASSBs.
Introduction
The development of next-generation batteries with high energy density and enhanced safety is required for emerging applications, such as energy storage systems (ESS) and electric vehicles.1 All-solid-state batteries (ASSBs) with solid electrolytes (SEs) are promising candidates for next-generation batteries.2,3 ASSBs resolve the safety concerns of conventional Li-ion batteries by replacing flammable liquid electrolytes with nonflammable inorganic SEs.4 ASSBs with SEs also enable the use of metallic anodes that exhibit significantly higher energy densities than conventional anode materials.5 Recently, various types of post-Li batteries with new cations such as Na, K, and Mg have been investigated owing to their low cost and high energy density.6–11 Among the post-Li batteries, Na-ion batteries have attracted increasing attention because of the abundance of Na.12,13 Na ASSBs have been investigated for large-scale applications, such as ESS, which require high safety.14,15Sulfide SEs have been widely studied for applications in Na ASSBs owing to their high ionic conductivity of 1–10 mS cm−1 for Na3PS4, Na3SbS4 and Na11Sn2PS12.16–20 However, sulfide SEs are generally unstable in moisture and exhibit a narrow electrochemical stability window.21,22 Oxide SEs (NASICONs and β-alumina) are chemically stable and can exhibit a high ionic conductivity of ∼1 mS cm−1, but require a high-temperature sintering process to resolve the interfacial resistance.23,24 Recently, halide SEs have been reported as promising SEs owing to their wide electrochemical stability window and compatibility with high-voltage cathode materials.25–28 Li ternary chlorides, Li3MCl6, exhibit good chemical stability against high-voltage cathode materials (∼4 V) and have high ionic conductivity of 0.5–3 mS cm−1 for Li3YCl6, Li3InCl6 and Li3ScCl6.29–32
Although Na halides are expected to exhibit wide electrochemical stability,33 very few Na halide SEs, such as Na3YCl6, Na3ErCl6, Na2ZrCl6 and Zr-substituted Na3−xM1−xZrxCl6 (M = Y and Er)—all of which have low ionic conductivity below 10−4 S cm−1—have been reported.34–36 Owing to the ionic radius of Na (102 pm), being larger than that of Li (76 pm), Na3MCl6 exhibited different crystal structures of P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) with lower ionic conductivity than the crystal structures of Li3MCl6, such as C2/m and P
with lower ionic conductivity than the crystal structures of Li3MCl6, such as C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1.37 Theoretical studies predicted the phase-dependent ionic conductivities of Na3YBr6 and Na3YI6,38,39 but only a few studies have reported on the phases of Na bromides and iodides, Na3MX6 (X = Br and I).40 This study aims to provide guidelines for the design of novel Na halide SEs, Na3MX6 (X = Cl, Br and I), through systematic investigations of their structural preference, phase stability, electrochemical stability and transport properties.
m1.37 Theoretical studies predicted the phase-dependent ionic conductivities of Na3YBr6 and Na3YI6,38,39 but only a few studies have reported on the phases of Na bromides and iodides, Na3MX6 (X = Br and I).40 This study aims to provide guidelines for the design of novel Na halide SEs, Na3MX6 (X = Cl, Br and I), through systematic investigations of their structural preference, phase stability, electrochemical stability and transport properties.
This study shows that the structures of Na3MX6 are strongly dependent on the types and sizes of M and X. In particular, Na3MX6 generally exhibited P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and C2/m phases, while Na3MX6 with relatively small M cations preferred the NaMX4 (P212121) phase.41,42 Na3MCl6 and Na3MBr6 preferred the P
and C2/m phases, while Na3MX6 with relatively small M cations preferred the NaMX4 (P212121) phase.41,42 Na3MCl6 and Na3MBr6 preferred the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases, with the phase transitions depending on the radius of M. Na3MI6 preferred the C2/m phase and showed a high ionic conductivity (∼10−4 S cm−1). Anion mixing with Br in Na3MI6 further improved Na-ion migration, exhibiting a high ionic conductivity (∼10−3 S cm−1) that is two orders of magnitude higher than the value reported for competing Na halide SEs. The material design principles in this study offer substantial promise for the development of practical superionic Na halide SEs.
phases, with the phase transitions depending on the radius of M. Na3MI6 preferred the C2/m phase and showed a high ionic conductivity (∼10−4 S cm−1). Anion mixing with Br in Na3MI6 further improved Na-ion migration, exhibiting a high ionic conductivity (∼10−3 S cm−1) that is two orders of magnitude higher than the value reported for competing Na halide SEs. The material design principles in this study offer substantial promise for the development of practical superionic Na halide SEs.
Methods
First principles calculations were performed based on the density functional theory (DFT) with a plane-wave basis set, as implemented in the Vienna Ab initio Simulation Package (VASP).43,44 The projector augmented wave method (PAW) was used for the core and valence electron interactions45 and the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) was employed for the exchange–correlation energy functional.46 A van der Waals (vdW) density functional (optB86b-vdW) was used to address vdW interactions in layered Na halide structures.47 An energy cutoff of 520 eV was used for the plane-wave basis sets and the k-point mesh was determined using the Python Materials Genomics (pymatgen) package,48 including a k-point density of at least 1000 per atom. Ionic relaxations were performed until the forces were less than 0.01 eV Å−1, with a convergence criterion of 10−5 eV for the electronic self-consistency loop.The simulation cells of sodium halides Na3MX6 (X = Cl, Br and I) were generated based on the experimental structures of Na3MX6 that exhibited trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c (#163),49,50 monoclinic P21/n (#14),34,35 trigonal R
1c (#163),49,50 monoclinic P21/n (#14),34,35 trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (#148)51 and monoclinic C2/m (#12)29 crystal structures. The trigonal P
(#148)51 and monoclinic C2/m (#12)29 crystal structures. The trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (#164) Li chloride structure, Li3MX6,27 was also used to prepare Na3MX6 simulation cells. Among the possible ionic configurations for the partially occupied sites in the R
m1 (#164) Li chloride structure, Li3MX6,27 was also used to prepare Na3MX6 simulation cells. Among the possible ionic configurations for the partially occupied sites in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , P21/n and P
, P21/n and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phases, the Na3MX6 structure with the lowest total energy was used for subsequent calculations. Details of the structural information of C2/m and P
m1 phases, the Na3MX6 structure with the lowest total energy was used for subsequent calculations. Details of the structural information of C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phases are provided in Table S1.† Various metal elements in +3 oxidation states have been considered for ternary metal halides, Na3MX6, including group 3 elements (Sc, Lu and Y), group 13 elements (Al, Ga, In and Tl), group 15 elements (Bi) and lanthanides (Yb, Tm, Er, Ho, Dy, Tb, Gd, Sm, Nd and La). The transition metals with multiple oxidation states were excluded in this study. The phase stability of Na3MX6 (X = Cl, Br and I) was evaluated by calculating the decomposition energy, Ed, against the competing stable phases NaX and MX3. The metastable Na3MX6 phase with an Ed below 25 meV per atom was considered to be a stable phase, owing to stabilization by entropic effects and kinetic inhibition. Further experimental studies can be performed to identify the stable structure of Na3MX6, based on the theoretical works.
m1 phases are provided in Table S1.† Various metal elements in +3 oxidation states have been considered for ternary metal halides, Na3MX6, including group 3 elements (Sc, Lu and Y), group 13 elements (Al, Ga, In and Tl), group 15 elements (Bi) and lanthanides (Yb, Tm, Er, Ho, Dy, Tb, Gd, Sm, Nd and La). The transition metals with multiple oxidation states were excluded in this study. The phase stability of Na3MX6 (X = Cl, Br and I) was evaluated by calculating the decomposition energy, Ed, against the competing stable phases NaX and MX3. The metastable Na3MX6 phase with an Ed below 25 meV per atom was considered to be a stable phase, owing to stabilization by entropic effects and kinetic inhibition. Further experimental studies can be performed to identify the stable structure of Na3MX6, based on the theoretical works.
The Na-ion potential energy landscape in Na3MX6 was obtained using the bond-valence site energy (BVSE) method, as implemented in SoftBV software.52 The potential energy of the Na sites was calculated using the Morse-type interaction potential with a grid density of 0.1 Å. The Na-ion migration path was predicted using the isosurface of the Na-ion probability density and the minimum energy value between the migration paths for the Na-ion migration energy barrier was obtained. Na-ion diffusivity in Na3MX6 was examined using ab initio molecular dynamics (AIMD) simulations with an energy cutoff of 350 eV, Γ-point-only k-point grid and the NVT ensemble with a Nosé–Hoover thermostat. A 2 × 2 × 1 supercell was used for P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , and a 2 × 1 × 2 supercell was used for the C2/m structure for the AIMD calculations corresponding to 80 atoms for the P
, and a 2 × 1 × 2 supercell was used for the C2/m structure for the AIMD calculations corresponding to 80 atoms for the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and C2/m, and 120 atoms for R
1c, P21/n and C2/m, and 120 atoms for R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structures. The Na-ion diffusivity was evaluated using the mean squared displacement (MSD) at five different temperatures (700, 750, 800, 900 and 1000 K) for a window of 100 to 200 ps, with a time step of 2 fs. Data from the AIMD simulations were analyzed using the diffusion analysis module of the pymatgen package.48 The total mean squared displacement (TMSD) and effective ion jumps were calculated to evaluate the relative standard deviation of diffusivity based on previous studies.53,54 The diffusion coefficient, D, was derived using the TMSD of Na ions as a function of the time interval, Δt:
structures. The Na-ion diffusivity was evaluated using the mean squared displacement (MSD) at five different temperatures (700, 750, 800, 900 and 1000 K) for a window of 100 to 200 ps, with a time step of 2 fs. Data from the AIMD simulations were analyzed using the diffusion analysis module of the pymatgen package.48 The total mean squared displacement (TMSD) and effective ion jumps were calculated to evaluate the relative standard deviation of diffusivity based on previous studies.53,54 The diffusion coefficient, D, was derived using the TMSD of Na ions as a function of the time interval, Δt:
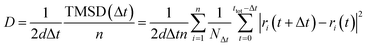 | (1) |
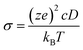 | (2) |
The electrochemical stability of Na3MX6 (X = Cl, Br and I) was investigated using the Materials Project (MP) database.55 The grand potential phase diagram as a function of the chemical potential of Na was obtained using the pymatgen package48 to evaluate the electrochemical stability window of Na3MX6. The total energies of Na3MX6 were updated using equivalent settings in the MP for the calculations. The oxidation and reduction potentials with their phase equilibria were examined to determine the electrochemical stability of Na3MX6. Na3MX6 compounds that were unstable against phase decomposition were excluded from the electrochemical stability calculations.
Results
The most stable structure of Na3MX6 (X = Cl, Br and I) among trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, monoclinic P21/n, trigonal R
1c, monoclinic P21/n, trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , monoclinic C2/m and trigonal P
, monoclinic C2/m and trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 was determined by comparing the total energies of the phases, as shown in Fig. S1–S3 and Table S2.† Although the energy differences among the phases are small and several phases can be considered as the most stable phase, there exists a general trend for phase transitions among the structures, as a function of the size of cation (M) and anion (X). The phase preference for Na3MCl6 agrees with a previous work37 showing that Na3MCl6 with relatively small M cations prefers the trigonal P
m1 was determined by comparing the total energies of the phases, as shown in Fig. S1–S3 and Table S2.† Although the energy differences among the phases are small and several phases can be considered as the most stable phase, there exists a general trend for phase transitions among the structures, as a function of the size of cation (M) and anion (X). The phase preference for Na3MCl6 agrees with a previous work37 showing that Na3MCl6 with relatively small M cations prefers the trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c phase, whereas Na3MCl6 with modestly large M cations prefers the monoclinic P21/n phase and Na3MCl6 with even larger M cations above 90 pm prefers the R
1c phase, whereas Na3MCl6 with modestly large M cations prefers the monoclinic P21/n phase and Na3MCl6 with even larger M cations above 90 pm prefers the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase, as shown in Fig. S1.† The phase preference of Na3MBr6 was found to be comparable to that of Na3MCl6 in the P
phase, as shown in Fig. S1.† The phase preference of Na3MBr6 was found to be comparable to that of Na3MCl6 in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases; however, the driving force for the phase transitions to P21/n and R
phases; however, the driving force for the phase transitions to P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) for Na3MBr6 was relatively weaker than for Na3MCl6, as shown in Fig. S1.† Therefore, phase transitions (from P
for Na3MBr6 was relatively weaker than for Na3MCl6, as shown in Fig. S1.† Therefore, phase transitions (from P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c to P21/n and from P21/n to R
1c to P21/n and from P21/n to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) require relatively larger M cations in Na3MBr6 compared with Na3MCl6. Na3MCl6 and Na3MBr6 preferred P
) require relatively larger M cations in Na3MBr6 compared with Na3MCl6. Na3MCl6 and Na3MBr6 preferred P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases, while Na3MI6 preferentially exhibited the C2/m phase over the other phases. The energy difference plot in Fig. S2† shows this phase preference of C2/m compared with other phases for Na3MI6. The energy differences for the P
phases, while Na3MI6 preferentially exhibited the C2/m phase over the other phases. The energy difference plot in Fig. S2† shows this phase preference of C2/m compared with other phases for Na3MI6. The energy differences for the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phases for Na3MX6 (X = Cl, Br and I) are listed in Table S2.† The energy difference among the phases was negligible for Na3MBr6 since they were in the phase transition region. The ground state of structure with the lowest energy should be examined to obtain the accurate results.
m1 phases for Na3MX6 (X = Cl, Br and I) are listed in Table S2.† The energy difference among the phases was negligible for Na3MBr6 since they were in the phase transition region. The ground state of structure with the lowest energy should be examined to obtain the accurate results.
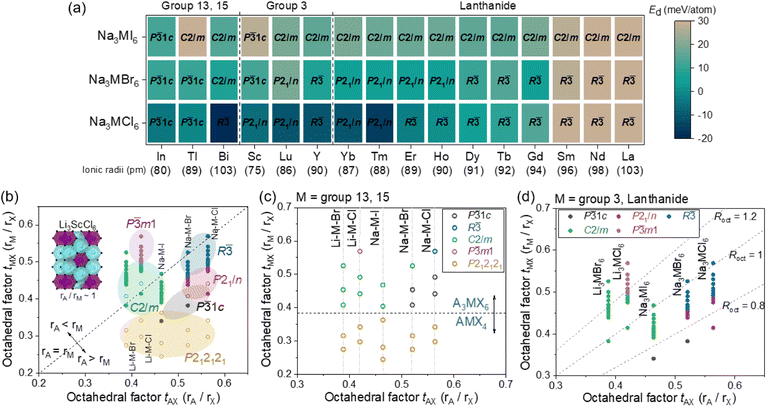
The phase stability of Na3MX6 (X = Cl, Br and I) was evaluated using the decomposition energy, Ed, against the competing stable phases, NaX and MX3. The most stable phase of MX3 among the experimental structures listed in Tables S3 and S4† was used to evaluate Ed. The Ed values for the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 structures are illustrated as a heat map in Fig. S3 and S4.† Na3MX6 phases with negative Ed values (dark blue) were considered stable against decomposition to NaX and MX3, whereas Na3MX6 phases with positive Ed values under 25 meV per atom were considered metastable phases owing to the entropic effects and kinetic barrier of decomposition. Na3MX6 phases with positive Ed values above 25 meV per atom (light brown) were considered unstable phases, which generally included large M cations (Mradii > 95 pm), such as Sm, Nd and La. Na3MCl6 typically exhibit stable phases, whereas most Na3MBr6 and Na3MI6 exhibit metastable or unstable phases. The Na3MI6Ed values are higher than those for Na3MBr6, suggesting that the relatively large X in Na3MX6 decreases phase stability. The most stable Na3MX6 phases with the lowest Ed value among the P
m1 structures are illustrated as a heat map in Fig. S3 and S4.† Na3MX6 phases with negative Ed values (dark blue) were considered stable against decomposition to NaX and MX3, whereas Na3MX6 phases with positive Ed values under 25 meV per atom were considered metastable phases owing to the entropic effects and kinetic barrier of decomposition. Na3MX6 phases with positive Ed values above 25 meV per atom (light brown) were considered unstable phases, which generally included large M cations (Mradii > 95 pm), such as Sm, Nd and La. Na3MCl6 typically exhibit stable phases, whereas most Na3MBr6 and Na3MI6 exhibit metastable or unstable phases. The Na3MI6Ed values are higher than those for Na3MBr6, suggesting that the relatively large X in Na3MX6 decreases phase stability. The most stable Na3MX6 phases with the lowest Ed value among the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phases are shown in Fig. 1(a) and Tables S5 and S6.†
m1 phases are shown in Fig. 1(a) and Tables S5 and S6.†
The Na3MX6 structures are strongly dependent on the sizes of M and X. The octahedral factor, t, was employed to investigate the structural preferences of Na3MX6. Defined as the ratio of the radius of cation to anion (r+/r−), this octahedral factor between M and X (tMX = rM/rX) effectively described the structure of the Li–M–X compound in an earlier study.25,56 Li–M–X was found to form MX8 cubes for high values of tMX, such as fluorides, while the structures changed to MX6 octahedra for lower values of tMX, such as chlorides (Li3MCl6). The Li–M–X compound exhibited an MX4 tetrahedron upon further decrease in tMX, forming LiMX4.25,56 The M–X structural changes in the Na–M–X compounds were consistent with these prior results for the Li–M–X compounds, suggesting that moderate values of tMX result in Na3MX6 phases, whereas lower values of tMX result in NaMX4 phases. Na–M–X compounds with relatively small cations, such as Al and Ga, showed low tMX values, exhibiting the NaMX4 (P212121) phase instead of the Na3MX6 phase, as shown in Table S7.†
The octahedral factor between A and X (tAX = rA/rX, A = Li and Na) and tMX was evaluated to investigate the structure of Na3MX6 in Fig. 1(b–d). Using the tAX and tMX as x and y values in the two-dimensional plot in Fig. 1(b), the structural preferences of A3MX6 among the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phases were assessed. Data that lie on the dashed line in Fig. 1(b) feature tAX that is equivalent to tMX, indicating that the sizes of octahedra of MX6 and AX6 are comparable (e.g., Li3ScCl6). Data points for A3MX6 lie above or below this dashed line when the size of M is larger or smaller than A, respectively. Na3MX6 (X = Cl, Br and I) is positioned below the dashed line because the ionic radius of Na (102 pm) is typically larger than that of the M cations. Most Li chlorides and bromides, Li3MX6 (X = Cl and Br), were found to lie above the dashed line because of the smaller ionic radius of Li (76 pm) compared with that of the M cations. Li fluorides and iodides (Li3MX6, X = F and I) were disregarded in this plot because they exceeded the span of t for Na3MX6, exhibiting high values of tMX above 0.6 for Li3MF6 and low values of tAX under 0.35 for Li3MI6.
m1 phases were assessed. Data that lie on the dashed line in Fig. 1(b) feature tAX that is equivalent to tMX, indicating that the sizes of octahedra of MX6 and AX6 are comparable (e.g., Li3ScCl6). Data points for A3MX6 lie above or below this dashed line when the size of M is larger or smaller than A, respectively. Na3MX6 (X = Cl, Br and I) is positioned below the dashed line because the ionic radius of Na (102 pm) is typically larger than that of the M cations. Most Li chlorides and bromides, Li3MX6 (X = Cl and Br), were found to lie above the dashed line because of the smaller ionic radius of Li (76 pm) compared with that of the M cations. Li fluorides and iodides (Li3MX6, X = F and I) were disregarded in this plot because they exceeded the span of t for Na3MX6, exhibiting high values of tMX above 0.6 for Li3MF6 and low values of tAX under 0.35 for Li3MI6.
In Fig. 1(b), the NaMX4 (P212121) phase for relatively small M cations with low values of tMX in Table S7† is represented in yellow. For Na3MX6 with higher values of tMX than those of NaMX4, the most stable structural phase among P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 is represented by black, red, blue, green and purple, respectively. Li3MX6 compounds (X = Cl and Br) generally exhibited the C2/m phase, whereas the P
m1 is represented by black, red, blue, green and purple, respectively. Li3MX6 compounds (X = Cl and Br) generally exhibited the C2/m phase, whereas the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase was the stable phase for Li3MCl6 with large M cations, corresponding to a high tMX above 0.5.57 Na3MI6 showed similar values of tAX and tMX (tAX ∼ 0.45 and 0.35 < tMX < 0.5) to Li3MCl6, resulting in a preference for the C2/m phase. As the size of the X anion increases (tAX > 0.5), Na3MX6 (X = Cl and Br) was found to prefer the P
m1 phase was the stable phase for Li3MCl6 with large M cations, corresponding to a high tMX above 0.5.57 Na3MI6 showed similar values of tAX and tMX (tAX ∼ 0.45 and 0.35 < tMX < 0.5) to Li3MCl6, resulting in a preference for the C2/m phase. As the size of the X anion increases (tAX > 0.5), Na3MX6 (X = Cl and Br) was found to prefer the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases to the C2/m phase, with P
phases to the C2/m phase, with P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c–P21/n–R
1c–P21/n–R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase transitions occurring for Na3MX6 (X = Cl and Br) with increased size of M (i.e., with larger tMX).
phase transitions occurring for Na3MX6 (X = Cl and Br) with increased size of M (i.e., with larger tMX).
The phase preferences of A3MX6 (A = Li and Na; X = Cl, Br and I) with M in the p-block (groups 13 and 15; M = Al, Ga, In, Tl and Bi) was observed to be slightly different, with phase transitions (from P212121 to C2/m, from P212121 to P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, from P
1c, from P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c to P21/n) occurring with relatively large M cations. For example, the group 3 element Sc (75 pm) exhibited phase transitions from P212121 to P
1c to P21/n) occurring with relatively large M cations. For example, the group 3 element Sc (75 pm) exhibited phase transitions from P212121 to P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c for Na3ScI6 and from P
1c for Na3ScI6 and from P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c to P21/n for Na3ScCl6, whereas the group 13 element In, with a relatively large ionic radius (80 pm), exhibited P212121 for NaInI4 and P
1c to P21/n for Na3ScCl6, whereas the group 13 element In, with a relatively large ionic radius (80 pm), exhibited P212121 for NaInI4 and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c for Na3InCl6. The difference in electronegativity between M and X is smaller for the p-block elements than for the d- and f-block elements (i.e., group 3 elements and lanthanides), resulting in weaker Coulomb interactions and different phase-transition trends.57 Hence, the phase transitions of A3MX6 with p-block elements occurred only with a relatively large M, for which the difference in electronegativity becomes appreciable. The data for A3MX6 with p-block elements are presented using open symbols in Fig. 1(b and c) and the phase preferences of A3MX6 in Fig. 1(b) are divided into two plots based on the M cation: Fig. 1(c) for group 13 and 15 elements and Fig. 1(d) for group 3 and lanthanide elements.
1c for Na3InCl6. The difference in electronegativity between M and X is smaller for the p-block elements than for the d- and f-block elements (i.e., group 3 elements and lanthanides), resulting in weaker Coulomb interactions and different phase-transition trends.57 Hence, the phase transitions of A3MX6 with p-block elements occurred only with a relatively large M, for which the difference in electronegativity becomes appreciable. The data for A3MX6 with p-block elements are presented using open symbols in Fig. 1(b and c) and the phase preferences of A3MX6 in Fig. 1(b) are divided into two plots based on the M cation: Fig. 1(c) for group 13 and 15 elements and Fig. 1(d) for group 3 and lanthanide elements.
Fig. 1(c) shows the preference of the MX4 tetrahedron for relatively small p-block elements with low values of tMX (<0.38), forming the NaMX4 (P212121) phase. Because this P212121 phase includes MX4 tetrahedron showing low ionic conductivity,26 M cations with small ionic radii may be neglected in the design of superionic Na–M–X SEs. The phase preference of A3MX6 for group 3 elements and lanthanides with relatively large ionic radii (>74 pm) is shown in Fig. 1(d). Here, the ratio of octahedral factors, Roct = tMX/tAX = rM/rA was used to classify the A3MX6 phases. The value of Roct is higher or lower than 1 when the cation M is larger or smaller than A, respectively. The Roct values were generally 1.0–1.3 for Li3MCl6 and they exhibited a phase transition from C2/m to P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 at a Roct value of approximately 1.2. The Roct values were generally 0.8–1.0 for Na3MX6 (X = Cl, Br and I) because of the large ionic radius of Na (102 pm). Na3MI6 maintained the C2/m phase in this range, whereas Na3MBr6 and Na3MCl6 exhibited a phase transition from P21/n to R
m1 at a Roct value of approximately 1.2. The Roct values were generally 0.8–1.0 for Na3MX6 (X = Cl, Br and I) because of the large ionic radius of Na (102 pm). Na3MI6 maintained the C2/m phase in this range, whereas Na3MBr6 and Na3MCl6 exhibited a phase transition from P21/n to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase at Roct values of approximately 0.85.
phase at Roct values of approximately 0.85.
The Na-ion potential energy landscapes for the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MX6 (Cl and Br) and the C2/m phase of Na3MI6 were predicted using the BVSE method. The experimental structures of Na3InCl6, Na3ErCl6, Na3GdCl6 and Na3GdI6 were used to examine Na-ion migration in the P
phases of Na3MX6 (Cl and Br) and the C2/m phase of Na3MI6 were predicted using the BVSE method. The experimental structures of Na3InCl6, Na3ErCl6, Na3GdCl6 and Na3GdI6 were used to examine Na-ion migration in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and C2/m phases, respectively. The isosurface of the Na-site energy (light blue) was obtained to visualize the Na-ion migration pathways, as shown in Fig. 2 and S5–S9.† The calculation results indicate that the trigonal P
and C2/m phases, respectively. The isosurface of the Na-site energy (light blue) was obtained to visualize the Na-ion migration pathways, as shown in Fig. 2 and S5–S9.† The calculation results indicate that the trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c and R
1c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MCl6 show 1D paths between octahedral sites (Oct.–Oct.) along the z-axis as well as 3D paths between octahedral sites via tetrahedral interstitial sites (Oct.–Tet.–Oct.). The monoclinic P21/n phase of Na3MCl6 exhibits 3D paths between octahedral and prism sites (Oct.–Prism) and between octahedral and prism sites via tetrahedral interstitial sites (Oct.–Tet.–Prism), agreeing with previous studies.37 The Na-ion migration paths in Na3InBr6 (P
phases of Na3MCl6 show 1D paths between octahedral sites (Oct.–Oct.) along the z-axis as well as 3D paths between octahedral sites via tetrahedral interstitial sites (Oct.–Tet.–Oct.). The monoclinic P21/n phase of Na3MCl6 exhibits 3D paths between octahedral and prism sites (Oct.–Prism) and between octahedral and prism sites via tetrahedral interstitial sites (Oct.–Tet.–Prism), agreeing with previous studies.37 The Na-ion migration paths in Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), Na3ErBr6 (P21/n) and Na3GdBr6 (R
1c), Na3ErBr6 (P21/n) and Na3GdBr6 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) were found to be consistent with the paths in Na3MCl6, as shown in Fig. 2, while the energy barrier between the migration paths was slightly decreased compared to Na3MCl6 (Fig. S5†). The Na-ion migration paths in Na3GdI6 for the C2/m phase include three-dimensional paths between octahedral sites connected by tetrahedral interstitial sites (Oct.–Tet.–Oct.). Details of the migration paths in Na3InBr6 (P
) were found to be consistent with the paths in Na3MCl6, as shown in Fig. 2, while the energy barrier between the migration paths was slightly decreased compared to Na3MCl6 (Fig. S5†). The Na-ion migration paths in Na3GdI6 for the C2/m phase include three-dimensional paths between octahedral sites connected by tetrahedral interstitial sites (Oct.–Tet.–Oct.). Details of the migration paths in Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), Na3ErBr6 (P21/n), Na3GdBr6 (R
1c), Na3ErBr6 (P21/n), Na3GdBr6 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and Na3GdI6 (C2/m) are presented in Fig. S6–S9,† respectively.
) and Na3GdI6 (C2/m) are presented in Fig. S6–S9,† respectively.
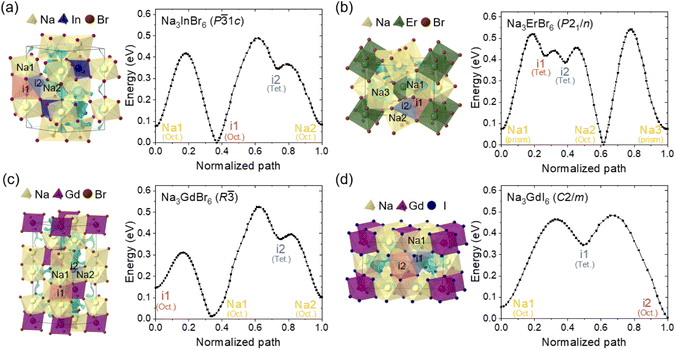 | ||
Fig. 2 Na-ion potential energy landscape of (a) Na3InBr6 (trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), (b) Na3ErBr6 (monoclinic P21/n), (c) Na3GdBr6 (trigonal R 1c), (b) Na3ErBr6 (monoclinic P21/n), (c) Na3GdBr6 (trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and (d) Na3GdI6 (monoclinic C2/m) calculated using the BVSE method, including Na-ion migration energy barriers along the migration paths. Details of migration paths are shown in Fig. S6–S9.† ) and (d) Na3GdI6 (monoclinic C2/m) calculated using the BVSE method, including Na-ion migration energy barriers along the migration paths. Details of migration paths are shown in Fig. S6–S9.† | ||
The Na-ion migration energy barriers (Ea) in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MX6 (M = In, Er, Gd; X = Cl, Br) and the C2/m phase of Na3GdI6 were predicted using BVSE, as shown in Fig. 2 and S5.† The trigonal P
phases of Na3MX6 (M = In, Er, Gd; X = Cl, Br) and the C2/m phase of Na3GdI6 were predicted using BVSE, as shown in Fig. 2 and S5.† The trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c and R
1c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MCl6 exhibited Ea of 0.45 and 0.35 eV, respectively, for the 1D paths between face sharing octahedral sites (Na1–i1), and Ea of 0.53 and 0.65 eV, respectively, for the 3D paths between octahedral sites through the interstitial tetrahedral site (i1–i2–Na2 and Na1–i2–Na2). Note that Ea for the 3D paths is the key determiner for long-range migration rates. The Ea values in the P21/n phase of Na3MCl6 were 0.60 eV for migration paths between octahedral and prism sites through tetrahedral interstitial sites (Na1–i1–i2–Na2) and 0.70 eV for the migration paths between octahedral and prism sites (Na2–Na3). The higher values of Ea for the R
phases of Na3MCl6 exhibited Ea of 0.45 and 0.35 eV, respectively, for the 1D paths between face sharing octahedral sites (Na1–i1), and Ea of 0.53 and 0.65 eV, respectively, for the 3D paths between octahedral sites through the interstitial tetrahedral site (i1–i2–Na2 and Na1–i2–Na2). Note that Ea for the 3D paths is the key determiner for long-range migration rates. The Ea values in the P21/n phase of Na3MCl6 were 0.60 eV for migration paths between octahedral and prism sites through tetrahedral interstitial sites (Na1–i1–i2–Na2) and 0.70 eV for the migration paths between octahedral and prism sites (Na2–Na3). The higher values of Ea for the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and P21/n phases indicate that the Na-ion diffusivity would be reduced for those phases. The P
and P21/n phases indicate that the Na-ion diffusivity would be reduced for those phases. The P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MBr6 exhibited slightly lower Ea than those of Na3MCl6 as shown in Fig. 2. The Ea for the 3D paths in the P
phases of Na3MBr6 exhibited slightly lower Ea than those of Na3MCl6 as shown in Fig. 2. The Ea for the 3D paths in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MBr6 were 0.49, 0.54 and 0.52 eV, respectively, suggesting an improvement in Na-ion migration in Na3MBr6. The Ea value for the C2/m phase of Na3GdI6 was computed as 0.48 eV for the 3D paths between octahedral sites through the interstitial tetrahedral sites (Na1–i1–i2), indicating that Na-ion diffusivity in the C2/m phase would be higher than in other phases. The Ea value for the 1D and 3D paths of Na3MX6 (M = In, Er, Gd; X = Cl, Br) and Na3GdI6 are listed in Table S8.†
phases of Na3MBr6 were 0.49, 0.54 and 0.52 eV, respectively, suggesting an improvement in Na-ion migration in Na3MBr6. The Ea value for the C2/m phase of Na3GdI6 was computed as 0.48 eV for the 3D paths between octahedral sites through the interstitial tetrahedral sites (Na1–i1–i2), indicating that Na-ion diffusivity in the C2/m phase would be higher than in other phases. The Ea value for the 1D and 3D paths of Na3MX6 (M = In, Er, Gd; X = Cl, Br) and Na3GdI6 are listed in Table S8.†
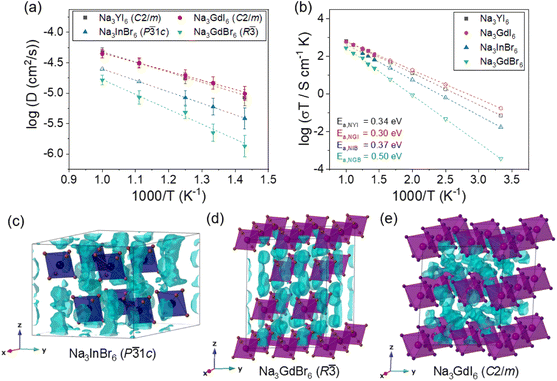
In addition to simple empirical BVSE calculations,58,59 further detailed analysis of Na-ion migration in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MX6 (X = Br and I) were performed using AIMD simulations. The Na-ion diffusivity in Na3InBr6 (P
phases of Na3MX6 (X = Br and I) were performed using AIMD simulations. The Na-ion diffusivity in Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), Na3ErBr6 (P21/n), Na3GdBr6 (R
1c), Na3ErBr6 (P21/n), Na3GdBr6 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ), Na3YI6 (C2/m) and Na3GdI6 (C2/m) were evaluated using the Na-ion mean squared displacement (MSD), as shown in Fig. S10.† Na3ErBr6 (P21/n) showed negligible Na-ion MSD over 100 ps at 900 K (Fig. S11†), suggesting the low ionic conductivity of Na3MBr6 with P21/n structure. According to earlier studies, the ionic conductivity of Na3ErBr6 should be approximately 10−9 S cm−1, reflecting the fact that inter-site hopping was not observed in the MSD plot at 900 K.60 The Na-ion diffusivities of Na3MBr6 were improved in the P
), Na3YI6 (C2/m) and Na3GdI6 (C2/m) were evaluated using the Na-ion mean squared displacement (MSD), as shown in Fig. S10.† Na3ErBr6 (P21/n) showed negligible Na-ion MSD over 100 ps at 900 K (Fig. S11†), suggesting the low ionic conductivity of Na3MBr6 with P21/n structure. According to earlier studies, the ionic conductivity of Na3ErBr6 should be approximately 10−9 S cm−1, reflecting the fact that inter-site hopping was not observed in the MSD plot at 900 K.60 The Na-ion diffusivities of Na3MBr6 were improved in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c and R
1c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases, and P
phases, and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c showed the highest diffusivity among the P
1c showed the highest diffusivity among the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MBr6. Note that, in Fig. 3(a), the Na-ion diffusivities of Na3InBr6 (P
phases of Na3MBr6. Note that, in Fig. 3(a), the Na-ion diffusivities of Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c) at 900 and 1000 K (open triangles) are extrapolated values from the lower-temperature simulations because Na3InBr6 melted at high temperature.
1c) at 900 and 1000 K (open triangles) are extrapolated values from the lower-temperature simulations because Na3InBr6 melted at high temperature.
As shown in Fig. 3(b), Na3GdBr6 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) exhibited activation energy of 0.50 eV and ionic conductivity of 1.2 × 10−6 S cm−1 at room temperature. Na-ion MSD was found to further improve in Na3InBr6 (P
) exhibited activation energy of 0.50 eV and ionic conductivity of 1.2 × 10−6 S cm−1 at room temperature. Na-ion MSD was found to further improve in Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), exhibiting activation energy of 0.37 eV and ionic conductivity of 5.8 × 10−5 S cm−1 at room temperature. The C2/m phase of Na3MI6 showed lower activation energy and higher ionic conductivity compared with the P
1c), exhibiting activation energy of 0.37 eV and ionic conductivity of 5.8 × 10−5 S cm−1 at room temperature. The C2/m phase of Na3MI6 showed lower activation energy and higher ionic conductivity compared with the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c and R
1c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases of Na3MBr6. Na3GdI6 and Na3YI6 exhibited activation energies of 0.30 and 0.34 eV and ionic conductivities of 5.9 × 10−4 and 2.4 × 10−4 S cm−1 at room temperature, respectively. The activation energies, ionic conductivities and error bounds are listed in Tables 1 and S9.† The activation energy and Na ionic conductivity of the C2/m phase of Na3YI6 showed good agreement with previous theoretical work39 reporting 0.32 eV and 3.5 × 10−4 S cm−1, respectively. In the earlier study, the high ionic conductivity of C2/m phase was predicted for Na3YCl6 and Na3YBr6,38 but P21/n phase was favorable structure for Na3YCl6, exhibiting low ionic conductivity approximately 10−9 S cm−1.35
phases of Na3MBr6. Na3GdI6 and Na3YI6 exhibited activation energies of 0.30 and 0.34 eV and ionic conductivities of 5.9 × 10−4 and 2.4 × 10−4 S cm−1 at room temperature, respectively. The activation energies, ionic conductivities and error bounds are listed in Tables 1 and S9.† The activation energy and Na ionic conductivity of the C2/m phase of Na3YI6 showed good agreement with previous theoretical work39 reporting 0.32 eV and 3.5 × 10−4 S cm−1, respectively. In the earlier study, the high ionic conductivity of C2/m phase was predicted for Na3YCl6 and Na3YBr6,38 but P21/n phase was favorable structure for Na3YCl6, exhibiting low ionic conductivity approximately 10−9 S cm−1.35
| Composition | Structure | σ at 300 K (mS cm−1) | E a (eV) |
|---|---|---|---|
| Na3InBr6 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c 1c |
0.058 | 0.37 |
| Na3ErBr6 | P21/n | 10−6 | N/A |
| Na3GdBr6 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
0.0012 | 0.50 |
| Na3YI6 | C2/m | 0.24 | 0.34 |
| Na3YI6 (ref. 39) | C2/m | 0.35 | 0.32 |
| Na3GdI6 | C2/m | 0.59 | 0.30 |
| Na3YBr3I3 | C2/m | 3.3 | 0.25 |
| Na3GdBr3I3 | C2/m | 7.5 | 0.21 |
The isosurfaces of the Na-ion probability densities were plotted using an isosurface value of 2P0 for Na3InBr6 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c), Na3GdBr6 (R
1c), Na3GdBr6 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and Na3GdI6 (C2/m) in Fig. 3(c–e), respectively, based on the Na-ion trajectories during 50 ps AIMD simulations at 800 K. As predicted from the relatively low values of Ea for the 1D paths in the P
) and Na3GdI6 (C2/m) in Fig. 3(c–e), respectively, based on the Na-ion trajectories during 50 ps AIMD simulations at 800 K. As predicted from the relatively low values of Ea for the 1D paths in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c and R
1c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases (Fig. 2), Na-ion isosurfaces were more connected for 1D paths along the z-axis, as shown in Fig. 3(c and d), S12 and S13.† The higher Ea for the 3D paths in R
phases (Fig. 2), Na-ion isosurfaces were more connected for 1D paths along the z-axis, as shown in Fig. 3(c and d), S12 and S13.† The higher Ea for the 3D paths in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases inhibited long-range diffusion along the xy plane, resulting in the low ionic conductivity of R
phases inhibited long-range diffusion along the xy plane, resulting in the low ionic conductivity of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) . The Na-ion diffusivity increased in the P
. The Na-ion diffusivity increased in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c phase for Na3MBr6 as diffusion along the 3D paths is facilitated in this phase, as shown in Fig. S12.† In Fig. 3(e) and S14,† it can be seen that the isosurfaces in Na3GdI6 are well connected through the 3D paths, verifying the high diffusivity in the C2/m phase.
1c phase for Na3MBr6 as diffusion along the 3D paths is facilitated in this phase, as shown in Fig. S12.† In Fig. 3(e) and S14,† it can be seen that the isosurfaces in Na3GdI6 are well connected through the 3D paths, verifying the high diffusivity in the C2/m phase.
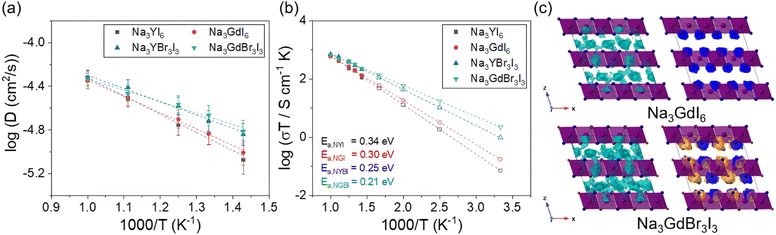
Anion mixing was performed to increase the ionic conductivity of the C2/m phase Na3MI6, based on previous studies showing that Cl–Br mixing enhanced the ionic conductivity of Li3MCl6 owing to the increase in disorder in chemical bonding.57,61,62 Na3MBrxI6−x (M = Y and Gd) structures with the lowest energy among 100 randomly generated simulation cells were used for the calculations. The phase stability of Na3MBrxI6−x was examined using the decomposition energy, Ed, as shown in Table S10.† Na3MBrxI6−x was found to be a metastable phase and it showed a phase transition from C2/m to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) as the ratio of Br in Na3MBrxI6−x increased (x > 3).
as the ratio of Br in Na3MBrxI6−x increased (x > 3).
The Na-ion diffusivity and conductivity of the C2/m phase in Na3MBr3I3 (M = Y and Gd) were evaluated using AIMD simulations, as shown in Fig. 4. The Arrhenius plot of the Na-ion diffusivity in Fig. 4(a) was obtained using the Na-ion MSD (Fig. S15†). Na3YBr3I3 and Na3GdBr3I3 exhibited activation energies of 0.25 and 0.21 eV and ionic conductivities of 3.3 × 10−3 and 7.5 × 10−3 S cm−1 at room temperature, respectively. Anion mixing with Br in the C2/m phase of Na3MI6 was found to be a valuable strategy to enhance the ionic conductivity. The predicted ionic conductivity of Na3GdBr3I3 (7.5 mS cm−1) is the highest value among the studied Na halide SEs. The activation energies, ionic conductivities and error bounds for Na3YBr3I3 and Na3GdBr3I3 are listed in Tables 1 and S11.† The isosurfaces of the ionic probability densities for Na3GdI6 and Na3GdBr3I3 are presented in Fig. 4(c) using an isosurface value of 2P0 based on the Na-ion trajectories from 50 ps AIMD simulations at 800 K. The ionic probability densities for Na, Br and I are shown in light blue, orange and blue, respectively. The isosurfaces of the Na-ion probability densities for Na3GdBr3I3 were found to be more connected through the 3D paths than those for Na3GdI6, confirming the higher Na-ion diffusivity in Na3GdBr3I3. Anion mixing likely increases disorder in the chemical bonding and enlarges the vibration of Br and I anions in the crystal lattice, which facilitates Na-ion migration. The isosurfaces of the ionic probability densities with views along various directions are shown in Fig. S16 and S17.†
The electrochemical stability window of Na3MX6 (X = Cl, Br and I) was evaluated using a grand potential diagram as a function of the chemical potential of Na. As shown in Fig. 5, Na3MCl6 and Na3MBr6 display high oxidation potential of approximately 3.9 and 3.7 V, respectively, suggesting good electrochemical stability against oxidation at high voltages. We point out that, under real conditions, oxidation reactions typically occur at potentials higher than these theoretical limits owing to the kinetic barrier for the phase decomposition reaction and the presence of protective decomposition layers at the interface. Therefore, Na3MCl6 and Na3MBr6 could be applied to ASSBs with high-voltage cathodes and they show substantial advantages compared with sulfide SEs with low oxidation potentials (<2.5 V), such as Na3PS4 and Na3SbS4.63 Na3MI6 exhibits an oxidation potential of approximately 3.0 V, suggesting lower electrochemical stability against oxidation than Na3MCl6 and Na3MBr6. Again, kinetic reaction barriers and decomposition layers may help to prevent the oxidation reaction. Interface coatings could be applied to passivate the oxidative decomposition of Na3MI6.33
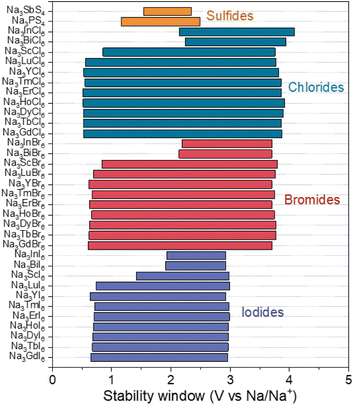 | ||
| Fig. 5 Electrochemical stability windows of Na halide (Na3MX6, X = Cl, Br and I) and sulfide (Na3PS4 and Na3SbS4) SEs. | ||
The reduction potentials of Na3MX6 (X = Cl, Br and I) were found to depend on the identity of the M element, agreeing with previous studies on Li halides Li3MX6 that electronegativity difference between M and X affected electrochemical stabilities.57 Stronger electron localization between M and X would decrease the reduction potential. The reduction potentials of Na3MX6 with p-block elements are approximately 2.1 V, whereas Na3MX6 with group 3 elements and lanthanides exhibit a much lower reduction potential of approximately 0.6 V. Overall, however, the Na3MX6 compounds generally show a wide electrochemical window. Reductive decomposition resulted in the formation of metallic compounds, as shown in Table S12,† enabling continuous reduction reactions of Na3MX6 by conducting electrons.64 Therefore, we suggest that interfacial coatings between the Na metal anode and Na3MX6 would be required to inhibit the continuous reductive decomposition of Na3MX. The oxidation and reduction potentials of Na3MX6 and the phase equilibria at these potentials are summarized in Table S12.†
Conclusions
In this study, we have provided design principles of superionic Na halide SEs through systematic analyses of the structural preference, phase stability, electrochemical stability and transport properties of Na3MX6 (X = Cl, Br and I). The structures of Na3MX6 are strongly dependent on the types and sizes of cations M and anions X, and the octahedral factors were found to be effective descriptors for predicting the stable phases of Na3MX6. Na3MX6 generally exhibits P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n, R
1c, P21/n, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and C2/m phases, while Na3MX6 with relatively small M cations exhibits the NaMX4 (P212121) phase. Na3MCl6 and Na3MBr6 prefer the P
and C2/m phases, while Na3MX6 with relatively small M cations exhibits the NaMX4 (P212121) phase. Na3MCl6 and Na3MBr6 prefer the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases and phase transitions from P
phases and phase transitions from P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c–P21/n–R
1c–P21/n–R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) were found to occur with increasing size of M. Na3MI6 showed octahedral factor values similar to those of the C2/m phase of Li3MCl6, indicating a preference for the C2/m phase over the P
were found to occur with increasing size of M. Na3MI6 showed octahedral factor values similar to those of the C2/m phase of Li3MCl6, indicating a preference for the C2/m phase over the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c, P21/n and R
1c, P21/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases. The effects of the structures of Na3MX6 on Na-ion migration were investigated using the BVSE method and AIMD simulations. The energy barriers of Na-ion migration in the R
phases. The effects of the structures of Na3MX6 on Na-ion migration were investigated using the BVSE method and AIMD simulations. The energy barriers of Na-ion migration in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and P21/n phases were found to be higher than those in the P
and P21/n phases were found to be higher than those in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c phase for Na3MCl6 and Na3MBr6, whereas the C2/m phase Na3MI6 showed a lower barrier than the other phases. AIMD simulations likewise revealed that the P
1c phase for Na3MCl6 and Na3MBr6, whereas the C2/m phase Na3MI6 showed a lower barrier than the other phases. AIMD simulations likewise revealed that the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c phase exhibits high ionic conductivity (∼10−5 S cm−1) relative to the other phases of Na3MBr6 and that the C2/m phase of Na3MI6 shows even higher ionic conductivity (∼10−4 S cm−1). Anion mixing with Br in Na3MI6 further enhanced Na-ion migration, resulting in a superb ionic conductivity of 7.5 × 10−3 S cm−1 for Na3GdBr3I3, which is the highest value among the reported Na halide SEs. Na3MCl6 and Na3MBr6 exhibit natively high oxidation potentials, enabling compatibility with high-voltage cathodes (∼4 V), whereas interfacial coatings would be required to use Na3MI6 with high-voltage cathodes. The material design principles in this work provide fundamental guidelines for the development of superionic Na halide SEs for high-voltage Na ASSBs.
1c phase exhibits high ionic conductivity (∼10−5 S cm−1) relative to the other phases of Na3MBr6 and that the C2/m phase of Na3MI6 shows even higher ionic conductivity (∼10−4 S cm−1). Anion mixing with Br in Na3MI6 further enhanced Na-ion migration, resulting in a superb ionic conductivity of 7.5 × 10−3 S cm−1 for Na3GdBr3I3, which is the highest value among the reported Na halide SEs. Na3MCl6 and Na3MBr6 exhibit natively high oxidation potentials, enabling compatibility with high-voltage cathodes (∼4 V), whereas interfacial coatings would be required to use Na3MI6 with high-voltage cathodes. The material design principles in this work provide fundamental guidelines for the development of superionic Na halide SEs for high-voltage Na ASSBs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the institutional program of the Korea Institute of Science and Technology (Project No. 2E31861 and 2E31864) and the National Supercomputing Center with supercomputing resources including technical support (KSC-2022-CRE-0039). The work by K. K. and B. W. was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract Number DE-AC52-07NA27344. B. W. acknowledges additional support from the Vehicle Technologies Office, Office of Energy Efficiency and Renewable Energy, U.S. Department of Energy.References
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef CAS.
- S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- P. Albertus, S. Babinec, S. Litzelman and A. Newman, Nat. Energy, 2018, 3, 16–21 CrossRef CAS.
- M. Cheng, Y. Wang, D. Zhang, S. Zhang, Y. Yang, X. Lv, J. Wang and Y. NuLi, J. Energy Chem., 2023, 76, 1–10 CrossRef CAS.
- S. Trano, F. Corsini, G. Pascuzzi, E. Giove, L. Fagiolari, J. Amici, C. Francia, S. Turri, S. Bodoardo, G. Griffini and F. Bella, ChemSusChem, 2022, 15, e202200294 CrossRef CAS PubMed.
- F. Bella, S. De Luca, L. Fagiolari, D. Versaci, J. Amici, C. Francia and S. Bodoardo, Nanomaterials, 2021, 11, 810 CrossRef CAS PubMed.
- M. Song, Y. Wang, B. Yu, W. Yang, G. Cheng, W. Cui and Z. Zhang, Chem. Eng. J., 2022, 450, 138176 CrossRef CAS.
- E. Manarin, F. Corsini, S. Trano, L. Fagiolari, J. Amici, C. Francia, S. Bodoardo, S. Turri, F. Bella and G. Griffini, ACS Appl. Polym. Mater., 2022, 4, 3855–3865 CrossRef CAS PubMed.
- A. Massaro, A. B. Muñoz-García, P. Maddalena, F. Bella, G. Meligrana, C. Gerbaldi and M. Pavone, Nanoscale Adv., 2020, 2, 2745–2751 RSC.
- W. Hou, X. Guo, X. Shen, K. Amine, H. Yu and J. Lu, Nano Energy, 2018, 52, 279–291 CrossRef CAS.
- Y. Lu, L. Li, Q. Zhang, Z. Niu and J. Chen, Joule, 2018, 2, 1747–1770 CrossRef CAS.
- C. Zhao, L. Liu, X. Qi, Y. Lu, F. Wu, J. Zhao, Y. Yu, Y.-S. Hu and L. Chen, Adv. Energy Mater., 2018, 8, 1703012 CrossRef.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100 CrossRef.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef CAS.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Angew. Chem., Int. Ed., 2016, 55, 9634–9638 CrossRef CAS PubMed.
- A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, Nat. Commun., 2019, 10, 5266 CrossRef CAS PubMed.
- Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93 RSC.
- T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett., 2020, 5, 146–151 CrossRef CAS.
- Y. Xiao, Y. Wang, S.-H. Bo, J. C. Kim, L. J. Miara and G. Ceder, Nat. Rev. Mater., 2020, 5, 105–126 CrossRef CAS.
- Y. Lee, J. Jeong, H. J. Lee, M. Kim, D. Han, H. Kim, J. M. Yuk, K.-W. Nam, K. Y. Chung, H.-G. Jung and S. Yu, ACS Energy Lett., 2022, 7, 171–179 CrossRef CAS.
- N. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, J. Mater. Sci., 2011, 46, 2821–2837 CrossRef CAS.
- M.-C. Bay, M. Wang, R. Grissa, M. V. F. Heinz, J. Sakamoto and C. Battaglia, Adv. Energy Mater., 2020, 10, 1902899 CrossRef CAS.
- J. Liang, X. Li, K. R. Adair and X. Sun, Acc. Chem. Res., 2021, 54, 1023–1033 CrossRef CAS PubMed.
- X. Li, J. Liang, X. Yang, K. R. Adair, C. Wang, F. Zhao and X. Sun, Energy Environ. Sci., 2020, 13, 1429–1461 RSC.
- S. Wang, Q. Bai, A. M. Nolan, Y. Liu, S. Gong, Q. Sun and Y. Mo, Angew. Chem., Int. Ed., 2019, 58, 8039–8043 CrossRef CAS PubMed.
- H. Kwak, S. Wang, J. Park, Y. Liu, K. T. Kim, Y. Choi, Y. Mo and Y. S. Jung, ACS Energy Lett., 2022, 7, 1776–1805 CrossRef CAS.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 CrossRef PubMed.
- X. Li, J. Liang, J. Luo, M. Norouzi Banis, C. Wang, W. Li, S. Deng, C. Yu, F. Zhao, Y. Hu, T.-K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, K. R. Adair and X. Sun, Energy Environ. Sci., 2019, 12, 2665–2671 RSC.
- J. Liang, X. Li, S. Wang, K. R. Adair, W. Li, Y. Zhao, C. Wang, Y. Hu, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, Y. Mo and X. Sun, J. Am. Chem. Soc., 2020, 142, 7012–7022 CrossRef CAS PubMed.
- L. Zhou, T.-T. Zuo, C. Y. Kwok, S. Y. Kim, A. Assoud, Q. Zhang, J. Janek and L. F. Nazar, Nat. Energy, 2022, 7, 83–93 CrossRef CAS.
- S. Yu, H. Park and D. J. Siegel, ACS Appl. Mater. Interfaces, 2019, 11, 36607–36615 CrossRef CAS PubMed.
- R. Schlem, A. Banik, M. Eckardt, M. Zobel and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 10164–10173 CrossRef CAS.
- E. A. Wu, S. Banerjee, H. Tang, P. M. Richardson, J.-M. Doux, J. Qi, Z. Zhu, A. Grenier, Y. Li, E. Zhao, G. Deysher, E. Sebti, H. Nguyen, R. Stephens, G. Verbist, K. W. Chapman, R. J. Clément, A. Banerjee, Y. S. Meng and S. P. Ong, Nat. Commun., 2021, 12, 1256 CrossRef CAS PubMed.
- H. Kwak, J. Lyoo, J. Park, Y. Han, R. Asakura, A. Remhof, C. Battaglia, H. Kim, S.-T. Hong and Y. S. Jung, Energy Storage Mater., 2021, 37, 47–54 CrossRef.
- D. Park, K. Kim, G. H. Chun, B. C. Wood, J. H. Shim and S. Yu, J. Mater. Chem. A, 2021, 9, 23037–23045 RSC.
- Y. Qie, S. Wang, S. Fu, H. Xie, Q. Sun and P. Jena, J. Phys. Chem. Lett., 2020, 11, 3376–3383 CrossRef PubMed.
- H. Huang, H.-H. Wu, C. Chi, Y. Yang, J. Zheng, B. Huang and S. Wang, J. Mater. Chem. A, 2021, 9, 26256–26265 RSC.
- A. Bohnsack and G. Meyer, Z. Anorg. Allg. Chem., 1997, 623, 837–843 CrossRef CAS.
- G. Mairesse, P. Barbier and J.-P. Wignacourt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 1573–1580 CrossRef.
- T. Staffel and G. Meyer, Z. Anorg. Allg. Chem., 1989, 574, 107–113 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- G. Friedrich, H. Fink and H. J. Seifert, Z. Anorg. Allg. Chem., 1987, 548, 141–150 CrossRef CAS.
- M. Beran and G. Meyer, Crystals, 2011, 1, 99–103 CrossRef CAS.
- G. Meyer, Z. Anorg. Allg. Chem., 1984, 517, 191–197 CrossRef CAS.
- H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2019, 75, 18–33 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18 CrossRef.
- Y. Liu, S. Wang, A. M. Nolan, C. Ling and Y. Mo, Adv. Energy Mater., 2020, 10, 2002356 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- Y. Yu, Z. Wang and G. Shao, J. Mater. Chem. A, 2021, 9, 25585–25594 RSC.
- K. Kim, D. Park, H.-G. Jung, K. Y. Chung, J. H. Shim, B. C. Wood and S. Yu, Chem. Mater., 2021, 33, 3669–3677 CrossRef CAS.
- R. Xiao, H. Li and L. Chen, Sci. Rep., 2015, 5, 14227 CrossRef CAS PubMed.
- D. Park, H. Park, Y. Lee, S.-O. Kim, H.-G. Jung, K. Y. Chung, J. H. Shim and S. Yu, ACS Appl. Mater. Interfaces, 2020, 12, 34806–34814 CrossRef CAS PubMed.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Chem. Mater., 2019, 31, 342–352 CrossRef CAS.
- Z. Liu, S. Ma, J. Liu, S. Xiong, Y. Ma and H. Chen, ACS Energy Lett., 2021, 6, 298–304 CrossRef CAS.
- A. Zevgolis, B. C. Wood, Z. Mehmedović, A. T. Hall, T. C. Alves and N. Adelstein, APL Mater., 2018, 6, 047903 CrossRef.
- H. Tang, Z. Deng, Z. Lin, Z. Wang, I.-H. Chu, C. Chen, Z. Zhu, C. Zheng and S. P. Ong, Chem. Mater., 2018, 30, 163–173 CrossRef CAS.
- L. M. Riegger, R. Schlem, J. Sann, W. G. Zeier and J. Janek, Angew. Chem., Int. Ed., 2021, 60, 6718–6723 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta05158c |
| This journal is © The Royal Society of Chemistry 2022 |