Criteria for evaluating lithium–air batteries in academia to correctly predict their practical performance in industry

Abstract

Although the market share for Li-ion batteries (LiBs) has continuously expanded, the limited theoretical energy density of conventional LiBs will no longer meet the advanced energy storage requirements. Lithium–air batteries (LABs) are potential candidates for next-generation rechargeable batteries because of their extremely high theoretical energy density. However, the reported values for the actual energy density of LABs are much lower than those for LiBs, mainly due to the excess amount of electrolyte in the cell. In the present review article, the practical energy density is estimated for the representative LABs reported in academia, and the critical factors for improving the energy density of LABs are summarized. The criteria for evaluating LABs in laboratory-based experiments are also proposed for accurately predicting the performance of practical cells in industry.

---

Shoichi Matsuda

Shoichi Matsuda is a Senior Researcher at the National Institute for Materials Science (NIMS), Japan. He studied chemistry in The University of Tokyo and received his PhD in 2015. After that, he joined NIMS as an ICYS (International Center for Young Scientists) researcher and then got a tenured position in 2017. He has been participating in the “Specially Promoted Research for Innovative Next Generation Batteries (ALCA-SPRING)” project since 2016. His current research interests are lithium-metal based rechargeable batteries and data-driven automated experiments.

Manai Ono

Manai Ono is a Postdoctoral Researcher at the National Institute for Materials Science (NIMS), Japan. She majored in applied chemistry at Meiji University. She obtained an ME (2014) and Doctor of Engineering (2017) from the University of Yamanashi. She worked for TAKAHATA PRECISION Co., LTD from 2010 to 2018 and studied synthesis of alkaline polyelectrolytes for Fuel Cell at the Fuel Cell Nanomaterials Center, University of Yamanashi, Japan. She has been participating in lithium–air battery research at NIMS since 2018 as a member of TechnoPro, Inc. and as a postdoctoral researcher since 2020.

Shoji Yamaguchi

Shoji Yamaguchi is currently a NIMS Specialist Staff at the National Institute for Materials Science (NIMS). He received his M.S. and PhD from Osaka University in 1981 and 1995, and studied at Johns Hopkins University from 1988 to 1991. He worked at Mitsubishi Chemical Corporation from 1981 to 2018. He was a principal researcher in the commercialization of the world's first core–shell type graphite anode material in 1996. He was GM of Battery System Designs Laboratory and Battery Materials Department at Mitsubishi Chemical Corporation and has contributed to the lithium-ion battery industry for 17 years. After that, he joined NIMS in 2019 and works as Director of NIMS Battery Research Platform to support the “Specially Promoted Research for Innovative Next Generation Batteries (ALCA-SPRING)” project from 2019 to 2021.

Kohei Uosaki

Kohei Uosaki is a Fellow, Executive Advisor to the President, and Director of the NIMS-SoftBank Advanced Technologies Development Center of NIMS and has been Professor Emeritus of Hokkaido University since 2010. He received his PhD from Flinders University and worked at Mitsubishi Petrochemical, Oxford University and Hokkaido University where he stayed for 30 years as an Assistant, Associate and Full Professor. He has published more than 450 original papers on surface physical chemistry. Currently, he is leading the “Specially Promoted Research for Innovative Next Generation Batteries (ALCA-SPRING)” project in Japan. He was awarded the Society Award of The Chemical Society of Japan (2010) and of The Surface Science Society of Japan (2014). He is a Fellow of the RSC, ISE, ECS, and CSJ.

---

1. Introduction

The demand for the development of rechargeable batteries with high energy densities has been increasing in recent years. Although Li-ion batteries (LiBs), which have been used since 1991, have responded well to market needs, the energy density of conventional LiBs does not meet the requirements of advanced energy storage devices, such as next-generation vehicles and flying objects, including drones and unmanned aerial vehicles, which slowly charge during the day and discharge overnight. Lithium–air batteries (LABs), which have the potential to achieve energy densities two to five times higher than those of LiBs, are potential candidates for next-generation rechargeable batteries for the above-mentioned application field. In the last few decades, there has been huge progress in LAB technology from the view point of materials science, such as the development of a stable electrolyte against oxygen reactive species, the hierarchical porous carbon electrode, and the protective layer of lithium metal electrodes. These research accomplishments have been well summarized in recent review papers (ref. 1 and 2). Although the superior cycle performance of LABs has been widely reported in the literature in the field of academia, their commercialization has not been achieved yet. In fact, most of the current research mainly focuses on the evaluation of individual components at the material level, and only a few studies have evaluated the cell level performance of LABs under practical conditions with the appropriate technological parameters (ref. 3–6). Even for next-generation rechargeable batteries other than LAB, such large gaps between academia and industry in the research activity have been pointed out (ref. 7–10). In this mini-review article, we summarize the crucial factors required for realizing LABs with high practical energy density based on the results of energy density simulations. In addition, the criteria for evaluating materials are proposed for correctly predicting their potential at the practical cell level.

2. Design principle of LABs with practical high energy density

A typical LAB is composed of a Li–metal foil, separator, Li-ion-conducting non-aqueous electrolyte, porous carbon electrode, and gas diffusion layer. During discharge, the dissolution of Li metal proceeds at the negative electrode. The generated electrons are transferred to the positive electrode through an external circuit and used for the reduction of atmospheric oxygen, forming insoluble Li₂O₂ as a discharge product. In the charging process, the reverse reaction should proceed, and the total reaction is shown as follows:

Positive electrode: O₂ + 2Li⁺ + 2e⁻ = Li₂O₂

Negative electrode: Li = Li⁺ + e⁻

For the energy density of LAB, 3150 W h kg⁻¹ can be theoretically obtained by multiplying an assumed operating voltage of 2.7 V with a specific capacity of 1168 A h kg⁻¹ based on the reaction 2Li + O₂ = Li₂O₂. However, owing to the presence of inactive components in the practical LAB cell, such as an electrolyte, separator and current collector, the cell level energy density significantly decreases compared with the theoretical value. To estimate the practical energy density of a LAB, it is necessary to accurately understand the effects of various parameters on the energy density. The energy density of the LAB is defined by dividing the amount of energy output during the discharge process by the total weight of the cell components as follows:

Energy density [W h kg⁻¹] = average discharge voltage [V] × areal capacity [mA h cm⁻²]/mass loading of cell components [mg cm⁻²].

Herein, the effects of various cell components on the energy density of a LAB were investigated. In the following energy density simulation, we do not include the weight of oxygen, sealing film and tab lead for simplifying the calculation. First, we selected the following cell parameters, which are commonly used in typical LAB experiments in the literature; mass loading of positive electrode = 1 mg cm⁻², 2000 mA h g^{electrode−1}, utilization ration of positive electrode = 50%, 50 μm thickness of lithium metal as a negative electrode, glass fiber-based separator, electrolyte amount = 50 mg cm⁻², areal capacity = 1 mA h cm⁻² (details are shown in the ESI†). In this case, the energy density of the LAB was estimated to be less than 50 W h kg⁻¹ (Fig. 1a), which is much lower than that of conventional LiBs. Considering the fact that the areal capacity of commercialized LiB is 2–5 mA h cm⁻², we changed the mass loading of the positive electrode from 1 mg cm⁻² to 4 mg cm⁻² for yielding an areal capacity of 4 mA h cm⁻². In addition, it can be seen that the electrolyte comprises more than 64% of the cell weight. Considering the fact that the weight percentage of the electrolyte in commercialized LiBs is approximately 30–40%, the amount of electrolyte in LABs should be decreased to improve their energy density. The amount of electrolyte can be decreased by replacing the thick glass fiber-based separator with a thin PO-based separator and decreasing the electrolyte injection ratio in the porous carbon electrode from 100% to 60%. As a result, the weight percentage of the electrolyte decreased to 57%, and the energy density reached 240 W h kg⁻¹ (Fig. 1b). In this case, most of the electrolyte was present in the porous carbon electrode. By replacing the carbon electrode of 8000 mA h g^{electrode−1}, the amount of electrolyte stored in the electrode can further decrease. As a result, the weight percentage of the electrolyte decreased to 31%, and the energy density reached 466 W h kg⁻¹ (Fig. 1c).

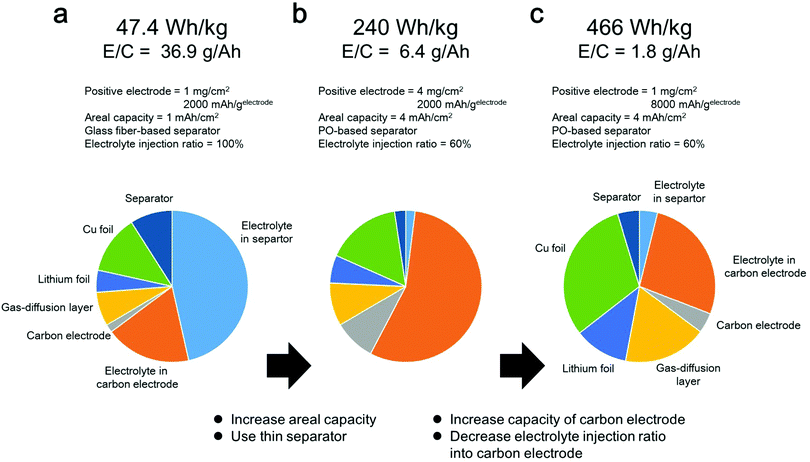Fig. 1 Energy density simulation of LAB. (a–c) Technological parameters used for energy density simulation and weight fractions of cell components calculated using the parameters listed in Table S1 (ESI†). (a) Areal capacity = 1 mA h cm⁻², glass fiber separator, capacity of carbon electrode = 2000 mA h g^{electrode−1}, mass loading of carbon electrode = 4 mg cm⁻² and electrolyte injection ratio in carbon electrode = 100%. (b) Areal capacity = 4 mA h cm⁻², polyolefin separator, capacity of carbon electrode = 2000 mA h g^{electrode−1}, mass loading of carbon electrode = 4 mg cm⁻² and electrolyte injection ratio in carbon electrode = 60%. (c) Areal capacity = 4 mA h cm⁻², polyolefin separator, capacity of carbon electrode = 8000 mA h g^{electrode−1}, mass loading of carbon electrode = 1 mg cm⁻² and electrolyte injection ratio in carbon electrode = 60%.

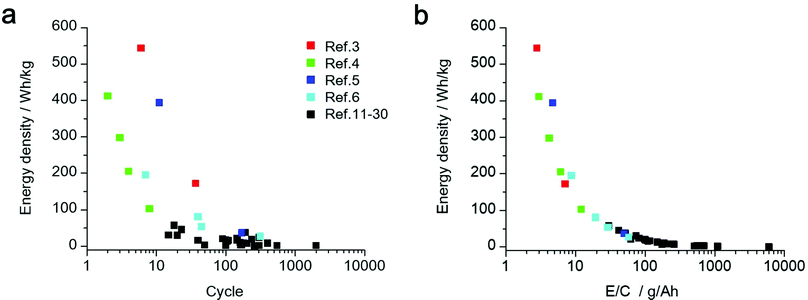
Based on the results obtained using the above energy density simulation, it was apparent that the amount of electrolyte and areal capacity are important parameters for determining the energy density of the LAB. Herein, we estimate the cell level energy density of the LAB reported in the literature (ref. 3–6, 11–30). In the cases where important parameters, such as the amount of electrolyte or details of the separator, were not described in their experimental section, we used the values that are generally used in the field of LABs to estimate their energy density. We restrict our target only to non-aqueous electrolyte-based LABs operated at room temperature for a fair comparison of their performance.

In Fig. 2a, the estimated energy density and cycle number of the discharge/charge test are plotted. Although there are many reports that demonstrate the successful operation of a LAB with prolonged discharge/charge processes for more than 100 cycles, their energy density at the practical cell level was lower than 50 W h kg⁻¹. In contrast, for the LABs with an energy density over 300 W h kg⁻¹, the cycle number was less than 20 cycles. Details of the LAB energy density estimation can be found in Tables S1, S2 and the supporting data file (ESI†). In addition, a brief summary of LAB energy density estimation and the weight percentage of cell components are shown in Table S2 and Fig. S1 (ESI†). If the important technological parameter is not described in the literature, we utilized a standard value for the estimation of the energy density of LABs. The details are described in Note S1 (ESI†). We also estimate the possible maximum energy density of “Advanced type of LABs” by performing a calculation utilizing the technological parameter of a next-generation material, such as thin current collector and light-weight gas-diffusion layer (Table S3, ESI†).

Fig. 2 Estimated cell-level energy density of the LAB reported in the literature. (a) Relationships between energy density and cycle life of LAB. (b) Relationships between energy density and the ratio of the electrolyte weight to cell capacity (E/C, g A⁻¹ h⁻¹).

In Fig. 2b, the estimated energy density of LABs was plotted against the ratio of the electrolyte weight to cell capacity (E/C, g A⁻¹ h⁻¹), which is used as an empirical parameter of the electrolyte amount in the field of LiBs. A clear correlation between two factors can be seen, suggesting that the E/C can be utilized as a practical indicator for estimating the cell level energy density of LABs based on the experimental data in the literature. Interestingly, all the LABs with E/C over 50 g A⁻¹ h⁻¹ exhibited an energy density lower than 50 W h kg⁻¹, suggesting that an excess amount of electrolyte (>50 mg cm⁻²) and/or operation at low areal capacity conditions (<1 mA cm⁻²) diminish the cell level energy density. These results clearly revealed that the value of E/C should be controlled lower than 10 g A⁻¹ h⁻¹ for realizing LABs with an energy density over 300 W h kg⁻¹.

3. Critical technologies for LABs with practically high energy density

Numerous studies on LABs have been published over the last decade. However, most of the current research mainly focuses on the evaluation of individual components at the material level, and only a few studies have evaluated the performance of LABs under practical conditions using appropriate technological parameters. As mentioned in the previous section, the evaluation of battery performance under a limited amount of electrolyte and high areal capacity conditions is crucial for realizing LABs with a high energy density at the practical cell level. In the following section, we summarize the critical technologies and the criteria for performance evaluation of LABs with high practical energy density.

3.1 Design principle of porous carbon based positive electrodes

Based on the results of the energy density simulation, the improvement in the energy capacity of the porous carbon-based positive electrode is beneficial for maximizing the energy density of LABs. Importantly, the energy capacity of the electrode should be evaluated by the unit of capacity per mass of the electrode (mA g^{electrode−1}), not by the capacity per mass of carbon (mA g^carbon−1). That is, the mass of inactive components in the electrode, such as the binder and substrate material should also be taken into account. It is a well-known fact that binder-free CNT based self-standing membranes can be easily prepared, for example, by a simple vacuum filtration technique. However, in the case of carbon black powders, the binder and substrate material should be utilized for preparing a self-standing membrane with sufficient mechanical strength. In this case, the weight ratio of the carbon material should be maximized by decreasing the amount of binder and substrate without diminishing the mechanical strength of the membrane for improving the capacity of the electrode (mA g^{electrode−1}). For the material design and evaluation of the electrode, the mass loading is also an important parameter. When the mass loading of the electrode is too small (0.1–0.2 mg cm⁻²), the areal capacity is also relatively small. For example, even if the 4000 mA h g^{electrode−1} is used, the areal capacity is 0.4–0.8 mA h cm⁻². Thus, for development of the positive electrode achieving the LABs with practically high energy density design, the mass loading should be higher than 1 mg cm⁻². In this case, the areal capacity higher than 4 mA h cm⁻² can be realized. For the evaluation of a positive electrode material, their performance should be evaluated at a wide mass loading region to correctly understand their potential for practical application. In high mass loading conditions, the hierarchical pore structure of the electrode should be designed. In addition to the mesopore structure for storing the deposited Li₂O₂, the formation of an interconnected micron-sized macropore is beneficial for enhancing the oxygen transport through the electrode (ref. 31–37).

3.2 Electrolyte injection technology

For minimizing the amount of the electrolyte in LAB cells, the electrolyte in the pores of the carbon electrode should be quantitatively controlled. Ideally, the surface of the porous carbon electrode should be completely wetted with the electrolyte to enable the efficient transfer of Li ions. In addition, the voids in the electrode should not be completely filled with the electrolyte to ensure that the oxygen transport channels from a gas diffusion layer. However, in reality, the electrolyte distribution in the carbon electrode is inhomogeneous, especially when the ratio of the electrolyte amount to the electrode pore volume (i.e., electrolyte volume fraction) is to be small. Under such conditions, Li₂O₂ formed during discharge is segregated in the region where the electrolyte is localized, thereby clogging the electrode pores. Therefore, a suitable electrolyte injection technology should be utilized. Actually, several electrolyte injection techniques have been demonstrated for their effectiveness of improving the performance of LABs (ref. 38), such as the “inkjet method”, which employs a piezoelectric element to emit nanoliter-scale electrolyte droplets, and the “stamping method”, which uses two highly hydrophilic filters as electrolyte transfer agents allowing the uniformly spread electrolyte to be transferred to the carbon electrode sandwiched between them. The details of each electrolyte injection technique are summarized in Fig. S2 (ESI†).

3.3 Performance evaluation of electrolyte

With respect to selecting an electrolyte for the LAB, a non-aqueous electrolyte is a promising candidate as a solvent because of its wide potential window and high wettability with electrodes and separators (ref. 39 and 40). Although aqueous electrolyte-based LABs have been reported as alternative candidates, concerns regarding the high volatility of water and its high reactivity against lithium electrodes remain (ref. 41 and 42). From the viewpoint of volatility, ionic liquid- and polymer-based electrolytes are attractive; however, their low conductivity limits the LAB from operating under practical current density conditions at room temperature (ref. 43–46).

For realizing prolonged cycles of LABs with a high practical energy density, the side reactions at the positive and negative electrodes should be minimized, especially to suppress decomposition of the electrolyte. Considering the case that the electrochemical reaction efficiency is 95% and the solvent is decomposed by one-electron reaction, 0.6 mg cm⁻² of solvent is decomposed during just one discharge/charge reaction with an areal capacity of 4 mA h cm⁻² (we consider the Mw of the solvent to be 100 g mol⁻¹). In case the initial amount of electrolyte is 20 mg cm⁻² (E/C = 5 g A⁻¹ h⁻¹), the amount of decomposed electrolyte corresponds to 6%. In this case, it was estimated that all the solvents completely decomposed in just 35 cycles, revealing the importance of suppressing the side reactions. In addition, the volatilization should also be seriously considered as the amount of electrolyte is strictly controlled in LABs with a high energy density design. Therefore, in laboratory-based studies, the performance of electrolyte (solvent, redox mediator) should be evaluated not only by the conventional discharge/charge tests but also by the reaction efficiency of the electrode reaction. In addition, it is also important to quantify the amount of electrolyte remaining in the cell after the repeated discharge/charge cycles. Such information is critical for correctly predicting the cycle performance of LABs at the practical cell level.

3.4. Challenges in LABs with lean-electrolyte

In order to realize LABs with a practically high energy density at the cell level, the problems particular to limited electrolyte conditions, so called “lean-electrolyte”, should be taken into account. The importance of the investigation of lithium negative electrodes in a lean-electrolyte system has been recognized in recent years (ref. 47–49). Even for the reaction at the oxygen positive electrodes, the peculiar issues regarding the lean-electrolyte system also exist. For example, the movement of electrolyte inside of the porous carbon electrode associated with the reversible formation/decomposition of lithium peroxide should be considered. Actually, under the condition that the amount of electrolyte is strictly limited, a unique cell failure mechanism was reported (ref. 38), that is, a sudden increase in over-potential during the initial stage of the charging process (Fig. S3, ESI†). One possible explanation is the physical squeezing of the electrolyte from the porous carbon electrode driven by the formation of lithium peroxide during discharge. That is, the electrolyte is pushed out and does not completely return to the porous carbon electrode, even though lithium peroxide decomposes during charging. Considering the importance of decreasing the amount of electrolyte for realizing LABs with high practical energy density, the understanding of this phenomenon is quite important, and an advanced analytical technique should be adopted to deepen our understanding of this degradation mechanism.

3.5. Multi-stacked cell

From a practical viewpoint, multiple LAB cells must be densely stacked, similar to conventional LiBs, to realize high energy density at the cell level. In such stacked situations, a proper cell configuration is required to ensure that oxygen can effectively pass through the entire positive electrode via the gas-diffusion layer (Fig. 3a). In fact, a fabricated 4 cm × 5 cm sized 10 cell stacked LAB exhibited a stable discharge/charge performance (ref. 50), in which the effective cell area was 200 cm², 100 times larger than that of the conventional coin-type cells (S = 2 cm²), which are commonly used in laboratory experiment in academia (Fig. 3b). In a coin-type cell, the oxygen is supplied from the top part of the positive electrode. In sharp contrast, in the stacked cell configuration, oxygen needs to be transported in the horizontal direction in the gas diffusion layer. Then, oxygen need to be further transported to the vertical direction to go through the whole part of the positive electrode. For practical implementation of LABs, the development of a gas-diffusion layer is highly important, which realizes efficient oxygen transport. The performance of the gas-diffusion layer should be evaluated in a suitable cell configuration, in which the oxygen supply is allowed only through the horizontal direction of the gas-diffusion layer. Although simulation-based studies have been reported for oxygen transport phenomenon in LAB (ref. 51 and 52), the ideal material properties and configuration of the gas-diffusion layer have not been identified, and further studies are required.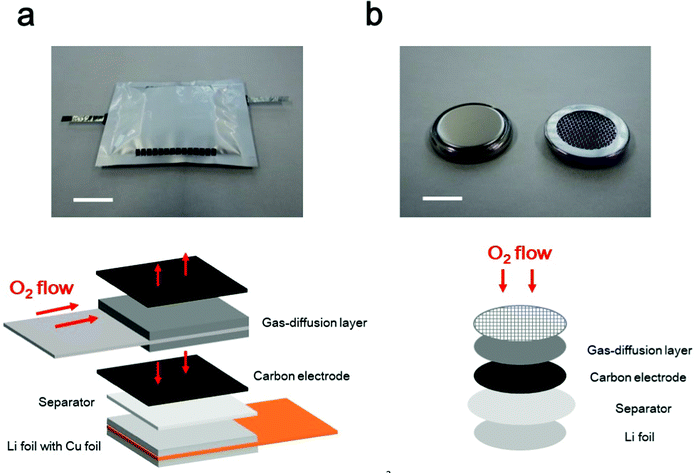

Fig. 3 Photographic and schematic images of LAB cells. (a) Multi-stacked LAB cell, and (b) coin-type LAB cell. The scale bars in the photographic images are 20 mm in (a) and 10 mm in (b).

Based on the above discussion, the performance of LABs should be evaluated at the suitable cell configuration, ideally the universal standardized cell should be utilized for sharing the experimental results obtained by various research groups. However, in reality, the home-made type cells were utilized for LAB experiments and such lack of standardization is one main reason for the limited acceleration of the research development of LABs. From that point of view, we propose a single-layered cell with a 2 cm × 2 cm sized electrode as a possible candidate for standard LAB cells, in which oxygen can be transported through the gas-diffusion layer only in the vertical direction and not in the horizontal direction. In addition, by restraining the top and bottom of the cell with a rigid substrate and tuning the contraction of the spring, the confining pressure inside the cell can be quantitatively controlled. The details of cell configuration are described in Fig. S4 (ESI†). Notably, the design of this cell can be easily extended to a large stacked type cell configuration by enlarging the electrode size (2 cm × 2 cm → 4 cm × 5 cm → 10 cm × 10 cm) and increasing the number of stacking layers (single cell → 2 layers stacked cell (bi-cell) → 10 layers stacked cell).

4. Summary and outlook

In this article, we overview the key technology for realizing LABs with high energy density at the practical cell level. The energy density estimation of LABs reported in the literature revealed that the cell level energy density of most of the LABs was less than 50 W h kg⁻¹ because the cell contains an excess amount of electrolyte and/or the cell is operated at relatively small areal capacity conditions. To achieve an energy density higher than 300 W h kg⁻¹, which surpasses the level of conventional LiBs, the ratio of amount of electrolyte against the areal capacity (E/C, g A⁻¹ h⁻¹) should be controlled to be less than 5 g A⁻¹ h⁻¹.

For rechargeable battery systems equipped with a lithium metal electrode, such as lithium/NMC and lithium/sulfur, recent studies investigated the cell level performance under practical conditions with the appropriate technological parameters (ref. 39–41, 45, 46, 53 and 54). As results, the specific issues in practical cell design have been widely recognized in their research community, resulting in the close collaboration between academia and industry. Even for the research development of LABs, advanced studies in academia should be performed under appropriate technological parameters to accurately predict the possibility of using LABs at the practical cell level.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The present work was partially supported by the ALCA-SPRING (Advanced Low Carbon Technology Research and Development Program – Specially Promoted Research for Innovative Next Generation Batteries) Project of the Japan Science and Technology Agency (JST: Grant Number JPMJAL1301). A part of this work was carried out at the SoftBank-NIMS Advanced Technologies Development Center as a joint research between NIMS and SoftBank Corp..

References

1. W.-J. Kwak, R. Sharma, D. Sharon, C. Xia, H. Kim, L. R. Johnson, P. G. Bruce, L. F. Nazar, Y.-K. Sun, A. A. Frimer, M. Noked, S. A. Freunberger and D. Aurbach, Chem. Rev., 2020, 120, 6626.
2. T. Liu, J. P. Vivek, E. W. Zhao, J. Lei, N. Garcia-Araez and C. P. Grey, Chem. Rev., 2020, 120, 6558.
3. S. Matsuda, E. Yasukawa, T. Kameda, S. Kimura, S. Yamaguchi, Y. Kubo and K. Uosaki, Cell Rep. Phys. Sci., 2021, 2, 100506.
4. S. Zhao, L. Zhang, G. Zhang, H. Sun, J. Yang and S. Lu, J. Energy Chem., 2020, 45, 74.
5. W. Chen, W. Yin, Y. Shen, Z. Huang, X. Li, F. Wang, W. Zhang, Z. Deng, Z. Zhang and Y. Huang, Nano Energy, 2018, 47, 353.
6. Y. J. Lee, S. H. Park, S. H. Kim, Y. Ko, K. Kang and Y. J. Lee, ACS Catal., 2018, 8, 2923.
7. Z. Lin, T. Liu, X. Ai and C. Liang, Nat. Commun., 2019, 9, 5262.
8. J. Betz, G. Bieker, P. Meister, T. Placke, M. Winter and R. Schmuch, Adv. Energy Mater., 2019, 9, 1803170.
9. Y. Cao, M. Li, J. Lu, J. Liu and K. Amine, Nat. Nanotechnol., 2019, 14, 200.
10. M. Ue, K. Sakaushi and K. Uosaki, Mater. Horiz., 2020, 7, 1937.
11. X. Zou, K. Liao, D. Wang, Q. Lu, C. Zhou, P. He, R. Ran, W. Zhou, W. Jin and Z. Shao, Energy Storage Mater., 2020, 27, 297.
12. M. Song, H. Tan, X. Li, A. I. Y. Tok, P. Liang, D. Chao and H. J. Fan, Small Methods, 2020, 4, 1900274.
13. Y. Ma, L. Wei, Y. Gu, J. Hu, Y. Chen, P. Qi, X. Zhao, Y. Peng, Z. Deng and Z. Liu, Adv. Funct. Mater., 2020, 30, 2007218.
14. P. Wang, C. Li, S. Dong, X. Ge, P. Zhang, X. Miao, R. Wang, Z. Zhang and L. Yin, Adv. Energy Mater., 2019, 9, 1900788.
15. L. Ye, M. Liao, H. Sun, Y. Yang, C. Tang, Y. Zhao, L. Wang, Y. Xu, L. Zhang, B. Wang, F. Xu, X. Sun, Y. Zhang, H. Dai, P. G. Bruce and H. Peng, Angew. Chem., Int. Ed., 2019, 58, 2437.
16. Y. Yu, Y. Bin Yin, J. L. Ma, Z. W. Chang, T. Sun, Y. H. Zhu, X. Y. Yang, T. Liu and X. B. Zhang, Energy Storage Mater., 2019, 18, 382.
17. T. Liu, X. Feng, X. Jin, M. Shao, Y. Su, Y. Zhang and X. Zhang, Angew. Chem., Int. Ed., 2019, 58, 18240.
18. F. Guo, T. Kang, Z. Liu, B. Tong, L. Guo, Y. Wang, C. Liu, X. Chen, Y. Zhao, Y. Shen, W. Lu, L. Chen and Z. Peng, Nano Lett., 2019, 19, 6377.
19. Z. Huang, J. Ren, W. Zhang, M. Xie, Y. Li, D. Sun, Y. Shen and Y. Huang, Adv. Mater., 2018, 30, 1803270.
20. G. Sun, Q. Zhao, T. Wu, W. Lu, M. Bao, L. Sun, H. Xie and J. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 6327.
21. X. Xin, K. Ito and Y. Kubo, Electrochim. Acta, 2018, 261, 323.
22. M. Asadi, B. Sayahpour, P. Abbasi, A. T. Ngo, K. Karis, J. R. Jokisaari, C. Liu, B. Narayanan, M. Gerard, P. Yasaei, X. Hu, A. Mukherjee, K. C. Lau, R. S. Assary, F. Khalili-Araghi, R. F. Klie, L. A. Curtiss and A. Salehi-Khojin, Nature, 2018, 555, 502.
23. H.-J. Shin, W.-J. Kwak, D. Aurbach and Y.-K. Sun, Adv. Funct. Mater., 2017, 27, 1605500.
24. Y. Lin, B. Moitoso, C. Martinez-Martinez, E. D. Walsh, S. D. Lacey, J.-W. Kim, L. Dai, L. Hu and J. W. Connell, Nano Lett., 2017, 17, 3252.
25. B. G. Kim, J.-S. Kim, J. Min, Y.-H. Lee, J. H. Choi, M. C. Jang, S. A. Freunberger and J. W. Choi, Adv. Funct. Mater., 2016, 26, 1747.
26. X. Xin, K. Ito and Y. Kubo, Carbon, 2016, 99, 167–173.
27. J. Kim, J. M. Carlin, S. A. Smith, J. Yin and Y. L. Joo, Electrochem. Commun., 2016, 70, 43.
28. C. Shu, R. Huang, J. Wang and D. Su, RSC Adv., 2015, 5, 103019.
29. W.-B. Luo, S.-L. Chou, J.-Z. Wang, Y.-C. Zhai and H.-K. Liu, Small, 2015, 11, 2817.
30. T. Liu, M. Leskes, W. Yu, A. J. Moore, L. Zhou, P. M. Bayley, G. Kim and C. P. Grey, Science, 2015, 350, 530.
31. K. Sakai, S. Iwamura and S. R. Mukai, J. Electrochem. Soc., 2017, 164, A3075.
32. K. Sakaushi, S. J. Yang, T. P. Fellinger and M. Antonietti, J. Mater. Chem. A, 2015, 3, 11720.
33. A. Dutta, K. Ito and Y. Kubo, J. Mater. Chem. A, 2019, 7, 23199.
34. A. N. Mistry, F. Cano-Banda, D. Law, A. Hernandez-Guerrero and P. P. Mukherjee, J. Mater. Chem. A, 2019, 7, 8882.
35. M. Olivares-Marín, M. Aklalouch and D. Tonti, Nanomaterials, 2019, 9, 1.
36. C. Shen, J. Xie, T. Liu, M. Zhang, P. Andrei, L. Dong, M. Hendrickson, E. J. Plichta and J. P. Zheng, J. Electrochem. Soc., 2018, 165, A2833.
37. S. M. Xu, X. Liang, Z. C. Ren, K. X. Wang and J. S. Chen, Angew. Chem., Int. Ed., 2018, 57, 6825.
38. S. Matsuda, S. Yamaguchi, E. Yasukawa, H. Asahina, H. Kakuta, H. Otani, S. Kimura, T. Kameda, Y. Takayanagi, A. Tajika, Y. Kubo and K. Uosaki, ACS Appl. Energy Mater., 2021, 4, 2563.
39. H.-G. Jung, J. Hassoun, J.-B. Park, Y.-K. Sun and B. Scrosati, Nat. Chem., 2012, 4, 579.
40. W. Walker, V. Giordani, J. Uddin, V. S. Bryantsev, G. V. Chase and D. Addison, J. Am. Chem. Soc., 2013, 135, 2076.
41. N. B. Mercier, R. A. Wong, M. L. Thomas, A. Dutta, K. Yamanaka, C. Yogi, T. Ohta and H. R. Byon, Sci. Rep., 2014, 4, 7127.
42. G. A. Elia and J. Hassoun, Sci. Rep., 2015, 5, 12307.
43. G. A. Elia, J. Hassoun, W.-J. Kwak, Y.-K. Sun, B. Scrosati, F. Mueller, D. Bresser, S. Passerini, P. Oberhumer, N. Tsiouvaras and J. Reiter, Nano Lett., 2014, 14, 6572.
44. J. O. Park, M. Kim, J.-H. Kim, K. H. Choi, H. C. Lee, W. Choi, S. B. Ma and D. Im, J. Power Soruces, 2019, 419, 112.
45. S. J. Visco, V. Y. Nimon, A. Petrov, K. Pridatko, N. Goncharenko, E. Nimon, L. D. Jonghe, Y. M. Volfkovich and D. A. Bograchev, J. Solid State Electrochem., 2014, 18, 1443.
46. H. Nemori, X. Shang, H. Minami, S. Mitsuoka, M. Nomura, H. Sonoki, Y. Morita, D. Mori, Y. Takeda, O. Yamamoto and N. Imanishi, Solid State Ionics, 2018, 317, 136.
47. S. Chen, C. Niu, H. Lee, Q. Li, L. Yu, W. Xu, J.-G. Zhang, E. J. Dufek, M. S. Whittingham, S. Meng, J. Xiao and J. Liu, Joule, 2019, 3, 1.
48. H. Li, Joule, 2019, 3, 908.
49. J. Liu, Z. Bao, Y. Cui, E. J. Dufek, J. B. Goodenough, P. Khalifah, Q. Li, B. Y. Liaw, P. Liu, A. Manthiram, Y. S. Meng, V. R. Subramanian, M. F. Toney, V. V. Viswanathan, M. S. Whittingham, J. Xiao, W. Xu, J. Yang, X.-Q. Yang and J.-G. Zhang, Nat. Energy, 2019, 4, 180186.
50. Y. Kubo and K. Ito, ECS Trans., 2014, 62, 129.
51. H. C. Lee, J. O. Park, M. Kim, H. J. Kwon, J. H. Kim, K. H. Choi, K. Kim and D. Im, Joule, 2019, 3, 542.
52. Y. Wang, L. Hao and M. Bai, J. Electrochem. Soc., 2021, 168, 070517.
53. M. Zhao, B. Li, H. Peng, H. Yuan, J. Wei and J. Huang, Angew. Chem., Int. Ed., 2020, 59, 12636.
54. S. Chung, C. Chang and A. Manthiram, Adv. Funct. Mater., 2018, 28, 1801188.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh01546j

---