Open Access Article
Open Access ArticleExploration of defined 2-dimensional working electrode shapes through additive manufacturing†
Alejandro
Garcia-Miranda Ferrari
 ,
Nicholas J.
Hurst
,
Elena
Bernalte
,
Nicholas J.
Hurst
,
Elena
Bernalte
 ,
Robert D.
Crapnell
,
Robert D.
Crapnell
 ,
Matthew J.
Whittingham
,
Dale A. C.
Brownson
,
Matthew J.
Whittingham
,
Dale A. C.
Brownson
 and
Craig E.
Banks
and
Craig E.
Banks
 *
*
Faculty of Science and Engineering, Manchester Metropolitan University, Chester Street, M1 5GD, UK. E-mail: c.banks@mmu.ac.uk; Tel: +44 (0)1612471196
First published on 6th October 2022
Abstract
In this work, the electrochemical response of different morphologies (shapes) and dimensions of additively manufactured (3D-printing) carbon black (CB)/poly-lactic acid (PLA) electrodes are reported. The working electrodes (WE) are printed using standard non-conductive PLA based filament for the housing and commercial Protopasta (carbon black/PLA) filament for the electrode and connection parts. Discs, squares, equilateral triangles and six-point stars with varying working electrode (WE) widths from 2 to 10 mm are evaluated herein towards the well-known near-ideal outer sphere redox probe hexaamineruthenium(III) chloride (RuHex). The results obtained show that triangular and squared electrodes exhibit a faster heterogeneous electron transfer (HET) rate constant (k°) than those of discs and stars, the latter being the slowest one. The results reported here also show a trend between the WE dimension and the reversibility of the electrochemical reaction, which decreases as the WE size increases. It is also observed that the ratio of the geometrical and electroactive area (%realarea) decreases as the overall WE size increases. On the other hand, these four WE shapes were applied toward the well-known and benchmarking detection of ascorbic acid (AA), uric acid (UA), β-nicotinamide adenine dinucleotide (NADH) and dopamine (DA). Moreover, electroanalytical detection of real acetaminophen (ACOP) samples is also showcased. The different designs for the working electrode proposed in this manuscript are easily changed to any other desired shapes thanks to the additive manufacturing methodology, these four shapes being just an example of what additive manufacturing can offer to experimentalists and to electrochemists in particular. Additive manufacturing is shown here as a versatile and rapid prototyping tool for the production of novel electrochemical sensing platforms, with scope for this work to be able to impact a wide variety of electroanalytical applications.
Introduction
Additive manufacturing (AM)/3D-printing has become recently popular in research due to its ability to create intricate designs, quick and affordable prototyping turnaround, and its bespoke capabilities. In electrochemistry research, additive manufacturing has been reported for the production of tailored cell designs,1,2 flow cells,3 thermal sensing,4,5 fully printed all-in-one setups6,7 and many others. Most of the work regarding the manufacture of tailored electrodes has been focusing on fused filament fabrication (FFF) methods, which allows a very affordable point of entry, low-waste and rapid prototypings.8 FFF feeds a heated thermoplastic filament continuously through an extruder which will allow for the controlled deposition of the final product layer-by-layer.9Historically, mercury electrodes were one of the first choices for working electrode materials in the last century; however, in the last decades, they have been replaced due to their known dangers10 by solid precious metals (gold (Au), silver (Ag) and platinum (Pt)) and later carbon/graphitic electrodes, which are known by their overall low background currents, wide potential range and chemical inertness.11,12 It is because of these features that graphite, in its many forms, is a great material of choice when designing conductive filaments for AM applications. These can be manufactured by embedding carbon black or graphene into a thermoplastic filament matrix, such as PLA or acrylonitrile butadiene styrene (ABS). Conductive FFF filaments can be widely purchased, however it is becoming a trend the bespoke production of them for some applications such as batteries,13 water splitting14 and electrochemical sensing.15 It is important to also note that, when applied to electroanalytical sensing, the performance of these AM electrodes is directly related to the characteristics of the WE's surface, being the activation of WE a point of attention when optimising their sensing performance. Electrochemical cycling,8 laser treatment16 or chemical reductions17 are often the applied strategies to remove the excess of plastic to unveil and increase the amount of carbon within the surface of the working electrode. Since the application of AM to the electrochemistry field, majority of the experimentalists do not use a defined electrode area for their experiments, being the “lollipop” design the most common due to its easiness of printing14,15,18–28 and similarities to the well-studied screen-printed platforms. The lollipop design is a simple flat disc with a rectangular tab for connecting the electrode to the potentiostat, being an easy to design and print figure. However, the issue with this design is the incapacity to fully control the area of the electrode which is immersed in the solution and in contact with the electrolyte.
In this manuscript we explore, for the first time, the effect of geometrical shape and dimensions of additively manufactured carbon black (CB)-based PLA working electrodes towards their electrochemical performance. Accordingly, heterogeneous electron transfer (HET) are evaluated using the near-ideal outer sphere hexaamineruthenium(III) chloride (RuHex) as redox probe and subsequently, the electroanalytical performances of the different WE's shapes are critically analysed towards other well-known redox species such as ascorbic acid, uric acid, β-nicotinamide adenine dinucleotide and dopamine. Finally, we demonstrate in this work the applicability of the best WE shape to detect acetaminophen in real pharmaceutical sample.
Experimental section
Materials
All chemicals used were of analytical grade and were used as received without any further purification. All solutions were prepared with deionised water of resistivity not less than 18.2 MΩ cm. Hexaamineruthenium(III) chloride (RuHex), ascorbic acid (AA), uric acid (UA), β-nicotinamide adenine dinucleotide (NADH), dopamine (DA), phosphate buffered saline (PBS) tablets and sodium hydroxidewere purchased from Merck (Gillingham, UK). Potassium chloride was purchased from Fisher Scientific (Loughborough, UK). The commercial conductive PLA/carbon black filament (ProtoPasta) was purchased from Farnell (Leeds, UK). Note that we have utilised this filament in a different system and more details of its physiochemical characterisation can be found in ref. 6. The working electrodes (WE) shapes are discs, squares, equilateral triangles and six-point stars with varying widths of working electrodes from 2 to 10 mm as shown in Fig. S1.† The connection tab for these was chosen to be 18 mm, which corresponds to the shortest connection possible that allows comfortable use and connection of the devices. Note that it has recently been reported the effect of graphitic screen-printed electrode's connection lengths to their electrochemical performance.29 Real samples were sourced from a local shop, consisting of 500 mg tablet of acetaminophen (ACOP).Additive manufacturing
The additive manufacturing electrodes (AMEs) were produced using fused filament fabrication (FFF), on a RAISE3D E2 independent dual-extruder (IDEX) printer (RAISE3D, California, US) using commercial conductive PLA/carbon black (PLA/CB, ProtoPasta, 1.75 mm) and non-conductive Premium PLA (RAISE3D, 1.75 mm). All designs and STL files were produced using Autodesk® Fusion 360®, then sliced and converted to G-code files using ideaMaker 4.0.1 (RAISE3D, California, US). The printing orientation is horizontal, where the non-conductive PLA was printed using a layer height of 0.1 mm, shell width of 1 mm with a gyroid infill of 20% and infill speed of 70 mm s−1. The conductive PLA/CB was printed with 100% infill at 35 mm s−1 speed. The prints had a purge block located close to the cells, as well as a skirt to help prime the nozzle prior to printing the first layer and between each extruder change.Electrochemical experiments
An μ-Autolab type (III) potentiostat (Utrecht, the Netherlands) was used in conjunction with NOVA 2.1.4 (Utrecht, the Netherlands) to carry out electrochemical measurements using a three-electrode configuration. The AMEs were used as the working electrodes, a nickel wire coil was used as the counter electrode and an Ag/AgCl electrode was used as the reference. Solutions of RuHex were degassed thoroughly for at least 15 minutes with nitrogen prior to any electrochemical measurement.Activation of the AMEs was achieved electrochemically in NaOH as described in the literature.30 Briefly, the AMEs were connected as the working electrode in conjunction with a nickel wire coil counter and Ag/AgCl reference electrode and placed in a solution of NaOH (0.5 M). Chronoamperometry was used to activate the AME by applying a set voltage of +1.4 V for 200 s, followed by applying −1.0 V for 200 s. The AMEs were then thoroughly rinsed with deionised water and dried under nitrogen before further use.
The HET rate constants,  , were calculated as an average of 3 sets of 10 different scan rates (5, 10, 15, 25, 50, 75, 100, 150, 250 and 500 mV s−1), where each set used a new AME. These were performed using the near ideal outer-sphere redox probe RuHex (in 0.1 M KCl) using the well-known31 and widely utilised Nicholson method,32 for quasi-reversible electrochemical reactions via the following formula:33
, were calculated as an average of 3 sets of 10 different scan rates (5, 10, 15, 25, 50, 75, 100, 150, 250 and 500 mV s−1), where each set used a new AME. These were performed using the near ideal outer-sphere redox probe RuHex (in 0.1 M KCl) using the well-known31 and widely utilised Nicholson method,32 for quasi-reversible electrochemical reactions via the following formula:33
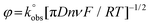 | (1) |
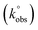 can be calculated via the gradient when plotting φ against [πDnνF/RT]−1/2. In cases where ΔEp is bigger than 212 mV, the following equation should be implemented:
can be calculated via the gradient when plotting φ against [πDnνF/RT]−1/2. In cases where ΔEp is bigger than 212 mV, the following equation should be implemented: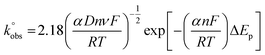 | (2) |
The electroactive area of the electrode, Areal, is calculated using the Randles–Ševćik equation at non-standard conditions for quasi- (3) and irreversible (4) electrochemical processes when appropriate:37
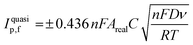 | (3) |
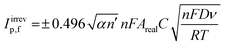 | (4) |
The detection of all analytes using cyclic voltammetry (CV) was performed at a scan rate of 50 mV s−1 and standard addition method was used for calibration (n = 3). Differential pulse voltammetry (DPV, 10 mV s−1) was used for the detection of ACOP in real samples at potential range from 0.0 to 0.8 V, with a step potential of 5 mV, modulation amplitude of 25 mV, modulation time of 0.05 s and interval time of 0.5 s. For the electrochemical detection of real ACOP samples, the tablets were initially dissolved in 250 mL of PBS, followed by a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 dilution for its analysis. External calibration was applied for the quantification of ACOP in real samples by applying DPV.
100 dilution for its analysis. External calibration was applied for the quantification of ACOP in real samples by applying DPV.
Also it is important to note that there have been investigations since the 1960s reporting that the current and potential distribution in electrodes depend on the geometry, the conductivity of the solution, the activation overpotential, the concentration overpotential and special effects near and in the electrodes.38 In our case, where we explore different WE geometries through AM, it is expected that the current distribution will be affected by the potential difference across the interface, which depends on the local current density. Therefore, the solution near the electrode is no longer an equi-potential surface, and since higher current densities involve larger overpotentials, the activation overpotentials and over-voltages will tend to make the current distributions more uniform across the overall of the electrode.38–41 This has been particularly reported at high current densities and large electrodes, where there is a non-uniform current distribution across the surface, being the current near the centre governed (predominantly) by ohmic effects, but near the edges the electrode kinetics become important (where non-uniformity is predominant).42 This would translate into higher current densities at the edges of the WE. This has often been applied to models with micro- and macro-profiles, but in regards of the profile of the reported AMEs herein, it is currently not possible to create a mathematical model and profile distribution due to their complex (nano-) geometry. However, this has often been applied and investigated towards micro-electronics, electro-metallurgy and battery research, it is often overlooked when applied to electroanalytical applications and needs further efforts to explore their implications.
Please note that in this manuscript we are not comparing our in-house produced AMEs against any traditional electrode, such as glassy carbon, due to this being only commercially available in set sizes and only in circular shapes. This said, the authors would expect that the electrocatalytic behaviour of traditional electrode materials would be more competitive than the AMEs reported herein, however additively manufacture electrodes allow experimentalists to manufacture them in any shape and size, which in real terms, means to design the electrode's geometrical area to any wanted one, allowing for more versatile designs to counteract AME's limitations.
Results and discussion
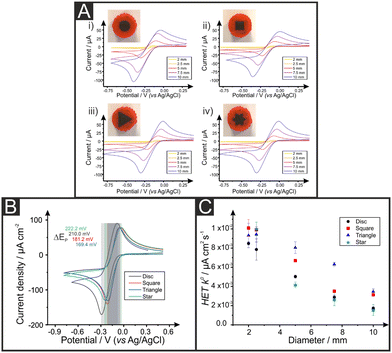
Fig. 1A shows a real-time photograph of FFF printing of additive manufacturing electrodes (AMEs), showcasing the ability of printing 100 electrodes at the same time, with different shapes and/or dimensions. Fig. 1B shows a computer-aided design (CAD) design of a 5 mm equilateral triangle electrode and Fig. 1C offers an overview comparison of the 3D-printed 7.5 mm (diameter/width) disc, square, equilateral triangle, and star electrodes shapes. Given the above insights, in this manuscript we report the electrochemical performance of a range of AM graphitic composite electrodes with different planar shapes: disc, square, triangle and star. We changed the geometrical shape of the planar electrode towards the calculation of their heterogeneous electron transfer (HET), rate constant (k°), real electroactive area (Areal), %realarea (percentage comparison from Areal to geometrical area (Ageo)) and their electroanalytical performance towards the detection of ascorbic acid (AA), uric acid (UA), β-nicotinamide adenine dinucleotide (NADH) and dopamine (DA). Due to the manufacturing freedom that additive manufacturing offers, herein we manufacture and compare different planar electrode geometries of additively manufactured for the first time.Electrochemical characterisation
First, we characterise our electrochemical systems (including all shapes and dimensions) by testing them against the near-ideal outer sphere redox probe hexaammineruthenium(III) chloride (RuHex) in order to calculate the k°, Areal and %realarea. RuHex was chosen because it is a near-ideal outer-sphere electron transfer redox probe that is only dependent on the electronic structure (DoS) of carbon-based electrode materials and therefore, one of the optimal probes to use when studying carbon surfaces’ electrochemistry.31,43–45As mentioned before, circular disc, square, equilateral triangle and (6 point) star were the chosen WE's shapes as shown in Fig. S1.† These designs were manufactured in the following 5 different dimensions: 2, 2.5, 5, 7.5 and 10 mm of WE widths, respectively.
Fig. 2A shows representative RuHex voltammograms recorded at 50 mV s−1 for the different electrode dimensions and shapes, confirming the expected increase in electrochemical signals when larger electrodes are used regardless of their geometric form. This is due to their increased surface area. Table 1 shows the geometrical area (Ageo), HET rate constant (k°), peak-to-peak (ΔEp) separation, real electroactive area (Areal) and %realarea for each of the AMEs. Please, note that these values are calculated as described in the Experimental Section. Peak-to-peak (ΔEp) values for RuHex indicate the reversibility of the electrochemical process and are in agreement with the values known to be only related to the electronic density of states.46 Upon closer inspection of the k°, it is observed that triangular electrodes exhibit the overall (slightly) faster HET values for RuHex, being the star and discs the slower ones. For comparative purposes, RuHex cyclic voltammograms are depicted in the Fig. 2B. Likewise, the peak-to-peak values are 162, 168, 200 and 225 mV for the triangle, square, disc and star electrodes, respectively (RuHex; 50 mV s−1), confirming their observed different electrode transfer. Moreover, as summarised in Table 1 and represented in Fig. 2C, it is evident the decrease of the k° values when the dimension of the electrode increases despite their shape. The highest k° value (10.1 × 10−3 cm s−1) was recorded for the 2 mm width square, while the lowest k° value (1.51 × 10−3 cm s−1) was recorded for the 10 mm star AME. This could also be due to the increase in the internal pathway of the graphite composite electrodes, leading to an increase in their internal resistance.29 Please note that these differences do not seem to be statistically significant to draw any conclusive difference among the different AME shapes.
| WE ∅/mm | Disc | Square | Triangle | Star | |
|---|---|---|---|---|---|
| a NP = not printable. | |||||
| a geo/cm2 | 2 | 0.0314 | 0.0314 | 0.0314 | NPa |
| 2.5 | 0.0491 | 0.491 | 0.492 | 0.491 | |
| 5 | 0.196 | 0.196 | 0.196 | 0.196 | |
| 7.5 | 0.466 | 0.466 | 0.466 | 0.466 | |
| 10 | 0.785 | 0.785 | 0.785 | 0.785 | |
| Avg. k°/cm s−1 | 2 | 8.49 (±0.49) × 10−3 | 1.01 (±0.073) × 10−2 | 9.32 (±0.70) × 10−3 | NPa |
| 2.5 | 7.85 (±1.14) × 10−3 | 9.90 (±1.43) × 10−3 | 9.42 (±0.85) × 10−3 | 9.99 (±0.075) × 10−3 | |
| 5 | 5.03 (±0.25) × 10−3 | 6.69 (±0.089) × 10−3 | 8.04 (±0.88) × 10−3 | 4.19 (±0.43) × 10−3 | |
| 7.5 | 2.89 (±0.040) × 10−3 | 3.51 (±0.020) × 10−3 | 6.30 (±1.81) × 10−3 | 2.65 (±0.24) × 10−3 | |
| 10 | 1.73 (±0.031) × 10−3 | 3.13 (±0.18) × 10−3 | 3.46 (±2.31) × 10−3 | 1.55 (±0.98) × 10−3 | |
| ΔEp/mV (at 50 mV s−1) | 2 | 125 | 112 | 129 | NPa |
| 2.5 | 130 | 132 | 127 | 111 | |
| 5 | 200 | 168 | 162 | 225 | |
| 7.5 | 286 | 260 | 231 | 394 | |
| 10 | 374 | 341 | 315 | 413 | |
| Avg. Areal/cm2 | 2 | 0.030 (±0.0018) | 0.023 (±0.0043) | 0.023 (±0.0014) | NPa |
| 2.5 | 0.049 (±0.0027) | 0.037 (±0.0042) | 0.038 (±0.0038) | 0.038 (±0.00083) | |
| 5 | 0.200 (±0.0059) | 0.159 (±0.010) | 0.145 (±0.0059) | 0.153 (±0.012) | |
| 7.5 | 0.433 (±0.015) | 0.321 (±0.0029) | 0.345 (±0.0043) | 0.311 (±0.029) | |
| 10 | 0.636 (±0.057) | 0.536 (±0.0027) | 0.559 (±0.016) | 0.503 (±0.042) | |
| %Realarea | 2 | 94.8 (±5.6) | 72.7 (±13.8) | 74.7 (±4.5) | NPa |
| 2.5 | 99.5 (±5.5) | 75.1 (±8.6) | 77.3 (±7.6) | 78.4 (±1.7) | |
| 5 | 102.1 (±3.0) | 80.9 (±5.3) | 73.7 (±3.0) | 77.7 (±6.3) | |
| 7.5 | 93.0 (±3.2) | 68.9 (±0.6) | 74.1 (±0.9) | 66.7 (±6.2) | |
| 10 | 80.9 (±7.3) | 68.2 (±0.3) | 71.2 (±1.9) | 64.0 (±5.4) | |
Attention was next turned to calculating the electroactive area (Areal) of the range of different AM electrodes using their respective Randles–Ševćik equation37 (see Experimental Section for further details). The Areal for the different electrodes is included in Table 1, including the ratio between the geometrical and electroactive area expressed as a percentage (%realarea). The overall %realarea values follow a decreasing trend when the dimensions of the electrode increase for all the different shapes, meaning that the electroactive area does not increase as much as the geometric one. This could be due to the internal electrode resistance and polymeric nature of the graphite/PLA filament, where PLA is electrochemically inactive (in contrast to traditional electrodes such as glassy carbon, where all the material is active and a linear increase of %realarea would be expected). Overall, the above results indicate that as the dimension of the working electrode increases, the reversibility of the electrochemical reaction (and therefore its HET kinetics) decreases, so does the electroactive area for all the four electrodes’ shapes tested herein. The AME shape with the highest %realarea across all sizes is the disc (varying from 80.9 to 102.1%), while the lowest %realarea is exhibited by the star electrode (ranging from 64.0 to 78.4%).
Electroanalytical applications
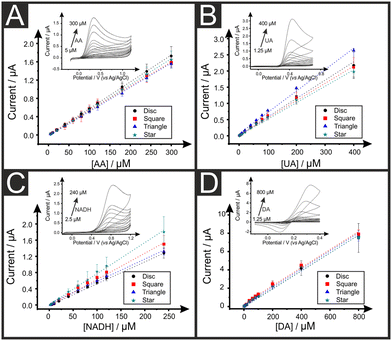
We now turn to exploring the electroanalytical performance of the AMEs towards the detection of relevant biological analytes, namely ascorbic acid (AA), uric acid (UA), β-nicotinamide adenine dinucleotide (NADH) and dopamine (DA) using the 2.5 mm width electrodes, as it was almost the one exhibiting the faster HET values for all geometric forms and it could be successfully 3D-printed for all shapes. Like for other carbon electrodes,47 it is described in the literature the need of a post-printing enhancement of the electrochemical properties so called “activation method” prior the utilisation of AMEs in electroanalytical applications. Note that this method is unnecessary for the above RuHex studies, due to the near ideal outer-sphere nature of the redox probe, being this method only beneficial for the further electroanalytical sensing applications. Several literature reports have addressed this pre-conditioning of the electrode's surface by chemical, physical or electrochemical treatments to successfully increase the active surface area and its electron transfer rates.6,7 Herein, we apply the method developed by Kalinke et al.8 Such method is based on the use of NaOH while a potential-controlled electrochemical method (namely chronoamperometry) is applied to promote PLA's saponification, which exposes the active material's active sites and electrochemical active area. This results in the increasing of the C/O ratio and therefore the improvement of the electrochemical performance of inner-sphere redox probes.The calibration plots for AA, UA, NADH and DA using all the electrode shapes are depicted in Fig. 3, with examples of the respective calibration voltammograms as insets. These were AA with disc electrodes, UA with square electrodes, NADH with triangle electrodes and DA with star electrodes. Fig. S2† includes all the voltammograms for each of the four analytes and each of the four electrodes shapes. The electrochemical sensitivity, limit of detection (LOD) and coefficient of determination (R2) values are included in Table 2. A very good linear behaviour is observed for all AMEs in all redox probes as R2 values are successfully ranged between 0.994 and 0.999. Moreover, it is observed that there are no significant differences between the four electrodes shapes in terms of their electroanalytical performance towards AA, UA, and DA. This is likely to indicate that the observed differences can be attributed to their respective calculated deviations. It is detected, however, a higher variation in the sensitivity of the four AMEs in the detection of NADH possibly due to the more complexity of the redox process of this molecule. Note that no significant differences between the four electrode shapes are observed herein, and, although small LOD differences are observed between the different electrode shapes, the higher LODs are reported when using square electrodes, which are likely due to their slightly higher background noise in their recorded voltammograms. These observations could be due to the sizes of the electrodes and their current distributions, in addition to the diffusion regimes where the AMEs being big enough that planar diffusion governs the electrochemical process and therefore the shape of the electrode does not play a relevant part with these dimensions.45 Also again, please note that these differences do not seem to be statistically significant.
| Analyte | Shape | ||||
|---|---|---|---|---|---|
| Disc | Square | Triangle | Star | ||
| AA | Sensitivity/μA μM−1 | 6.55 × 10−3 | 6.01 × 10−3 | 6.33 × 10−3 | 5.89 × 10−3 |
| LOD/μM | 0.54 | 2.13 | 0.75 | 0.64 | |
| R 2 | 0.999 | 0.998 | 0.999 | 0.999 | |
| UA | Sensitivity/μA μM−1 | 5.51 × 10−3 | 5.35 × 10−3 | 5.03 × 10−3 | 6.65 × 10−3 |
| LOD/μM | 0.12 | 0.36 | 0.26 | 0.19 | |
| R 2 | 0.996 | 0.995 | 0.995 | 0.995 | |
| NADH | Sensitivity/μA μM−1 | 5.44 × 10−3 | 6.40 × 10−3 | 7.64 × 10−3 | 5.60 × 10−3 |
| LOD/μM | 0.79 | 0.53 | 0.50 | 0.48 | |
| R 2 | 0.998 | 0.995 | 0.997 | 0.996 | |
| DA | Sensitivity/μA μM−1 | 9.43 × 10−3 | 9.91 × 10−3 | 9.52 × 10−3 | 9.74 × 10−3 |
| LOD/μM | 0.37 | 1.29 | 0.50 | 0.64 | |
| R 2 | 0.994 | 0.993 | 0.994 | 0.997 | |
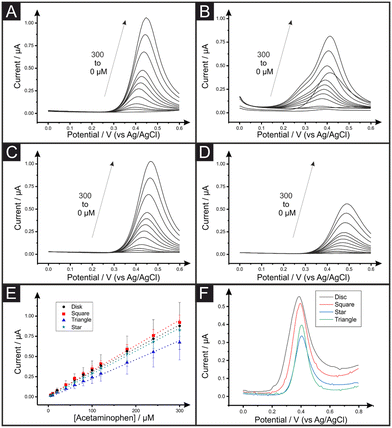
Lastly, we apply the AMEs to the electrochemical determination of acetaminophen (ACOP) and the analysis of this compound in a commercial tablet accordingly diluted in PBS (0.01 M, pH = 7.4). A series of calibration plots was performed for each AME shape by differential pulse voltammetry (DPV). Fig. 4 shows the DPV signals of increasing amounts of ACOP for the square (A), triangle (B), disc (C) and star (D) shaped electrodes and their respective calibration plot of ACOP (E). The analytical sensitivity, limit of detection (LOD) and coefficient of determination (R2) are reported in Table 3. The analytical sensitivity for the ACOP determination varies from 5.89 × 10−3 to 6.55 × 10−3 μA μM−1 with star and disc electrodes respectively. It is evident upon inspection of Table 3 that there are no substantial differences between the four electrode shapes in terms of their ACOP determination. Interestingly, square electrodes are showing the highest LOD for ACOP by DPV similarly to the previous reported AA and DA determination by CV. Fig. 4F shows the DPV responses for the unknown samples of over-the-counter ACOP tablets. The samples were prepared as explained within the Experimental Section. As shown in Table 3, the concentration of the ACOP commercial tablets was experimentally calculated to be a recovery value of 102.3%, 96.9%, 80.3% and 122.6% for the disc, square, star and triangle shaped AMEs. Higher recovery values reported for the triangle electrodes can be explained by an overestimation in the quantification peak while using external calibration plots. This can be due to the appearance of a shoulder in the ACOP DPV signals at higher concentrations (Fig. 4B). On the other hand, the noticeable underestimation in the ACOP recovery using star electrode could be due to the restriction in the anodic potential range recorded during ACOP calibration (Fig. 4D). Nevertheless, all the 2.5 mm AMEs developed in this work are successfully applied for the electroanalytical detection of ACOP in real samples without further pre-treatment.
| Analyte | Shape | ||||
|---|---|---|---|---|---|
| Disc | Square | Triangle | Star | ||
| ACOP | Sensitivity/μA μM−1 | 6.55 × 10−3 | 6.01 × 10−3 | 6.33 × 10−3 | 5.89 × 10−3 |
| LOD/μM | 0.54 | 2.13 | 0.75 | 0.64 | |
| R 2 | 0.999 | 0.998 | 0.999 | 0.999 | |
| Sample recovery/% | 102.3 | 96.9 | 122.6 | 80.3 | |
As a future perspective comment, the expansion of commercial and research 3D printers has allowed it to become mainstream, helping bringing costs down and increasing its accessibility. Please do take into consideration that the results reported herein could and are likely to differ when commercial 3D printers increase their resolution. This expected improved resolution in future commercial printers will help increasing the printability and reproducibility of AM devices, allowing to print even more complex or smaller designs.
Conclusions
We have explored, for the first time, the use of additively manufactured disc, square, triangle and star working electrodes towards RuHex, ascorbic acid (AA), uric acid (UA), NADH, dopamine (DA) and acetaminophen (ACOP), in different WE dimensions ranging from 2 to 10 mm width. Increasing the working electrode sizes results in decreased electrochemical HET properties when using all the four shapes. We have found that triangular electrodes exhibit the overall faster HET values for RuHex, the star-shaped being the slower ones, however statistically non-significant differences are reported. The electroanalytical performance of the four types of electrodes with 2.5 mm width was tested towards common analytes such as AA, UA, DA and NADH, however non-representative differences were observed when the shapes of the electrodes were compared. Real tablet samples of ACOP were tested, with recoveries ranging between 80.3% and 122.6% with the star and triangle-shaped AMEs, respectively. Herein, we want to highlight the ability of additive manufacturing to print more complex shapes and structures to experimentalists, in addition to carefully considering the dimension and shape of newly designed working electrodes. Future work should study the diffusion profiles and current distribution at micro-electrodes and how can this be applied to produce beneficial voltammetric profiles towards analytes of interest.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. G.-M. F. and E. B. would like to acknowledge their respective Innovate UK funding for their Knowledge Transfer Partnerships (KTP reference: 11606 and 12021 respectively).References
- G. D. da Silveira, R. F. Quero, L. P. Bressan, J. A. Bonacin, D. P. de Jesus and J. A. F. da Silva, Ready-to-use 3D-printed electrochemical cell for in situ voltammetry of immobilized microparticles and Raman spectroscopy, Anal. Chim. Acta, 2021, 1141, 57–62 CrossRef PubMed.
- M. F. Dos Santos, V. Katic, P. L. Dos Santos, B. M. Pires, A. L. Formiga and J. A. Bonacin, 3D-printed low-cost spectroelectrochemical cell for in situ Raman measurements, Anal. Chem., 2019, 91(16), 10386–10389 CrossRef.
- J. Scremin, I. V. J. Dos Santos, J. P. Hughes, A. G.-M. Ferrari, E. Valderrama, W. Zheng, X. Zhong, X. Zhao, E. J. Sartori and R. D. Crapnell, Platinum nanoparticle decorated vertically aligned graphene screen-printed electrodes: electrochemical characterisation and exploration towards the hydrogen evolution reaction, Nanoscale, 2020, 12(35), 18214–18224 RSC.
- K. Betlem, A. Kaur, A. D. Hudson, R. D. Crapnell, G. Hurst, P. Singla, M. Zubko, S. Tedesco, C. E. Banks and K. Whitehead, Heat-Transfer Method: A Thermal Analysis Technique for the Real-Time Monitoring of Staphylococcus aureus Growth in Buffered Solutions and Digestate Samples, ACS Appl. Bio Mater., 2019, 2(9), 3790–3798 CrossRef.
- R. D. Crapnell, W. Jesadabundit, A. Garcia-Miranda Ferrari, N. C. Dempsey-Hibbert, M. Peeters, A. Tridente, O. Chailapakul and C. E. Banks, Toward the Rapid Diagnosis of Sepsis: Detecting Interleukin-6 in Blood Plasma Using Functionalized Screen-Printed Electrodes with a Thermal Detection Methodology, Anal. Chem., 2021, 93(14), 5931–5938 CrossRef PubMed.
- R. D. Crapnell, E. Bernalte, A. Garcia-Miranda Ferrari, M. J. Whittingham, R. J. Williams, N. J. Hurst and C. E. Banks, All-in-One Single-Print Additively Manufactured Electroanalytical Sensing Platforms, ACS Meas. Sci. Au, 2021, 167–176 Search PubMed.
- M. J. Whittingham, R. D. Crapnell, E. J. Rothwell, N. J. Hurst and C. E. Banks, Additive manufacturing for electrochemical labs: an overview and tutorial note on the production of cells, electrodes and accessories, Talanta Open, 2021, 100051 CrossRef.
- R. M. Cardoso, C. Kalinke, R. G. Rocha, P. L. Dos Santos, D. P. Rocha, P. R. Oliveira, B. C. Janegitz, J. A. Bonacin, E. M. Richter and R. A. Munoz, Additive-manufactured (3D-printed) electrochemical sensors: A critical review, Anal. Chim. Acta, 2020, 1118, 73–91 CrossRef CAS.
- B. Redwood, F. Schöffer and B. Garret, The 3D printing handbook: technologies, design and applications, 3D Hubs, 2017 Search PubMed.
- J. Wang, Stripping Analysis, in Encyclopedia of Electrochemistry, 2007 Search PubMed.
- A. Hayat and J. L. Marty, Disposable Screen Printed Electrochemical Sensors: Tools for Environmental Monitoring, Sensors, 2014, 14(6), 10432–10453 CrossRef CAS.
- R. W. Murray, A. G. Ewing and R. A. Durst, Chemically modified electrodes. Molecular design for electroanalysis, Anal. Chem., 1987, 59(5), 379A–390A Search PubMed.
- V. Gupta, F. Alam, P. Verma, A. Kannan and S. Kumar, Additive manufacturing enabled, microarchitected, hierarchically porous polylactic-acid/Lithium iron phosphate/carbon nanotube nanocomposite electrodes for high performance Li-Ion batteries, J. Power Sources, 2021, 494, 229625 CrossRef.
- J. P. Hughes, P. L. dos Santos, M. P. Down, C. W. Foster, J. A. Bonacin, E. M. Keefe, S. J. Rowley-Neale and C. E. Banks, Single step additive manufacturing (3D printing) of electrocatalytic anodes and cathodes for efficient water splitting, Sustainable Energy Fuels, 2020, 4(1), 302–311 RSC.
- C. W. Foster, H. M. Elbardisy, M. P. Down, E. M. Keefe, G. C. Smith and C. E. Banks, Additively manufactured graphitic electrochemical sensing platforms, Chem. Eng. J., 2020, 381, 122343 CrossRef.
- D. P. Rocha, V. N. Ataide, A. de Siervo, J. M. Gonçalves, R. A. Muñoz, T. R. Paixão and L. Angnes, Reagentless and sub-minute laser-scribing treatment to produce enhanced disposable electrochemical sensors via additive manufacture, Chem. Eng. J., 2021, 130594 CrossRef.
- E. Redondo, J. Muñoz and M. Pumera, Green activation using reducing agents of carbon-based 3D printed electrodes: Turning good electrodes to great, Carbon, 2021, 175, 413–419 CrossRef.
- C. W. Foster, M. P. Down, Y. Zhang, X. Ji, S. J. Rowley-Neale, G. C. Smith, P. J. Kelly and C. E. Banks, 3D Printed Graphene Based Energy Storage Devices, Sci. Rep., 2017, 7(1), 42233 CrossRef PubMed.
- C. Y. Foo, H. N. Lim, M. A. Mahdi, M. H. Wahid and N. M. Huang, Three-Dimensional Printed Electrode and Its Novel Applications in Electronic Devices, Sci. Rep., 2018, 8(1), 7399 CrossRef PubMed.
- P. L. dos Santos, V. Katic, H. C. Loureiro, M. F. dos Santos, D. P. dos Santos, A. L. B. Formiga and J. A. Bonacin, Enhanced performance of 3D printed graphene electrodes after electrochemical pre-treatment: Role of exposed graphene sheets, Sens. Actuators, B, 2019, 281, 837–848 CrossRef CAS.
- C. Kalinke, N. V. Neumsteir, G. d. O. Aparecido, T. V. d. B. Ferraz, P. L. dos Santos, B. C. Janegitz and J. A. Bonacin, Comparison of activation processes for 3D printed PLA-graphene electrodes: electrochemical properties and application for sensing of dopamine, Analyst, 2020, 145(4), 1207–1218 RSC.
- A. M. López Marzo, C. C. Mayorga-Martinez and M. Pumera, 3D-printed graphene direct electron transfer enzyme biosensors, Biosens. Bioelectron., 2020, 151, 111980 CrossRef.
- K. P. A. Kumar, K. Ghosh, O. Alduhaish and M. Pumera, Metal-plated 3D-printed electrode for electrochemical detection of carbohydrates, Electrochem. Commun., 2020, 120, 106827 CrossRef CAS.
- C. Iffelsberger, S. Ng and M. Pumera, Catalyst coating of 3D printed structures via electrochemical deposition: Case of the transition metal chalcogenide MoSx for hydrogen evolution reaction, Appl. Mater. Today, 2020, 20, 100654 CrossRef.
- L. Wang and M. Pumera, Covalently modified enzymatic 3D-printed bioelectrode, Microchim. Acta, 2021, 188(11), 374 CrossRef CAS PubMed.
- C. Kalinke, N. V. Neumsteir, R. de Oliveira, P. Janegitz, B. C. Bonacin and J. A., Sensing of L-methionine in biological samples through fully 3D-printed electrodes, Anal. Chim. Acta, 2021, 1142, 135–142 CrossRef CAS.
- J. Muñoz and M. Pumera, 3D-Printed COVID-19 immunosensors with electronic readout, Chem. Eng. J., 2021, 425, 131433 CrossRef.
- C. Kalinke, P. R. de Oliveira, N. V. Neumsteir, B. F. Henriques, G. de Oliveira Aparecido, H. C. Loureiro, B. C. Janegitz and J. A. Bonacin, Influence of filament aging and conductive additive in 3D printed sensors, Anal. Chim. Acta, 2022, 1191, 339228 CrossRef CAS PubMed.
- M. J. Whittingham, N. J. Hurst, R. D. Crapnell, A. Garcia-Miranda Ferrari, E. Blanco, T. J. Davies and C. E. Banks, Electrochemical Improvements Can Be Realized via Shortening the Length of Screen-Printed Electrochemical Platforms, Anal. Chem., 2021, 93(49), 16481–16488 CrossRef CAS PubMed.
- E. M. Richter, D. P. Rocha, R. M. Cardoso, E. M. Keefe, C. W. Foster, R. A. Munoz and C. E. Banks, Complete additively manufactured (3D-printed) electrochemical sensing platform, Anal. Chem., 2019, 91(20), 12844–12851 CrossRef CAS PubMed.
- A. Garcia-Miranda Ferrari, C. W. Foster, P. Kelly, D. A. C. Brownson and C. E. Banks, Determination of the Electrochemical Area of Screen-Printed Electrochemical Sensing Platforms, Biosensors, 2018, 8(2), 53 CrossRef.
- R. S. Nicholson, Theory and Application of Cyclic Voltammetry for Measurement of Electrode Reaction Kinetics, Anal. Chem., 1965, 37(11), 1351–1355 CrossRef CAS.
- S. J. Rowley-Neale, D. A. C. Brownson and C. E. Banks, Defining the origins of electron transfer at screen-printed graphene-like and graphite electrodes: MoO2 nanowire fabrication on edge plane sites reveals electrochemical insights, Nanoscale, 2016, 8(33), 15241–15251 RSC.
- D. Brownson and C. E. Banks, The Handbook of Graphene Electrochemistry, 2014, p. 208 Search PubMed.
- F. E. Galdino, C. W. Foster, J. A. Bonacin and C. E. Banks, Exploring the electrical wiring of screen-printed configurations utilised in electroanalysis, Anal. Methods, 2015, 7(3), 1208–1214 RSC.
- C. W. Foster, M. P. Down, Y. Zhang, X. Ji, S. J. Rowley-Neale, G. C. Smith, P. J. Kelly and C. E. Banks, 3D Printed Graphene Based Energy Storage Devices, Sci. Rep., 2017, 7, 42233 CrossRef.
- A. Bard and L. Faulkner, Electrochemical Methods: Fundamentals and Applications. John Wiley & Sons, Inc, 2001 Search PubMed.
- R. H. Rousselot and S. Barnartt, Répartition du potentiel et du courant dans les électrolytes, J. Electrochem. Soc., 1960, 107(2), 40C CrossRef.
- J. Deconinck, The Current Distribution in Electrochemical Systems, in Current Distributions and Electrode Shape Changes in Electrochemical Systems, Springer Berlin Heidelberg, Berlin, Heidelberg, 1992, pp. 1–55 Search PubMed.
- W. Jaenicke, Chem. Ing. Tech., 197446125–125, Electrochemical Systems, Von J. S. Newman., Prentice-Hall, Inc., London – Englewood Cliffs 1973. XIV, 432 S., zahlr. Abb., geb. £ 9.50, DOI:10.1002/cite.330460315.
- N. Ibl, Distribution du courant dans les systemes électrochimiques, Techniques de L′ingénieur D, 1976, vol. 902, pp. 1–78 Search PubMed.
- N. Ibl, Current Distribution, in Comprehensive Treatise of Electrochemistry: Electrodics: Transport, ed. E. Yeager, J. O. M. Bockris, B. E. Conway and S. Sarangapani, Springer US, Boston, MA, 1983, pp. 239–315 Search PubMed.
- R. C. Alkire, P. N. Barlett and J. Lipkowski, Electrochemistry of Carbon Electrodes, Wiley, 2016, vol. 1, p. 450 Search PubMed.
- D. A. C. Brownson, A. Garcia-Miranda Ferrari, S. Ghosh, M. Kamruddin, J. Iniesta and C. E. Banks, Electrochemical properties of vertically aligned graphenes: tailoring heterogeneous electron transfer through manipulation of the carbon microstructure, Nanoscale Adv., 2020, 5319–5328 RSC.
- R. G. Compton and C. E. Banks, Understanding Voltammetry, World Scientific Publishing Company, 3rd edn, 2018 Search PubMed.
- A. D. Clegg, N. V. Rees, O. V. Klymenko, B. A. Coles and R. G. Compton, Marcus Theory of Outer-Sphere Heterogeneous Electron Transfer Reactions: Dependence of the Standard Electrochemical Rate Constant on the Hydrodynamic Radius from High Precision Measurements of the Oxidation of Anthracene and Its Derivatives in Nonaqueous Solvents Using the High-Speed Channel Electrode, J. Am. Chem. Soc., 2004, 126(19), 6185–6192 CrossRef CAS.
- M. Mahbubur Rahman and J.-J. Lee, Sensitivity control of dopamine detection by conducting poly(thionine), Electrochem. Commun., 2021, 125, 107005 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an01412b |
| This journal is © The Royal Society of Chemistry 2022 |