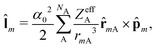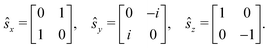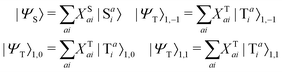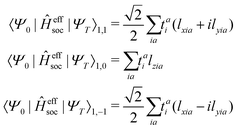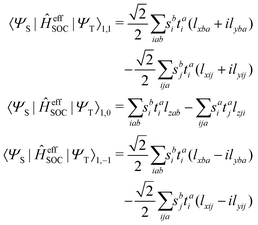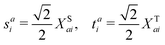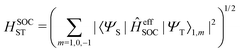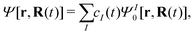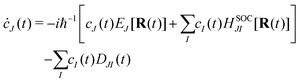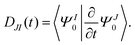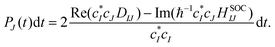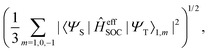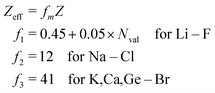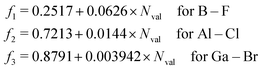An efficient implementation of spin–orbit coupling within the framework of semiempirical orthogonalization-corrected methods for ultrafast intersystem crossing dynamics†
Received
29th July 2021
, Accepted 12th September 2021
First published on 14th September 2021
Abstract
We implement spin–orbit coupling (SOC) within the framework of semiempirical orthogonalization-corrected methods (OMx). The excited-state wavefunction is generated from configuration interaction with single excitations (CIS). The SOC Hamiltonian in terms of the one-electron Breit–Pauli operator with effective nuclear charges is adopted in this work. Benchmark calculations show that SOCs evaluated using the OMx/CIS method agree very well with those obtained from time-dependent density functional theory. As a particularly attractive application, we incorporate SOCs between singlet and triplet states into Tully's fewest switches surface hopping algorithm to enable excited-state nonadiabatic dynamics simulations, treating internal conversion and intersystem crossing on an equal footing. This semiempirical dynamics simulation approach is applied to investigate ultrafast intersystem crossing processes in core-substituted naphthalenediimides.
1 Introduction
The ability to unravel nonadiabatic dynamics processes in photophysical and photochemical phenomena is crucial in many fields of research, including photovoltaics, photocatalysis, photosynthesis and so on.1–8 Theoretical models to study these photoinduced ultrafast internal conversion (IC) and intersystem crossing (ISC) processes involve time evolution of many electronic states, which often requires nonadiabatic molecular dynamics (NAMD) simulation methods,9–13 such as trajectory-based surface hopping14 and multiple spawning15 approaches. Here, excited-state electronic structure properties including potential energy surfaces, energy gradients, nonadiabatic couplings and spin–orbit couplings (SOCs) of a manifold of electronic states are usually generated “on-the-fly” from electronic structure methods.16
Rapid progress in advanced electronic structure algorithms has extensively extended the rage of applicability of NAMD methods. For example, high-level wavefunction methods, such as the complete active space self-consistent field (CASSCF),17,18 multi-reference configuration interaction (MRCI)19,20 and complete active-space second-order perturbation (CASPT2)21 methods, have been applied to accurately describe the excited-state dynamics of small nucleobase molecules.13 These high-level methods have also been generalized to larger systems, such as the 51-atom provitamin D3 molecule, through a combination of advanced algorithms and GPU-acceleration.22 In contrast, single-reference methods, such as coupled cluster (CC) methods,23–26 algebraic-diagrammatic construction (ADC) methods,27,28 and time-dependent density functional theory (TDDFT),29,30 enable NAMD simulations of medium-size systems,1,10 such as vitamin D photosynthesis31 and benzene excimer formation.32 However, the applicability of NAMD methods to large systems is still challenging using these ab initio methods due to the high computational costs.
A particularly appealing possibility is to generalize semiempirical methods to NAMD dynamics simulations for large systems. For example, floating occupation molecular orbital CI (FOMO-CI),33 semiempirical orthogonalization-corrected methods (OMx) MRCI,34–36 time-dependent density functional tight binding (TDDFTB)37 and the collective electronic oscillator (CEO) method applied at the Austin model 1 (AM1) level of theory in combination with a configuration interaction singles (CIS) formalism38 have been successfully applied to a large variety of photoinduced ultrafast processes in organic molecules. Recently, Liu and Thiel combined the OMx methods including orthogonalization models OM1, OM2, and OM339,40 with configuration interaction with single excitations (CIS), which includes all single excitations,41 and the spin–flip extended configuration interaction with single excitations (SF-XCIS) method, which treats the ground state and excited states in a fully balanced manner and properly describes conical intersections involving the ground state.42 Due to the explicit inclusion of Pauli exchange, the OMx/CIS and OMx/SF-XCIS methods give a promising description of excited-state properties and dynamic processes. Furthermore, to apply these methods for simulating intersystem crossing dynamics requires the evaluation of SOCs between singlet and triplet states.
A rigorous calculation of SOCs would use relativistic quantum mechanics, namely the Dirac equation, and include many-body interactions. In practical calculations, approximate schemes including variational methods, such as the zeroth-order regular approximation (ZORA),43–45 and perturbative methods, such as the Breit–Pauli approximation,46–49 have been proposed to reduce the computational costs. Here, the SOC Hamiltonian using the Breit–Pauli operator can be directly evaluated from excited-state wavefunctions and this has been widely implemented in quantum chemistry packages.50–54 The Breit–Pauli operator contains one- and two-electron terms originating from the interaction of the electron spin with the orbital angular momentum. In addition, a reduced screened-nuclear charge method has also been proposed as a reformulation of the Breit–Pauli operator in terms of a single-electron operator together with effective nuclear charges.46–49
In this work, we present efficient evaluation of spin–orbit coupling within the framework of OMx/CIS. The simplest method using the one-electron term of the Breit–Pauli operator has been adopted for the SOC calculations. A scaling parameter, the effective nuclear charge, approximately accounts for the missing two-electron spin–orbit term in the Breit–Pauli operator. The formula of the effective nuclear charges used for OMx/CIS without reoptimization was originally derived by fitting experimental results for fine structure splittings in Π states of diatomic hydrides for the multiconfiguration self-consistent field (MCSCF) method with the effective core potential (ECP) basis set.46,47 By incorporating the SOCs into Tully's fewest switches algorithm for surface hopping (FSSH),9,14,55–57 one of most widely used mixed quantum-classical dynamics methods, we generalize the OMx/CIS method for simulating both internal conversion and intersystem crossing dynamics in large systems.
This paper is organized as follows. Section 2 gives a brief description of the theoretical methodology, covering the OMx methods, excited-state properties and spin–orbit couplings computed within the semiempirical OMx/CIS framework, and then the generalized FSSH method. More details about the numerical implementation of SOCs within the framework of OMx/CIS are discussed in Section 3. In Section 4, we benchmark SOCs for a set of small molecules evaluated at the OMx/CIS level with respect to the TDDFT and TDDFTB methods. After that, we present nonadiabatic dynamics simulations of ultrafast intersystem crossing processes in core-substituted naphthalenediimides,58–62 which accounts for the high fluorescence quantum yields. A summary is given in Section 5.
2 Theoretical methodology
Let's introduce the notation used throughout this work. Lowercase italics i,j label occupied molecular orbitals; a,b label virtual molecular orbitals; and p,q,r,s label arbitrary molecular orbitals. Greek letters μ,ν label atomic orbitals (AOs). Two-electron integrals are defined as| | 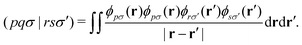 | (1) |
ϕpσ is the pth molecular orbital and εpσ is the corresponding molecular orbital energy. σ is the spin index and α,β indicate different spins. N is the number of basis functions. NA is the number of atoms. Vectors and matrices are written in bold type.
2.1 OMx methods
Assuming the zero-differential-overlap approximation, the OMx working equation is given aswhere C is the molecular orbital (MO) coefficient and E is the diagonal matrix of the corresponding MO energies. The Fock matrix is given in the basis of molecular orbitals as| | 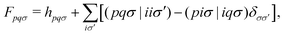 | (3) |
where h is the one-electron core Hamiltonian including one-electron energies, semiempirical core–electron attractions, valence orthogonalization corrections, penetration integrals and effective core potentials (see ref. 39 for a detailed expression). The explicit inclusion of orthogonalization terms in the OMx methods offers significant improvements in the description of asymmetric splitting of bonding and antibonding orbitals, which is crucial for performing excited-state dynamics simulations.35,36,39,40
In order to achieve a low-scaling quantum-chemical method, the OMx methods expand the molecular orbitals ϕ in a set of orthogonal minimal valence atomic orbitals χ⊥,
| | 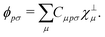 | (4) |
Standard four-center two-electron integrals scale as
O(
N4). In the OMx method, only the two-center two-electron integrals (
μAνA|
λBκB) involved in the Fock matrix are evaluated by the analytical integrals over the contracted Gaussian valence orbitals with a uniform Klopman–Ohno scaling.
39 This leads to a much lower computational scaling as
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
N2). In OM2 and OM3, there exist three-center orthogonalization corrections that in principle scale as
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
N3) for matrix multiplications. The feature of the low-scaling computational cost enables the application of the OMx methods to study large systems containing hundreds of atoms.
2.2 CIS method
The singlet and triplet excitation configurations can be expressed as| | 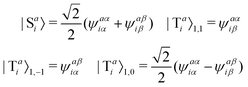 | (5) |
where the subscript (l,m) indicates the angular and magnetic quantum numbers, respectively, and “S” and “T” indicate singlet and triplet configurations, respectively. Here, we assume a single excitation promoting an electron from an occupied orbital i to an unoccupied orbital a.
The CIS wavefunction is defined as
| | 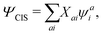 | (6) |
with
ψai defined in
eqn (5). The excitation energy
ωI and the amplitude
XI can be obtained from the CIS eigenvalue equation,
The matrix elements of
A are defined in the basis of molecular orbitals as follows
| | 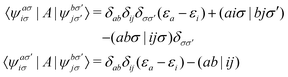 | (8) |
In this work, we assume closed-shell molecular orbitals used throughout this work. For simplicity, we drop the spin labels and rewrite
eqn (9) as
| | 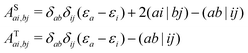 | (9) |
The summation over the spin index is absorbed in the coefficients. The Coulomb part (
ai|
bj) vanishes for triplet excitations since the single excitation,
i →
a, has opposite spin for |T
ai〉
1,1 and |T
ai〉
1,−1 or the integral cancels itself out for |T
ai〉
1,0. The transition vectors
X satisfy
The
Ith excitation energy is given by
To extract a few excited states within a specified energy window for large systems, the Davidson iterative algorithm63 is one of the most widely used methods to diagonalize the eigenvalue equation. It reduces the scaling of the OMx/CIS method from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n6) to
(n6) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n3) by projecting the eigenvalue equation onto an appropriate subspace instead of diagonalizing the whole matrix. Considering that only two-center two-electron integrals are required in eqn (9), the OMx/CIS method is computationally efficient for excited-state dynamics simulations of molecular systems with dozens of atoms.
(n3) by projecting the eigenvalue equation onto an appropriate subspace instead of diagonalizing the whole matrix. Considering that only two-center two-electron integrals are required in eqn (9), the OMx/CIS method is computationally efficient for excited-state dynamics simulations of molecular systems with dozens of atoms.
2.3 Spin–orbital coupling
The Dirac equation, describing the wavefunction with four components, is in principle a rigorous scheme to account for spin–orbit coupling. However, due to its high computational cost, approximate strategies are frequently used to evaluate spin–orbital coupling in practical calculations. In this work, we have implemented the simplest spin–orbit Hamiltonian via the one-electron Breit–Pauli operator and embodied effective nuclear charges| | 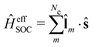 | (12) |
where ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) m is the orbital angular momentum operator for electron m,
m is the orbital angular momentum operator for electron m,| | 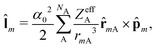 | (13) |
and ŝ is the spin angular momentum operator,| | 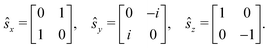 | (14) |
ZeffA is the effective charge on nucleus A and fine-structure constant α0 = e/mec.
Given singlet and triplet wavefunctions
| | 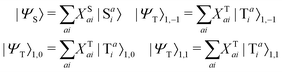 | (15) |
the spin–orbit couplings between a singlet ground state and a triplet excited state are
| | 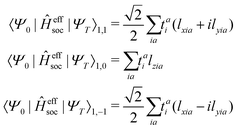 | (16) |
and the spin–orbit couplings between singlet and triplet excited states are
| | 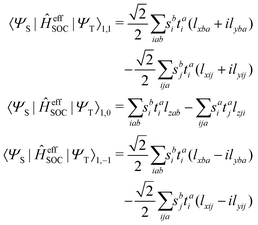 | (17) |
Here, we define
| | 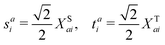 | (18) |
which are the CIS amplitudes defined in most quantum chemistry packages.
The total spin–orbit coupling between one pair of singlet and triplet states is given as
| | 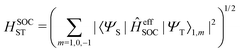 | (19) |
2.4 Generalized trajectory surface-hopping method
The trajectory surface-hopping (TSH) method is a popular tool to study ultrafast ISC processes. For example, the TSH method has been combined with Landau–Zener,64 Zhu–Nakamura theory,65 or “on-the-fly” SOCs for ISC dynamics simulations.11–13 In the latter case, the Tully's fewest switches TSH method has been applied to study ISC processes in both spin-adiabatic and spin-diabatic representations.13,66–71 When the SOC is relatively small and the states closely approach each other, it is promising to perform the TSH dynamics in the spin-diabatic representation.68,72–74
Considering the spin–orbit coupling as a perturbation interaction in the Hamiltonian68–70
| | | Ĥ[r,R(t)] = Ĥ0[r,R(t)] + ĤSOC[r,R(t)] | (20) |
where
Ĥ0 is the spin-free part of the Hamiltonian, the time-dependent wavefunction can be expressed in terms of eigenstates of
Ĥ0| | 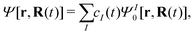 | (21) |
with
| | | Ĥ0ΨI0[r,R(t)] = EI[R(t)]ΨI0[r,R(t)] | (22) |
and
cI being the coefficient of the
I-th electronic state. Inserting
eqn (21) into the time-dependent Schrödinger equation, the generalized FSSH working equation is given as
| | 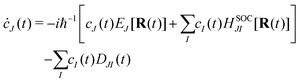 | (23) |
The nonadiabatic coupling is defined as
| | 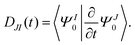 | (24) |
The detailed expression of
DIJ within the framework of OMx/CIS is formulated in ref.
41. The hopping probability from state
I to state
J is written as
| | 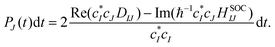 | (25) |
In this work, a simple spin-diabatic representation with each state considered as a single electronic state has been used to account for the spin–orbit coupling.68,72–74 The effective SOCs are defined as
| | 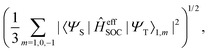 | (26) |
namely, we approximate it by averaging over the interactions between the singlet and the three triplet sublevels (this is analogous to the definition of the effective SOC used in ref.
68). In this way, the effective SOC values for singlet–triplet transitions are the same in either direction. This approach suffers from an incorrect description of intersystem crossing in certain cases as the sign change of SOCs occurs as the two states come close in energy. As such, Granucci and coworkers have recommended, when possible, the spin-adiabatic representation to be used, which needs the diagonalization of the full electronic Hamiltonian.
67,69,71 However, in complex molecular systems, this situation is expected to rarely happen and therefore we are able to use the spin-diabatic approach to obtain a qualitative result as long as one is aware of its limitations.
The surface hopping method implemented in the spin-adiabatic representation has been successfully used in studying ultrafast intersystem crossing for nucleobases and DNA molecules,13,75,76 and transition metal complexes.77 Due to the lack of a calculation of energy gradients including SOCs in most quantum chemistry software packages, some approximations should be introduced in the spin-adiabatic representation as discussed in ref. 13. In this work, we demonstrate a proof-of-principle application of the OMx/CIS method to ISC dynamics. Further work is needed in the future to explore better representations of the effective SOC Hamiltonian or to interface the MNDO program to advanced dynamics simulation software, such as SHARC,13 and NEXTON-X,50 to enable more choice of the spin basis representation.
3 Implementation
An efficient implementation of excited-state calculations including vertical excitation energies, analytic excite-state gradients and nonadiabatic couplings within the framework of OMx/CIS has been realized in the semiempirical MNDO electronic structure package.78 In this work, we focus on the implementation of the spin–orbital coupling at the OMx/CIS level and combining it with the generalized trajectory surface-hopping method. The CIS wavefunction can be explicitly extracted from the OMx/CIS calculation. One main task is to implement orbital angular momentum integrals over contracted Gaussian atomic orbitals (STO-3G for hydrogen and ECP-3G for carbon, nitrogen, oxygen, and fluorine). Since these integrals are one-electron integrals and only a minimal atomic basis is used in the OMx method, we adopt the Obara and Saika scheme for evaluating the matrix elements of orbital angular momentum operators in eqn (13).
As stated above, we have implemented a reduced screened-nuclear charge method in this work. The effective nuclear charges (Zeff),46,79
| | 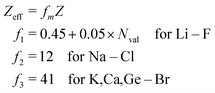 | (27) |
which are empirical parameters in the single-electron spin–orbit Hamiltonian of
eqn (12), are determined for main group elements by using experimental results for the fine structure splittings in Π states of diatomic hydrides. Here,
Z is the true nuclear charge and
Nval is the number of valence electrons. Note that
eqn (27) was initially optimized for the MCSCF/SBK method with the ECP basis set designed by Stevens, Basch and Krauss.
80 However, as shown in the following benchmark, incorporating this
Zeff expression in the OMx/CIS methods, the accuracy of SOCs is also quite promising.
For the evaluation of SOCs with all-electron basis sets, a different expression of Zeff should be used81
| | 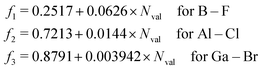 | (28) |
which is applied in the TDDFT calculations for a more reasonable comparison with OMx/CIS.
Integral derivatives with respect to nuclear coordinates that appear in the one-electron and two-electron terms of excited-state gradients and nonadiabatic coupling are evaluated with the central finite difference (CFD) method. The evaluation of spin–orbital coupling does not need integral derivatives, while the orbital angular momentum operator results in one-electron integrals over higher angular momentum Gaussian functions. The overall computational cost of SOCs is still relatively low. In the integral calculations for OMx, one adjustable parameter ζ that scales the exponents of all Gaussian primitives has been introduced for fine-tuning of the computational accuracy. These scale factors are optimized to be greater than 1 in the OMx methods. For the SOC evaluations, all scale factors ζ are set to be 1 since the nuclear charges have been scaled to fit the experimental results.46
4 Results
All spin–orbit coupling calculations are performed using the one-electron Breit–Pauli operator with an effective nuclear charge approximation implemented in modified MNDO78 and Q-Chem52 electronic structure packages. The molecular structures for the SOC benchmark calculations are obtained from the literature36,82 and drawn with VESTA.83 For comparison purposes, different effective nuclear charge expressions of eqn (27) and (28) are used in MNDO and Q-Chem, respectively. Excited-state wavefunctions are generated using OMx/CIS from MNDO or linear-response TDDFT (LR-TDDFT) from Q-Chem.
4.1 Spin–orbit coupling
The molecular structures for the benchmark calculations are shown in Fig. 1. Correlation-consistent basis set cc-pVTZ is applied to all LR-TDDFT calculations. Due to the lack of parameterization of sulfur atoms in OM1 and OM3, we only present OM2 results for thymine derivatives (g–j) and the psoralen series (k–m). As discussed in ref. 82, the SOCs evaluated with different density functionals showed an obvious discrepancy. For example, the SOCs evaluated with PBE and ωB97XD differ by about 30 cm−1 for S0/T1 of 2-thiothymine while the difference among various hybrid functionals is much smaller. Therefore, in this work one typical hybrid functional (B3LYP)84 and one popular long-range corrected functional (ωB97XD)85 are chosen for comparison. In addition, SOCs evaluated with TDDFTB (data from ref. 82) for thymine derivatives and psoralen derivatives are presented for comparison.
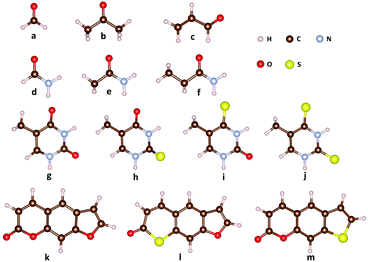 |
| | Fig. 1 Molecular structures for the spin–orbit coupling benchmark calculations: (a) formaldehyde, (b) acetone, (c) acrolein, (d) formamide, (e) acetamide, (f) propanamide, (g) thymine, (h) 2-thiothymine, (i) 4-thiothymine, (j) 2,4-thiothymine, (k) 7H-furo[3,2-g][1]benzopyran-7-one (psoralenOO), (l) 7H-thiopyrano[3,2-f][1]benzofuran-7-one (psoralenOS), and (m) 2H-thieno[3,2-g][1]benzopyran-2-one (psoralenSO). | |
Table 1 lists the SOCs for formaldehyde, acetone and acrolein, in which there exist lowest-lying n → π* singlet and triplet excited states followed by the p → π* excited state. In comparison with LR-TDDFT, the OMx/CIS methods give a qualitatively correct description of strong SOCs, namely 1gs/3nπ* and 1nπ*/3ππ*, for the three molecular systems. These results are also consistent with the El-Sayed rule that states that a radiationless transition from the lowest singlet states to the triplet manifold is relative large if this transition involves a change of molecular orbital type. In detail, the SOCs of 1nπ*/3ππ* evaluated with OMx/CIS agree quite well with those evaluated with LR-TDDFT in formaldehyde and acetone, while in acrolein the SOCs of 1nπ*/3ππ* evaluated with OMx/CIS and LR-TDDFT differ by about 10 cm−1. For the SOCs of 1gs/3nπ* in the three systems, the OMx/CIS methods obviously underestimate them by about 10 cm−1 compared with LR-TDDFT. However, the weak SOCs evaluated with the OMx/CIS methods are almost the same as those evaluated with LR-TDDFT.
Table 1 SOCs (in cm−1) for formaldehyde, acetone and acrolein computed with OMx/CIS and LR-TDDFT using B3LYP and ωB97XD
|
|
1gs/3ππ* |
1gs/3nπ* |
1nπ*/3ππ* |
1nπ*/3nπ* |
| Formaldehyde |
| OM1 |
0 |
49 |
45 |
0 |
| OM2 |
0 |
49 |
44 |
0 |
| OM3 |
0 |
50 |
40 |
0 |
| B3LYP |
0 |
61 |
46 |
0 |
| ωB97XD |
0 |
60 |
45 |
0 |
| Acetone |
| OM1 |
0 |
46 |
45 |
0 |
| OM2 |
1 |
43 |
43 |
0 |
| OM3 |
1 |
44 |
42 |
0 |
| B3LYP |
0 |
57 |
44 |
0 |
| ωB97XD |
0 |
57 |
44 |
0 |
| Acrolein |
| OM1 |
1 |
45 |
16 |
0 |
| OM2 |
1 |
43 |
15 |
0 |
| OM3 |
1 |
42 |
12 |
0 |
| B3LYP |
0 |
54 |
25 |
0 |
| ωB97XD |
0 |
54 |
23 |
0 |
Analogous to formaldehyde, acetone and acrolein, another set of molecules including formamide, acetamide and propanamide also have a carbonyl group that leads to lowest-lying n → p* states. However, this state has a much high excitation energy due to the amino-group substituent. Table 2 lists the SOCs between singlet states and low-lying triplet states in formamide, acetamide and propanamide. Compared with formaldehyde, acetone and acrolein, the SOCs of 1gs/3nπ* and 1nπ*/3ππ* in formamide, acetamide and propanamide only slightly decrease. The SOCs evaluated with OM1/CIS, OM2/CIS and OM3/CIS with respect to the LR-TDDFT results are very close each other except that the OM3/CIS method gives a relatively large value for the weak SOC of 1gs/3ππ*. In addition, the difference in the SOCs between OM1/CIS and OM3/CIS is obvious, especially for 1nπ*/3ππ*.
Table 2 SOCs (in cm−1) for formamide, acetamide and propanamide computed with OMx/CIS and LR-TDDFT using B3LYP and ωB97XD
|
|
1gs/3ππ* |
1gs/3nπ* |
1nπ*/3ππ* |
1nπ*/3nπ* |
| Formamide |
| OM1 |
2 |
46 |
42 |
1 |
| OM2 |
3 |
45 |
39 |
1 |
| OM3 |
11 |
44 |
35 |
1 |
| B3LYP |
1 |
54 |
39 |
0 |
| ωB97XD |
1 |
53 |
39 |
0 |
| Acetamid |
| OM1 |
2 |
44 |
42 |
0 |
| OM2 |
2 |
42 |
39 |
0 |
| OM3 |
3 |
41 |
37 |
1 |
| B3LYP |
0 |
52 |
40 |
0 |
| ωB97XD |
0 |
52 |
34 |
0 |
| Propanamide |
| OM1 |
2 |
44 |
42 |
0 |
| OM2 |
3 |
41 |
39 |
0 |
| OM3 |
4 |
41 |
36 |
0 |
| B3LYP |
0 |
51 |
39 |
0 |
| ωB97XD |
0 |
51 |
39 |
0 |
Table 3 lists SOCs for thymine and its thio-derivatives, including 2-thiothymine, 4-thiothymine and 2,4-thiothymine, evaluated with OM2/CIS and LR-TDDFT. As the heavy sulfur atom is introduced, the SOCs in the three sulfur-substituted thymine derivatives are significantly larger than those in thymine. On the other hand, due to the distorted out-of-plane structure, there exists strong n/mixing in the HOMO and HOMO-1 orbitals of 2-thiothymine. As such, 2-thiothymine has strong SOCs for 1gs/3ππ* and 1nπ*/3ππ*, which break the El-Sayed rule. This is different from the other three thymine derivatives with planar structures. For all cases shown in Table 3, the SOCs predicted by the OM2/CIS method are quite close to the LR-TDDFT results with a largest error of 24 cm−1. In contrast, as discussed in ref. 82, the difference between LR-TDDFT/ωB97XD and TDDFTB is as large as ∼140 cm−1 for S1/T2 in 2-thiothymine. For weak SOCs, OM2/CIS gives quite reasonable results.
Table 3 SOCs (in cm−1) for thymine, 2-thiothymine, 4-thiothymine, and 2,4-thiothymine computed with OM2/CIS and LR-TDDFT using B3LYP and ωB97XD
|
|
1gs/3ππ* |
1gs/3nπ* |
1nπ*/3ππ* |
1nπ*/3nπ* |
| Thymine |
| OM2 |
4 |
35 |
10 |
6 |
| TD-B3LYP |
5 |
38 |
18 |
3 |
| TD-ωB97XD |
5 |
40 |
17 |
1 |
| TDDFTB |
5 |
39 |
32 |
4 |
| 2-Thiothymine |
| OM2 |
102 |
152 |
150 |
44 |
| TD-B3LYP |
108 |
151 |
132 |
68 |
| TD-ωB97XD |
108 |
153 |
141 |
50 |
| TDDFTB |
180 |
129 |
85 |
197 |
| 4-Thiothymine |
| OM2 |
2 |
110 |
120 |
1 |
| TD-B3LYP |
2 |
130 |
137 |
2 |
| TD-ωB97XD |
1 |
131 |
133 |
1 |
| TDDFTB |
1 |
175 |
206 |
0 |
| 2,4-Thiothymine |
| OM2 |
5 |
111 |
123 |
1 |
| TD-B3LYP |
3 |
135 |
135 |
3 |
| TD-ωB97XD |
2 |
134 |
136 |
1 |
| TDDFTB |
1 |
119 |
119 |
0 |
Psoralen and its thio-derivatives have been well studied in previous work.82,86,87Table 4 shows four typical SOCs evaluated with OM2/CIS and LR-TDDFT. As the size of the systems increases, the ordering of excited states becomes more complicated when different methods are used. In order to perform a reliable comparison, SOCs between different electronic states are identified by the dominant excitation configuration for different methods. As usual, the calculated SOCs from different theoretical methods differ by less than 1 cm−1 in the weak SOC case. The strong SOCs are systematically underestimated by OM2/CIS, especially for psoralenOS. In the case of S1/T4 for psoralenOS, the SOCs between OM2/CIS and TD-B3LYP differ by 27 cm−1 while TDDFTB significantly overestimates it by 27 cm−1. In addition, TDDFTB remarkably underestimates the SOC of S0/T5 for psoralenOO while OM2/CIS shows a much smaller deviation with respect to LR-TDDFT.
Table 4 SOCs (in cm−1) for psoralenOO, psoralenOS and psoralenSO computed with OMx/CIS and LR-TDDFT using B3LYP and ωB97XD
|
|
OM2 |
B3LYP |
ωB97XD |
TDDFTB |
| PsoralenOO |
| S0/T1 |
0 |
1 |
1 |
0 (S0/T3) |
| S0/T5 |
33 |
44 (S0/T4) |
48 |
32 (S0/T2) |
| S1/T1 |
0 |
1 |
1 |
0 (S2/T3) |
| S1/T5 |
6 |
9 (S1/T4) |
10 |
12 (S2/T2) |
| PsoralenOS |
| S0/T1 |
1 |
0 |
0 |
0 (S0/T3) |
| S0/T4 |
51 (S0/T3) |
72 |
77 |
75 (S0/T2) |
| S1/T1 |
0 |
0 |
0 |
0 (S2/T3) |
| S1/T4 |
8 (S1/T3) |
35 |
32 |
62 (S2/T2) |
| PsoralenSO |
| S0/T1 |
1 |
0 |
1 |
0 (S0/T3) |
| S0/T5 |
33 |
43 (S0/T4) |
48 |
30 (S0/T2) |
| S1/T1 |
1 |
1 |
1 |
1 (S2/T3) |
| S1/T5 |
5 |
4 (S1/T4) |
6 |
5 (S2/T2) |
Overall, the SOCs evaluated with the semiempirical OMx/CIS methods show good agreement with those obtained from LR-TDDFT with B3LYP and ωB97XD and the cc-pVTZ basis set. However, due to the minimal valence basis used in the OMx methods and the error from the CIS method, OMx/CIS systematically underestimates the SOCs for the benchmark molecular set. Considering that a scale factor ζ of 1 has been used without optimization for calculations of SOCs, it is possible to improve the accuracy of SOCs evaluated at the OMx/CIS level via optimizing each scale factor for different atoms.
4.2 Excited-state dynamics
In the past few years, core-substituted naphthalenediimides (c-NDIs) have aroused lots of interest as building blocks for application in photovoltaics, artificial photosysthesis and so on.88–95 Typically, c-NDIs exhibit larger quantum fluorescence yields than the non-core-substituted naphthalenediimides. This mainly results from the change of excitation configurations in the lowest excited state induced by the core substituents. In this work, we apply the generalized surface hopping approach based on the OMx/CIS method to study ultrafast intersystem-crossing dynamics in a red naphthalenediimide (rNDI) dye.
In this work, all calculations are performed for an analogue of rNDI (m-rNDI), in which a hydrogen atom is substituted by the bromine atom, as shown in Fig. 2. Vertical excitation energies and dominant excitations evaluated with OM2/CIS and LR-TDDFT/ωB97XD/cc-pVTZ (TD-ωB97XD) for m-rNDI are listed in Table 5. In the MNDO package, there do not exist parameters for the bromine atom. Therefore, we perform the excited-state calculation with parameters of the fluorine atom. For singlet excited states, OMx/CIS gives a very reasonable description of the excitation energies and dominant excitation configurations, while it slightly underestimates the excitation energies of S2 (nH−2 → πL). A sequence of triplet excited states with dominant excitation of πH → πL, πH−1 → πL and nH−2 → πL predicted by OM2/CIS is also consistent with those from TD-ωB97XD. The ultrafast intersystem crossing in rNDI takes place after an initial πH−1 → πL excitation, namely S0 → S4.
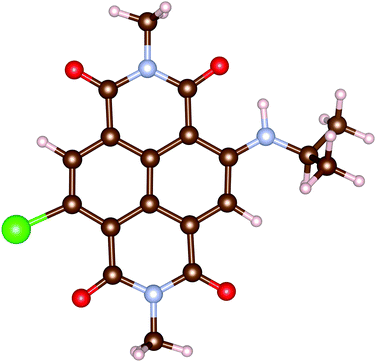 |
| | Fig. 2 Molecule structures of m-rNDI. | |
Table 5 Vertical excitation energies (in eV) and dominant excitations evaluated with OM2/CIS and LR-TDDFT/ωB97XD/cc-pVTZ for m-rNDI. The subscripts “H” and “L” indicate the HOMO and LUMO molecular orbitals. The subscripts “H−i” and “L−i” indicate the HOMO−i and LUMO−i molecular orbitals
|
|
OM2 |
ωB97XD |
| ΔE (eV) |
Dominant excitation |
ΔE (eV) |
Dominant excitation |
| S1 |
3.15 |
πH → πL (0.94) |
3.05 |
πH → πL (0.97) |
| S2 |
3.72 |
nH−2 → πL (0.79) |
4.05 |
nH−2 → πL (0.79) |
| S3 |
3.95 |
nH−7 → πL (0.54) |
4.06 |
πH−1 → πL (0.91) |
|
|
|
nH−6 → πL (0.35) |
|
|
| S4 |
4.00 |
πH−1 → πL (0.76) |
4.44 |
πH → πL+1 (0.68) |
|
|
|
|
|
πH−3 → πL (0.63) |
| T1 |
2.08 |
πH → πL (0.90) |
1.83 |
πH → πL (0.93) |
| T2 |
2.77 |
πH−1 → πL (0.81) |
2.40 |
πH−1 → πL (0.86) |
| T3 |
3.31 |
πH−5 → πL (0.51) |
3.34 |
πH → πL+1 (0.65) |
|
|
|
πH → πL+1 (0.48) |
|
πH−9 → πL (0.40) |
| T4 |
3.5 |
nH−2 → πL (0.74) |
3.7 |
nH−2 → πL (0.73) |
Table 6 shows some typical SOCs for m-rNDI computed with OM2/CIS and TD-ωB97XD. Explicit OM2/CIS calculations with parameters of the fluorine atom result in relatively small SOCs since the bromine atom is much heavier than the fluorine atom. As a compromise scheme, we set the effective nuclear charge Zeff to be 1435, which is Zeff of the bromine atom obtained from eqn (27), and consequently the scale factor for the Gaussian basis functions to be 0.9, which roughly reproduces SOCs evaluated with TD-ωB97XD. As shown in Table 6, good agreement of SOCs between OM2/CIS and TD-ωB97XD is obtained. Here, typical strong SOCs are observed between πH → πL and nH−2 → πL. However, the SOC between πH−1 → πL and nH−2 → πL, namely (S4/T4) at the OM2/CIS level (S3/T4 for TD-ωB97XD), is quite small compared to the former one. This implies that the direct intersystem crossing from the second bright excited state S4 to the triplet state may be very slow due to the small SOC. There are unavoided surface crossings between singlet and triplet states. For example, the energies of S3 and S4 are very close to each other, and the surface crossing is unavoided in rNDI. Similarly, unavoided surface crossings also happen between S2 and T4/T5. In our numerical simulations, we identified the excited state according to the excitation configuration to avoid problems induced by unavoided surface crossings.
Table 6 Typical SOCs (in cm−1) for m-rNDI computed with OM2/CIS and TDDFT/ωB97XD/cc-pVTZ
|
|
S1/T4 |
S2/T1 |
S2/T2 |
S2/T3 |
| OM2 |
94 |
96 |
20 |
136 |
| ωB97XD |
98 |
104 |
15 |
132 |
|
|
S4/T1 |
S4/T2 |
S4/T3 |
S4/T4 |
| OM2 |
1 |
0 |
1 |
11 |
| ωB97XD |
5 |
1 |
2 (S4/T4) |
7 (S3/T4) |
As a pilot application of the generalized surface hopping approach based on our semiempirical OM2/CIS method, we perform excited-state dynamics simulations after an initial S0 → S4 excitation for m-rNDI to gain deep insight into ultrafast intersystem crossing dynamics. To account for the solvent effect, a Langevin thermostat was used to keep the temperature constant at 298 K with a friction coefficient γ of 2.0 ps−1.41,96 The velocity-Verlet algorithm was used with a time step of 0.5 fs for the nuclear motion. 500 independent surface hopping trajectories of 2 ps were run.
Fig. 3 shows the time evolution of the populations of the lowest-lying singlet and triplet excited states averaged over all trajectories on the OM2/CIS potential surface. It is clear that the decay of the second bright state S4 take place within a very short time scale (<100 fs). However, as the population of S4 decreases, the population of S2 increases very rapidly, while at the same time there is only little population of triplet states. This reveals that the dominant decay channel of S4 is through internal conversion to lower singlet states, namely 1ππ* → 1nπ*. After 100 fs, with most S4 decaying to S2, there are two competing decay channels: one is a radiationless transition to S1 through internal conversion, and the other is a transition to triplet states through intersystem crossing. As shown in Fig. 3, the populations of the S1 and triplet states are almost equivalent at 1 ps. However, after that, the population of the triplet states, especially T1, continuously increases. Overall, we conclude that ultrafast intersystem crossing after an initial excitation to the second bright state in rNDI mainly takes place between 1nπ* and 3ππ* instead of between 1ππ* and 3nπ*.
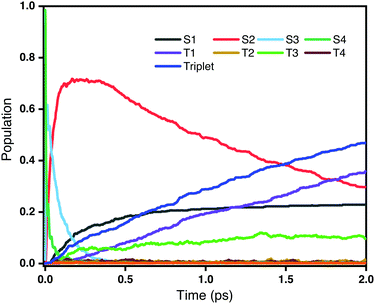 |
| | Fig. 3 Populations of different excited states as a function of time obtained from the fraction of trajectories in each state at the CIS/OM2 level. The initial excitation is S0 → S4. | |
5 Conclusion
We have presented efficient evaluation of SOC within the framework of OMx/CIS. The SOC Hamiltonian in terms of the one-electron Breit–Pauli operator and embodied effective nuclear charges is employed to evaluate SOCs between singlet states and a manifold of triplet states. Benchmark calculations on a set of small molecules show good agreement between the OMx/CIS method using the effective core potential basis set and the hybrid LR-TDDFT method using the all-electron basis set. However, analogous to the fact that the OMx/CIS method frequently underestimates molecular excitation energies,41 the SOCs computed with OMx/CIS also show systematic deviations from those computed with LR-TDDFT. It is possible to optimize parameters, especially the scale factor ζ for integrals over Gaussian basis functions, to alleviate these deviations.
One particularly attractive application of the implementation of SOCs based on OMx/CIS is to extend the FSSH algorithm to simulate both internal conversion and intersystem crossing, namely radiationless transitions between electronic states with different spin multiplicity. Due to the high efficiency of the OMx/CIS method, all excited-state properties, including excitation energies, analytical energy gradients, nonadiabatic couplings and SOCs, can be computed “on the fly” with much less computational costs compared to ab initio methods. This semiempirical dynamics simulation method is able to provide a computationally accessible and reasonable description of photoinduced dynamics in large molecular systems consisting of hundreds of atoms on time scales of tens of picoseconds. As an initial application of this method, we perform a nonadiabatic dynamics simulation of c-NDIs after S0 → S4 excitation and interpret the ultrafast intersystem crossing dynamics process which takes place on a very short time scale comparable to that for internal conversion processes.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (21688102, 22073086, 21803065, 21933011 and 21873112), by the National Key Research and Development Program of China (2016YFA0200604), and Anhui Initiative in Quantum Information Technologies (AHY090400).
References
- A. V. Akimov, A. J. Neukirch and O. V. Prezhdo, Chem. Rev., 2013, 113, 4496–4565 CrossRef CAS PubMed.
- S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115–164 RSC.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- A. Kubacka, M. Fernández-García and G. Colón, Chem. Rev., 2012, 112, 1555–1614 CrossRef CAS PubMed.
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- F. Segatta, L. Cupellini, M. Garavelli and B. Mennucci, Chem. Rev., 2019, 119, 9361–9380 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- L. Wang, R. Long and O. V. Prezhdo, Annu. Rev. Phys. Chem., 2015, 66, 549–579 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- B. F. Curchod and T. J. Martńez, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
-
J. C. Tully, in Modern Methods for Multidimensional Dynamics Computations in Chemistry, ed. D. L. Thompson, World Scientific, Singapore, 1998, pp. 34–72 Search PubMed.
- M. Ben-Nun, J. Quenneville and T. J. Martńez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- S. Pratihar, X. Ma, Z. Homayoon, G. L. Barnes and W. L. Hase, J. Am. Chem. Soc., 2017, 139, 3570–3590 CrossRef CAS PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- K. Ruedenberg, M. W. Schmidt, M. M. Gilbert and S. T. Elbert, Chem. Phys., 1982, 71, 41–49 CrossRef CAS.
-
K. Hirao, Recent advances in multireference methods, World Scientific, Singapore, 1999, vol. 4 Search PubMed.
- H. Lischka, M. Dallos, P. G. Szalay, D. R. Yarkony and R. Shepard, J. Chem. Phys., 2004, 120, 7322–7329 CrossRef CAS PubMed.
-
K. Andersson and B. O. Roos, in Modern electronic structure theory, ed. D. R. Yarkony, World Scientific, Singapore, 1995, vol. 2 of Advanced Series in Physical Chemistry, pp. 55–109 Search PubMed.
- J. W. Snyder, B. F. E. Curchod and T. J. Martínez, J. Phys. Chem. Lett., 2016, 7, 2444–2449 CrossRef CAS PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1996, 105, 1451–1459 CrossRef CAS.
- S. A. Kucharski, M. Wloch, M. Musial and R. J. Bartlett, J. Chem. Phys., 2001, 115, 8263–8266 CrossRef CAS.
- S. V. Levchenko and A. I. Krylov, J. Chem. Phys., 2004, 120, 175–185 CrossRef CAS PubMed.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95 CAS.
-
M. E. Casida, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific, River Edge, NJ, 1995, ch. 5, vol. I of Recent Advances in Computational Chemistry, pp. 155–192 Search PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- C. Cisneros, T. Thompson, N. Baluyot, A. C. Smith and E. Tapavicza, Phys. Chem. Chem. Phys., 2017, 19, 5763–5777 RSC.
- T. M. Cardozo, A. P. Galliez, I. Borges, F. Plasser, A. J. A. Aquino, M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2019, 21, 13916–13924 RSC.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- A. Koslowski, M. E. Beck and W. Thiel, J. Comput. Chem., 2003, 6, 714–726 CrossRef PubMed.
- W. Thiel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 145–157 CAS.
- D. Tuna, Y. Lu, A. Koslowski and W. Thiel, J. Chem. Theory Comput., 2016, 12, 4400–4422 CrossRef CAS PubMed.
- R. Mitrić, U. Werner, M. Wohlgemuth, G. Seifert and V. Bonačić-Koutecký, J. Phys. Chem. A, 2009, 113, 12700–12705 CrossRef PubMed.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171–3212 CrossRef CAS PubMed.
- P. O. Dral, X. Wu, L. Spörkel, A. Koslowski and W. Thiel, J. Chem. Theory Comput., 2016, 12, 1097–1120 CrossRef CAS PubMed.
- P. O. Dral, X. Wu, L. Spörkel, A. Koslowski, W. Weber, R. Steiger, M. Scholten and W. Thiel, J. Chem. Theory Comput., 2016, 12, 1082–1096 CrossRef CAS PubMed.
- J. Liu and W. Thiel, J. Chem. Phys., 2018, 148, 154103 CrossRef PubMed.
- J. Liu and W. Thiel, J. Chem. Phys., 2018, 148, 244108 CrossRef PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 10, 9783 CrossRef.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505 CrossRef CAS.
- S. Koseki, M. S. Gordon, M. W. Schmidt and N. Matsunaga, J. Phys. Chem., 1995, 99, 12764–12772 CrossRef CAS.
- S. Koseki, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 1998, 102, 10430–10435 CrossRef CAS.
- D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592 Search PubMed.
- S. G. Chiodo and N. Russo, J. Comput. Chem., 2009, 30, 832–839 CrossRef CAS PubMed.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
-
Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kús, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Dop, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, P. A. Pieniazek, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, N. Sergueev, S. M. Sharada, S. Sharmaa, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, V. Vanovschi, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhou, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xua, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 Search PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
-
TURBOMOLE V. 6.3.1, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633 CAS.
- E. Fabiano, T. W. Keal and W. Thiel, Chem. Phys., 2008, 349, 334–347 CrossRef CAS.
- L. Spörkel and W. Thiel, J. Chem. Phys., 2016, 144, 194108 CrossRef PubMed.
- V. Wintgens, P. Valat, J. Kossanyi, L. Biczok, A. Demeter and T. Berces, J. Chem. Soc., Faraday Trans., 1994, 90, 411 RSC.
- T. C. Barros, S. Brochsztain, V. G. Toscano, P. Berci Filho and M. J. Politi, J. Photochem. Photobiol., A, 1997, 111, 97 CrossRef CAS.
- S. Alp, S. Erten, C. Karapire, B. Koz, A. O. Doroshenko and S. Icli, J. Photochem. Photobiol., A, 2000, 135, 103 CrossRef CAS.
- M. S. Refat, I. Grabchev, J. M. Chovelon and G. Ivanova, Spectrochim. Acta, Part A, 2006, 64, 435 CrossRef CAS PubMed.
- O. Yushchenko, G. Licari, S. Mosquera-Vazquez, N. Sakai, S. Matile and E. Vauthey, J. Phys. Chem. Lett., 2015, 6, 2096–2100 CrossRef CAS PubMed.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137(833), 696–702 Search PubMed.
- C. Xu, L. Yu, C. Zhu, J. Yu and Z. Cao, Sci. Rep., 2016, 6, 26768 CrossRef CAS PubMed.
- B. Maiti and G. C. Schatz, J. Chem. Phys., 2003, 119, 12360–12371 CrossRef CAS.
- G. Granucci, M. Persico and G. Spighi, J. Chem. Phys., 2012, 137, 22A501 CrossRef PubMed.
- G. Cui and W. Thiel, J. Chem. Phys., 2014, 14, 124101 CrossRef PubMed.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- B. F. E. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, J. Chem. Phys., 2016, 144, 101102 CrossRef PubMed.
- J. Peng, Y. Xie, D. Hu and Z. Lan, J. Chem. Phys., 2019, 150, 164126 CrossRef PubMed.
- B. Fu, B. C. Shepler and J. M. Bowman, J. Am. Chem. Soc., 2011, 133, 7957–7968 CrossRef CAS PubMed.
- B. F. Habenicht and O. V. Prezhdo, J. Am. Chem. Soc., 2012, 134, 15648–15651 CrossRef CAS PubMed.
- F. Franco de Carvalho and I. Tavernelli, J. Chem. Phys., 2015, 143, 224105 CrossRef CAS PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095 CrossRef CAS PubMed.
- L. Martínez-Fernández, I. Corral, G. Granucci and M. Persico, Chem. Sci., 2014, 5, 1336–1347 RSC.
- A. J. Atkins and L. González, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
-
W. Thiel, MNDO99 program, Max-Planck-Institut für Kohlenforschung, Mülheim, Germany, 2007. Available from the author upon private communication Search PubMed.
- S. Koseki, N. Matsunaga, T. Asada, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2019, 123, 2325–2339 CrossRef CAS PubMed.
- W. J. Stevens, H. Basch and M. Krauss, J. Chem. Phys., 1984, 81, 6026–6033 CrossRef.
- S. G. Chiodo and M. Leopoldini, Comput. Phys. Commun., 2014, 185, 676–683 CrossRef CAS.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. G. Chiodo and N. Russo, Chem. Phys. Lett., 2010, 490, 90–96 CrossRef CAS.
- J. Pirillo, B. De Simone and N. Russo, Theor. Chem. Acc., 2016, 135, 8 Search PubMed.
- S. Bhosale, A. L. Sisson, P. Talukdar, A. Fürstenberg, N. Banerji, E. Vauthey, G. Bollot, J. Mareda, C. Röger and F. Würthner, Science, 2006, 313, 84 CrossRef CAS PubMed.
- A. L. Sisson, N. Sakai, N. Banerji, A. Fürstenberg, E. Vauthey and S. Matile, Angew. Chem., Int. Ed., 2008, 47, 3727 CrossRef CAS PubMed.
- N. Sakai, M. Lista, O. Kel, S.-i. Sakurai, D. Emery, J. Mareda, E. Vauthey and S. Matile, J. Am. Chem. Soc., 2011, 133, 15224 CrossRef CAS PubMed.
- N. Sakai, J. Mareda, E. Vauthey and S. Matile, Chem. Commun., 2010, 46, 4225 RSC.
- D. Villamaina, M. M. A. Kelson, S. V. Bhosale and E. Vauthey, Phys. Chem. Chem. Phys., 2014, 16, 5188 RSC.
- S. V. Bhosale, S. V. Bhosale, M. B. Kalyankar and S. J. Langford, Org. Lett., 2009, 11, 5418 CrossRef CAS PubMed.
- C. Röger and F. Würthner, J. Org. Chem., 2007, 72, 8070 CrossRef PubMed.
- F. Würthner, A. Shahadat, C. Thalacker and T. Debaerdemaeker, Chem. – Eur. J., 2002, 8, 4742 CrossRef.
- M. G. Paterlini and D. M. Ferguson, Chem. Phys., 1998, 236, 243–252 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03477d |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Zhenggang
Lan
*a,
Zhenggang
Lan
 b and
Jinlong
Yang
b and
Jinlong
Yang
 *a
*a
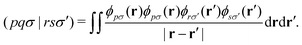
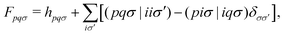
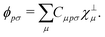
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2). In OM2 and OM3, there exist three-center orthogonalization corrections that in principle scale as
(N2). In OM2 and OM3, there exist three-center orthogonalization corrections that in principle scale as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N3) for matrix multiplications. The feature of the low-scaling computational cost enables the application of the OMx methods to study large systems containing hundreds of atoms.
(N3) for matrix multiplications. The feature of the low-scaling computational cost enables the application of the OMx methods to study large systems containing hundreds of atoms.
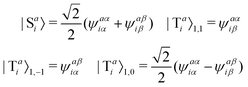
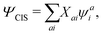
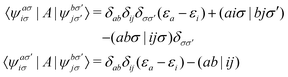
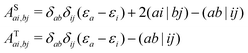
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n6) to
(n6) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n3) by projecting the eigenvalue equation onto an appropriate subspace instead of diagonalizing the whole matrix. Considering that only two-center two-electron integrals are required in eqn (9), the OMx/CIS method is computationally efficient for excited-state dynamics simulations of molecular systems with dozens of atoms.
(n3) by projecting the eigenvalue equation onto an appropriate subspace instead of diagonalizing the whole matrix. Considering that only two-center two-electron integrals are required in eqn (9), the OMx/CIS method is computationally efficient for excited-state dynamics simulations of molecular systems with dozens of atoms.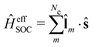
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) m is the orbital angular momentum operator for electron m,
m is the orbital angular momentum operator for electron m,