Systematic evaluation of bundled SPC water for biomolecular simulations

Abstract

In bundled SPC water models, the relative motion of groups of four water molecules is restrained by distance-dependent potentials. Bundled SPC models have been used in hybrid all-atom/coarse-grained (AA/CG) multiscale simulations, since they enable to couple atomistic SPC water with supra-molecular CG water models that effectively represent more than a single water molecule. In the present work, we systematically validated and critically tested bundled SPC water models as solvent for biomolecular simulations. To that aim, we investigated both thermodynamic and structural properties of various biomolecular systems through molecular dynamics (MD) simulations. Potentials of mean force of dimerization of pairs of amino acid side chains as well as hydration free energies of single side chains obtained with bundled SPC and standard (unrestrained) SPC water agree closely with each other and with experimental data. Decomposition of the hydration free energies into enthalpic and entropic contributions reveals that in bundled SPC, this favorable agreement of the free energies is due to a larger degree of error compensation between hydration enthalpy and entropy. The Ramachandran maps of Ala₃, Ala₅, and Ala₇ peptides are similar in bundled and unrestrained SPC, whereas for the (GS)₂ peptide, bundled water leads to a slight overpopulation of extended conformations. Analysis of the end-to-end distance autocorrelation times of the Ala₅ and (GS)₂ peptides shows that sampling in more viscous bundled SPC water is about two times slower. Pronounced differences between the water models were found for the structure of a coiled-coil dimer, which is instable in bundled SPC but not in standard SPC. In addition, the hydration of the active site of the serine protease α-chymotrypsin depends on the water model. Bundled SPC leads to an increased hydration of the active site region, more hydrogen bonds between water and catalytic triad residues, and a significantly slower exchange of water molecules between the active site and the bulk. Our results form a basis for assessing the accuracy that can be expected from bundled SPC water models. At the same time, this study also highlights the importance of evaluating beforehand the effects of water bundling on the biomolecular system of interest for a particular multiscale simulation application.

---

1 Introduction

Molecular dynamics (MD) simulations have become an indispensable tool for studying biological systems.^1–3 However, one major bottleneck of conventional all-atom (AA) MD simulations is that the huge computational effort involved imposes severe limitations on the systems and processes that can be studied, both concerning the system sizes and time scales. In biomolecular simulations, the majority of this effort is dedicated to computing interactions involving solvent molecules. To overcome these limitations, efficient coarse-grained (CG) models have been developed.⁴ By combining several atoms into CG beads, such models can increase computational efficiency by several orders of magnitude and thus significantly extend the spatial and temporal scales accessible to molecular simulations. Particularly promising in terms of the achievable speed-up are those CG models that either employ an implicit solvent model, or retain an explicit description of the solvent but combine several individual solvent molecules into a single supra-molecular CG solvent bead. Such CG approaches have been successfully used to study a wide range of biomolecular processes.^4,5 However, not surprisingly in light of the approximations inherent to coarse-graining, CG models necessarily have their limitations as well. For example, most CG models that provide a substantial computational speed-up cannot accurately describe details of the conformational dynamics of proteins, such as transitions between conformational states or the (transient) formation of secondary structure elements.

Multiscale simulations aim to achieve a balance between accuracy and efficiency by combining different levels of resolution. Multiscale methods can be classified into serial (or sequential) and parallel (or hybrid) approaches.⁶ In the serial approaches, the different models are used one after another: first, information from an atomistic simulation is used to parameterize a CG model. Then, back-mapping methods⁷ can be used to convert structures obtained from a CG simulation back into the underlying atomistic ensembles. In the parallel or hybrid schemes, by contrast, different resolution models are used for certain components or parts of the system. Hence, atomistic and coarse-grained representations are simultaneously present in the same simulation system, thus requiring direct interactions between them. One way to achieve this is to partition the simulation system into different spatial regimes. Often, the phenomena of interest are rather local, such as, e.g., the binding of a small molecule to a binding site or conformational changes within a (part of a) biological macromolecule. In such cases, AA/CG methods in which an AA model (for the small subsystem of interest) is coupled to a CG description for the remainder (mostly solvent) can be computationally very efficient.

In the adaptive resolution multiscale methods,^8–12 the solute of interest is described at the all-atom level and embedded in a (usually spherical) shell of atomistic solvent molecules, which in turn is surrounded by CG solvent. A healing region of a particular width is introduced, in which the molecules gradually switch their resolution on-the-fly upon diffusing into or out of the atomistic zone. In this region, forces⁹ or potentials¹² are scaled to enact smooth switching between the different levels of resolution. Adaptive resolution simulations in which a supra-molecular CG solvent is used require mapping of a group of atomistic solvent molecules to a single CG site located at the center of mass of these atomistic molecules. To map the atomistic coordinates in such a way that a low-energy CG configuration is obtained is impossible if the individual atomistic solvent molecules diffuse independently.¹³ To enable this mapping in multiscale simulations, atomistic bundled SPC water models^14,15 have been developed, in which distance restraints are used to confine the relative motion of water molecules in groups of four. This choice was motivated by the corresponding four-to-one mapping of atomistic and CG water in the widely used CG-Martini force field,^16–18 to which the bundled SPC models can thus be coupled. Recent applications have employed bundled SPC water in adaptive resolution simulations of solvents^15,19 and a protein in water.²⁰ These hybrid AA/CG simulations provided a computational speed-up of up to a factor 12 as compared to a fully atomistic system of the same size.¹⁵ Integrating the equations of motion in the AA and CG subsystems with different time steps would further boost efficiency. Of course, the computational efficiency gain that can be achieved for a particular simulation system depends on the system size and the ratio of atomistic and CG particles, though. The accuracy of such multiscale approaches depends critically on the properties of the bundled water, which is used as the inner shell solvent surrounding the solute of interest. However, thus far, the effects of bundling the water molecules on the structural and thermodynamic properties of the embedded biomolecular solutes have not been explored in much detail.

Here, we systematically evaluate and critically test bundled SPC water as solvent for various biomolecular systems. We did not perform AA/CG multiscale simulations, but focused on fully all-atom simulations in bundled SPC as compared to reference simulations in standard (unrestrained) water. This approach does not provide any computational speed-up, but it allowed us to study the effects of bundling the water molecules without possible additional influences of an AA/CG boundary. We calculated potentials of mean force (PMFs) of dimerization of selected pairs of amino acid side chains as well as free energies of hydration of amino acid side chains. These hydration free energies were decomposed into the enthalpic and entropic contributions. Furthermore, we investigated the conformational sampling of different polypeptides and a dimeric coiled-coil structure. Finally, we explored the effect of bundling the solvent molecules on the hydration of the active site of the protein α-chymotrypsin (α-CT). Our results show that for many of the investigated thermodynamic properties, the bundled SPC models yield results in agreement with unrestrained SPC and experiments. However, differences are observed for the structural sampling of the coiled-coil dimer and the arrangement of water molecules in the α-CT active site.

2 Methods

All simulations were performed with Gromacs (Ver. 4.6.3).^21,22 The Gromos force field (53a6)²³ was used for the amino acid side chain analogues and polypeptides (Ala_n and (GS)₂). For the coiled-coil dimer and α-chymotrypsin, in addition to the Gromos 54a7 (ref. 24) force field, the Amber (99SB-ILDN)^25,26 force field was used. The SPC,²⁷ SPC/E,²⁸ or bundled SPC¹⁴ water models were used for the solvent. The temperature was maintained at 300 K using either a velocity rescaling thermostat²⁹ (time constant τ_T = 0.1 ps) or, in case of the thermodynamic integration (TI) calculations, a Langevin thermostat (SD integrator in Gromacs, τ_T = 2 ps). For constant pressure, the simulation box was isotropically scaled according to the Berendsen scheme³⁰ with a reference pressure of 1 bar, τ_p = 1 ps and compressibility 4.5 × 10⁻⁵ bar⁻¹. In the simulations with the Gromos force fields, the non-bonded interactions were truncated at 1.4 nm, with the charge-group based neighbor list updated every 20 fs. The electrostatic interactions beyond the cut-off were corrected with a reaction field approach using a dielectric constant of ε_rf = 78. In the simulations with the Amber force field, particle-mesh Ewald (PME) long-range electrostatics³¹ with a grid spacing of 0.12 nm and cubic spline interpolation was used. In these simulations, short-range electrostatic and Lennard-Jones interactions were treated with a Verlet buffered neighbor list,³² with potentials smoothly shifted to zero at a 1.0 nm cut-off. Analytical dispersion corrections were added to energy and pressure to account for the truncation of the Lennard-Jones interactions at this 1.0 nm cut-off. All constraints, including all internal degrees of freedom of the bundled water molecules, were solved with the LINCS algorithm,^33,34 apart from the simulations with the standard (non-bundled) water models, in which SETTLE³⁵ was used for the waters. The constraints allowed for an integration time step of 2 fs in the MD simulations.

2.1 Bundled SPC water

In the bundled SPC water models,^14,15 four SPC water molecules are grouped together by imposing restrictions on their relative movement. This model was developed to be consistent with the mapping scheme of the CG-Martini force field, in which four atomistic water molecules are represented by a single CG site. The bundling is achieved by using a half-harmonic distance restraining potential applied on all grouped oxygen atoms. The onset of the restraining potential was set to 0.3 nm, slightly beyond the first peak of the oxygen–oxygen radial distribution function (at 0.28 nm). In addition, the oxygen–oxygen Lennard-Jones C₁₂ repulsion parameter was altered to mitigate the effects of the restraining potential on the properties of the SPC water. The different SPC water models are compared in Table 1. Two different models, differing in the force constant for the distance restraint, k_dr, were proposed by Fuhrmans and coworkers¹⁴ and were investigated in this study. Although the alternative bundled SPC model suggested by Nagarajan and coworkers¹⁵ was not included in the present study, due to the similarity of the models, we expect that many of the reported findings are at least qualitatively relevant for that model as well.

Table 1 Parameters for the water models

Model	k dr (kJ mol^−1 nm^−2)	C 12 (kJ mol^−1 nm^12)
Bundled SPC (MOD1)	1000	3.25000 × 10^−6
Bundled SPC (MOD2)	4000	3.45000 × 10^−6
SPC	n/a	2.63413 × 10^−6

---

2.2 Potentials of mean force

Potentials of mean force (PMFs) were calculated for pairs of amino acid side chain analogues and Na⁺–Cl⁻ in SPC, SPC/E, and both bundled water models (MOD1 and MOD2). The systems used here are identical to our previous work.³⁶ The following solute pairs were simulated: apolar (Phe–Phe, Val–Val), polar (Ser–Ser, NMA–NMA) and charged (Na⁺–Cl⁻, Lys⁺–Glu⁻). The list of all amino acid side chain analogues used in this work, including those used in the hydration free energy calculations (see below), is given in Table 2.

Table 2 Amino acid analogues used in this work

Amino acid	Abbrev.	Analogue
Alanine	Ala (A)	Methane
Asparagine	Asn (N)	Acetamide
Cysteine	Cys (C)	Methanethiol
Glutamine	Gln (Q)	Propionamide
Leucine	Leu (L)	Isobutane
Methionine	Met (M)	Methyl ethyl sulfide
Backbone	NMA	n-Methylacetamide
Phenylalanine	Phe (F)	Toluene
Serine	Ser (S)	Methanol
Threonine	Thr (T)	Ethanol
Tryptophan	Trp (W)	3-Methylindole
Tyrosine	Tyr (Y)	p-Cresol
Valine	Val (V)	Propane

---

The constraint method, as outlined previously,^36,37 was used for the PMF calculations. The constraint procedure involves a set of distance constraint simulations from which the PMF is calculated as , where 〈f_c〉_r is the average force on a constraint between the centers of mass of two solute molecules separated by distance r. The PMF at R_m, the maximum distance used, is set to zero. All systems were solvated with either 2400 SPC (or SPC/E) molecules or 600 bundled SPC water clusters (corresponding to 2400 water molecules) in a periodic rhombic dodecahedron simulation box with a size of 5.0 nm. The distance range (0.25 to 2.2 nm) and spacing (0.05 nm) is identical to the previous work.³⁶ Additional distances were added in certain cases to explore in detail the local features of the PMF profiles. In total, ca. 40 constraint simulations were performed for each system. For each distance, the system was energy minimized (1000 steepest descent steps) and simulated for 11 ns, with constraint forces saved every 100 fs. For the PMF calculations, the first 1 ns of the trajectories was discarded. Statistical errors were estimated from the limiting values of the block averages,³⁸ as implemented in the g_analyze tool of the Gromacs distribution. Our results in unrestrained SPC agree with the dimerization free energies obtained by de Jong and coworkers³⁹ from counting the relative monomer/dimer populations in extended MD simulations.

2.3 Hydration free energy

Thermodynamic integration (TI) was used to determine the hydration free energies, ΔG_hyd, for the uncharged (at pH 7.0) amino acid side chain analogues listed in Table 2. Each analogue was solvated with 460 bundled SPC water clusters (corresponding to 1840 individual water molecules) in a cubic simulation box of 3.8 nm. For the free energy calculations, the number of LINCS iterations for the rotational correction was increased to 8. Both electrostatic and Lennard Jones (LJ) interactions between the solvent and the solute were gradually turned off using a coupling parameter λ. Soft-core potentials were used for to avoid singularities,

V_sc(r) = (1 − λ)V_o([ασ⁶λ + r⁶]^(1/6))

where V_o(r) is the original hard-core pair potential, σ = 0.3 nm the interaction range, and α = 0.6 the potential height. The states λ = 0 and λ = 1 are the fully coupled and uncoupled states, respectively. The basic λ-spacing was set to 0.025. However, a finer spacing of Δλ = 0.005 was used for λ ≤ 0.1 to capture the curvature of the derivative of the Hamiltonian, ∂H/∂λ, close to the early transition region. In total, 58 λ-points were simulated for 1 ns each, with ∂H/∂λ saved every 100 fs. The hydration free energy was obtained by integrating the 〈∂H/∂λ〉-over-λ curve using the trapezoidal rule. Statistical errors were estimated using block averaging (as described above), and these errors were integrated to give the total error in ΔG_hyd. The errors are below 1.8 kJ mol⁻¹ in all cases (see ESI†).

To determine the hydration enthalpies, ΔH_hyd, extended 110 ns MD simulations of the following systems were carried out: (i) the entire solute–solvent system, (ii) only solvent (comprising the same number of solvent molecules as in the entire system), and (iii) only the solute molecule in vacuo. The simulation parameters were identical to the ones described above, with the exception that instead of Langevin temperature coupling, the leap-frog integrator and the velocity rescaling²⁹ thermostat (τ_T = 0.1 ps) were used. For the simulations of the solute in vacuo, no cut-offs were used for the non-bonded interactions, and overall translation and rotation were removed. Finally, the hydration enthalpy was calculated as ΔH_hyd = 〈U_system〉 − 〈U_solvent〉 − 〈U_solute〉. The pΔV contribution, which for the simulated systems is smaller than the statistical errors,⁴⁰ was neglected. The entropy was obtained from the difference, TΔS_hyd = ΔH_hyd − ΔG_hyd. Statistical errors in ΔH_hyd and TΔS_hyd are below 1.5 and 2.1 kJ mol⁻¹, respectively, in all cases (see ESI†).

2.4 Conformational sampling of peptides

The starting structures for the poly-alanine peptides Ala₃, Ala₅ and Ala₇ as well as the (GS)₂ peptide were generated with pymol. For the Ala_n peptides, the N- and C-termini were acetylated and amidated, respectively. For (GS)₂, the termini were charged (zwitterion). The structures were solvated in 2400 SPC or 600 bundled SPC water clusters in a periodic rhombic dodecahedron unit cell of 5.0 nm. Following a short energy minimization, the systems were simulated under NpT conditions for 200 ns. Coordinates were saved every 2 ps. Final analysis was done rejecting the first 5 ns of the trajectories.

2.5 Coiled-coil dimer

The starting structure for our simulations was taken from the first model of the NMR ensemble in PDB 1U0I.⁴¹ The dimer was solvated in a periodic rhombic dodecahedron box and Na⁺ and Cl⁻ counterions were added to achieve a concentration of ≈150 mM. In the simulations with the Gromos 54a7 protein force field, we observed rapid unfolding of the helix dimer, even in standard (non-bundled) SPC. Thus, we resorted to the Amber (99SB-ILDN) force field, with either the SPC or bundled SPC water models. The final systems comprised of ca. 16 000 atoms. The systems were initially energy minimized (2000 steepest descent steps), followed by a 125 ps NVT simulation at 200 K with position restraints on all protein atoms (force constant 1000 kJ mol⁻¹ nm⁻²). Finally, for each system, three independent production simulations (different random seeds were used to generate the initial velocities) were run for 500 ns in the NpT ensemble at p = 1 bar and T = 300 K. Thus, the total accumulated simulation time of the coiled-coil is 4.5 μs.

2.6 Protein hydration

The starting structure for α-chymotrypsin was taken from PDB 4CHA.⁴² The protonation states of the titratable residues were adjusted according to pK_a values predicted by Propka.⁴³ Care was taken that all disulphide bonds were properly taken into account. His-57 was protonated on Nδ to enable the formation of the hydrogen bonds with Asp-102 and Ser-195. The overall system size was ca. 30 000 atoms. The equilibration and simulation protocol was the same as used for the coiled-coil dimer (see above), with the exception that here, simulation times were only 100 ns. As for the coiled-coil, simulations in SPC and bundled SPC models MOD1 and MOD2 were carried out with both the Gromos 54a7 and Amber 99SB-ILDN force fields. For the latter, additional simulations in TIP4P-Ew⁴⁴ water were carried out.

3 Results and discussion

3.1 Potentials of mean force

First, we will discuss the PMF profiles for apolar side chain analogues and then proceed with the polar and charged pairs.

The PMF for the Phe–Phe pair is shown in Fig. 1A. The profile in unrestrained SPC (black) shows a strong contact minimum at 0.55 nm with a relative free energy of −3.0 kJ mol⁻¹. A small barrier of 0.3 kJ mol⁻¹ at 0.85 nm is followed by a solvent-separated shallow minimum at 1.0 nm. The results for SPC/E are similar to SPC, with a slightly less deep contact minimum of −2.7 kJ mol⁻¹ (ESI†). Our Phe–Phe PMF is very similar to the benzene–benzene PMF obtained by Villa and coworkers⁴⁶ with the Gromos 53a6 force field and SPC/E water. The PMF in bundled SPC MOD1 (red) is similar to unrestrained SPC, with a few notable differences. The contact minimum is deeper (−3.9 kJ mol⁻¹), and the solvent-separated minimum is slightly shifted, lower in energy, and significantly broader. In MOD2 (blue), the first minimum is raised (to −3.1 kJ mol⁻¹) compared to MOD1. The desolvation peak (0.5 kJ mol⁻¹) is higher than in SPC, and a second shallow minimum occurs at 1.05 nm. The deviations of the PMF profiles in the bundled water models with respect to SPC are shown as inset in Fig. 1A. The overall root mean square deviation (RMSD) between the PMFs in bundled and unrestrained SPC is 0.5 and 0.1 kJ mol⁻¹ for MOD1 and MOD2, respectively (Table 3). With respect to SPC/E, these RMSDs are significantly higher (3.2 and 2.9 kJ mol⁻¹ for MOD1 and MOD2, respectively).

Fig. 1 PMFs in bundled SPC (red and blue curves for MOD1 and MOD2, respectively) as compared to the reference PMFs in unrestrained SPC (black). Insets show the deviation from the reference.

Table 3 RMSD of the PMF profiles in bundled SPC with respect to SPC and SPC/E

System	MOD1 (kJ mol^−1)		MOD2 (kJ mol^−1)
	SPC	SPC/E	SPC	SPC/E
Ser–Ser	0.4	0.2	0.5	0.4
NMA–NMA	0.3	0.3	0.4	0.5
Phe–Phe	0.5	3.2	0.1	2.9
Val–Val	0.3	1.7	0.4	1.7
Na^+–Cl^−	1.2	0.9	1.9	1.2
Lys^+–Glu^−	1.3	0.7	1.5	0.8

---

The PMF profile for Val–Val is similar to Phe–Phe, as shown in Fig. 1B. The contact minima in all water models are located at 0.5 nm. The dimers are more stable in MOD1 (−3.0 kJ mol⁻¹) and MOD2 (−3.3 kJ mol⁻¹) compared to SPC (−2.5 kJ mol⁻¹) and SPC/E (−2.0 kJ mol⁻¹). The desolvation barrier at 0.7 nm is similar, irrespective of the water model. As observed for Phe–Phe, the solvent-separated minimum is shallower and shifted by 0.15 nm in bundled water compared to SPC and SPC/E. The RMSD of the PMF profiles (inset) shows an oscillating behavior. The RMSD of the PMF profiles is very low, 0.3 and 0.4 kJ mol⁻¹ for MOD1 and MOD2, respectively. The PMFs in SPC/E are provided in ESI.†

The Ser–Ser PMF in Fig. 1C shows that, in addition to a contact minimum at 0.45 nm, an additional sharp minimum exists at a shorter distance (0.33 nm). This peculiar feature differentiates this PMF profile from the others. In unrestrained SPC (black), the free energies of these two minima are −1.1 and −0.3 kJ mol⁻¹, respectively. The relative energies in bundled SPC models MOD1 and MOD2 (+0.7 and +1.3 kJ mol⁻¹, respectively) are higher for the sharp minimum. The minimum at 0.45 nm is similar to SPC for both MOD1 and MOD2. The solvent-separated minimum is shifted from 0.75 nm in SPC to 0.95 nm in bundled SPC, although the desolvation peak remains roughly unchanged.

Fig. 1D shows the PMF for a pair of NMA molecules. The global minimum is at 0.45 nm for all solvent models, with similar free energies of the contact minima (−2.3 kJ mol⁻¹ in SPC compared to −2.7 kJ mol⁻¹ in MOD1 and −2.2 kJ mol⁻¹ in MOD2). The overall RMSDs between the PMFs in unrestrained SPC and bundled SPC are similarly low for both Ser–Ser and NMA–NMA (Table 3).

The PMFs of Na⁺–Cl⁻ are shown in Fig. 1E. In unrestrained SPC (black), a minimum at 0.25 nm (−11.4 kJ mol⁻¹) is separated by a barrier at 0.35 nm (+4.7 kJ mol⁻¹) from the second minimum at 0.50 nm (−5.3 kJ mol⁻¹). In bundled SPC, the locations of these points are similar, but the relative free energies are different. In particular, the first minimum is less deep (−7.6 and −5.8 kJ mol⁻¹ for MOD1 and MOD2, respectively). In contrast to the side chain analogues, the position of the second minimum is not shifted in bundled SPC, as a result of the small size of the ions. Due to the free energy difference between the contact minima in unrestrained and bundled SPC, the overall RMSD between the PMFs is significant, 1.2 and 1.9 kJ mol⁻¹ for MOD1 and MOD2, respectively (Table 3). In this respect, the bundled SPC models compare more favorably to unrestrained SPC/E, where the free energy of the contact minimum (−8.1 kJ mol⁻¹) is similar. This agreement is most likely due to the more similar static dielectric permittivities of SPC/E (ε_r = 71) and bundled SPC¹⁹ (ε_r = 77), whereas ε_r = 66 for SPC. Indeed, the same effect is observed for the charged Lys⁺–Glu⁻ pair (Fig. 1F), where the relative free energy of the contact minimum is −3.2 kJ mol⁻¹ for unrestrained SPC/E and both bundled SPC models, as compared to −4.3 kJ mol⁻¹ for unrestrained SPC.

In conclusion, the dimerization free energy profiles of the investigated molecules are overall very similar in bundled SPC water as compared to unrestrained SPC. One significant and recurring difference is that the solvent-separated minima are broader in bundled SPC. This may, at least to some extent, be a solvent packing effect, as reflected by the oxygen–oxygen RDF of bundled SPC itself that displays shifted and broadened minima.¹⁴ For the dimerization of larger molecules, however, we anticipate some stronger effects of the bundling potentials. For example, upon binding of two large (apolar) molecular surfaces, such as upon protein–protein encounter, bundling may well have an effect on the expulsion of the last hydration layers, since the water molecules have to get excluded from the contact interface in groups of four. Additional scenarios that, by design, cannot be expected to be captured with bundled water are files of single water molecules or interactions mediated by single water molecules, be it at protein–protein interfaces or within proteins. The performance of bundled water in simulations of a helix–helix dimer involving an apolar contact interface as well as the hydration of an enzyme active site will be discussed below.

3.2 Hydration free energy

The hydration free energies of side chain analogues in different solvent models are shown in Fig. 2 and summarized in ESI.† The values in bundled SPC are comparable with both experiment⁴⁵ and unrestrained SPC.⁴⁰ The free energies are consistently underestimated (too negative), with larger differences for polar residues. The hydration free energy for small hydrophobic side chains and Phe match the experimental values. The mean absolute error (MAE) in ΔG_hyd with respect to experiment is 2.4 and 3.7 kJ mol⁻¹ for MOD1 and MOD2, respectively (Table 4). When compared to SPC as a reference, these errors reduce to 1.0 and 2.3 kJ mol⁻¹. A close agreement between the hydration free energies in unrestrained and bundled SPC was also reported by Fuhrmans and coworkers for ΔG_hyd of butane and ethanol.¹⁴

Fig. 2 Calculated values of ΔG_hyd for side chain analogues in unrestrained SPC (black triangles, data taken from ref. 40), MOD1 (red circles) and MOD2 (blue squares) compared to experimental values⁴⁵ (black circles).

Table 4 Mean absolute errors (in kJ mol⁻¹) of ΔG_hyd, ΔH_hyd, and TΔS_hyd obtained with bundled SPC water with respect to experiment and unrestrained SPC simulations

Solvent	ΔGhyd		ΔHhyd		TΔShyd
	Expt	SPC	Expt	SPC	Expt	SPC
SPC	1.6	—	2.7	—	3.4	—
MOD1	2.4	1.0	5.4	3.7	4.4	3.1
MOD2	3.7	2.3	5.8	4.0	4.9	3.9

---

As opposed to ΔG_hyd, hydration enthalpy and entropy are more sensitive to structural rearrangements of solvent molecules in the hydration shells around the solute. The hydration enthalpy for different solvent models is shown in Fig. 3A and ESI.† The MAE for ΔH_hyd is significantly larger than for ΔG_hyd (Table 4), suggesting that error compensation led to the more favorable agreement of ΔG_hyd with experiment. This observation can be rationalized considering that hydration enthalpy is dominated by water–water interactions. The internal energy per water molecule is −33.8 and −31.6 kJ mol⁻¹ for bundled water MOD1 and MOD2, respectively, which significantly differs from unrestrained SPC (−42.0 kJ mol⁻¹). By design, the internal energy of bundled water has to be higher (less negative) due to the entropy loss as a result of the restraining potentials. Thus, when decomposing the free energy into enthalpic and entropic components, a larger degree of compensation is expected.

Fig. 3 The hydration enthalpy (A) and entropy (B) for side chain analogues in SPC (black triangles, data from ref. 40), MOD1 (red circles) and MOD2 (blue squares). Experimental values⁴⁷ are shown as black filled circles.

Hydration enthalpies are either overestimated (too positive), as in case of small hydrophobic residues, or underestimated (too negative), as observed for the polar side chains (Fig. 3A). The too positive hydration enthalpy of hydrophobic side chains in unrestrained SPC was attributed to the hydration volume and thermal expansion coefficient.⁴⁰ To confirm this, we calculated the isobaric thermal expansion coefficients, α_P, of MOD1 and MOD2. Indeed, the obtained values of 8.0 × 10⁻⁴ K⁻¹ for MOD1 and 9.0 × 10⁻⁴ K⁻¹ for MOD2 are higher than for unrestrained SPC (α_P = 7.4 × 10⁻⁴ K⁻¹), thus accounting for the observed too positive ΔH_hyd. For polar side chains, additional effects play a role, a detailed investigation of which is beyond the scope of the present work.

The hydration entropy is shown in Fig. 3B. Both bundled SPC models either under- or overestimate TΔS_hyd. The overall MAE with respect to unrestrained SPC is 3.1 and 3.9 kJ mol⁻¹ for MOD1 and MOD2, respectively. Like for the enthalpies, the hydration entropies of polar side chains are underestimated and those of the small hydrophobic side chains (Ala, Val and Leu) overestimated. As a consequence, error compensation leads to ΔG_hyd that is close to experiment. One notable exception is Phe, where both ΔH_hyd and TΔS_hyd closely match experimental values for both bundled SPC models.

3.3 Conformational sampling of peptides

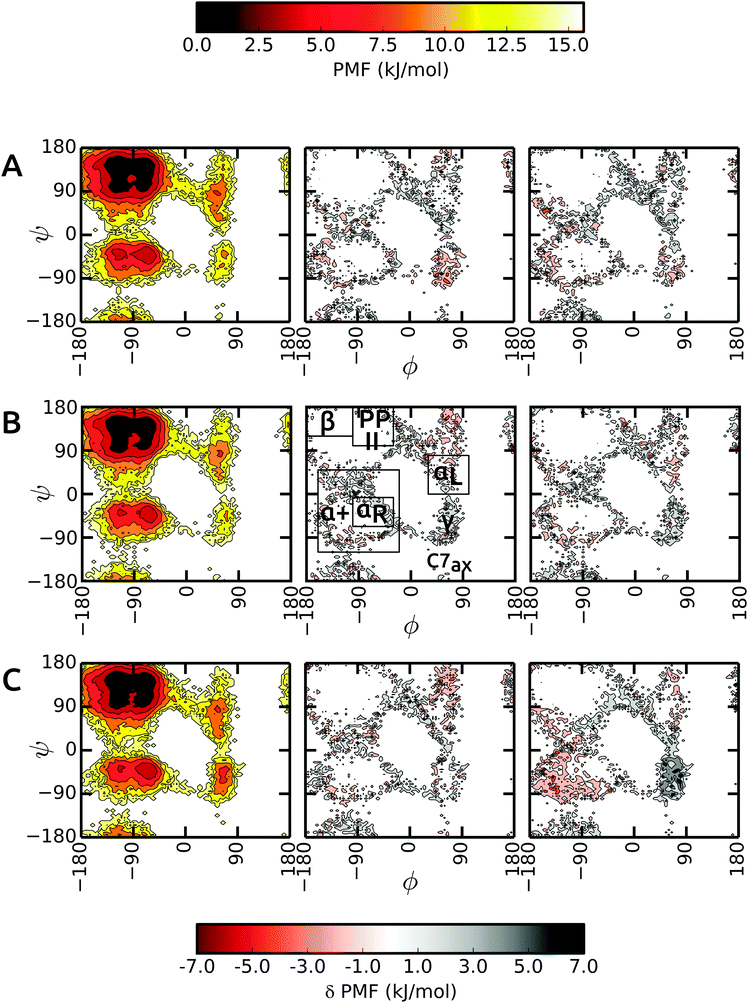
We start the discussion with the results in unrestrained SPC and then highlight the differences in bundled SPC as compared to these reference simulations. Overall, the PMFs in the investigated water models are very similar, with differences of the order of 1–2 k_BT. Fig. 4 shows the Ramachandran map of the central residues of blocked Ala₃ (A), Ala₅ (B) and Ala₇ (C). Overall, the sampling in unrestrained SPC (left panels) is similar across all peptides. For comparison, we divide the Ramachandran map in a similar way to Best and coworkers:⁴⁸α+ basin, −160° < ϕ < −20° and −120° < ψ < 50°, containing the right α-helical region α_R, −100° < ϕ < −30° and −67° < ψ < −7°; ppII basin, −100° < ϕ < −30° and 100° < ψ < 180°; β-basin −180° < ϕ < −100° and 120° < ψ < 180°; and α_L-basin located at 30° < ϕ < 100° and 0° < ψ < 80°.

Fig. 4 Comparison of backbone ϕ/ψ PMFs for the central residue in Ala₃ (A), Ala₅ (B), and Ala₇ (C). For the bundled SPC models MOD1 (middle panels) and MOD2 (right panels), the deviation from the reference PMF in unrestrained SPC (left panels) is plotted.

As observed previously,⁴⁸ the Gromos force field exhibits a broader minimum in the ppII region and a subdued C5 minimum. Additional features include two similar minima in the α+ basin. In addition, C7_ax is not well-populated with the Gromos 53a6 force field. The transition region connecting α_R and γ is slightly more prominent in the longer Ala₇, along with a more pronounced γ region (around ψ = −75°, ϕ = −90°). The sampling in Ala₃ is very similar in the bundled SPC models as depicted in Fig. 4A (middle and right panel). The major minima are well characterized. The only differences occur in the periphery of the dominant ϕ/ψ regions, which however we at least partly attribute to the larger statistical errors in these lower-populated regions at the rims of the wells. In addition, the γ region is stabilized in bundled SPC. A similar picture is obtained for Ala₅ (Fig. 4B). For Ala₇, by contrast, there are a few noticeable differences between the Ramachandran maps (Fig. 4C). In MOD2, the lower half of the α+ region is considerably more favorable compared to SPC, whereas the γ region is too high in free energy. In MOD1, the α_L region is oversampled.

The ϕ/ψ sampling was explored further by comparing the populations of the various regions (Table 5). In spite of the overall similarity, there are differences in the ppII and β regions. The ppII region is the most favored region in all polypeptides, irrespective of the solvent model. In unrestrained SPC, this region accounts for about 33% of the overall population, which is slightly higher than for bundled models MOD1 and MOD2. Furthermore, the higher propensity of ppII compared to β is more evident in SPC, where the difference between the populations is 7.1%, 5.8%, and 7.9% for Ala₃, Ala₅, and Ala₇ respectively. In bundled water, these differences are smaller (4.2%, 2.2%, and 3.5% in MOD1 and 3.1%, 2.8%, and 2.3% in MOD2). The α+ region is consistently more favored in MOD2 compared to the other solvents, with the largest difference observed for Ala₇.

Table 5 Populations of different ϕ/ψ regions in Ala_n peptides. The data is for the central residue. The number of hydrogen bonds with water molecules is also given. Statistical errors are below 2% and 0.05 for populations and H-bonds, respectively

Solute	Solvent	% α+	% αR	% αL	% ppII	% β	# hbonds
Ala3	SPC	13.6	7.0	0.9	32.7	25.6	8.1
	MOD1	14.2	7.1	0.7	30.3	26.1	8.3
	MOD2	14.5	7.2	0.7	29.2	26.1	8.4
Ala5	SPC	12.4	6.7	0.8	32.6	26.8	12.0
	MOD1	11.8	6.0	1.0	30.1	27.9	12.3
	MOD2	13.4	7.0	1.0	29.6	26.8	12.4
Ala7	SPC	11.8	6.7	1.0	33.5	25.6	15.8
	MOD1	12.0	6.6	1.1	29.8	26.3	16.3
	MOD2	16.5	8.5	1.0	28.3	26.0	16.5

---

In addition to the alanine peptides, we investigated the conformational sampling of the (GS)₂ peptide, which is frequently used in experiments as a model for flexible polypeptide linkers. Fig. 5 compares the end-to-end distance distributions in the different water models. In unrestrained SPC, the peptide explores a diverse range of compact and extended structures, with preference for the latter. In bundled SPC, these extended structures are even more favored. The populations of the compact structures (both minima at 0.35 and 0.6 nm combined) are 19%, 15%, and 14% for unrestrained SPC, MOD1 and MOD2, respectively.

Fig. 5 Distribution of end-to-end distance of (GS)₂ in SPC (black), MOD1 (red), and MOD2 (blue). The end-to-end distance is calculated between the terminal N and C atoms.

In the compact structures with 0.6 nm end-to-end distance, a single water molecule bridges the charged NH₃⁺ and COO⁻ termini. The bundling potentials make it more difficult for individual water molecules to adopt such a bridging position, hence reducing the population of this compact structure. The similar effect was also observed in an additional simulation of zwitterionic (instead of blocked) Ala₇ (results not shown). In previous simulations of (GS)₂ employing the CHARMM22 force field,⁴⁹ the compact conformation was found to be more favorable than the extended conformation, at odds with our present findings obtained with the Gromos 53a6 force field in combination with any of the used water models, including unrestrained SPC. Taken together, our results suggest that the conformational sampling in the investigated peptides is largely determined by the protein force field and less so by the water model.

3.4 First solvation shells

Next, we compare the water–peptide hydrogen bonds in the different solvent models. Table 5 (last column) shows that for all investigated alanine peptides, the average number of H-bonds is similar in all water models. To investigate the local water environment in the vicinity of the peptides in more detail, we analyzed the radial distribution of water molecules around the side chains of Ala₅ and (GS)₂. The RDFs are shown in Fig. 6. For Ala₅, the RDF of water oxygen atoms around the CH₃ group of the central Ala residue shows only one minimum at 0.53 nm in unrestrained SPC (Fig. 6A), whereas in bundled SPC, an additional shallow broad minimum at larger distances (0.75 nm) is observed. Similar results were obtained for Ala₃ and Ala₇ (data not shown). For (GS)₂, the RDF between water oxygen and the side chain Oγ atom shows a shifted and shallow second minimum in the bundled SPC models. As discussed earlier, this could be a consequence of differential solvent packing due to the bundling potentials.

Fig. 6 The RDFs between peptides and water oxygen atoms. (A) CH₃ group of central residue in Ala₅. (B) Oγ of (GS)₂ Ser residue.

3.5 Kinetics

Until now, our analysis focused solely on thermodynamic and structural properties. However, the bundling potentials could also affect the kinetics and thus the efficiency with which configurational space is sampled in the simulations. Fuhrmans and coworkers¹⁴ reported that the viscosity of the bundled SPC models is 0.85 and 0.99 mPa s for MOD1 and MOD2, respectively, which is higher than for SPC (0.5 mPa s). To investigate whether and how this difference affects the sampling efficiency, we calculated the autocorrelation functions of the end-to-end distances in Ala₅ and (GS)₂ (Fig. 7). Since the transitions between compact and extended structures, as described by the end-to-end distance, involve some dislocation of solvent molecules, we expected that this property would be sensitive to solvent viscosity. Indeed, the autocorrelation functions in Fig. 7 show that sampling is slowed down in bundled SPC. For Ala₅, single-exponential fits of the autocorrelation decay yielded time constants of 240, 420, and 400 ps in unrestrained SPC, MOD1, and MOD2, respectively; the corresponding values for (GS)₂ are 128, 234, and 243 ps. This observed retardation correlates with the roughly 2-fold higher viscosity of bundled water.

Fig. 7 Autocorrelation of the end to end distances of Ala₅ (solid) and (GS)₂ (dashed) peptides in SPC (black), MOD1 (red) and MOD2 (blue).

3.6 Coiled-coil dimer

The dimeric coiled-coil represents a challenging test case for protein force fields, as described previously.^48,50 Here, we probe the influence of different water models, including bundled SPC. The dimer structure comprises of two helices that form an interface via a stretch of hydrophobic Ala, Ile, and Leu residues, whereas charged residues (Glu and Lys) are exposed to the solvent. In light of the results from our free energy calculations (see above), we expect that this specific arrangement of hydrophobic and hydrophilic residues renders this system susceptible to solvation effects. In particular, it can be assumed that entropic contributions due to the rearrangement of water molecules around the hydrophobic residues play an important role for the assembly of the helix dimer. The specific details of this rearrangement may be altered by the bundling potentials. Our choice of the coiled-coil dimer as a suitable, sensitive system to study subtle effects of the solvent model is further supported by previous simulations, which showed that this coiled-coil helix dimer is, in many force fields, only marginally stable as compared to alternative conformations.^48,50 The native contact analysis (Fig. 8) shows that in unrestrained SPC, the coiled-coil structure and dimer interface are very well preserved on the time scale of the simulations. The deviations from the first structure in the NMR ensemble are minor and comparable to the differences between the different structures in the NMR ensemble itself (inset). We thus conclude that in SPC, the coiled-coil merely undergoes thermal fluctuations around a minimum-energy conformation that closely resembles the NMR structure. This is also supported by the backbone RMSD analysis, see ESI.†

Fig. 8 Native contacts of the coiled-coil dimer structure in the course of the MD simulations, using the first model in the NMR ensemble as a reference. Native contacts were calculated according to Best et al.⁵¹ The time traces in (A)–(C) show the three independent simulations (colored in cyan, green, and magenta) in SPC, MOD1, and MOD2, respectively. The inset in (A) shows the variation of the 20 structures in the NMR ensemble. (D) Probability distributions, obtained from the final 200 ns of each simulation.

By contrast, in bundled SPC, large structural deviations were observed (Fig. 8B and C). These deviations involve partial unfolding of the helices and an increase in the solvent-accessible surface area. For both MOD1 and MOD2, a very large degree of unfolding was observed in one out of three simulations, although significant deviations were observed in all cases (Fig. 8D). These results show that the bundling restraints can have a dramatic effect in certain, sensitive cases in which several, structurally diverse states that are comparable in free energy are kinetically accessible during the simulations.

3.7 Protein hydration

Finally, to further investigate local solvation effects, we switch to the active site of the serine protease α-chymotrypsin (α-CT). This active site constitutes a complex and confined environment and is thus a challenging test case for the bundled water models, in particular also because water molecules inside proteins usually do not tend to occur in groups of four. As shown in Fig. 9, the catalytic triad (His-57, Asp-102, Ser-195) is located between two β-barrels at the enzyme surface and is accessible to the solvent. In the X-ray crystal structure, electron density could be resolved for several water molecules close to the active site,⁴² see Fig. 9. Water plays a crucial role in the enzymatic mechanism, because as part of the mammalian digestive system, α-CT selectively hydrolyzes peptide bonds next to large hydrophobic residues.⁵² The function of the enzyme is achieved by a charge relay system formed by a hydrogen bond network involving the catalytic triad residues.

Fig. 9 Structure of α-chymotrypsin with the catalytic triad (His-57, Asp-102, Ser-195). Crystallographic waters involved in hydrogen bonding with residues in the triad are shown in ball-and-stick representation.

In all solvent models, the overall protein structure is stable on the 100 ns simulation time scale, as evident from the backbone RMSD (Fig. 10A). Stable protein structures in bundled SPC simulations have also been reported previously for lysozyme¹⁴ and ubiquitin.²⁰Fig. 10B and C show the distance distributions of the hydrogen bonds between catalytic triad residues. In standard (non-bundled) SPC, the Ser-195–His-57 hydrogen bond is established for 60% of the simulation time (using cut-offs of 0.35 nm for the donor–acceptor distance and 30 degrees for the hydrogen–donor–acceptor angle, respectively). Likewise, the Asp-102–His-57 hydrogen bond is very stable in SPC, with one hydrogen bond present for 81% of the total simulation time, and even two hydrogen bonds (both carboxylic acid oxygens hydrogen-bonding to the His-57 NH) established in 36% of the frames. Both, the Ser-195–His-57 and the Asp-102–His-57 hydrogen bonds are significantly destabilized in bundled SPC. For bundled SPC models MOD1 and MOD2, the Ser-195–His-57 hydrogen bond occupancy drops to 20% and 10%, respectively. For the single and double Asp-102–His-57 hydrogen bonds, the percentages drop to 58%/35% and 21%/16% for MOD1 and MOD2, respectively.

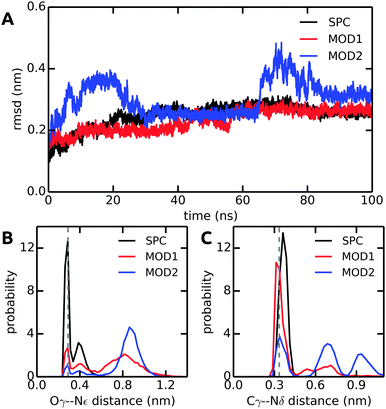Fig. 10 Comparison of structural parameters of α-CT in unrestrained SPC, MOD1, and MOD2. (A) Backbone RMSD. (B) Ser-195 Oγ–His-57 Nε distance distribution. (C) Asp-102 Cγ–His-57 Nδ distance distribution. The distances in the X-ray crystal structure are shown as dashed lines. The results shown here were obtained with the Gromos 54a7 force field; see ESI† for the corresponding Amber 99SB-ILDN results.

To investigate the reasons for this differential stability of the hydrogen bonds between catalytic triad residues and to more thoroughly characterize the hydration of the active site, we analyzed the water molecules in the catalytic triad region. Upon setting up our simulations from the crystal structure, all crystallographic water molecules were removed, since it was not feasible to include them in the bundled SPC setup.‡ In the course of the MD simulations, the active site readily became rehydrated. First, we counted the number of water oxygen atoms within 0.6 nm of the center of mass of His-57, which is close to the geometric center of the active site. A water molecule was counted if its oxygen atom was within this cut-off. The analysis was repeated with different cut-offs (between 0.5 and 0.75 nm), with qualitatively similar results (data not shown). For unrestrained SPC, an average of 3.1 water molecules were found close to the catalytic triad, similar to the number of water molecules resolved in the crystal structure (Table 6). By contrast, for bundled SPC, an average of 4.5 and 10.9 water molecules (in MOD1 and MOD2, respectively) populate the active site region. This pronounced difference is also reflected in the number of hydrogen bonds that these water molecules form with the active site residues (Table 6). Due to their larger number, bundled SPC water molecules more successfully compete with intra-residue hydrogen bonds and form more hydrogen bonds with active site residues than standard SPC.

Table 6 Average number of waters in the active site and hydrogen bonds between water and catalytic triad residues

	# water	# hbonds
		Ser-195		Asp-102		His-57
		Backbone	Side chain	Back bone	Side chain	Back bone	Side chain
X-ray^42	4.0	1.0	1.0	1.0	—	1.0	—
SPC	3.1	0.3	1.6	0.3	1.0	1.2	0.7
MOD1	4.5	0.2	1.8	0.0	1.8	1.2	1.9
MOD2	10.9	1.0	1.6	0.1	3.4	1.6	2.4

---

In addition, to characterize the dynamics of the active site hydration, we analyzed the residence times of the water molecules in the vicinity of the catalytic triad region. This was done by counting the time periods (τ_i) that every unique water molecule spend within the cut-off sphere, as defined above. These time periods were accumulated, i.e., also included rebinding of water molecules to the active site region. A mean residence time defined was as 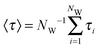.^53,54 In standard (non-bundled) SPC, more than 4300 unique water molecules (out of the total 8546 water molecules in the simulation box) visited the active site region during the 100 ns simulation, indicating that the active site hydration was well sampled on this time scale. Most of the active site water molecules stayed for less than 0.1 ns before exchanging with bulk waters, with a mean residence time of only 66 ps. The maximum residence time observed for any of the water molecules was 2.5 ns. By contrast, in the bundled SPC simulations, fewer unique water molecules visited the active site region (2609/8536 and 2815/8536 for MOD1 and MOD2, respectively), and the mean residence times were slightly longer (164 and 370 ps for MOD1 and MOD2, respectively). However, in this case, these mean residence times are less meaningful, since—unlike for standard SPC—the distributions are skewed and have a significant contribution of the long-time regime. Most strikingly, the maximum residence time found for a single water molecule belonging to a bundled 4-water cluster was 12 ns for MOD1, and even 87 ns for MOD2. Such long water residence times could overcompensate any speed-up of a hybrid AA/CG set-up, at least if one is interested in properties related to active site hydration. The slow down of water exchange kinetics may result from the fact that, to access or leave the partially buried active site region, the clusters of 4 water molecules have to deform, which is energetically penalized by the bundling distance restraints.

4 Summary and conclusions

In this work, we have critically evaluated two different bundled SPC water models as solvents for biomolecular systems. These bundled water models, which differ in the strength of the distance restraining potentials used to bundle the water molecules in groups of four, have previously been used in hybrid AA/CG adaptive resolution multiscale simulations,^15,19,20 because they enable the group-wise mapping of several AA solvent molecules to a single supra-molecular CG solvent molecule upon diffusional exchange across the resolution boundary. To investigate the effects of the bundling potentials in the absence of possible additional effects due to an AA/CG boundary, we carried out fully atomistic simulations in bundled SPC. A systematic approach was adopted to study both, thermodynamic (for small molecules) as well as structural properties (for larger biomolecular systems). To assess the performance of the bundled water models, the results were compared with simulations in standard (unrestrained) water as well as with experimental data, where available. For the investigated thermodynamic properties, such as potentials of mean force (PMF) between pairs of amino acid side chains in water as well as hydration free energies of uncharged side chains, we found a good agreement between bundled SPC and standard water models, with minor differences of the order of 1–2 k_BT. Likewise, the conformational space sampled by the polyalanine peptides Ala₃, Ala₅, and Ala₇ is very similar in all water models. We attribute this close agreement to the observation that also in bundled water, the largely tetrahedral structure of hydrogen bonds is well-preserved and the orientational polarization of the water molecules by the environment is realistically described.^14,15 For the more polar (GS)₂ peptide, in bundled SPC, more extended conformations are favored over compact conformations, because single bundled water molecules do not readily adopt a bridging position between the peptide termini. Small differences were also found for the structure of the first solvation shells around the peptides. In terms of sampling efficiency, for the investigated peptides, the bundled SPC water models are slightly less efficient than standard SPC, with a slow-down in the kinetics by a factor of ca. 2.

Significant differences between the water models were found for the larger biomolecular systems studied, such as the structure of the dimeric coiled-coil protein and the hydration of the active site of the enzyme α-chymotrypsin. For the coiled-coil dimer, severe structural distortions and loss of native contacts occurred in the bundled SPC simulations, but not in standard (unrestrained) SPC. These results suggest that, for sensitive systems in which the natively folded state is thermodynamically and kinetically only marginally more stable than alternative conformations, subtle solvation effects due to water bundling can have a pronounced influence on the structural ensemble sampled in the simulations. Likewise, we observed differences between the solvent models for the hydration of the active site of α-chymotrypsin, which is located close to the enzyme surface and accessible to solvent. In bundled water, a larger number of water molecules entered the active site region, leading to the formation of more hydrogen bonds between water and catalytic triad residues at the cost of intra-residue hydrogen bonds. Nevertheless, the overall structure of the enzyme was highly stable, irrespective of the solvent model used in the simulations. The α-chymotrypsin structure is less vulnerable to solvent effects, because in contrast to the coiled-coil dimer, it has a very stable fold including several disulphide bonds. In addition, the exchange of water molecules between the active site and the bulk was hindered for bundled water, with a maximum residence time of tens of ns, as opposed to 2 ns for standard SPC. This kinetic trap may impose severe sampling limitations, especially for the hydration dynamics of partially buried regions. In general, for the investigated thermodynamic, kinetic, as well as structural properties, out of the two bundled SPC models studied (MOD1 and MOD2), the model with the larger force constant of the bundling potential (MOD2) yielded slightly inferior results, although the major differences were observed between bundled and non-bundled (standard) water.

In conclusion, our results show that hybrid multiscale simulation approaches involving bundled water as inner shell solvent can, for some biomolecular systems, be comparably accurate as conventional fully atomistic models. At the same time, the shortcomings of the bundled water models become evident, for example in processes where the molecular nature of individual single waters plays a crucial role, such as the solvation of the α-chymotrypsin active site described here, single-file water molecules (e.g., in aquaporins or nanotubes), or interactions mediated by single waters (e.g., in protein–ligand binding). However, using bundled water may also not be recommendable in situations where its limitations are less obvious, as highlighted by our simulations of the coiled-coil dimer. Thus, it remains to be carefully tested for every simulation system beforehand whether it is recommendable to use bundled water as inner shell solvent in a multiscale setup.

Acknowledgements

The German Research Foundation supported this work (Cluster of Excellence RESOLV (EXC 1069), Emmy Noether grant SCHA1574/3-1 to L.S.).

References

1. M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652.
2. R. O. Dror, R. M. Dirks, J. P. Grossman, H. Xu and D. E. Shaw, Annu. Rev. Biophys., 2012, 41, 429–452.
3. W. F. van Gunsteren, D. Bakowies, R. Baron, I. Chandrasekhar, M. Christen, X. Daura, P. Gee, D. P. Geerke, A. Glättli, P. H. Hünenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. A. van der Vegt and H. B. Yu, Angew. Chem., Int. Ed., 2006, 45, 4064–4092.
4. Coarse-Graining of Condensed Phase and Biomolecular Systems, ed. G. A. Voth, CRC Press/Taylor and Francis, Boca Raton, FL, 2009.
5. H. I. Ingólfsson, C. A. Lopez, J. J. Uusitalo, D. H. de Jong, S. M. Gopal, X. Periole and S. J. Marrink, WIRES Comput. Mol. Sci., 2014, 4, 225–248.
6. G. S. Ayton, W. G. Noid and G. A. Voth, Curr. Opin. Struct. Biol., 2007, 17, 192–198.
7. C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357–4366.
8. C. F. Abrams, J. Chem. Phys., 2005, 123, 234101.
9. M. Praprotnik, L. Delle Site and K. Kremer, J. Chem. Phys., 2005, 123, 224106.
10. M. Praprotnik, L. Delle Site and K. Kremer, Annu. Rev. Phys. Chem., 2008, 59, 545–571.
11. A. Heyden and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 217–221.
12. B. Ensing, S. O. Nielsen, P. B. Moore, M. L. Klein and M. Parrinello, J. Chem. Theory Comput., 2007, 3, 1100–1105.
13. M. Praprotnik, S. Matysiak, L. Delle Site, K. Kremer and C. Clementi, J. Phys.: Condens. Matter, 2007, 19, 292201.
14. M. Fuhrmans, B. P. Sanders, S. J. Marrink and A. H. de Vries, Theor. Chem. Acc., 2009, 125, 335–344.
15. A. Nagarajan, C. Junghans and S. Matysiak, J. Chem. Theory Comput., 2013, 9, 5168–5175.
16. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
17. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810.
18. D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697.
19. J. Zavadlav, M. N. Melo, S. J. Marrink and M. Praprotnik, J. Chem. Phys., 2014, 140, 054114.
20. J. Zavadlav, M. N. Melo, A. V. Cunha, A. H. de Vries, S. J. Marrink and M. Praprotnik, J. Chem. Theory Comput., 2014, 10, 2591–2598.
21. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
22. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
23. C. Oostenbrink, A. Villa, A. E. Mark and W. F. van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676.
24. N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843–856.
25. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725.
26. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
27. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces, ed. B. Pullman, D. Reidel Publishing, 1981, pp. 331–338.
28. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
29. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
30. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
31. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
32. S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650.
33. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
34. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
35. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
36. T. A. Wassenaar, H. I. Ingólfsson, M. Prieß, S. J. Marrink and L. V. Schäfer, J. Phys. Chem. B, 2013, 117, 3516–3530.
37. B. Hess, C. Holm and N. F. A. van der Vegt, J. Chem. Phys., 2006, 124, 164509.
38. B. Hess, J. Chem. Phys., 2002, 116, 209–217.
39. D. H. de Jong, X. Periole and S. J. Marrink, J. Chem. Theory Comput., 2012, 8, 1003–1014.
40. B. Hess and N. F. A. van der Vegt, J. Phys. Chem. B, 2006, 110, 17616–17626.
41. D. A. Lindhout, J. R. Litowski, P. Mercier, R. S. Hodges and B. D. Sykes, Biopolymers, 2004, 75, 367–375.
42. H. Tsukada and D. M. Blow, J. Mol. Biol., 1985, 184, 703–711.
43. H. Li, A. D. Robertson and J. H. Jensen, Proteins, 2005, 61, 704–721.
44. H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678.
45. R. Wolfenden, L. Andersson, P. M. Cullis and C. C. Southgate, Biochemistry, 1981, 20, 849–855.
46. A. Villa, C. Peter and N. F. A. van der Vegt, J. Chem. Theory Comput., 2010, 6, 2434–2444.
47. G. Makhatadze and P. L. Privalov, J. Mol. Biol., 1993, 232, 639–659.
48. R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273.
49. F. Rao and M. Spichty, J. Comput. Chem., 2012, 33, 475–483.
50. R. B. Best, K. A. Merchant, I. V. Gopich, B. Schuler, A. Bax and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18964–18969.
51. R. B. Best, G. Hummer and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17874–17879.
52. L. Hedstrom, Chem. Rev., 2002, 102, 4501–4523.
53. I. Muegge and E. W. Knapp, J. Phys. Chem., 1995, 99, 1371–1374.
54. A. R. Bizzarri and S. Cannistraro, J. Phys. Chem. B, 2002, 106, 6617–6633.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04784b

‡ It would of course be possible – and in fact is usually recommendable – to retain the crystal waters in the simulations with standard (non-bundled) water, but for consistency we decided to remove them in these cases as well.

---