Calculating limits of detection and defining working ranges for multi-signal calibration methods

Abstract

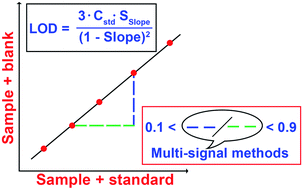
Multi-signal calibration methods, such as multi-energy calibration (MEC) and multi-isotope calibration (MICal), have increasingly been used to improve the efficiency of spectrochemical instrumental analyses. As MEC and MICal are adopted by an increasing number of laboratories, questions on their working ranges, the most appropriate calibration standard concentration (C_std) to be used, and the best approach to calculate limits of detection (LOD) and quantification (LOQ) have been raised. In this study, we evaluate the effects of working with different combinations of C_std and analyte concentration in the sample (C_sam) on the accuracy of MEC and MICal. Chromium, Cu and Mo are used as models for MEC determinations by microwave-induced plasma optical emission spectrometry (MIP OES) and inductively coupled plasma OES (ICP OES), and MICal determinations by ICP mass spectrometry (ICP-MS), respectively. We use the error propagation approach to determine LODs and LOQs, evaluate the effect of employing different values of C_std in these calculations, and compare the results with those from external standard calibration (EC) using the IUPAC approach. Finally, we apply MEC and MICal to analyze certified reference materials and compare the results with those from the traditional standard additions (SA) method. Although presenting usually higher LODs and LOQs compared to EC, MEC and MICal generally provide trueness similar to, and sometimes better than, SA. LOD and LOQ calculations based on the error propagation approach provide robust results, and trueness and precision depend on the calibration slope and the analyte level in the sample. The best results for MEC and MICal are found when working within the 0.1 < calibration slope < 0.9 range. A simple pre-analysis test comparing the analytical signal recorded for the sample (I_sam) and a calibration standard (I_std) may ensure such conditions if 0.11 < I_sam/I_std < 9.00. MEC and MICal are simple and efficient alternatives to EC and SA. They are particularly effective for minimizing matrix effects and analyzing complex-matrix samples.