A spectrum of p-atic symmetries and defects in confluent epithelia

Abstract

Topological defects provide a unifying language to describe how orientational order breaks down in active and living matter. Considering cells as elongated particles confluent, epithelial tissues can be interpreted as nematic fields and their defects have been linked to extrusion, migration, and morphogenetic transformations. Yet, epithelial cells are not restricted to nematic order: their irregular shapes can express higher rotational symmetries, giving rise to $p$-atic order with $p>2$. Here we introduce a framework to extract $p$-atic fields and their defects directly from experimental images. Applying this method to MDCK cells, we find that all symmetries from $p=2$ to $p=6$ generate 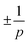$\pm \frac{1}{p}$ defects. Surprisingly, the statistics reveal an even–odd asymmetry, with odd $p$ producing more defects than even $p$, consistent with geometric frustration arguments based on tilings. In contrast, no strong positional or orientational correlations are found between nematic and hexatic defects, suggesting that different symmetries coexist largely independently. These results demonstrate that epithelial tissues should not be described by nematic order alone, but instead host a spectrum of $p$-atic symmetries. Our work provides experimental evidence for this multivalency of order and offers a route to test and refine emerging $p$-atic liquid crystal theories of living matter.