Effective patchiness from critical points of a coarse-grained protein model with explicit shape and charge anisotropy
Abstract
Colloidal model systems are successful in rationalizing emergent phenomena like aggregation, rheology and phase behaviour of protein solutions. Colloidal theory in conjunction with isotropic interaction models is often employed to estimate the stability of such solutions. In particular, a universal criterion for the reduced second virial coefficient at the critical point 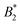 is frequently invoked which is based on the behavior of short-range attractive fluids (Noro–Frenkel rule,
is frequently invoked which is based on the behavior of short-range attractive fluids (Noro–Frenkel rule, 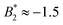 ). However, if anisotropic models for the protein–protein interaction are considered, e.g. the Kern–Frenkel (KF) patchy particle model, the value of the
). However, if anisotropic models for the protein–protein interaction are considered, e.g. the Kern–Frenkel (KF) patchy particle model, the value of the 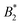 criterion is shifted to lower values and explicitly depends on the number of patches. If an explicit shape anisotropy is considered, as e.g. in a coarse-grained protein model, the normalization of
criterion is shifted to lower values and explicitly depends on the number of patches. If an explicit shape anisotropy is considered, as e.g. in a coarse-grained protein model, the normalization of 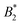 becomes ambiguous to some extent, as no unique exclusion volume can be defined anymore. Here, we investigate a low-resolution, coarse-grained model for the globular protein bovine serum albumin (BSA) and study effects of charge-anisotropy on the phase diagram (determined by simulations) at the isoelectric point. We present methods of assigning an “effective patchiness” to our protein model by comparing its critical properties to the KF model. We find that doubling the native charges increases the critical temperature Tc by ≈14% and that our BSA model can be compared to a 3 to 5 patch KF model. Finally, we argue that applying existing
becomes ambiguous to some extent, as no unique exclusion volume can be defined anymore. Here, we investigate a low-resolution, coarse-grained model for the globular protein bovine serum albumin (BSA) and study effects of charge-anisotropy on the phase diagram (determined by simulations) at the isoelectric point. We present methods of assigning an “effective patchiness” to our protein model by comparing its critical properties to the KF model. We find that doubling the native charges increases the critical temperature Tc by ≈14% and that our BSA model can be compared to a 3 to 5 patch KF model. Finally, we argue that applying existing 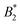 criteria from colloidal theory should be done with care, due to multiple, physically plausible ways of how to assign effective diameters to shape-anisotropic models.
criteria from colloidal theory should be done with care, due to multiple, physically plausible ways of how to assign effective diameters to shape-anisotropic models.

- This article is part of the themed collection: Colloidal interactions, dynamics and rheology


 Please wait while we load your content...
Please wait while we load your content...