Rayleigh anomaly induced phase gradients in finite nanoparticle chains

Abstract

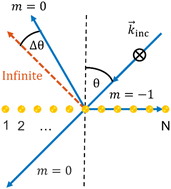
Collective optical interactions in infinite nanoparticle arrays have been studied intensively over the past decade. However, analysis of finite arrays has received significantly less attention. Here, we theoretically and numerically show that the collective interaction in finite nanoparticle chains can support phase gradients that shift the diffraction pattern with respect to infinite chains. Specifically, we demonstrate that this phenomenon occurs for resonating nanoparticles in a narrow spectral range around the Rayleigh anomaly condition, i.e., when a certain diffraction order radiates at a grazing angle. This reveals that the Rayleigh anomaly, which is associated with intensity changes, can also induce angular anomalies in finite arrays. To study the effect theoretically, we develop a novel analytical approach based on the discrete dipole approximation. Within this framework, we find an approximate closed-form solution to the particles’ dipole moments. We show that our solution can be expressed in two different ways, one based on a combinatorial calculation, and the other on a recursive calculation, and discuss the unique physical interpretation emerging from each of them. Our results are of potential importance in a wide range of practical applications from LIDARs to beam shaping schemes.