Motion of an active particle with dynamical disorder
Abstract
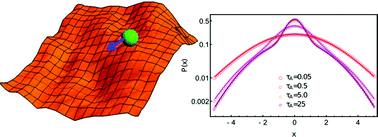
We propose a model for investigating the motion of a single active particle in a heterogeneous environment where the heterogeneity may arise due to crowding, conformational fluctuations and/or slow rearrangement of the surroundings. Describing the active particle in terms of the Ornstein–Uhlenbeck process (OUP) and incorporating heterogeneity in a thermal bath using two separate models, namely “diffusing diffusivity” and “switching diffusion”, we explore the essential dynamical properties of the particle for its one-dimensional motion. In addition, we show how the dynamical behavior is controlled by dynamical variables associated with active noise such as strength and persistence time. Our model is relevant in the context of single particle dynamics in a crowded environment, driven by activity.


 Please wait while we load your content...
Please wait while we load your content...