Colloidal clustering and diffusion in a convection cell array
Abstract
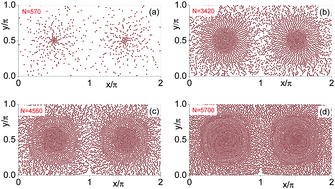
We numerically investigated the clustering of a uniform suspension of finite-size disks in a linear array of two-dimensional convection cells. We observed that, due to steric interactions, the disks tend to form coherently rotating spatial structures at the center of each cell, as a combined effect of advection and pair collisions. Micellar, ring-like and hexatic patterns emerge in the deterministic regime, depending on the suspension density, but dissolve in the presence of thermal fluctuations. Moreover, pair collisions suffice to activate cell crossings even by noiseless disks and, therefore, cause athermal diffusion. The robustness of such collision induced effects is studied against the opposing action of thermal noise, transverse biases, and particle self-propulsion.


 Please wait while we load your content...
Please wait while we load your content...