The contact angle of an evaporating droplet of a binary solution on a super wetting surface

Abstract

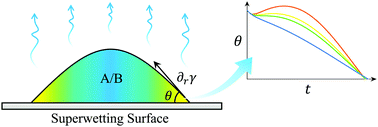
We study the dynamics of the contact angle of a droplet of a binary solution evaporating on a super wetting surface. Recent experiments have shown that although the equilibrium contact angle of such a droplet is zero, the contact angle can show complex time dependence before reaching the equilibrium value. We analyse such phenomena by extending our previous theory for the dynamics of an evaporating single component droplet to a double component droplet. We show that the time dependence of the contact angle can be quite complex. Typically, it first decreases slightly, and then increases and finally decreases again. Under certain conditions, we find that the contact angle remains constant over a certain period of time during evaporation. We study how the plateau or peak contact angle depends on the initial composition and the humidity. This theory explains the experimental results reported previously.