Topological principles of protein folding

Abstract

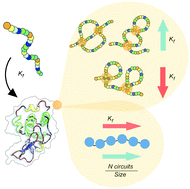
What is the topology of a protein and what governs protein folding to a specific topology? This is a fundamental question in biology. The protein folding reaction is a critically important cellular process, which is failing in many prevalent diseases. Understanding protein folding is also key to the design of new proteins for applications. However, our ability to predict the folding of a protein chain is quite limited and much is still unknown about the topological principles of folding. Current predictors of folding kinetics, including the contact order and size, present a limited predictive power, suggesting that these models are fundamentally incomplete. Here, we use a newly developed mathematical framework to define and extract the topology of a native protein conformation beyond knot theory, and investigate the relationship between native topology and folding kinetics in experimentally characterized proteins. We show that not only the folding rate, but also the mechanistic insight into folding mechanisms can be inferred from topological parameters. We identify basic topological features that speed up or slow down the folding process. The approach enabled the decomposition of protein 3D conformation into topologically independent elementary folding units, called circuits. The number of circuits correlates significantly with the folding rate, offering not only an efficient kinetic predictor, but also a tool for a deeper understanding of theoretical folding models. This study contributes to recent work that reveals the critical relevance of topology to protein folding with a new, contact-based, mathematically rigorous perspective. We show that topology can predict folding kinetics when geometry-based predictors like contact order and size fail.