A global transform for the general formulation of liquid viscosities with significant linearizing benefits: a case study on ionic liquid mixtures†
Abstract
Among the different thermophysical properties of significant importance in the study of transport phenomena, viscosity has long defied attempts at presenting a unified model applicable to both pure compounds and binary mixtures within extended temperature and composition ranges. Similar to the role that ln(Psat.)–T−1 profiles play in linearizing vapor pressure data, here it is contended for the first time that it is highly beneficial to study viscosity in the 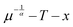 space, as opposed to the commonly used logarithmic space. Within this framework, the groundbreaking Lewis–Squires model is modified and extended to mixtures by studying 184 binary systems with 89 distinct ILs and 17 polar and nonpolar solutes. The dataset covers a total of 1104 isotherms with 10 909 data points, having quite an extensive range of viscosities, from 0.447 to 113 733 (mPa s). Breaking a highly regarded convention upheld for decades, the proposed model does not stipulate the availability of pure state viscosity and/or volumetric data over the whole temperature range, which acts as a bottleneck for the current literature models that have all been cast in the same mold inspired by thermodynamic mixing rules. In practice, without utilizing any volumetric properties, a single pure solvent viscosity datum at any reference temperature is the only requirement in the interpolative mode, which is complemented by the binary viscosity data at the reference isotherm of choice in the extrapolative mode of the proposed model that is concurrently applicable to both pure components and binary mixtures. An AARD of 2.82% was obtained in estimating the binary viscosity data using the new algorithm, while deviations of 13.58%, 6.79%, 6.17%, and 3.41% were obtained for the Grunberg and Nissan, Fang and He, Jouyban–Acree, and Eyring-MTSM models, respectively. Moreover, for extrapolation of the binary data measured at room temperature, a capability exclusive to the proposed model, an overall AARD of 5.66% was obtained for the mixtures of interest. With significant inherent flexibility, the new methodology could also be employed to represent the uncommon composition dependence of certain IL systems exhibiting multiple local extrema, with AARDs close to half of those of the current models.
space, as opposed to the commonly used logarithmic space. Within this framework, the groundbreaking Lewis–Squires model is modified and extended to mixtures by studying 184 binary systems with 89 distinct ILs and 17 polar and nonpolar solutes. The dataset covers a total of 1104 isotherms with 10 909 data points, having quite an extensive range of viscosities, from 0.447 to 113 733 (mPa s). Breaking a highly regarded convention upheld for decades, the proposed model does not stipulate the availability of pure state viscosity and/or volumetric data over the whole temperature range, which acts as a bottleneck for the current literature models that have all been cast in the same mold inspired by thermodynamic mixing rules. In practice, without utilizing any volumetric properties, a single pure solvent viscosity datum at any reference temperature is the only requirement in the interpolative mode, which is complemented by the binary viscosity data at the reference isotherm of choice in the extrapolative mode of the proposed model that is concurrently applicable to both pure components and binary mixtures. An AARD of 2.82% was obtained in estimating the binary viscosity data using the new algorithm, while deviations of 13.58%, 6.79%, 6.17%, and 3.41% were obtained for the Grunberg and Nissan, Fang and He, Jouyban–Acree, and Eyring-MTSM models, respectively. Moreover, for extrapolation of the binary data measured at room temperature, a capability exclusive to the proposed model, an overall AARD of 5.66% was obtained for the mixtures of interest. With significant inherent flexibility, the new methodology could also be employed to represent the uncommon composition dependence of certain IL systems exhibiting multiple local extrema, with AARDs close to half of those of the current models.



 Please wait while we load your content...
Please wait while we load your content...