Direction reversing active Brownian particle in a harmonic potential
Abstract
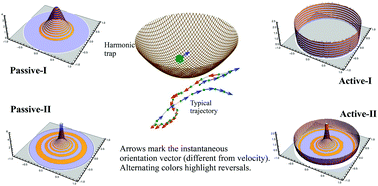
We study the two-dimensional motion of an active Brownian particle of speed v0, with intermittent directional reversals in the presence of a harmonic trap of strength μ. The presence of the trap ensures that the position of the particle eventually reaches a steady state where it is bounded within a circular region of radius v0/μ, centered at the minimum of the trap. Due to the interplay between the rotational diffusion constant DR, reversal rate γ, and the trap strength μ, the steady state distribution shows four different types of shapes, which we refer to as active-I & II, and passive-I & II phases. In the active-I phase, the weight of the distribution is concentrated along an annular region close to the circular boundary, whereas in active-II, an additional central diverging peak appears giving rise to a Mexican hat-like shape of the distribution. The passive-I is marked by a single Boltzmann-like centrally peaked distribution in the large DR limit. On the other hand, while the passive-II phase also shows a single central peak, it is distinguished from passive-I by a non-Boltzmann like divergence near the origin. We characterize these phases by calculating the exact analytical forms of the distributions in various limiting cases. In particular, we show that for DR ≪ γ, the shape transition of the two-dimensional position distribution from active-II to passive-II occurs at μ = γ. We compliment these analytical results with numerical simulations beyond the limiting cases and obtain a qualitative phase diagram in the (DR, γ, μ−1) space.


 Please wait while we load your content...
Please wait while we load your content...