Trapping, gliding, vaulting: transport of semiflexible polymers in periodic post arrays

Abstract

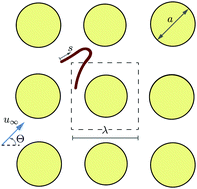
The transport of deformable particles through porous media underlies a wealth of applications ranging from filtration to oil recovery to the transport and spreading of biological agents. Using direct numerical simulations, we analyze the dynamics of semiflexible polymers under the influence of an imposed flow in a structured two-dimensional lattice serving as an idealization of a porous medium. This problem has received much attention in the limit of reptation and for long-chain polymer molecules such as DNA that are transported through micropost arrays for electrophoretic chromatographic separation. In contrast to long entropic molecules, the dynamics of elastic polymers results from a combination of scattering with the obstacles and flow-induced buckling instabilities. We identify three dominant modes of transport that involve trapping, gliding and vaulting of the polymers around the obstacles, and we reveal their essential features using tools from dynamical systems theory. The interplay of these scattering dynamics with transport and deformations in the imposed flow results in the long-time asymptotic dispersion of the center of mass, which we quantify in terms of a hydrodynamic dispersion tensor. We then discuss a simple yet efficient chromatographic device that exploits the competition between different modes of transport to sort filaments in a dilute suspension according to their lengths.