Integral equation theory for a mixture of spherical and patchy colloids: analytical description

Abstract

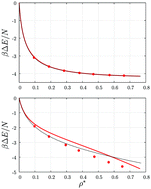
An analytic theory for the structure and thermodynamics of two-component mixtures of patchy and spherical colloids is developed. The theory is based on an analytical solution of the multidensity Ornstein–Zernike equation supplemented by the associative Percus–Yevick closure relations. We derive closed-form analytic expressions for the partial structure factors and thermodynamic properties using the energy route for the model with arbitrary number of patches and any hard-sphere size ratio of the particles. To assess the accuracy of the theoretical predictions we compare them against existing and newly generated set of computer simulation data. In our numerical calculations we consider the model with equal hard-sphere sizes and one patch. Very good agreement between results of the theory and simulation for the pair correlation functions, excess internal energy and pressure is observed for almost all values of the system density, temperature and composition studied. Only in the region of low concentrations of spherical colloids the theoretical results become less accurate.