Adiabatic motion and statistical mechanics via mass-zero constrained dynamics
Abstract
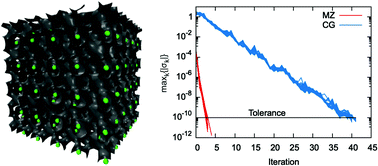
In recent work [Coretti et al., J. Chem. Phys., 2018, 149, 191102], a new algorithm to solve numerically the dynamics of the shell model for polarization was presented. The approach, broadly applicable to systems involving adiabatically separated dynamical variables, employs constrained molecular dynamics to strictly enforce the condition that the force on the fast degrees of freedom, modeled as having zero mass, is null at each time step. The algorithm is symplectic and fully time reversible, and results in stable and efficient propagation. In this paper we complete the discussion of the mechanics of mass-zero constrained dynamics by showing how to adapt it to problems where the fast degrees of freedom must satisfy additional conditions. This extension includes, in particular, the important case of first principles molecular dynamics. We then consider the statistical mechanics of the mass-zero constrained dynamical system demonstrating that the marginal probability sampled by the dynamics in the physical phase space recovers the form of the Born–Oppenheimer probability density. The effectiveness of the approach and the favorable scaling of the algorithm with system size are illustrated in test calculations of solid Na via orbital-free density functional dynamics.
- This article is part of the themed collection: Frontiers in Molecular Simulation of Solvated Ions, Molecules and Interfaces


 Please wait while we load your content...
Please wait while we load your content...