Revisiting the Stokes–Einstein relation for glass-forming melts
Abstract
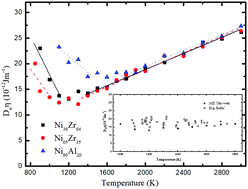
Molecular dynamics simulations of Ni36Zr64, Cu65Zr35 and Ni80Al20 were carried out over a broad range of temperature (900–3000 K) to investigate the Stokes–Einstein (SE) relation for glass-forming melts. Our results reproduce experimental structural and transport properties. Results show that the breakdown temperature of the SE relation (TSE) equals the dynamical crossover temperature (TA) and both are roughly twice the glass-transition temperature (Tg) for the three glass-forming melts (TSE = TA ≈ 2.0Tg). The product of the individual component self-diffusion coefficient and viscosity Dαη can be roughly regarded as a constant at the transition zone (a small temperature range around TSE) in which the temperature behaviors of self-diffusion coefficient and viscosity switch from high-temperature Arrhenius to a low-temperature VFT behavior. Below TSE, the decoupling of component diffusion coefficients was found. In particular, the decoupling of component diffusion coefficients can be ascribed to the decoupling of the partial pair structural correlation of components, which can be clearly reflected by the intersection of the high-temperature and low-temperature behaviors of the ratio between the partial pair correlation entropy of components (Sβ2/Sα2). Furthermore, the ratio between the partial pair correlation entropy of components may be used to predict the validity of the SE relation, in the absence of both transport coefficients and atomic coordinates.


 Please wait while we load your content...
Please wait while we load your content...